多孔腔体内对流传热现象普遍存在于化工、能源、环境等相关领域,例如换热器的优化设计、电子器件的冷却以及颗粒堆积型流化床中吸放热过程等[1-3]。
近年来很多学者采用有限元法、有限差分法等传统方法,对多孔腔体内对流传热现象进行数值模拟研究。Nithiarasu P等[4]采用有限差分法对饱含多孔介质的方腔内自然对流进行模拟,研究表明多孔介质的孔隙度、Da数、Ra数对腔体内对流传热有较大的影响。M. Sankar等[5]采用有限容积方法研究了具有局部间断等温边界的方腔内自然对流,分析了Da数、孔隙度等参数对腔内对流传热的影响,并与全热边界进行对比,结果表明:合理布置局部等温边界的腔体中产生的对流传热强度比全热边界情况更高。
格子Boltzmann方法(LBM)是近年来发展起来的一种介观模拟方法,具有程序简单、计算并行好、处理边界条件容易等特点,在多孔介质内传热传质领域得到了很好的应用。Haghshenas等[6]利用LBM从介观尺度研究了孔隙度和Ra数对填充多孔介质开口腔体内自然对流换热的影响。Guo等[7]采用LBM研究了均匀多孔介质方腔中充满了粘度随温度变化流体的自然对流现象,结果表明:当方腔壁面温差较大,工质黏度随温度变化显著时对腔体内对流传热影响较大,在可变粘度下流体流线和等温线均表现出不对称特性。Wang等[8]提出了改进的介观尺度LBGK模型用于解决多孔介质内不可压缩热流体流动问题,并指出可以通过调节额外参数改变弛豫时间的数值。王佐等[9]构建了一种非正交矩阵的MRT模型用以模拟轴对称热流动,结果表明该模型具有更好的数值稳定性与计算效率。
对于方腔内自然对流的研究,大多学者集中在处理垂直壁面加热、水平壁面绝热的情况,而一些学者研究了倾斜腔体的情况。Kefayati等[10]在考虑Soret和Dufour效应下,从介观尺度采用有限元格子Boltzmann方法研究倾斜方腔内充满幂律流体的自然对流传热的规律。Huelsz G等[11]采用LBM研究了Ra数、倾斜角度θ对腔体内自然对流传热的影响规律,分析了平均Nu数、流线及等温线随倾斜角度θ(0°~360°)的分布特点。Hamady等[12]通过实验方法研究了倾斜角度θ(0°~180°)、Ra数(104~106)范围方腔内自然对流传热现象,并描绘了平均Nu的变化规律。Zhang等[13]采用MRT-LBM方法研究了内置四个高温方块的空腔中充满纳米级磁流体的对流传热现象,分析了倾斜角度θ(0°~90°)腔体内流线及等温线的分布规律。
在实际的大多数生产领域中,倾斜腔体在机械电子器件冷却、建筑物保温及太阳能集热器中能量储存等方面有较大的应用前景,吸引了越来越多的学者对饱含多孔介质倾斜方腔内传递现象进行研究,由于研究中存在方腔倾斜角度变化范围不足、边界条件处理不符合实际情况及模拟结果精确度不够等因素,使得对多孔腔体内对流传热规律的探讨不够充分。本文在前人研究的基础上,讨论了内置高温方块的倾斜多孔腔体中传递现象,研究了多孔腔体倾角θ、孔隙度ε、Da数、Ra数等参数对腔体内传热传质特性的影响规律。
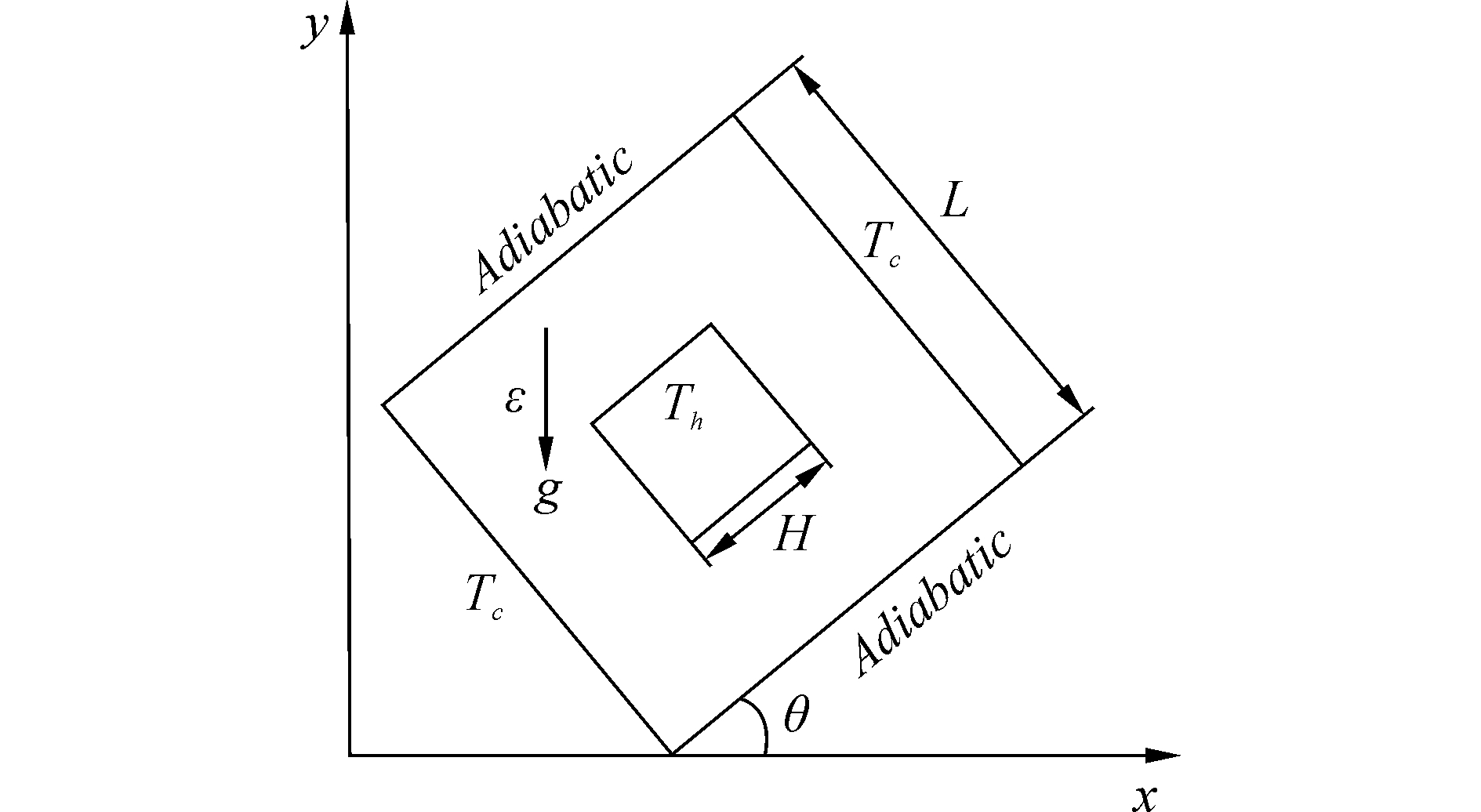
1 计算模型的建立二维方腔中心放置一个发热方块,方块表面温度为Th,宽度为H;外部方腔左右壁面温度为Tc,其他壁面绝热、绝质,宽度为L,两个方块宽度比定义为A=H/L,设定A=0.4。发热方块与腔体之间填充了各向同性、刚性、均质的多孔介质材料;方腔的倾斜角度为θ,如图 1所示。
|
Download:
|
| 图 1 物理模型 Fig. 1 Physical model | |
假设流体不可压缩,为方便处理由于温差引起的浮升力项,引入Boussinesq假设。采用修正的Brinkman-Darcy-Forchheimer渗流模型描述腔体内的复杂流动现象,结合能量方程,多孔介质表征单元体积尺度下流体流动传热的广义Navier-Stokes方程为[4]
| $ \nabla \cdot \mathit{\boldsymbol{u}} = 0 $ | (1) |
| $ {\partial _t}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{u}} \cdot \nabla \left( {\frac{\mathit{\boldsymbol{u}}}{\varepsilon }} \right) = - \frac{1}{\rho }\nabla \left( {\varepsilon p} \right) + {\nu _e}{\nabla ^2}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{F}} $ | (2) |
| $ \sigma {\partial _t}T + \mathit{\boldsymbol{u}} \cdot \nabla T = \nabla \cdot \left( {{a_e}\nabla T} \right) $ | (3) |
式中:u、p、T分别为流体的体积平均速度、压力和温度,ε为多孔腔体孔隙度,νe为有效黏性系数,ae为热扩散系数。σ为多孔腔体内固体相(下标s)与流体相(下标f)的热容之比:
| $ \sigma = \varepsilon + \left( {1 - \varepsilon } \right){\left( {\rho {c_p}} \right)_s}/{\left( {\rho {c_p}} \right)_f}。$ |
式(2)中最后一项F为流体在多孔腔体中所受的合外力,其计算式为
| $ \mathit{\boldsymbol{F}} = - \frac{{\varepsilon \nu }}{K}\mathit{\boldsymbol{u}} - \frac{{1.75}}{{\sqrt {150\varepsilon K} }}\left| \mathit{\boldsymbol{u}} \right|\mathit{\boldsymbol{u}} + \varepsilon G $ | (4) |
式中:右边第一项为线性(Darcy)介质阻力,第二项为非线性(Forchheimer)介质阻力,第三项为浮升力;K为多孔介质的渗透率,K=ε3dp2/[150(1-ε)2],dp为多孔介质内固体颗粒的有效半径。G为浮升力,G=-gβT(T-Tm)(sin θi+cos θj),βT、Tm分别为流体的热膨胀系数、平均温度。
2 格子Boltzmann模型基于Guo等[14]提出的耦合LBM模型,采用D2Q9模型描述腔体内流场和温度场,其演化方程为
| $ \begin{array}{*{20}{c}} {{f_i}\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_i}\delta t,t + \delta t} \right) = {f_i}\left( {\mathit{\boldsymbol{x}},t} \right) + }\\ {\frac{1}{{{\tau _f}}}\left[ {f_i^{eq}\left( {\mathit{\boldsymbol{x}},t} \right) - {f_i}\left( {\mathit{\boldsymbol{x}},t} \right)} \right] + \delta t{\mathit{\boldsymbol{F}}_i}} \end{array} $ | (5) |
| $ \begin{array}{*{20}{c}} {{g_i}\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_i}\delta t,t + \delta t} \right) = {g_i}\left( {\mathit{\boldsymbol{x}},t} \right) + }\\ {\frac{1}{{{\tau _T}}}\left[ {g_i^{eq}\left( {\mathit{\boldsymbol{x}},t} \right) - {g_i}\left( {\mathit{\boldsymbol{x}},t} \right)} \right]} \end{array} $ | (6) |
| $ f_i^{eq} = {\omega _i}\rho \left[ {1 + \frac{{{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{u}}}}{{c_s^2}} + \frac{{{{\left( {{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{u}}} \right)}^2}}}{{2\varepsilon c_s^4}} - \frac{{\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{u}}}}{{2\varepsilon c_s^2}}} \right] $ | (7) |
| $ g_i^{eq} = {\omega _i}T\left[ {1 + \frac{{{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{u}}}}{{c_s^2}}} \right] $ | (8) |
式中:fi、gi分别表示密度、温度分布函数;fieq、gieq为相应的平衡态分布函数;声速cs=c/
| $ \mathit{\boldsymbol{e}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&{ - 1}&0&1&{ - 1}&{ - 1}&1\\ 0&0&1&0&{ - 1}&1&1&{ - 1}&{ - 1} \end{array}} \right] $ |
式(5)中的外力项为
| $ {\mathit{\boldsymbol{F}}_i} = {\omega _i}\rho \left( {1 - \frac{1}{{2{\tau _f}}}} \right)\left[ {\frac{{{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{F}}}}{{c_s^2}} + \frac{{\mathit{\boldsymbol{uF}}:\left( {{\mathit{\boldsymbol{e}}_i}{\mathit{\boldsymbol{e}}_i} - c_s^2\mathit{\boldsymbol{I}}} \right)}}{{2\varepsilon c_s^4}}} \right] $ | (9) |
流体密度、温度可以由分布函数得出:
| $ \rho = \sum\limits_i {{f_i}} ,\sigma T = \sum\limits_i {{g_i}} $ |
多孔腔体内流体速度u通过计算临时速度v求解:
| $ \mathit{\boldsymbol{v}} = \frac{1}{\rho }\sum\limits_i {{e_i}{f_i}} + \frac{{\delta t}}{2}\varepsilon G $ | (10) |
| $ \mathit{\boldsymbol{u}} = \frac{\mathit{\boldsymbol{v}}}{{{c_0} + \sqrt {c_0^2 + {c_1}\left| \mathit{\boldsymbol{v}} \right|} }} $ | (11) |
式中:
相关的νe、ae可表示为
| $ \begin{array}{l} {\nu _e} = \left( {{\tau _f} - 0.5} \right)\delta tR{T_m},\\ {a_e} = \sigma \left( {{\tau _T} - 0.5} \right)\delta tR{T_m} \end{array} $ | (12) |
局部Nusselt数(Nu)及平均Nusselt数(Nuave)定义如下:
| $ Nu = - \frac{L}{{\Delta T}}{\left( {\frac{{\partial T}}{{\partial x}}} \right)_w},N{u_{{\rm{ave}}}} = \frac{1}{{4L}}\sum\limits_{i = 1}^4 {\int_0^L {Nu{\rm{d}}l} } $ | (13) |
其中,局部Nusselt数采用五点差分格式计算,平均Nusselt数是沿四周热壁面线积分求和取平均值所得。
描述多孔腔体内对流传热特性的无量纲特征参数有:Da=K/L2,Pr=ν/ae,Ra=gβΔTL3/(νae),J=νe/ν。
为了深入了解多孔腔体内传递规律,分别讨论孔隙度ε(ε=0.4,0.7,1.0),Da数(Da=10-4,10-2),Ra数(105~107)等参数对腔体内对流传热的影响。本文中其他参数设置为常数,σ=1,J=1,Pr=1.0。网格密度采用200×200,方腔壁面及高温方块边界处理均采用非平衡态外推格式[15-16]。
3 数值结果及讨论 3.1 程序验证为了验证程序的正确性,首先模拟了竖直腔体内自然对流问题,分别计算冷壁面上Nuave数、最大Numax及其位置YNu,方腔中间宽度位置x方向速度分量u的最大值umax及其位置Yu max,方腔中间高度位置y方向速度分量v的最大值vmax及其位置Xv max,并将计算结果与文献[17]进行比较,结果如表 1所示。由表 1可知,计算数据相差很小,表明文中模型处理腔体对流传热具有很好的适用性;其次,模拟了倾斜腔体内孔隙度ε=1.0,Da=106,倾角θ=45°时自然对流传热现象,并与文献[11]模拟结果对比,如图 2所示,得到的流场和温度场分布非常吻合;最后,模拟了饱含多孔介质的腔体内自然对流传热,计算热壁面上Nuave数,并与文献[4]有限差分法结果进行比较,结果如表 2所示。可以看出,文中LBM结果与文献中数值相近,绝对误差都在2%以内,充分验证了文中LBM处理腔体对流传热的可靠性。
| 表 1 空腔内自然对流的比较 Tab.1 Comparison of natural convection in a cavity |

|
Download:
|
| 图 2 倾斜空腔流线、等温线分布对比(Ra=105、Pr=0.71、θ=45°) Fig. 2 Comparison of streamlines and isotherms in an inclined square cavity(Ra=105、Pr=0.71、θ=45°) | |
| 表 2 热壁面上Nuave数的比较 Tab.2 Comparison of average Nusselt number at hot sidewall |
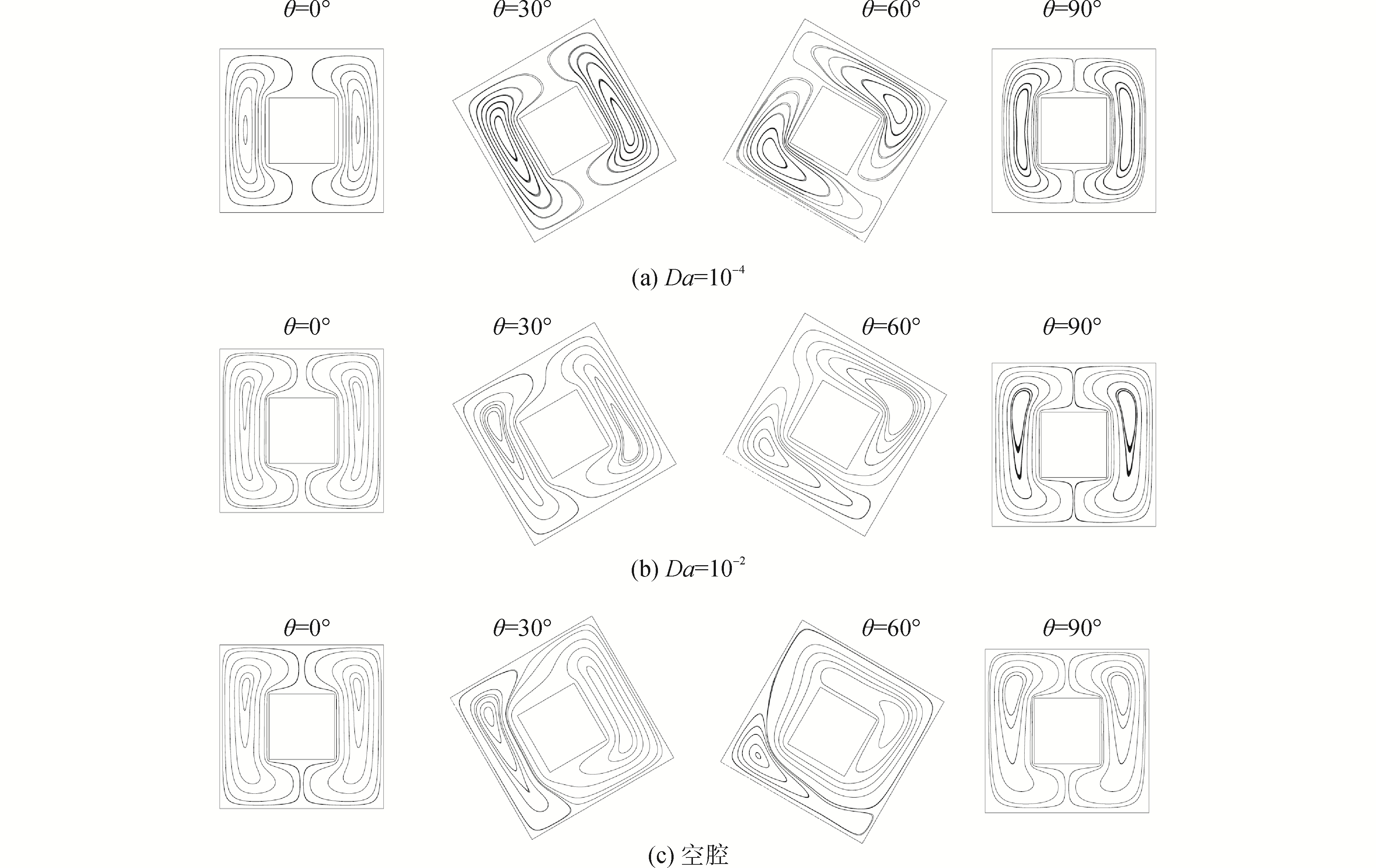
为了直观反映腔体内对流传热的情况,图 3、图 4分别给出了Ra=105时,内置高温方块的多孔腔体中流体流线、等温线随Da数、倾角θ变化的分布规律。当倾角θ=0°时,方腔水平放置、浮升力只作用于y方向。
|
Download:
|
| 图 3 不同倾角和Da数下的等温线图(Ra=105) Fig. 3 Isotherms for different inclination angles and Darcy number with Ra=105 | |

|
Download:
|
| 图 4 热壁面上Nuave数的比较 Fig. 4 Comparison of average Nusselt number at hot sidewall | |
由于高温方块两侧流动区域及边界条件的设置是相同的,使得腔体内流线及等温线分布规律严格地关于腔体中心的高温方块对称分布。Da=10-4时,腔体内高温方块左右两侧的水平中心线位置分别出现一个漩涡,并且旋转方向相反;腔体内流体温度分布较为均匀,等温线关于高温方块严格的左右对称分布、以及近似的上下对称分布。原因在于,Da数较小时,渗透率相对较小,多孔腔体内流体流动受到线性和非线性介质阻力的作用较大,浮升力的作用可以忽略不计,热对流作用很弱,传热方式以热传导为主,使得流线和等温线分布出现近似上下对称分布的情况。Da数较大或空腔时,y方向浮升力作用加强,腔体中两个漩涡会同时向顶部移动,漩涡的形状及大小均会发生变化,演变成尾翼形状;温度场中等温线也不再近似上下对称分布,内置高温方块上侧的等温线分布较为稀疏,而下侧等温线分布较为密集。随着倾角θ的变化,由于浮升力只是作用于y方向,使得流线及等温线分布均会表现出倾斜的情况。当倾角θ=30°时,Da=10-4时,腔体中流线关于高温方块中心对称分布,左侧的涡心向顶部移动,右侧的涡心向底部移动;温度场中等温线也会发生倾斜,倾角θ越大,等温线倾斜的越严重。Da=10-2时,腔体中右侧的流线会绕过高温方块,流线不再出现对称分布规律,等温线的倾斜程度更大;对于空腔的情况,这种不对称、倾斜现象表现得更明显。这是因为,Da较大时,渗透率增大,介质阻力作用相对较弱,浮升力占合外力比例增大,随着倾角的增大,冷却壁面相对于高温方块的位置在y方向上逐渐占优,冷却/加热壁面之间的热对流得到充分发展。当倾角θ=60°时,腔体内流线及等温线的分布规律与θ=30°情况类似。当倾角θ=90°时,方腔上下壁面为冷却壁面,左右壁面为绝热壁面,边界条件相对于高温方块看作对称布置,使得流线及等温线呈现对称分布规律。与倾角θ=0°情况不同的是,腔体中两个漩涡为扁平状。原因在于,受到腔体横向空间的限制,左右壁面为绝热壁面时,流体只能向腔体顶部或底部对流传热而形成的。
为了定量的比较孔隙度ε对方腔内对流传热的影响,图 5给出了Da=10-2、Ra=105时,不同孔隙度ε下热壁面上Nuave数随倾角θ变化关系。由图 5可知,3条曲线随着倾角θ的增大呈现逐渐减小的变化趋势。考虑热壁面上Nuave数,孔隙度ε从0.4增大到1.0(空腔情况)的过程中,θ=0°时Nuave数增大了8.4%,θ=90°时Nuave数仅仅增大了2.3%。由此可知,由于受到方腔空间结构的限制,以及冷却/加热边界相对位置的影响,冷却边界布置在方腔的左右壁面比布置在上下壁面时,更能够促进腔体内对流传热的强度。同时可以看出,固定倾角θ时,孔隙度越大,介质阻力越小,流体与高温方块之间的自然对流传热能力越强。

|
Download:
|
| 图 5 不同孔隙度下热壁面Nuave数随倾斜角度变化 Fig. 5 Average Nusselt number at the hot wall versus inclination angle for different porosity | |
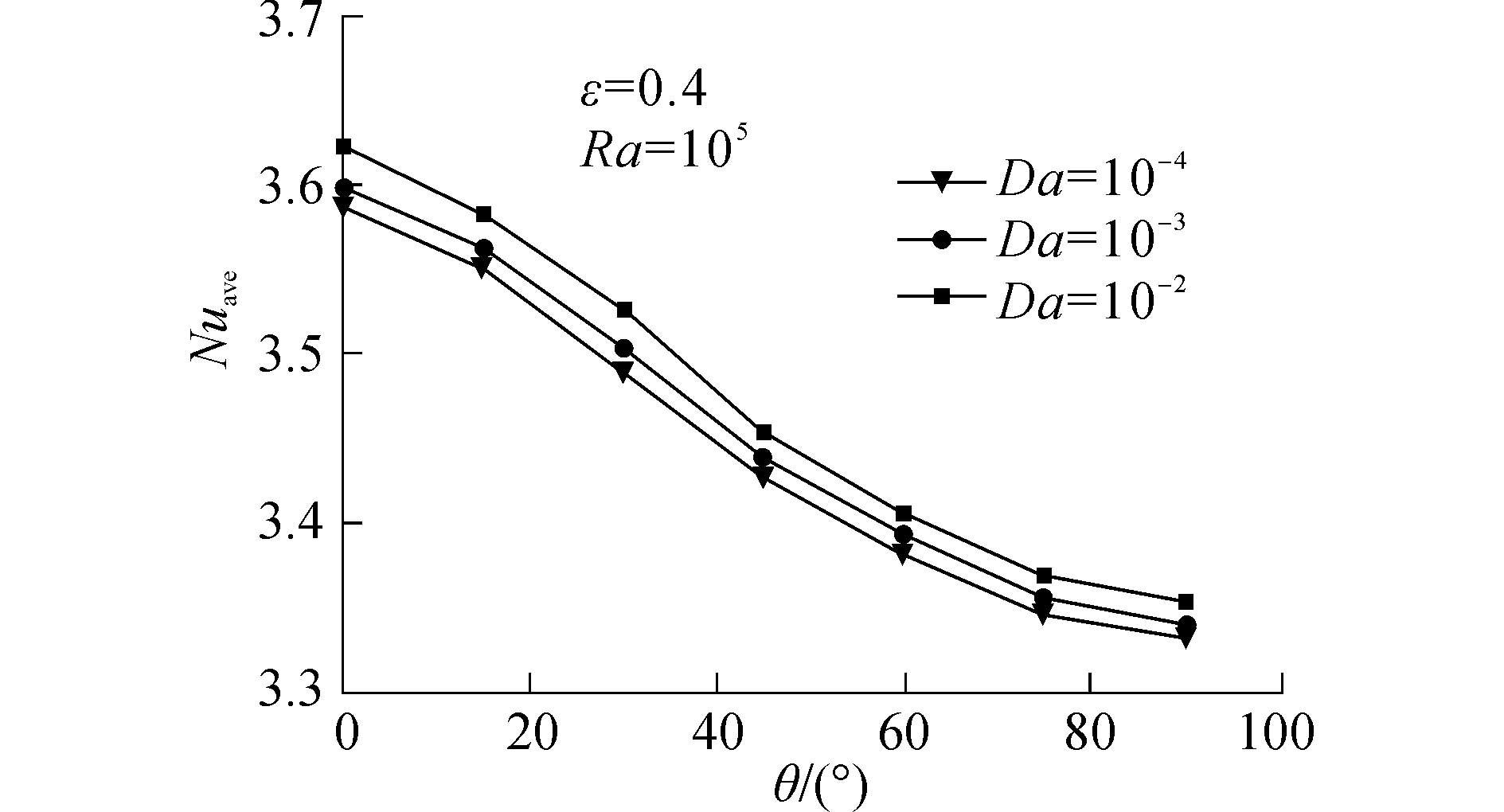
图 6给出了ε=0.4、Ra=105时,不同Da数下热壁面上Nuave数随倾角θ的变化规律。由图 6可知,随着倾角θ的增大,3条曲线均表现出“倒S”型减小的变化趋势。倾角θ从0°增大到90°的过程中,Da=10-4、10-3、10-2时热壁面上Nuave数分别降低了7.15%、7.16%、7.23%。对于相同的倾斜角度的情况,增大Da数时,热壁面上Nuave数会增大。这是因为增大Da数时,渗透率相对较大,介质阻力的作用相对较小,腔体内流体渗流速度会增大,从而促进了腔体内对流传热强度。
|
Download:
|
| 图 6 不同Da数下热壁面Nuave数随倾斜角度变化 Fig. 6 Average Nusselt number at the hot wall versus inclination angle for different Darcy number | |
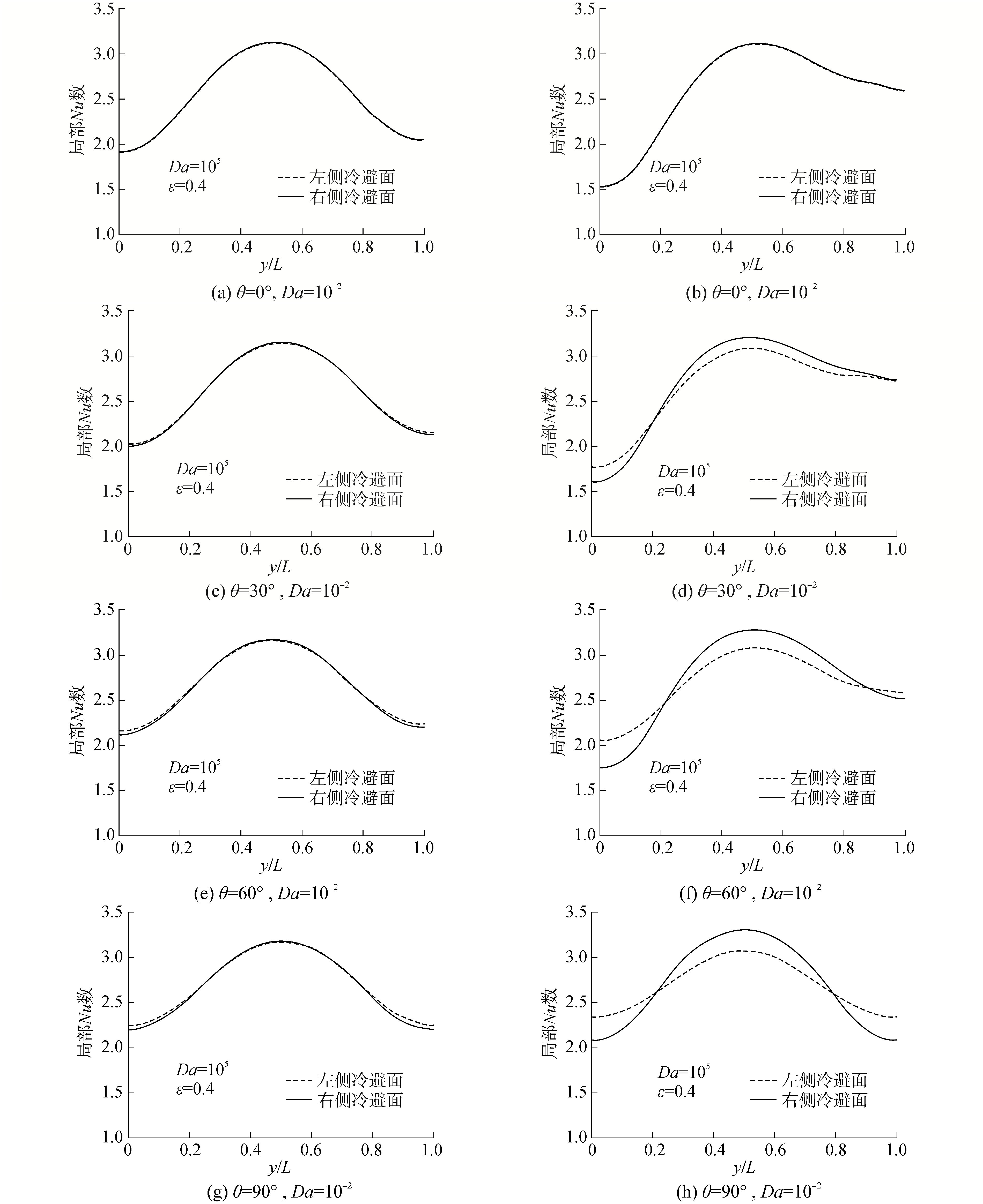
图 7为Ra=105、ε=0.4时,不同Da数下冷壁面上局部Nu数分布图。由图 7可知,冷壁面上局部Nu数均呈现先增加、后减小的变化趋势。当Da数较小为10-4时,左、右侧冷壁面上局部Nu数差别较小,此时多孔腔体内流体传热方式以导热为主。当Da数较大为10-2时,随着腔体倾角的增加,左侧冷壁面在两侧位置区域产生的局部Nu数大于右侧冷壁面对应区域的数值,而中间位置的数值较小。这是因为Da数较大时,多孔腔体内流体受到介质阻力较小,渗透率较大,使得左、右侧冷壁面上局部Nu数区别明显。随着倾角的增加,与右侧冷壁面相比,由于左侧冷壁面位于腔体的下方,在壁面两侧位置沿着浮升力方向有较大的流体流动空间,使得流体对流传热强度比较活跃,局部Nu数较大;而壁面中间位置,由于受到高温方块位置的影响,限制了流体流动的空间,使得局部Nu数较小。
|
Download:
|
| 图 7 不同Da数下冷壁面上局部Nu数分布图 Fig. 7 Local Nusselt number at the cold walls with different Darcy number | |
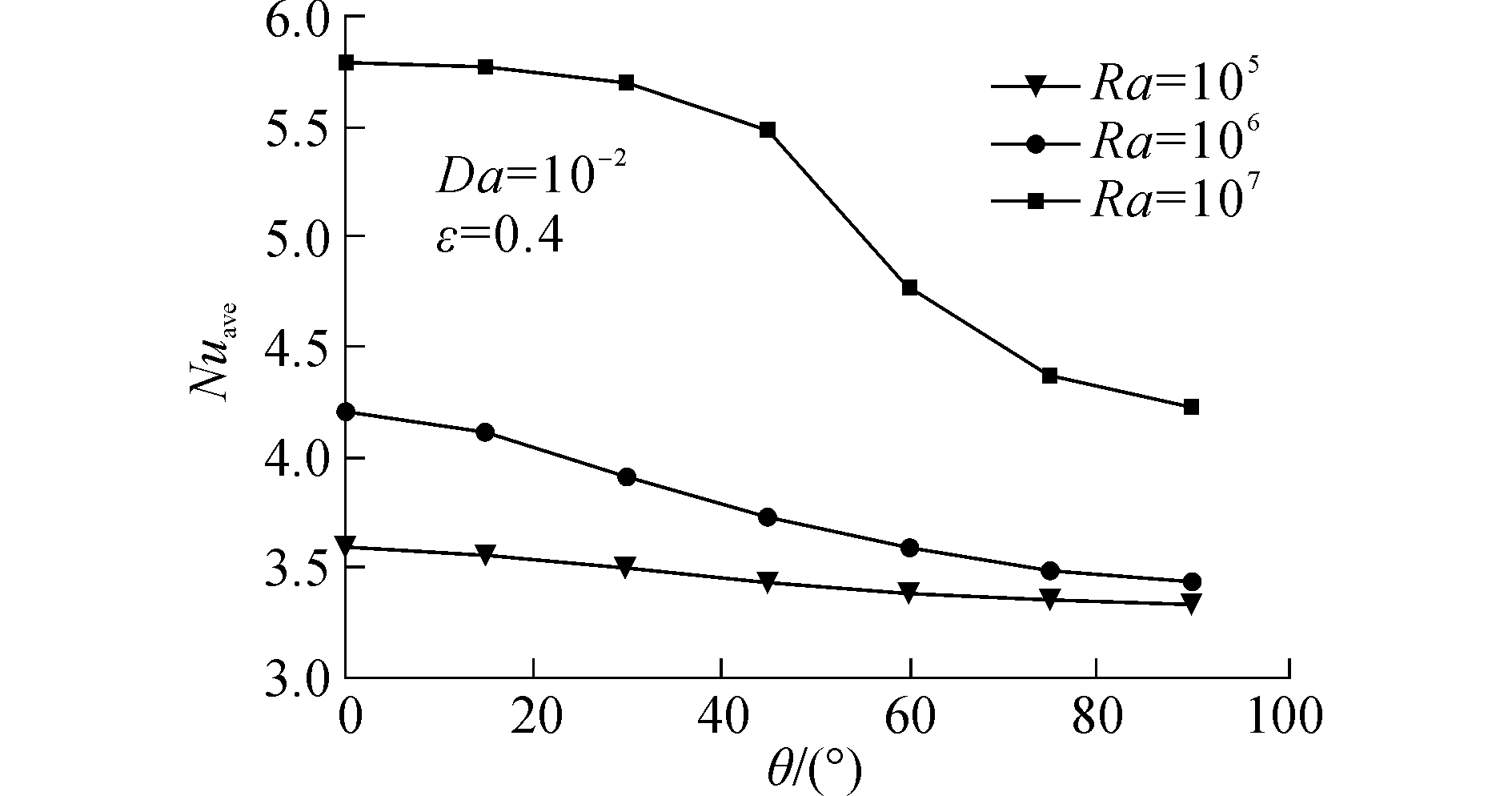
图 8反映了Da=10-4、ε=0.4时,热壁面上Nuave数随倾角θ的变化规律。由图 8可知,当Ra数较小为105时,随着倾角θ从0°增大到90°过程中,热壁面上Nuave数减少了7.15%,此时对传热影响不大。随着Ra数的增大,热壁面上Nuave数减少的较为明显。当Ra数较大为107时,随着倾角θ从0°增大到90°过程中,热壁面上Nuave数减少了27.02%,此时对腔体内对流传热影响较大。并且,在倾角θ=45°的附近倾斜区域,热壁面上Nuave数变化的较快。这是因为,流体受到的浮升力只作用于y方向,θ<45°时,方腔绝热壁面在y方向占优,流体不仅在冷却、加热壁面之间流动,在绝热壁面附近也得到了充分的发展;而θ>45°时,方腔冷却壁面在y方向占优,流体仅在冷却、加热壁面之间流动,腔体内流体整体循环流动效果不好,从而降低了对流传热强度。
|
Download:
|
| 图 8 不同Ra数下热壁面Nuave数随倾斜角度变化 Fig. 8 Average Nusselt number at the hot wall versus inclination angle for different Rayleigh number | |
1) 方腔倾斜使得腔内流场流线和温度场等温线发生偏移变形,其偏移程度受Da数大小影响。
2) 方腔内孔隙度对传热的影响与腔体倾斜角度相关,倾斜角增大会抑制方腔对流传热强度。
3) 热壁面上Nuave随倾角增大呈现特定变化规律,增大孔隙度ε、Da数、Ra数时,均可以增强流体与热壁面之间的自然对流传热能力。
| [1] |
DUBOIS F, LIN Chaoan, TEKITEK M M. Anisotropic thermal lattice Boltzmann simulation of 2D natural convection in a square cavity[J]. Computers & fluids, 2016, 124: 278-287. (  0) 0)
|
| [2] |
JAMI M, MOUFEKKIR F, MEZRHAB A, et al. New thermal MRT lattice Boltzmann method for simulations of convective flows[J]. International journal of thermal sciences, 2016, 100: 98-107. DOI:10.1016/j.ijthermalsci.2015.09.011 (  0) 0)
|
| [3] |
AHMED S E, OZTOP H F, AL-SALEM K. Natural convection coupled with radiation heat transfer in an inclined porous cavity with corner heater[J]. Computers & fluids, 2014, 102: 74-84. (  0) 0)
|
| [4] |
NITHIARASU P, SEETHARAMU K N, SUNDARARAJAN T. Natural convective heat transfer in a fluid saturated variable porosity medium[J]. International journal of heat and mass transfer, 1997, 40(16): 3955-3967. DOI:10.1016/S0017-9310(97)00008-2 (  0) 0)
|
| [5] |
SANKAR M, BHUVANESWARI M, SIVASANKARAN S, et al. Buoyancy induced convection in a porous cavity with partially thermally active sidewalls[J]. International journal of heat and mass transfer, 2011, 54(25/26): 5173-5182. (  0) 0)
|
| [6] |
HAGHSHENAS A, NASR M R, RAHIMIAN M H. Numerical simulation of natural convection in an open-ended square cavity filled with porous medium by lattice Boltzmann method[J]. International communications in heat and mass transfer, 2010, 37(10): 1513-1519. DOI:10.1016/j.icheatmasstransfer.2010.08.006 (  0) 0)
|
| [7] |
GUO Zhaoli, ZHAO Tianshou. Lattice Boltzmann simulation of natural convection with temperature-dependent viscosity in a porous cavity[J]. Progress in computational fluid dynamics, 2005, 5(1/2): 110-117. DOI:10.1504/PCFD.2005.005823 (  0) 0)
|
| [8] |
WANG Liang, MI Jianchun, GUO Zhaoli. A modified lattice Bhatnagar-Gross-Krook model for convection heat transfer in porous media[J]. International journal of heat and mass transfer, 2016, 94: 269-291. DOI:10.1016/j.ijheatmasstransfer.2015.11.040 (  0) 0)
|
| [9] |
王佐, 张家忠, 王恒. 非正交多松弛系数轴对称热格子Boltzmann方法[J]. 物理学报, 2017, 66(4): 044701. WANG Zuo, ZHANG Jiazhong, WANG Heng. Non-orthogonal multiple-relaxation-time lattice Boltzmann method for axisymmetric thermal flows[J]. Acta physica sinica, 2017, 66(4): 044701. (  0) 0)
|
| [10] |
KEFAYATI G R. Mesoscopic simulation of magnetic field effect on natural convection of power-law fluids in a partially heated cavity[J]. Chemical engineering research and design, 2015, 94: 337-354. DOI:10.1016/j.cherd.2014.08.014 (  0) 0)
|
| [11] |
HUELSZ G, RECHTMAN R. Heat transfer due to natural convection in an inclined square cavity using the lattice Boltzmann equation method[J]. International journal of thermal sciences, 2013, 65: 111-119. DOI:10.1016/j.ijthermalsci.2012.09.009 (  0) 0)
|
| [12] |
HAMADY F J, LLOYD J R, YANG H Q, et al. Study of local natural convection heat transfer in an inclined enclosure[J]. International journal of heat and mass transfer, 1989, 32(9): 1697-1708. DOI:10.1016/0017-9310(89)90052-5 (  0) 0)
|
| [13] |
ZHANG Tao, CHE Defu. Double MRT thermal lattice Boltzmann simulation for MHD natural convection of nanofluids in an inclined cavity with four square heat sources[J]. International journal of heat and mass transfer, 2016, 94: 87-100. DOI:10.1016/j.ijheatmasstransfer.2015.11.071 (  0) 0)
|
| [14] |
GUO Zhaoli, ZHAO T S. A lattice Boltzmann model for convection heat transfer in porous media[J]. Numerical heat transfer, part B:fundamentals, 2005, 47(2): 157-177. DOI:10.1080/10407790590883405 (  0) 0)
|
| [15] |
何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009. HE Yaling, WANG Yong, LI Qing. Lattice Boltzmann method:theory and applications[M]. Beijing: Science Press, 2009. (  0) 0)
|
| [16] |
郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009. GUO Zhaoli, ZHENG Chuguang. Theory and applications of lattice Boltzmann method[M]. Beijing: Science Press, 2009. (  0) 0)
|
| [17] |
PENG Y, SHU C, CHEW Y T. Simplified thermal lattice Boltzmann model for incompressible thermal flows[J]. Physical review E, 2003, 68: 026701. DOI:10.1103/PhysRevE.68.026701 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


