蒸汽弹射起飞是舰载机主要的舰上起飞方式之一。与滑跃起飞[1]相比,借助蒸汽弹射器产生的弹射力,重型舰载机可在无甲板风环境下弹射升空。与电磁弹射[2]相比,蒸汽弹射器[3]是世界范围内运用最广泛、使用时间最长、技术较为成熟、可靠性较强的弹射器。它具有抗电磁干扰的能力。能够较好地满足航母作战的需求。
国外很早就进行了蒸汽弹射器的研究。SLAVIN F J[3]介绍了蒸汽弹射器的结构,列出了储汽筒和气缸的设计准则。文献[4]对蒸汽弹射器的热力学过程进行了分析研究;美国海军工程中心[5]提供了蒸汽弹射器弹射质量车的试验数据。美军标[6]提供了牵制杆最小释放载荷的数学模型。美军标[7]提出,可以将蒸汽弹射器提供的弹射力表示为弹射冲程的函数曲线。Small[8]指出前轮拖拽弹射方式优于传统的钢丝绳弹射方式。Lucas[9]提出了舰载机弹射起飞的安全准则。
国内从20世纪90年代开始已经公开发表弹射器研究的技术成果。赵险峰[10]建立了舰载机蒸汽弹射系统的数学模型,为蒸汽弹射系统的研究打下了良好的基础。余晓军等[11]建立了蒸汽弹射器的动力学模型。程刚等[12]在一定的假设条件下,对蒸汽弹射系统的动力学和热力学过程进行了研究。张雷等[13]在等熵过程和等体积传热过程基础上,建立了蒸汽弹射器的热力学模型。高俊东等[14]阐明了发射阀的结构和基本工作原理,并建立了蒸汽弹射器的数学模型。朱齐丹等[15]建立了蒸汽弹射器数学模型和舰载机六自由度动力学模型,分析了不同偏心距情况下舰载机的运动姿态。文献[16-17]将弹射器模型简化为弹射力随弹射器行程变化的曲线。
目前公开文献中,尚未见有综合考虑蒸汽弹射器模型、牵引释放装置模型和弹射系统动力学模型条件下,包括施加预紧力阶段、弹射力加载阶段和弹射滑跑阶段的全过程质量车蒸汽弹射系统的研究。本文针对储汽筒压力、气缸压力和质量车加速度3个蒸汽弹射系统关键参数,进行了理论分析与仿真验证。通过部分参数与实验数据[5]对比,说明了本文建模方法的正确性,同时对弹射系统的其他参数进行了研究。
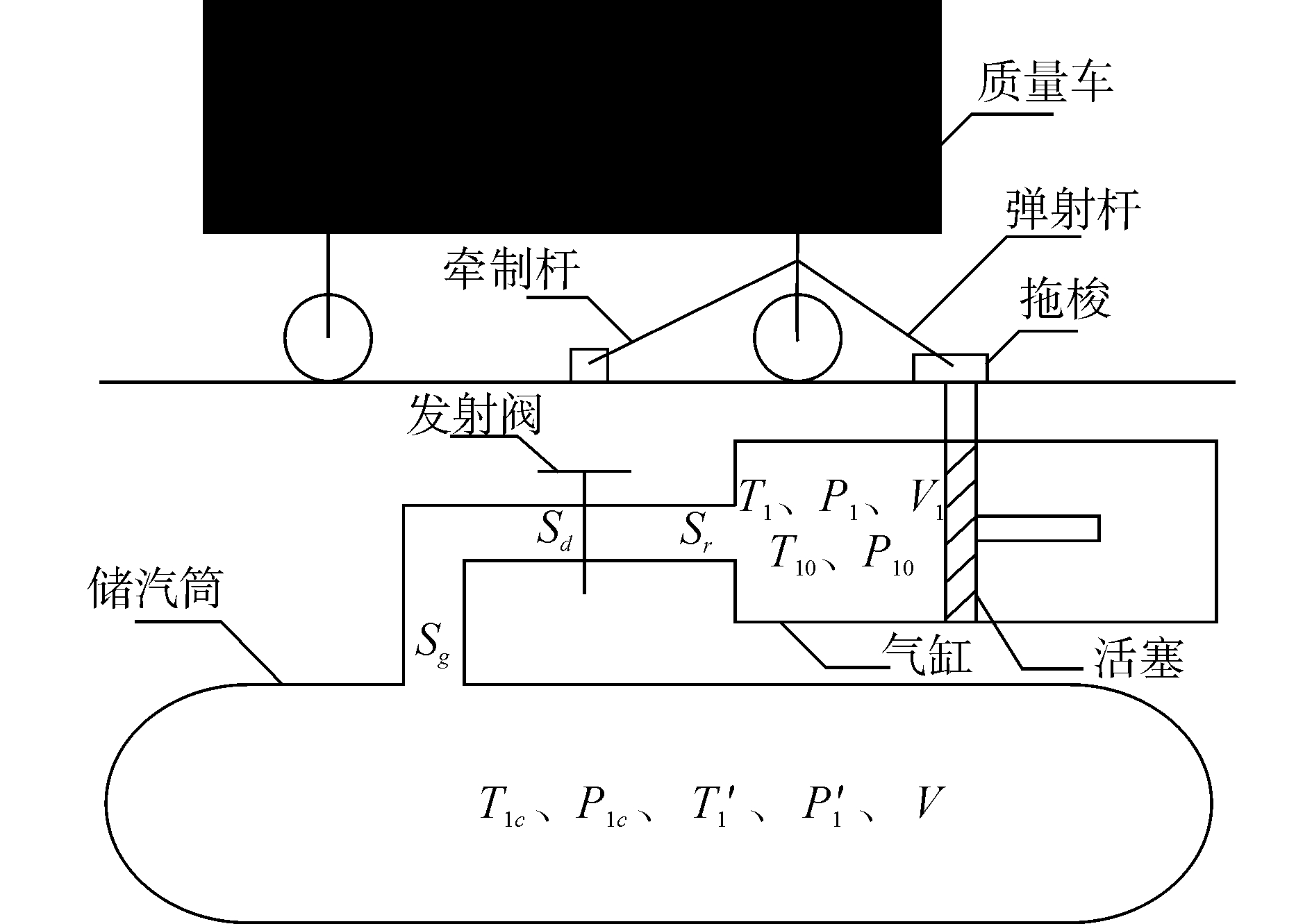
1 质量车蒸汽弹射系统及弹射过程质量车蒸汽弹射系统主要由蒸汽弹射器、牵引释放装置和质量车等部件组成,其简化模型如图 1所示。图中,储汽筒的容积为V;储汽筒内水蒸汽初始温度和压强分别为T1c和P1c;储汽筒内水蒸汽t时刻的温度和压强分别为T′1和P′1;储汽筒放汽的出口面积为Sg;发射阀流通面积为Sd;汽缸入口面积为Sr;汽缸进汽腔初始温度和压强分别为T10和P10;t时刻汽缸进汽腔的温度、压强和体积分别为T1、P1和V1。
|
Download:
|
| 图 1 质量车蒸汽弹射系统示意图 Fig. 1 The schematic of deadload steam catapult system | |
质量车弹射系统的弹射过程如下:开启发射阀,储汽筒内的高温高压蒸汽经过发射阀和管道流入气缸,气缸内的蒸汽压力逐渐增大,当达到一定值时,牵制杆张紧力达到最小释放载荷,牵制杆断裂,活塞和质量车开始同步向前运动,当活塞达到动力冲程时,弹射杆脱离拖梭,质量车进入自由滑跑,活塞进入水力制动装置,然后开启排气阀,复位机构将活塞复位到初始位置,准备下一次的弹射。
弹射过程可划分为3个阶段,具体如图 2所示。第1个阶段为施加预紧力阶段,目的是使滑车、弹射杆、质量车和牵制杆之间紧密连接,防止松脱,使质量车可靠静止的停在航母甲板上。第2个阶段是弹射力加载阶段,牵制杆断开是第2个阶段结束标志;第3个阶段是弹射滑跑阶段。当质量车到达弹射器末端,弹射滑跑结束,弹射力突卸。

|
Download:
|
| 图 2 蒸汽弹射仿真阶段划分 Fig. 2 Phases of steam catapult | |
蒸汽弹射器主要由储汽筒、发射阀、汽缸和活塞组成,如图 1所示。下面分别建立储汽筒模型、发射阀模型以及汽缸模型。
2.1.1 储汽筒模型本文的储汽筒模型为干式储汽筒模型,其结构类似于蒸汽蓄热器,它能在较短的时间内释放出大量高温高压蒸汽,而蒸汽来自于增压锅炉燃烧所产生的,在向汽缸放汽的过程中,储汽筒内水蒸汽的质量、压强和温度会随之下降。为了对储汽筒放汽的热力学过程进行建模,现进行下述假设:
1) 在系统工作过程中,将储汽筒放汽的过程假定为绝热放汽过程,由于储汽筒放汽过程持续时间约为3 s,假设在此过程中储汽筒与外界不存在热交换;
2) 储汽筒为刚性容器,忽略压强和温度导致的体积变化。
3) 储汽筒放汽过程为准静态过程,可以近似认为在每一时刻,储汽筒内热力学变化量都无限接近于一平衡态,满足状态方程。
4) 忽略储汽筒放汽过程中,高温高压蒸汽与储汽筒壁之间的摩擦损失。
5) 认为在储汽筒和气缸之间的管道中,高温高压蒸汽做绝热稳定流动。
储汽筒放汽过程的等熵过程方程:
| $ {{T'}_1} = {T_{1c}}{\left( {\frac{{{P_{1c}}}}{{{{P'}_1}}}} \right)^{\frac{{1 - \kappa }}{\kappa }}} $ | (1) |
圣维南质量流量公式:
| $ {Q_{m1}} = \left\{ \begin{array}{l} {A_q}\frac{{{{P'}_1}}}{{\sqrt {{{T'}_1}} }}\sqrt {\frac{{2\kappa }}{{\kappa - 1}}\frac{1}{{{R_g}}}\left( {{{\left( {\frac{{{P_1}}}{{{{P'}_1}}}} \right)}^{\frac{2}{\kappa }}} - {{\left( {\frac{{{P_1}}}{{{{P'}_1}}}} \right)}^{\frac{{\kappa + 1}}{\kappa }}}} \right)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{P_1} > {P_k}\\ {A_q}\frac{{{{P'}_1}}}{{\sqrt {{{T'}_1}} }}\sqrt {{{\left( {\frac{2}{{\kappa + 1}}} \right)}^{\frac{{\kappa + 1}}{{\kappa - 1}}}}\frac{\kappa }{{{R_g}}}} \;\;\;\;{P_1} \le {P_k} \end{array} \right. $ | (2) |
式中:Rg为高温高压蒸汽的气体常数;κ为比热比,又称绝热指数。
临界压强:
| $ {P_k} = {{P'}_1} \times {\left( {\frac{2}{{\kappa + 1}}} \right)^{\frac{\kappa }{{\kappa - 1}}}} $ | (3) |
为将式(2)表示成气动元件组合后的等效有效截面积S的函数,令Aq=S。
储汽筒和气缸之间管道的等效有效截面积:
| $ S = \frac{1}{{\sqrt {\frac{1}{{S_g^2}} + \frac{1}{{S_d^2}} + \frac{1}{{S_r^2}}} }} $ | (4) |
根据热力学第一定律,储汽筒绝热放汽过程的能量方程:
| $ {{i'}_1}{\rm{d}}{M_s} = - {\rm{d}}{U_1} $ | (5) |
式中: dU1为储汽筒内蒸汽内能减少量;i′1为储汽筒流出单位质量蒸汽所带走的能量(即蒸汽的比焓);dMs为储汽筒流出蒸汽的质量。
储汽筒内蒸汽内能减少量:
| $ {\rm{d}}{U_1} = {c_v}d\left( {{{T'}_1}{{M'}_1}} \right) $ | (6) |
式中:M′1为储汽筒内蒸汽的质量, cv为定容热容。
储汽筒内蒸汽流出带走能量:
| $ {{i'}_1}{\rm{d}}{M_s} = {c_p}{{T'}_1}{\rm{d}}{M_s} $ | (7) |
将式(6)和式(7)代入式(5),可得
| $ {c_p}{{T'}_1}{\rm{d}}{M_s} = - {c_v}{\rm{d}}\left( {{{T'}_1}{{M'}_1}} \right) $ | (8) |
根据理想气体状态方程:
| $ {{P'}_1}V = {{M'}_1}{R_g}{{T'}_1} $ | (9) |
定压热容和定容热容关系:
| $ {c_p} - {c_v} = {R_g},\frac{{{c_p}}}{{{c_v}}} = \kappa $ | (10) |
将式(9)~(10)代入式(8),可得
| $ \kappa {R_g}{{T'}_1}{\rm{d}}{M_s} = - V{\rm{d}}{{P'}_1} $ | (11) |
方程两边同除dt,并将Qm1=dMs/dt代入式(11),得
| $ \frac{{{\rm{d}}{{P'}_1}}}{{{\rm{d}}t}} = - \frac{{\kappa {R_g}{{T'}_1}{Q_{m1}}}}{V} $ | (12) |
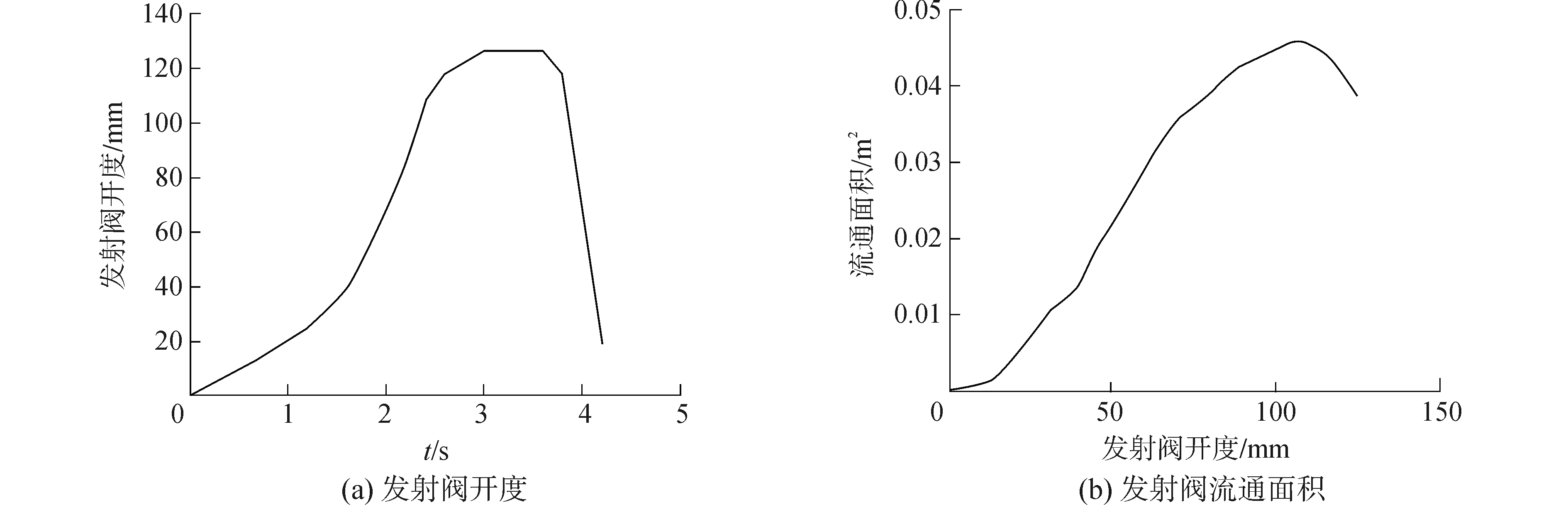
发射阀是蒸汽弹射系统的核心装置之一,通过调节发射阀开度和发射阀流通面积,可以得到不同的弹射能量。为了使发射阀的模型更加符合实际情况,本文使用试验数据[5]的发射阀开度和发射阀流通面积。如图 3所示。
|
Download:
|
| 图 3 发射阀模型 Fig. 3 The model of launch valves | |
为了对气缸的热力学过程进行建模,现进行下述假设:
1) 假设气缸与外界不存在热交换;
2) 气缸为刚性容器,忽略压强和温度导致的体积变化。
3) 气缸充汽过程为准静态过程,可以近似认为在每一时刻,气缸内热力学变化量都无限接近于一平衡态,满足状态方程。
4) 忽略气缸充汽过程中,高温高压蒸汽与气缸壁之间的摩擦损失。
5) 认为在储汽筒和气缸之间的管道中,高温高压蒸汽做绝热稳定流动。
取汽缸无杆腔侧蒸汽(工质)为热力系统时,根据热力学第一定律可得
| $ {\rm{d}}Q = {{i'}_1}{\rm{d}}{M_s} = {\rm{d}}U + {\rm{d}}W $ | (13) |
式中: dQ为汽缸无杆腔侧蒸汽与外界交换的热量,i′1为从储汽筒流进汽缸内单位质量蒸汽所带进的能量(即蒸汽的比焓),dMs为进入汽缸的蒸汽质量,dU为气缸内蒸汽内能增加量,dW为气缸内蒸汽体积膨胀所做的功。
整个充气过程时间较短,汽缸内蒸汽来不及通过器壁与外界进行热交换,这样的充汽过程可视为绝热充气过程。对于绝热充气,dQ=0。
气缸内蒸汽内能增加量:
| $ {\rm{d}}U = {c_v}{\rm{d}}\left( {{T_1}{M_1}} \right) $ | (14) |
式中M1为汽缸内的蒸汽质量。
容积变化功:
| $ {\rm{d}}W = {P_1}{\rm{d}}{V_1} $ | (15) |
带进气缸的蒸汽能量:
| $ {{i'}_1}{\rm{d}}{M_s} = {c_p}{{T'}_1}{\rm{d}}{M_s} $ | (16) |
将式(14)~(16)代入式(13),可得
| $ {c_p}{{T'}_1}{\rm{d}}{M_s} = {c_v}{\rm{d}}\left( {{T_1}{M_1}} \right) + {P_1}{\rm{d}}{V_1} $ | (17) |
理想气体状态方程:
| $ {P_1}{V_1} = {M_1}{R_g}{T_1} $ | (18) |
将式(18)和式(10)代入式(17)并求导,得
| $ \kappa {R_g}{{T'}_1}{\rm{d}}{M_s} = {V_1}{\rm{d}}{P_1} + \kappa {P_1}{\rm{d}}{V_1} $ | (19) |
方程两边同除dt,将Qm1=dMs/dt代入式(19),并化简:
| $ \frac{{{\rm{d}}{P_1}}}{{{\rm{d}}t}} = \frac{{\kappa {R_g}{{T'}_1}{Q_{m1}}}}{{{V_1}}} - \frac{{\kappa {P_1}}}{{{V_1}}}\frac{{{\rm{d}}{V_1}}}{{{\rm{d}}t}} $ | (20) |
| $ {V_1} = {V_{10}} + {A_1}X = {A_1}\left( {{X_{10}} + X} \right) $ | (21) |
式中:V10为气缸无杆腔初始体积,A1为无杆腔侧蒸汽对活塞的作用面积,X为活塞的位移,X10为活塞的初始位移。
将式(21)代入式(20),可得
| $ \frac{{{\rm{d}}{P_1}}}{{{\rm{d}}t}} = \frac{{\kappa {R_g}{{T'}_1}{Q_{m1}}}}{{{A_1}\left( {{X_{10}} + X} \right)}} - \frac{{\kappa {P_1}}}{{{X_{10}} + X}}\frac{{{\rm{d}}X}}{{{\rm{d}}t}} $ | (22) |
弹射力方程:
| $ {F_T} = 2\left( {{P_1}{A_1} - {P_2}{A_2}} \right) $ | (23) |
式中:A2为有杆腔侧蒸汽对活塞的作用面积, P2为汽缸有杆腔侧压力, T2为汽缸有杆腔侧温度。
2.2 牵引释放装置数学模型 2.2.1 弹射杆数学模型牵引释放装置与蒸汽弹射器和质量车的连接关系如图 1所示。
弹射力是由气缸内的高温高压蒸汽对活塞施加的压力产生的,弹射杆轴向力为T。将它按纵向进行分解,弹射杆牵引力为
| $ {T_1} = T\cos {\theta _c} $ | (24) |
式中θc为弹射角。
弹射杆轴向力的竖直分量:
| $ {T_2} = {T_1}\tan {\theta _c} $ | (25) |
牵制杆释放装置作用于施加预紧力阶段和弹射力加载阶段,质量车受牵制杆的牵制力作用,静止在航母甲板上,整个质量车处于静平衡状态。牵制杆有一个最小释放载荷,弹射杆上的拉力增加时,牵制杆上的拉力也增加,当牵制杆上的拉力达到最小释放载荷时,牵制杆被拉断,牵制力突卸。
参考美军标[6],牵制杆最小释放载荷为
| $ {R_{\min }} = 1.35 \times \left( {\frac{{P + f + 0.5G}}{{\cos \beta }}} \right) $ | (26) |
式中:P为发动机推力, G为舰载机设计重量, f为预紧力, β为牵制角。
将牵制杆轴向力按纵向进行分解,牵制杆牵制力为
| $ {R_1} = R\cos \beta $ | (27) |
牵制杆轴向力的竖直分量:
| $ {R_2} = {R_1}\tan \beta $ | (28) |
为了便于建模计算,在质量车蒸汽弹射系统的动力学建模时,需要进行一定的假设如下:
1) 不考虑甲板运动,即不考虑舰面纵摇、舰面横摇和舰面生沉运动;
2) 质量车为刚性车身,即不考虑质量车的变形;
3) 质量车质量集中在质心上,即质量车的质量被认为集中于一个假想点;
4) 不考虑质量车轮胎的压缩变形,轮胎受到弹射力和牵制力的作用会发生形变,本文忽略此形变;
5) 质量车弹射过程前处于完全对中状态,无偏航角,即弹射跑道与质量车的对称平面平行;
6) 弹射过程中,不考虑侧向载荷及湍流的影响,即不考虑侧向甲板风及湍流的影响;
7) 弹射过程中,弹射角和牵制角为定值,轮胎受到弹射力和牵制力的作用会发生形变,这样弹射角和牵制角也会发生相应的变化,本文忽略轮胎的形变,则弹射角和牵制角为定值;
8) 活塞为刚性体,即不考虑活塞的变形;
9) 活塞质量集中在质心上,即活塞的质量被认为集中于一个假想点。
2.3.2 施加预紧力阶段数学模型1) 活塞施加预紧力阶段数学模型。
活塞在此阶段处于静止状态。其纵向平衡方程:
| $ {F_Y} - f - {T_1} = 0 $ | (29) |
式中:FY为预紧力,f为活塞摩擦力。
活塞摩擦力:
| $ f = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \left( {{m_1}g - {T_1}\tan {\theta _c}} \right){\mu _2},\\ \left( {{T_1}\tan {\theta _c} - {m_1}g} \right){\mu _2}, \end{array}&\begin{array}{l} {m_1}g \ge {T_2}\\ {m_1}g < {T_2} \end{array} \end{array}} \right. $ | (30) |
式中:m1为活塞的质量,μ2为活塞与气缸之间的摩擦系数。
将式(30)代入式(29),得
| $ {T_1} = \left\{ \begin{array}{l} \frac{{{F_Y} - {m_1}g{\mu _2}}}{{1 - {\mu _2}\tan {\theta _c}}},\;\;\;\;{m_1}g \ge {T_2}\\ \frac{{{F_Y} + {m_1}g{\mu _2}}}{{1 + {\mu _2}\tan {\theta _c}}}\;\;\;\;\;{m_1}g < {T_2} \end{array} \right. $ | (31) |
2) 质量车施加预紧力阶段数学模型。
质量车在此阶段处于静止状态。其纵向平衡方程:
| $ {T_1} - {f_1} - {f_2} - {R_1} = 0 $ | (32) |
式中:f1为前轮受到的摩擦力,f2为后轮受到的摩擦力。
前轮受到的摩擦力:
| $ {f_1} = {N_1}{\mu _1} $ | (33) |
式中:μ1为舰面摩擦因数,N1为质量车前轮受到的甲板支反力。
后轮受到的摩擦力:
| $ {f_2} = {N_2}{\mu _1} $ | (34) |
式中N2为质量车后轮受到的甲板支反力。
将式(25)、(28)、(33)和(34)代入式(32),得
| $ {R_1} = \frac{{{T_1}\left( {1 - {\mu _1}\tan {\theta _c}} \right) - mg{\mu _1}}}{{{\mu _1}\tan \beta + 1}} $ | (35) |
1) 活塞弹射力加载阶段静力学模型。
活塞在此阶段处于静止状态。其纵向平衡方程:
| $ {F_Y} + {F_T} - f - {T_1} = 0 $ | (36) |
2) 质量车弹射力加载阶段静力学模型。
质量车在此阶段处于静止状态。其纵向平衡方程:
| $ {T_1} - {f_1} - {f_2} - {R_1} = 0 $ | (37) |
1) 活塞弹射滑跑阶段动力学模型。
活塞纵向动力学方程:
| $ {F_T} - f - {T_1} = {m_1}{a_1} $ | (38) |
式中a1代表活塞加速度。
2) 质量车弹射滑跑阶段动力学模型。
质量车纵向动力学方程:
| $ {T_1} - {f_1} - {f_2} - D = ma $ | (39) |
式中:m代表质量车质量,a代表质量车加速度,D为质量车受到的空气阻力。
风洞试验及文献均认为空气阻力与速度的平方成正比,本文将空气阻力计算模型表示为
| $ D = \frac{1}{2}{C_D}A\rho {V^2} $ | (40) |
式中:CD为阻力系数,A为质量车迎风面积,ρ为空气密度,V为质量车速度。
根据质量车加速度和活塞的加速度相等,可得
| $ \begin{array}{l} a = \frac{{\left( {{F_T} + {m_1}g{\mu _2}} \right)\left( {1 - {\mu _1}\tan {\theta _c}} \right)}}{{m\left( {1 + {\mu _2}\tan {\theta _c}} \right) + {m_1}\left( {1 - {\mu _1}\tan {\theta _c}} \right)}} - \\ \;\;\;\;\frac{{\left( {D + G{\mu _1}} \right)\left( {1 + {\mu _2}\tan {\theta _c}} \right)}}{{m\left( {1 + {\mu _2}\tan {\theta _c}} \right) + {m_1}\left( {1 - {\mu _1}\tan {\theta _c}} \right)}} \end{array} $ | (41) |
质量车蒸汽弹射系统仿真计算所需的条件如下:质量车质量为26 354 kg,储汽筒初始压力为1.38 MPa,蒸汽弹射器类型为C13类型。
3.1 储汽筒压力 3.1.1 理论分析由式(12)可知,储汽筒压力的导数与比热比、蒸汽的气体常数、储汽筒内温度、质量流和储汽筒体积相关,且储汽筒内压力的导数不大于0,所以储汽筒内的压力随着时间不增加。质量流的变化能够导致储汽筒内压力的导数发生变化,而发射阀的开度能够控制蒸汽流通管道内的质量流,所以,发射阀开度的变化是储汽筒内压力变化的主要原因。
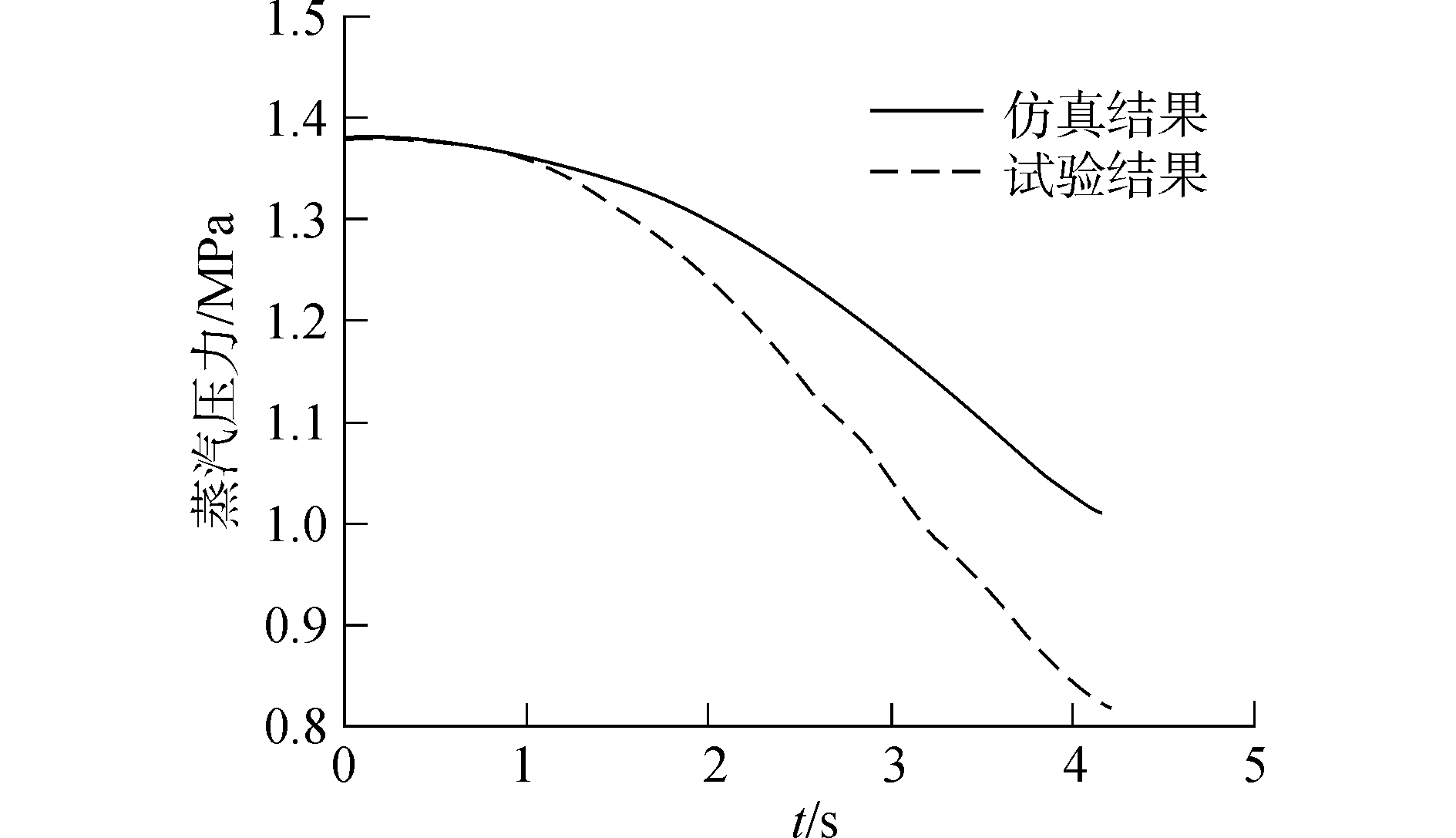
3.1.2 仿真验证储汽筒内蒸汽压力的仿真结果和试验结果的对比情况如图 4所示,由图 4的仿真结果可知:
|
Download:
|
| 图 4 储汽筒压力对比 Fig. 4 The contrast figure of accumulator pressure | |
1) 储汽筒内压力在整个弹射过程中呈不断减小的趋势。这同理论分析中的结果相符。
2) 由于仿真考虑的是理想情况,即储汽筒不与外界发生热交换,储汽筒放汽过程中,高温高压蒸汽与储汽筒壁之间没有摩擦损失,蒸汽管道及气缸没有蒸汽泄露等。仿真中储汽筒的压降低于试验中储汽筒的压降。
3.2 气缸压力 3.2.1 理论分析由式(22)可知,气缸压力的导数,与比热比、蒸汽的气体常数、储汽筒内温度、质量流、蒸汽对活塞的作用面积、活塞的初始位移、活塞的位移、气缸压力和活塞的速度相关,且气缸压力的导数由式(22)右侧被减数项与减数项的差值决定。
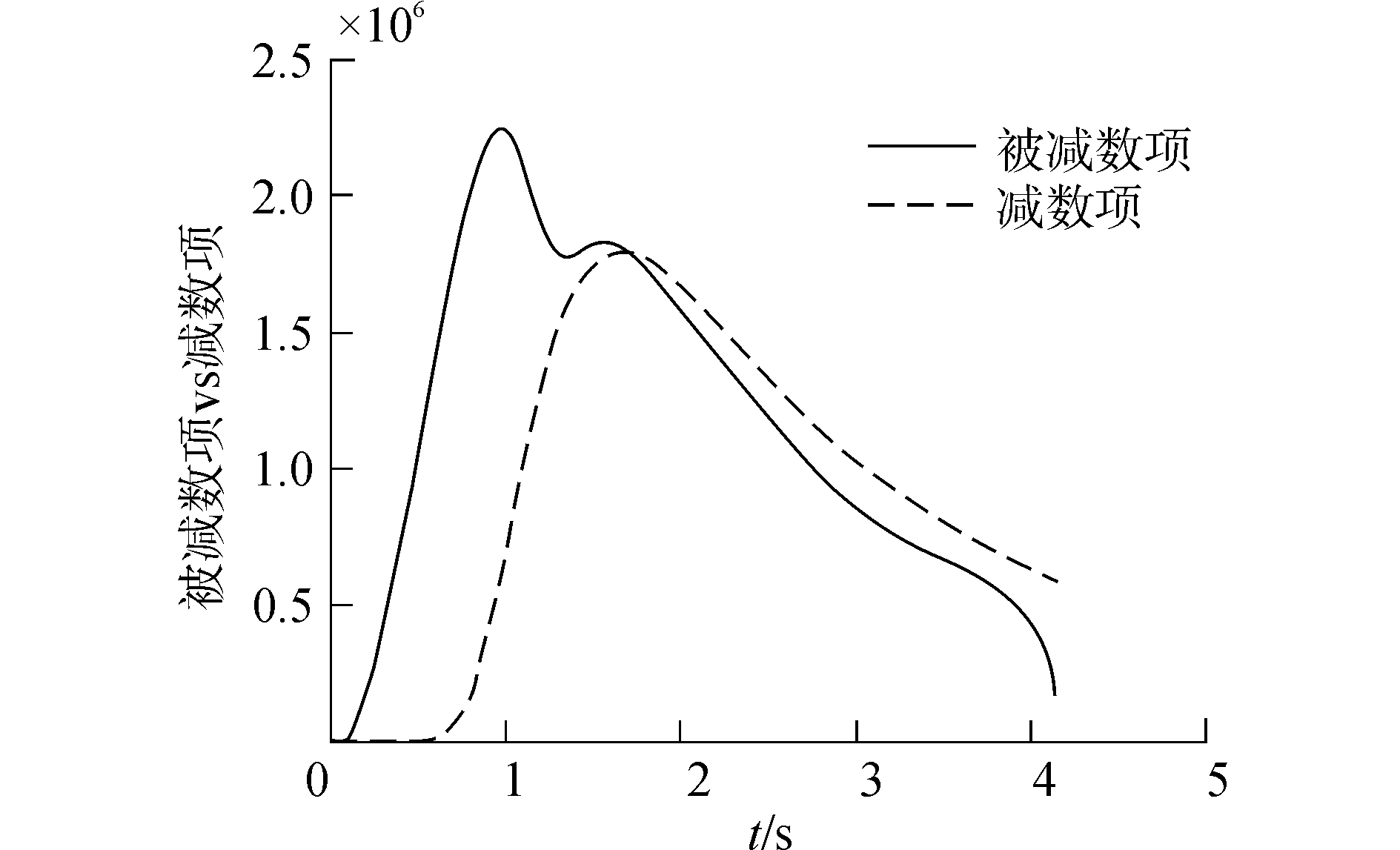
3.2.2 仿真验证图 5为式(22)中被减数项与减数项的对比图,图 6为气缸内蒸汽压力的仿真结果和试验结果的对比图,由图 5和图 6的仿真结果可知:
|
Download:
|
| 图 5 被减数项与减数项对比 Fig. 5 The contrast figure of minuend and reduction item | |

|
Download:
|
| 图 6 气缸压力对比 Fig. 6 The contrast figure of cylinder pressure | |
1) 由减数项的仿真结果曲线可知,牵制杆突卸时刻为0.616 s。此后,活塞和质量车开始运动。
2) 在第1.702 s之前,减数项小于被减数项,气缸压力的导数大于0,气缸内压力持续增加;在第1.702 s以后,减数项开始大于被减数项,气缸内压力持续减小;
3) 气缸内压力与弹射力对应,可以通过设计被减数项和减数项来得到气缸压力,进而得到理想的弹射力。
3.3 质量车加速度 3.3.1 理论分析由式(41)可知,质量车加速度,与弹射力、活塞质量、重力加速度、活塞与气缸之间的摩擦系数、弹射角、甲板摩擦系数、质量车受到的空气阻力和质量车质量相关。且弹射力是质量车加速度变化的主要原因。
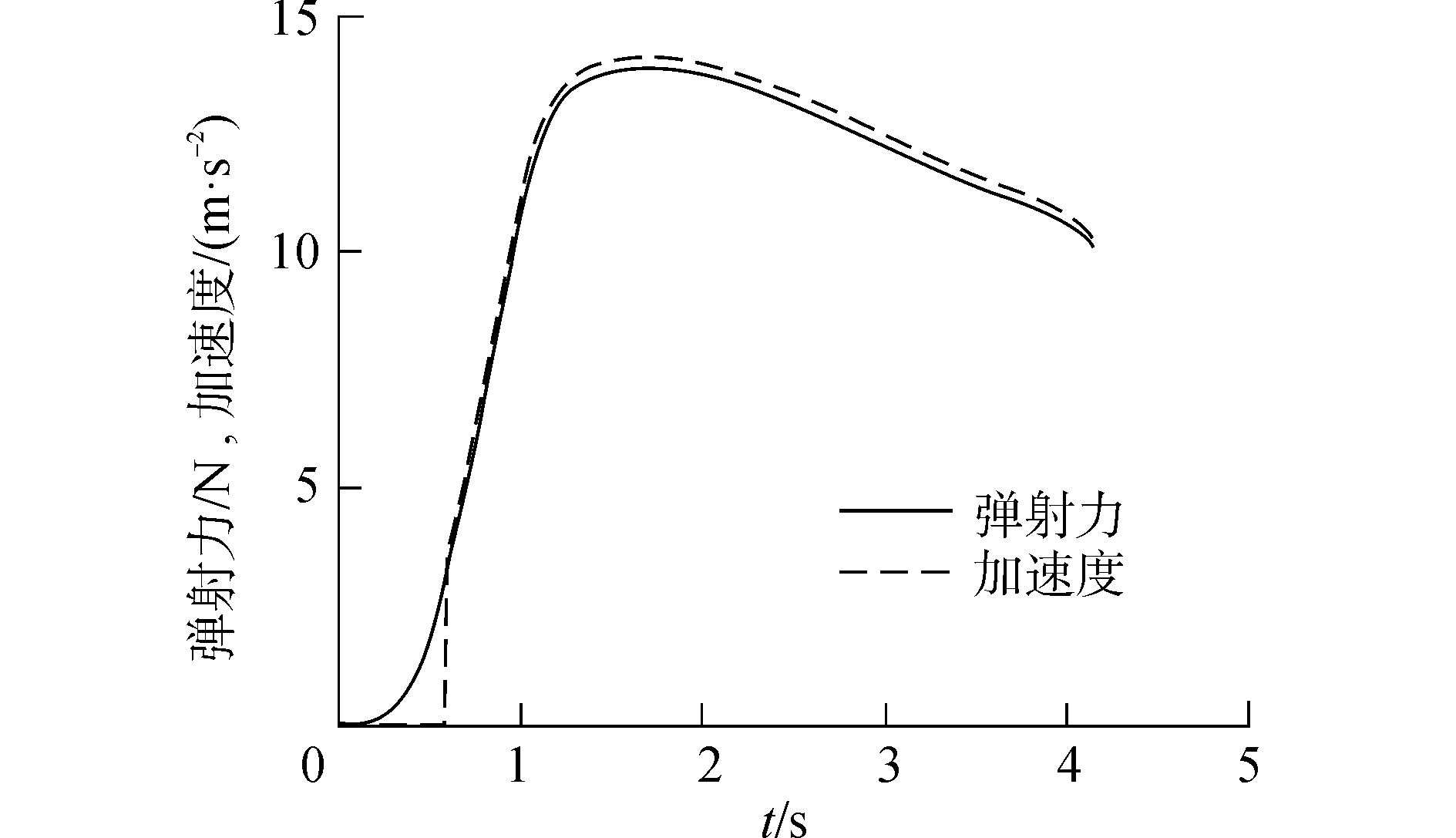
3.3.2 仿真验证图 7描述了弹射力曲线与质量车加速度曲线的趋势对比图,图 8描述了质量车加速度的仿真结果和试验结果对比图,由图 7和图 8的仿真结果可知:
|
Download:
|
| 图 7 弹射力与质量车加速度趋势对比 Fig. 7 The contrast figure of catapult force and deadload acceleration trend | |

|
Download:
|
| 图 8 质量车加速度对比 Fig. 8 The contrast figure of deadload acceleration | |
1) 弹射力曲线和质量车加速度的曲线趋势基本吻合,所以弹射力是质量车加速度变化的主要原因。
2) 由于弹射力由气缸压力主导,而在第1.702 s之前,气缸压力持续增加,导致质量车加速度持续增加;在第1.702 s以后,气缸内压力持续减小,导致质量车加速度持续减小。
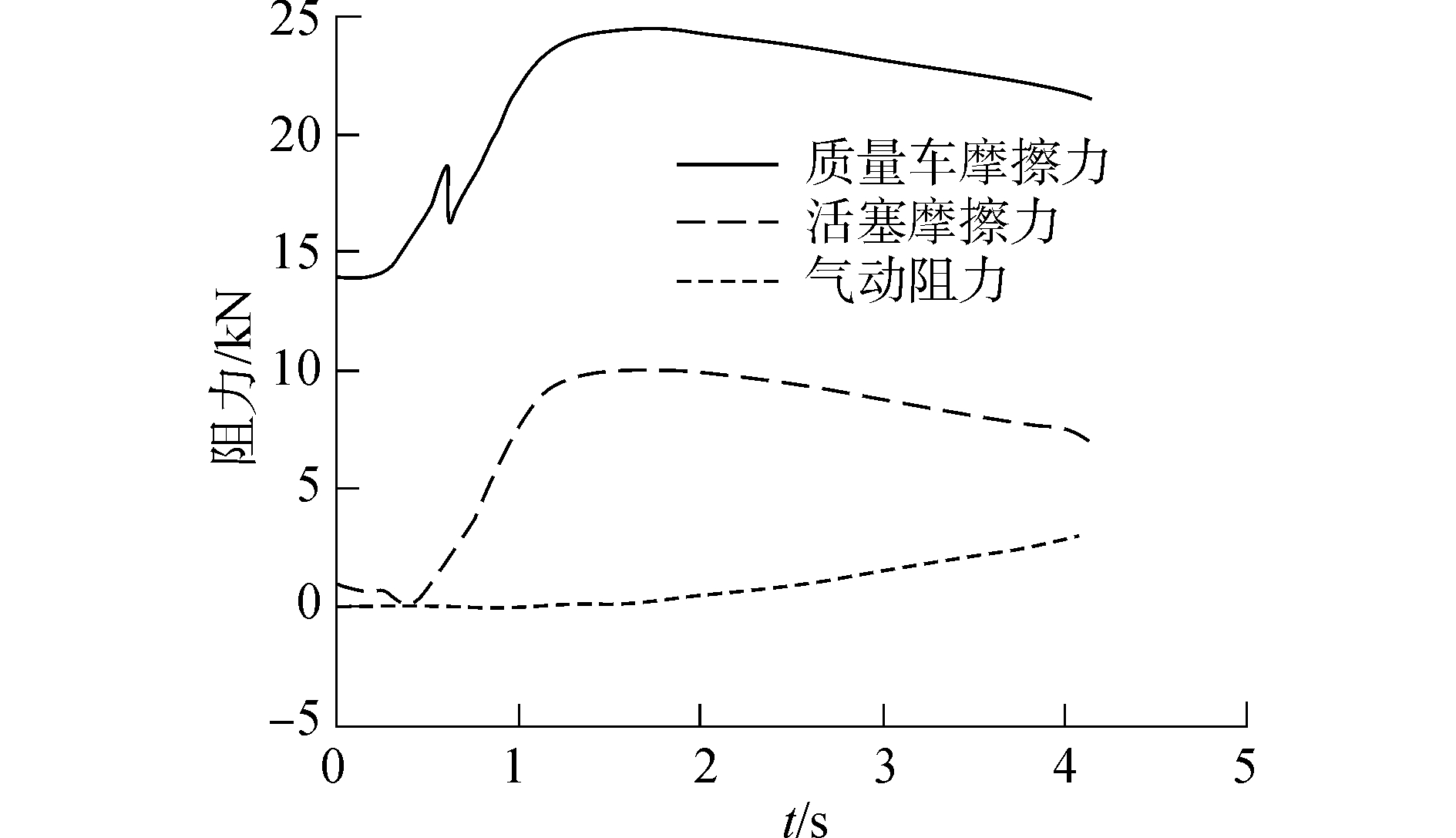
3.4 蒸汽弹射系统受到的阻力图 9描述了质量车弹射系统所受阻力的对比情况,由图 9的仿真结果可知:
|
Download:
|
| 图 9 蒸汽弹射系统受到的阻力 Fig. 9 The resistance of steam catapult system | |
1) 在蒸汽弹射系统受到的三个阻力当中,质量车受到的摩擦阻力最大,空气阻力最小。
2) 在牵制杆突卸时刻,由于牵制力和牵制杆轴向力的竖直分量突然消失,质量车摩擦阻力会突然减小,后来由于弹射杆轴向力逐渐增大,导致质量车摩擦力逐渐增大。
3) 由于弹射杆轴向力的竖直分量逐渐增加,导致活塞的摩擦力逐渐减小,直到在弹射力加载的某一时刻,弹射杆轴向力的竖直分量等于活塞的重力,此时活塞摩擦力为零,后来由于弹射杆轴向力逐渐增大,导致活塞摩擦力也逐渐增大。
3.5 蒸汽弹射器关键参数图 10为蒸汽弹射器的一些关键数据曲线,由图 10的仿真结果可知:

|
Download:
|
| 图 10 蒸汽弹射器关键数据曲线 Fig. 10 The key data curve of steam catapult system | |
1) 质量流的变化趋势与发射阀开度的变化趋势一致。
2) 弹射力随冲程的变化曲线可以看作一个分段函数,即前一段斜率为负,后一段斜率为正的分段函数。
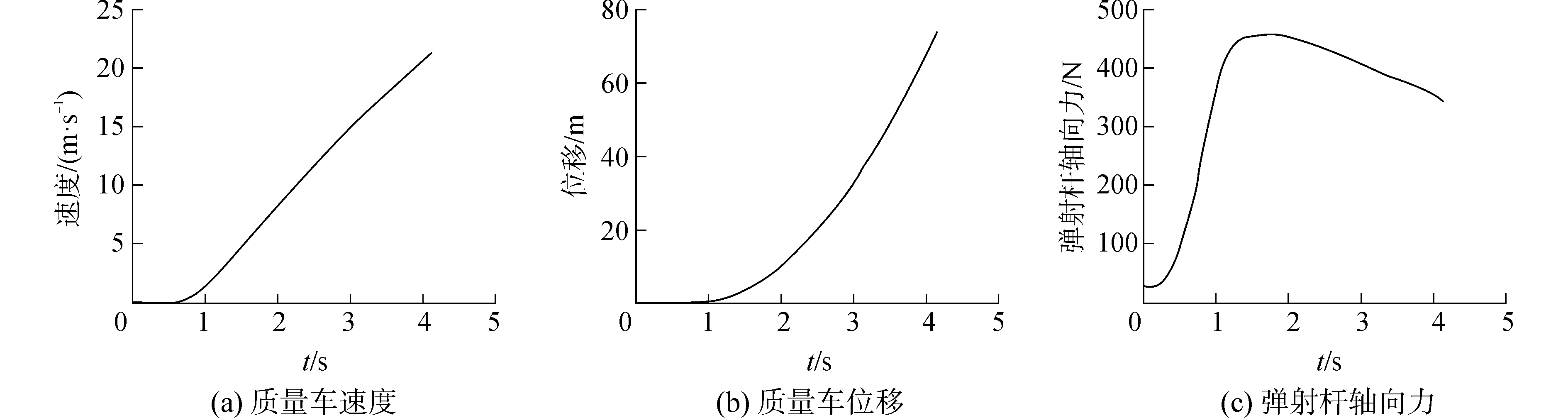
3.6 其他关键参数图 11为质量车蒸汽弹射系统其他关键数据曲线,由图 11的仿真结果可知:
|
Download:
|
| 图 11 其他关键数据曲线 Fig. 11 Other key data curve | |
1) 牵制力突卸之后,质量车的速度和位移逐渐增加。
2) 由于在发射阀开启之前,张紧系统会对蒸汽弹射系统施加预紧力,这导致弹射启动时刻,弹射杆就已经存在力;弹射杆轴向力与弹射力和气缸压力相关,且弹射杆轴向力的峰值大于弹射力的峰值。
4 结论1) 通过对储汽筒压力、气缸压力和质量车加速度三个蒸汽弹射系统关键参数进行理论分析与仿真验证,并与实验数据进行对比,验证了本文建模方法的正确性。本文的仿真结果对蒸汽弹射系统的设计及实验提供了参考。
2) 通过建立包括施加预紧力阶段、弹射力加载阶段和弹射滑跑阶段的全过程质量车蒸汽弹射的仿真模型。这样更加符合工程实际情况。本文所建立的模型可对蒸汽弹射器、牵引释放装置和负载之间的相互作用关系研究提供参考。
3) 仿真结果表明:在蒸汽弹射系统的三个阻力当中,质量车摩擦力影响最大,空气阻力影响最小;弹射力与冲程的曲线可以看成前一段斜率为正,后一段斜率为负的分段函数;弹射杆轴向力的峰值大于弹射力的峰值。
| [1] |
刘星宇, 许东松, 王立新. 滑跃起飞中机舰参数的适配性分析[J]. 北京航空航天大学学报, 2011, 37(6): 644-648, 653. LIU Xingyu, XU Dongsong, WANG Lixin. Match features of aircraft-carrier parameters during ski-jump takeoff[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(6): 644-648, 653. (  0) 0)
|
| [2] |
DOYLE M R, SAMUEL D J, CONWAY T, et al. Electromagnetic aircraft launch system-EMALS[J]. IEEE transactions on magnetics, 1995, 31(1): 528-533. DOI:10.1109/20.364638 (  0) 0)
|
| [3] |
SLAVIN F J. Aircraft steam catapults[J]. Mechanical engineering, 1969, 91: 42-46. (  0) 0)
|
| [4] |
U.S. Naval Air Engineering Center. Steam catapult performance prediction program documentation[R]. AD704528, 1970.
(  0) 0)
|
| [5] |
U.S. Naval Air Engineering Center. Evaluation of advanced method for steam catapult performance prediction with shipboard test data[R]. AD742804, 1972.
(  0) 0)
|
| [6] |
NAVY. MIL-A-8863C, Airplane strength and rigidity ground loads for navy acquired airplanes[S]. New York: NAVY, 1993.
(  0) 0)
|
| [7] |
MIL-STD-2066, Catapulting and arresting gear forcing functions for aircraft structural design[S]. New Jersey: Department of the Navy, 1982.
(  0) 0)
|
| [8] |
SMALL D B. Full scale tests of nose tow catapulting[C]//Proceedings of the 1st AIAA Annual Meeting. Reston, 1964: 1-3.
(  0) 0)
|
| [9] |
LUCAS C B. Catapult criteria for a carrier-based aircraft AD702814[R]. Washington DC: Defense Technical Information Center, 1968.
(  0) 0)
|
| [10] |
赵险峰. 航母舰载机蒸汽弹射系统的数学仿真研究[J]. 舰载武器, 1996(3): 45-53. ZHAO Xianfeng. Study on the mathematical simulation of the steam catapult system of carrier-based aircraft[J]. Shipborne weapons, 1996(3): 45-53. (  0) 0)
|
| [11] |
余晓军, 高翔, 钟民军. 蒸汽弹射器的动力学仿真研究[J]. 船海工程, 2005(3): 1-4. YU Xiaojun, GAO Xiang, ZHONG Minjun. Simulation on dynamics of the steam-powered catapult[J]. Ship & ocean engineering, 2005(3): 1-4. DOI:10.3963/j.issn.1671-7953.2005.03.002 (  0) 0)
|
| [12] |
程刚, 倪何, 孙丰瑞. 舰载蒸汽弹射系统建模与仿真研究[J]. 武汉理工大学学报(交通科学与工程版), 2010, 34(2): 301-305. CHENG Gang, NI He, SUN Fengrui. Modeling and simulation research on naval steam-power aircraft launch system[J]. Journal of Wuhan University of Technology (transportation science & engineering), 2010, 34(2): 301-305. DOI:10.3963/j.issn.1006-2823.2010.02.022 (  0) 0)
|
| [13] |
张雷, 冯蕴雯, 薛小锋, 等. 舰载机蒸汽弹射动力学仿真分析[J]. 航空计算技术, 2012, 42(6): 29-33. ZHANG Lei, FENG Yunwen, XUE Xiaofeng, et al. Dynamics simulation of carrier-based aircraft steam catapult[J]. Aeronautical computing technique, 2012, 42(6): 29-33. DOI:10.3969/j.issn.1671-654X.2012.06.008 (  0) 0)
|
| [14] |
高俊东, 崔帅, 冯蕴雯, 等. 舰载机蒸汽弹射器热力学仿真分析[J]. 机械科学与技术, 2013, 32(7): 963-967. GAO Jundong, CUI Shuai, FENG Yunwen, et al. Simulation and analysis of thermodynamics for carrier-based aircraft steam catapult[J]. Mechanical science and technology for aerospace engineering, 2013, 32(7): 963-967. (  0) 0)
|
| [15] |
朱齐丹, 刘恒, 李晓琳. 舰载机偏心情况下弹射起飞研究[J]. 飞行力学, 2016, 34(2): 10-14. ZHU Qidan, LIU Heng, LI Xiaolin. Research on carrier-based aircraft catapult launching in the case of different eccentricity[J]. Flight dynamics, 2016, 34(2): 10-14. (  0) 0)
|
| [16] |
于浩, 聂宏. 舰载机偏中心定位弹射起飞弹射杆载荷分析[J]. 航空学报, 2010, 31(10): 1953-1959. YU Hao, NIE Hong. Launch bar load analysis of carrier-based aircraft during off-center catapult launch[J]. Acta aeronautica et astronautica sinica, 2010, 31(10): 1953-1959. (  0) 0)
|
| [17] |
刘星宇, 许东松, 王立新. 舰载飞机弹射起飞的机舰参数适配特性[J]. 航空学报, 2010, 31(1): 102-108. LIU Xingyu, XU Dongsong, WANG Lixin. Match characteristics of aircraft-carrier parameters during catapult takeoff of carrier-based aircraft[J]. Acta aeronautica et astronautica sinica, 2010, 31(1): 102-108. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


