对非线性大时滞系统实现快速稳定控制是过程控制工程中的一个难题。随着科技的进步、被控对象的日益复杂以及对控制品质要求的提高, 传统的控制方法例如PID控制,对于复杂的非线性大时滞系统控制效果不甚理想。现有的一些先进的控制方法大多是基于模型的,但是非线性大时滞系统的模型不易建立,即使建立成功,模型也会存在复杂、高阶次难于应用于先进控制器设计或者精度低难以反映系统内在动态的问题,达不到想要的控制效果[1]。
无模型控制是基于被控系统的输入输出数据,不需要建立被控系统的数学模型,计算量小,容易实现,非常适合于复杂的非线性系统[2]。它是以非线性途径设计出来的控制方法,因而用来控制非线性复杂对象时, 表现出了它的优良控制品质,但是基本无模型算法对于大时滞的被控对象,动态控制效果不理想,难以有效的快速跟踪控制[3-4]。本文根据被控对象具有大的时间滞后特点,设计了带有滞后时间输入变化率约束项的无模型自适应控制方法,推导了双输入双输出的无模型控制律,使其能应用于更多实际系统控制中。
压缩式制冷系统是典型的非线性大时滞系统,具有多输入、多输出,强耦合及难以建立可以实现控制的精确数学模型等特性[5-6]。现有的控制方法存在一些问题:首先PID在控制蒸发器过热度时会产生震荡,并且对工况及环境变化的适应性差;其次,制冷系统模型不易建立,依赖模型的先进控制方法不易实现;最后,实际制冷系统存在很大的滞后问题,现有的基于PID的控制方法难以实现对大时滞系统的快速有效控制[7-8]。针对上述问题,本文设计了压缩式制冷系统的无模型控制方法,选取了大时滞对象和制冷系统进行仿真实验。
1 无模型自适应控制算法对于一个离散系统,假定[u(k-1), y(k)]和[u(k), y(k+1)],是相邻采样时刻的观测数据,且u(k)≠u(k-1)。系统的泛模型为
| $ \left\{ \begin{array}{l} y\left( {k + 1} \right) - y\left( k \right) = \varphi \left( k \right)\left( {u\left( k \right) - u\left( {k - 1} \right)} \right)\\ \Delta y\left( {k + 1} \right) = \varphi \left( k \right)\Delta u\left( k \right) \end{array} \right. $ | (1) |
式中φ(k)是其特征参量。
基本MFAC算法控制率求取方法[9]描述如下
| $ \begin{array}{*{20}{c}} {u\left( k \right) = u\left( {k - 1} \right) + }\\ {\frac{{\rho \varphi \left( k \right)}}{{\lambda + {{\left\| {\varphi \left( k \right)} \right\|}^2}}}\left[ {{y^ * }\left( {k + 1} \right) - y\left( k \right)} \right]} \end{array} $ | (2) |
| $ \begin{array}{*{20}{c}} {\hat \varphi \left( k \right) = \hat \varphi \left( {k - 1} \right) + \frac{{\eta \Delta u\left( {k - 1} \right)}}{{\mu + {{\left\| {\Delta u\left( {k - 1} \right)} \right\|}^2}}} \cdot }\\ {\left[ {\Delta y\left( k \right) - \hat \varphi \left( {k - 1} \right)\Delta u\left( {k - 1} \right)} \right]} \end{array} $ | (3) |
式中:ε是一个充分小的正数;权重系数λ既可以确保分母不为零,又可以限制Δu(k)变化范围;μ的存在则限制了参数φ(k)的变化。
2 大时滞系统的无模型控制算法 2.1 单输入单输出时滞系统的无模型自适应控制算法考虑滞后时间常数τ对大时滞系统的影响,为更好地控制大时滞对象,在基本MFAC算法基础上,特别地针对大时间滞后系统,在算法中加入τ。在控制输入准则函数中选取带间隔滞后时间τ的两组输入值之间的变化率作为输入准则中的一个重要的约束参数,即称之为带有滞后时间的输入变化率的约束项[10]:[(u(k)-u(k-1-τ))/T]2, 式中T为采样周期,则输入准则函数为
| $ \begin{array}{*{20}{c}} {\min J\left[ {u\left( k \right)} \right] = {{\left[ {{y^ * }\left( {k + 1} \right) - y\left( {k + 1} \right)} \right]}^2} + }\\ {\eta {{\left[ {\frac{{u\left( k \right) - u\left( {k - 1 - \tau } \right)}}{T}} \right]}^2} + }\\ {\lambda {{\left[ {u\left( k \right) - u\left( {k - 1} \right)} \right]}^2}} \end{array} $ | (4) |
在伪偏导数估计准则函数中,同样加入了带有滞后时间的输入变化约束项:[u(k-1)-u(k-2-τ)],来代替基本MFAC算法中的Δu(k-1)项。则伪偏导数估计准则函数的描述如下
| $ \begin{array}{*{20}{c}} {\min J\left[ {\varphi \left( k \right)} \right] = \left[ {{y^ * }\left( k \right) - y\left( {k - 1} \right) - } \right.}\\ {{{\left. {\varphi \left( k \right)\left[ {u\left( {k - 1} \right) - u\left( {k - 2 - \tau } \right)} \right]} \right]}^2} + }\\ {\mu {{\left[ {\varphi \left( k \right) - \varphi \left( {k - 1} \right)} \right]}^2}} \end{array} $ | (5) |
将式(1)代入式(4)、(5),分别对u(k)和φ(k)求偏导可得设计的MFAC算法,描述如下
| $ \begin{array}{*{20}{c}} {u\left( k \right) = u\left( {k - 1} \right) + \frac{{\rho \varphi \left( k \right)}}{{\lambda + {{\left\| {\varphi \left( k \right)} \right\|}^2} + \frac{\eta }{{{T^2}}}}} \cdot }\\ {\left[ {{y^ * }\left( {k + 1} \right) - y\left( k \right)} \right] + \frac{{\left( {\eta /{T^2}} \right)}}{{\lambda + {{\left\| {\varphi \left( k \right)} \right\|}^2} + \frac{\eta }{{{T^2}}}}} \cdot }\\ {\left[ {u\left( {k - 1 - \tau } \right) - u\left( {k - 1} \right)} \right]} \end{array} $ | (6) |
φ(k)=φ(1),若
| $ \begin{array}{*{20}{c}} {\varphi \left( k \right) = \varphi \left( {k - 1} \right) + }\\ {\frac{{\xi \left[ {u\left( {k - 1} \right) - u\left( {k - 2 - \tau } \right)} \right]}}{{\mu + {{\left\| {u\left( {k - 1} \right) - u\left( {k - 2 - \tau } \right)} \right\|}^2}}} \cdot }\\ {\left\{ {\Delta y\left( k \right) - \varphi \left( {k - 1} \right)\left[ {u\left( {k - 1} \right) - u\left( {k - 2 - \tau } \right)} \right]} \right\}} \end{array} $ | (7) |
式中:y*(k+1)是系统的期望输出;y(k)表示系统的真实输出;T为采样时间;ξ、ρ、η、λ、μ是权重系数;ε是一个充分小的正数;η限制了我们提出的滞后输入变化率的变化,和λ一起影响伪偏导数的变化。
2.2 多输入多输出时滞系统的无模型自适应控制算法为了将新型的无模型自适应控制方法应用到更多实际系统控制中,本文推导给出了针对双输入双输出时滞系统的无模型控制律,具体控制律设计和伪偏导数估计的推导过程如下:令U(k)=[u1(k) u2(k)]T, Y(k)=[y1(k) y2(k)]T,对于双输入双输出离散系统,其泛模型为
| $ \begin{array}{*{20}{c}} {\left[ \begin{array}{l} {y_1}\left( {k + 1} \right) - {y_1}\left( k \right)\\ {y_2}\left( {k + 1} \right) - {y_2}\left( k \right) \end{array} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{\varphi _{11}}\left( k \right)}&{{\varphi _{12}}\left( k \right)}\\ {{\varphi _{21}}\left( k \right)}&{{\varphi _{22}}\left( k \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_1}\left( k \right) - {u_1}\left( {k - 1} \right)}\\ {{u_2}\left( k \right) - {u_2}\left( {k - 1} \right)} \end{array}} \right]} \end{array} $ | (8) |
一方面,希望实际输出与给定值的偏差平方和最小,输出快速跟随给定;另一方面,采用泛模型代替非线性系统时相邻采样时刻的Δu(k)不能太大,故文中使用式(9)所表示的目标函数:
| $ \begin{array}{*{20}{c}} {\min J\left[ {\mathit{\boldsymbol{U}}\left( k \right)} \right] = {{\left[ {y_1^ * \left( {k + 1} \right) - {y_1}\left( {k + 1} \right)} \right]}^2} + }\\ {{{\left[ {y_2^ * \left( {k + 1} \right) - {y_2}\left( {k + 1} \right)} \right]}^2} + }\\ {{\lambda _1}{{\left[ {{u_1}\left( k \right) - {u_1}\left( {k - 1} \right)} \right]}^2} + }\\ {{\lambda _2}{{\left[ {{u_2}\left( k \right) - {u_2}\left( {k - 1} \right)} \right]}^2}} \end{array} $ | (9) |
为了处理大滞后问题,加入了带有滞后时刻输入变化率的约束项: [(u1(k)-u1(k-1-τ))/T]2、[(u2(k)-u2(k-1-τ))/T]2,则设计的输入准则函数如下式:
| $ \begin{array}{*{20}{c}} {\min J\left[ {\mathit{\boldsymbol{U}}\left( k \right)} \right] = {{\left[ {y_1^ * \left( {k + 1} \right) - {y_1}\left( {k + 1} \right)} \right]}^2} + }\\ {{{\left[ {y_2^ * \left( {k + 1} \right) - {y_2}\left( {k + 1} \right)} \right]}^2} + {\lambda _1}\left[ {{u_1}\left( k \right) - } \right.}\\ {{{\left. {{u_1}\left( {k - 1} \right)} \right]}^2} + {\lambda _2}{{\left[ {{u_2}\left( k \right) - {u_2}\left( {k - 1} \right)} \right]}^2} + }\\ {{\eta _1}{{\left[ {\left( {{u_1}\left( k \right) - {u_1}\left( {k - 1 - \tau } \right)} \right)/T} \right]}^2} + }\\ {{\eta _2}{{\left[ {\left( {{u_2}\left( k \right) - {u_2}\left( {k - 1 - \tau } \right)} \right)/T} \right]}^2}} \end{array} $ | (10) |
将式(8)代入式(10),并分别对u1和u2求偏导得到
| $ \begin{array}{*{20}{c}} {\min \frac{{\partial J\left[ {U\left( k \right)} \right]}}{{\partial {u_1}\left( k \right)}} = 2\left[ {y_1^ * \left( {k + 1} \right) - {y_1}\left( k \right) - } \right.}\\ {{\varphi _{11}}\left( k \right)\left( {{u_1}\left( k \right) - {u_1}\left( {k - 1} \right)} \right) - {\varphi _{12}}\left( k \right)\left( {{u_2}\left( k \right) - } \right.}\\ {\left. {\left. {{u_2}\left( {k - 1} \right)} \right)} \right]\left( { - {\varphi _{11}}\left( k \right)} \right) + 2\left[ {y_2^ * \left( {k + 1} \right) - } \right.}\\ {{y_2}\left( k \right) - {\varphi _{21}}\left( k \right)\left( {{u_1}\left( k \right) - {u_1}\left( {k - 1} \right)} \right) - }\\ {\left. {{\varphi _{22}}\left( k \right)\left( {{u_2}\left( k \right) - {u_2}\left( {k - 1} \right)} \right)} \right]\left( { - {\varphi _{21}}\left( k \right)} \right) + }\\ {2{\lambda _1}\left[ {{u_1}\left( k \right) - {u_1}\left( {k - 1} \right)} \right] + }\\ {2{\eta _1}\left[ {\left( {{u_1}\left( k \right) - {u_1}\left( {k - 1 - \tau } \right)} \right)/T} \right]/{T^2}} \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {\min \frac{{\partial J\left[ {U\left( k \right)} \right]}}{{\partial {u_2}\left( k \right)}} = 2\left[ {y_1^ * \left( {k + 1} \right) - {y_1}\left( k \right) - } \right.}\\ {{\varphi _{11}}\left( k \right)\left( {{u_1}\left( k \right) - {u_1}\left( {k - 1} \right)} \right) - }\\ {\left. {{\varphi _{12}}\left( k \right)\left( {{u_2}\left( k \right) - {u_2}\left( {k - 1} \right)} \right)} \right]\left( { - {\varphi _{12}}\left( k \right)} \right) + }\\ {2\left[ {y_2^ * \left( {k + 1} \right) - {y_2}\left( k \right) - {\varphi _{21}}\left( k \right)\left( {{u_1}\left( k \right) - } \right.} \right.}\\ {\left. {\left. {{u_1}\left( {k - 1} \right)} \right) - {\varphi _{22}}\left( k \right)\left( {{u_2}\left( k \right) - {u_2}\left( {k - 1} \right)} \right)} \right] \cdot }\\ {\left( { - {\varphi _{22}}\left( k \right)} \right) + 2{\lambda _2}\left[ {{u_2}\left( k \right) - {u_2}\left( {k - 1} \right)} \right] + }\\ {2{\eta _2}\left[ {\left( {{u_2}\left( k \right) - {u_2}\left( {k - 1 - \tau } \right)} \right)/T} \right]/{T^2}} \end{array} $ | (12) |
令式(11)、(12)恒等于零。最终, 控制率[u1(k) u2(k)]T通过求解由式(13)、(14)组成的二元一次方程组得到
| $ \begin{array}{*{20}{c}} {\left[ {\varphi _{11}^2\left( k \right) + \varphi _{21}^2\left( k \right) + {\lambda _1} + \frac{{{\eta _1}}}{{{T^2}}}} \right]{u_1}\left( k \right) + }\\ {\left[ {{\varphi _{11}}\left( k \right){\varphi _{12}}\left( k \right) + {\varphi _{21}}\left( k \right){\varphi _{22}}\left( k \right)} \right]{u_2}\left( k \right) = }\\ {\frac{{{\eta _1}{u_1}\left( {k - 1 - \tau } \right)}}{{{T^2}}} + {\lambda _1}{u_1}\left( {k - 1} \right) + {\varphi _{21}}\left( k \right) \cdot }\\ {\left[ {y_2^ * \left( {k + 1} \right) - {y_2}\left( k \right) + {\varphi _{21}}\left( k \right){u_1}\left( {k - 1} \right) + } \right.}\\ {\left. {{\varphi _{22}}\left( k \right){u_2}\left( {k - 1} \right)} \right] + {\varphi _{11}}\left( k \right)\left[ {y_1^ * \left( {k + 1} \right) - } \right.}\\ {\left. {{y_1}\left( k \right) + {\varphi _{11}}\left( k \right){u_1}\left( {k - 1} \right) + {\varphi _{12}}\left( k \right){u_2}\left( {k - 1} \right)} \right]} \end{array} $ | (13) |
| $ \begin{array}{*{20}{c}} {\left[ {{\varphi _{11}}\left( k \right){\varphi _{12}}\left( k \right) + {\varphi _{21}}\left( k \right){\varphi _{22}}\left( k \right)} \right]{u_1}\left( k \right) + }\\ {\left[ {\varphi _{12}^2\left( k \right) + \varphi _{22}^2\left( k \right) + {\lambda _2} + \frac{{{\eta _2}}}{{{T^2}}}} \right]{u_2}\left( k \right) = }\\ {\frac{{{\eta _2}{u_2}\left( {k - 1 - \tau } \right)}}{{{T^2}}} + {\lambda _2}{u_2}\left( {k - 1} \right) + {\varphi _{22}}\left( k \right) \cdot }\\ {\left[ {y_2^ * \left( {k + 1} \right) - {y_2}\left( k \right) + {\varphi _{21}}\left( k \right){u_1}\left( {k - 1} \right) + } \right.}\\ {\left. {{\varphi _{22}}\left( k \right){u_2}\left( {k - 1} \right)} \right] + {\varphi _{12}}\left( k \right)\left[ {y_1^ * \left( {k + 1} \right) - } \right.}\\ {\left. {{y_1}\left( k \right) + {\varphi _{11}}\left( k \right){u_1}\left( {k - 1} \right) + {\varphi _{12}}\left( k \right){u_2}\left( {k - 1} \right)} \right]} \end{array} $ | (14) |
式中: λ1、λ2、η1和η2都是权重系数, λ1和λ2可以限制Δu(k)的变化范围,保证泛模型替代非线性系统的合理性。式(13)、(14)中只有特征参量φ(k)未知,需要伪偏导数的参数估计。
φ(k)是泛模型的特征参量。一方面,希望实际输出与泛模型输出之间的偏差平方和最小,使得泛模型近似于实际模型;另一方面,采用泛模型代替非线性系统时,相邻采样时刻的Δφ(k)不能变化太大,故文中使用下式(15)所表示的目标函数:
| $ \begin{array}{*{20}{c}} {\min J\left[ {\varphi \left( k \right)} \right] = {{\left[ {y_1^ * \left( k \right) - {y_1}\left( k \right)} \right]}^2} + }\\ {{{\left[ {y_2^ * \left( k \right) - {y_2}\left( k \right)} \right]}^2} + {\mu _{11}}{{\left[ {{\varphi _{11}}\left( k \right) - {\varphi _{11}}\left( {k - 1} \right)} \right]}^2} + }\\ {{\mu _{12}}{{\left[ {{\varphi _{12}}\left( k \right) - {\varphi _{12}}\left( {k - 1} \right)} \right]}^2} + {\mu _{21}}\left[ {{\varphi _{21}}\left( k \right) - } \right.}\\ {{{\left. {{\varphi _{21}}\left( {k - 1} \right)} \right]}^2} + {\mu _{22}}{{\left[ {{\varphi _{22}}\left( k \right) - {\varphi _{22}}\left( {k - 1} \right)} \right]}^2}} \end{array} $ | (15) |
同样,考虑滞后时间常数τ对大时滞系统的影响,我们加入了带有滞后时刻的输入变化率的约束项u1(k-1)-u1(k-2-τ),u2(k-1)-u2(k-2-τ),进而得到伪偏导数估计准则函数描述如下
| $ \begin{array}{*{20}{c}} {\min J\left[ {\varphi \left( k \right)} \right] = \left[ {y_1^ * \left( k \right) - {y_1}\left( {k - 1} \right) - } \right.}\\ {{\varphi _{11}}\left( {k - 1} \right)\left[ {{u_1}\left( {k - 1} \right) - {u_1}\left( {k - 2 - \tau } \right)} \right] - }\\ {{{\left. {{\varphi _{12}}\left( {k - 1} \right)\left[ {{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)} \right]} \right]}^2} + }\\ {\left[ {y_2^ * \left( k \right) - {y_2}\left( {k - 1} \right) - {\varphi _{21}}\left( {k - 1} \right)\left[ {{u_1}\left( {k - 1} \right) - } \right.} \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right] - {\varphi _{22}}\left( {k - 1} \right)\left[ {{u_2}\left( {k - 1} \right) - } \right.}\\ {{{\left. {\left. {{u_2}\left( {k - 2 - \tau } \right)} \right]} \right]}^2} + {\mu _{11}}{{\left[ {{\varphi _u}\left( k \right) - {\varphi _{11}}\left( {k - 1} \right)} \right]}^2} + }\\ {{\mu _{12}}{{\left[ {{\varphi _{12}}\left( k \right) - {\varphi _{12}}\left( {k - 1} \right)} \right]}^2} + {\mu _{21}}\left[ {{\varphi _{21}}\left( k \right) - {\varphi _{21}}\left( {k - } \right.} \right.}\\ {{{\left. {\left. 1 \right)} \right]}^2} + {\mu _{22}}{{\left[ {{\varphi _{22}}\left( k \right) - {\varphi _{22}}\left( {k - 1} \right)} \right]}^2}} \end{array} $ | (16) |
式(16)分别对φ11(k)、φ12(k)、φ21(k)、φ22(k)求偏导可得:
| $ \begin{array}{*{20}{c}} {\min \frac{{\partial J\left[ {\varphi \left( k \right)} \right]}}{{\partial {\varphi _{11}}\left( k \right)}} = - 2\left[ {y_1^ * \left( k \right) - {y_1}\left( {k - 1} \right) - } \right.}\\ {\left( {{\varphi _{11}}\left( k \right) - \Delta {\varphi _{11}}\left( k \right)} \right)\left( {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right) - \left( {{\varphi _{12}}\left( k \right) - \Delta {\varphi _{12}}\left( k \right)} \right) \cdot }\\ {\left. {\left( {{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)} \right)} \right]\left[ {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right] + 2{\mu _{11}}\left[ {{\varphi _{11}}\left( k \right) - {\varphi _{11}}\left( {k - 1} \right)} \right]} \end{array} $ | (17) |
| $ \begin{array}{*{20}{c}} {\min \frac{{\partial J\left[ {\varphi \left( k \right)} \right]}}{{\partial {\varphi _{12}}\left( k \right)}} = - 2\left[ {y_1^ * \left( k \right) - {y_1}\left( {k - 1} \right) - } \right.}\\ {\left( {{\varphi _{11}}\left( k \right) - \Delta {\varphi _{11}}\left( k \right)} \right)\left( {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right) - \left( {{\varphi _{12}}\left( k \right) - \Delta {\varphi _{12}}\left( k \right)} \right) \cdot }\\ {\left. {\left( {{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)} \right)} \right]\left[ {{u_2}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_2}\left( {k - 2 - \tau } \right)} \right] + 2{\mu _{12}}\left[ {{\varphi _{12}}\left( k \right) - {\varphi _{12}}\left( {k - 1} \right)} \right]} \end{array} $ | (18) |
| $ \begin{array}{*{20}{c}} {\min \frac{{\partial J\left[ {\varphi \left( k \right)} \right]}}{{\partial {\varphi _{21}}\left( k \right)}} = - 2\left[ {y_2^ * \left( k \right) - {y_2}\left( {k - 1} \right) - } \right.}\\ {\left( {{\varphi _{21}}\left( k \right) - \Delta {\varphi _{21}}\left( k \right)} \right)\left( {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right) - \left( {{\varphi _{22}}\left( k \right) - \Delta {\varphi _{22}}\left( k \right)} \right) \cdot }\\ {\left. {\left( {{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)} \right)} \right]\left[ {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right] + 2{\mu _{21}}\left[ {{\varphi _{21}}\left( k \right) - {\varphi _{21}}\left( {k - 1} \right)} \right]} \end{array} $ | (19) |
| $ \begin{array}{*{20}{c}} {\min \frac{{\partial J\left[ {\varphi \left( k \right)} \right]}}{{\partial {\varphi _{22}}\left( k \right)}} = - 2\left[ {y_2^ * \left( k \right) - {y_2}\left( {k - 1} \right) - } \right.}\\ {\left( {{\varphi _{21}}\left( k \right) - \Delta {\varphi _{21}}\left( k \right)} \right)\left( {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right) - \left( {{\varphi _{22}}\left( k \right) - \Delta {\varphi _{22}}\left( k \right)} \right) \cdot }\\ {\left. {\left( {{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)} \right)} \right]\left[ {{u_2}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_2}\left( {k - 2 - \tau } \right)} \right] + 2{\mu _{22}}\left[ {{\varphi _{22}}\left( k \right) - {\varphi _{22}}\left( {k - 1} \right)} \right]} \end{array} $ | (20) |
令式(17)~(20)恒等于零,分别求一元一次方程,可得伪偏导数:
| $ \begin{array}{*{20}{c}} {{\varphi _{11}}\left( k \right) = {\varphi _{11}}\left( {k - 1} \right) + }\\ {\frac{{{u_1}\left( {k - 1} \right) - {u_1}\left( {k - 2 - \tau } \right)}}{{{\mu _{11}} + {{\left\| {{u_1}\left( {k - 1} \right) - {u_1}\left( {k - 2 - \tau } \right)} \right\|}^2}}}\left[ {y_1^ * - } \right.}\\ {{y_1}\left( {k - 1} \right) - {\varphi _{11}}\left( {k - 1} \right)\left( {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right) - {\varphi _{12}}\left( {k - 1} \right)\left( {{u_2}\left( {k - 1} \right) - } \right.}\\ {\left. {\left. {{u_2}\left( {k - 2 - \tau } \right)} \right)} \right]} \end{array} $ | (21) |
| $ \begin{array}{*{20}{c}} {{\varphi _{12}}\left( k \right) = {\varphi _{12}}\left( {k - 1} \right) + }\\ {\frac{{{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)}}{{{\mu _{12}} + {{\left\| {{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)} \right\|}^2}}}\left[ {y_1^ * - } \right.}\\ {{y_1}\left( {k - 1} \right) - {\varphi _{11}}\left( {k - 1} \right)\left( {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right) - {\varphi _{12}}\left( {k - 1} \right)\left( {{u_2}\left( {k - 1} \right) - } \right.}\\ {\left. {\left. {{u_2}\left( {k - 2 - \tau } \right)} \right)} \right]} \end{array} $ | (22) |
| $ \begin{array}{*{20}{c}} {{\varphi _{21}}\left( k \right) = {\varphi _{21}}\left( {k - 1} \right) + }\\ {\frac{{{u_1}\left( {k - 1} \right) - {u_1}\left( {k - 2 - \tau } \right)}}{{{\mu _{21}} + {{\left\| {{u_1}\left( {k - 1} \right) - {u_1}\left( {k - 2 - \tau } \right)} \right\|}^2}}}\left[ {y_2^ * - } \right.}\\ {{y_2}\left( {k - 1} \right) - {\varphi _{21}}\left( {k - 1} \right)\left( {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right) - {\varphi _{22}}\left( {k - 1} \right)\left( {{u_2}\left( {k - 1} \right) - } \right.}\\ {\left. {\left. {{u_2}\left( {k - 2 - \tau } \right)} \right)} \right]} \end{array} $ | (23) |
| $ \begin{array}{*{20}{c}} {{\varphi _{22}}\left( k \right) = {\varphi _{22}}\left( {k - 1} \right) + }\\ {\frac{{{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)}}{{{\mu _{22}} + {{\left\| {{u_2}\left( {k - 1} \right) - {u_2}\left( {k - 2 - \tau } \right)} \right\|}^2}}}\left[ {y_2^ * - } \right.}\\ {{y_2}\left( {k - 1} \right) - {\varphi _{21}}\left( {k - 1} \right)\left( {{u_1}\left( {k - 1} \right) - } \right.}\\ {\left. {{u_1}\left( {k - 2 - \tau } \right)} \right) - {\varphi _{22}}\left( {k - 1} \right)\left( {{u_2}\left( {k - 1} \right) - } \right.}\\ {\left. {\left. {{u_2}\left( {k - 2 - \tau } \right)} \right)} \right]} \end{array} $ | (24) |
式中μ11、μ12、μ21、μ22是权重系数。
3 仿真研究为验证本文设计算法的有效性,分别使用本文设计的无模型控制算法和基本MFAC算法进行仿真实验比较研究。选取典型的大时滞系统进行仿真实验比较。仿真过程中,被控系统数学模型仅用于产生输入输出的实验数据,而不参与控制策略的设计。
3.1 一阶大时滞系统仿真引入一阶大时滞系统进行仿真比较分析:
| $ G\left( s \right) = \frac{1}{{40s + 1}}{{\rm{e}}^{ - {\rm{20s}}}} $ | (25) |
使用本文所设计的无模型控制算法,各参数选择如下:ξ=1,ρ=1, η=1, λ=500, μ=1.2,则本文所设计的无模型控制方法和基本MFAC控制算法的Matlab仿真比较结果如图 1所示。通过仿真结果可以看出:本文所设计算法和基本MFAC算法都能对一阶大时滞对象进行稳定的控制,超调较小并且输出稳定;但是本文所设计的控制算法具有明显较小的上升时间,而且响应速度远远大于基本MFAC算法,因此具有更好的控制性能。

|
Download:
|
| 图 1 一阶大时滞系统阶跃响应曲线 Fig. 1 The step response curves of the first-order large-delay system | |
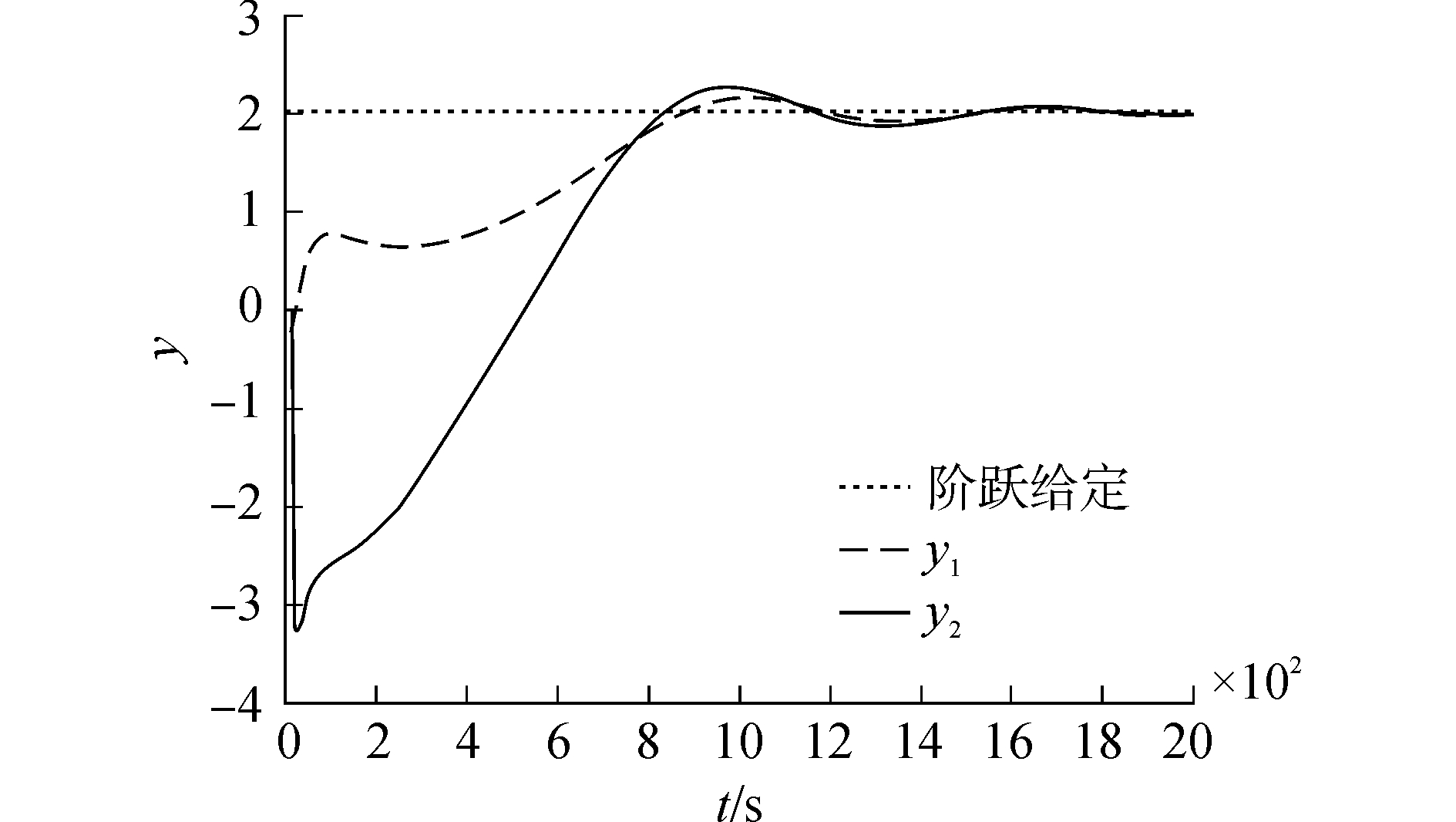
选取经典的双输入双输出大时滞系统Wood-Berry精馏塔模型[11]如式(26)作为仿真对象,使用本文设计的算法和基本MFAC算法进行仿真比较研究,本文所设计算法控制参数选择如下:η1=1.6,η2=1.6,μ11=1,μ12=1,μ21=1,μ22=1,仿真结果如图 2、3所示。通过仿真结果不难看出,两种算法都略有超调和震荡,但本文设计算法的响应速度和动态性能明显优于基本MFAC算法,并且能较好地达到控制要求。
|
Download:
|
| 图 2 基本MFAC算法阶跃响应曲线 Fig. 2 The step response curves of basic MFAC algorithm | |

|
Download:
|
| 图 3 本文算法阶跃响应曲线 Fig. 3 Step response curve of this algorithm | |
| $ \mathit{\boldsymbol{G}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {\frac{{12.8{{\rm{e}}^{ - s}}}}{{16.7s + 1}}}&{\frac{{ - 18.9{{\rm{e}}^{ - 3s}}}}{{21s + 1}}}\\ {\frac{{6.6{{\rm{e}}^{ - 7s}}}}{{10.9s + 1}}}&{\frac{{ - 19.4{{\rm{e}}^{ - 3s}}}}{{14.4s + 1}}} \end{array}} \right] $ | (26) |
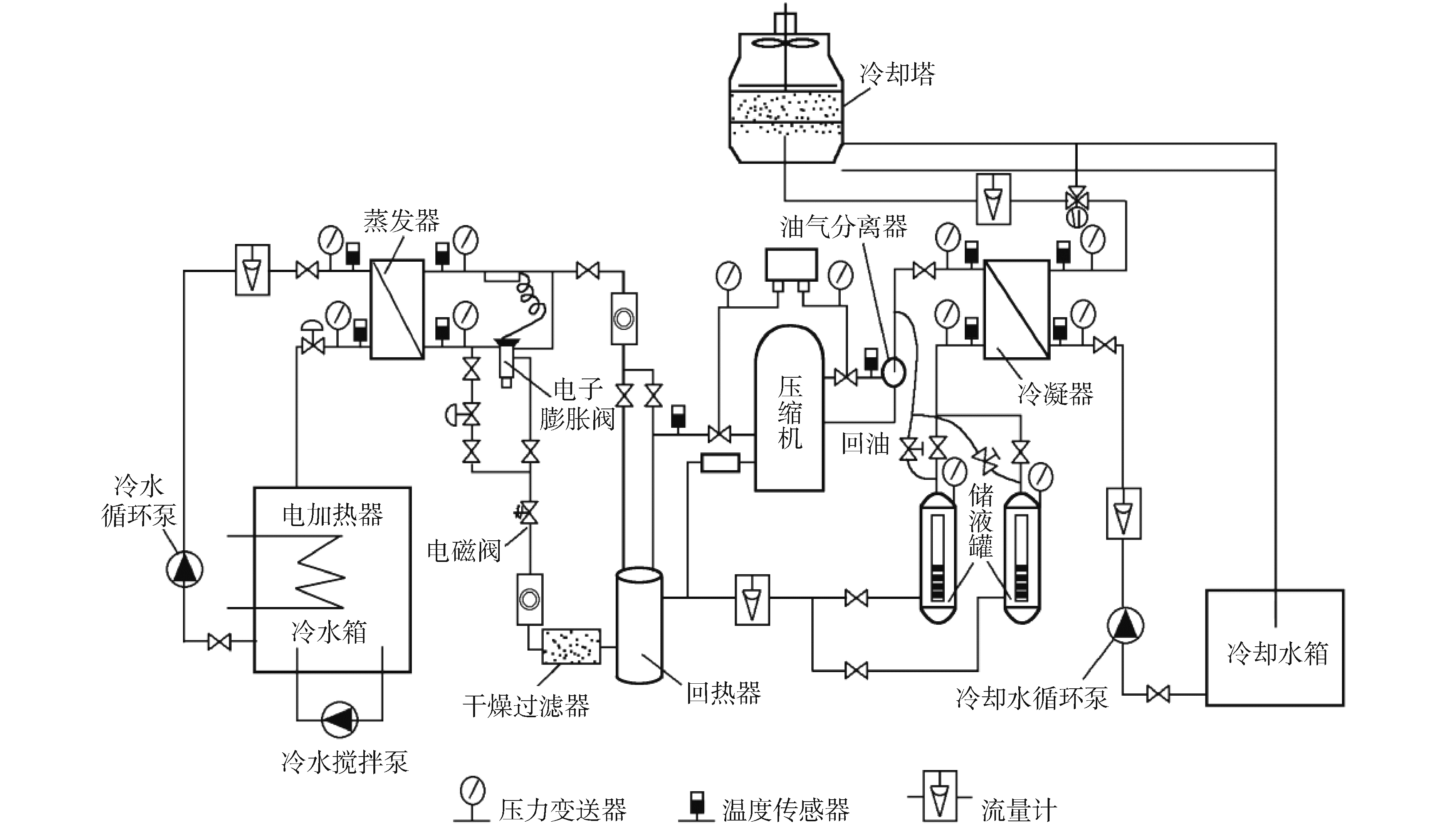
压缩式制冷系统实验平台[5]由电子膨胀阀、板式换热器、活塞式压缩机、气液热交换器、储液器等设备组成,系统装置如图 4所示。技术参数如下:蒸发器传热面积F=2.88 m2, 换热量30 kW;冷凝器传热面积F=3.02 m2, 换热量35 kW;回热器传热面积F=0.78 m2;压缩机功率7 460 N;冷却水泵扬程32 m,流量8.4 m3/h;冷冻水泵扬程27.4 m,流量7.8 m3/h;冷却水塔冷却能力35.17 kW;电子膨胀阀流量系数Kvs=0.63 m3/h, 制冷量74 kW;电加热器功率30 kW可调。
|
Download:
|
| 图 4 压缩式制冷系统装置 Fig. 4 Device of compression refrigeration system | |
基于最小二乘法的ARX模型,采用Matlab中的系统辨识工具箱进行辨识得到以压缩机频率、电子膨胀阀开度为输入,以蒸发温度、过热度为输出的制冷系统二阶传递函数矩阵,数学模型为
| $ \left[ {\begin{array}{*{20}{c}} {\Delta {T_s}}\\ {\Delta {T_e}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{ - 0.825}}{{38s + 1}}{{\rm{e}}^{ - 9s}}}&{\frac{{1.84}}{{35s + 1}}{{\rm{e}}^{ - 26s}}}\\ {\frac{{0.778}}{{35s + 1}}{{\rm{e}}^{ - 10s}}}&{\frac{{ - 0.752}}{{41s + 1}}{{\rm{e}}^{ - 28s}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {v_a}}\\ {\Delta f} \end{array}} \right] $ | (27) |
式中:ΔTs和ΔTe分别表示制冷剂过热度和制冷剂蒸发温度的变化量;Δva和Δf分别表示电子膨胀阀开度和压缩机频率的变化量。
4.2 制冷系统控制方案针对压缩式制冷系统辨识模型中的纯滞后环节及其强耦合的特性,将带有滞后时间输入变化率约束项的无模型自适应控制方法应用到控制方案中,制冷系统的整体控制方案如图 5所示。本文采用了恒定蒸发温度控制和变最小稳定过热度控制相结合的控制方案,一个回路是恒定蒸发温度控制,通过调节压缩机频率来控制蒸发温度;另一个回路是变最小过热度控制,通过调节电子膨胀阀使蒸发器过热度快速跟随给定。最小过热度设定值根据最小稳定过热度曲线查得, 最小稳定过热度曲线可根据文献[5]中的实验方法测取。

|
Download:
|
| 图 5 压缩式制冷系统无模型控制方案 Fig. 5 Model-free control scheme for compression refrigeration syste | |
制冷系统辨识模型在式(27)中给出,此辨识模型仅用于仿真时模拟实际系统产生输入输出数据,而不参与控制器的设计。分别使用本文设计的无模型控制算法和基本MFAC算法进行Matlab仿真比较研究:仿真1:过热度设定值阶跃变化(7 ℃变为8 ℃), 蒸发温度设定值不变,本文设计算法各控制参数选择如下:η1=1,η2=1,μ11=10,μ12=10,μ21=10,μ22=10;仿真2:过热度设定值不变, 蒸发温度设定值阶跃变化(5 ℃变为6 ℃)。本文设计算法各控制参数选择如下:η1=1.5,η2=1.5,μ11=8,μ12=8,μ21=8,μ22=8。不同控制算法作用下,制冷系统的过热度和蒸发温度的阶跃响应曲线分别在图 6、7中给出。

|
Download:
|
| 图 6 仿真1的过热度和蒸发温度阶跃响应曲线 Fig. 6 The superheat and the evaporation temperature step response curves in simulation 1 | |
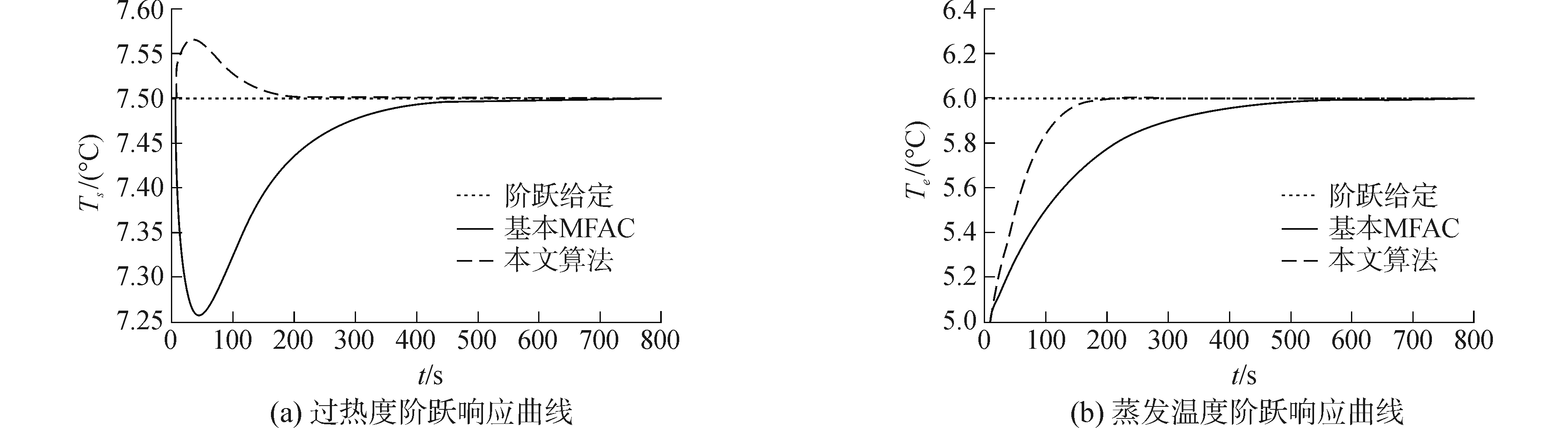
|
Download:
|
| 图 7 仿真2的过热度和蒸发温度阶跃响应曲线 Fig. 7 The superheat and the evaporation temperature step response curves in simulation 2 | |
从仿真图 6、7可以看出,制冷系统过热度阶跃响应曲线和蒸发温度阶跃响应曲线在两种算法控制下都很好地满足了控制要求,超调较小并且系统输出稳定,本文算法控制下的过热度和蒸发温度之间的耦合问题被大大削弱。图 6表明, 当跟踪过热度设定值时, 本文所提算法的控制作用下的实际过热度的调节时间明显减小; 图 7表明, 当跟踪蒸发温度设定值时, 本文所提算法的控制作用下的实际蒸发温度的调节时间明显减小。可见,本文控制方法使系统的动态性能显著提高。
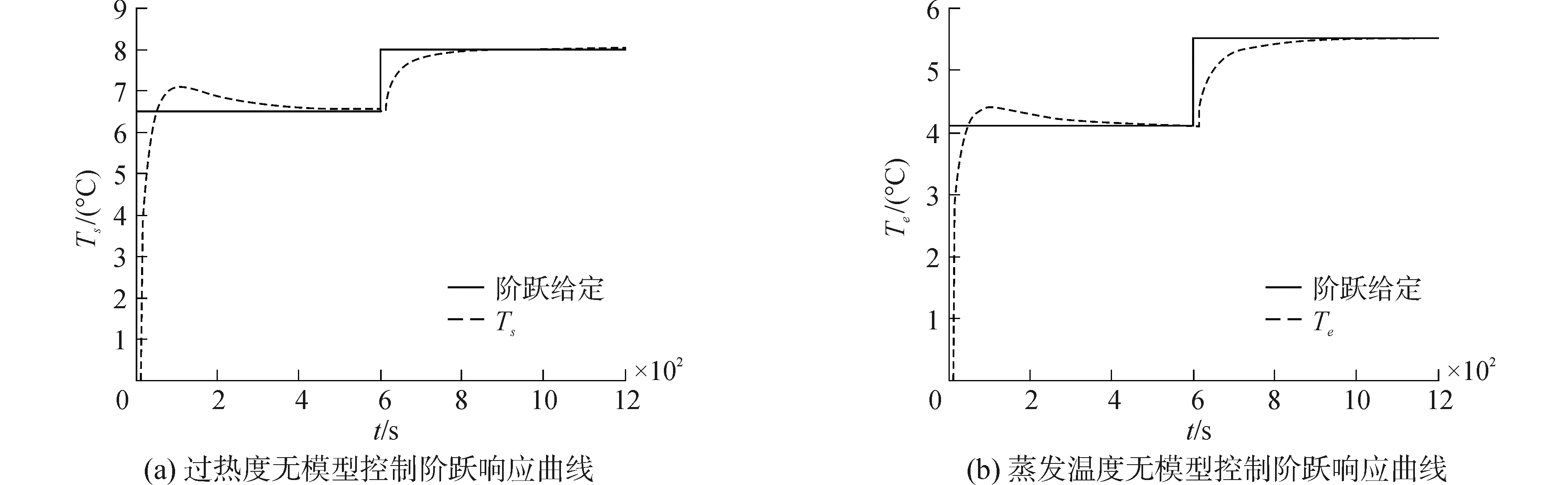
为了验证文中所提算法对于变化的给定信号的跟踪能力,本文引入了带有两次阶跃的给定信号,系统的响应曲线如图 8所示。控制参数选择如下:η1=1.2,η2=1.2,μ11=1,μ12=1,μ21=1,μ22=1。从仿真结果明显可以看出,文中所提算法控制下的制冷系统过热度和蒸发温度对于变化的给定信号具有很好的跟踪能力,系统输出稳定并且拥有良好的动态性能。无模型控制方法,能够很好地处理制冷系统纯滞后的问题, 提高了闭环系统的稳定性和动态性能。
|
Download:
|
| 图 8 制冷系统无模型控制阶跃响应 Fig. 8 Model-free control step response of refrigeration system | |
1) 选取典型的单输入单输出和双输入双输出大时滞系统进行了仿真实验。仿真结果表明,本文所设计的控制算法具有较小的超调,能在更短的时间内取得稳定的跟踪结果,输出稳定且动态性能良好。
2) 将无模型自适应控制算法应用到压缩式制冷系统控制器设计中,采用制冷系统二阶模型进行了控制方案的仿真验证。仿真结果表明,本文设计算法控制下的过热度和蒸发温度能够对于给定信号实现快速稳定的跟踪,并且对于变化的给定信号也具有良好的跟踪能力,缓解了系统的耦合问题,验证了控制算法的有效性。
本文工作是基于制冷系统的二阶传递函数矩阵建立的仿真实验,未来将在制冷机组实验平台上验证控制算法的有效性。本文将无模型自适应控制算法应用到压缩式制冷系统控制器设计中,有效缓解了传统PID方法在控制蒸发器过热度时动态性能差的现象。无模型控制算法避开了复杂的制冷系统不易建模、难以精确建模的问题,为更多难以建模的控制对象提供了控制思路。本文提出的带有滞后时间输入变化率约束项的无模型自适应控制方法具有良好的动态性能,在未来的工作中将继续研究其在更多复杂系统控制领域的应用。
| [1] |
WANG Xiaofeng, LI Xing, WANG Jianhui, et al. Data-driven model-free adaptive sliding mode control for the multi degree-of-freedom robotic exoskeleton[J]. Information sciences, 2016, 327: 246-257. DOI:10.1016/j.ins.2015.08.025 (  0) 0)
|
| [2] |
GIGLIO S, MAGGIORI M, STROEBEL J. No-Bubble condition:model-free tests in housing markets[J]. Econometrica, 2016, 84(3): 1047-1091. DOI:10.3982/ECTA13447 (  0) 0)
|
| [3] |
KALDMÄE A, CALIFANO C, MOOG C H. Integrability for nonlinear time-delay systems[J]. IEEE transactions on automatic control, 2016, 61(7): 1912-1917. DOI:10.1109/TAC.2015.2482003 (  0) 0)
|
| [4] |
金尚泰, 侯忠生. 一类非线性大滞后系统的改进无模型自适应控制[J]. 控制理论与应用, 2008, 25(4): 623-626. JIN Shangtai, HOU Zhongsheng. An improved model-free adaptive control for a class of nonlinear large-lag systems[J]. Control theory & applications, 2008, 25(4): 623-626. (  0) 0)
|
| [5] |
程保华.制冷系统动态建模及优化控制方法研究[D].天津: 天津大学, 2013. CHENG Baohua. Dynamic modeling of refrigeration sys-tem and research on optimization control method[D]. Tianjin: Tianjin University, 2013. (  0) 0)
|
| [6] |
OH J S, BINNS M, PARK S, et al. Improving the energy efficiency of industrial refrigeration systems[J]. Energy, 2016, 112: 826-835. DOI:10.1016/j.energy.2016.06.119 (  0) 0)
|
| [7] |
CHEN Jianyong, JARALL S, HAVTUN H, et al. A review on versatile ejector applications in refrigeration systems[J]. Renewable and sustainable energy reviews, 2015, 49: 67-90. DOI:10.1016/j.rser.2015.04.073 (  0) 0)
|
| [8] |
HU Kaiyong, ZHU Jialing, ZHANG Wei, et al. Effects of evaporator superheat on system operation stability of an organic Rankine cycle[J]. Applied thermal engineering, 2016, 111: 793-801. (  0) 0)
|
| [9] |
ZHU Yuanming, HOU Zhongsheng. Data-driven MFAC for a class of discrete-time nonlinear systems with RBFNN[J]. IEEE transactions on neural networks and learning systems, 2014, 25(5): 1013-1020. DOI:10.1109/TNNLS.2013.2291792 (  0) 0)
|
| [10] |
陈琛, 何小阳. 一种大时滞系统的无模型自适应控制改进算法[J]. 计算技术与自动化, 2012, 31(3): 10-13. CHEN Chen, HE Xiaoyang. An improved algorithm of model-free adaptive control for large time-delay system[J]. Computing technology and automation, 2012, 31(3): 10-13. DOI:10.3969/j.issn.1003-6199.2012.03.003 (  0) 0)
|
| [11] |
LIU Tao, ZHANG Weidong, GU Danying. Analytical multiloop PI/PID controller design for two-by-two processes with time delays[J]. Industrial & engineering chemistry research, 2005, 44(6): 1832-1841. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


