2. 智能康复装置与检测技术教育部工程研究中心, 天津 300130;
3. 国家康复辅具研究中心, 北京 100176
2. Engineering Research Center of Intelligent Rehabilitation, Ministry of Education, Tianjin 300130, China;
3. National Research Center for Rehabilitation Technical Aids, Beijing 100176, China
下肢外骨骼机器人是一种可穿戴的人机一体化装置,通过跟踪穿戴者的期望轨迹完成日常生活中的常见运动。外骨骼系统能够增强使用者的力量和耐力,可用于军事、医学、康复等不同领域。引起世界各国学者的广泛关注[1-2]。
建立面向控制的下肢外骨骼模型是对其进行稳定性控制的基础[3]。精确的模型可以很好的反映外骨骼系统的特性,从而设计相对应的控制系统;但过于复杂的模型将增大控制器设计的难度,反而可能影响控制效果[4]。下肢外骨骼模型具有非线性和强耦合的特点[5-6],其输入力矩包括穿戴者提供的主动力矩和机械结构提供的辅助力矩。在穿戴者是偏瘫患者的情况下,人的主动力矩只占极小的一部分,一般可以忽略[7]。但对于有一定行为能力的穿戴者来说,主动力矩在外骨骼的驱动力矩中占据很大的一部分,并且主动力矩具有不确定性,对主动力矩的处理是实现系统稳定的关键问题之一[8]。文献[9]仅利用系统的鲁棒性处理主动力矩的干扰,降低了系统的控制精度。文献[10]成比例地分配人机的力矩输入,但所构成的系统适用范围很小,不能很好地应对运行过程中的突发情况。文献[11]提出通过系统的运行状态构造观测器,估计穿戴者的主动力矩输入,但观测器仅设计膝关节的部分,未考虑髋关节部分主动力矩的输入影响,具有一定的局限性。
本文针对主动力矩不确定问题,对气动肌肉构建的下肢外骨骼系统进行动力学分析,建立面向控制的下肢外骨骼摆动相模型,反映各关节间的相互作用。通过设计干扰观测器估计穿戴者在摆动相提供的主动力矩,由此设计相应的滑模控制器。对控制系统进行稳定性证明,并利用实验平台对所设计系统进行了仿真验证。
1 基于拉格朗日的动力学建模相对于上肢而言,下肢运动具有明显的周期性特点,通过足底压力传感器,将整个步态周期分为摆动期和支撑期两个阶段。在摆动期过程中,通过控制气动肌肉充放气来模拟人体拮抗肌,驱动下肢外骨骼为穿戴者提供助力;在支撑期过程中,气动肌肉放气结束,保持最大长度,下肢外骨骼跟随穿戴者的运动,无需进行控制。为了建立面向控制的下肢外骨骼摆动期动力学模型,现将模型进行如下的处理[12]:
1) 对躯干部分和下肢系统共同建模会增加模型的复杂性,提高了控制器设计的难度。而躯干部分对下肢运动的影响无法忽略,因此对髋关节进行坐标设置。将髋关节的速度和加速度信息建立到模型中,利用髋关节信息作为干扰来代替躯干部分对下肢运动的影响。
2) 气动肌肉在控制过程中长度和质心位置都会发生变化。为了简化气动肌肉在下肢运动过程中造成的影响,假设气动肌肉在控制过程中可以完全跟随人的运动状态,利用腿部的两固定点间的距离代替气动肌肉的长度,并认为气动肌肉的质心始终在气动肌肉的中心位置。
通过以上处理,将外骨骼系统简化为图 1所示的连杆模型。取向前的方向为x轴正方向,向下的方向为y轴正方向,建立如图 1所示的坐标系及系统模型描述。

|
Download:
|
| 图 1 下肢外骨骼模型 Fig. 1 Lower extremity exoskeleton model | |
在图 1中,髋关节为p0,膝关节为p7,气动肌肉1分别与腰部和膝关节连接于p3和p5,气动肌肉2分别与大腿和小腿连接于p1和p9,大腿、小腿、气动肌肉1、气动肌肉2的质心依次为p2、p8、p4、p6。
运用拉格朗日动力学对图 1所示的外骨骼模型进行分析,得到系统的微分方程:
| $ \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\ddot \theta }} + \mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right)\mathit{\boldsymbol{\dot \theta }} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\theta }} \right) = \mathit{\boldsymbol{\tau }} + {\mathit{\boldsymbol{\tau }}_h} $ | (1) |
其中:
| $ \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{\theta }} \right) = \left[ {\begin{array}{*{20}{c}} {{F_{11}}}&{{F_{12}}}\\ {{F_{21}}}&{{F_{22}}} \end{array}} \right] $ |
| $ \begin{array}{*{20}{c}} {{F_{11}} = \frac{1}{4}r_5^2{m_3} + \frac{1}{3}\left( {{m_1}{l_2} + {m_2}{l_3}} \right) + \left( {l_2^2 + r_4^2} \right){m_4} + }\\ {\left[ {2{r_4}{l_2}{m_4} + \frac{1}{2}{r_5}\left( {{r_1} + {l_2}} \right){m_3}} \right]\cos {\theta _2} + \frac{1}{4}r_3^2 + }\\ {\frac{1}{4}\left( {{r_1} + {l_2}} \right)2{m_3}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{F_{12}} = - \frac{1}{4}{r_5}\left( {{r_1} + {l_2}} \right){m_3}\cos {\theta _1}\cos \left( {{\theta _2} - {\theta _1}} \right) - }\\ {{r_4}{l_2}{m_4}\cos {\theta _1}\cos \left( {{\theta _2} - {\theta _1}} \right) - }\\ {\frac{1}{4}r_5^2{m_3} - r_4^2{m_4} - \frac{1}{3}{m_2}{l_3}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{F_{21}} = - \frac{1}{4}{r_5}\left( {{r_1} + \frac{1}{2}} \right){m_3}\cos {\theta _1}\cos \left( {{\theta _2} - {\theta _1}} \right) - }\\ {{r_4}{l_2}{m_4}\cos {\theta _1}\cos \left( {{\theta _2} - {\theta _1}} \right) - }\\ {\frac{1}{4}r_5^2{m_3} - r_4^2{m_4} - \frac{1}{3}{m_2}{l_3}} \end{array} $ |
| $ {F_{22}} = \frac{1}{4}r_5^2{m_3} + r_4^2{m_4} + \frac{1}{3}{m_2}{l_3} $ |
| $ \mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right) = \left[ {\begin{array}{*{20}{c}} {{H_{11}}}&{{H_{12}}}\\ {{H_{21}}}&{{H_{22}}} \end{array}} \right] $ |
| $ \begin{array}{*{20}{c}} {{H_{11}} = {r_5}\left( {{r_1} + {l_2}} \right)\left( {\frac{1}{2}{m_2} + \frac{1}{4}{m_3}} \right)\sin \left( {2{\theta _1} - {\theta _2}} \right){{\dot \theta }_2} + }\\ {3{r_4}{l_2}{m_4}\sin \left( {2{\theta _1} - {\theta _2}} \right){{\dot \theta }_2}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{H_{12}} = \frac{1}{4}{r_5}\left( {{r_1} + {l_2}} \right){m_3}\cos {\theta _1}\sin \left( {{\theta _2} - {\theta _1}} \right){{\dot \theta }_2} + }\\ {{r_4}{l_2}{m_4}\cos {\theta _1}\sin \left( {{\theta _2} - {\theta _1}} \right){{\dot \theta }_2}} \end{array} $ |
| $ {H_{21}} = \left[ {\frac{1}{4}{r_5}\left( {{r_1} + {l_2}} \right){m_3} + {r_4}{l_2}{m_4}} \right]\sin \left( {2{\theta _1} - {\theta _2}} \right){{\dot \theta }_1} $ |
| $ \begin{array}{*{20}{c}} {{H_{22}} = \frac{1}{4}{r_5}\left( {{r_1} + {l_2}} \right){m_3}\cos {\theta _1}\sin \left( {{\theta _2} - {\theta _1}} \right){{\dot \theta }_1} + }\\ {{r_4}{l_2}{m_4}\cos {\theta _1}\sin \left( {{\theta _2} - {\theta _1}} \right){{\dot \theta }_1}} \end{array} $ |
| $ \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\theta }} \right) = {\left[ {\begin{array}{*{20}{c}} {{G_1}}&{{G_2}} \end{array}} \right]^{\rm{T}}} $ |
| $ \begin{array}{*{20}{c}} {{G_1} = \left\{ {\left[ {{m_1}{r_1} + \frac{1}{2}{r_3}{m_2} + \frac{1}{2}\left( {{r_1} + {l_2}} \right){m_3} + {l_2}{m_4}} \right]\cos {\theta _1} + } \right.}\\ {\left. {\left( {{r_4}{m_4} - \frac{1}{2}{r_5}{m_3}} \right)\cos \left( {{\theta _2} - {\theta _1}} \right)} \right\}{{\ddot x}_0} - }\\ {\left\{ {\left[ {{m_1}{r_1} + \frac{1}{2}{r_3}{m_2} + {l_2}{m_4} + \frac{1}{2}\left( {{r_1} + {l_2}} \right){m_3}} \right]\sin {\theta _1} + } \right.}\\ {\left. {\left( {{r_4}{m_4} + \frac{1}{2}{r_5}{m_3}} \right)\sin \left( {{\theta _2} - {\theta _1}} \right)} \right\}{{\ddot y}_0} - }\\ {\left( {{r_2}{m_1} + {l_2}{m_2}} \right)g\sin {\theta _1} + {r_4}{m_2}g\sin \left( {{\theta _2} - {\theta _1}} \right)} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{G_2} = - \left[ {\frac{1}{2}{r_5}{m_3}\cos \left( {{\theta _2} - {\theta _1}} \right) + {r_4}{m_4}\cos \left( {{\theta _2} - {\theta _1}} \right)} \right]{{\ddot x}_0} - }\\ {\left[ {\frac{1}{2}{r_3}{m_3}\sin \left( {{\theta _2} - {\theta _1}} \right) + {r_4}{m_4}\sin \left( {{\theta _2} - {\theta _1}} \right)} \right]{{\ddot y}_0} - }\\ {{r_4}{m_2}g\sin \left( {{\theta _2} - {\theta _1}} \right)} \end{array} $ |
式中:m1、m2、m3、m4依次为大腿、小腿和气动肌肉1、2的质量,l2、l3依次为大、小腿长度,l1为气动肌肉1与腰部连接点p3到髋关节p0的距离,r1为气动肌肉2与大腿连接点p1到髋关节p0的距离,r2为大腿质心p2到髋关节p0的距离,r3为气动肌肉1与大腿连接点p5到髋关节p0距离,r4为小腿质心p8到膝关节p7的距离,r5为气动肌肉2与小腿连接点p9到膝关节p7的距离, τ=[τ1 τ2]T为髋关节和膝关节的外骨骼力矩,τh=[τh1 τh2]T为髋关节和膝关节的穿戴者肌肉力矩,
基于下肢外骨骼模型设计相应的控制系统,针对主动力矩设计相应的干扰观测器,利用李雅普诺夫函数证明系统的稳定性。
2.1 控制系统设计通过数学模型可知,下肢外骨骼系统膝关节和髋关节具有非线性和强耦合的特点,因此对下肢外骨骼系统设计滑模控制器。
滑模控制与其他控制方法的不同之处在于,系统的结构不是固定的,而是可以在动态过程中根据系统当前状态有目的地不断变化,迫使系统按照预定滑动模态的状态轨迹运动,提高系统的鲁棒性和抗干扰能力[13]。
在下肢外骨骼系统控制过程中,将穿戴者提供的主动力矩作为一种干扰输入。由于滑模控制具有不连续性,仅利用系统的鲁棒性克服干扰容易产生抖振现象。本文通过设计干扰观测器,在滑模控制律中加入干扰估计值对干扰加以补偿,从而有效地降低抖振。根据下肢外骨骼系统和滑模变结构的特点,设计控制系统,如图 2所示。

|
Download:
|
| 图 2 系统控制框图 Fig. 2 System control block diagram | |
设d=τh,针对模型的特点设计非线性干扰观测器:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot z}} = \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\left( {\mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right) + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\theta }} \right) - \mathit{\boldsymbol{\tau }}} \right) - \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\hat d}}\\ \mathit{\boldsymbol{\hat d}} = \mathit{\boldsymbol{z}} + \mathit{\boldsymbol{p}}\left( {\mathit{\boldsymbol{\dot \theta }}} \right) \end{array} \right. $ | (2) |
| $ \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right) = {\mathit{\boldsymbol{A}}^{ - 1}}{\mathit{\boldsymbol{F}}^{ - 1}}\left( \mathit{\boldsymbol{\theta }} \right) $ | (3) |
| $ \mathit{\boldsymbol{p}}\left( {\mathit{\boldsymbol{\dot \theta }}} \right) = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{\dot \theta }} $ | (4) |
令
| $ {\mathit{\boldsymbol{A}}^{ - {\rm{T}}}} + {\mathit{\boldsymbol{A}}^{ - {\rm{1}}}} - {\mathit{\boldsymbol{A}}^{ - {\rm{T}}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{A}}^{ - {\rm{1}}}} \ge \xi \mathit{\boldsymbol{I}} $ | (5) |
式中
定义干扰观测器的观测误差为
| $ \mathit{\boldsymbol{\tilde d}} = \mathit{\boldsymbol{d}} - \mathit{\boldsymbol{\hat d}} $ | (6) |
对式(6)进行求导,并将式(2)代入,得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot {\tilde d}}} = \mathit{\boldsymbol{\dot d}} - \mathit{\boldsymbol{\hat d}} = \mathit{\boldsymbol{\dot d}} - \mathit{\boldsymbol{\dot z}} - \mathit{\boldsymbol{\dot p}}\left( {\mathit{\boldsymbol{\dot \theta }}} \right) = }\\ {\mathit{\boldsymbol{\dot d}} - \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\left( {\mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }}} \right)\mathit{\boldsymbol{\dot \theta }} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\theta }} \right) - \mathit{\boldsymbol{\tau }}} \right) + \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\hat d}} - }\\ {\mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{\theta }} \right)\ddot \theta = }\\ {\mathit{\boldsymbol{\dot d}} + \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\hat d}} - \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{d = }}}\\ {\mathit{\boldsymbol{\dot d}} - \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\tilde d}}} \end{array} $ | (7) |
假设相对于干扰观测器,动态特性干扰的变化是缓慢的,即
| $ \mathit{\boldsymbol{\dot {\tilde d}}} + \mathit{\boldsymbol{L}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\tilde d}} = 0 $ | (8) |
将式(3)代入式(8),得
| $ \begin{array}{l} \mathit{\boldsymbol{\dot {\tilde d}}} = - {\mathit{\boldsymbol{A}}^{ - 1}}{\mathit{\boldsymbol{F}}^{ - 1}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\tilde d}}\\ {{\mathit{\boldsymbol{\dot {\tilde d}}}}^{\rm{T}}} = - {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}{\mathit{\boldsymbol{F}}^{ - {\rm{T}}}}\left( \mathit{\boldsymbol{\theta }} \right){\mathit{\boldsymbol{A}}^{ - {\rm{T}}}} \end{array} $ | (9) |
在外骨骼设计中,为了尽量减小外骨骼对人体的负担,要求m3和m4小于穿戴者大小腿的质量,则F为正定阵,设计系统的Lyapunov函数为
| $ {V_o} = {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{A\tilde d}} $ | (10) |
对式(10)进行求导,并代入式(9),得
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot V}}}_o} = {{\mathit{\boldsymbol{\dot {\tilde d}}}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{A\tilde d}} + {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\dot F}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{A\tilde d}} + }\\ {{{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{A\dot {\tilde d}}} = - {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {\mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\dot F}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)\mathit{\boldsymbol{\tilde d}}} \end{array} $ | (11) |
构造不等式:
| $ \mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\dot F}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{A}}^{\rm{T}}} \ge \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} $ | (12) |
式中,Γ>0为实对称正定阵,存在Γ′,有
| $ {{\tilde V}_o} \le - {{\mathit{\boldsymbol{\tilde d}}}^T}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \tilde d}} = - \mathit{\boldsymbol{ \boldsymbol{\varGamma} '}}{V_o} $ | (13) |
式中Γ′>0。由式(8)可得观测器误差方程解为
| $ \mathit{\boldsymbol{\tilde d}}\left( t \right) = \mathit{\boldsymbol{\tilde d}}\left( {{t_0}} \right)\exp \left( { - \mathit{\boldsymbol{L}}\left( \theta \right) \cdot t} \right) $ | (14) |
通过以上的稳定性分析可知,干扰观测器指数收敛,收敛精度取决于参数Γ,Γ值越大,收敛速度越快,精度越高。
2.3 滑模控制律设计设关节的理想角度为θd,跟踪误差为e=θ-θd,定义滑模函数为
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} e}} $ | (15) |
式中,
设计系统的滑模控制器为
| $ \begin{array}{l} \mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{F}}{{\mathit{\boldsymbol{\ddot \theta }}}_d} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} F}}{{\mathit{\boldsymbol{\dot \theta }}}_d} - \mathit{\boldsymbol{ \boldsymbol{\varLambda} F\dot \theta }} + \mathit{\boldsymbol{H}}{{\mathit{\boldsymbol{\dot \theta }}}_d} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} H}}{\mathit{\boldsymbol{\theta }}_d} - \\ \;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varLambda} H\theta }} + \mathit{\boldsymbol{G}} - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\hat d}} \end{array} $ | (16) |
式中:
对式(15)求导,然后将式(16)代入
| $ \mathit{\boldsymbol{F\dot s}} = - \mathit{\boldsymbol{Hs}} - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\mathit{\boldsymbol{s}} + \mathit{\boldsymbol{\tilde d}} $ | (17) |
设计闭环系统的Lyapunov函数为
| $ V = {V_o} + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Fs}} $ | (18) |
由于干扰观测器指数收敛,则
| $ \begin{array}{*{20}{c}} {\dot V = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{F\dot s}} + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Fs + }}{{\dot V}_o} = }\\ {{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( { - \mathit{\boldsymbol{Hs}} - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\mathit{\boldsymbol{s}} + \mathit{\boldsymbol{\tilde d}}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Fs + }}{{\dot V}_o} = }\\ { - \mathit{\boldsymbol{\eta }}\left\| \mathit{\boldsymbol{s}} \right\| - {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\tilde d}} + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\dot F}} - 2\mathit{\boldsymbol{H}}} \right)\mathit{\boldsymbol{s}} + {{\dot V}_o} = }\\ { - \mathit{\boldsymbol{\eta }}\left\| \mathit{\boldsymbol{s}} \right\| - {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\tilde d}} + \frac{1}{2}{{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\dot F}} - 2\mathit{\boldsymbol{H}}} \right)\mathit{\boldsymbol{\tilde d}} \le 0} \end{array} $ | (19) |
令
| $ - \mathit{\boldsymbol{\eta }}\left\| s \right\| - {s^{\rm{T}}}\mathit{\boldsymbol{\tilde d}} \equiv 0 $ | (20) |
| $ {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\dot F}} - 2\mathit{\boldsymbol{H}}} \right)\mathit{\boldsymbol{\tilde d}} \equiv 0 $ | (21) |
从而s≡0,
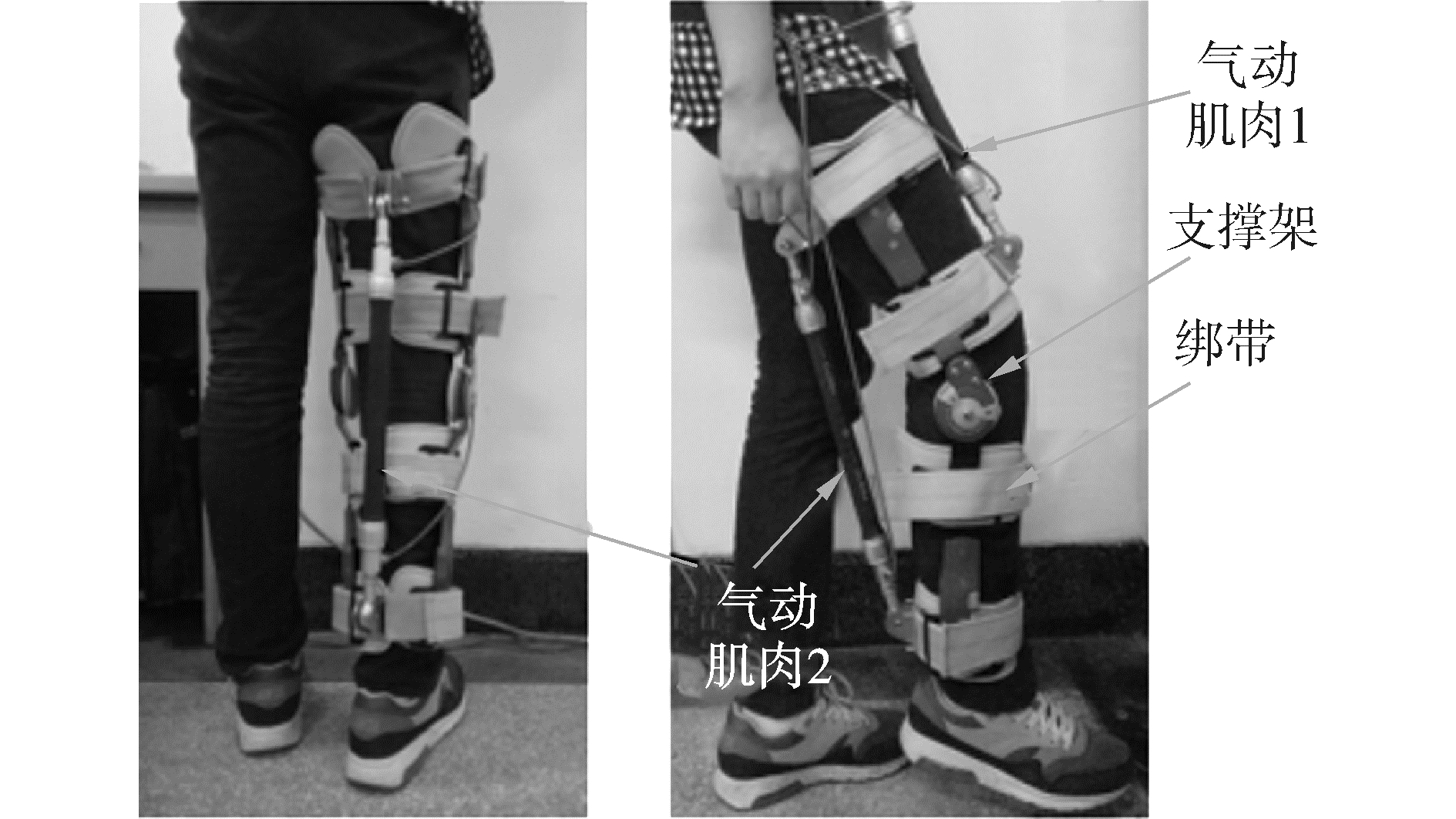
为验证所设计闭环系统的性能,对其进行仿真验证。取中国男生的平均身高l=1.75 m和平均体重m=60 kg作为模型的参数输入,根据文献[14]中公布的数据得到相应的人体参数,确定图 3所示的下肢外骨骼系统模型中与穿戴者有关的大小腿质量和长度、外骨骼穿戴位置等参数,与外骨骼自身长度和质量参数,在表 1中一起列出。
|
Download:
|
| 图 3 下肢外骨骼实验装置 Fig. 3 The experimental device of lower limb exoskeleton | |
| 表 1 外骨骼系统主要参数 Table 1 Main parameters of exoskeleton system |
将表 1中参数代入下肢外骨骼模型式(1)得到式(1)各项的具体形式为
| $ {F_{11}} = 2.007\;1 + 0.209\;6\cos {\theta _2} $ |
| $ {F_{12}} = - 0.346\;6 - 0.104\;8\cos {\theta _1}\cos \left( {{\theta _2} - {\theta _1}} \right) $ |
| $ {F_{21}} = - 0.346\;6 - 0.104\;8\cos {\theta _1}\cos \left( {{\theta _2} - {\theta _1}} \right) $ |
| $ {F_{22}} = 0.346\;6 $ |
| $ {H_{11}} = 0.420\;6\sin \left( {2{\theta _1} - {\theta _2}} \right){{\dot \theta }_2} $ |
| $ {H_{12}} = 0.104\;8\cos {\theta _1}\sin \left( {{\theta _2} - {\theta _1}} \right){{\dot \theta }_2} $ |
| $ {H_{21}} = 0.104\;8\sin \left( {2{\theta _1} - {\theta _2}} \right){{\dot \theta }_1} $ |
| $ {H_{22}} = 0.104\;8\cos {\theta _1}\sin \left( {{\theta _2} - {\theta _1}} \right){{\dot \theta }_1} $ |
| $ \begin{array}{*{20}{c}} {{G_1} = \left[ {2.092\;7\cos {\theta _1} + 0.201\;6\cos \left( {{\theta _2} - {\theta _1}} \right)} \right]{{\ddot x}_0} - }\\ {\left[ {1.502\;6\sin {\theta _1} - 0.291\;4\sin \left( {{\theta _2} - {\theta _1}} \right)} \right]{{\ddot y}_0} - }\\ {29.065\;3\sin {\theta _1} + 3.583\;0\sin \left( {{\theta _2} - {\theta _1}} \right)} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{G_2} = - 0.291\;4\cos \left( {{\theta _2} - {\theta _1}} \right){{\ddot x}_0} - 0.321\;6\sin \left( {{\theta _2} - } \right.}\\ {\left. {{\theta _1}} \right){{\ddot y}_0} - 3.583\;0\sin \left( {{\theta _2} - {\theta _1}} \right)} \end{array} $ |
在摆动相过程,角度的变化与力矩的输入线性相关,因此假设主动力矩干扰模型为d(θ)=kθ,将该模型作为实际干扰的输入,其中k=[k1 k2]。考虑各关节的动态特性,设髋关节系数k1=2,膝关节系数k2=1,θ=[θ1 θ2]T为髋关节和膝关节的期望角度,是通过采集人体平地行走过程中的实际关节角度得到。
3.2 仿真实验结果干扰观测器采用式(2)~(4)的形式,为了保证观测效果,取主动干扰力矩[0.5 0.05]T作为实际干扰的初始输入。根据
控制器的形式如式(16)所示,采用饱和函数代替连续函数,取边界层厚度为0.2。系数矩阵为

|
Download:
|
| 图 4 髋关节和膝关节的跟随效果 Fig. 4 Tracking effects of hip and knee joints | |
|
Download:
|
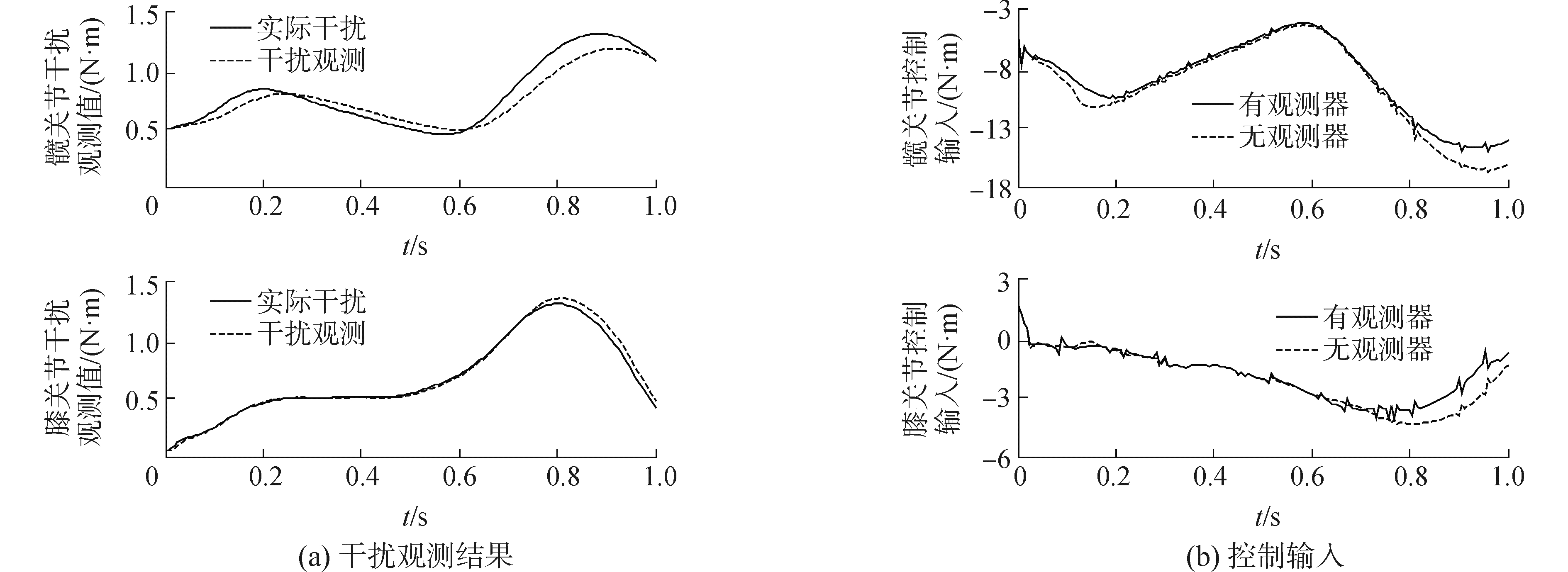
| 图 5 控制系统仿真结果 Fig. 5 Control system simulation results | |
由图 5(a)可以看出,干扰观测器对干扰具有良好的观测能力。由图 4可以看出,在有初始设置误差且干扰较小的情况下,两种方法均可消除误差并跟随关节角度和角速度的变化。但是如主动力矩的干扰增大,无观测器的控制方法不再能很好地跟随角度的变化趋势,运行轨迹误差明显,并随着干扰的增大而增大;而增加干扰观测器的控制器仍可很好地跟随期望轨迹的变化,说明干扰观测器可以为控制器提供必要的补偿,从而使整个闭环系统具有更好的跟随能力。得到髋关节和膝关节相应的控制器输入(即控制器输出)如图 5(b)所示,由于干扰观测器对控制器进行了补偿,从而减小了控制器的输出,避免控制器输出因为变化幅度太大调整不及时造成控制误差。
3.3 实物验证利用图 3所示的装置进行实物仿真实验,进一步验证控制方法的可行性。本文首先根据仿真实验数据,经过离线计算得到气动肌肉的控制量,进而进行开环验证实验,式(22)~(26)为气动肌肉控制量转化公式。
气动肌肉的力学表达特性[15]为
| $ \mathit{\boldsymbol{P}} = \left( {\mathit{\boldsymbol{F}} + 168} \right)/\left( {289 - 1\;528\varepsilon + 2\;468{\varepsilon ^2}} \right) $ | (22) |
式中:P为气动肌肉内气体的压强,ε为气动肌肉的收缩率,气动肌肉1的收缩率与髋关节角度的关系为
| $ {\varepsilon _1} = 1 - \sqrt {5.151\;2 + 3.498\;0\cos {\theta _1}} $ | (23) |
气动肌肉2的收缩率与膝关节角度的关系为
| $ {\varepsilon _2} = 1 - \sqrt {0.504\;8 + 0.495\;3\cos {\theta _2}} $ | (24) |
气动肌肉1为大腿提供的力矩与力的关系:
| $ {F_1} = \frac{{{\tau _1}}}{{\sin \beta \sqrt {1.01 + b\cos {\theta _1}} }} $ | (25) |
| $ \beta = {\theta _1} - \arctan \frac{{a\sin {\theta _1}}}{{0.1 + a\cos {\theta _1}}} $ |
气动肌肉2为大腿提供的力矩与力的关系:
| $ {F_2} = {\tau _2}/\left( {c + a\cos {\theta _2}} \right) $ | (26) |
式中:a=0.342 8, b=0.685 6, c=0.282 4。
将仿真系统得到的力矩转化为压强输入到气动肌肉中,利用角度传感器测量髋关节与膝关节角度,与期望轨迹相比较,验证控制算法的有效性。如图 6所示,外骨骼系统可以很好地跟随期望轨迹的变化,进一步证明了控制方案的有效性。

|
Download:
|
| 图 6 模拟实验结果 Fig. 6 Simulated experimental results | |
1) 对由气动肌肉组建的下肢外骨骼做了一系列合理的假设,利用拉格朗日原理对下肢外骨骼进行了动力学分析,然后建立面向控制的动力学模型,仿真验证证明,该模型可以很好地反映下肢外骨骼的动力学特性,为外骨骼建模提供一定思路。
2) 利用干扰观测器对下肢行走过程中,由穿戴者提供的主动力矩进行估计,并对控制器进行相应的补偿,从而提升外骨骼的抗干扰能力。并通过设计相应的仿真实验和实物实验,验证了控制算法的有效性,干扰观测器可以有效解决主动力矩的不确定性。
虽然进行了一定的硬件实验验证,但是由于外骨骼硬件设备的不足,可完成动作的幅度具有一定的局限性,致使髋关节与膝关节角度的运动趋势与仿真实验一致,但最大角度均明显偏小。下一步的研究重点是优化外骨骼机构设计,为控制算法验证提供更优越的硬件平台。
| [1] |
HUO Weiguang, MOHAMMED S, MORENO J C, et al. Lower limb wearable robots for assistance and rehabilitation:a state of the art[J]. IEEE systems journal, 2016, 10(3): 1068-1081. DOI:10.1109/JSYST.2014.2351491 (  0) 0)
|
| [2] |
YOUNG A J, FERRIS D P. State of the art and future directions for lower limb robotic exoskeletons[J]. IEEE transactions on neural systems and rehabilitation engineering, 2017, 25(2): 171-182. DOI:10.1109/TNSRE.2016.2521160 (  0) 0)
|
| [3] |
TSAI A C, LUH J J, LIN T T. A novel STFT-ranking feature of multi-channel EMG for motion pattern recognition[J]. Expert systems with applications, 2015, 42(7): 3327-3341. DOI:10.1016/j.eswa.2014.11.044 (  0) 0)
|
| [4] |
贾山, 韩亚丽, 路新亮, 等. 基于人体特殊步态分析的下肢外骨骼机构设计[J]. 机器人, 2014, 36(4): 392-401, 410. JIA Shan, HAN Yali, LU Xinliang, et al. Design of lower extremity exoskeleton based on analysis on special human gaits[J]. Robot, 2014, 36(4): 392-401, 410. (  0) 0)
|
| [5] |
MEFOUED S. A second order sliding mode control and a neural network to drive a knee joint actuated orthosis[J]. Neurocomputing, 2015, 155: 71-79. DOI:10.1016/j.neucom.2014.12.047 (  0) 0)
|
| [6] |
ZHU Yanhe, CUI Jinxiang, ZHAO Jie. Biomimetic design and biomechanical simulation of a 15-DOF lower extremity exoskeleton[C]//IEEE International Conference on Robotics and Biomimetics. Shenzhen, China, 2013: 1119-1124.
(  0) 0)
|
| [7] |
隋立明, 张立勋. 气动肌肉驱动步态康复训练外骨骼装置的研究[J]. 哈尔滨工程大学学报, 2011, 32(9): 1244-1248. SUI Liming, ZHANG Lixun. Development of an actuated exoskeleton with pneumatic muscles for gait rehabilitation training[J]. Journal of Harbin Engineering University, 2011, 32(9): 1244-1248. DOI:10.3969/j.issn.1006-7043.2011.09.026 (  0) 0)
|
| [8] |
NAGARAJAN U, AGUIRRE-OLLINGER G, GOSWAMI A. Integral admittance shaping:a unified framework for active exoskeleton control[J]. Robotics and autonomous systems, 2016, 75: 310-324. DOI:10.1016/j.robot.2015.09.015 (  0) 0)
|
| [9] |
LIU Yanjun, GAO Ying, TONG Shaocheng, et al. Fuzzy approximation-based adaptive backstepping optimal control for a class of nonlinear discrete-time systems with dead-zone[J]. IEEE transactions on fuzzy systems, 2016, 24(1): 16-28. DOI:10.1109/TFUZZ.2015.2418000 (  0) 0)
|
| [10] |
杨秀霞, 杨晓冬, 王亭, 等. 下肢携行外骨骼系统建模及控制[J]. 舰船电子工程, 2016, 36(4): 45-48. YANG Xiuxia, YANG Xiaodong, WANG Ting, et al. Model and control of lower extreme exoskeleton system[J]. Ship electronic engineering, 2016, 36(4): 45-48. DOI:10.3969/j.issn.1672-9730.2016.04.012 (  0) 0)
|
| [11] |
MOHAMMED S, HUO Weiguang, HUANG Jian, et al. Nonlinear disturbance observer based sliding mode control of a human-driven knee joint orthosis[J]. Robotics and autonomous systems, 2016, 75: 41-49. DOI:10.1016/j.robot.2014.10.013 (  0) 0)
|
| [12] |
丛德宏, 徐心和. 磁流变液智能假腿的摆动相控制[J]. 系统仿真学报, 2006, 18(Z2): 916-918, 922. CONG Dehong, XU Xinhe. Swing phase control of intelligent lower limb prosthesis using magnetorheological fluid damper[J]. Journal of system simulation, 2006, 18(Z2): 916-918, 922. DOI:10.3969/j.issn.1004-731X.2006.z2.260 (  0) 0)
|
| [13] |
刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407-418. LIU Jinkun, SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control theory & applications, 2007, 24(3): 407-418. (  0) 0)
|
| [14] |
刘静民.中国成年人人体惯性参数国家标准的制定[D].北京: 北京体育大学, 2004. LIU Jingmin. Establishment of national standard about inertial parameters of Chinese adults[D]. Beijing: Beijing Sport University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10043-2004134368.htm (  0) 0)
|
| [15] |
ANDRIKOPOULOS G, NIKOLAKOPOULOS G, MANESIS S. Novel considerations on static force modeling of pneumatic muscle actuators[J]. IEEE/ASME transactions on mechatronics, 2016, 21(6): 2647-2659. DOI:10.1109/TMECH.2016.2585503 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


