2. 齐齐哈尔大学 机电工程学院, 黑龙江 齐齐哈尔 161006;
3. 国网黑龙江省电力有限公司 经济技术研究院, 黑龙江 哈尔滨 150036
2. College of Mechanical Engineering, Qiqihar University, Qiqihar 161006, China;
3. Economic Research Institute, State Grid Heilongjiang Electric Power Company Limited, Harbin 150036, China
无人水下航行器(unmanned underwater vehicle,UUV)在现代海洋环境中扮演着越来越重要的角色,在真实的海洋环境下受到很多不确定因素的影响[1],如执行任务的变化、海洋环境的变化以及各种威胁的变化等,因此需要UUV在这种复杂的海洋环境下具备一定的自主决策能力,最主要的技术难点是自主决策模型适应动态变化的海洋环境态势。UUV在海洋环境的自主决策过程中,对海洋环境及自身状态进行威胁评估可以促进自主决策水平的提高,一方面,对海洋环境及自身状态的评估有助于更加快地感知海洋环境态势,提高自主决策的实时性;另一方面,对海洋环境及自身状态的评估可以增强对海洋环境态势的理解,提高自主决策的正确性,从而更好地将信息优势转化为决策优势。
国内外学者对威胁评估已经进行了许多探索性的研究,主要的理论方法有:灰色关联法[2-3]、层次分析法[4]、多属性决策理论[5]、模糊逻辑方法[6]、贝叶斯网络等。国外的威胁评估技术在理论研究和应用方面等发展比国内更趋于成熟,据公开发表的文献,美国开发出包括美国陆军分析系统TCAC(Technical Control and Analysis Center)、战场管理和目标检测系统BETA(Battle field Exploitation and Target Acquisition system)等比较好的原型系统;英国开发出IKBS(Intelligent Knowledge-Based Systems),用于本国军舰传感器与无线数据链及信号情报融合;南非研制出威胁估计系统Future,用来辅助海军检测周围海域的威胁事件;加拿大利用模糊理论,贝叶斯网络等研制出TADMUS(tactical decision making under stress)系统。在以上理论中基于贝叶斯网络(Bayesian network,BN)理论在对不完全、不精确、不确定信息进行推理时具有重要优势,贝叶斯网络推理方法不仅应用在推理预测中[7],还可以应用于战场的态势估计中。目前利用静态BN进行战场态势估计的算法难以适应战场环境的动态变化[8-9];虽然在态势估计应用方面,利用动态贝叶斯网络(dynamic bayesian network,DBN)能适应复杂环境的动态变化,但是由专家给出相应的网络参数,在推理的整个过程中参数保持不变,不能随环境的变化而发生变化,所以无法保证推理结果的准确性和实时性[10-12]。现阶段针对DBN参数学习方法的研究不多,大多数应用常用的EM算法,由于EM算法具有极易收敛到局部以及收敛速度慢的缺点,所以针对大样本条件下网络参数学习的问题,很难达到网络参数学习实时性的要求。
本文设计基于动态贝叶斯网络的威胁评估模型以及决策推理模型,采用遗传算法实现了离散动态贝叶斯网络参数学习,模型网络参数的最大似然估计函数作为遗传算法的适应度函数,最终获得优良的网络参数,进而加强模型对海洋环境的快速适应的能力。
1 任务描述与动态贝叶斯网络构建 1.1 任务决策需求假设UUV在执行任务时经过相关海域从起点到目的点,受到海洋环境变化、自身状态变化以及其他未知变化的影响,这些影响会威胁到UUV的航行安全。有必要对UUV进行威胁评估,由于UUV的威胁评估受到众多的因素制约和限制,这里只考虑一些简化情形,即UUV任务决策模型由自身危险以及海洋环境威胁为主,自身危险包括UUV传感器失灵、漏水检测、能源监测、卡舵、推进器故障等;海洋环境威胁包括海流、障碍物、海底地形、海水密度等。
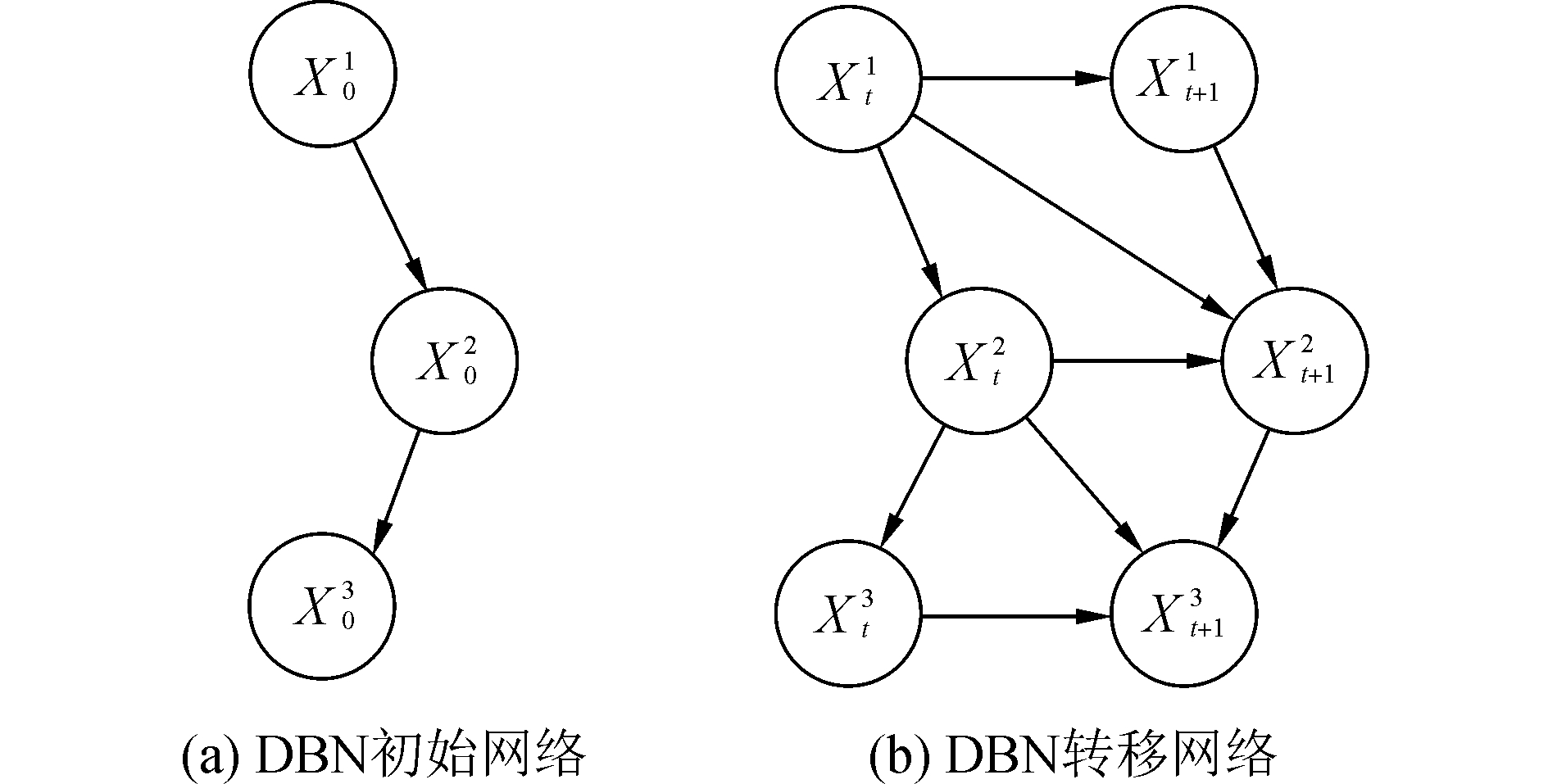
1.2 动态贝叶斯网络构建给出动态贝叶斯网络(DBN)的数学定义[13-14]:一个DBN可以定义为(B1, B→),其中B1表示最初的BN,即先验网络,图 1中任一节点的先验概率为P(X1),B→表示由两个以上时间片段的BN组成的图形。若用P(Xt|Xt-1)表示已知任一变量t-1时刻状态时,t时刻状态发生的概率,Xti表示第i个变量t时刻的取值,Pa(Xti)为其父节点。N表示有N个变量存在。当只有两个时间片段(2TBN)时,有
|
Download:
|
| 图 1 DBN表示图 Fig. 1 DBN representation | |
| $ P\left( {{X_t}|{X_{t - 1}}} \right) = \prod\limits_{i = 1}^N P \left( {X_t^i|Pa\left( {X_t^i} \right)} \right) $ | (1) |
同样可以得出动态贝叶斯网络中任一节点的联合分布概率:
| $ \begin{array}{c} P\left( {X_{1:T}^{\left( {1:N} \right)}} \right) = \prod\limits_{i = 1}^N {{P_{{B_1}}}} \left( {X_1^i|Pa\left( {X_1^i} \right)} \right) \times \\ \prod\limits_{t = 2}^T {\prod\limits_{i = 1}^N {{P_{B \to }}} \left( {X_t^i|Pa\left( {X_t^i} \right)} \right)} \end{array} $ | (2) |
利用DBN进行UUV威胁评估时,首先必须解决网络的构建问题。网络模型的构建主要是围绕海洋环境及自身状态的事件展开,有三个部分:确定网络的节点变量;建立网络的威胁模型;对各节点进行概率分配,即完成参数学习。
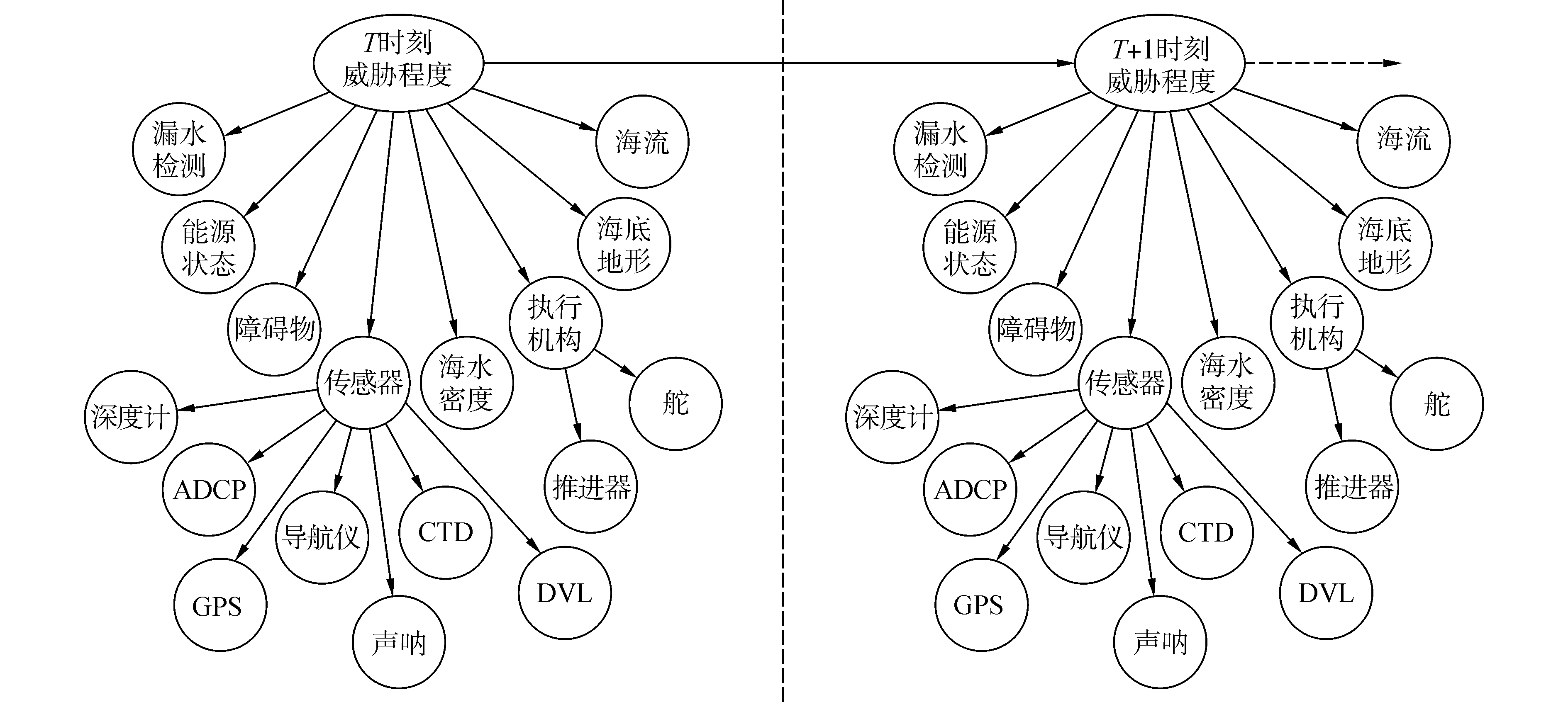
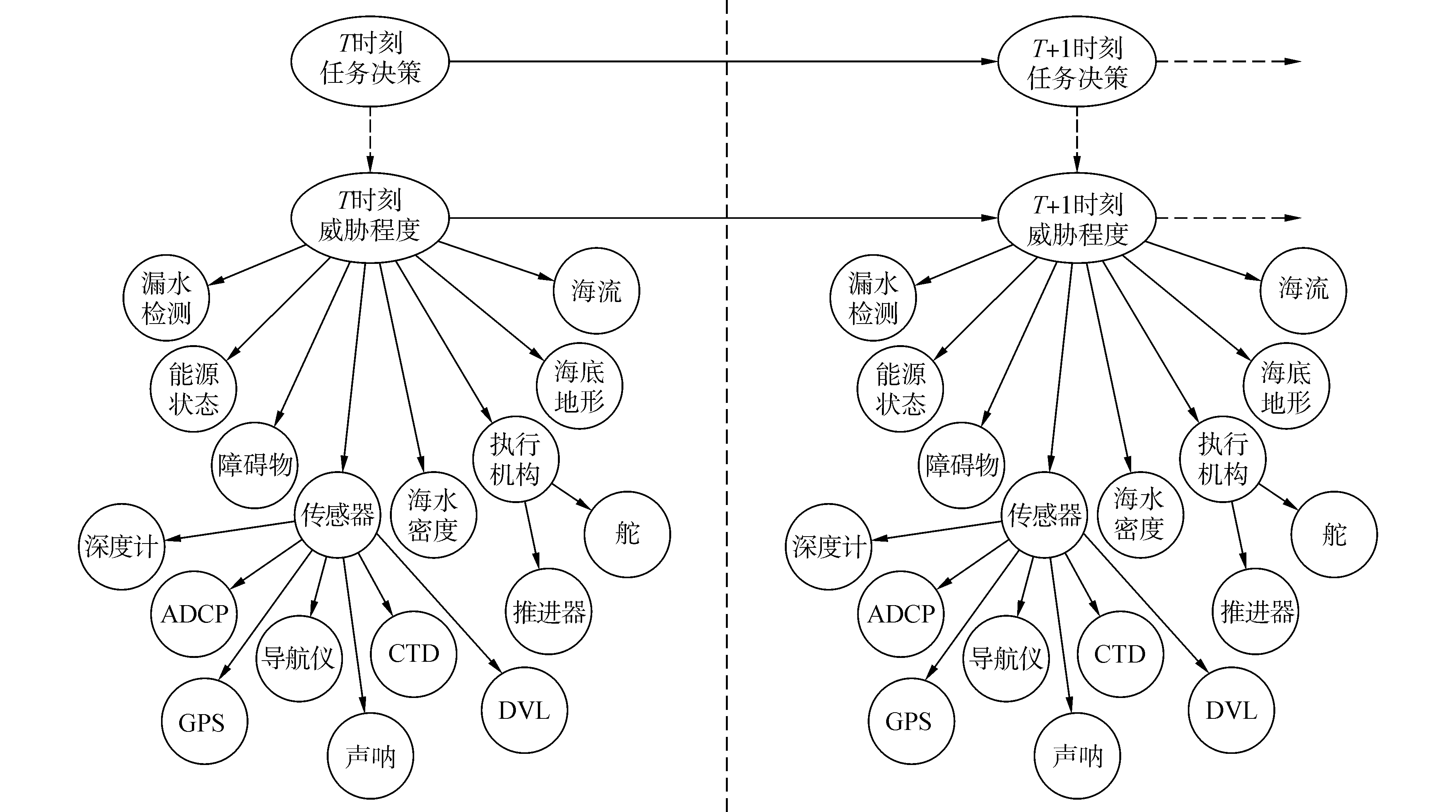
本文采用专家知识来建立UUV威胁评估动态贝叶斯网络模型,如图 2所示,图中的贝叶斯网络按照时间轴展开。其中威胁程度是隐变量,其他变量是可观测的。威胁程度节点表示UUV威胁评估的全局态势,最下面的可观测节点表示影响UUV威胁评估的海洋环境事件和自身状态事件,事件来源于UUV携带传感器所获得的数据和UUV自身的状态信息。连接各节点之间的有向弧表示节点间的因果关系,其依赖强度用条件概率表来描述。根据构建的威胁评估模型,通过自底向上的推理,逐级达到对海洋环境、自身状态发生事件的识别,进而获得对UUV威胁程度的感知,为UUV自主决策提供依据,最后给出UUV决策推理模型,如图 3所示。
|
Download:
|
| 图 2 基于动态贝叶斯网络的UUV威胁估计模型 Fig. 2 Threat estimation model of UUV based on dynamic Bayesian network | |
|
Download:
|
| 图 3 基于动态贝叶斯网络的UUV决策推理模型 Fig. 3 Decision reasoning model of UUV based on dynamic Bayesian network | |
对于海洋环境和自身状态事件来说,当处于不同情况时,事件对UUV的威胁程度也是不一样的。图 3中网络模型各节点的状态集合分别定义为:任务决策R(t)={忽略,处理威胁}为UUV做出的决策;威胁程度W(t)={高,低}。假如UUV以4 kn的速度巡航,当前视声呐测得UUV与障碍物之间距离小于50 m时,视为威胁程度高,距离大于50 m时,视为威胁程度低,即定义障碍物Z(t)={高,低}为UUV受到的威胁程度的状态;海流对UUV的影响也非常大,当海流流向与UUV的航向相反或偏差较大时,或海流速度大于5 kn时,航迹会改变,则视为威胁程度高,否则视为威胁程度低,即定义海流L(t)={高,低}为海流对UUV的威胁程度的状态,海底地形D(t)={高,低}为海底地形对UUV的威胁程度,海水密度M(t)={高,低}为海水密度对UUV的威胁程度;传感器包括深度计、GPS、声呐、ADCP、导航仪、CTD,DVL,即可以定义传感器C(t)={正常,故障}为传感器工作的状态,漏水检测J(t)={正常,漏水}为UUV漏水的程度;执行机构包括舵和推进器,即执行机构Q(t)={正常,故障}为UUV执行机构的工作状态,能源状态N(t)={充足,不足}为UUV的能源状态。威胁评估模型中的条件概率是由专家知识给出的,具有一定的主观性,专家根据检测到的实际数据给出一定威胁程度(概率)。DDBN决策推理模型的真实条件概率如表 1所示。
| 表 1 真实的贝叶斯网络参数 Table 1 Real Bayesian network parameters |
贝叶斯网络的参数学习本质上是在网络结构已建立的条件下,学习网络上所有节点的概率分布。最初的贝叶斯网络的概率分布表是由专家知识提供的,这种方法导致与观测数据产生较大的偏差。目前算法是从观测数据中学习网络参数的概率分布,具有较强的适应性。
观测数据分为两种,即完备和不完备。完备数据的参数学习方法有:最大似然估计(MLE)方法和贝叶斯方法。对于不完备数据的学习,常用几种方法有Monte-Carlo方法、Gaussian逼近,以及期望极大化算法求ML或MAP等。近期出现一些参数学习的新方法,基于相容渐进性的BCL算法、基于参数约束的参数学习[15]、积极学习算法的参数学习[16]、并行的EM算法等。状态空间模型往往包括一些必要的参数θ,用以定义状态空间的转移概率模型P(Xt|Xt-1)和观测概率模型P(Yt|Xt)。学习意味着从大量的数据中估计这些参数θ,这也称作系统辨识。本文采用最大似然估计(maximum likelihood estimation,MLE)方法。
2.1 最大似然估计(MLE)最大似然估计(MLE)是由Spiegelhalter于1992年提出的,通过计算给定父节点集的值时,计算节点不同取值的概率,并作为该节点的条件概率参数。最大似然估计的基本原理是试图寻找使得似然函数最大的参数。
给出贝叶斯网络拓扑结构G以及独立同分布的观测数据集D={Y1, Y2, …, YN},每个观测数据可以是一个向量或向量的时间序列,则数据集的似然函数为模型参数的函数:
| $ P\left( {D|\theta ,G} \right) = \prod\limits_{i = 1}^N P \left( {{Y_i}|\theta ,G} \right) $ | (3) |
MLE参数可以通过最大似然函数来获得,或等价地使用对数似然,即
| $ \begin{array}{c} L\left( \theta \right) = \sum\limits_{i = 1}^N {\log P\left( {{Y_i}|\theta ,G} \right)} = \\ \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{q_j}} {P\left( {Y_i^j|Y_i^{pa\left( j \right)},{\theta ^j}} \right)} } = \\ \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{q_j}} {\sum\limits_{k = 1}^{{m_j}} {{n_{ijk}}\log \left( {{\theta _{ijk}}} \right)} } } \end{array} $ | (4) |
定义样本的特征函数nijk如下
| $ {n_{ijk}} = \left\{ \begin{array}{l} 1,在{Y_j}中,{P_a}\left( j \right) = k\\ 0,其他 \end{array} \right. $ | (5) |
式中:j为贝叶斯网络中的节点;Pa(j)为节点j的父节点集;k为节点j的父节点的数目,θj为给定父节点条件下Yj的条件概率。
2.2 DDBN参数学习遗传算法设计遗传算法(genetic algorithm,GA)是模拟达尔文的遗传选择和自然淘汰的生物进化机制的计算模型[17],它在解空间寻优的过程中具有自动获取和积累有关搜索空间知识的能力,并能快速适应地检验搜索进程,随机产生初始种群,从而进行评估、遗传运算、选择、经多代繁殖,最后适者生存,经过数次循环往复,使种群素质和种群中个体的素质不断提高,并通过种群中个体的多样性进而多点搜索解空间,最终得到全局最优解。
采用GA进行参数学习的详细设计步骤如下:
1) 初始化DDBN的网络参数θ0,同时对威胁估计模型进行实时采样,得到一组数据。
2) 编码方式采用二进制编码,对GA种群进行初始化。这里的参数为各节点条件概率的集合, 即{Z(t), L(t), D(t), M(t), C(t), J(t), Q(t), N(t)}, 集合中元素介于区间[0, 1]内,为了减小个体长度,元素编码的时候只用小数位来表示。例如0.23,则小数位相应的二进制表示为00111011,保留小数点后8位精度。即集合的元素个体长度为8,集合中8个元素,所以集合的长度大小为64,种群大小为100,初始种群是随机产生的。
3) 给定最大遗传代数为100,判断是否满足结束条件。
4) 取最大似然函数L(θ)作为遗传算法的适应度函数F(x),保留最优个体。
| $ F\left( x \right) = \max \left\{ { - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{q_j}} {\sum\limits_{k = 1}^{{m_j}} {{n_{ijk}}\log \left( {{\theta _{ijk}}} \right)} } } } \right\} $ | (6) |
5) 选择策略:正比选择策略,对于个体i,设其适应值为Fi,种群规模为100,则该个体的选择概率可以表示为式(7),得到选择概率后,采用轮盘赌来实现选择操作。
| $ {P_i} = \frac{{{F_i}}}{{\sum\limits_{i = 1}^{100} {{F_i}} }} $ | (7) |
令PP0=0,
交叉:采用多切点交叉法,对于两个选定的个体P1和P2,随机选取8个切点,交换多个切点之间的子串,即完成交叉操作,这里选取交叉概率为Pc=0.9。
变异:指在种群中按变异概率任选若干基因位改变其位值,对二进制编码来说,就是反转位值。这里选取变异概率为Pm=0.03。
6) 不断更新遗传算法的种群,目标函数如式(8)所示,将通过计算得到的网络参数θt+1替换上一时刻网络参数θt,同时进行实时数据采样。
| $ L\left( \theta \right) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{q_j}} {\sum\limits_{k = 1}^{{m_j}} {{n_{ijk}}\log \left( {{\theta _{ijk}}} \right)} } } $ | (8) |
假设UUV以4 kn速度执行任务,从起始点到目的点的过程中遇到障碍物,根据UUV携带传感器感知的威胁源数据,对图 3所建立的UUV决策推理模型分为4个时间片(这个时间片只是仿真时确定的时间段,与UUV控制周期没有关系)进行采样,每个时间片(1 min)采30组数据,对模型的贝叶斯网络参数进行初始化:即Z(t)={高}={0.5};L(t)={高}={0.5};D(t)={高}={0.5};M(t)={高}={0.5};C(t)={正常}={0.5};J(t)={正常}={0.5};Q(t)={正常}={0.5};N(t)={充足}={0.5},然后采用遗传算法(GA)对决策模型的网络参数进行学习,最后进行威胁评估的验证。
3.1 GA进行参数学习的有效性验证遗传算法进行参数学习的步骤见2.2节。分时间片学习模型网络参数,第1时间片下所学参数结果如表 2所示,第4时间片下所学参数结果如表 3所示。其他时间片不一一列出。
| 表 2 第1时间片下的贝叶斯网络参数学习结果 Table 2 The first time under Bayesian network parameters learning results |
| 表 3 第4时间片下的贝叶斯网络参数学习结果 Table 3 The fourth time under Bayesian network parameters learning results |
由表 2和表 3中所学习的贝叶斯网络参数可以看出,当UUV航行接近目的点时,由UUV携带的传感器感知目的点附近的威胁源数据,并且对数据进行采样,实时地更新贝叶斯网络参数。
似然度的取值体现数据与模型参数的匹配度,即似然度值越大则说明该参数越真实,匹配程度越高。下面对模型第1个时间片和第4个时间片采样的数据组的似然度进行比较验证。将第1个时间片和第4个时间片的样本数据组分别通过遗传算法进行参数学习,遗传算法的迭代优化曲线如图 4所示。从图 4中可以看出,任务初期(第1时间片)由于样本数据的数量比较少,其似然度的值比较小,随着参数学习迭代次数的增加,模型的对数似然度缓慢增加并且渐渐收敛,此时的参数与真实的网络参数相比差距大。最后的第4个时间片测得的样本数据的数量随着时间片的增多而逐渐增加,经过120组样本数据之后,其似然度值最大,匹配程度最高,即最终学习得到的贝叶斯网络参数接近于真实的网络参数。因此,随着时间的推移,通过参数学习的模型似然度会渐渐逼近真实模型。

|
Download:
|
| 图 4 遗传算法的迭代优化曲线 Fig. 4 Iterative optimization curve of genetic algorithm | |
利用Netica软件,结合基于动态贝叶斯网络的UUV威胁估计模型结构和参数,对执行任务中遇到障碍物来进行仿真威胁评估。
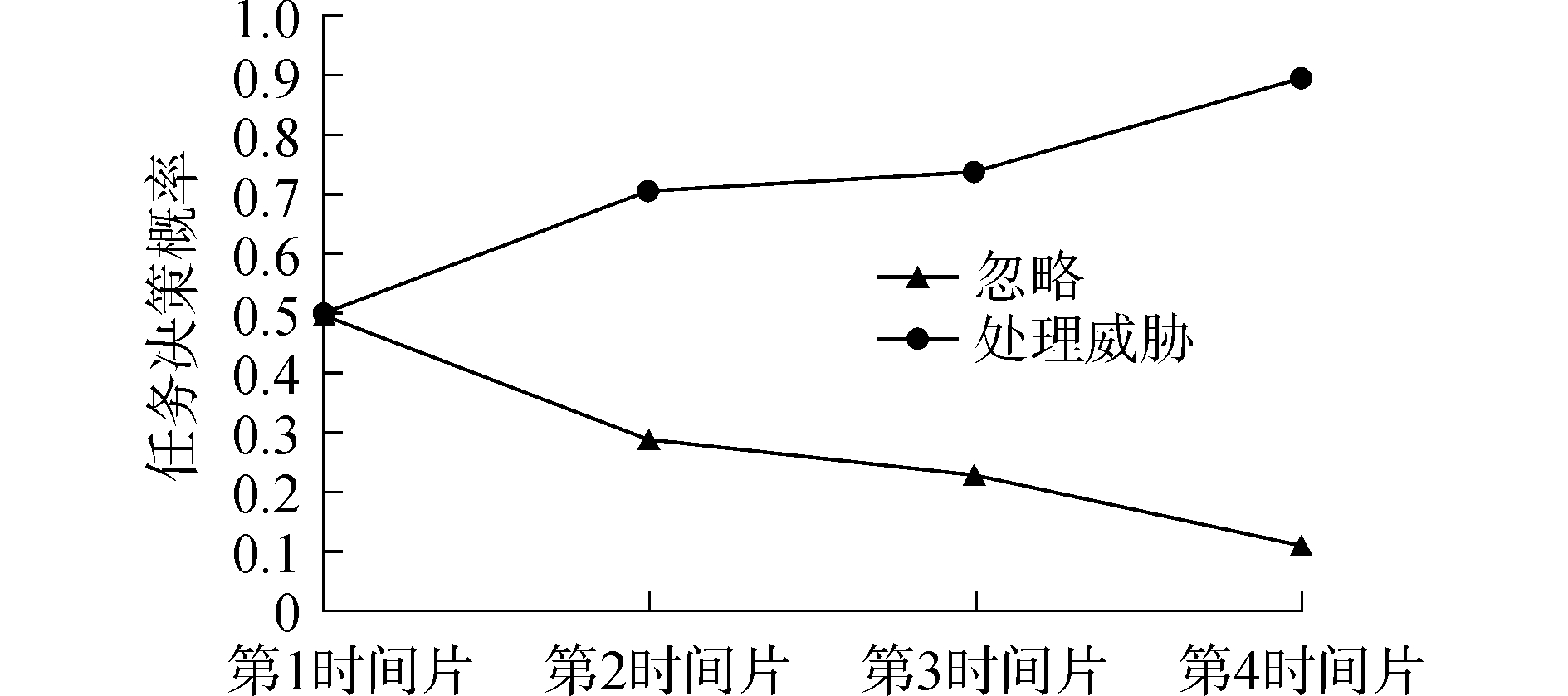
将上述4个时间片所学的参数代入UUV决策推理模型,最终进行概率推理,得到UUV不确定海洋环境下的决策结果,结果如图 5所示。由上述分析和结果看出随着时间片的展开,收集到的信息逐渐增多,推理预测的节点值精确性在不断提高,由此可见基于DDBN的威胁评估模型可以有效地学习上一时刻的经验和知识,并充分运用到下一时刻的模型推理去。该图同样也可以说明GA算法学习得到的网络参数的正确性,为有效的推理模型提供了可靠的参数保障。所以说UUV依据威胁目标当前时刻的威胁程度,能够实时地进行复杂海洋环境下的自主决策。
|
Download:
|
| 图 5 UUV海洋环境任务决策概率推理 Fig. 5 Marine environment task decision probability reasoning of UUV | |
1) 设计的基于动态贝叶斯网络的威胁评估模型以及决策推理模型,采用遗传算法实现了DDBN参数学习,能够使决策推理模型中的贝叶斯网络参数随海洋环境实时更新,随着数据数量的增加并进行不断地修正,最终趋近于真实的网络参数。
2) 通过仿真实验以及参数学习前后模型的似然度比较,验证了遗传算法进行参数学习的有效性,为UUV的海洋环境任务决策提供准确的参数保证,确保了UUV自主动态任务决策的合理性和准确性。
今后将进一步深化动态贝叶斯网络参数的在线学习方法研究,以实现准确可信的在线推理决策提供网络参数保证。
| [1] |
DUNN P. Navy unmanned undersea vehicle (UUV) master plan[C]//Unmanned Underwater Vehicle Showcase 2000 Conference Proceedings. PGI Spearhead Ltd, 2000.
(  0) 0)
|
| [2] |
夏春林, 周德云, 冯琦. 基于变权灰色关联法的目标威胁评估[J]. 火力与指挥控制, 2014, 39(4): 54-57. XIA Chunlin, ZHOU Deyun, FENG Qi. Target threat assessment based on the method of variable weight grey incidence[J]. Fire control & command control, 2014, 39(4): 54-57. DOI:10.3969/j.issn.1002-0640.2014.04.014 (  0) 0)
|
| [3] |
李特, 冯琦, 张堃. 基于熵权灰色关联和D-S证据理论的威胁评估[J]. 计算机应用研究, 2013, 30(2): 380-382. LI Te, FENG Qi, ZHANG Kun. Threat assessment based on entropy weight grey incidence and D-S theory of evidence[J]. Application research of computers, 2013, 30(2): 380-382. DOI:10.3969/j.issn.1001-3695.2013.02.016 (  0) 0)
|
| [4] |
王百合, 黄建国, 张群飞. 基于层次分析法的水下多目标威胁评估模型[J]. 舰船科学技术, 2006, 28(6): 75-77. WANG Baihe, HUANG Jianguo, ZHANG Qunfei. Underwater multi-target threat evaluation model based on analytic hierarchy process[J]. Ship science and technology, 2006, 28(6): 75-77. (  0) 0)
|
| [5] |
王毅, 刘三阳, 张文, 等. 属性权重不确定的直觉模糊多属性决策的威胁评估方法[J]. 电子学报, 2014, 42(12): 2509-2514. WANG Yi, LIU Sanyang, ZHANG Wen, et al. Threat assessment method with uncertain attribute weight based on intuitionistic fuzzy multi-attribute decision[J]. Acta electronica sinica, 2014, 42(12): 2509-2514. DOI:10.3969/j.issn.0372-2112.2014.12.025 (  0) 0)
|
| [6] |
王新增, 慈林林, 李俊山, 等. 恶劣气象条件对无人机飞行航迹的威胁评估[J]. 飞行力学, 2010, 28(5): 84-87. WANG Xinzeng, CI Linlin, LI Junshan, et al. Threat evaluation of hazardous weather conditions to the flight path of UAV[J]. Flight dynamics, 2010, 28(5): 84-87. (  0) 0)
|
| [7] |
马静. 贝叶斯网络的战场作战意图评估方法[J]. 西安工业大学学报, 2010, 30(4): 397-401. MA Jing. Assessment of operational intention in battlefield based on Bayesian network[J]. Journal of Xi'an Technological University, 2010, 30(4): 397-401. DOI:10.3969/j.issn.1673-9965.2010.04.020 (  0) 0)
|
| [8] |
王三民, 王宝树. 贝叶斯网络在战术态势评估中的应用[J]. 系统工程与电子技术, 2004, 26(11): 1620-1623, 1679. WANG Sanmin, WANG Baoshu. Application of Bayesian networks in tactical situation assessment[J]. Systems engineering and electronics, 2004, 26(11): 1620-1623, 1679. DOI:10.3321/j.issn:1001-506X.2004.11.024 (  0) 0)
|
| [9] |
王晓帆, 王宝树. 基于贝叶斯网络和直觉模糊推理的态势估计方法[J]. 系统工程与电子技术, 2009, 31(11): 2742-2746. WANG Xiaofan, WANG Baoshu. Situation assessment method based on Bayesian network and intuitionistic fuzzy reasoning[J]. Systems engineering and electronics, 2009, 31(11): 2742-2746. (  0) 0)
|
| [10] |
史建国, 高晓光, 李相民. 基于离散模糊动态贝叶斯网络的空战态势评估及仿真[J]. 系统仿真学报, 2006, 18(5): 1093-1096, 1100. SHI Jianguo, GAO Xiaoguang, LI Xiangmin. Modeling air combat situation assessment by using fuzzy dynamic Bayesian network[J]. Journal of system simulation, 2006, 18(5): 1093-1096, 1100. DOI:10.3969/j.issn.1004-731X.2006.05.002 (  0) 0)
|
| [11] |
NASEEM A, SHAH S T H, KHAN S A, et al. Decision support system for optimum decision making process in threat evaluation and weapon assignment:Current status, challenges and future directions[J]. Annual reviews in control, 2017, 43: 169-187. DOI:10.1016/j.arcontrol.2017.03.003 (  0) 0)
|
| [12] |
MA Shidong, ZHANG Hongzhi, YANG Guoqing. Target threat level assessment based on cloud model under fuzzy and uncertain conditions in air combat simulation[J]. Aerospace science and technology, 2017, 67: 49-53. DOI:10.1016/j.ast.2017.03.033 (  0) 0)
|
| [13] |
NICULESCU R S, MITCHELL T, RAO R B. Bayesian network learning with parameter constraints[C]//Advances in Neural Information Processing Systems, 2005: 1-48.
(  0) 0)
|
| [14] |
TONG S, KOLLER D. Active learning for parameter estimation in Bayesian networks[C]//Proceedings of the 13th International Conference on Neural Information Processing Systems. Denver, CO: MIT Press, 2000: 647-653.
(  0) 0)
|
| [15] |
ZHOU Yun, FENTON N, NEIL M. Bayesian network approach to multinomial parameter learning using data and expert judgments[J]. International journal of approximate reasoning, 2014, 55(5): 1252-1268. DOI:10.1016/j.ijar.2014.02.008 (  0) 0)
|
| [16] |
BASU M. Modified particle swarm optimization for nonconvex economic dispatch problems[J]. International journal of electrical power & energy systems, 2015, 69: 304-312. (  0) 0)
|
| [17] |
王小平, 曹立民. 遗传算法——理论、应用与软件实现[M]. 西安: 西安交通大学出版社, 2002. WANG Xiaoping, CAO Limin. Theory application and so ftware implement of genetic algorithm[M]. Xi'an: Xi'an Jiaotong University Press, 2002. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


