随着互联网、物联网、智慧城市等数字化技术的发展,传感器、移动终端等各类数据收集设备将人类的衣食住行各类信息以数字化形式存储起来,从而催生了大数据时代的到来。在发掘数据潜在价值的过程中,如何保障个人的隐私安全,尤其是如何避免数据挖掘带来的隐私泄露,是数据科学目前亟待解决的关键问题。随着数据挖掘技术在应用层面的普及,面向挖掘的隐私安全问题开始受到了关注,隐私保护领域的研究焦点正逐渐向隐私保护数据挖掘领域偏移。针对数据发布的隐私保护技术已得到了广泛的研究,其中基于聚类挖掘技术的数据发布隐私保护技术是学术界研究的一个热点方向[1]。文献[2]研究了Map Reduce架构下基于k-均值聚类的数据隐私保护技术,其结果显示,所提方法能达到差分隐私需求,具有较好的保护效果。采用聚类技术保护隐私的研究已经延伸到对敏感轨迹数据的保护,为防止攻击者通过两次聚类劫取用户隐私信息,文献[3]采用杂交式的聚集手段,构建了一个隐私保护模型,对初次聚类的结果再次聚类后再发布,所发布的轨迹数据在簇的固有特征方面保持较好。通过反复聚类来保护隐私的研究思路在文献[4]中得到了应用,其研究反复利用聚类方法,对敏感字段关联程度类似的记录进行k-匿名操作,该方法每次处理的簇较小,算法效率高,且保护性能可达到k-匿名的隐匿水平。文献[5]对于个性化轨迹隐私保护做出了深入的研究,其方法首先对关键轨迹做出标记并且根据隐私级别产生各移动对象的敏感属性,再根据信息损失最小化作为优化准则来删除关键移动点,此方法在数据可用性和隐私保护性方面达到了较好折中。
兼顾了个体不同隐私需求的隐匿方法具有较强的操作针对性,保护效果较好,保护后发布的数据可用性较高,该领域的研究正逐渐成为隐私保护领域的前沿课题。文献[6]基于k-匿名的思想,根据用户自定义的隐私安全性分离相似的安全等级,提出了一种自顶向下的个性化泛化回溯算法,该方法通过动态构建泛化树结构,能有效防止同质攻击和背景知识攻击。文献[7]在定义敏感属性值个性隐私敏感因子和个性隐私保护需求度的概念的基础上,提出了一种基于熵分类的个性化(α, k)-匿名模型,该方法在满足个性化服务需求的同时,其近似信息损失度较小。文献[8]基于轨迹的相似性和方向性,通过构建轨迹匿名区域,提出了一种个性化轨迹匿名模型,有效解决了轨迹k-匿名集的选择问题。文献[9]根据轨迹间距离和方向度量轨迹间边权,构造规模可变的个性化轨迹图模型,提出了一种基于贪心策略寻找近似最优的k条轨迹构建轨迹k-匿名集的方法,有效解决了轨迹匿名数据的个性化需求问题。文献[10]针对传统方法对所有移动对象提供同等程度的隐私保护,不能满足保护的个性化需求问题,提出了一种面向轨迹数据发布的个性化隐私保护方法,在隐私保护和数据可用性方面达到了较好的平衡。
1 隐私数据模型描述及相关定义对于原始数据模型A=(A1, A2, …, An)下的一条数据表示为d=(a1, a2, …, an),其中,ai为数据的属性,若存在i(i=1, 2, …, n)使得ai是敏感的,不愿意他人知晓,则称此记录d为一条隐私数据,而数据产生者对隐私数据项敏感程度的量化表示,称为隐私度。给定原始数据模式A=(A1, A2, …, An),对应的隐私度模式为S=(S1, S2, …, Sn),则隐私数据模型定义为序偶﹤A, S﹥,该模型下的一条隐私数据表示为n重组d=(d1, d2, …, dn),其中di=﹤ai, si﹥为有序二重组,ai为属性Ai对应的一个原始数据值,si为ai对应的隐私度。另记dj=(aj1, aj2, …, ajn)为原始数据模式A=(A1, A2, …, An)的第j个元组,设dj各个属性对应的隐私度依次为sj1, sj2, …, sjn,则aj的元组敏感度定义为sj=u1s1+u2s2+…+unsn, 即sj是第j个属性隐私度的线性组合,其系数为属性敏感度。
定义1(隐私关系) 隐私数据集合D中的一条记录为多重组d=(d1, d2, …, dn), 序偶di=﹤ai, si﹥∈d,ai为字段Ai上的原始数据值,si为ai对应的隐私度。称卡氏积D×D的下述子集为D上的隐私关系
| $ \begin{array}{l} R = \left\{ {\left\langle {d, d'} \right\rangle } \right.|d, d' \in D, {d_i} = \left\langle {{a_i}, {s_i}} \right\rangle \in d, {{d'}_i} = \left\langle {} \right.\\ \left. {\left. {{{a'}_i}, {{s'}_i}} \right\rangle \in d', {s_i} \ge {{s'}_i}} \right\} \end{array} $ |
若D上的两条记录d和d'具有隐私关系,即﹤d, d'﹥∈R则记为
| $ d \ge d' $ |
定义2(隐私偏序) 记原始数据模式A=(A1, A2, …, An)下收集的隐私数据集合为D,A'=(Ai, Ai+1, …, Ai+k)为A的一个属性子集(k≤n),对应的隐私度子模式为S'=(Si, Si+1, …, Si+k),D中每条记录去掉A'和S'中未出现的属性字段后所得的子集记为D',并设R'为D'上的隐私关系,则称序偶﹤R', D'﹥为隐私偏序集合,简称隐私偏序。
定义3(隐私秩) 记d∈D为隐私数据集D中的一条隐私数据,则隐私数据d的隐私秩定义为
| $ \left| d \right\rangle = - \sum\limits_{d' \in D} {\underline {{\rm{sign}}\left( {d - d'} \right)} } | $ | (1) |
式中:
定义4(极小隐私集) 设﹤D, R﹥为一个隐私偏序,若数据集合B⊆D,对于隐私数据b∈B,且B中不存在隐私数据x,使得b≠x且b≥x,那么隐私数据b∈B称为B的一个极小隐私元。B的所有极小隐私元构成的集合,定义为B的极小隐私集。
定义5(首隐私极元) 设隐私偏序﹤D, R﹥,B⊆D,E为B的极小隐私集,则称E中隐私秩最小的隐私数据e为B的一个首隐私极元。
定义6(偏序隐私层) 所谓偏序隐私层是指,逐渐删掉极小隐私集的过程,规定原始隐私数据集的第一个极小隐私集对应的层数为1,删掉第一个极小隐私集后,剩余数据集的极小隐私集对应的层数为2,依次类推,层数逐次增加1,直到删完所有数据为止。
定义7(隐私线序集) 隐私偏序经过拓扑分类后,由三元组﹤隐私数据记录指针,偏序隐私层号,相对隐私秩﹥构成的拓扑分类队列,称为隐私线序集。
2 隐私偏序的拓扑分类隐私偏序的拓扑分类是指对不同隐私数据的敏感性进行排序。如果﹤D', R'﹥是非空有限集合的偏序集合,拓扑分类的目标是在D'上构造一个线序R",对于∀a, b∈D',使得每当﹤a, b﹥∈R'时,有﹤a, b﹥∈R"。
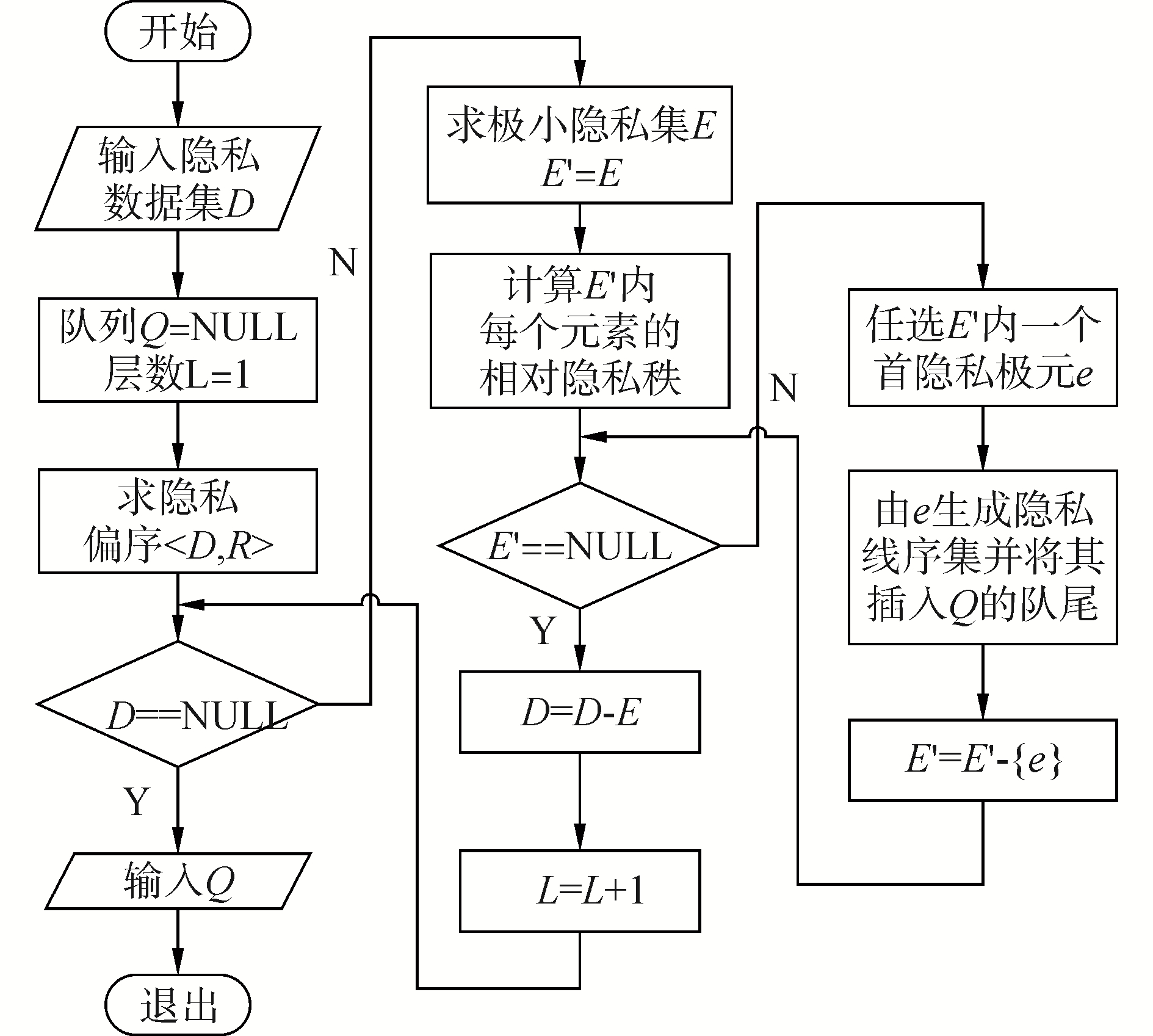
隐私偏序的拓扑分类,其本质是求一个隐私数据的线序,为此本研究设置一个队列Q,用于存储隐私数据经过拓扑分类后的结果,该队列的每个节点除了存储一条隐私数据外(只需存储该条记录指针或ID),还存储偏序隐私层的序号和极小隐私集内的相对隐私秩。本研究将此队列Q称为隐私线序集。隐私偏序的拓扑分类流程如图 1所示。
|
Download:
|
| 图 1 隐私偏序的拓扑分类流程图 Fig. 1 Partial classification of privacy partial order | |
下面通过算法形式描述隐私数据的拓扑分类过程。
算法1(privacy topology, PT):隐私偏序拓扑分类算法。
输入:隐私数据集D。
输出:隐私线序集Q。Q中存储三类值:隐私数据记录指针、偏序隐私层号和相对隐私秩。
初始化队列Q为空,置层数L=1;
生成隐私偏序﹤D, R﹥;
WHILE D不空DO
求D的极小隐私集E,置E'=E;
FOR EACH e IN E DO
计算e在E内的相对隐私秩
END FOR
WHILE E不空DO
任选E内一个首隐私极元e;
置Q队尾节点的指针指向e,置层数为L,置相对隐私秩为|e〉;
置E'=E'-{e};
END WHILE
置D=D-E;
层数L=L+1;
END WHILE
RETURN Q;
算法结束。
隐私偏序的拓扑分类结果刻画了隐私需求的个性化差异,这是实施个性化隐私保护的关键。后续研究将此拓扑分类结果作为一个视图,进行个性化隐私多视图聚类。
3 个性化隐私多视图聚类隐私数据是一种多视图数据,不同视图提供了对隐私数据不同角度的观察轮廓,且视图之间存在密切联系,对隐私数据进行多视图聚类,能揭示视图内部的元组之间以及不同视图之间的内在联系,不同聚类簇体现了不同的隐私个性化需求,这有助于提高隐私保护操作的个性化程度。本研究基于原始数据、隐私度、元组敏感度、隐私线序集等多个视图,对隐私数据进行多视图聚类,对不同聚类簇以及同簇内部的不同元组施加程度有别的个性化保护操作。
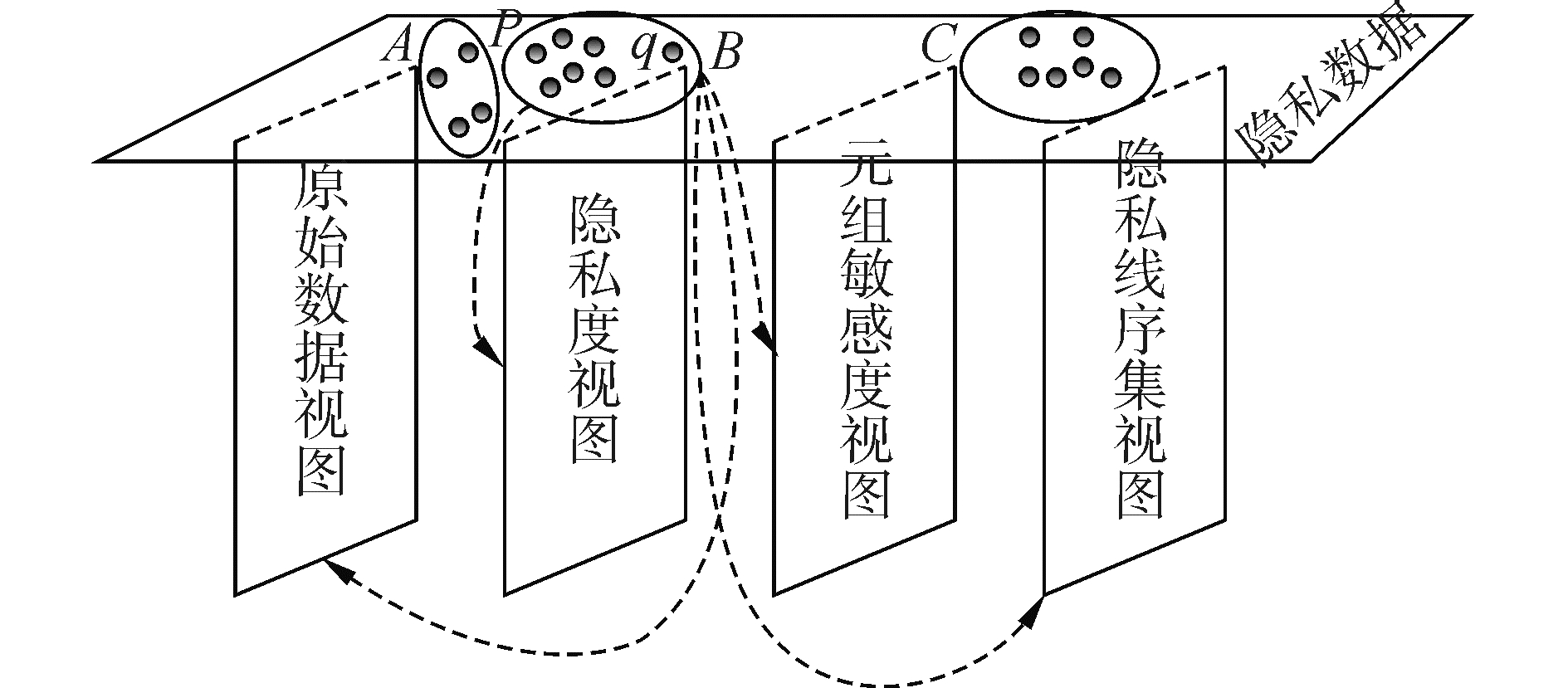
图 2中,聚类簇A、B、C是在原始数据、隐私度、元组敏感度、隐私线序集等多个视图共同作用下的三个聚类结果。需要注意的是,尽管点p距离聚类簇B很近,经典的单视图聚类算法一般将点p归为聚类簇B的点,但是在多视图聚类情况下,点p可能被排除在聚类簇B之外。另一个例外是点q,单视图聚类时该点一般难以归为聚类簇B的点,但在多视图聚类情况下,由于它与多个视图之间的紧密联系,却归为了聚类簇B的点。可见,多视图聚类充分利用了各个视图的信息及其之间的联系对数据对象进行有效聚类,其聚类结果更加合理,在其上进行个性化隐私保护更有效。
|
Download:
|
| 图 2 隐私数据多视图聚类示意图 Fig. 2 Multi-view clustering diagram of privacy data | |
记第i个视图的样本矩阵表示为X(i),构造如下所示的多视图k-均值聚类目标函数[14]
| $ \begin{array}{l} \;\;\;\;\mathop {\min }\limits_{{C^{\left( i \right)}}, G, {\lambda ^{\left( i \right)}}} \sum\limits_{i = 1}^M {{{\left( {{\lambda ^{\left( i \right)}}} \right)}^\gamma }} {\left\| {{\mathit{\boldsymbol{X}}^{\left( i \right)}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}^{\left( i \right)}}} \right\|_2}, \\ {\rm{s}}{\rm{.t}}.\;\;{\mathit{\boldsymbol{G}}_{jk}} \in \left\{ {0, 1} \right\}, \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{G}}_{jk}} = 1, } \sum\limits_{k = 1}^K {{\lambda ^{\left( i \right)}} = 1.} \end{array} $ | (2) |
式中:C(i)为第i个视图的聚类中心矩阵;G为聚类指示矩阵,由约束条件可知,其每行有一个1,其余全为0,若Gjk=1,表明第j个样本在第k个聚类簇中;λ(i)为第i个视图的权重;γ是控制权重分布的调节参数。M为视图个数,本研究包括原始数据、隐私度、元组敏感度和隐私线序集等4个视图。在此目标函数中,指示矩阵G实现了不同视图的关联。
上述目标函数的求解过程可参见文献[11],下面给出该多视图k-均值聚类算法的过程描述。
输入:隐私数据的每个视图数据X(i),聚类簇数目期望值K,调节参数γ。i=1, 2, 3, 4。
输出:聚类指示矩阵G,各视图的聚类中心矩阵C(i)及权重λ(i)。i=1, 2, 3, 4。下同。
随机填充矩阵G使得每行恰有一个1,其余全为0;生成对角矩阵D(i)。
WHILE UNTIL 收敛或超过设定的执行次数
计算对角阵
更新中心矩阵:
| $ {\mathit{\boldsymbol{C}}^{\left( i \right)}} = {\mathit{\boldsymbol{X}}^{\left( i \right)}}{{\mathit{\boldsymbol{\tilde D}}}^{\left( i \right)}}\mathit{\boldsymbol{G}}{\left( {{\mathit{\boldsymbol{G}}^T}{\mathit{\boldsymbol{D}}^{\left( i \right)}}\mathit{\boldsymbol{G}}} \right)^{ - 1}}。$ |
更新聚类指示矩阵G:
| $ \begin{array}{l} \;\mathop {\min }\limits_G \sum\limits_{i = 1}^4 {{{\mathit{\boldsymbol{\tilde D}}}^i}} \left\| {{\mathit{\boldsymbol{X}}^{\left( i \right)}} - {\mathit{\boldsymbol{C}}^{\left( i \right)}}} \right\|_2^2, \\ {\rm{s}}{\rm{.t}}.\;\;{\mathit{\boldsymbol{G}}_{jk}} \in \left\{ {0, 1} \right\}, \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{G}}_{jk}} = 1} \end{array} $ |
更新对角矩阵Djj(i)=(2||e(i)j||)-1,其中,e(i)j是E(i)=X(i)-GC(i)的第j行。
更新权重
H(i)=Tr{(X(i)-C(i)GT)D(i)(X(i)-C(i)GT)T}。
END WHILE
本节通过研究隐私数据的多视图聚类技术,利用隐私数据多视图k-均值聚类算法得到个性化隐私多视图聚类结果,为后续提出的个性化匿名算法提供了基础。
4 个性化匿名算法本文用平均偏序隐私层号和平均相对隐私秩作为多视图聚类簇的敏感性评估准则。由偏序隐私层的意义可知,其层号越大,敏感性越高;而相对隐私秩是同一个极小隐私集内刻画隐私数据间敏感性强弱的关系测度,因此用平均偏序隐私层号和平均相对隐私秩评估聚类簇敏感性是合理的。
聚类簇的敏感性评估过程中,平均偏序隐私层号和平均相对隐私秩分别作为主、次关键字,即偏序隐私层的优先级大于相对隐私秩。
关于对不同敏感度的聚类簇如何施加不同程度保护操作的问题,本研究在算法选择上是开放的,具有保护程度差别的算法皆适用。不失一般性,本文选取经典的k-匿名算法对不同簇进行保护。在k-匿名算法中,k值代表不可区别的记录条数,其值是保护能力强弱的直接指标,k的取值越大,保护程度越高,反之则保护能力越低。
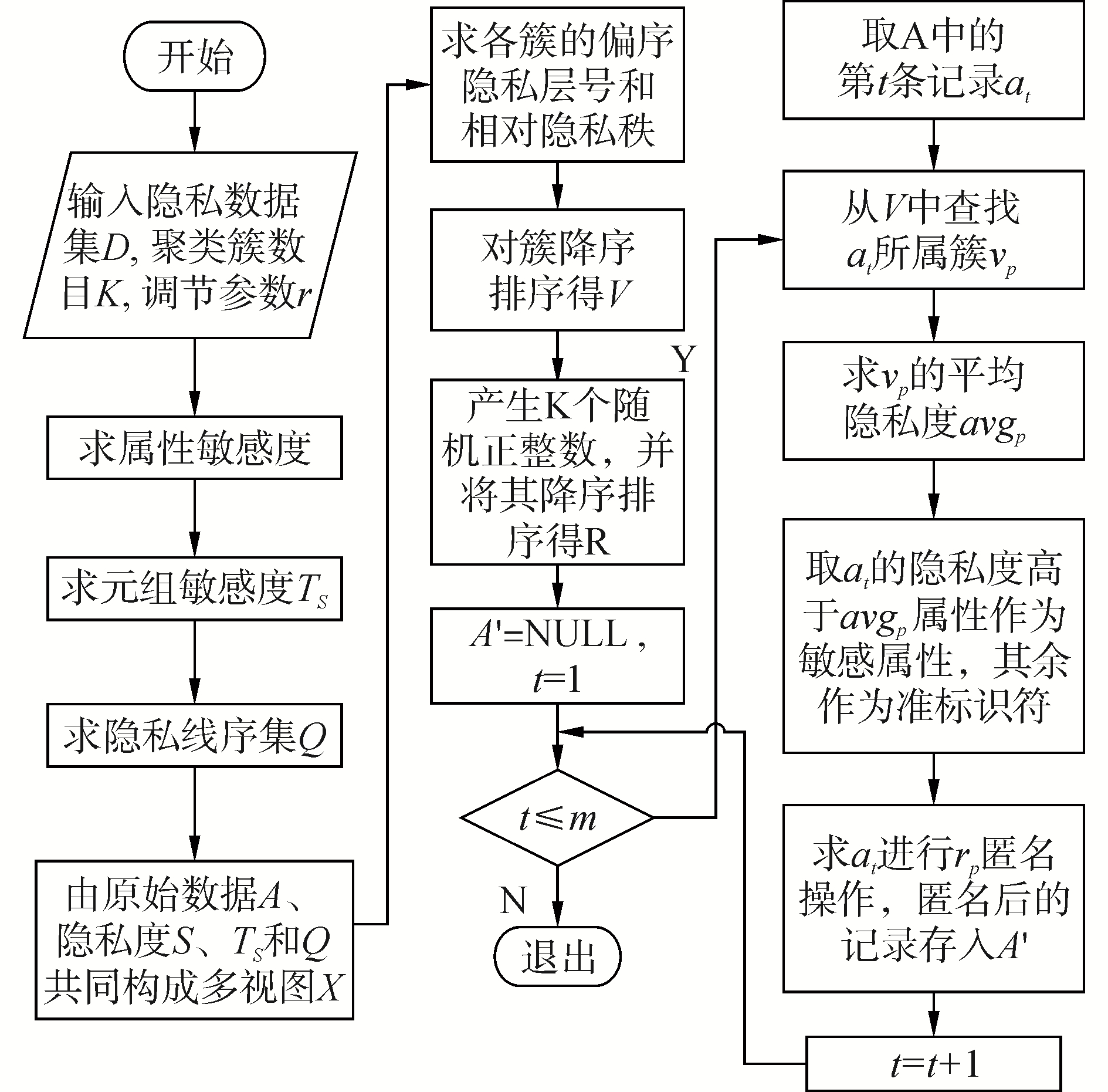
本文为降低问题复杂性,将k值设定为K以内可重复的随机正整数,其中K为多视图k-均值聚类算法的输入参数,即多视图聚类簇数目期望值。图 3给出了面向聚类的个性化隐私保护操作的执行流程。
|
Download:
|
| 图 3 面向聚类的个性化隐私保护操作执行流程 Fig. 3 Personalized privacy protection operation execution process for clustering | |
下面给出算法的详细执行步骤。
算法3(personal privacy oriented clustering,PPOC):面向聚类的个性化匿名算法。
输入:
1) 隐私数据D,包括原始数据记录表
2) 多视图聚类簇数目期望值K及调节参数γ;
输出:保护后的发布数据A'。
对S进行主成分分析,取第一主成分系数u(1)=(u1, u2, …, un)作为属性敏感度;
1) 求S每行记录Sj=(sj1, sj2, …, sjn)的元组敏感度:Sj=u(1)sjT,置Ts=(S1, S2, …, Sm)T;
2) Q=PT(D);调用算法1。
3) 置X(1)=A,X(2)=S,X(3)=Ts,X(4)=Q,X={X(i)|i=1, 2, 3, 4};
4) [G, C, λ]=PMVC(X,K,γ);调用算法2,
G为聚类指示矩阵, C={C(i)|i=1, 2, 3, 4}是每个视图的聚类中心,λ={λ(i)|i=1, 2, 3, 4}为每个视图的权重。
5) FOR EACH G的列指示的聚类簇DO
6) 基于Q,计算每个聚类簇对应的平均偏序隐私层号和平均相对隐私秩;
7) END FOR
8) 分别以平均偏序隐私层号和平均相对隐私秩为主、次关键字,对聚类簇降序排序,排序后的聚类簇序列记为V=(v1, v2, …, vK);
9) 产生K内可重复的K个随机正整数序列R,并降序排序得R=(r1, r2, …, rK);
10) 置A'为空;
11) FOR t FROM 1 TO m DO
① 取A中的第t条记录at;
② 基于G,查找at所属聚类簇vp;
③ 求vp的平均隐私度avgp;
④ 取at隐私度高于avgp属性作为敏感属性,其余作为准标识符;
⑤ 对at进行rp-匿名操作,匿名后的记录存入A';
12) END FOR
13) 返回A'。
5 实验仿真及结果分析为考察本文所提出的面向聚类的个性化隐私保护算法的有效性,本节比较本文所提算法PPOC与经典算法KP3和GDTMs在不用数据规模下的信息损失和算法效率并展开仿真实验验证。
实验数据取自UCI机器学习网站上Adult数据集,从Adult数据集中删除具有缺失项的数据后,共获得46 195条完整数据记录。实验将考察信息损失和算法效率两个方面的有效性,将本文所提算法PPOC与文献[6]提出的算法(简称KP3算法)和文献[4]的算法(简称GDTMs算法)进行比较。算法PPOC的参数γ设置为0.5,算法GDTMs的参数ρ设置为10%。
5.1 信息损失分析信息损失(information loss, IL)是数据可用性的一个间接测度,是隐私保护算法有效性的一个重要指标。本文对不同敏感度聚类簇保护时,可施加保护操作算法的选择是开放的,针对所采用的可变k-匿名策略,本文用非均衡熵来刻画算法的信息损失。
不同数据规模下的信息损失结果如图 4所示,其中簇数目值K设定为30。选取数据集总数的10%~55%的数据进行实验,故图 4中横坐标表示数据集总数的倍数。

|
Download:
|
| 图 4 不同数据规模下的信息损失 Fig. 4 Information loss under different data sizes | |
由图 4(a)可以看出,信息损失随着数据规模的增加而呈现出上升趋势。在数据规模增加的过程中,被隐匿的记录数增多,故信息损失量也加大,这与事实是相符的。
尽管图 4(a)的结果显示,数据规模影响了信息损失,但并不能据此认为本文算法不适用于大规模数据。用信息损失与数据规模相除,获得平均信息损失,其结果如图 4(b)所示。图 4(b)的结果表明,数据规模在增加的过程中,平均信息损失却在下降。此结果表明,本文所提算法在数据集规模较大时平均信息损失较小。
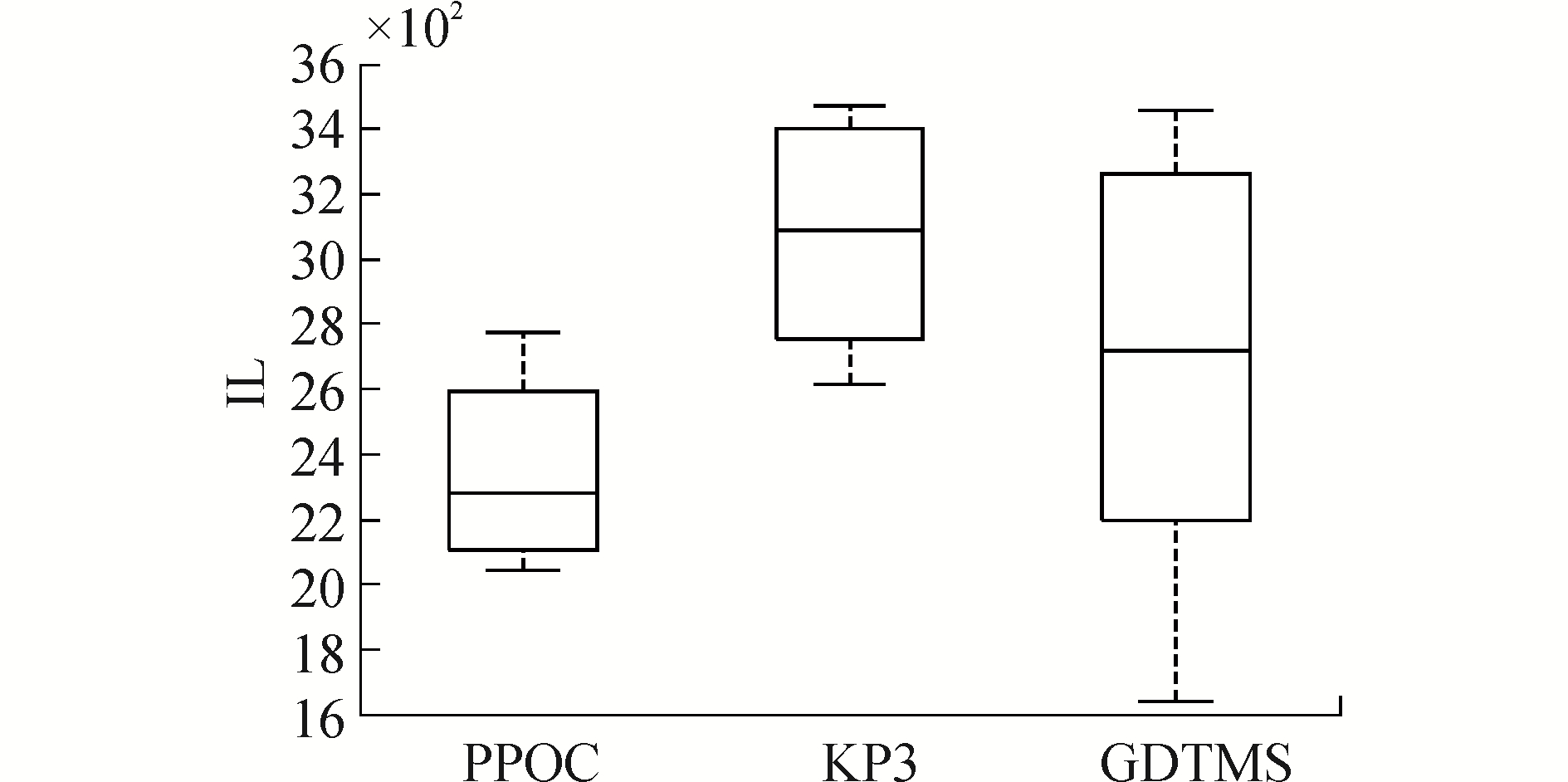
图 5所示的箱盒图给出了不同算法的信息损失比较情况,其中簇数目值K设定为30,数据规模设定为数据集总数的五分之一。由图 5可以看出,本文所提算法PPOC的均值显著低于被比算法,说明PPOC信息损失相对较小。
|
Download:
|
| 图 5 不同算法的信息损失比较 Fig. 5 Information loss under different data sizes | |
在PPOC算法中,对不同聚类簇所施加的隐私保护强度有别,高敏感簇保护强,而低敏感簇强度弱;另外PPOC重点保护的是敏感度高的属性值。简言之,PPOC算法的个性化保护是具有针对性的,所以其信息损失偏低的实验结果与预期相符。
5.2 算法效率分析本实验将从数据规模对运行时间的影响考察算法效率,并比较PPOC算法与KP3算法和GDTMs算法的效率。与前述实验类似,每组实验重复进行10次,取平均值作为最终结果。
图 6给出了不同数据规模下的运行时间,其中簇数目值K设定为30。选取数据集总数的10%至55%的数据进行实验,图 6中的横坐标表示数据集总数的倍数。

|
Download:
|
| 图 6 不同数据规模下的运行时间 Fig. 6 Run time under different data sizes | |
由图 6可以看出,在数据规模增加的过程中,运行时间持续上升。考察运行时间的上升趋势发现,其时间花费与数据规模几乎呈线性递增趋势。这一结果表明,数据规模是影响运行时间的一个重要因素。
但是并不是增加了等量规模数据,运行时间就一定对等升高。考察图 6中0.2倍和0.4倍规模数据情况,它们的运行时间增量显然小于其他情况下的运行时间增量。再考察0.15倍和0.45倍规模数据情况,其运行时间增量却较大。
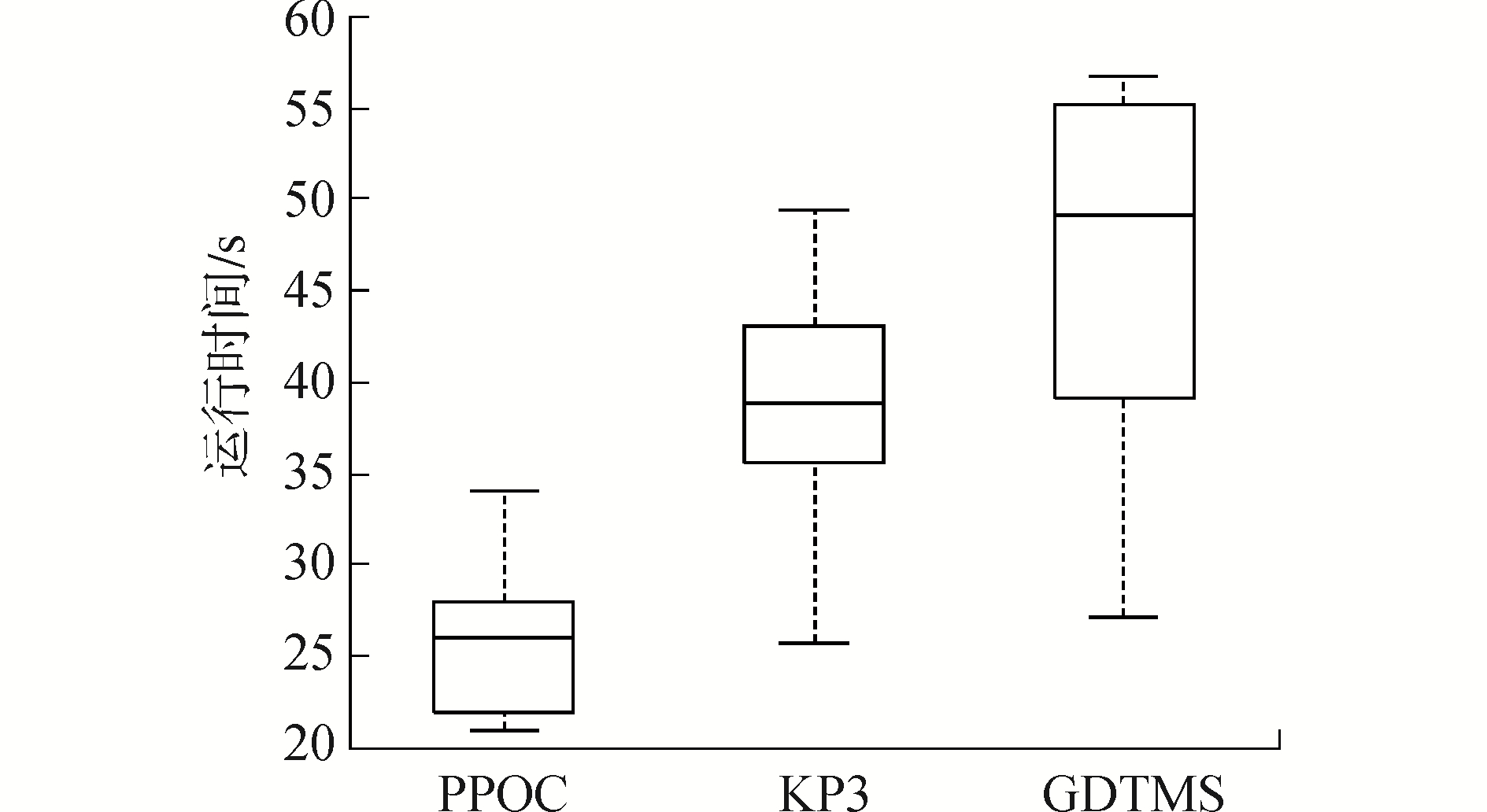
为验证所提算法的执行效率,实验进一步将所提PPOC算法与KP3和GDTMs两个经典算法的运行效率进行对比分析。图 7给出了不同算法的运行时间比较情况,其中簇数目值K=30,数据规模设定为数据集总数的五分之一。
|
Download:
|
| 图 7 不同算法的运行时间 Fig. 7 Run time for different algorithms | |
图 7是三个算法比较的箱盒图,重点考察平均值、极值和四分位数三个指标。由图 7可以看出,三个算法的平均运行时间具有显著差异,其中PPOC的平均运行时间显著低于被比算法,可见本研究进行有针对性的个性化保护是高效的。
另一方面,图 7的极值和四分位数显示,与GDTMs算法相比,PPOC算法和KP3算法的运行时间波动相对较小。此结果表明,本文所提算法稳定性较好。
综上所述,本研究所提算法的信息损失总量受数据规模的影响,而运行时间主要受数据规模的影响,与KP3和GDTMs算法相比,所提算法具有较低的信息损失和较好的运行效率,其优势表现在平均运行时间低,且算法执行效率相对较稳定, 实验验证了所提算法的有效性。
6 结论1) 通过原始数据和隐私度共同描述的隐私数据模型对隐私数据进行拓扑分类以解决不同隐私数据敏感性的排序问题,在此基础上获得了多视图隐私数据,再基于多视图聚类技术提出了一种个性化匿名方法。
2) 充分利用了不同视图间的互补信息,提高了隐私保护的针对性和效率。
3) 实现了在不同敏感需求的簇上施加程度有别的保护操作,解决了隐私保护的个性化需求问题。
4) 真实数据集上的实验结果表明,所提算法具有较低的信息损失和较好的数据可用性。
| [1] |
倪巍伟, 陈耿, 崇志宏, 等. 面向聚类的数据隐藏发布研究[J]. 计算机研究与发展, 2012, 49(5): 1095-1104. NI Weiwei, CHEN Geng, CHONG Zhihong, et al. Privacy-preserving data publication for clustering[J]. Journal of computer research and development, 2012, 49(5): 1095-1104. (  0) 0)
|
| [2] |
李洪成, 吴晓平, 陈燕. MapReduce框架下支持差分隐私保护的k-means聚类方法[J]. 通信学报, 2016, 37(2): 124-130. LI Hongcheng, WU Xiaoping, CHEN Yan. K-means clustering method preserving differential privacy in MapReduce framework[J]. Journal on communications, 2016, 37(2): 124-130. (  0) 0)
|
| [3] |
吴英杰, 唐庆明, 倪巍伟, 等. 基于聚类杂交的隐私保护轨迹数据发布算法[J]. 计算机研究与发展, 2013, 50(3): 578-593. WU Yingjie, TANG Qingming, NI Weiwei, et al. A clustering hybrid based algorithm for privacy preserving trajectory data publishing[J]. Journal of computer research and development, 2013, 50(3): 578-593. (  0) 0)
|
| [4] |
OLIVEIRA S R M, ZAANE O R. Privacy preserving clustering by data transformation[J]. Journal of information and data management, 2010, 1(1): 37-52. (  0) 0)
|
| [5] |
KOMISHANI E G, ABADI M. A generalization-based approach for personalized privacy preservation in trajectory data publishing[C]//Proceedings of the 6th International Symposium on Telecommunications. Tehran, Iran, 2012: 1129-1135.
(  0) 0)
|
| [6] |
VAIDYA J, CLIFTON C. Privacy-preserving k-means clustering over vertically partitioned data[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, August 24-27, 2003, Washington DC, USA. New York: ACM Press, 2003: 206-215.
(  0) 0)
|
| [7] |
康海燕, 杨孔雨, 陈建明. 基于K-匿名的个性化隐私保护方法研究[J]. 山东大学学报(理学版), 2014, 49(9): 142-149. KANG Haiyan, YANG Kongyu, CHEN Jianming. A method of personalized privacy preservation based on k-anonymization[J]. Journal of Shandong University (natural science), 2014, 49(9): 142-149. DOI:10.6040/j.issn.1671-9352.2.2014.320 (  0) 0)
|
| [8] |
王波, 杨静, 张健沛. 基于熵分类的个性化隐私匿名方法[J]. 吉林大学学报(工学版), 2013, 43(1): 179-185. WANG Bo, YANG Jing, ZHANG Jianpei. Entropy-based classification approach for personalized privacy anonymity[J]. Journal of Jilin University (engineering and technology edition), 2013, 43(1): 179-185. (  0) 0)
|
| [9] |
GAO Sheng, MA Jianfeng, SUN Cong, et al. Balancing trajectory privacy and data utility using a personalized anonymization model[J]. Journal of network and computer applications, 2014, 38: 125-134. DOI:10.1016/j.jnca.2013.03.010 (  0) 0)
|
| [10] |
杨静, 张冰, 张健沛, 等. 基于图划分的个性化轨迹隐私保护方法[J]. 通信学报, 2015, 36(3): 2015053. YANG Jing, ZHANG Bing, ZHANG Jianpei, et al. Personalized trajectory privacy preserving method based on graph partition[J]. Journal on communications, 2015, 36(3): 2015053. (  0) 0)
|
| [11] |
KOMISHANI E G, ABADI M, DELDAR F. PPTD:preserving personalized privacy in trajectory data publishing by sensitive attribute generalization and trajectory local suppression[J]. Knowledge-based systems, 2016, 94: 43-59. DOI:10.1016/j.knosys.2015.11.007 (  0) 0)
|
| [12] |
WEI W, LEI C, QIAN Z. Outsourcing high-dimensional healthcare data to cloud with personalized privacy preservation[J]. Computer networks, 2015, 88(9): 136-148. (  0) 0)
|
| [13] |
XIAO P, Weizhang C, Lei W, et al. Protecting personalized privacy against sensitivity homogeneity attacks over road networks in mobile services[J]. Frontiers of computer science, 2016, 10(2): 370-382. DOI:10.1007/s11704-015-4528-9 (  0) 0)
|
| [14] |
CAI Xiao, NIE Feiping, HUANG Heng. Multi-view k-means clustering on big data[C]//Proceedings of the IJCAI '13 Twenty-Third International Joint Conference on Artificial Intelligence. Beijing, China, 2013: 2598-2604.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


