潜艇在水下航行时,要实现水平面上的航行方向调整和垂直面上的航行深度调整,主要是通过操纵艉舵、围壳舵(或者是艏舵)来完成的。打舵时,舵上产生的水动力作用在潜艇艇体上,使潜艇产生相应的运动变化和航行状态的调整,因此舵的水动力性能对潜艇的操纵性表现有直接的影响。舵的外形及水动力优化是船舶操纵性研究领域的热点问题[1-4],而对于潜艇操纵面的优化设计,研究者和设计师在开展传统的艉部十子型舵水动力性能优化的基础上[5-6],提出了X型舵、H型舵、木字舵等多种尾操纵面的样式和分离式操舵方法[7-10]。由于潜艇在水下运动时,要兼顾航行的稳定性和机动性,所以国内外多型潜艇艉操纵面采用了稳定翼加转动舵的组合形式,前部的稳定翼与艇体固连,在提高潜艇航行稳定性的同时还可以对后部的可转动舵起到保护作用[11],这种设计类似于襟翼舵,但又不同于一般的襟翼舵[6]。从公开的潜艇外形对比来看,国内外对潜艇艉部稳定翼加转动舵组合形式的布局存在较大的差异。德国的214型潜艇、英国的机敏级潜艇、俄罗斯的北风之神级潜艇等新型潜艇艉部稳定翼和舵采用了的是一种共翼型设计,即艉舵与稳定翼组合成完整的翼型剖面,舵轴靠前缘布置,稳定翼和舵的间隙很小;而国内潜艇从公开的图片上看,艉部稳定翼和艉舵的布局是:后部的艉舵具有独立完整的翼剖面线型,舵轴布置在水动力作用中心附近,前部稳定翼的剖面线型不完整,稳定翼与舵之间有较大的间隙。从定性的认识上看,共翼型舵在转舵过程中,舵与稳定翼的线型能够保持连续光顺,而非共翼型舵的布局可能会使得舵翼结合部的流场恶化。
为了分析共翼型舵的技术优势,本文采用模型试验和数值模拟计算的方法,对比研究了共翼型舵和非共翼型舵在水动力性能和流场特征,总结了共翼型舵的优势和不足。
1 舵的模型根据共翼型舵和非共翼型舵的型线特点和几何形状特点,结合试验研究所用循环水洞工作段的参数,研究中所用的共翼型舵及非共翼型舵外形尺寸如图 1所示。

|
Download:
|
| 图 1 舵模型总体尺寸 Fig. 1 Main size of the rudder model | |
两种舵各外形尺寸相同,且每一横剖面处完整的线型相同,只是在稳定翼和转动舵分割处分别采用共翼型与非共翼型的方式,最小间距都为1 mm。共翼型舵的舵轴处于首部圆弧的圆心处,舵轴线距离舵尾段87.0 mm;非共翼型舵的舵轴处于舵首部端点向后30%弦长位置处,舵轴线距离舵尾段73.0 mm,两种舵的转动部分投影面积相等。
2 舵水动力性能的对比分析舵作为一种操纵设备,最基础的水动力性能是在一定偏转角度(即舵角)下能够产生垂直于来流方向上的升力性能以及所需的转矩大小,其阻力表现尽管也很重要,但是对于整个船体或潜艇艇体而言所占比例是极小的。
分别采用循环水洞试验测量的方法和数值模拟计算的方法开展了共翼型舵模型和非共翼型舵模型的水动力性能对比研究。
2.1 舵水动力性能的试验测量在循环水洞中开展了两种舵的水动力性能测量试验,主要测量了两种舵在不同舵角下的升力、阻力与舵轴转矩。需要注意的是,由于稳定翼和转动舵距离很近,翼和舵的流场和水动力会有相互的耦合效应,因此在试验中分别测量了前部稳定翼的升力、后部转动舵的升力以及转动舵的舵轴力矩随舵角的变化。试验所用的水洞设备、舵模型以及舵在水洞中的安装分别如图 2和图 3所示。水洞的试验工作段横截面为600 mm×600 mm,工作段长2 600 mm。试验中水流速度为3.87 m/s,水流速度的稳速精度在0.3%以内。

|
Download:
|
| 图 2 试验水洞 Fig. 2 Experimental water tunnel | |

|
Download:
|
| 图 3 舵模型及其试验安装 Fig. 3 Rudder model and its arrangement in water tunnel | |
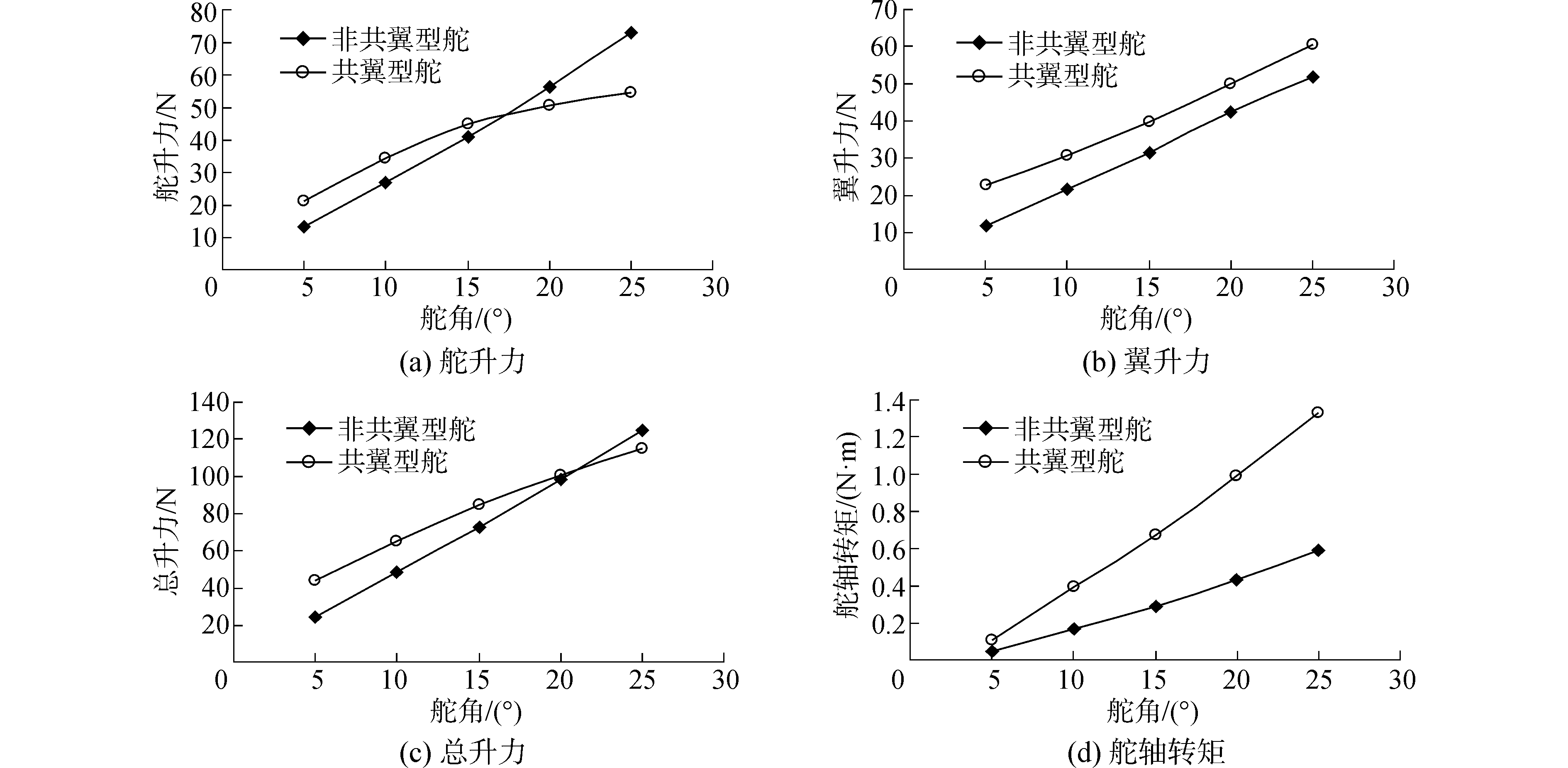
图 4给出了共翼型舵与非共翼型舵的转动舵升力、稳定翼升力、舵与翼总的升力以及两种舵的舵轴力矩随舵角的变化。从图 4可以看出:1)对于稳定翼和转动舵的组合操纵面,操舵后产生的升力包括舵上升力和稳定翼上升力两部分,稳定翼上升力不可忽视;2)对比表明,共翼型舵相对于非共翼型舵而言,前部稳定翼上的升力明显增大,且在小舵角时增加的幅度非常明显;3)本研究中所用的共翼型舵在20°以内的中、小舵角水动力性能优于非共翼型舵,在大舵角情况下的水动力性能恶化,所以应结合潜艇操纵运动中实际使用舵角情况和操纵性指标要求,综合考虑共翼型舵的应用问题以及水动力性能的优化问题;4)由于共翼型舵舵轴位置大幅前移,使得其舵轴力矩明显大于非共翼型舵。
|
Download:
|
| 图 4 舵水动力性能的对比 Fig. 4 Comparison on the hydrodynamic force of rudder | |
采用计算流体力学(CFD)方法对舵翼组合操纵面的水动力性能和流场进行模拟计算。对于舵翼组合操纵面的计算,需要重点关注两种舵的流场细节,特别是舵翼结合部位置的涡结构和舵面处的流动分离现象,因此运用分离涡模型进行舵的水动力性能和流场模拟计算。该方法在求解流动基本控制方程——Navier-Stockes方程的过程中,对湍流的模拟采用了时均雷诺应力项的方法与大涡模拟方法相结合的方式[12]。即在壁面湍流边界层内,对微尺度且可认为不受物体外形影响的湍流进行模式处理,从而节省计算资源;而在外部区域采用大涡模拟以更充分和更高精度地对“大尺度”流动进行准确求解。
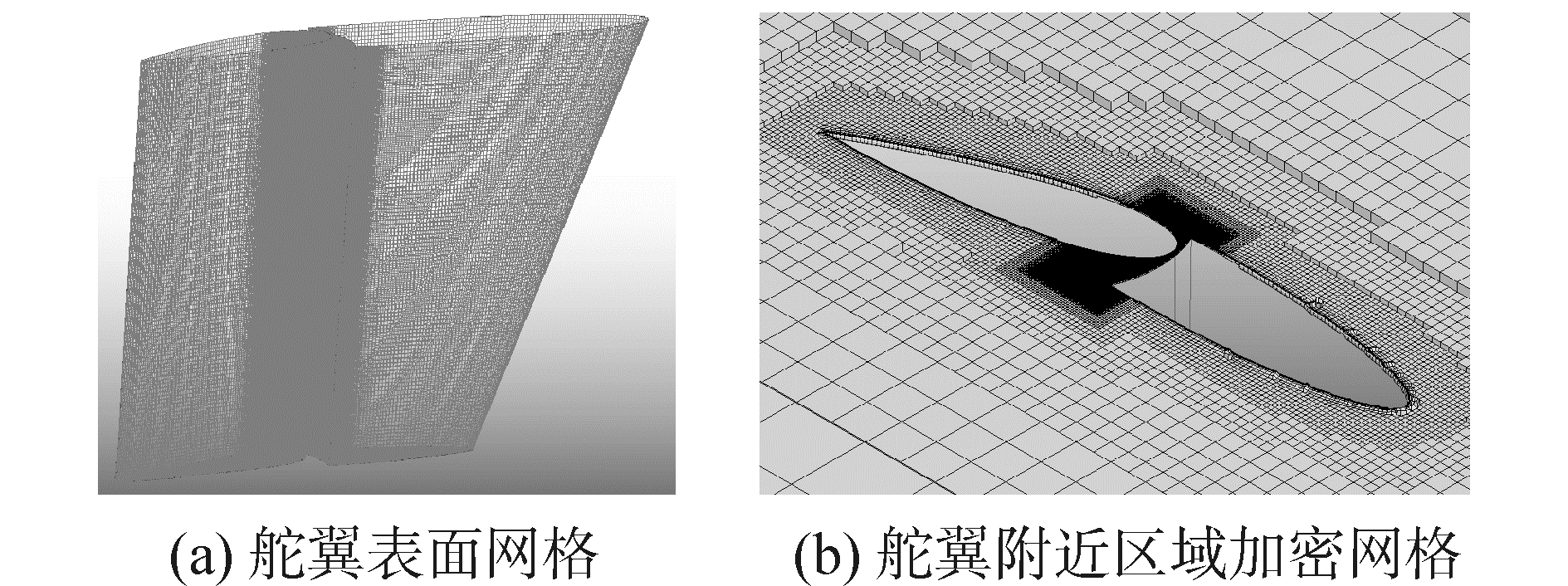
计算所用模型完全按照试验模型建立,并按照水洞工作段和舵在水洞中的安装位置建立计算流域(2 600 mm×600 mm×600 mm),计算流域前方进口设置为速度入口边界条件,后方出口设置为压力出口边界条件,四周设置为壁面条件。舵翼表面计算网格如图 5所示,在舵翼结合部设置了加密块,整个流域计算网格数量为1.224×107。
|
Download:
|
| 图 5 计算网格 Fig. 5 Computational grid | |
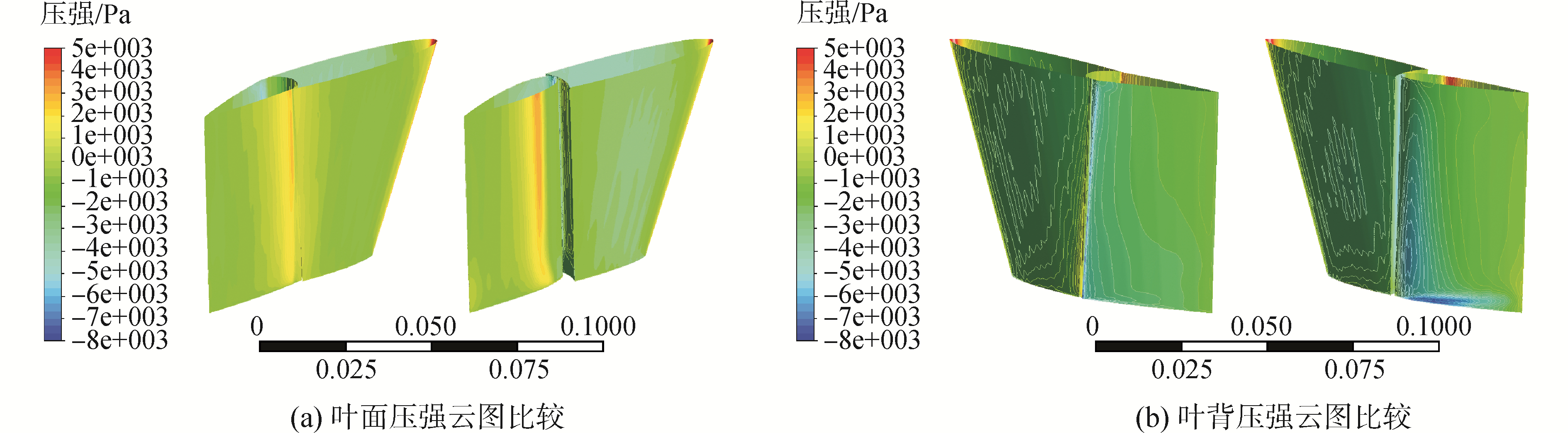
在来流流速3.87 m/s的条件下,分别计算了5°、15°、25°三种舵角下的流场和水动力,以代表小舵角、中舵角和大舵角典型工况。图 6~8分别给出了这三种舵角下共翼型舵(左侧图)和非共翼型舵(右侧图)叶面和叶背上的压力云图。

|
Download:
|
| 图 6 舵角5°时压强云图的比较 Fig. 6 Comparison on the pressure contour at rudder angle of 5° | |
|
Download:
|
| 图 7 舵角15°时压强云图的比较 Fig. 7 Comparison on the pressure contour at rudder angle of 15° | |

|
Download:
|
| 图 8 舵角25°时压强云图的比较 Fig. 8 Comparison on the pressure contour at rudder angle of 25° | |
从图12~14的比较可以看出,在5°舵角时,共翼型舵叶面正压力区域较大且分布较均匀,叶背的负压值较大;在15°舵角时,共翼型舵叶面的正压力区域(特别是在舵翼结合部和前部稳定翼处)范围较大;在25°舵角时,非共翼型舵的后部舵叶叶背导边处有较强的负压区。上述压力分布云图的对比可以通过总的水动力数值结果的比较进一步反映(如表 1所示)。
| 表 1 舵水动力的计算结果 Tab.1 Computational result of the rudder hydrodynamics |
从表 1的水动力计算结果可以看出,翼升力、舵升力及舵轴转矩随舵角的变化规律与试验结果一致,且与压力云图的分布规律相吻合,计算结果的数值与图 8~11中的试验测量数值相比达到工程精度要求。

|
Download:
|
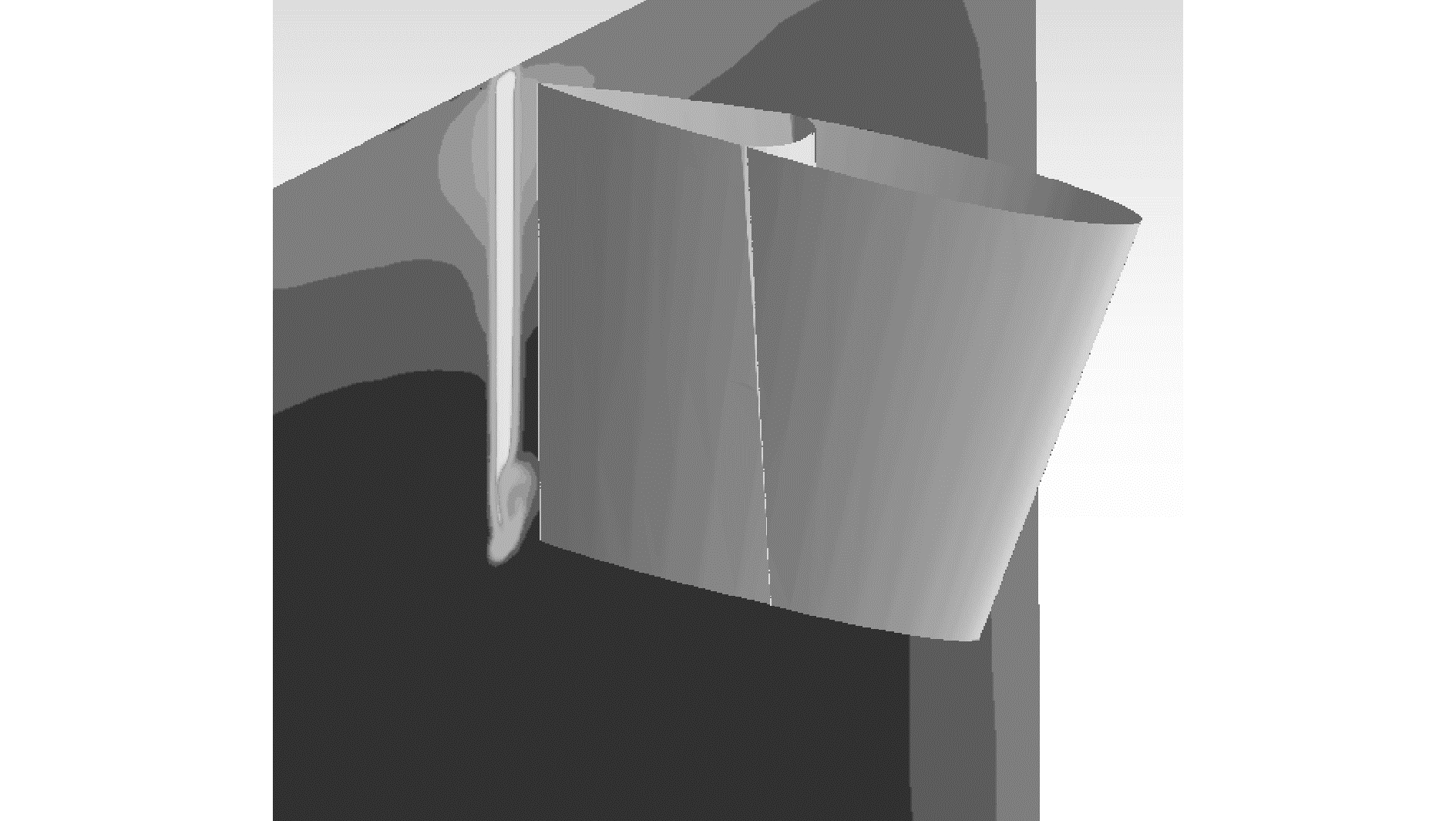
| 图 9 剖面流线图的比较 Fig. 9 Comparison on the section streamlines | |
|
Download:
|
| 图 10 尾流截面的位置 Fig. 10 Section position for the wake | |
|
Download:
|
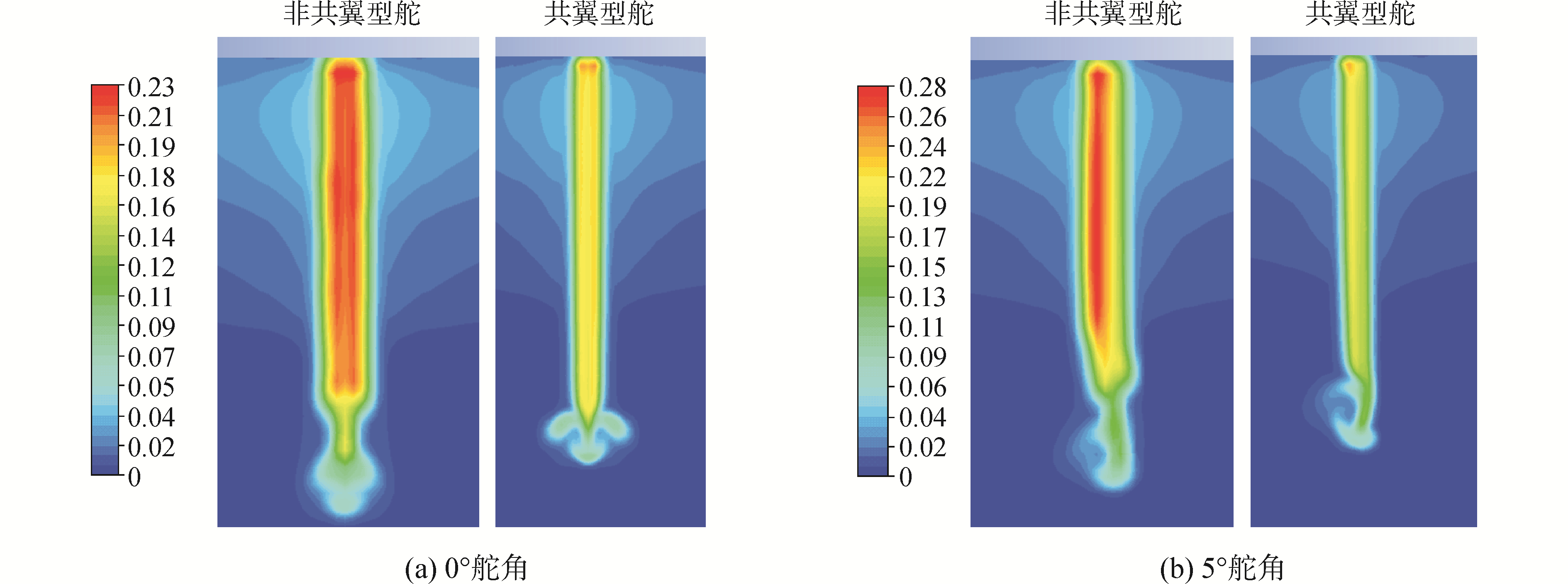
| 图 11 尾流湍流度的比较 Fig. 11 Comparison on the turbulent intensity of the rudder wake | |
第2节的研究显示出共翼型舵与非共翼型舵的水动力性能有很大的差异,为了从流场结构的角度探究差异形成的原因,进一步开展了两种舵的流场特征对比分析。水洞试验过程中未开展流场测量,因此流场特征研究根据数值计算模拟来进行。由水动力计算结果与试验测量结果的对比表明二者规律一致且数值具有较高精度,可以认为舵的流场计算精度虽然无法验证,但是两种舵的流场结构差异应该是符合实际的,并最终通过宏观的水动力上的差异体现出来。
3.1 舵水平剖面上流场的对比在数值模拟计算结果中,截取了两种舵在展长中点位置处水平剖面上的流线图,进行了5°、15°、25°舵角下的流线分布对比(如图 9所示)。
从计算对比可以看出:1)非共翼型舵由于稳定翼与舵过渡处线型不连续,所以各舵角下过渡位置都会形成涡流,这种涡流对前面的稳定翼和后面舵的水动力都有不利影响,而共翼型舵方案由于稳定翼与舵的线型是光滑过渡的,所以消除了过渡位置涡流;2)共翼型舵在小舵角时有较好的流线品质,因而其升力性能明显好于非共翼型舵,但大舵角时舵面上形成分离涡,导致类似于机翼的失速现象产生,水动力性能随之明显下降;3)非共翼型舵在小舵角时主体处于前部稳定翼的尾流中,工作环境差升力性能不好;大舵角时,舵的导边和主体可以突出稳定翼尾流区、受稳定翼尾流的影响小,完整翼型的水动力性能优势能够显现出来。共翼型舵从整体上看,导边迎流处无法形成攻角,而对于完整的舵而言,在来流攻角作用下导边附近的叶背叶面压力差对升力的贡献最大,所以共翼型舵在大舵角工况下水动力性能会变差。
3.2 舵尾部横截面上流场特性的对比在潜艇总体设计上,推进器布置在尾部操纵面之后,尾部操纵面的流场扰动会顺艇体直接进入推进器。抑制进入推进器流场的不均匀度和湍流脉动是控制潜艇推进器振动噪声的重要方面,因此开展了两种舵尾流特征的对比。由于潜艇在静音航行时,不可能使用大角度工况,所以只对比了0°舵角和5°舵角两种舵的尾部流场特性。尾部流场横截面所取的位置是在舵尾端向下游0.5倍的最大厚度处(如图 10所示),舵尾流湍流度的比较对比结果如图 11所示。
从图 11的对比可以看出,共翼型舵在小角度和0°时尾流的湍流度强度明显小于非共翼型舵,对于改善处于舵尾流影响中的推进器入流品质是有利的。潜艇推进器入流湍动能减小、流动更为均匀稳定,将会有利于改善推进器的振动噪声性能和空泡性能。
4 结论1) 共翼型舵能够避免舵翼结合部处的涡流,保持流线的光顺,在小舵角工况时水动力性能和尾流的均匀性、稳定性明显优于传统的非共翼型舵。
2) 非共翼型舵在小舵角时舵翼结合部处的流场较差,并且舵的主体处于前部稳定翼的尾流中,所以水动力较差,但在大攻角时能够突破尾流影响,舵完整翼型的水动力性能显著提升;而共翼型在大舵角时叶背容易产生流动分离涡,水动力性能下降。
3) 共翼型舵的舵轴前移,导致其各舵角时的舵轴转矩显著大于非共翼型舵的舵轴转矩,这是共翼型舵从原理上就会存在的固有不足。
本文开展了共翼型舵与传统非共翼型平衡舵水动力性能上的比较研究,既得到了共翼型舵的优势也发现了其不足,后续将围绕共翼型舵大攻角时流动分离控制、舵轴转矩控制以及艇体边界层条件影响下的两种舵结构的性能对比等问题,开展深入研究,服务于共翼型舵技术的工程应用。
| [1] |
LIU Jialun, QUADVLIEG F, HEKKENBERG R. Impacts of the rudder profile on manoeuvring performance of ships[J]. Ocean engineering, 2016, 124: 226-240. DOI:10.1016/j.oceaneng.2016.07.064 (  0) 0)
|
| [2] |
MOLLAND A F, TURNOCK S R. Marine rudders and control surfaces[M]. Amsterdam, London: Elsevier, Butterworth-Heinemann, 2007: 42-44.
(  0) 0)
|
| [3] |
KIM H J, KIM S H, OH J K, et al. A proposal on standard rudder device design procedure by investigation of rudder design process at major Korean shipyards[J]. Journal of marine science and technology, 2012, 20(4): 450-458. (  0) 0)
|
| [4] |
LIU Jialun, HEKKENBERG R. Sixty years of research on ship rudders:effects of design choices on rudder performance[J]. Ships and offshore structures, 2017, 12(4): 495-512. DOI:10.1080/17445302.2016.1178205 (  0) 0)
|
| [5] |
祝享元, 黄胜, 郭春雨, 等. 桨后扭曲舵的理论设计及水动力性能计算[J]. 哈尔滨工程大学学报, 2008, 29(2): 126-129. ZHU Xiangyuan, HUANG Sheng, GUO Chunyu, et al. Design and performance of a skew rudder behind a propeller[J]. Journal of Harbin Engineering University, 2008, 29(2): 126-129. (  0) 0)
|
| [6] |
杨立, 张华, 沈定安, 等. 舵型参数对襟翼舵升力特性影响的数值计算研究[J]. 中国造船, 2017, 58(1): 19-27. YANG Li, ZHANG Hua, SHEN Ding'an, et al. Numerical research on influence of parameters of flap-rudder on its lift performance[J]. Shipbuilding of China, 2017, 58(1): 19-27. (  0) 0)
|
| [7] |
PARK J Y, KIM N, SHIM Y K. Experimental study on hydrodynamic coefficients for high-incidence-angle maneuver of a submarine[J]. International journal of naval architecture and ocean engineering, 2017, 9(1): 100-113. DOI:10.1016/j.ijnaoe.2016.08.003 (  0) 0)
|
| [8] |
DUBBIOSO G, BROGLIA R, ZAGHI S. CFD analysis of turning abilities of a submarine model[J]. Ocean engineering, 2017, 129: 459-479. DOI:10.1016/j.oceaneng.2016.10.046 (  0) 0)
|
| [9] |
王京齐, 潘子英, 施生达. 水下航行体分片式艉水平舵操纵性水动力试验[J]. 海军工程大学学报, 2013, 25(4): 52-55, 78. WANG Jingqi, PAN Ziying, SHI Shengda. Model test study for maneuverability hydrodynamics of submarine's stern horizontal rudders in different subsection[J]. Journal of Naval University of Engineering, 2013, 25(4): 52-55, 78. (  0) 0)
|
| [10] |
CIOBACA V. Validation of numerical simulations for separation control on high-lift configuration[D]. Braunschweig: German Aerospace Center, 2014: 45-48. http://www.researchgate.net/publication/288129044_Validation_of_numerical_simulations_forr_separation_control_on_high-lift_configurations
(  0) 0)
|
| [11] |
吴宝山, 潘子英, 陈纪军, 等. 潜艇组合翼舵的水动力非线性特性研究[J]. 船舶力学, 2008, 12(1): 54-58. WU Baoshan, PAN Ziying, CHEN Jijun, et al. Investigation on nonlinear characteristics of normal force on stern-plane of submarine by CFD simulation[J]. Journal of ship mechanics, 2008, 12(1): 54-58. (  0) 0)
|
| [12] |
LIU Zhihua, XIONG Ying, TU Chengxu. The method to control the submarine horseshoe vortex by breaking the vortex core[J]. Journal of hydrodynamics, ser. B, 2014, 26(4): 637-645. DOI:10.1016/S1001-6058(14)60070-6 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


