疲劳破坏是船舶与海洋工程结构破坏的主要模式之一。多年来,船舶结构的疲劳断裂问题一直是造船界所关注的课题[1]。目前,船舶结构疲劳寿命的预报大多基于确定性方法,得到的疲劳分析结果也是确定的损伤值。然而,船舶结构的疲劳分析中涉及的疲劳载荷计算、S-N曲线以及Miner线性累积损伤模型等存在很大的不确定因素,疲劳分析结果必然存在可靠性问题[2-3]。Ang等[4]对LNG船的疲劳分析表明,通过确定性的方法校核满足疲劳强度要求,但疲劳热点在设计寿命周期内失效概率竟然达到20%左右。因此有必要采用基于结构可靠性理论方法进行船舶结构疲劳寿命的预报,进而从概率统计的角度对结构的疲劳寿命作出合理的预测。
Muhammed等[5]总结了基于S-N曲线简化分析方法的船舶与海洋工程疲劳可靠性分析方法,并分析了各不确定性因素对船舶与海洋工程结构物可靠性指标的影响关系。Garbatov等[6]对船舶与海洋工程疲劳可靠性分析中涉及的船舶主尺度、船型、波浪散布图、波浪谱及浪向角、焊接点形状、名义应力的不完整性等因素做了全面地分析对比,并给出了详尽的对比结果。国内方面,何文涛[7]采用Kriging代理模型和裂纹扩展方法研究了船体典型节点的疲劳寿命可靠性问题。徐帅[8]针对LNG船典型热点采用JC法计算疲劳可靠性指标, 并研究极限疲劳损伤值、S-N曲线和疲劳载荷等变量对可靠性指标的敏感性。胡毓仁等[1, 9], 在这方面也做了相当多的工作。
上述研究中,大多数采用疲劳分析的简化分析方法,或者基于简化的应力响应分析的谱分析法,且只考虑少数工况以减少工作量。本文采用整船有限元分析、考虑全浪向全工况的谱分析直接计算方法,给出了船体结构的疲劳可靠性分析的直接计算方法,并以高性能三体船为例进行了算例分析。
1 船体疲劳强度计算方法 1.1 应力范围的概率密度函数在疲劳强度可靠性的频域直接计算中,应力范围的概率密度函数的确定是首先要解决的问题。
对于每一个短期海况,根据随机过程理论可知,应力峰值服从Rayleigh分布,采用概率论中随机变量函数的概率密度的计算方法,可得应力范围的概率密度函数为
| $ {f_S}\left( S \right) = \frac{S}{{4{m_0}}}\exp \left( { - \frac{{{S^2}}}{{8{m_0}}}} \right)\;\;\;\;0 \le S < + \infty $ | (1) |
式中:m0为应力响应谱的零次矩,通过响应谱的功率谱密度获得。
在假定船舶结构为线性系统的前提下,应力的响应谱GXX(ωe)为
| $ {G_{XX}}\left( {{\omega _e}} \right) = {\left| {{H_\sigma }\left( {{\omega _e}} \right)} \right|^2} \cdot {G_{\eta \eta }}\left( {{\omega _e}} \right) $ | (2) |
式中:Gηη(ωe)为以遭遇频率ωe表达的波能谱,Hσ(ωe)为应力响应传递函数。
应力响应传递函数通常通过基于三维势流理论的波浪载荷计算和基于热点应力的整船有限元分析方法确定。
1.2 应力参数的定义为便于后续疲劳可靠性的分析,定义应力参数如下:
对于短期分布,定义第i海况中应力参数为
| $ {\mathit{\Omega }_i} = {f_{{L_i}}}{\rm{E}}{\left( {{S^m}} \right)_i} = {f_{{L_i}}}\int\limits_0^{ + \infty } {{S^m}{f_{{S_i}}}\left( S \right){\rm{d}}S} $ | (3) |
式中:fLi为第i海况中的应力范围作用的平均频率,fSi(S)为第i海况应力范围短期分布的概率密度函数。
对于长期分布,定义应力参数为
| $ \begin{array}{*{20}{c}} {\mathit{\Omega } = \sum\limits_{i = 1}^k {{\gamma _i}{\mathit{\Omega }_i}} = \sum\limits_{i = 1}^k {{\gamma _i}{f_{{L_i}}}{\rm{E}}{{\left( {{S^m}} \right)}_i}} = }\\ {\sum\limits_{i = 1}^k {{\gamma _i}{f_{{L_i}}}\int\limits_0^{ + \infty } {{S^m}{f_{{S_i}}}\left( S \right){\rm{d}}S} } } \end{array} $ | (4) |
式中:γi为第i海况作用的时间占整个载荷谱回复周期的比例,k为海况个数。
将式(1)代入式(4),可得应力参数:
| $ \begin{array}{*{20}{c}} {\mathit{\Omega } = \sum\limits_{i = 1}^k {{\gamma _i}{\mathit{\Omega }_i}} = \sum\limits_{i = 1}^k {{\gamma _i}{f_{{L_i}}}{{\left( {2\sqrt 2 {\sigma _{{X_i}}}} \right)}^m}\mathit{\Gamma }\left( {\frac{m}{2} + 1} \right)} = }\\ {{{\left( {2\sqrt 2 } \right)}^m}\mathit{\Gamma }\left( {\frac{m}{2} + 1} \right)\sum\limits_{i = 1}^k {{\gamma _i}f_{{L_i}{\sigma _{{X_i}}}}^m} } \end{array} $ | (5) |
假设所考虑的船舶在第i海况和第j航向中航行时间为Tij期间的累积损伤度Dij为
| $ {D_{ij}} = \frac{{{T_{ij}}{f_{0ij}}}}{A}\int\limits_0^{ + \infty } {{S^m}{f_{Sij}}\left( S \right){\rm{d}}S} $ | (6) |
式中f0ij为该应力交变过程的跨零率。
整个寿命期总的疲劳累积损伤为
| $ D = \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^p {{D_{ij}}} } = \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^p {\frac{{{T_{ij}}{f_{0ij}}}}{A}\int\limits_0^{ + \infty } {{S^m}{f_{Sij}}\left( S \right){\rm{d}}S} } } $ | (7) |
式中p为航向个数。
考虑到短期海况和长期海况应力参数的定义,损伤可表达为
| $ D = \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^p {{D_{ij}}} } = \frac{T}{A}\sum\limits_{i = 1}^k {\sum\limits_{j = 1}^p {{\gamma _i}{\mathit{\Omega }_{ij}}} } = \frac{T}{A}\mathit{\Omega } $ | (8) |
疲劳寿命的随机性质因素主要由S-N曲线、疲劳载荷计算以及Miner线性累积损伤模型的不确定因素组成。其中,S-N曲线的不确定因素由参数A体现。
以随机变量B表示疲劳载荷的计算过程中不确定性,真实的应力范围可表示为
| $ {S_a} = BS $ | (10) |
从而,计及真实应力范围后的应力参数为
| $ {\mathit{\Omega }_a} = {B^m}\mathit{\Omega } $ | (11) |
应力参数Ω仍根据应力范围的计算结果S来计算,作为确定值处理,而疲劳载荷计算过程中的不确定因素则通过随机变量B来计及。
以随机变量Δ考虑Miner线性累积损伤破环时的随机性,结构发生疲劳破坏时:
| $ D = \Delta $ | (12) |
考虑上述不确定因素后,结构的疲劳寿命可写成
| $ {T_f} = \frac{{\Delta A}}{{{B^m}\mathit{\Omega }}} $ | (13) |
依照结构可靠性理论的基本原理,安全余量为
| $ Z = {T_f} - {T_D} = \frac{{\Delta A}}{{{B^m}\mathit{\Omega }}} - {T_D} $ | (14) |
式中A、B、Δ为基本随机变量。
在船舶与海洋工程领域,基本随机变量A、B、Δ通常认为服从对数正态分布,从而形成计算结构疲劳寿命可靠度的对数正态格式。
在此假设下,安全余量可等效写成
| $ \begin{array}{*{20}{c}} {Z = \ln {T_f} - \ln {T_D} = \ln \left( {\frac{{\Delta A}}{{{B^m}\mathit{\Omega }}}} \right) - \ln {T_D} = }\\ {\ln \Delta + \ln A - m\ln B - \ln \mathit{\Omega } - \ln {T_D}} \end{array} $ | (15) |
式中lnA、lnB、lnΔ为正态分布随机变量。
依照式(13),疲劳寿命Tf也为对数正态分布随机变量,其中值和标准差分别为
| $ {{\tilde T}_f} = \frac{{\tilde \Delta \tilde A}}{{{{\tilde B}^m}\mathit{\Omega }}} $ | (16) |
| $ {C_{{T_f}}} = {\left[ {\left( {1 + C_\Delta ^2} \right)\left( {1 + C_A^2} \right){{\left( {1 + C_B^2} \right)}^{{m^2}}} - 1} \right]^{1/2}} $ | (17) |
随机变量lnTf的中值和标准差分别为
| $ {\mu _{\ln {T_f}}} = \ln {{\tilde T}_f} = \ln \left( {\frac{{\tilde \Delta \tilde A}}{{{{\tilde B}^m}\mathit{\Omega }}}} \right) $ | (18) |
| $ \begin{array}{*{20}{c}} {{\sigma _{\ln {T_f}}} = {{\left[ {\ln \left( {1 + C_{{T_f}}^2} \right)} \right]}^{1/2}} = }\\ {{{\left\{ {\ln \left[ {\left( {1 + C_\Delta ^2} \right)\left( {1 + C_A^2} \right){{\left( {1 + C_B^2} \right)}^{{m^2}}}} \right]} \right\}}^{1/2}}} \end{array} $ | (19) |
结构疲劳寿命可靠性指标及可靠度为
| $ \beta = \frac{{{\mu _{\ln {T_f}}} - \ln {T_D}}}{{{\sigma _{\ln {T_f}}}}} = \frac{{\ln {{\tilde T}_f} - \ln {T_D}}}{{{\sigma _{\ln {T_f}}}}} = \frac{{\ln \left( {\frac{{{{\tilde T}_f}}}{{{T_D}}}} \right)}}{{{{\left[ {\ln \left( {1 + C_{\ln {T_f}}^2} \right)} \right]}^{1/2}}}} $ | (20) |
| $ {p_r} = \mathit{\Phi }\left( \beta \right) $ | (21) |
高速三体船作为一种具有优良耐波性等特点的新型高性能船型,具有极大的发展潜力[10-12]。其特有的连接桥结构,应力集中问题严重,疲劳强度问题显得特别突出。各国船级社规范中关于三体船的疲劳分析方法涉及不多。本文以某高速三体船为例,采用前面所述方法对连接桥结构进行疲劳寿命的可靠性分析。
3.1 有限元模型及分析部位三体船的船体外形及结构复杂, 热点应力计算采用局部细划网格镶入在全船有限元模型中的直接计算方法, 并采用结构净厚度[13]。依据三体船结构特点,疲劳校核部位在全船强度计算基础上并结合船体在不同浪向、频率下的结构应力响应,经过对比和筛选,确定结构强度较为薄弱的连接桥4个部位:
1) 连接桥及湿甲板首端与主船体间断处;
2) 连接桥中部湿甲板与主船体相交处;
3) 连接桥中部主体部位纵骨穿越强框架处;
4) 连接桥中部湿甲板与片体相交处。
3.2 波浪载荷计算及传递函数的计算本文采用基于三维线性势流理论计算船舶波浪载荷和运动响应。计算航速取为零。航向角取为0°~330°,间隔为30°,共计12个浪向,计算波浪圆频率ω取为0.1~2.9,步长为0.1共计29个。波浪载荷响应参数确定之后,利用波浪载荷计算软件WALCS进行计算,得到各规则波中的船体运动响应、剖面载荷响应及船体水动压力分布。限于篇幅,本文只给出迎浪情况、波浪圆频率ω=0.7 rad/s时船体水动压力分布,其施加在有限元模型后如图 2所示。

|
Download:
|
| 图 1 全船有限元分析模型 Fig. 1 The whole FE model of trimaran | |

|
Download:
|
| 图 2 迎浪下船体水动压力分布 Fig. 2 The hydrodynamic pressure on ship′s surface in head sea | |
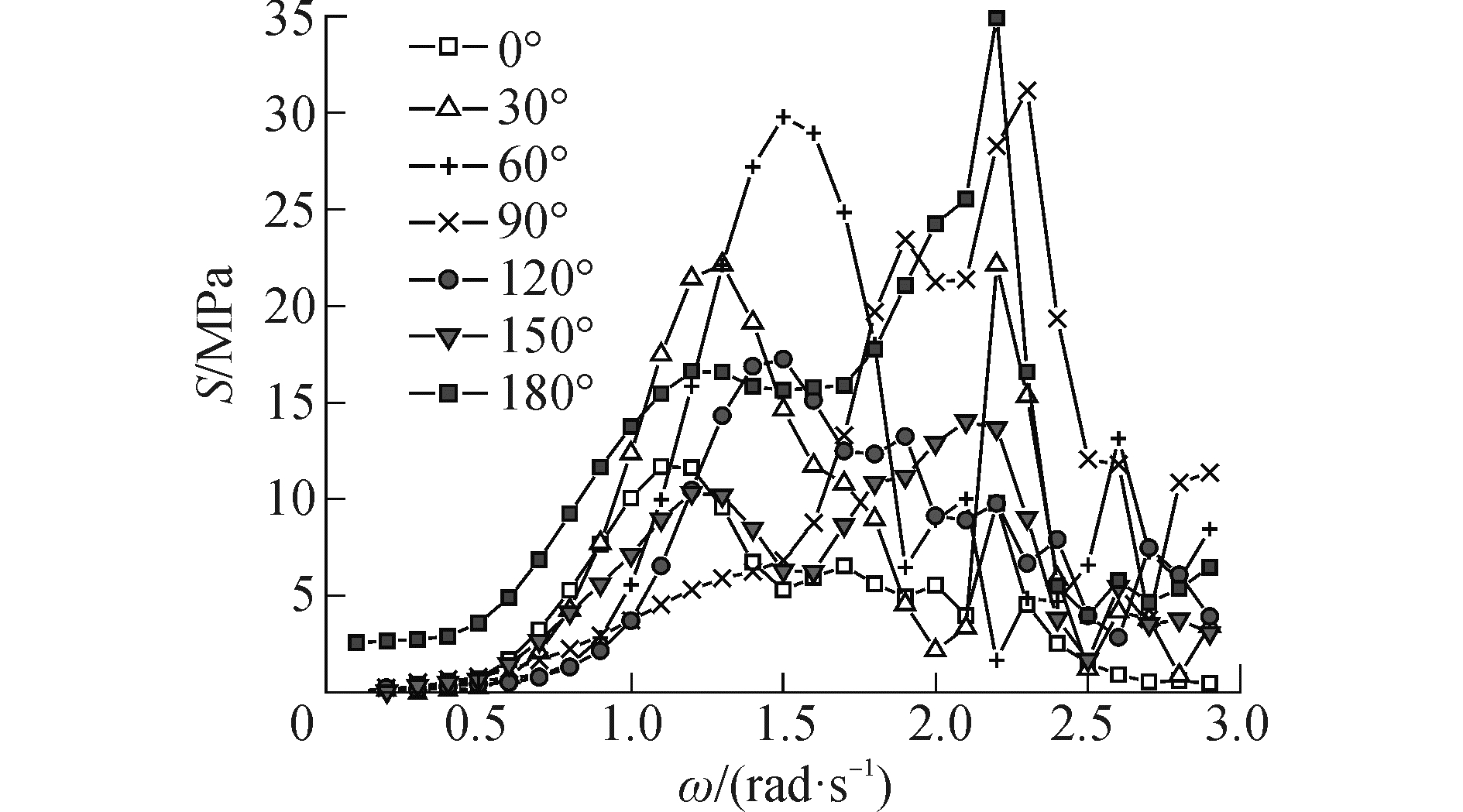
依照传递函数概念,将航向角为θ,圆频率为ω的单位波幅规则波下的外部水动压力和与船体运动有关的各种惯性力施加到船体结构有限元模型上,得到应力响应,其结果就是传递函数的值。限于篇幅关系,本文只给出热点3部位应力响应传递函数,如图 3所示。
|
Download:
|
| 图 3 热点3应力响应传递函数 Fig. 3 The stress transfer function of hotspot 3 | |
依照相关文献[1, 3],累积损伤和S-N曲线的中值和变异系数取为
| 表 1 疲劳寿命可靠度计算结果 Tab.1 Result of fatigue life′s reliability |
由表 1中的疲劳寿命可靠度的计算结果可以看出,疲劳寿命的可靠度在疲劳损伤较为严重的区域较小,且随着疲劳寿命的增加而增大,疲劳损伤很小的区域,发生疲劳失效的概率基本不存在,疲劳寿命的可靠度随着疲劳载荷变异系数的增大而减小。
4 结论1) 疲劳寿命可靠度计算算例表明,疲劳寿命的可靠度问题在疲劳损伤较为严重的区域较为严重,疲劳寿命可靠度大小与疲劳载荷不确定性因素的变异系数取值较为敏感。
2) 疲劳载荷以及其他影响疲劳寿命的不确定性因素的概率统计参数的准确确定,对疲劳寿命可靠性的精准计算是相当重要的。
| [1] |
胡毓仁, 陈伯真. 船舶与海洋工程结构疲劳可靠性分析[M]. 北京: 人民交通出版社, 1996: 110-114. HU Yuren, CHEN Bozhen. Fatigue reliability analysis of the ship and ocean engineering structures[M]. Beijing: China Communications Press, 1996: 110-114. (  0) 0)
|
| [2] |
DOSHI K, ROY T, PARIHAR Y S. Reliability based inspection planning using fracture mechanics based fatigue evaluations for ship structural details[J]. Marine structures, 2017, 54: 1-22. DOI:10.1016/j.marstruc.2017.03.003 (  0) 0)
|
| [3] |
MAHMOUD H, RIVEROS G. Fatigue reliability of a single stiffened ship hull panel[J]. Engineering structures, 2014, 66: 89-99. DOI:10.1016/j.engstruct.2014.02.007 (  0) 0)
|
| [4] |
ANG A H S, CHEUNG M C, SHUGAR T A, et al. Reliability-based fatigue analysis and design of floating structures[J]. Marine structures, 2001, 14(1/2): 25-36. (  0) 0)
|
| [5] |
MUHAMMED A, STACEY A. Probabilistic S-N fatigue assessment methods for welded joints in offshore structures[C]//Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering. Estoril, Portugal: ASME, 2008: 335-354. http://www.researchgate.net/publication/267604823_Probabilistic_S-N_Fatigue_Assessment_Methods_for_Welded_Joints_in_Offshore_Structures
(  0) 0)
|
| [6] |
GARBATOV Y, SOARES C G. Assessment of the uncertainties introduced by different fatigue damage models for ship structural details[C]//Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai: ASME, 2010: 549-559. https://www.researchgate.net/publication/263085873_Assessment_of_the_Uncertainties_Introduced_by_Different_Fatigue_Damage_Models_for_Ship_Structural_Details
(  0) 0)
|
| [7] |
HE Wentao, LIU Jingxi, XIE De. Probabilistic life assessment on fatigue crack growth in mixed-mode by coupling of Kriging model and finite element analysis[J]. Engineering fracture mechanics, 2015, 139: 56-77. DOI:10.1016/j.engfracmech.2015.03.040 (  0) 0)
|
| [8] |
徐帅. 基于谱分析法的LNG船疲劳可靠性分析[D]. 武汉: 华中科技大学, 2011: 24-26. XU Shuai. Fatigue reliability for LNG carrier using spectral-based analysis[D]. Wuhan: Huazhong University of Science And Technology, 2011: 24-26. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D187633 (  0) 0)
|
| [9] |
CUI Weicheng. Relation between crack growth rate curve and S-N curve for metal fatigue[J]. Journal of ship mechanics, 2002, 6(6): 93-106. (  0) 0)
|
| [10] |
卢晓平, 郦云, 董祖舜. 高速三体船研究综述[J]. 海军工程大学学报, 2005, 17(2): 43-48, 52. LU Xiaoping, LI Yun, DONG Zushun. A research summary on high speed trimaran[J]. Journal of naval university of engineering, 2005, 17(2): 43-48, 52. (  0) 0)
|
| [11] |
FANG M C, CHEN T Y. A parametric study of wave loads on trimaran ships traveling in waves[J]. Ocean engineering, 2008, 35(8/9): 749-762. (  0) 0)
|
| [12] |
WANG Yingguang. Spectral fatigue analysis of a ship structural detail-A practical case study[J]. International journal of fatigue, 2010, 32(2): 310-317. DOI:10.1016/j.ijfatigue.2009.06.020 (  0) 0)
|
| [13] |
甄春博, 王天霖, 于鹏垚. 基于直接计算的三体船结构疲劳强度影响因素分析[J]. 中国舰船研究, 2017, 12(3): 86-90. ZHEN Chunbo, WANG Tianlin, YU Pengyao. Influencing factor analysis for direct calculation of trimaran structure's fatigue strength[J]. Chinese journal of ship research, 2017, 12(3): 86-90. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


