2. 中国海洋大学 环境科学与工程学院, 山东 青岛 266100
2. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China
风能是一种新型的可再生能源,相比陆地上的风力发电,海上风力发电有一定的优势[1]。海上风力发电已经成为当下有效实用的新型可再生能源,减少了人们对化石燃料的依赖,海上风机系统的研究成为当务之急[2]。海上风机基础主要以单桩为主,因其结构较为简单,占用面积小,承载力高,沉降量小且均匀,适用范围广,使用比例高达60%以上[3]。
海上风机所处的海洋环境导致了桩基础长期承受波浪荷载、风荷载、潮流荷载等,增加了风机结构分析的难度。对于不同的波浪理论,波浪荷载有一定差异,应用最多的是经过深度衰减修正的小振幅波、Airy线性波和Stokes非线性波浪理论。戴国亮等[4]根据东海大桥的水文资料,对比了在不同波浪理论下的波浪参数以及桩基所受的波浪力,进一步考虑了潮流对波浪的影响。李德源等[5]采用三维线性波理论,将Morison方程推广到空间体系,研究了海上风机塔架的动力响应。GalvãN[6]考虑了桩土相互作用,建立了风机在波浪作用下的动力响应模型,探讨了不同土体参数对风机支撑系统动力响应的影响。Seong[7]进一步考虑了桩土结构物的相互作用,采用离心试验分析了风机系统的自振频率等动力特性。目前,大部分学者的研究主要集中在不同波浪理论下海上风机基础的静力特性和线性波作用下的动力响应,对于风机支撑结构在不同波浪理论下的动力响应研究相对较少。
本文通过建立风机系统有限元模型,探讨了风机支撑系统的弯矩、加速度、速度的变化规律以及振动特性,对比分析了不同波浪理论下风机支撑系统的动力响应。
1 波浪理论与数学模型 1.1 微振幅波浪理论该理论由Airy[8]提出,适用于浅水区域(h/L≤0.5),假定波浪在传播过程中不发生变形,其波形为正弦(余弦)曲线,波剖面方程为
| $ \eta \left( {t,x} \right) = \frac{H}{2}\cos \left( {kx - \sigma t} \right) $ | (1) |
式中:H为波高;k为波数,k=2π/L,L为波长;σ为波浪角频率。d为水深,相对水深(d/L)是影响波动性质的主要因素。
水平速度:
| $ u\left( {t,z} \right) = \sigma {G_s}\left( {z,d,L} \right)\eta \left( {t,x} \right) $ | (2) |
| $ {G_s} = \frac{{\cosh \left( {t,z} \right)}}{{dt}} $ | (3) |
式中:Gs为小振幅波深度衰减函数。
加速度:
| $ a = \frac{{du\left( {t,z} \right)}}{{dt}} $ | (4) |
当小振幅波的假设和基本理论不一致,在水平面波浪速度的表达不连续,此时需要利用经深度衰减修正的函数P(x, y),即
| $ g\left( {z,d,{L_n},\eta } \right) = \frac{{\cosh \left( {kz\frac{d}{{\eta + d}}} \right)}}{{\sinh \left( {kd} \right)}} $ | (5) |
式中:
最早由Stokes[10]提出,水深适用范围比Airy波更广,假设波浪为有限振幅,得到无限水深的五阶近似解,其波面方程以级数形式展开:
| $ \eta \left( {t,x} \right) = \sum\limits_1^n {\frac{H}{2}\cos \left( {kx - \sigma t} \right)} $ | (6) |
其余详细方程本文未列出。但值得注意的是Airy波即为Stokes波的一阶形式。
1.4 桩-土相互作用海上风机桩基础主要根据美国石油研究院(API)建议的P-y曲线来设计[11-12],P-y曲线法就是在水平力H的作用下,泥面以下深度X处的土反力P与该点桩的挠度y之间的关系曲线,本文采用Winkler地基模型,把桩周土离散为若干单独作用的弹簧,应用P-y曲线法[13-14],基本方程如下
| $ {\rm{EI}}\frac{{{{\rm{d}}^4}y}}{{{\rm{d}}{x^4}}} + bP\left( {x,y} \right) = 0 $ | (7) |
式中:P(x, y)为地基反力,y值为挠度,x值为沿桩身的长度,EI为桩的抗弯刚度,b为桩截面的计算宽度。式(7)综合反应了桩周土的非线性、桩的刚度和外载荷作用性质等特点。
王腾等通过水平荷载下的单桩模型试验,以API砂土的P-y曲线表达式为基础,得到了黄河粉土的P-y曲线表达式为[15]
| $ P = 1.26{P_u}\tanh \left( {kzy/{P_u}} \right) $ | (8) |
式中:Pu为承载力极限,k为初始地基反力模量,z为深度。并加以验证,该式(8)适用于黄河粉土。P-y曲线计算基于式(8),桩基及土体参数见上文。
1.5 瞬态分析动力方程瞬态分析就是时间历程分析,用于计算风机系统在循环荷载作用下的动力响应。其基本运动方程如下
| $ \mathit{\boldsymbol{M}}\left\{ {\mathit{\boldsymbol{\ddot U}}\left( t \right)} \right\} + \mathit{\boldsymbol{C}}\left\{ {\mathit{\boldsymbol{\dot U}}\left( t \right)} \right\} + \mathit{\boldsymbol{K}}\left\{ {\mathit{\boldsymbol{U}}\left( t \right)} \right\} = \left\{ {\mathit{\boldsymbol{F}}\left( t \right)} \right\} $ | (9) |
式中:M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵,
在进行循环荷载作用下的瞬态分析时,必须确定阻尼系数。本文采用比例阻尼法:
| $ \mathit{\boldsymbol{C}} = \alpha \mathit{\boldsymbol{M}} + \beta \mathit{\boldsymbol{K}} $ | (10) |
根据振型分解法,可分别求出阻尼系数α、β:
| $ \zeta = \frac{\alpha }{{2{\omega _i}}} + \frac{{\beta {\omega _i}}}{2} $ | (11) |
式中:ζ为振型阻尼比,对于海上风机,建议取值0.02~0.05,本论文取0.03[16];ωi为风机系统的i阶固有圆频率,根据ω=2πf得到。
2 风机有限元模型黄河三角洲拟建3.6 MW海上风机发电系统,风轮和机舱总重290 t。海面以上为风机塔架和三叶式风轮,叶片长度65 m,叶轮直径122 m。塔架与过渡段视为整体,长64 m,直径从4 m过渡到3 m。基础形式采用单桩基础,设计桩径4 m,壁厚55 mm,桩长30 m,插入海床面以下20 m,海床土体主要为粉土,粘聚力c=12 kPa,内摩擦角φ=25°,如图 1所示。50年一遇的最大风速为31 m/s[17],海水深度为10 m,流速在2.5~40 cm/s,采用50年一遇的波浪荷载,有效波高6.7 m,有效周期8.6 s[18]。风机叶片材料采用环氧玻璃钢,其余结构材料均采用同一种钢材。
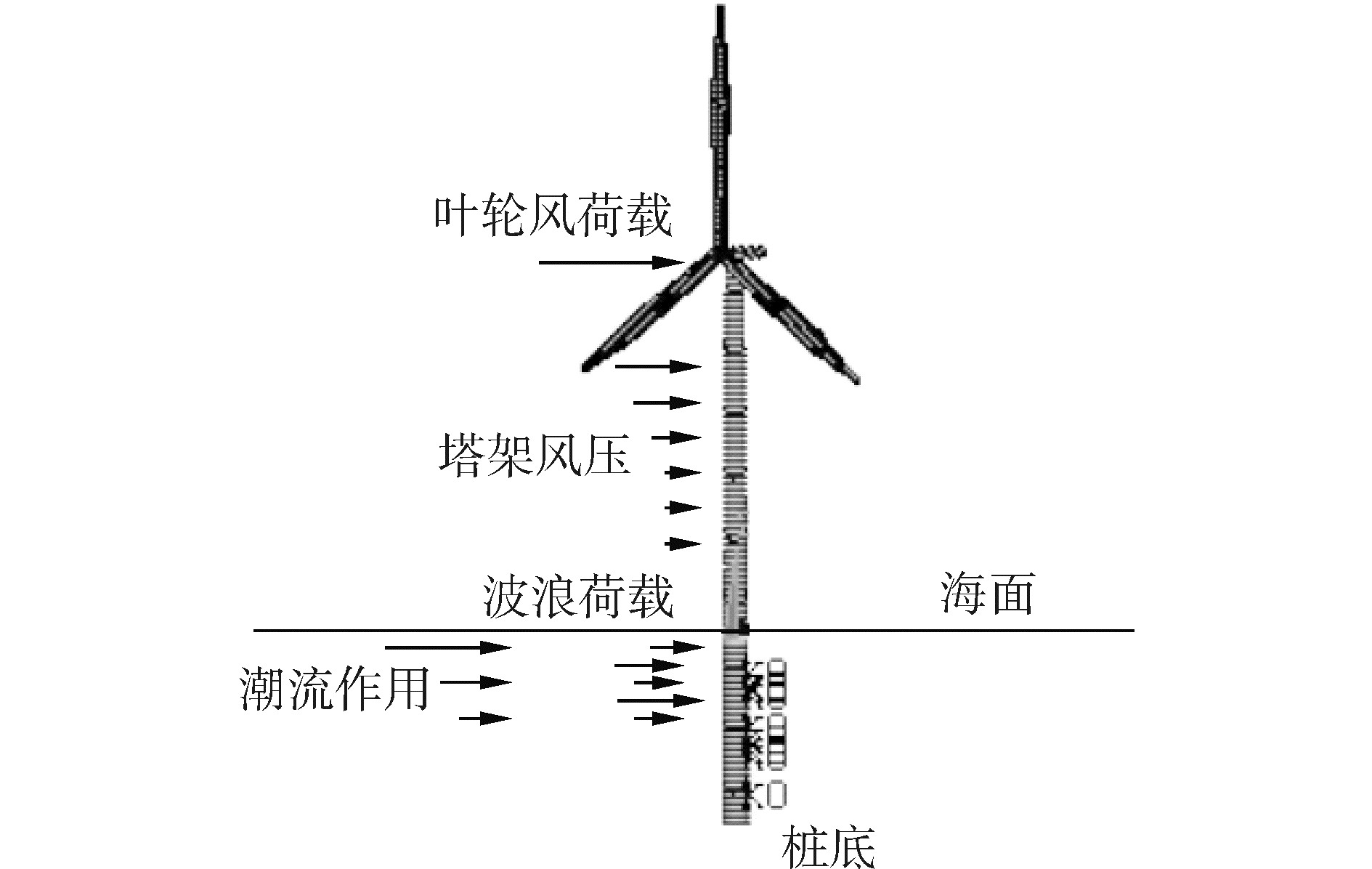
|
Download:
|
| 图 1 风机系统模型 Fig. 1 Model of wind turbine system | |
有限元模型采用PIPE16、PIPE59、COMBIN39和BEAM188四种单元类型。PIPE16单元用于机舱、轮毂和海床面以下桩体结构,不考虑塑性。PIPE59用于海床面以上的桩体结构,可以考虑塑性。COMBIN39用于模拟桩土相互作用的关系,需要输入P-y曲线。
波浪荷载以及潮流作用通过Water Table输入,其中波浪和潮流耦合作用最大相位角φ=61°通过APDL语言进行全方位搜索得到,桩底反力与不同相位角的关系如图 2。

|
Download:
|
| 图 2 桩底反力与相位角的关系 Fig. 2 The relationships between phase angle and reaction force in bottom of pile | |
模态分析时采用Block Lanczos法,提取前5阶模态,3种波浪理论下风机的自振频率和振型基本一致,本文仅列出Stokes五阶波浪理论下的前五阶振型,如图 3,1~5阶频率分别为0.163、0.169、0.186、0.200和0.243 Hz.见表1。风机模型在低阶振动时,主要为叶片的转动和摆动以及塔架的摆动,在高阶自振时,才会出现单桩基础的振动,说明风机在低阶自振时对桩基的影响不大,主要是叶片、机舱、轮毂和塔架的振动。

|
Download:
|
| 图 3 风机的前五阶振型 Fig. 3 The first five order modes of wind turbine | |
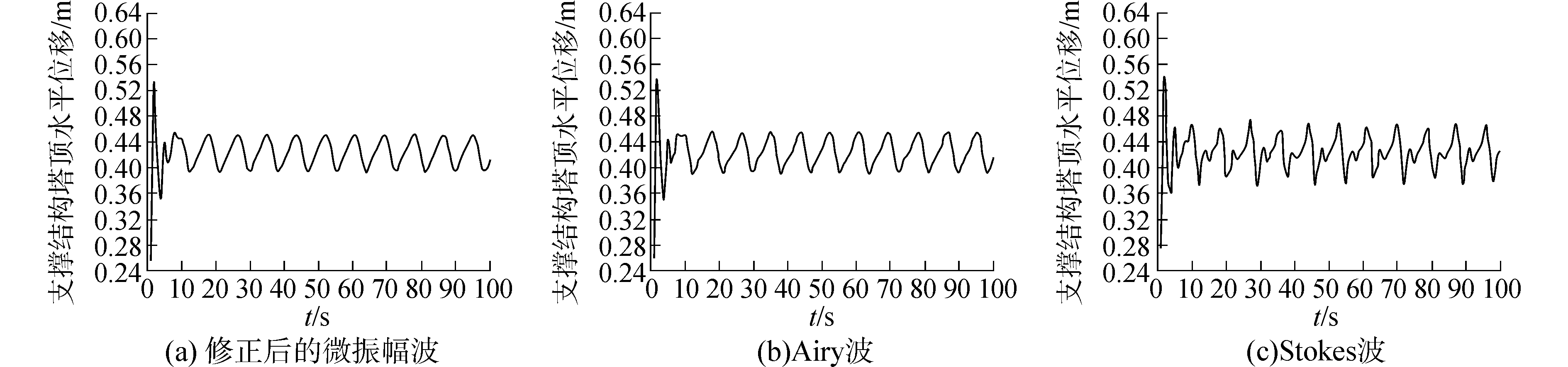
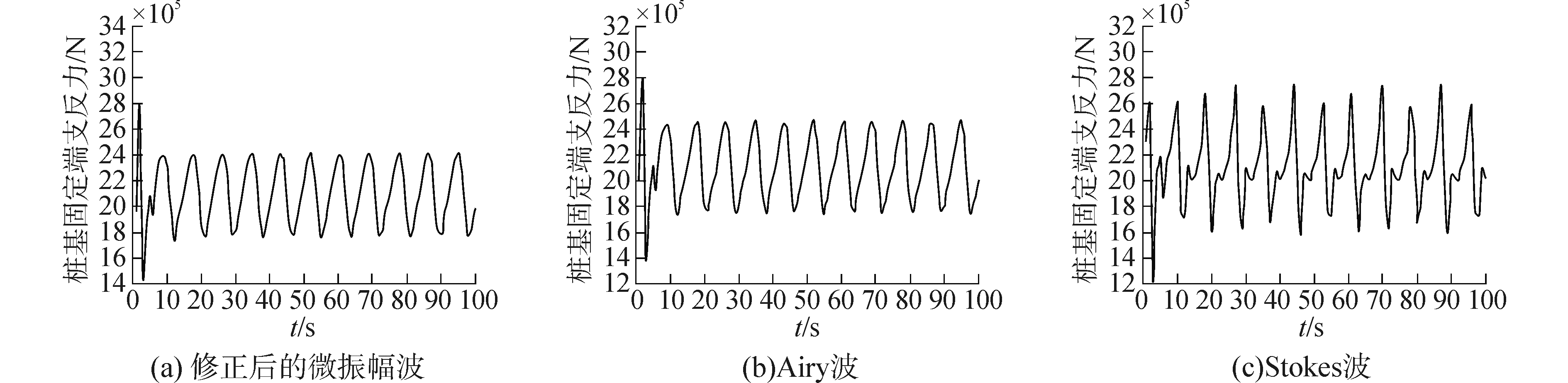
基于式(9)~(10),瞬态分析采用完全法,风荷载通过前述风速,由风压理论计算得到,阻尼系数α、β由模态分析得出的前两阶自振频率代入式(11)求得。图 4~6分别为经修正的小振幅波、Airy波以及Stokes五阶波浪理论作用下风机支撑结构塔顶水平位移、危险位置弯矩和桩底支反力的时程曲线。图 4~6均表明:荷载作用前期,变量随时间无规律变化,而后期呈固定波形,由于本文将风荷载以静力处理,前期主要为风浪流共同作用,后期仅为波浪潮流耦合作用,设计时应选取各变量的最大值。前两种波浪属于线性波,波形为简单正弦波,而Stokes波浪呈现出明显的非线性。经修正的小振幅波和Airy波作用下各变量的时程曲线基本一致,但各变量的峰值不同,风浪流作用下塔顶水平位移、弯矩和桩底支反力分别为0.5 331 m和0.5 364 m、0.392 ×108 N ·m和0.394 ×108 N ·m、0.278 ×107 N和0.28×107 N;波浪潮流作用下分别为0.4 507 m和0.4 560 m、0.338 ×108 N ·m和0.347 ×108 N ·m、0.239 ×107 N和0.25×107 N。最大弯矩均出现在海床以下4 m位置附近,但Stokes五阶波浪理论下弯矩最大,其次是Airy波和修正后的微振幅波。Airy波作用下各变量均比经修正的小振幅波大。Stokes五阶波浪理论下,风浪流作用下塔顶水平位移、弯矩和桩底支反力分别为0.542 5 m、0.369 ×108 N ·m、0.263 ×107 N;波浪潮流作用下分别为0.461 7 m、0.381×108 N ·m、0.268×107 N。风浪流作用下桩顶水平位移较波流作用下的大,而弯矩和桩底反力相反。对比三种波浪理论,Stokes五阶波浪对整个支撑系统的影响最显著,其次是Airy波和经修正的小振幅波。
|
Download:
|
| 图 4 不同波浪理论下塔顶水平位移时程曲线 Fig. 4 Time curves with the horizontal displacement of the top tower under different wave theories | |

|
Download:
|
| 图 5 不同波浪理论下危险位置的弯矩时程曲线 Fig. 5 Time curves with the moment of the dangerous location under different wave theories | |
|
Download:
|
| 图 6 不同波浪理论下桩底支反力时程曲线 Fig. 6 Time curves with the reaction force of bottom under different wave theories | |
图 7为第2 s响应时,3种波浪理论作用下支撑结构各点的水平位移、速度、加速度和转角,不同波浪理论下塔顶至桩底各点数据差值逐渐减小,两种线性波理论的变化规律基本一致,Stokes五阶波浪理论作用下的塔顶位移和转角与前两种差异虽不明显,但可辨别,原因可能是不同工况下波浪参数取值影响。其中速度和加速度值差异显著,Stokes五阶波浪理论作用相对两种线性波理论变化更大。

|
Download:
|
| 图 7 沿支撑结构各点的水平位移、速度、加速度和转角 Fig. 7 Horizontal displacement, velocity, acceleration and rotation along supporting system under different wave theories | |
图 7说明了不同的波浪理论对风机支撑结构的动力响应有显著的影响,由于关键位置的弯矩和动力响应对于风机结构设计和风机的疲劳设计起决定性作用,因此必须选择合适的波浪理论,分析风机在风浪流荷载下的动力响应,为风机承载设计和疲劳设计提供基础资料。海上风机大多安装在浅水海域,须考虑波浪的非线性,运用Stokes波浪理论得出的各时程曲线相对另两种波浪理论具有显著的非线性,因此结果更接近实际。
4 结论1) 风机支撑系统的动力响应取决于风浪流共同作用,而波浪相位角是波流耦合作用的影响因素。进行风机动力分析时,必须考虑波浪的相位角。文中波流耦合作用最大时的相位角为φmax=61°,最小为φmin=14°。
2) 线性波浪理论和Stokes五阶波浪理论下风机支撑系统的自振频率和振型基本一致,仅在高阶自振时,才会出现单桩基础的振动,说明风机在低阶自振时对桩基的影响不大,主要是叶片、机舱、轮毂和塔架的振动,避免了共振的发生。
3) 两种线性波理论的变化规律基本一致,Stokes五阶波浪理论作用下的塔顶位移和转角与前两种相差1.7%左右,其中速度最大相差66.3%,加速度最大相差15.5%,差异较大。Stokes五阶波浪对整个支撑系统的影响最显著,其次是Airy波和经修正的小振幅波。Stokes波浪理论下的动力响应具有明显非线性,对于浅水海域,结果更接近实际。不同工况组合对支撑结构动力响应的影响有待进一步研究。
| [1] |
SALWA T, BOKHOVE O, KELMANSON M A. Variational modelling of wave-structure interactions with an offshore wind-turbine mast[J]. Journal of engineering mathematics, 2017, 107(1): 61-85. DOI:10.1007/s10665-017-9936-4 (  0) 0)
|
| [2] |
吴姗姗, 王双, 彭洪兵, 等. 我国海上风电产业发展思路与对策建议[J]. 经济纵横, 2017(1): 68-73. WU Shanshan, WANG Shuang, PENG Hongbing, et al. Development thought and suggestions on offshore wind power industry in China[J]. Economic review, 2017(1): 68-73. (  0) 0)
|
| [3] |
王淼, 吴云青, 苏萌, 等. 单桩式基础应用于我国海上风电的可行性探讨[J]. 电力建设, 2013, 34(4): 63-66. WANG Miao, WU Yunqing, SU Meng, et al. Application of single pile foundation in offshore wind power in China[J]. Electric power construction, 2013, 34(4): 63-66. (  0) 0)
|
| [4] |
戴国亮, 龚维明, 沈景宁, 等. 东海大桥海上风电场基础波浪理论分析[J]. 岩土工程学报, 2013, 35(S1): 456-461. DAI Guoliang, GONG Weiming, SHEN Jingning, et al. Wave theory analysis of foundation of offshore wind farm near East Sea Bridge[J]. Chinese journal of geotechnical engineering, 2013, 35(S1): 456-461. (  0) 0)
|
| [5] |
李德源, 刘胜祥, 张湘伟. 海上风力机塔架在风波联合作用下的动力响应数值分析[J]. 机械工程学报, 2009, 45(12): 46-52. LI Deyuan, LIU Shengxiang, ZHANG Xiangwei. Dynamical response numerical analysis of the Offshore Wind Turbine Tower under combined action of wind and wave[J]. Journal of mechanical engineering, 2009, 45(12): 46-52. (  0) 0)
|
| [6] |
GALVÍN P, ROMERO A, SOLÍS M, et al. Dynamic characterisation of wind turbine towers account for a monopile foundation and different soil conditions[J]. Structure and infrastructure engineering, 2017, 13(7): 942-954. DOI:10.1080/15732479.2016.1227342 (  0) 0)
|
| [7] |
SEONG J T, HA J G, KIM J H, et al. Centrifuge modeling to evaluate natural frequency and seismic behavior of offshore wind turbine considering SFSI[J]. Wind energy, 2017, 20(10): 1787-1800. DOI:10.1002/we.v20.10 (  0) 0)
|
| [8] |
AIRY G B. On tidal and wave[M]. London: Encyclopedia Metropolitan, 1845: 241-396.
(  0) 0)
|
| [9] |
WHEERLER J D. Method for calculating forces produced by irregular waves[J]. Journal of petroleum technology, 1970, 22(3): 359-367. DOI:10.2118/2712-PA (  0) 0)
|
| [10] |
STOKES G G. On the theory of oscillatory waves[J]. Transactions of the Cambridge philosophical society, 1847, 8(310): 441-473. (  0) 0)
|
| [11] |
MATLOCK H, REESE L C. Generalized solutions for laterally loaded piles[J]. Journal of the soil mechanics and foundations division, 1960, 86(5): 63-94. (  0) 0)
|
| [12] |
GAZIOGLU S M, O'NEILL M W. Evaluation of P-y relationships in cohesive soils[C]//Proceeding of the Conference on Analysis and Design of Pile Foundations. San Francisco, California, 1984: 174-213. http://www.researchgate.net/publication/285683478_EVALUATION_OF_P-Y_RELATIONSHIPS_IN_COHESIONLESS_SOILS
(  0) 0)
|
| [13] |
苏静波, 邵国建, 刘宁. 基于P-y曲线法的水平受荷桩非线性有限元分析[J]. 岩土力学, 2006, 27(10): 1781-1785. SU Jingbo, SHAO Guojian, LIU Ning. Nonlinear finite element analysis of piles under lateral load based on P-y curves[J]. Rock and soil mechanics, 2006, 27(10): 1781-1785. DOI:10.3969/j.issn.1000-7598.2006.10.028 (  0) 0)
|
| [14] |
JEONG S, KIM Y, KIM J. Influence on lateral rigidity of offshore piles using proposed P-y curves[J]. Ocean engineering, 2011, 38(2/3): 397-408. (  0) 0)
|
| [15] |
王腾, 王天霖. 粉土P-y曲线的试验研究[J]. 岩土力学, 2009, 30(5): 1343-1346. WANG Teng, WANG Tianlin. Experimental research on silt P-y curves[J]. Rock and soil mechanics, 2009, 30(5): 1343-1346. (  0) 0)
|
| [16] |
杨进, 刘书杰, 姜伟, 等. ANSYS在海洋石油工程中的应用[M]. 北京: 石油工业出版社, 2010. YANG Jin, LIU Shujie, JIANG Wei, et al. Application of ANSYS in marine petroleum engineering[M]. Beijing: Petroleum Industry Press, 2010. (  0) 0)
|
| [17] |
李高伟, 韩美, 张东启. 1961-2013年黄河三角洲气候变化趋势研究[J]. 人民黄河, 2017, 39(1): 30-37. LI Gaowei, HAN Mei, ZHANG Dongqi. Climatic change tendency in yellow river delta during 1961-2013[J]. Yellow River, 2017, 39(1): 30-37. (  0) 0)
|
| [18] |
WANG Hu, LIU Hongjun. Evaluation of storm wave-induced silty seabed instability and geo-hazards:a case study in the Yellow River delta[J]. Applied ocean research, 2016, 58: 135-145. DOI:10.1016/j.apor.2016.03.013 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


