小水线面双体船(small water-plane area twin hull,SWATH)由于具有形状细长、面积较小的水线面和深置于水中、排水体积较大的下体,因而受到的波浪干扰力较小,在大风浪中的失速和运动响应均较小,具有较好的稳定性和优良的耐波性[1-3]。众多学者针对SWATH的耐波性进行了大量研究后发现,与常规单体船的耐波性预报相比,SWATH的耐波性计算更为复杂,其难点主要体现在:两片体间的水动力干扰、粘性和稳定鳍的影响[4]。开展耐波性计算时,一般需分别求解SWATH船体、粘性和稳定鳍的水动力系数和波浪干扰力。
Lee[4-12]等基于二维切片法,采用半经验的方法来计入粘性和稳定鳍的影响,求解SWATH的耐波性,得到了满足工程使用的结果。但存在理论上的缺陷,如忽视了流体的三维流动、高速时预报结果失真等。而目前基于三维势流理论针对SWATH耐波性的研究尚不多见。
由于SWATH船型的特殊性,模型试验仍是进行SWATH耐波性研究的重要手段[13]。Qian等[14-20]针对SWATH的静水阻力、水动力系数、波浪中运动和波浪增阻等水动力性能开展了试验研究。
SWATH船通常安装有稳定鳍来改善纵向运动稳定性,并可起到一定的减摇效果。采用主动控制式稳定鳍可以进一步提高减摇效果,但针对大型SWATH船,由于主动控制需要克服较大的力矩,因而大型SWATH多选择在合适的位置安装固定式稳定鳍。
线性势流理论一般假设船体在受到微幅波的扰动时,其运动响应随波高变化是线性的。但实际上,当波高变化时,船体的运动响应会呈现出非线性特征。Bouscasse[3]和Castiglione[21]针对高速双体船Delft 372,分别通过模型试验和数值计算研究了波高变化对船体运动响应和波浪增阻的影响。两者的结果均表明,波高变化对船体运动响应非线性的影响在共振区附近较为明显。而关于波高变化引起SWATH船运动响应非线性的研究并不多见。
本文针对一条安装有固定式稳定鳍的SWATH模型开展了顶浪规则波中模型试验,分析了航速和稳定鳍纵向位置变化对SWATH纵向运动性能的影响,以及波高变化对船体运动响应非线性的影响。
1 试验模型及测试设备 1.1 试验模型试验模型为木模,将其命名为SWATH-M,其主要参数见表 1。图 1给出了模型水线以下部分的侧视图和横剖图。模型艏艉安装有稳定鳍,表 2给出了稳定鳍的主要参数,其中纵向位置以船中为参考。
| 表 1 SWATH-M主要参数 Tab.1 General properties of SWATH-M |

|
Download:
|
| 图 1 模型示意图 Fig. 1 SWATH-M model | |
| 表 2 稳定鳍主要参数 Tab.2 Main parameters of stabilizing fins |
与常规单体船不同,SWATH的推力轴线距重心较远,且水线面较小,若拖点垂向位置仍位于重心,则与实际船航行时相比,相当于增加了一个埋艏力矩,影响船体姿态和水动力测试结果。图 2给出了试验时的模型安装图。拖曳装置可释放模型的升沉、纵摇,约束其他运动自由度。使用该拖曳装置进行试验时,拖点的纵向位置与重心纵向位置相同,而垂向位置为推力轴线高度。

|
Download:
|
| 图 2 拖点在推力轴线时的模型 Fig. 2 Experimental setup with the towing point at the axis of thrust | |
试验在中国特种飞行器研究所高速拖曳水池里完成。试验水池长、宽和水深分别为510 m、6.5 m和5 m。造波机为16片摇板式,浪高仪固定在造波机前方60 m处测量波高。升沉测量采用拉线式位移传感器测量,误差小于1%。纵摇测量采用TC-11A型垂直陀螺仪,测量误差小于0.1°。
2 试验结果及分析 2.1 试验工况试验工况包括:顶浪规则波中不同航速下的耐波性试验、鳍纵向位置变化耐波性试验,以及变波高耐波性试验。表 3给出了试验工况。模型航速Vm为0.282~1.127 m/s,对应的傅汝德数Fn为0.054~0.215(
| 表 3 试验工况 Tab.3 Experimental cases |
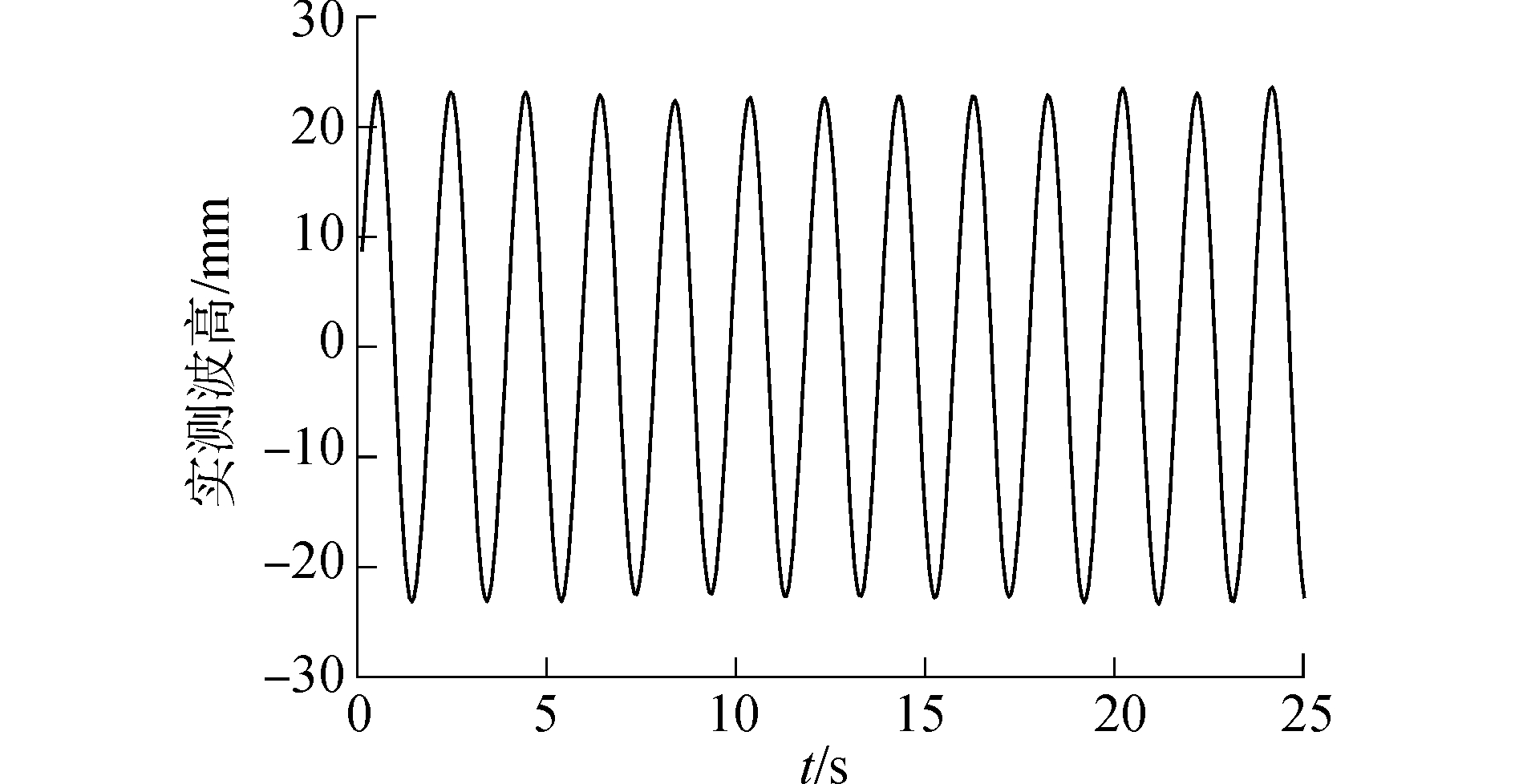
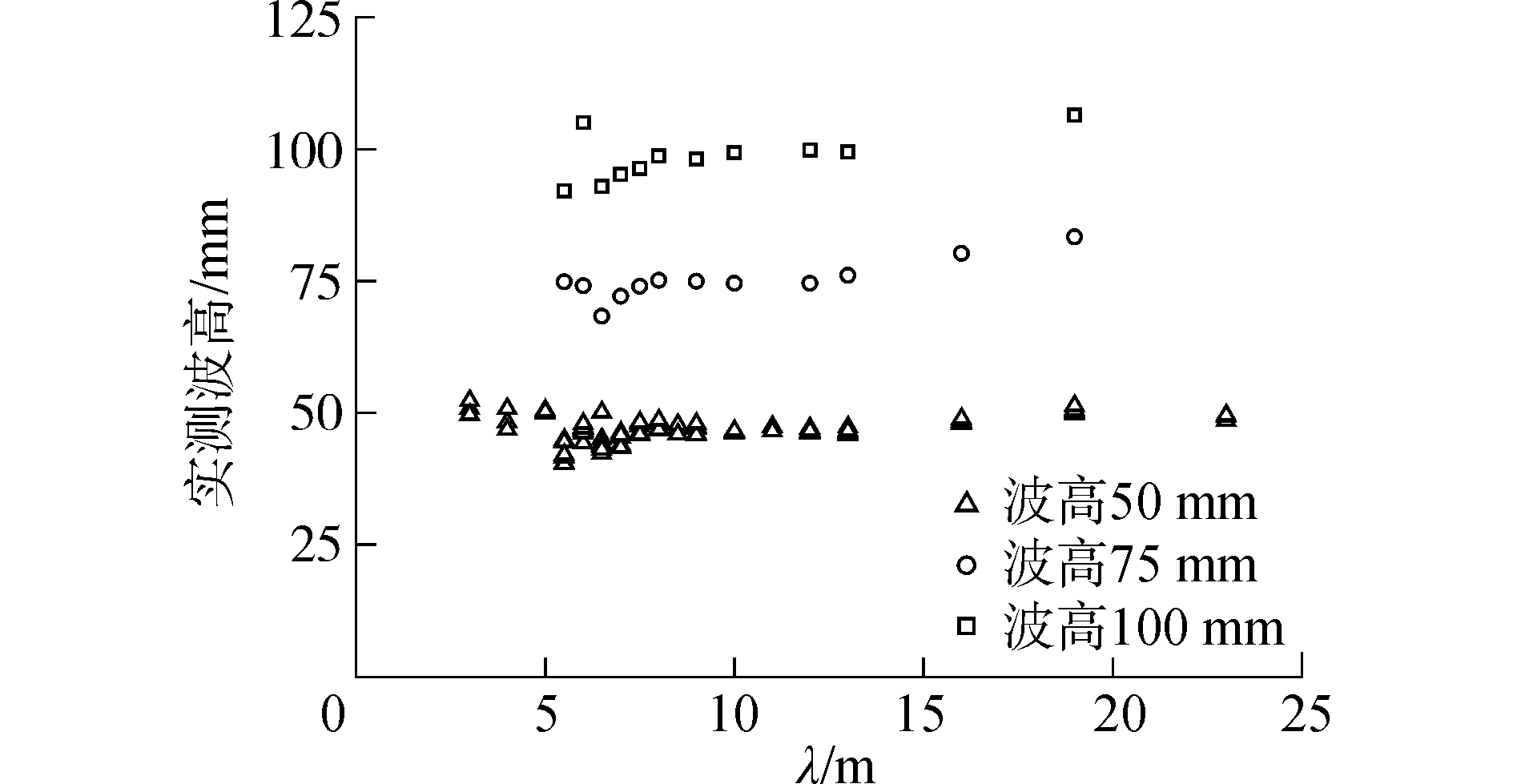
图 3给出了波长6 m时的一段波幅时历曲线,图 4给出了不同试验工况时的实测波高统计值。可以发现,虽然不同波长的实测波幅较为稳定,但实测波高与目标波高存在一定的误差。在对试验结果进行分析时,必须以实测波高对测量结果进行无因次化处理。
|
Download:
|
| 图 3 λ=6 m波幅时历曲线 Fig. 3 Time history of wave amplitude (λ=6 m) | |
|
Download:
|
| 图 4 试验实测波高 Fig. 4 Wave height of measurement | |
定义垂荡传递函数TF3为Za/ζa,纵摇传递函数TF5=θa/(ζka)。其中,k为波数(k=2π/λ),ζa为入射波波幅,λ为入射波波长。
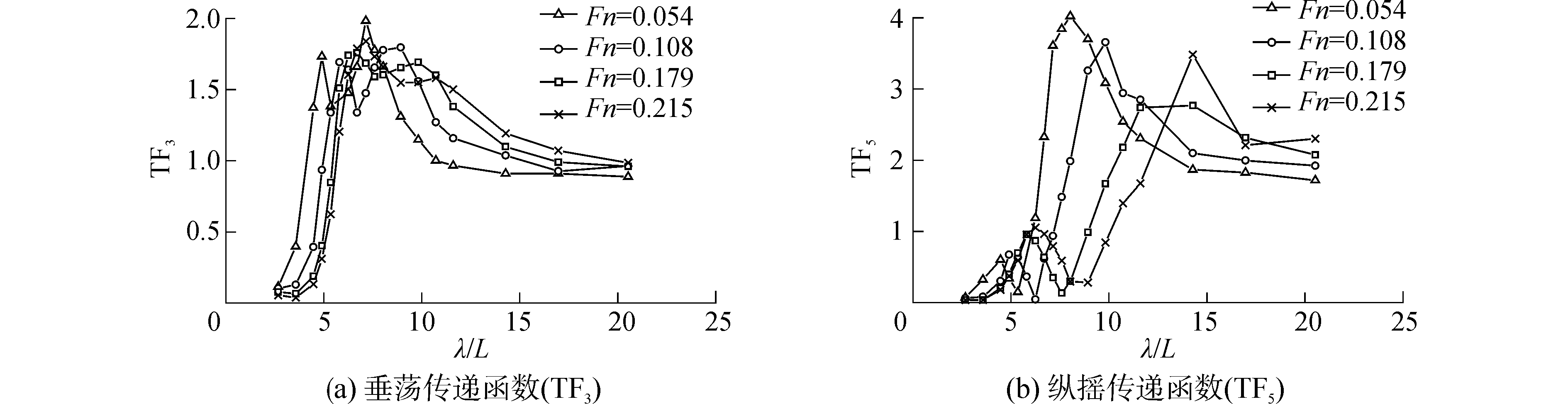
2.3 航速的影响图 5给出了拖点垂向高度在推力轴线时,不同航速下模型的运动传递函数。可以看出,不同航速下,船体的垂荡传递函数和纵摇传递函数均随着波长变化呈现出双极值。航速对垂荡传递函数极值的影响较小;而纵摇传递函数短波中的极值随着航速增加而增大,长波中的极值随着航速增加先减小后增大。相同航速,垂荡传递函数的两个极值大小较为接近;而纵摇传递函数的两个极值大小差别较大,长波中的极值明显大于短波中的极值,至少为短波中极值的2.9倍。
|
Download:
|
| 图 5 不同航速时的运动传递函数 Fig. 5 Transfer functions of motion responses at different speed versus non-dimensional wave length | |
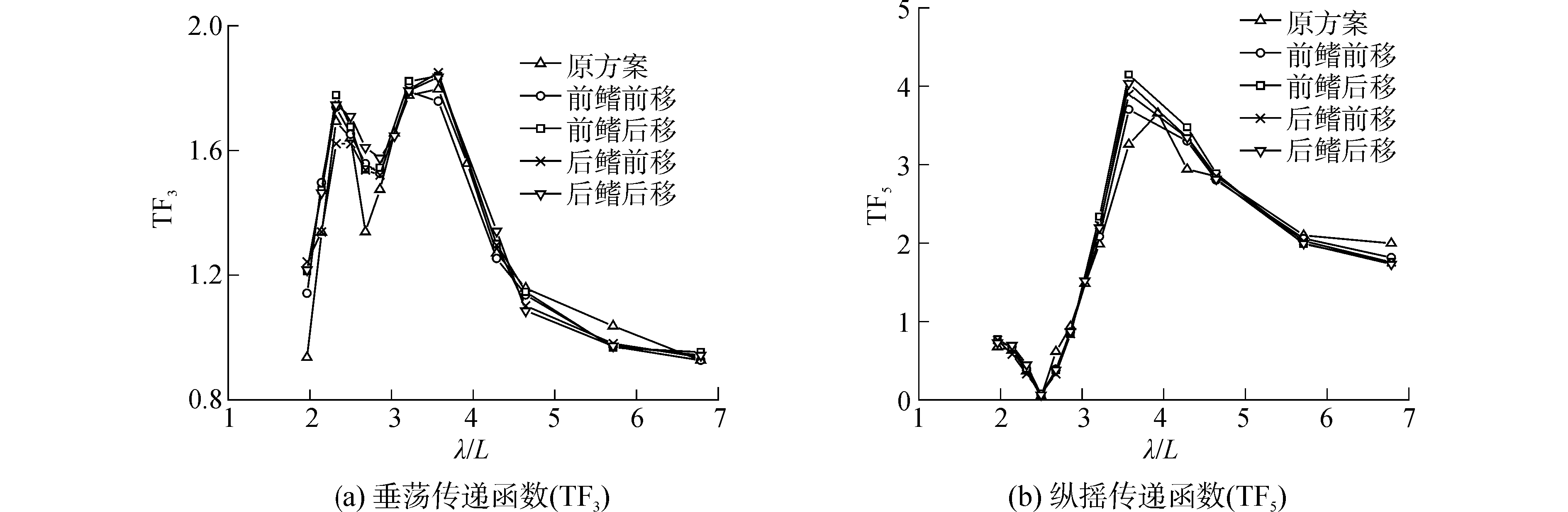
原方案与变换不同稳定鳍纵向位置时的船体运动传递函数对比如图 6和图 7所示。总体来看,不同稳定鳍纵向位置对应的垂荡传递函数和纵摇传递函数差别不大,可能是由于稳定鳍的纵向位置改变较小(纵向移动距离约为0.035LWL),导致作用于船体的水动力没有显著变化。
|
Download:
|
| 图 6 Fn=0.108时的运动传递函数对比 Fig. 6 Transfer functions of motion responses at Fn=0.108 | |

|
Download:
|
| 图 7 Fn=0.215时的运动传递函数对比 Fig. 7 Transfer functions of motion responses at Fn=0.215 | |
对比前鳍前移和前鳍后移两个方案可以发现,前鳍后移时,模型的垂荡传递函数和纵摇传递函数在共振区附近略有增加。对比后鳍前移和后鳍后移两个方案可以发现,后鳍前移时,模型的垂荡传递函数在第一个共振区附近略有增加;而纵向传递函数基本没有变化。
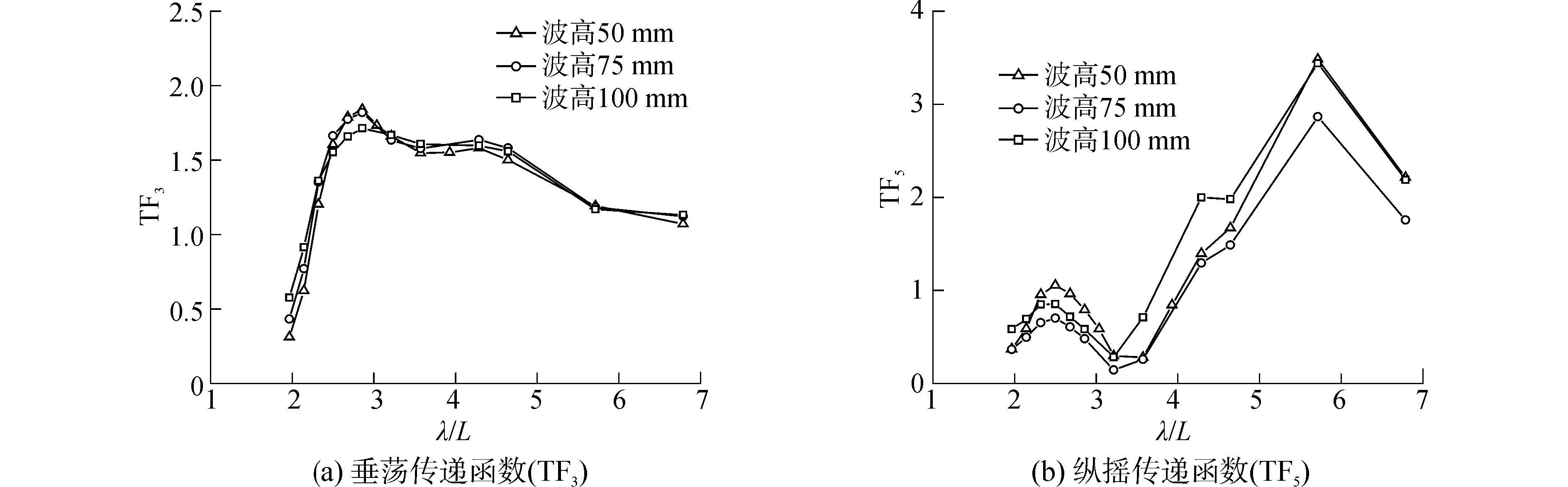
2.5 波高的影响图 8和图 9给出了不同波高时的模型纵向运动传递函数。可以看出,波长相同而波高不同时,模型的垂荡传递函数和纵摇传递函数均存在差别,特别是在共振区附近,体现了船体运动随波高变化的非线性特征。

|
Download:
|
| 图 8 Fn=0.108时的运动传递函数对比 Fig. 8 Transfer functions of motion responses at Fn=0.108 | |
|
Download:
|
| 图 9 Fn=0.215时的运动传递函数对比 Fig. 9 Transfer functions of motion responses at Fn=0.215 | |
Fn=0.108时,在共振区附近,不同波高对应的运动传递函数差别显著,波高100 mm时的垂荡传递函数和纵摇传递函数最小,符合运动非线性的规律。而Fn=0.215时,船体的垂荡传递函数在共振区附近差别不明显;纵摇传递函数差别显著,但在长波中,波高100 mm时的纵摇传递函数数值最大,而波高75 mm时的纵摇传递函数数值最小。
现从模型受力分析产生上述现象的原因:对SWATH模型运动产生影响的水动力包括由入射波浪产生的傅汝德-克雷洛夫力、波浪遇到船体反射引起的绕射力、船体运动产生的辐射力、水的粘性引起的粘性力和稳定鳍产生的升力。由于SWATH本身的线型特点,其受到的傅汝德-克雷洛夫力,绕射力和辐射力相对较小,而受到的粘性力和稳定鳍升力较大。
稳定鳍升力与模型的航速密切相关。低速时,稳定鳍的升力较小,而波浪对模型受到的水动力贡献较大。因此,当波高变化时,模型的运动响应随波高变化呈现出较明显的非线性特征。而高速时,稳定鳍升力迅速增加,对模型受到的水动力有较大贡献,此时波高变化对模型受到的水动力的影响相对较弱,模型运动响应的非线性特征变得不明显。
此外,当波高较大时,模型的运动增加,稳定鳍距离自由液面的高度减小,稳定鳍会受到自由液面的影响,其产生的水动力发生一定的变化。同时,在共振区附近,模型的连接桥部位会出现入水现象,也对模型的运动产生一定影响。
3 结论1) 不同航速下,船体的垂荡传递函数和纵摇传递函数均随着波长变化呈现出双极值。航速对垂荡传递函数极值的影响较小;而纵摇传递函数短波中的极值随着航速增加而增大,长波中的极值随着航速增加先减小后增大。
2) 稳定鳍纵向位置移动3.5%设计水线长时,对模型的运动响应影响不大。
3) 随着波高增加,模型运动响应的非线性特征突出表现在共振区附近,在低速时更为显著。
| [1] |
KOS S, BRČIĆ D, FRANČIĆ V. Comparative analysis of conventional and SWATH passenger catamaran[C]//Proceedings of Mednarodno Posvetovanje o Prometni znanosti. Portorož, 2009. http://www.researchgate.net/publication/229034772_Comparative_analysis_of_conventional_and_SWATH_passenger_catamaran
(  0) 0)
|
| [2] |
BRIZZOLARA S, VERNENGO G. Automatic optimization computational method for unconventional S.W.A.T.H. ships resistance[J]. International journal of mathematical models and methods in applied sciences, 2011, 5(5): 882-889. (  0) 0)
|
| [3] |
BOUSCASSE B, BROGLIA R, STERN F. Experimental investigation of a fast catamaran in head waves[J]. Ocean engineering, 2013, 72: 318-330. DOI:10.1016/j.oceaneng.2013.07.012 (  0) 0)
|
| [4] |
LEE C M. Theoretical prediction of motion of small-waterplane-area, twin-hull (SWATH) ships in waves[R]. SPD-76-0046, 1976. http://www.researchgate.net/publication/235132381_Theoretical_Prediction_of_Motion_of_Small-Waterplane-Area_Twin-Hull_(SWATH)_Ships_in_Waves
(  0) 0)
|
| [5] |
LEE C M, CURPHEY R M. Prediction of motion, stability, and wave load of Small-Waterplane-Area, Twin-Hull ships[C]//Proceedings of Annual Meeting. Jersey City, NJ, USA, 1977: 94-130. http://www.researchgate.net/publication/284048927_Prediction_of_motion_stability_and_wave_load_of_Small-Waterplane-Area_Twin-Hull_Ships
(  0) 0)
|
| [6] |
HONG Y S. Improvements in the prediction of heave and pitch motions for SWATH ships[R]. SDR-0928-02, 1980.
(  0) 0)
|
| [7] |
MCCREIGHT K K, STAHL R. Vertical plane motions of SWATH (Small Waterplane area Twin Hull) ships in regular waves[R]. SPD-1076-01, 1983.
(  0) 0)
|
| [8] |
MCCREIGHT K K. Predicting the motions of SWATH ships in waves. A validated mathematical model[R]. CRDKNSWC/HD-1350-03, 1995. https://www.researchgate.net/publication/277761649_Predicting_the_Motions_of_SWATH_Ships_in_Waves._A_Validated_Mathematical_Model
(  0) 0)
|
| [9] |
李向群. SWATH船型的耐波性研究[J]. 上海船舶运输科学研究所学报, 1988(2): 41-46. LI Xiangqun. A study on the seakeeping ability of SWATH[J]. Journal of Shanghai ship and Shipping Research Institute, 1988(2): 41-46. (  0) 0)
|
| [10] |
董祖舜, 董文才. 小水线面双体船纵向运动稳定性的简化判据及分析[J]. 中国造船, 1994(4): 36-48. DONG Zushun, DONG Wencai. A simplified criterion and an analysis of some influence factors on longitudinal motion stability of Small Waterplane Area Twin-Hull ships[J]. Shipbuilding of China, 1994(4): 36-48. (  0) 0)
|
| [11] |
刘志华, 董文才, 熊鹰. 小型高速SWATH船下体型线研究[J]. 船舶工程, 2004, 26(6): 4-8. LIU Zhihua, DONG Wencai, XIONG Ying. Study on lines of lower hull of small-sized high-speed SWATH ship[J]. Ship engineering, 2004, 26(6): 4-8. (  0) 0)
|
| [12] |
毛筱菲. 小水线面双体船在波浪中的运动响应预报[J]. 船海工程, 2005(4): 13-15. MAO Xiaofei. Numerical study of the motion response prediction of SWATH ship in waves[J]. Ship & ocean engineering, 2005(4): 13-15. (  0) 0)
|
| [13] |
孙小帅, 姚朝帮, 叶青. 小水线面双体船波浪中纵向运动性能模型试验研究[J]. 国防科技大学学报, 2017, 39(4): 161-167. SUN Xiaoshuai, YAO Chaobang, QE Qing. Experimental investigation on the seakeeping performance of small waterplane area twin hull in head waves[J]. Journal of National University of Defense Technology, 2017, 39(4): 161-167. DOI:10.11887/j.cn.201704025 (  0) 0)
|
| [14] |
QIAN Peng, YI Hong, LI Yinghui. Numerical and experimental studies on hydrodynamic performance of a small-waterplane-area-twin-hull (SWATH) vehicle with inclined struts[J]. Ocean engineering, 2015, 96: 181-191. DOI:10.1016/j.oceaneng.2014.12.039 (  0) 0)
|
| [15] |
LEE C M, MURRAY L O. Experimental investigation of hydrodynamic coefficients of a small-waterplane area, twin-hull model[R]. SPD 747-01, 1977. http://adsabs.harvard.edu/abs/1977STIN...7726338L
(  0) 0)
|
| [16] |
FEIN J A, STAHL R. Head and following wave exciting force experiments on two SWATH configurations[R]. SPD-0928-01, 1980. http://trid.trb.org/view/162003
(  0) 0)
|
| [17] |
NUMATA E. Experimental study of SWATH model rolling in beam waves[R]. SIT-DL-81-9-2200, 1981. https://www.researchgate.net/publication/235127678_Experimental_Study_of_SWATH_Model_Rolling_in_Beam_Waves
(  0) 0)
|
| [18] |
HART C J, KIESOW R O. Vertical plane oscillation experiments on a series of Two-Dimensional SWATH Demi-hull sections[R]. DTRC-87/SHD-1253-01, 1988. http://agris.fao.org/openagris/search.do?recordID=AV2012050397
(  0) 0)
|
| [19] |
HART C J, WATERS R T, HICKOK J. Rotating arm experiment for an extended strut SWATH ship as represented by SWATH-6E[R]. SPD-0698-03, 1983. http://trid.trb.org/view/419164
(  0) 0)
|
| [20] |
POLLACK J G. Motion comparison between a 64-foot SWATH and a 65-foot monohull[R]. NBDL-85R001, 1985. https://www.researchgate.net/publication/235076420_Motion_Comparison_between_a_64-Foot_Swath_and_a_65-Foot_Monohull
(  0) 0)
|
| [21] |
CASTIGLIONE T, STERN F, BOVA S, et al. Numerical investigation of the seakeeping behavior of a catamaran advancing in regular head waves[J]. Ocean engineering, 2011, 38(16): 1806-1822. DOI:10.1016/j.oceaneng.2011.09.003 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


