2. 江西理工大学 建筑与测绘工程学院, 江西 赣州 341000
2. School of Architectural and Surveying & Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
非饱和区井孔入渗法在地质勘探、矿山开采及工农业生产中具有广泛的应用,如利用钻井注水试验推求地层的饱和渗透系数[1-2]、煤层钻井注水以降低粉尘浓度[3]、田间入渗试验推求田间土壤饱和导水率[4]、离子型稀土矿山原地浸矿作业[5-6]等。对于非饱和区井孔入渗注液流量的确定,最初人们假定从井孔入渗到土体的水只形成一个饱和区,饱和区周围形成了水体的自由面,水体就在自由面所包围的区域内运动,从而提出了基于饱和区渗流理论的各种经验公式[7-9]。然而,事实已经证明[10],水由井孔入渗土体时,首先渗入非饱和区,将非饱和区变成饱和区,饱和区的范围逐渐从井边向井附近扩展,入渗基本稳定时,在井孔附近只有较小范围的饱和区,而大片地区是饱和程度不一的非饱和区。吴良骥通过有限差分算例分析得到了地下水埋藏很深时井孔入渗量的经验公式[11],但该拟合公式缺乏理论基础,拟合系数复杂且没有明显的规律,难以推广应用。赵伟霞等通过室内井孔入渗实验研究了三种土壤小范围短历时入渗规律,并假定恒定水头井入渗近似为以井内积水表面积为入渗面的一维入渗,建立了适用于恒定水头井入渗的修正Green-Ampt模型[12],但并未给出稳渗流量计算公式。2000年的《注水试验规程》[1]提供了地下水位以上钻井降水头注水试验方法,但由于计算公式与影响条件十分复杂,目前一般应用较少而处于研究和积累资料阶段[13]。2007年的《水利水电工程注水试验规程》[2]将该方法修正为地下水位线以上的钻井常水头注水试验方法,并给出了相应的渗透系数计算公式和适用条件。然而,张贻火等[14-15]的研究发现,该试验方法的渗透系数计算公式和适用条件具有较大的局限性,甚至存在矛盾的地方,应用十分不便。因此,目前对于非饱和区井孔入渗注液流量的计算缺乏准确可靠的计算模型。
本文选取龙南典型离子型稀土矿山,开展单孔注液入渗现场试验。基于非饱和渗流达西定律,建立非饱和区常水头井稳渗流量模型,并以现场试验验证模型的准确性。本文研究成果可为确定离子型稀土原地浸矿工艺的合理注液流量参数提供依据。
1 单孔注液现场试验 1.1 试验矿山简介选取江西龙南某离子型稀土矿山作为试验矿山(图 1),该矿山位于龙南县南约10 km处的某稀土矿区,试验矿山海拔在300~400 m,其山顶、山脊比较平坦,沟谷切割深度小于80 m,坡度一般小于15°,具有完整的天然底板。试验矿山的矿体厚度较大,一般在10 m左右,具有赣南裸脚式离子型稀土矿的典型特征,符合试验要求。

|
Download:
|
| 图 1 试验矿山 Fig. 1 Test mine | |
在试验矿山上选择典型测试点,先平整场地至矿体出露,利用环刀取样,通过室内土工试验测试矿土的基本物理力学参数,得到矿土的天然密度为1.63 g/cm3,天然含水量为15.3%,平均孔隙比为0.92,液限为39.47%,塑限为30.34%。利用振动筛分机与激光粒度分析仪测试矿土的粒径累积曲线,如图 2所示,经分析可知该矿土土质类型为砂土。

|
Download:
|
| 图 2 粒径累计曲线 Fig. 2 Particle size accumulation curve | |
非饱和土的体积含水率和渗透系数均是土体基质吸力的函数,分别称作水分特征曲线和渗透特征曲线,是描述土体非饱和渗流的基本本构模型,并且这些曲线随着土质、颗粒级配、土体密度以及流体的性质不同而不同,变化很大,至今尚未提出较成熟的研究结果,不同学者提出了不同的拟合模型。常用的Van Genuchten模型表达式[16]:
| $ \left\{ \begin{array}{l} \theta \left( \psi \right) = {\theta _{\rm{r}}} + \frac{{{\theta _{\rm{s}}} - {\theta _{\rm{r}}}}}{{{{\left[ {1 + {{\left( {\frac{\mathit{\Psi }}{\lambda }} \right)}^n}} \right]}^m}}}\\ k\left( \theta \right) = {k_s}{S^{0.5}}{\left( {1 - {{\left( {1 - {S^{\frac{1}{m}}}} \right)}^m}} \right)^2} \end{array} \right. $ | (1) |
式中:θs为饱和体积含水率;θr为残余体积含水率;Ψ为土体基质吸力,kPa;λ、m、n为拟合参数,m=1-1/n;ks为饱和渗透系数,m/d;S为土体相对饱和度,其计算公式为
| $ S = \frac{{\theta - {\theta _{\rm{r}}}}}{{{\theta _{\rm{s}}} - {\theta _{\rm{r}}}}} = \frac{1}{{{{\left[ {1 + {{\left( {\frac{\mathit{\Psi }}{\lambda }} \right)}^n}} \right]}^m}}} $ | (2) |
为了获得矿土非饱和渗流本构模型,常用方法是通过试验测试土体的含水率-基质吸力关系曲线,通过选用的本构模型方程进行拟合。
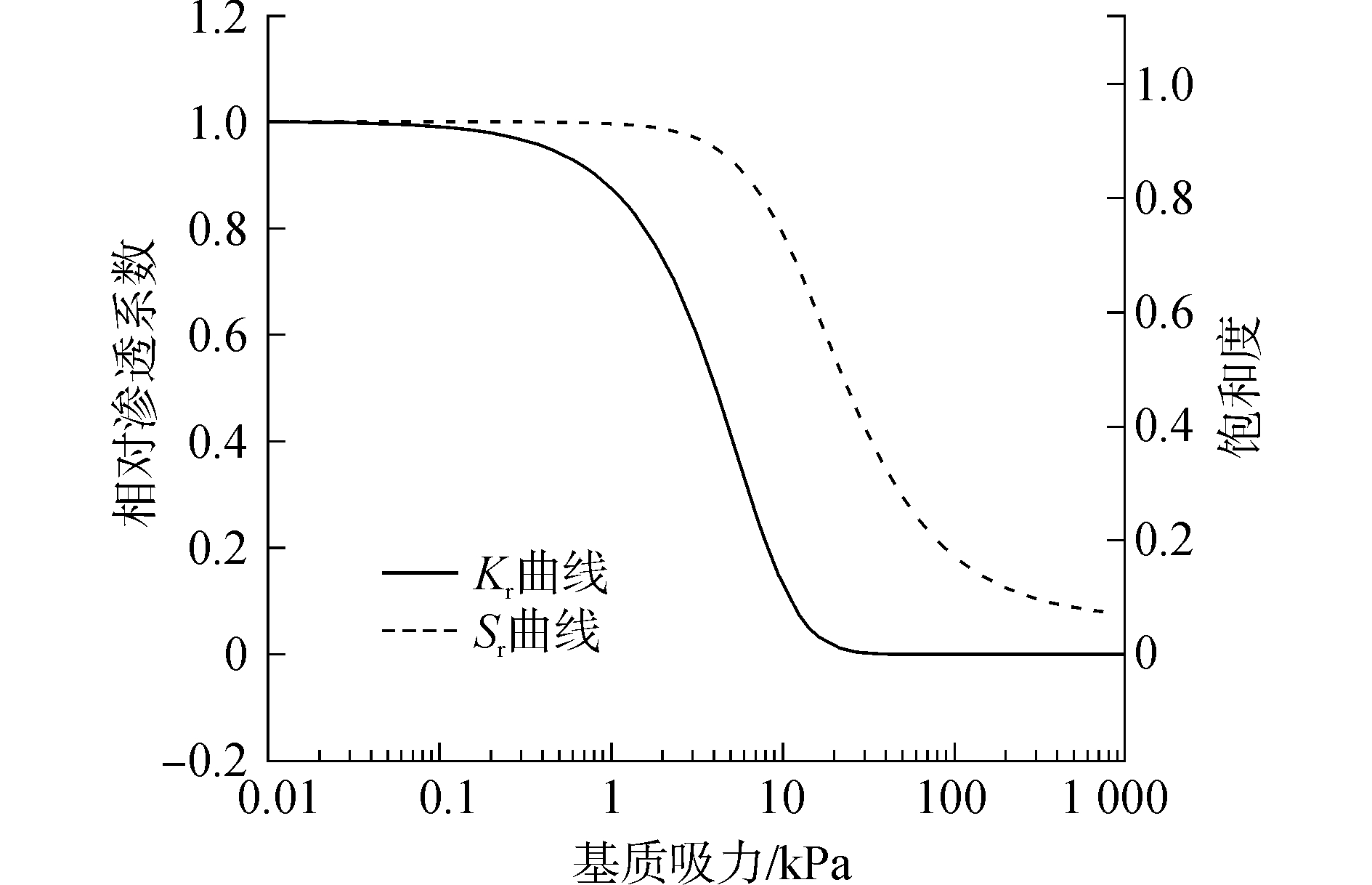
在矿山合适位置开辟一块1 m×1 m的区域,埋入8根TEN型张力计(图 3),张力计长度为30 cm,基质吸力量测范围为0~100 kPa。仪器静置至读数稳定后记录基质吸力测试结果,并取样测试各张力计附近土体的含水率,结果汇总于表 1。同时通过室内常水头渗流实验测得矿土平均饱和渗透系数Ks为0.5 m/d。利用Van Genuchten模型对表 1的测试数据进行拟合,拟合结果见表 2,归一化的拟合曲线见图 4。

|
Download:
|
| 图 3 基质吸力现场测试 Fig. 3 Matrix suction field test | |
| 表 1 基质吸力-含水率测试结果 Tab.1 Test results of matrix suction-moisture content |
| 表 2 渗流本构模型参数拟合结果 Tab.2 Parameter fitting results of the seepage constitutive model |
|
Download:
|
| 图 4 渗流本构模型拟合曲线 Fig. 4 The seepage constitutive model fitting curve | |
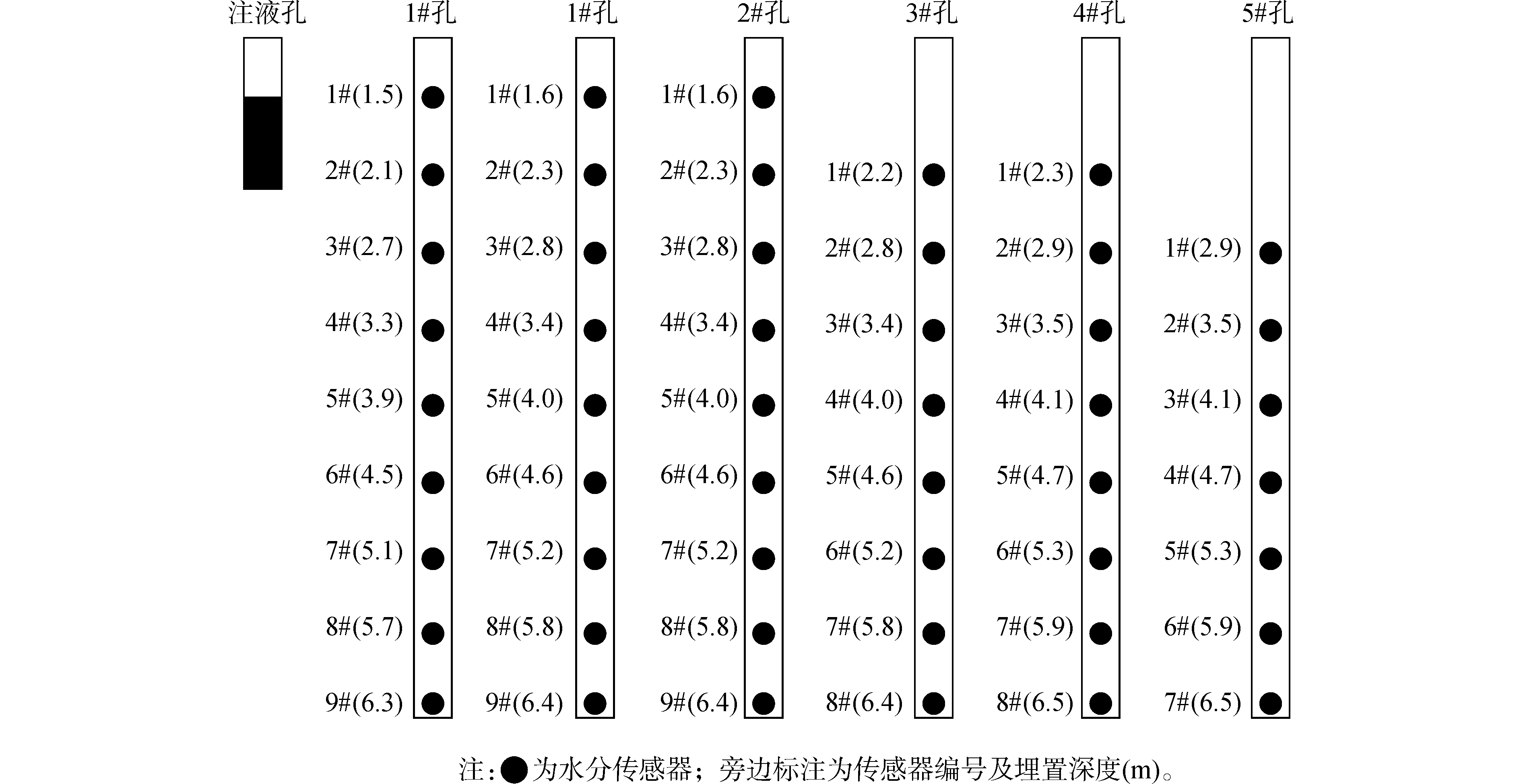
沿稀土矿山山脊线上相隔较远距离(10 m开外)选择5个合适的试验点(图 5),利用洛阳铲钻取5个直径为18 cm、孔深2~3 m的注液孔,并连以供水管网以供试验,每根水管安装一个水龙头和一个水表,以控制并量测注液流量。在每个注液孔周围钻取6个直径为18 cm、孔深6 m左右的水分传感器埋置孔,埋置孔距注液孔的直线距离按0.5 m递增,即埋置孔距注液孔的直线距离分别为0.5、1.0、1.5、2.0、2.5和3.0 m,试验钻孔平面布置图如图 6所示。各埋置孔内按不同间距埋设数量不等的FDS-100水分传感器,具体数量与位置如图 7所示。将各水分传感器的数据线全部连接至主机采集器,试验开始后每隔3 min自动采集并存储一次数据,并定时将采集器中存储数据连接至电脑进行分析处理。

|
Download:
|
| 图 5 现场注水试验(3#孔) Fig. 5 Field water injection test (3# hole) | |

|
Download:
|
| 图 6 水分传感器埋置孔平面图 Fig. 6 The floor plan of moisture sensor hole | |
|
Download:
|
| 图 7 水分传感器布置立面图 Fig. 7 Water sensor layout elevation | |
为使试验区域土体恢复至初始状态,试验在传感器埋设完成两个月后进行。本次单孔注液试验为定流量注液试验,5个注液孔的注液流量分别为3、2.4、1.8、1.2、0.6 m3/d。试验以大部分水分传感器读数趋于稳定为结束标志,实际试验时间为10 d。试验过程中采用数显型液位变送器定时量测每个注液孔内的水头。
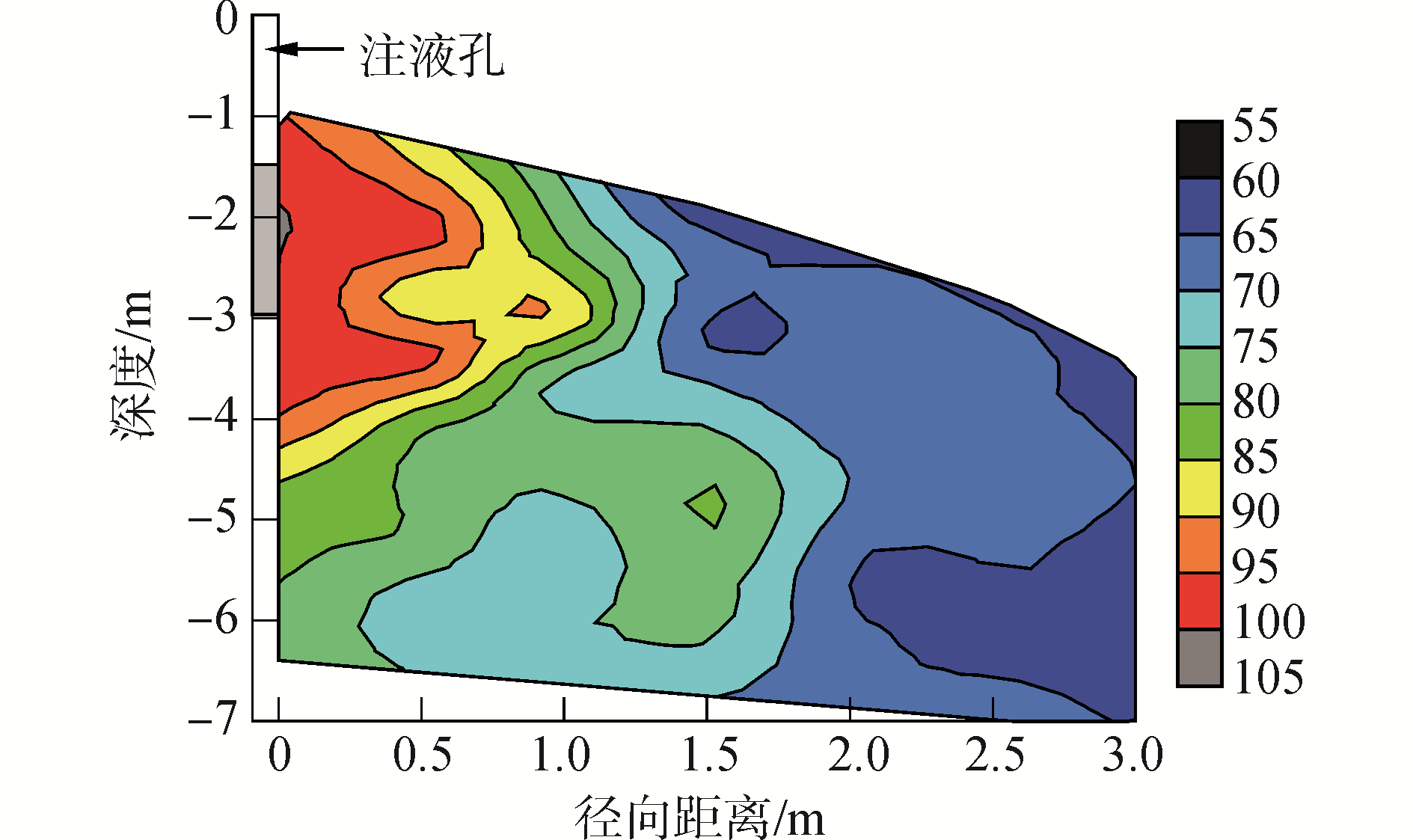
试验得到了各注液流量下注液孔周围土体含水率随时间的变化规律、拟稳渗条件下注液孔周围土体含水率空间分布规律及孔内稳定水头。图 8为3#注液孔稳渗后饱和度云图(其余各孔结果类似),由图可知,入渗基本稳定时,在注液孔附近只有较小范围的饱和区,而大片地区是饱和程度不一的非饱和区,且饱和度随着距注液孔距离的增大而逐渐降低。
|
Download:
|
| 图 8 单孔注液饱和度云图(3#孔) Fig. 8 Saturation cloud map of single-hole water injection(3# hole) | |
由于试验传感器测量误差及传感器埋置孔土体扰动等原因,云图中饱和度等值线形状不太规则,为进一步验证单孔注液饱和度等值线的形状特征,在单孔注液试验的同时开展单孔注液染色试验,在试验矿山选择一处地势平整的试验点,采用洛阳铲钻取一个孔深2.0 m,孔直径18 cm的注液孔,孔内连续注入浓度为4.0 g/L的亮蓝溶液,单孔注液流量为1.2 m3/d,总注液量为2.4 m3。注液完成5 d后,以注液孔为中心,沿竖向开挖,染色范围如图 9所示。从图 9可以看出,注液孔孔底以上部分的染色范围近似为椭球体,因此说明了单孔注液饱和度等值面近视为椭球面。

|
Download:
|
| 图 9 单孔注液亮蓝染色试验 Fig. 9 Brilliant blue dyeing test of single-hole water injection | |
若以Sr =80%等值面围成的椭球区域视为单孔注液影响范围,影响范围在孔底径向的长度为影响半径,将单孔注液试验结果汇总于表 3。
| 表 3 单孔注液试验结果 Tab.3 The test results of single-hole water injection |
当砂土的饱和度Sr>80%时,可将土体视为饱和状态[17-18]。因此,对于龙南离子型稀土矿单孔注液(准)稳态入渗过程,取Sr=80%等值面围成的近似椭球体区域为研究对象,将Sr=80%等值面视为概化湿润锋面,可将该(准)稳态入渗过程等效为以孔内水头H0及Sr=80%等值面上基质吸力Sf为驱动力的入渗问题,利用达西定律可以得到入渗流量的计算公式:
| $ {Q_{\rm{s}}} = {K_{\rm{e}}}{I_{\rm{e}}}{A_{\rm{e}}} $ | (3) |
式中:Qs为注液孔稳渗流量,m3/d;Ke为椭球体区域等效渗透系数,m/d,由于该区域视为饱和区域,取Ke=Ks;Ie为椭球体区域等效水力梯度,无量纲;Ae为注液孔给水面积,m2; Ae=πR02+2πR0H0=2πR0 (R0 /2+H0),R0为注液孔半径,m; H0为注液孔内水头,m。
注液孔壁积水表面上各点的水头压力存在差异,从液位表面到孔底水头压力值从0直线变化至H0,本文忽略这种差异,取孔壁积水表面上各点的恒定水头值为H0,则可由下式计算椭球体区域的等效水力梯度Ie:
| $ {I_{\rm{e}}} = \frac{{{Z_{\rm{f}}} + {H_0} + {h_{\rm{f}}}}}{{{Z_{\rm{f}}}}} $ | (4) |
式中:Zf为孔壁到概化湿润锋面的等效厚度,m;hf为概化湿润锋面上平均基质势,m。
由文献[19]可知,某一等含水率面上的平均基质吸力可基于非饱和土的土水特征曲线和渗透系数方程确定。根据文献[20]中湿润锋面上平均基质吸力的算法,类比可得Sr=80%椭球面上平均基质势按下式计算:
| $ {h_{\rm{f}}} = \frac{1}{{{\gamma _{\rm{w}}}}}\int_0^{{\psi _{0.8}}} {{K_{\rm{r}}}\left( \psi \right){\rm{d}}\psi } $ | (5) |
式中:ψ0.8为土体Sr=80%对应的基质吸力,Pa;rw为水的重度,kN/m3;Kr(ψ)为相对渗透系数函数。
对于椭球体研究区域,其体积和表面积可计算:
| $ V = \frac{4}{3}{\rm{ \mathsf{ π} }}{a^2}b $ | (6) |
| $ {A_{{\rm{ell}}}} = 2{\rm{ \mathsf{ π} }}a\sqrt {{a^2} + \frac{2}{3}ab + \frac{7}{3}{b^2}} $ | (7) |
式中:V为椭球体体积,m3;Aell为椭球体表面积,m2;a为椭球体长半轴,m;b为椭球体短半轴,m。
根据体积等效原理[12],概化湿润锋等效厚度Zf为
| $ {Z_{\rm{f}}} = \frac{V}{{{A_{{\rm{ell}}}}}} = \frac{{2ab}}{{\sqrt {9{a^2} + 6ab + 21{b^2}} }} $ | (8) |
将式(5)、(8)代入式(4),可得
| $ \begin{array}{*{20}{c}} {{I_{\rm{e}}} = 1 + \frac{{\sqrt {9{a^2} + 6ab + 21{b^2}} }}{{2ab}} \cdot }\\ {\left( {{H_0} + \frac{{\int_0^{{\psi _{0.8}}} {{K_{\rm{r}}}\left( \psi \right){\rm{d}}\psi } }}{{{\gamma _{\rm{w}}}}}} \right)} \end{array} $ | (9) |
令非饱和土渗透特征值
| $ \begin{array}{*{20}{c}} {{Q_{\rm{s}}} = 2{\rm{ \mathsf{ π} }}{R_0}\left( {\frac{{{R_0}}}{2} + {H_0}} \right){K_s} \cdot }\\ {\left[ {1 + \frac{{\sqrt {9{a^2} + 6ab + 21{b^2}} }}{{2ab}}\left( {{H_0} + \frac{F}{{{\gamma _{\rm{w}}}}}} \right)} \right]} \end{array} $ | (10) |
式(10)即为原地浸矿单孔注液稳渗流量计算模型表达式,模型表达式中含有非饱和土渗透特征值F0.8,该值表征着非饱和区总体(不是对个别含水量而言的)透水的一种特性,其大小反映了土体非饱和区相对透水能力。
2.2 模型的验证以表 3中试验结果作为单孔注液稳渗流量模型验证的计算依据,同时采用SEEP/W建立单孔注液入渗轴对称有限元模型,计算5种试验工况下的渗流流量,作为对比分析的依据之一。根据土体非饱和渗透本构模型公式(1),计算得F0.8=4.655 kPa,各注液孔稳渗流量计算结果见表 4,各注液孔稳渗流量对比结果见图 10。由表 3和图 9可知,单孔注液稳渗流量数值计算值与试验实测值比较吻合,模型计算值比试验实测值大多偏小,且误差绝对值随着H0/D的增大而增大,这是因为:单孔注液入渗基本稳定时,在注液孔附近会形成较小范围的饱和区,这相当于增加了注液孔的直径,且饱和区范围会随着H0/D的增大而增大,但这个范围难以在试验中进行测量,本文稳渗流量模型没有考虑这方面的影响,因此造成模型计算值偏小,模型误差绝对值随着H0/D的增大而增大。对于原地浸矿注液孔而言,孔内水头一般在0.5~1.0 m,模型误差绝对值在12%以内,满足工程要求,因此,对于原地浸矿工程而言,本文稳渗流量计算模型是适用的。
| 表 4 单孔注液稳渗流量计算结果 Tab.4 The calculation results of single-hole water injection steady seepage flow |

|
Download:
|
| 图 10 单孔注液稳渗流量与孔内水头的变化曲线 Fig. 10 The curve of the single-hole injection steady seepage flow vs. water head | |
进一步分析表 4中各参数变化趋势可知,随着注液孔内水头H0的增加,Sr ≥80%近似椭球体的形状和大小也会发生改变,体现在椭球体长、短轴方向的改变及椭球体体积、面积的变大;概化湿润峰的厚度Zf基本上与水头H0呈线性增加,其中5#孔的Zf值(最大值)相对于1#孔的Zf值(最小值)增大了64.8%,但各注液孔的等效水力梯度变化不大,其中5#孔的Ie值(最小值)相对于1#孔的Ie值(最大值)只减小了12.5%。因此,若取各注液孔等效水力梯度为各孔等效水力梯度的平均值
| $ {Q_{\rm{s}}} = 2{\rm{ \mathsf{ π} }}{R_0}\left( {\frac{{{R_0}}}{2} + {H_0}} \right)\overline {{I_{\rm{e}}}} {K_s} $ | (11) |
由式(11)可知,在注液孔半径R0不变的情况下,原地浸矿单孔注液稳渗流量Qs与孔内水头H0近似呈线性关系,这与图 10中的拟合结果也是基本吻合的。
4 结论1) 非饱和土渗透特征值F0.8是非饱和土总体(不是对个别含水量而言)透水能力的表征,其大小反映了土体非饱和区相对透水能力。将该特征值引入到原地浸矿单孔注液稳渗流量模型,能够很好地考虑非饱和区对原地浸矿单孔入渗规律的影响,提高了模型的准确度。
2) 原地浸矿单孔注液孔周等效水力梯度的计算比较困难,需要确定单孔注液入渗Sr ≥80%椭球体范围的形状。但不同孔内水头条件下等效水力梯度值的变化较小,固可取5次试验的平均值5.62,从而简化了稳渗流量计算模型,并从简化模型得出原地浸矿单孔注液稳渗流量Qs与孔内水头H0近似呈线性关系。
3) 单孔注液入渗基本稳定时,在注液孔附近会形成较小范围的饱和区,这相当于增加了注液孔的直径,但这个范围难以在试验中进行测量,本文稳渗流量模型没有考虑这方面的影响,因此造成模型计算值偏小,模型误差绝对值随着H0/D的增大而增大。对于原地浸矿注液孔而言,孔内水头一般在0.5~1.0 m,模型误差绝对值在12%以内,满足工程要求,表明单孔注液稳渗流量计算模型是有效的。
| [1] |
中国有色金属工业长沙勘察设计研究院. YS 5214-2000, 注水试验规程[S]. 北京: 中国计划出版社, 2001. China Nonferrous Metals Survey and Design Institute of Changsha. YS 5214-2000, Specification for injection test[S]. Beijing: China Planning Press, 2001. (  0) 0)
|
| [2] |
中华人民共和国水利部. SL 345-2007, 水利水电工程注水试验规程[S]. 北京: 中国水利水电出版社, 2008. The Ministry of Water Resource of the People's Republic of China. SL 345-2007, Code of water injection test for water and hydropower engineering[S]. Beijing: China Water & Power Press, 2008. (  0) 0)
|
| [3] |
吴兵, 于振江, 王紫薇, 等. 基于饱和-非饱和渗流的煤层注水数值模拟及应用[J]. 中国煤炭, 2015, 41(6): 102-105. WU Bing, YU Zhenjiang, WANG Ziwei, et al. The numerical simulation of coal seam water injection based on saturated-unsaturated seepage and applications[J]. China coal, 2015, 41(6): 102-105. (  0) 0)
|
| [4] |
BAGARELLO V, GIORDANO G. Comparison of procedures to estimate steady flow rate in field measurement of saturated hydraulic conductivity by the Guelph permeameter method[J]. Journal of agricultural engineering research, 1999, 74(1): 63-71. DOI:10.1006/jaer.1999.0437 (  0) 0)
|
| [5] |
罗仙平, 翁存建, 徐晶, 等. 离子型稀土矿开发技术研究进展及发展方向[J]. 金属矿山, 2014, 43(6): 83-90. LUO Xianping, WENG Cunjian, XU Jing, et al. Research progress on and development trend of exploitation technique of ion-absorbed type rare earth ore[J]. Metal mine, 2014, 43(6): 83-90. (  0) 0)
|
| [6] |
邓国庆, 杨幼明. 离子型稀土矿开采提取工艺发展述评[J]. 稀土, 2016, 37(3): 129-133. DENG Guoqing, YANG Youming. A review of the mining technologies of ion-absorbed rare earth mineral[J]. Chinese rare earths, 2016, 37(3): 129-133. (  0) 0)
|
| [7] |
SMEDEMA L K, RYCROFT D W. Land drainage[M]. Ithaca, New York: Cornell University Press, 1983.
(  0) 0)
|
| [8] |
CORNWELL F E. Flow from a Short Section of test-hole below ground water level[J]. Theory and problems of water percolation, 1953, 8(2): 66-68. (  0) 0)
|
| [9] |
GLOVER R E. Flow from a test-hole located above groundwater level[M]//ZANGAR C N. Theory and Problems of Water Percolation. Denver, Colorado: Bureau of Reclamation, 1953: 69-71.
(  0) 0)
|
| [10] |
DAY P R, LUTHIN J N. Sand-model experiments on the distribution of water-pressure under an unlined canal[J]. Soil science society of America journal abstract, 1954, 18(2): 133-136. DOI:10.2136/sssaj1954.03615995001800020005x (  0) 0)
|
| [11] |
吴良骥. 非饱和区对地下水埋藏很深井孔入渗的影响[J]. 水利水运科学研究, 1986(3): 33-45. WU Liangji. Effect of unsaturated region on the infiltration of the borehole above the water table far deep from ground surface[J]. Hydro-science and engineering, 1986(3): 33-45. (  0) 0)
|
| [12] |
赵伟霞, 张振华, 蔡焕杰, 等. 恒定水头井入渗Green-Ampt模型的改进与验证[J]. 水利学报, 2010, 41(4): 464-470. ZHAO Weixia, ZHANG Zhenhua, CAI Huanjie, et al. Improvement and verification of the Green-Ampt model for constant-head well permeameter[J]. Journal of hydraulic engineering, 2010, 41(4): 464-470. (  0) 0)
|
| [13] |
工程地质手册编写委员会. 工程地质手册[M]. 3版. 北京: 中国建筑工业出版社, 1992. Committee for the Compilation of Engineering Geology Handbook. The engineering geology manual[M]. 3rd ed.. Beijing: China Architecture & Building Press, 1992. (  0) 0)
|
| [14] |
张贻火. 钻孔注水试验方法浅析[J]. 资源环境与工程, 2008, 22(S1): 203-206. ZHANG Yihuo. Analyses of the borehole water injection test method[J]. Resources environment & engineering, 2008, 22(S1): 203-206. (  0) 0)
|
| [15] |
盛林. 常水头注水试验不同水头对渗透系数的影响[J]. 小水电, 2015, 182(2): 14-16, 31. SHENG Lin. The influence of different head to permeability coefficient in constant head water injection test[J]. Small hydro power, 2015, 182(2): 14-16, 31. (  0) 0)
|
| [16] |
VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil science society of America journal, 1980, 44(5): 892-898. DOI:10.2136/sssaj1980.03615995004400050002x (  0) 0)
|
| [17] |
东南大学, 浙江大学, 湖南大学, 等. 土力学[M]. 北京: 中国建筑工业出版社, 2010. Southeast University, Zhejiang University, Hunan University, et al. Soil Mechanics[M]. 3rd ed. Beijing: China Architecture & Building Press, 2010. (  0) 0)
|
| [18] |
谢定义. 非饱和土土力学[M]. 北京: 高等教育出版社, 2015. XIE Dingyi. Soil mechanics for unsaturated soils[M]. Beijing: Higher Education Press, 2015. (  0) 0)
|
| [19] |
SCHAAP M G, LEIJ F J. Improved prediction of unsaturated hydraulic conductivity with the Mualem-Van Genuchten model[J]. Soil science society of America, 2002, 64(3): 843-851. (  0) 0)
|
| [20] |
MEIN R G, FARRELL D A. Determination of wetting front suction in the green-Ampt equation[J]. Soil science society of America, 1974, 38(6): 872-876. DOI:10.2136/sssaj1974.03615995003800060014x (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


