2. 同济大学 土木工程防灾国家重点实验室, 上海 200092
2. State Key Laboratory for Disaster Prevention in Civil Engineering, Tongji University, Shanghai 200092, China
在以往的桥梁实际震害中,桥墩抗震性能的设计不足导致了很多桥梁结构的破坏,如Loma Prieta地震(1989年,Mw6.9)中的Cypress高架桥,Northridge地震(1994年,Mw6.7)中的Bull Creek Canyon海峡桥以及汶川地震(2008年,Mw7.9)中的百花大桥等。桥墩作为联系桥梁上部结构与基础的重要构件,其抗震性能的好坏直接影响着整个桥梁结构体系的抗震性能,因而有必要提高强震区域桥梁的桥墩抗震性能,来确保桥梁结构的安全性。
为提高桥墩的抗震性能,目前广泛采用的方法是基于桥梁结构的延性抗震设计方法,通过箍筋的约束作用来提高桥梁结构的抗震性能。然而对于强震区域的桥梁结构,这种方法往往需要使用配置大量的加密箍筋,在一定程度上提高了施工与工程质量控制的难度。另外,对于桥梁结构的某些特定部位,根本就没有足够的空间来布置大量箍筋。因而,有必要采用其他方法来提高桥墩的抗震性能。近年来,钢纤维混凝土逐渐应用于工程实际。钢纤维混凝土通过在普通混凝土中掺入钢纤维,能够有效地提高混凝土的抗拉、抗弯、抗冲击、耐疲劳以及延性等性能。因而,为了减少桥墩过密的箍筋数量,可以考虑使用钢纤维混凝土来提高桥墩整体的强度和塑性区域的延性。
目前,多数研究集中于钢纤维混凝土的材料性能和数值模拟方法的研究[1-5]。Mansour[6-7]分别对预制钢纤维混凝土板和具有不同配筋的钢纤维混凝土梁的抗弯性能进行了分析。Yadav等[8-10]则分别测试了钢纤维混凝土梁的抗剪和抗弯性能及极限承载能力。对于钢纤维混凝土墩柱的抗震性能分析而言,张于晔等对钢纤维混凝土墩柱进行了拟静力试验,并提出了相应的数值模拟方法[11-13]。然而,上述研究仅针对钢纤维混凝土的力学特性,较少涉及到钢纤维混凝土桥梁结构的整体抗震性能分析。因而,本文以两座采用钢纤维混凝土的连续刚构桥梁为例,分别建立三维有限元模型,选取了60条实测地震波,对桥梁结构进行非线性时程分析,并生成了桥梁结构的地震易损性曲线,以概率方法对钢纤维混凝土桥梁的抗震性能进行分析。
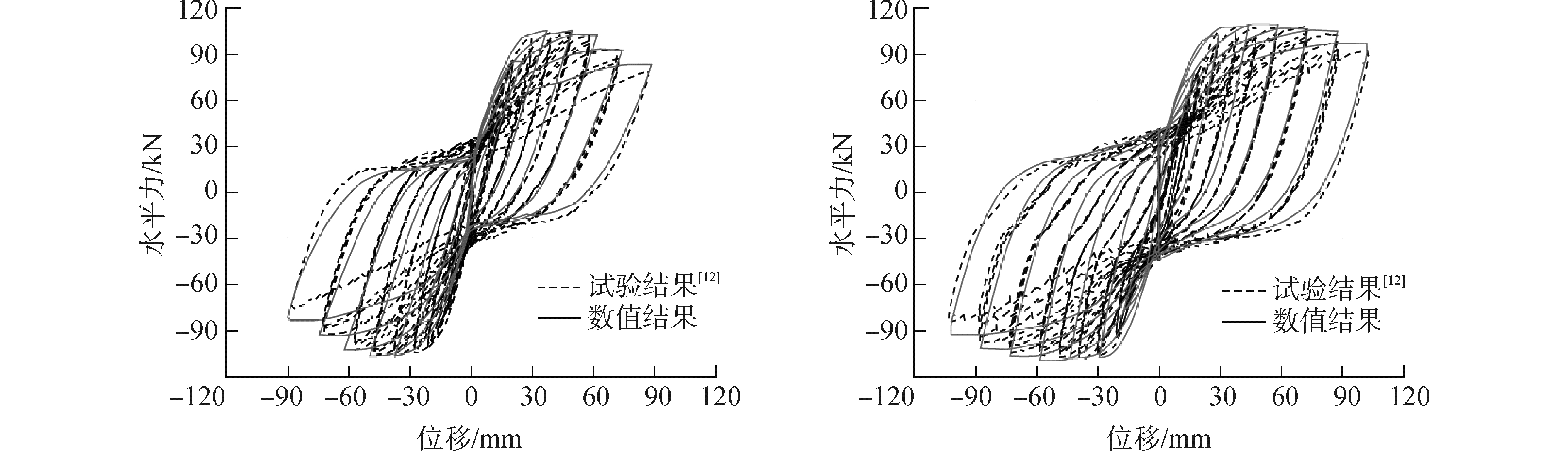
1 钢纤维混凝土模拟相比普通混凝土,钢纤维混凝土提高了混凝土的弹性模量、抗压强度以及相应的压应变,并且能够改变钢筋与混凝土的粘结滑移效应。在本文中,钢纤维混凝土采用OpenSees程序模拟,采用Conrete07本构模型、粘结滑移材料、纤维单元以及零长度单元来进行模拟。本文所使用的数值模拟方法通过与张于晔等[12]的拟静力试验结果对比进行了验证,来证明该方法的准确性,如图 1所示。
|
Download:
|
| 图 1 本文所使用方法与拟静力试验结果[12]的对比 Fig. 1 Comparison between numerical simulations with the cyclic loading tests | |
在本文的纤维单元中,普通混凝土以及钢纤维混凝土均采用Concrete07本构模型来进行模拟。Concrete07本构模型是Mander混凝土模型的改进型,由Chang和Mander在大量往复试验的基础上提出的,如图 2所示。由于钢纤维能够影响混凝土力学性能,因而本文采用Nataraja等[12]提出的公式计算钢纤维对混凝土力学性能的影响:

|
Download:
|
| 图 2 Concrete07本构关系图 Fig. 2 Force-deformation relationship of Concrete07 | |
| $ {f_c} = {f_{c0}} + 2.160\;4{R_I} $ | (1) |
| $ {\varepsilon _c} = {\varepsilon _{c0}} + 0.000\;6{R_I} $ | (2) |
| $ {R_I} = {W_f}{L_f}/{D_f} $ | (3) |
式中:fc0为普通混凝土抗压强度;εc0为与fc0对应的混凝土应变;fc为钢纤维混凝土抗压强度;εc为与fc对应的压应变;RI为钢纤维的增强指数;Wf为钢纤维的质量分数,一般认为取钢纤维体积分数Vf的3.2倍;Lf、Df分别为钢纤维长度和直径,本文采用长度50 mm以及直径10 mm的钢纤维来增强混凝土。出于经济性方面的考虑,本文所用的钢纤维用量为1%、3%以及5%。每个钢纤维用量对应的Concrete07模型参数如表 1。
| 表 1 Concrete07模型中各试件混凝土参数值 Tab.1 Concrete parameters adopted by Concrete07 model |
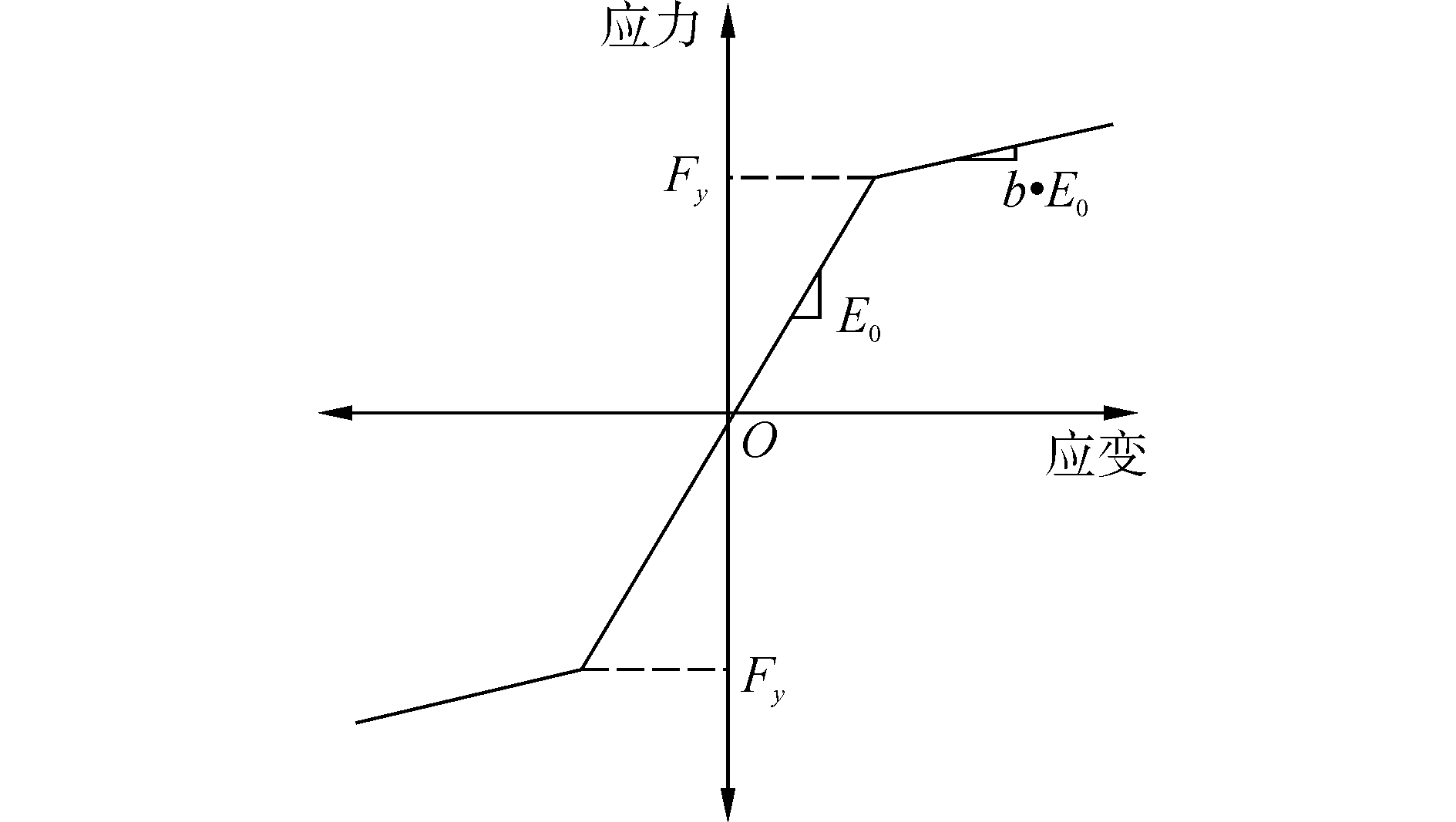
在地震荷载作用下,钢筋会出现线弹性段、屈服平台段、应变强化段和应变软化段。本文采用Steel01双线性模型近似考虑应变强化效应,其本构关系如图 3所示。
|
Download:
|
| 图 3 Steel01本构关系图 Fig. 3 Force-deformation relationship of Steel01 | |
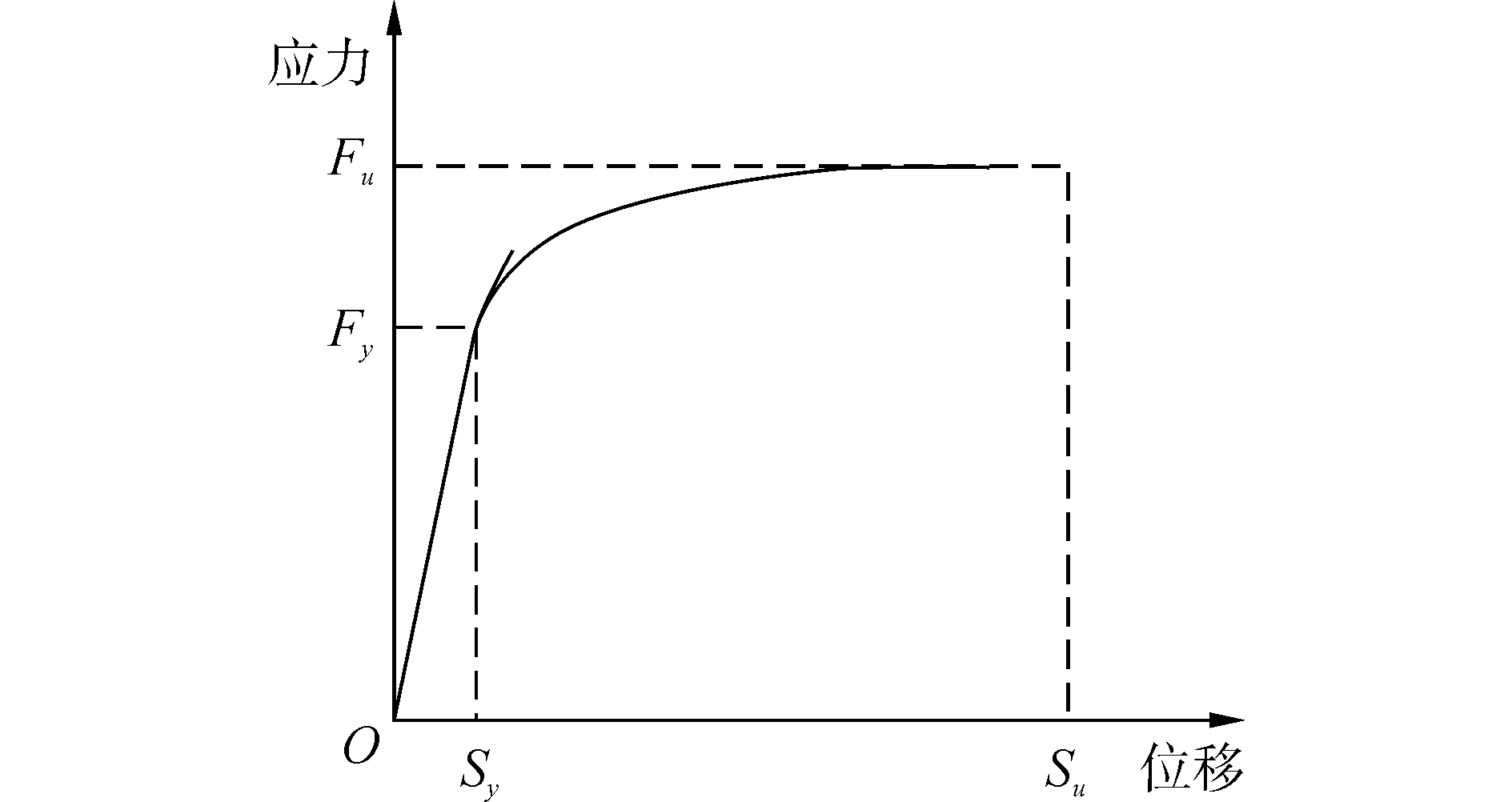
在地震反复荷载作用下,钢纤维能够显著影响钢筋与混凝土之间的黏结性能[13-14]。为更好地模拟这一影响,可在墩底处附加一个单独考虑纵向钢筋滑移变形的零长度单元,并采用粘结滑移材料Bond_SP01来考虑黏结滑移效应,其本构关系如图 4所示。
|
Download:
|
| 图 4 Bond_SP01本构关系图 Fig. 4 Force-deformation relationship of Bond_SP01 | |
本文中不同钢纤维用量的Bond_SP01材料的主要力学参数如表 2所示,其中fy为钢筋的屈服强度,fsu为钢筋的极限强度,参数取值按照实际所用钢筋确定。钢筋达到屈服应力时的粘结滑移量为Sy;钢筋达到极限应力时的滑移量为Su;钢筋的应力-滑移曲线初始硬化率为b(钢筋屈服时曲线切线刚度与初始刚度的比值);钢筋应力-滑移循环响应的“捏拢”因子为R,其中参数Sy可由文献[15-16]推荐的公式计算得到:
| 表 2 Bond_SP01模型中各参数取值 Tab.2 Mechanical properties in Bond_SP01 material model |
| $ {S_y} = {S_1}{{\rm{e}}^{1.8\left[ {{{\left( {{u_y}/u_m^{{\rm{SFRC}}}} \right)}^2} - 1} \right]}} $ | (7) |
| $ {u_y} = 0.78\sqrt {{f_c}} {\left( {\frac{{c + 0.45c{V_f}{L_f}/{D_f}}}{{{d_b}}}} \right)^{2/3}} $ | (8) |
| $ u_m^{{\rm{SFRC}}} = \left( {1 + 0.34\sqrt {{V_f}{L_f}/{D_f} - 0.25} } \right)u_m^{{\rm{RC}}} $ | (9) |
| $ u_m^{{\rm{RC}}} = 0.75\sqrt {{f_c}} {\left( {c/{d_b}} \right)^{2/3}} $ | (10) |
式中:uy为屈服粘结应力;um为最大粘结应力;S1=0.15c0,c0为纵向受力钢筋的净距,c为最小保护层混凝土厚度。
2 桥梁地震易损性分析目前,基于性能的地震工程框架已经广泛应用于基于性能的桥梁抗震设计方法中。桥梁地震易损性分析方法是基于性能的地震工程框架中较为重要的一环。常用的地震易损性分析方法有两种,分别为云图法(PSDA)和放缩法(IDA)。两种方法都能够考虑结构与地震波的不确定性,区别在于云图法并不需要反复放缩地震波,因而所要求的计算量较少。本文采用云图法计算地震易损性曲线,具体如下:
1) 构造地震需求模型(PSDM)。本文采用Cornell提出的幂运算定律,认为地震作用下结构的平均地震需求Sd与地震动参数(IM)符合对数线性关系,即
| $ \ln {S_d} = \ln a + b\ln {I_M} $ | (11) |
式中a和b是统计回归系数。
2) 假设地震作用下,结构的地震需求服从两个参数的对数正态分布[17],因而结构地震需求的方差,βd|IM,可以由下式计算:
| $ {\beta _{d\left| {{I_M}} \right.}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {\left[ {\ln {D_i} - \left( {\ln a + b\ln {I_{Mi}}} \right)} \right]^2} }}{{n - 2}}} $ | (12) |
式中:Di为第i条地震波的结构地震需求,n为考虑的地震波数量。
3) 得到上面两步的地震需求均值以及方差以后,地震易损性函数[18]可以表示为
| $ P\left[ {D \ge C\left| {{I_M}} \right.} \right] = 1 - \mathit{\Phi }\left( {\frac{{\ln C - \ln {S_d}}}{{{\beta _{d\left| {{I_M}} \right.}}}}} \right) $ | (13) |
式中:Φ(·)为标准正态分布函数,C为结构构件的能力。
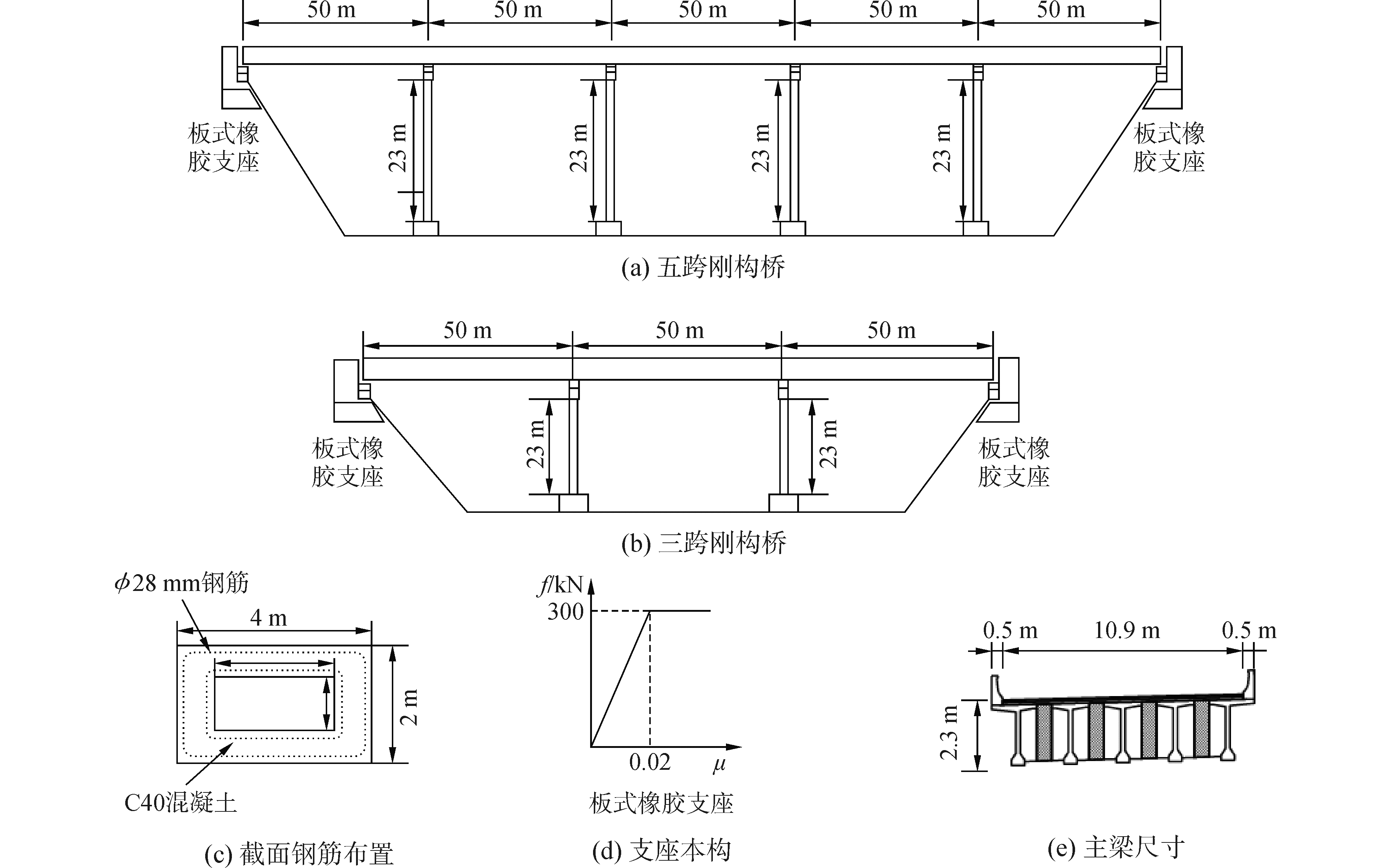
3 实例分析本文以两座连续刚构桥为例对桥墩使用钢纤维混凝土的桥梁结构进行地震易损性分析。两座桥单跨跨径均为50 m,桥墩高均为23 m,横截面为4×2 m的空心矩形截面,两端采用板式橡胶支座支撑。桥墩采用钢纤维混凝土,主梁采用C50普通混凝土,钢筋采用HRB335,桥墩纵向配筋率为0.8%,配箍率为0.6%。桥梁整体布置及细部构造如图 5所示。利用OpenSees有限元程序分别建立两座连续刚构桥梁的三维有限元模型。主梁采用线弹性单元模拟,而桥墩采用非线性纤维梁单元来模拟,桥梁两端的支座采用零长度单元模拟,并考虑桥台刚度对桥梁响应的影响。
|
Download:
|
| 图 5 桥梁结构整体布置及细部构造图 Fig. 5 Layout and details of reinforced concrete bridges | |
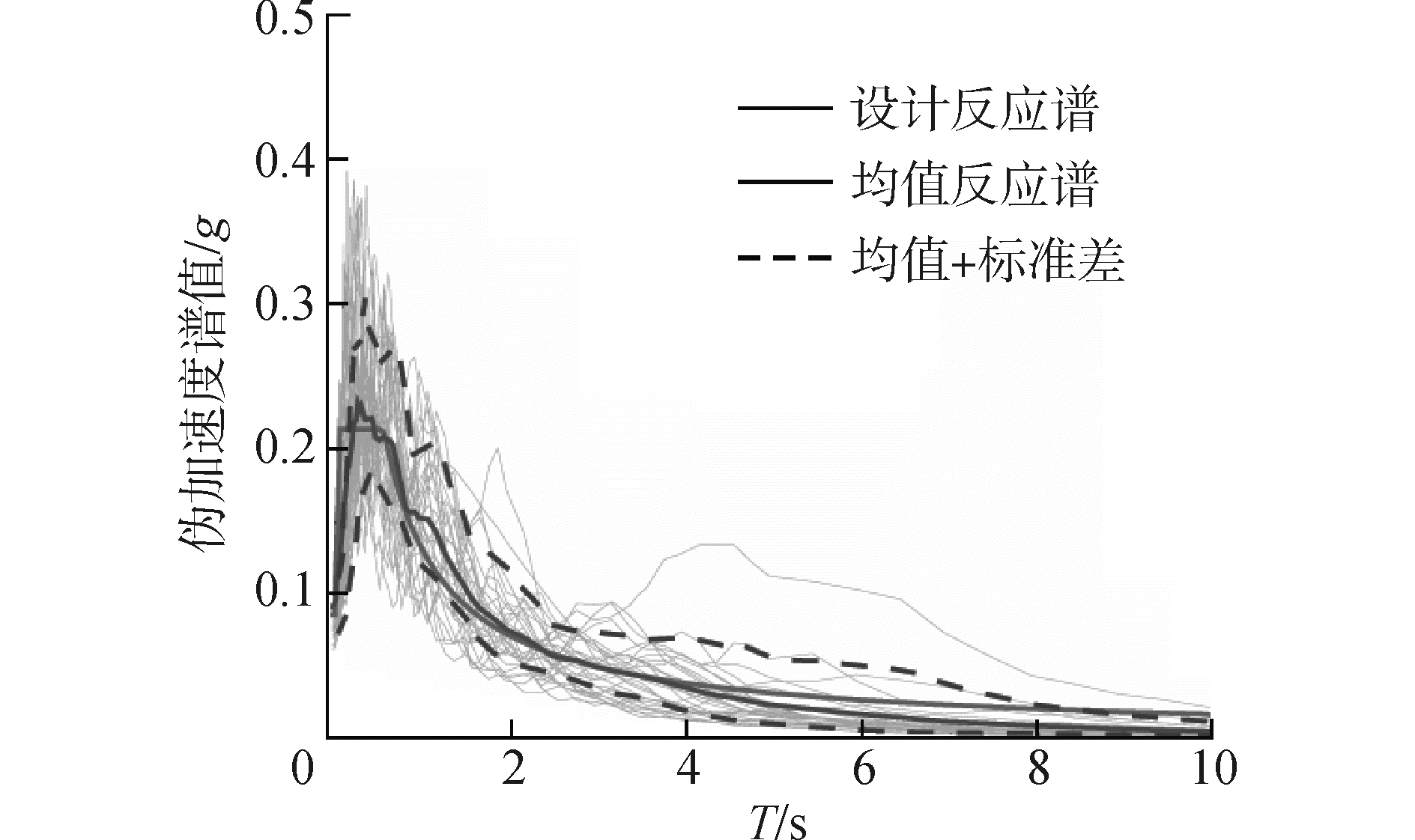
本文桥梁所处的场地为中软场地土,为Ⅲ类场地。因而本文的地震波选取采用如下标准:1)地震震级区间为6~8级;2)震中距区间为10~100 km(100 km的设置是为了避免过小的地震波);3)由于是Ⅲ类场地,Vs30的取值区间为300~700 m/s。根据前面的标准,本文从PEER强震数据平台中选取60条地震波,并以该桥地震安评报告提供的场地反应谱为目标对该60条地震波进行调幅,调幅后各条地震波的谱加速度曲线如图 6所示。对于地震动参数而言,本文以地震动峰值加速度(PGA)作为地震动强度参数。
|
Download:
|
| 图 6 选取的60条地震波反应谱 Fig. 6 Fesponse spectra of the selected 60 ground motions | |
在进行桥梁地震易损性分析时,需要定义损伤等级和损伤指标[19]。不同于连续梁桥,连续刚构桥墩在地震作用下有不只一处塑性铰区,因而无法采用桥墩特定部位的曲率延性系数来定义损伤指标。因此,本文采用墩顶位移作为工程需求参数(EDP)来定义桥墩整体的损伤指标。介于不同损伤等级的具体描述较为困难,本文以墩底截面最外层钢筋首次屈服时的墩顶位移作为轻微损伤的指标,并采用文献[20]所述方法通过在轻微损伤的基础上乘以相应的延性系数,来定义中等损伤、严重损伤和倒塌的损伤指标的数值。在本文中,中等损伤、严重损伤和倒塌对应的延性系数分别取2.25、2.9和4.6。损伤等级与损伤指标的定义如表 3所示。
| 表 3 损伤等级及损伤指标的定义 Tab.3 Definitions of damage states and DI criteria |
由表 3可知,在轻微损伤等级下,墩顶位移能力之间的差异较明显,混凝土中钢纤维用量达到5%时,相较普通混凝土桥墩(钢纤维用量为0),钢纤维能够提高36.8%的墩顶位移能力。
4 数据分析与讨论 4.1 地震需求概率模型本文使用图 6中的60条地震波,对两座连续刚构桥进行纵向激励,通过多次非线性时程分析,得到相应的墩顶位移,并采用上述方法建立概率地震需求模型,如图 7所示。由图 7可知,当钢纤维用量从0向5%增加时,无论是三跨还是五跨刚构桥,结构的地震需求都有略微的增大,这应该是由于钢纤维的加入使得混凝土的强度与刚度增加,从而增强了桥梁的整体刚度,从而使得桥梁的周期变短,地震响应增大。从图 7中还可以看出,相较三跨刚构桥而言,钢纤维用量对五跨刚构桥地震需求的影响更为明显,这可能是由于钢纤维对五跨刚构桥整体刚度的增加较为明显。但总体来看,不论是三跨还是五跨连续刚构桥,不同的钢纤维用量对于桥梁结构的地震需求影响都不是特别大。需要注意的是,图 7所示的概率地震需求模型具有较大的离散性,这与本文所选取的地震动离散性有关。

|
Download:
|
| 图 7 不同跨径下的桥梁概率地震需求模型 Fig. 7 Probabilistic seismic demand models of bridges with different spans | |
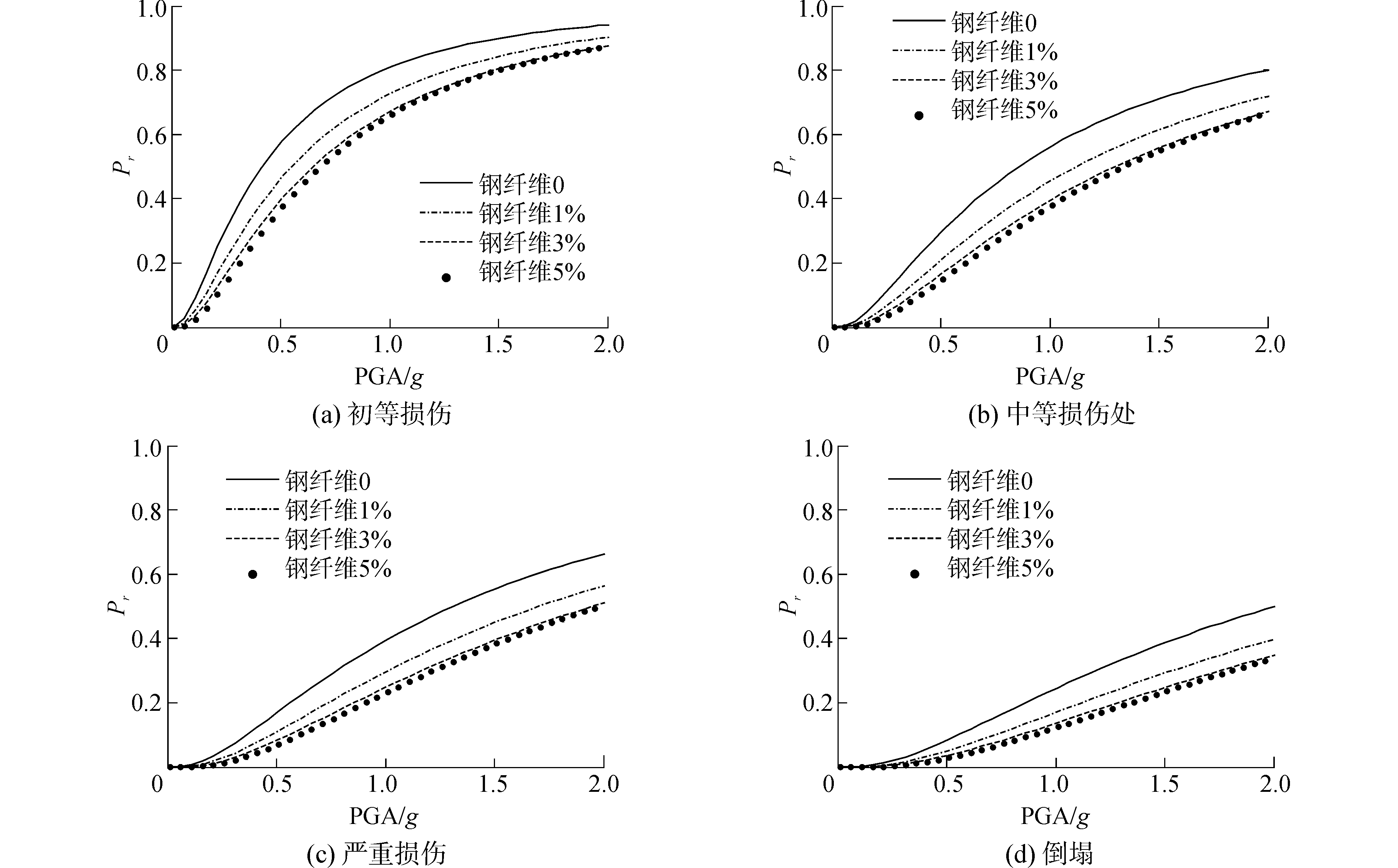
对于桥梁结构的抗震性能而言,单方面分析结构的地震需求或者抗震能力都无法准确说明结构抗震性能的改变,因而本文在研究钢纤维混凝土对刚构桥抗震性能的影响时,对两座不同跨径的刚构桥分别进行了地震易损性分析。在桥梁地震易损性分析中,分别计算得到了不同钢纤维用量时三跨与五跨刚构桥的地震易损性曲线,如图 8、9所示。
|
Download:
|
| 图 8 三跨连续刚构桥不同钢纤维用量下的易损性曲线 Fig. 8 Fragility curves of three span continuous rigid frame bridge with steel fiber concrete | |
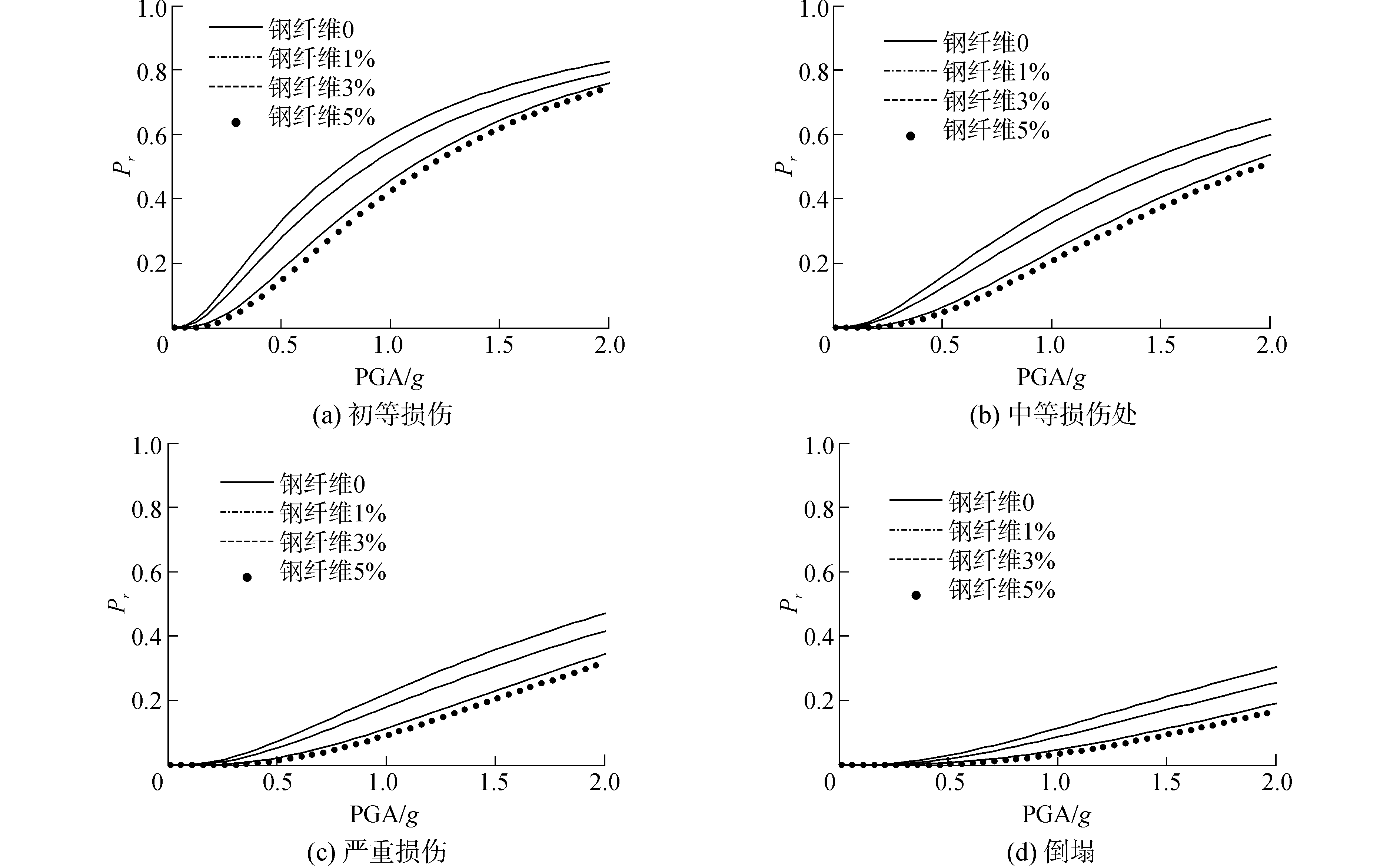
|
Download:
|
| 图 9 五跨连续刚构桥不同钢纤维用量的易损性曲线 Fig. 9 Fragility curves of five span continuous rigid frame bridge with steel fiber concrete | |
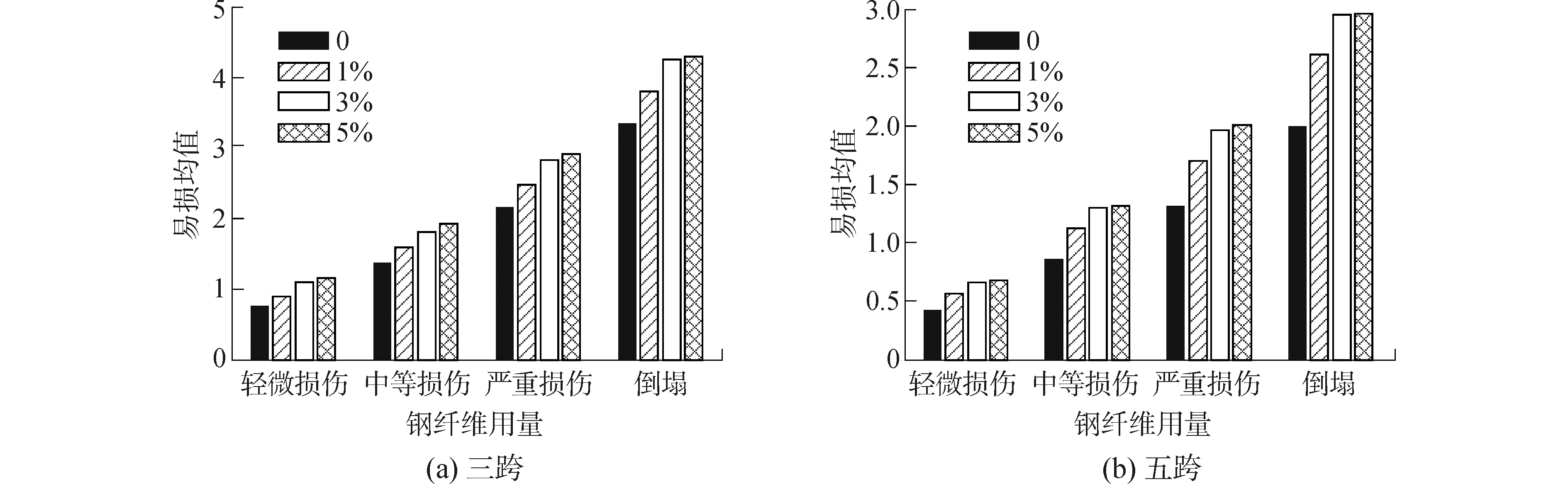
从图 8、9可以看出,相同钢纤维用量情况下,三跨连续刚构桥比五跨连续刚构桥更易损。这是由于五跨刚构桥周期较长,因而所受的地震荷载相对较小。对于不同跨径的桥梁结构,一定量的钢纤维的影响也可能不一样。当钢纤维用量为1%时,三跨刚构桥的易损概率的降低程度明显要比五跨刚构桥的降幅大。3%钢纤维的易损概率的降幅对于三跨刚构桥而言并不太明显,相反,对于五跨刚构桥,则相对更为明显。在相同损伤级别情况下,随着钢纤维用量的增多,其损伤概率将出现不同程度的降低,并且随着钢纤维用量的增多,其作用逐渐趋于一个稳定值。换言之,结合经济性因素,无论是三跨或者是五跨刚构桥,都会有一个最优的钢纤维用量值。从图 8、9中可以看到,对于本文所考虑的桥梁结构中,无论是三跨或者是五跨刚构桥,3%的钢纤维用量已经使得桥梁地震易损概率达到一个稳定的值,因而可以认为,3%是一个最优的钢纤维用量值。需要注意的是,这个最优值对于不同跨径、不同尺寸以及不同类型的桥梁可能是不同的。这些桥梁还需要结合具体的分析来讨论最优的钢纤维用量。为了确定钢纤维用量对于提升桥梁结构抗震性能的程度,本文采用易损均值来说明。易损均值采用易损概率为0.5时的PGA值来表示,结果如图 10所示,需要注意的是,易损均值越大,代表桥梁结构的抗震性能越好。
|
Download:
|
| 图 10 不同损伤等级下三跨与五跨连续刚构易损均值的比较 Fig. 10 Comparison of median fragility at different damage states for three and five span continuous rigid frame bridges | |
由图 10可知,对于不同的损伤等级而言,相同钢纤维用量的作用并不相同。举例而言,对于五跨刚构桥而言,在轻微损伤等级时,3%的钢纤维使得结构的易损均值从0.45g到0.6g左右,提高25%左右,而对于倒塌损伤等级而言,3%的钢纤维用量可以使得结构的易损均值从2.1g到2.9g左右,提高28%左右。另外,从图 10亦可知,对于相同的损伤等级,不同钢纤维用量的作用也并不相同,总体上这种作用呈逐渐减少的趋势。例如,对于三跨刚构桥而言,在严重损伤等级时,0、1%、3%以及5%钢纤维用量对应的易损均值为2.2g、2.4g、2.8g以及2.9 g。相比0%钢纤维的易损均值,相应的增幅为8.3%、21.4%以及24.1%,而相比前一个钢纤维用量(如1%相比0、3%相比1%),相应的增幅为8.3%、14.3%以及3.4%。虽然5%钢纤维对应的易损均值增幅最大,但相比3%钢纤维用量,5%钢纤维的作用增幅放缓(仅有3.4%)。因而,结合图 7~9,无论是三跨或者五跨刚构桥梁,3%钢纤维用量最为经济,作用效率最高,是本文所考虑桥梁的最优钢纤维用量。
4 结论1) 钢纤维可以有效提高混凝土材料的强度与刚度,使得桥梁结构在轻微损伤下具有更高的墩顶位移能力。
2) 采用钢纤维混凝土桥墩无法显著增加桥梁的地震需求,且对桥梁结构的概率地震需求模型的影响较小。
3) 在相同损伤级别情况下,随着钢纤维用量的增多,其损伤概率将出现不同程度的降低,并且随着钢纤维用量的增多,其作用逐渐趋于一个稳定值。对本文所考虑的桥梁结构而言,3%钢纤维用量最优,可以提升大约30%的桥梁抗震性能。
| [1] |
AGRAWAL A, JAIN T, AGARWAL S. Compressive strength testing of steel fiber reinforced concrete in different curing regimes[J]. International journal of engineering research & technology, 2014, 3(10): 1-5. (  0) 0)
|
| [2] |
Al-MATTARNEH H. Electromagnetic quality control of steel fiber concrete[J]. Construction and building materials, 2014, 73: 350-356. DOI:10.1016/j.conbuildmat.2014.09.101 (  0) 0)
|
| [3] |
李方元, 赵人达. 高强混凝土和钢纤维高强混凝土断裂性能试验研究[J]. 混凝土, 2002(8): 29-32. LI Fangyuan, ZHAO Renda. Crack performance test investigation of high performance concrete and steel fiber reinforced concrete[J]. Concrete, 2002(8): 29-32. (  0) 0)
|
| [4] |
高丹盈, 陈刚, SADRADDINH M N, 等. 钢筋与钢纤维混凝土的黏结-滑移性能及其关系模型[J]. 建筑结构学报, 2015, 36(7): 132-139. GAO Danying, CHEN Gang, SADRADDIN H M N, et al. Bond-slip behavior and constitutive model between rebar and steel fibre reinforced concrete[J]. Journal of building structures, 2015, 36(7): 132-139. (  0) 0)
|
| [5] |
KHALIFA E S. Analytical model for steel fiber concrete composite short-coupling beam[J]. Composites part B:engineering, 2014, 56: 318-329. DOI:10.1016/j.compositesb.2013.08.050 (  0) 0)
|
| [6] |
MANSOUR F R, BAKAR S A, IBRAHIM I S, et al. Flexural performance of a precast concrete slab with steel fiber concrete topping[J]. Construction and building materials, 2015, 75: 112-120. DOI:10.1016/j.conbuildmat.2014.09.112 (  0) 0)
|
| [7] |
MERTOL H C, BARAN E, BELLO H J. Flexural behavior of lightly and heavily reinforced steel fiber concrete beams[J]. Construction and building materials, 2015, 98: 185-193. DOI:10.1016/j.conbuildmat.2015.08.032 (  0) 0)
|
| [8] |
YADAV S, AMEERULLAH K, CHRYSELLE J. Shear behavior of steel fiber reinforced concrete beam[J]. International journal of Theoretical and Experimental Research (IJTER), 2014, 1(2): 30-33. (  0) 0)
|
| [9] |
SWAMY R N, AL-TA'AN S A. Deformation and ultimate strength in flexure of reinforced concrete beams made with steel fiber concrete[J]. Journal of the American concrete institute, 1981, 78(5): 395-405. (  0) 0)
|
| [10] |
QIAN Chunxiang, PATNAIKUNI I. Properties of high-strength steel fiber-reinforced concrete beams in bending[J]. Cement and concrete composites, 1999, 21(1): 73-81. DOI:10.1016/S0958-9465(98)00040-7 (  0) 0)
|
| [11] |
张于晔, 魏红一, 袁万城. 钢纤维混凝土桥墩抗震性能数值模拟与试验[J]. 同济大学学报(自然科学版), 2013, 41(6): 813-820. ZHANG Yuye, WEI Hongyi, YUAN Wancheng. Numerical and experimental study on seismic performance of bridge piers by steel fiber reinforced concrete[J]. Journal of Tongji University(Natural Science), 2013, 41(6): 813-820. (  0) 0)
|
| [12] |
ZHANG Yuye, HARRIES K A, YUAN Wancheng. Experimental and numerical investigation of the seismic performance of hollow rectangular bridge piers constructed with and without steel fiber reinforced concrete[J]. Engineering structures, 2013, 48: 255-265. DOI:10.1016/j.engstruct.2012.09.040 (  0) 0)
|
| [13] |
HARAJLI M H, GHARZEDDINE O. Effect of steel fibers on bond performance of steel bars in NSC and HSC under load reversals[J]. Journal of materials in civil engineering, 2007, 19(10): 864-873. DOI:10.1061/(ASCE)0899-1561(2007)19:10(864) (  0) 0)
|
| [14] |
CAMPIONE G, CUCCHIARA C, MENDOL L, et al. Experimental investigation on local bond-slip behaviour in lightweight fiber reinforced concrete under cyclic actions[C]//Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver, Canada: WCEE, 2004: 84-91. http://www.researchgate.net/publication/265037926_Experimental_Investigation_on_Local_Bond-Slip_Behavior_in_Lightweight_Fiber_Reinforced_Concrete_Under_Cyclic_Actions
(  0) 0)
|
| [15] |
ZHAO Jian, SRITHARAN S. Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J]. ACI structural journal, 2007, 104(2): 133-141. (  0) 0)
|
| [16] |
HARAJLI M H. Bond behavior in steel fiber-reinforced concrete zones under static and cyclic loading:experimental evaluations and analytical modeling[J]. Journal of materials in civil engineering, 2010, 22(7): 674-686. DOI:10.1061/(ASCE)MT.1943-5533.0000067 (  0) 0)
|
| [17] |
庞于涛, 袁万城, 沈国煜, 等. 基于结构易损性分析的公路桥梁可靠度研究[J]. 哈尔滨工程大学学报, 2012, 33(9): 1091-1096. PANG Yutao, YUAN Wancheng, YU Shenguo, et al. Reliability analysis of highway bridges based on structural vulnerability analysis[J]. Journal of Harbin Engineering University, 2012, 33(9): 1091-1096. (  0) 0)
|
| [18] |
袁万城, 王征南, 庞于涛, 等. 连续梁桥在主震-余震序列波下的地震易损性分析[J]. 哈尔滨工程大学学报, 2016, 37(12): 1671-1676. YUAN Wancheng, WANG Zhennan, PANG Yutao, et al. Seismic fragility analysis of a continuous girder bridge subject to an earthquake mainshock-aftershock sequence[J]. Journal of Harbin Engineering University, 2016, 37(12): 1671-1676. (  0) 0)
|
| [19] |
王晓伟, 叶爱君, 沈星, 等. 大跨度桥梁边墩横向减震体系的地震易损性分析[J]. 同济大学学报(自然科学版), 2016, 44(3): 333-340. WANG Xiaowei, YE Aijun, SHEN Xing, et al. Fragility Analysis on Transversal Isolation system for outer piers of long span bridges[J]. Journal of Tongji University (Natural Science), 2016, 44(3): 333-340. (  0) 0)
|
| [20] |
BANERJEE S, PRASAD G G. Seismic risk assessment of reinforced concrete bridges in flood-prone regions[J]. Structure and infrastructure engineering, 2013, 9(9): 952-968. DOI:10.1080/15732479.2011.649292 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


