我国是拥有五千年悠久历史的文明古国,不但自身的传统文化独具特色、自成体系,还不断借鉴和吸收多方外来文化。众所周知,古塔归属于古建筑的范畴,代表了我国古代高层建筑的最高水平,在世界建筑史上独树一帜[1]。小雁塔由于建筑造型优美,结构形式独特,且具有丰富的历史文化价值和艺术美学意义[2],在我国古塔建筑中占有及其重要的地位,2014年被联合国教科文组织列入《世界文化遗产名录》。然而,由于小雁塔结构建造历史久远,其本身已遭受不同程度的损伤和破坏,故其抗震性能显著降低。考虑到小雁塔结构的文物价值和历史意义,因此,对小雁塔结构的抗震保护工作显得极其重要。
近年来我国在古建筑保护研究领域也有不少研究成果,如张建霖等[3]对陕西地区的古塔现状进行了一些调查,并据此提出针对古塔的抗震加固分类方法,从六个方面确定指数来分类。姚谦峰等[4]利用软件对兴教寺塔进行抗震分析,并由此提出四点加固方法:塔体加箍、裂缝粘结、增设构造柱与圈梁和碳纤维加固。除此之外,陈东佐等[5]提出运用复位纠偏和加固补强技术对太原双塔进行复位纠偏和加固维修。陈平等[6]在勘察和揭露调查的基础上,采用“成孔—软化”方法对眉县净光寺塔实施了纠偏扶正,并取得了理想的效果。姚道平等[7]通过对六胜塔的地基基础和结构设计进行研究,提出用结合测试法进行石结构古塔的抗震性能分析。但是,由于小雁塔属于中国历史文物范畴,按照古塔保护“最小干预”原则,以上所述方法并不适合于小雁塔结构的抗灾变保护,故当前亟需一套针对古塔结构抗灾变保护的理论和方法。
结构振动控制是一种已被实际验证能够有效减小结构地震响应的新理论、新方法[8]。其中,消能减震技术因其构造简单,造价低廉,便于安装且不改变建筑物原貌等优点,成为目前发展较为成熟且被广泛应用的振动控制技术[9]。文中依据悬摆减震原理,结合形状记忆合金,设计并制作了一种新型形状记忆合金复合悬摆减震系统(shape memory alloy-suspension pendulum damping system,SMA-SPDS),且对提出的新型减震系统进行了试验研究;根据模型结构设计的相似性理论,设计制作了一个几何相似比为1/10的小雁塔模型结构,同时,利用大型有限元软件ANSYS对小雁塔模型结构的减震控制进行了模拟分析,将分析结果与振动台试验结果进行对比,验证ANSYS模拟结果的可靠性,并进行了小雁塔原型结构的减震控制分析。
1 SMA复合悬摆减震系统 1.1 构造设计利用SMA丝的相变伪弹性,结合调谐质量阻尼器原理,本文设计并制作了一种SMA复合悬摆减震系统,模型如图 1所示。阻尼器由质量块、丝材、吊杆、外框等几个部分组成。吊杆下端的丝杆与质量块中心处的螺孔相连,并由单向铰固定于外框顶部。单向铰垂直于摆动平面,吊杆上端圆孔穿入单向铰中的转轴,转轴仅两端与螺帽相连部分有螺纹,中部无螺纹且足够光滑,能够保证吊杆的自由转动。两端螺帽与吊杆上端通过两个等刚度弹簧对称连接,弹簧套在转轴上。两端螺帽处于松弛时,弹簧处于自由状态,对吊杆转动无影响。但当螺帽处于紧固状态时,弹簧产生水平推力,使吊杆转动并受到一定摩擦阻力,以此来为阻尼器装置提供阻尼。两组形状记忆合金丝对称布置于装置两侧,其中一端绕过定滑轮通过螺钉与滑块相连,另一端同建筑结构固定连接。当该减震系统遭受外部激励时(此处仅考虑质量块一个周期运动状态),如质量块产生向左运动,由于滑块与质量块两者之间采用“扣式”连接,此时滑块将拉动右侧SMA丝产生相对位移Δε,而左侧的丝材处于松弛状态;同理当质量块改变运动状态,向右侧运动时,左侧滑块被带动从而使左侧丝材拉紧并产生位移,而右侧丝材松弛。在质量块的整个周期运动过程中,SMA丝材经历了由拉紧到放张的循环过程,构成了饱满的滞回曲线,实现了对结构的耗能。

|
Download:
|
| 图 1 SMA复合悬摆减震系统示意图 Fig. 1 Diagram of SMA-SPDS | |
SMA复合悬摆减震系统归属于调谐类阻尼器,根据调谐类阻尼器性质[10],SMA复合悬摆减震系统的动力特性对结构的减震效果具有显著影响,因此,对该减震系统进行动力参数测试是很有必要的。为研究SMA质量复合悬摆阻尼器的装配精度、动力参数,将质量分别为30、45、46 kg,摆长为55 cm,丝材是1 mm的SMA质量复合悬摆系统放置于小型振动台上(图 2)进行动力测试。

|
Download:
|
| 图 2 减震系统试验装置 Fig. 2 Damping systemtest equipment | |
通过改变摆锤质量来实现不同阻尼器的组装,该试验仅测量阻尼器x方向的频率。试验中,当单向铰两端螺帽处于松弛状态时,即弹簧处于自由状态,测试奥氏体合金丝处于拉紧和松弛两种状态下该减震系统的振动频率值。以摆锤质量为30 kg为例,在摆锤质量块处放置位移传感器,奥氏体合金丝未张拉时,采用初位移法得到该减震系统位移衰退曲线如图 3(a)所示,再进行FFT频谱分析,得到该减震系统振动频率如图 3(b)所示。当拉紧奥氏体合金丝时,采用初位移法得到该减震系统位移衰退曲线如图 4(a)所示,再进行FFT频谱分析,得到阻尼器振动频率如图 4(b)所示。

|
Download:
|
| 图 3 SMA丝未张紧时测试曲线 Fig. 3 Test curves of SMA wire without tension | |

|
Download:
|
| 图 4 SMA丝张紧时测试曲线 Fig. 4 Test curves of SMA wire tension | |
SMA复合悬摆减震系统的等效阻尼可通过时域衰减曲线法求得,计算公式为[11]
| $ \begin{array}{l} \zeta = \frac{1}{n}\frac{{\lg \psi }}{{\sqrt {{{\left( {{\rm{ \mathsf{ π} lge}}} \right)}^2} + {{\left( {\lg \psi /n} \right)}^2}} }} = \\ \;\;\;\;\;\frac{1}{n}\frac{{\lg \psi }}{{\sqrt {1.862 + {{\left( {\lg \psi /n} \right)}^2}} }}, \end{array} $ | (1) |
式中:ψ=|Ak/Ak+1|为自由振动实测曲线上相邻n个波峰的位移峰值之比,n为选择的波峰数。上述三类减震系统根据式(1)计算方法求得的阻尼比范围为0.004 5~0.152 9。其中减震系统转轴外弹簧松弛和压紧状态下的位移时程曲线如图 5所示。

|
Download:
|
| 图 5 SMA-SPDS位移时程曲线 Fig. 5 Displacement time history curves of SMA-SPDS | |
形状记忆合金复合悬摆减振系统是附加在主结构中的一个子结构,主要包括质量块、弹簧、阻尼系统几个组成部分。其工作原理是:主结构受到动力荷载作用下产生振动时,质量块随之产生惯性运动。若有合理的子结构参数设计使减振系统的自振频率与主结构的自振频率符合某种关系时,减振子结构会与主结构形成“反共振”,即子结构将与主结构共同振动,但会输出与主结构运动同频率的反向荷载而减弱主结构的响应。实际上,减振子结构可以理解为应用共振原理对结构的某一个和某几个振型进行减振控制。
假设基底输入的加速度是均值为0的白噪声过程,且功率谱为So,可求得结构第i振型的反应方差为[12]
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\sigma _{{i^d}}^2 = {S_0}{\int_{ - \infty }^{ + \infty } {\left| {{h_i}\left( {j\omega } \right)} \right|} ^2}{\rm{d}}\omega = \\ \frac{{{S_0}\mathsf{ π}\left[ {\left( {B_0^2/{A_0}} \right)\left( {{A_2}{A_3} - {A_1}{A_4}} \right) + {A_3}\left( {B_1^2 - 2{B_0}{B_2}} \right) + {A_1}B_2^2} \right]}}{{{A_1}\left( {{A_2}{A_3} - {A_1}{A_4}} \right) - {A_0}A_3^2}} \end{array} $ | (2) |
式中:A0=ωi2ωd2, A1=2ξiωiωd2+2ξdωdωi2, A2=ωi2+(1+μiφsi2)ωd2+4ξiξdωdωi, A3=2ξiωi+2(1+μiϕsi2)ξdωd, A4=1, B0=(ηi+μiϕsi)ωd2, B1=2ξd(ηi+μiϕsi)ωd, B2=ηi。
其中,ϕsi为结构第i个振型向量的第s个元素值,μi=md/mi*,
未设置减震系统时,结构第i振型反应的方差为
| $ \sigma _i^2 = {S_0}{\int_{-\infty }^{ + \infty } {\left| {{H_i}\left( {{\rm{j}}\omega } \right)} \right|} ^2}{\rm{d}}\omega = \frac{{{\rm{ \mathsf{ π} }}{S_0}\eta _i^2}}{{2{\xi _i}\omega _i^3}}, $ | (3) |
式中:
减振系统在结构上的位置由位置向量E描述,其中E=[0 0 … 1 0 … 0]T∈Rn,仅布置减震系统楼层元素为1,其余全为0,式(2)中与向量E相关的向量是ϕsi,ϕsi反映了减振系统在结构上的位置对|h(jω)|2的贡献。
当ϕsi=0时,即减振系统设置于第i振型的曲线零点对应的质点处时,无论ξd的值是否为零,根据式(2)可以得出
当ϕsi≠0时,考虑ξd=0的情况,引入λi=ωd/ωi,λ=ω/ωi,则根据式(2)可知
为了取得最好的控制效果,除进行最佳位置选择外,还要进行减振系统的参数优化设计。在式(2)中引入了λi=ωd/ωi,将结构的第i振型的反应方差写为频率比的形式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sigma _{{i^d}}^2 = \frac{{{S_0}{\rm{ \mathsf{ π} }}}}{{\omega _i^3}} \cdot \\ \frac{{\left[{\left( {b_0^2/{a_0}} \right)\left( {{a_2}{a_3}-{a_1}{a_4}} \right) + {a_3}\left( {b_1^2-2{b_0}{b_2}} \right) + {a_1}b_2^2} \right]}}{{{a_1}\left( {{a_1}{a_3} -{a_1}{a_4}} \right) -{a_0}a_3^2}} \end{array} $ | (4) |
式中:a0=λi2,a1=2ξiλi2+2ξdλi,a2=1+(1+μiφsi2)λi2+4ξiξdλi,a3=2ξi+2(1+μiφsi2)ξdλi,a4=1,b0=(ηi+μiϕsi)λi2,b1=2ξd(ηi+μiϕsi)λi,b2=ηi。
令
为方便应用,可进行一些简化处理,如令ϕsi=1,ξi=0,此时
| $ \begin{array}{l} \sigma _{{i^d}}^2 = \frac{{{S_0}{\rm{ \mathsf{ π} }}}}{{2\omega _i^3}}\left\{ {\frac{{\left[{\left( {1 + {\mu _i}} \right)\left( {{\mu _i} + {\eta _i}} \right)\lambda _i^2-{\eta _i}} \right]}}{{{\xi _d}{\lambda _i}{\mu _i}}} + } \right.\\ \left. {\frac{{{{\left( {{\mu _i} + {\eta _i}} \right)}^2}\lambda _i^2{\mu _i} + 4\left( {1 + {\mu _i}} \right){{\left( {{\mu _i} + {\eta _i}} \right)}^2}\xi _d^2\lambda _i^2}}{{{\xi _d}{\lambda _i}{\mu _i}}} + } \right\} \end{array} $ | (5) |
由
| $ \lambda _i^* = \frac{1}{{1 + \mu }}\sqrt {\frac{{2{\eta _i} + {\eta _i}{\mu _i}-\mu _i^2}}{{2\left( {{\eta _i} + {\mu _i}} \right)}}}, $ | (6) |
| $ \xi _d^* = \sqrt {\frac{{{\mu _i}\left( {3{\mu _i}{\eta _i} + 4{\eta _i}-\mu _i^2} \right)}}{{8\left( {1 + {\mu _i}} \right)\left( {2{\eta _i} + {\mu _i}{\eta _i}-\mu _i^2} \right)}}}, $ | (7) |
一般情况下μi较ηi要小一个数量级,故可以忽略μi2项,式(7)可写为
| $ \xi _d^* = \sqrt {\frac{{{\mu _i}\left( {3{\mu _i} + 4} \right)}}{{8\left( {1 + {\mu _i}} \right)\left( {2 + {\mu _i}} \right)}}} $ | (8) |
可看出,系数ηi对最佳阻尼比ξd*影响较小。
3 小雁塔结构仿真与分析 3.1 小雁塔试验模型根据现场调查可知现小雁塔残高为43.3 m,塔身原为15层,现残存13层,14层大部分墙体被毁,塔底层层高6.84 m相对其上部层高较高,以上各层逐层减少,轮廓协调。基于模型相似理论,综合考虑振动台承载能力,采用欠人工质量模型设计了一个相似比为1/10的小雁塔模型结构,本次模型制作忽略了塔顶和内部楼梯的质量贡献,模型高度取4.0 m。模型立于200 mm厚钢筋混凝土底座上,模型底层与底座间采用钢筋锚固连接,试验时通过螺栓将底座固定在振动台上;模型墙体由砖砌筑而成,根据小雁塔原型结构的材料组成及性能,并考虑试验的相似性和可操作性,本次试验选取的小雁塔模型结构砌体材料经过强度测试选为20世纪50年代建筑的青砖,但尺寸进行了必要处理,砖的尺寸分别为110 mm×50 mm×25 mm和110 mm×50 mm×10 mm两种规格,砂浆材料选用石灰糯米浆,最终砌筑而成的小雁塔模型图如图 6所示。本次试验采用在小雁塔内添加钢块来使得结构的等效密度变大,因结构本身是内空,当人工质量分布在墙体上不需要准确模拟,模型设计可以简化,在墙两侧设置配重箱,将所有人工质量均添加进去,如图 7所示。

|
Download:
|
| 图 6 小雁塔模型图 Fig. 6 The Small Wild Goose Pagoda model | |

|
Download:
|
| 图 7 模型配重分布图 Fig. 7 Distribution of balance weight | |
根据《建筑设计抗震规范》(GB50011-2010)规定[13],本次试验选取两条实际强震记录El Centro波和江油波,一条人工波上海波,其为《上海市建筑抗震设计规程》推荐的人工拟合地震波,原场地类别为Ⅳ类,经SeismoSignal软件转化为Ⅱ类场地类别;将三条地震波加速度峰值分别按八度小震、八度中震和八度大震进行调幅。
3.3 试验与仿真对比本次有限元模拟分析借助ANSYS作为分析工具[14],采用整体式方法建模,为简化计算,将砌体和砂浆等效为一种各项同性均质材料,并选取单元solid64模拟小雁塔模型结构墙体,材料参数依据现场回弹测试和模型相似比,选取小雁塔模型结构弹性模量为1 200 MPa,泊松比为0.15,砖砌体密度取值为6 498 kN/m3,小雁塔模型结构有限元模型图如图 8所示。根据小雁塔原型结构现状条件,结合小雁塔模型结构,依据前述的优化理论,仅在小雁塔模型结构第1、2、5层布置SMA复合悬摆减震系统。在ANSYS中模拟SMA复合悬摆减震系统,可以采用简化的物理模型,采用特殊设置中的惯量和弹簧/阻尼器来模拟阻尼器,将质量点与弹簧/阻尼器串联,在惯量中定义质量参数,在弹簧/阻尼器中定义刚度和阻尼,故在此选用COMBIN40单元来模拟SMA复合悬摆减震系统。
|
Download:
|
| 图 8 小雁塔模型结构有限元模型图 Fig. 8 The finite element model of The Small Wild Goose Pagoda | |
基于小雁塔试验模型结构,可得出小雁塔模型结构各层地震响应,并与模拟分析结果对比,由于篇幅有限,仅对比结构在有控状态下,八度中震作用下El Centro波塔顶位移和加速度反应,如图 9所示。
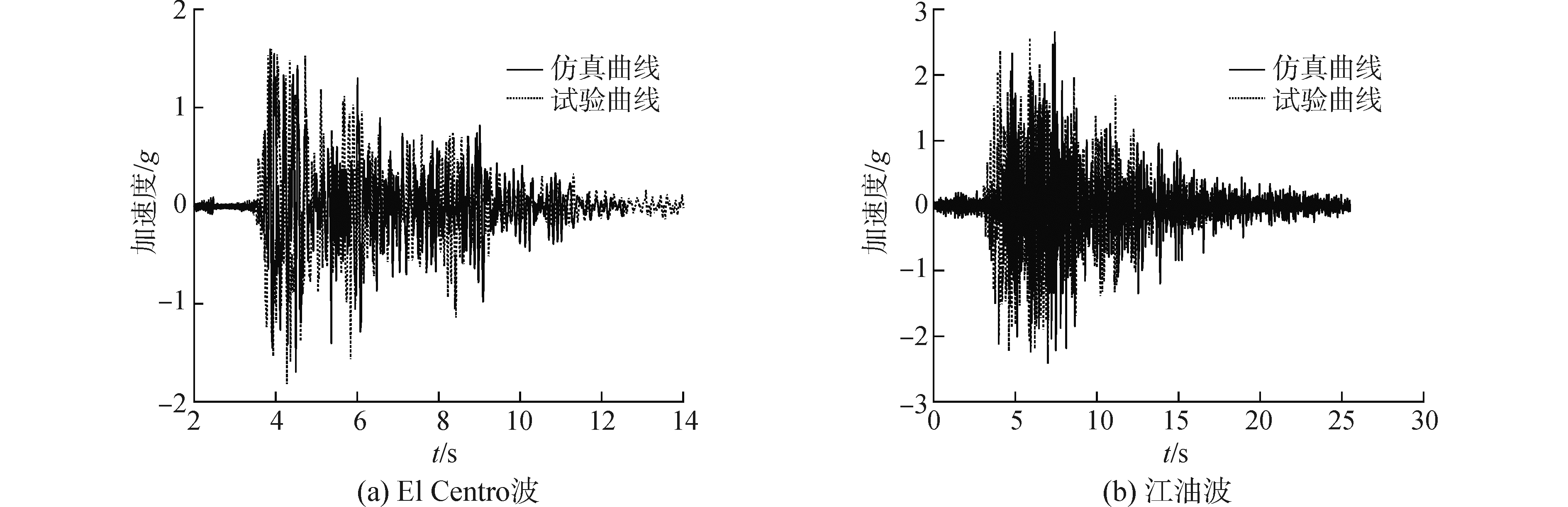
|
Download:
|
| 图 9 八度中震作用下塔顶模拟与试验对比图 Fig. 9 Comparison of top simulation and experiment under eight degree earthquake | |
对比塔顶加速度和位移时程曲线可以看出,由于试验过程中塔顶加速度的采样率与软件分析过程中的采样率并不相同,所以在地震反应较为明显的地方所发生的时间有较小的差异,但这并不影响分析。相比于软件计算得到的塔顶加速度时程曲线,试验记录的曲线对结构反应的表达较为明确,并且试验产生的塔顶加速度峰值反应小于软件计算所得,但是可以看出在结构反应较大的前10 s内,试验数据和软件计算都准确的表达了结构顶部加速度反应较大的时刻,曲线振动情况具有一定的相似性。在后10 s内,最大的区别在于12~13 s,软件计算所得结果同试验有较大差异,试验数据表示此时刻结构加速度反应并未出现较大波动,而软件计算则相反。在此之后,两者都表达了结构加速度反应较为平稳。但整体上试验值和仿真值具有较好的吻合,验证了利用ANSYS模拟小雁塔模型减震结构的可靠性。
3.4 小雁塔原型结构仿真分析为减小缩尺效应、施工误差等因素对小雁塔结构抗震性能影响,在此对小雁塔原型结构在有控和无控两种状态下进行地震响应分析。小雁塔原型结构材料参数通过查询相关文献,现场动力测试和回弹测试获得,杨氏模量取为E=1 200 MPa,泊松比为μ=0.15,密度为ρ=1 800 kN/m3。
通过现象调查发现,小雁塔东西方向由于洞口的存在而使其刚度受到削弱,所以在地震过程中很容易受到破环,本文重点研究东西方向的减震,所以仅对小雁塔原型结构进行单向的地震波输入,小雁塔在东西向平面内发生弯曲的前几阶振型分别是第二阶、第四阶和第七阶,其中第七阶振型参与系数过小,在此不作考虑。SMA-SPDS的安装位置优先选择受控振型位移向量较大处,根据模态分析可知,二阶振型下,位移向量最大值出现在顶楼13层,其次是12层;四阶振型位移向量最大值出现在13层,12层、11层、5层位移向量也较大,故控制结构的第二频率的阻尼器安装于结构的顶层,控制结构的第四频率的阻尼器安装于12层,几种减震方案设计如表 1所示。
| 表 1 减震方案 Tab.1 Damping scheme |
通常情况下,SMA-SPDS质量越大其减震效果越明显,在此考虑到安装空间限制,质量比取为0.01,其他优化参数值采用式(6)和式(8)计算。
选取El Centro波、Taft波、兰州波和TH1TG035波4组加速度时程曲线作为地震波输入,并对上述3种方案分别进行地震响应分析,可获得所述4种波在上述3种方案下的层间位移角对比图,如图 10所示。

|
Download:
|
| 图 10 层间位移角对比 Fig. 10 Comparison of story drift angle | |
可以看出,就整体情况而言,4组地震波中3种减振方案下结构的层间位移角均比原结构有不同程度的减小。其中方案3的减振效果最好,在El Centro波、Taft波、兰州波和TH1TG035波下的最大减振率分别可达到28.5%、21.4%、13.1%、14.3%。方案2的减振效果次之,在El Centro波、Taft波、兰州波和TH1TG035波下的最大减振率分别可达到14.8%、15.6%、10.7%、8.4%。方案1的减振效果稍小,在El Centro波、Taft波、兰州波和TH1TG035波下的最大减振率分别可达到12.1%、10.8%、7.2%、6.4%。此外,3种减振方案对于3~4层以下的楼层的减振效果都较小,而对于上中部分楼层的控制效果较好。由此可知,随着控制模态阶次的提高,需要相应的增加SMA-SPDS的数量;同时,小雁塔结构的控制效果也有明显提高。然而,综合考虑小雁塔实际工程的复杂性、成本控制、可操作性以及小雁塔原型结构的可观光性等因素,因此,本文建议考虑控制小雁塔原型结构前两阶振型。
4 结论1) 基于模型相似理论,设计并制作了一个缩尺比例为1/10的小雁塔模型结构,并利用有限元软件ANSYS对该模型结构进行模拟分析;结果表明小雁塔模型减震结构加速度和位移反应的试验值与模拟分析结果大致吻合,验证了ANSYS模拟分析可对小雁塔原型结构进行减震反应分析。
2) 针对小雁塔原型结构减震控制,提出了三种减震方案,并通过时程反应分析,获得三种减震方案的减震效果。结果表明,随着控制模态阶次的提高,需要相应的增加SMA-SPDS的数量;同时,小雁塔结构的控制效果也有明显提高。
3) 本文提出的新型小雁塔结构保护方案,严格遵循古塔结构抗震保护的“最小干预”原则,可有效减小塔身结构的震动响应,可将其应用于类似古塔的抗震保护中且对古塔抗震保护具有重要的参考价值和意义,同时,对古塔的抗震保护开辟了新思想、新方法。
| [1] |
罗哲文. 中国古塔[M]. 北京: 中国青年出版社, 1985.
(  0) 0)
|
| [2] |
沈远戈. 小雁塔抗震性能分析及地基构造研究[D]. 西安: 西安建筑科技大学, 2010. SHEN Yuange. Seismic behavior analysis and foundation construction research on Xiaoyan Pagoda[D]. Xi'an: Xi'an University of Architecture and Technology, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D193382 (  0) 0)
|
| [3] |
张建霖, 张洵安. 古塔抗震加固的调查与分类[J]. 建筑技术, 2003, 34(11): 839-840. ZHANG Jianlin, ZHANG Xun'an. Investigation and classification of ancient tower anti-seismic reinforcement[J]. Architecture technology, 2003, 34(11): 839-840. DOI:10.3969/j.issn.1000-4726.2003.11.018 (  0) 0)
|
| [4] |
姚谦峰, 卢俊龙, 张荫. 砖石古塔抗震加固对策探讨[J]. 工业建筑, 2007, 37(9): 115-118. YAO Qianfeng, LU Junlong, ZHANG Yin. Research on seismic reinforcement methods for masonry pagodas[J]. Industrial construction, 2007, 37(9): 115-118. (  0) 0)
|
| [5] |
陈东佐, 康玉庆. 浅谈山西太原双塔的复位纠偏与保护[J]. 山西地震, 2000(3): 32-34. CHEN Dongzuo, KANG Yuqing. Humble opinion of replacement and rectification for Twin-pagoda in Taiyuan and its protection and maintenance[J]. Earthquake research in Shanxi, 2000(3): 32-34. (  0) 0)
|
| [6] |
陈平, 赵冬, 王伟, 等. 眉县净光寺塔纠偏工程[J]. 西安建筑科技大学学报(自然科学版), 2003, 35(1): 44-47. CHEN Ping, ZHAO Dong, WANG Wei, et al. A study on the rectification of Jingguang Temple Pagoda in Meixian county[J]. Journal of Xi'an university of architecture & technology (natural science edition), 2003, 35(1): 44-47. (  0) 0)
|
| [7] |
姚道平, 谢志招, 许仪西, 等. 测试分析石结构古塔抗震性能[J]. 工程抗震与加固改造, 2009, 31(3): 107-112. YAO Daoping, XIE Zhizhao, XU Yixi, et al. Testing and analysis of the earthquake resistance performance of the stone structure's ancient tower[J]. Earthquake resistant engineering and retrofitting, 2009, 31(3): 107-112. (  0) 0)
|
| [8] |
CHAE Y B, KIM J K. Implementation of configuration dependent stiffness proportional damping for the dynamics of rigid multi-block systems[J]. Earthquake engineering and engineering vibration, 2003, 2(1): 87-97. DOI:10.1007/BF02857541 (  0) 0)
|
| [9] |
BILLAH A H M M, ALAM M S. Plastic hinge length of shape memory alloy (SMA) reinforced concrete bridge pier[J]. Engineering structures, 2016, 117: 321-331. DOI:10.1016/j.engstruct.2016.02.050 (  0) 0)
|
| [10] |
OK S Y, SONG J, PARK K S. Optimal performance design of bi-Tuned Mass Damper systems using multi-objective optimization[J]. KSCE journal of civil engineering, 2008, 12(5): 313-322. DOI:10.1007/s12205-008-0313-8 (  0) 0)
|
| [11] |
黄浩华. 地震模拟振动台的设计与应用技术[M]. 北京: 地震出版社, 2008.
(  0) 0)
|
| [12] |
苏荣华, 梁冰, 宋维源. 结构-TMD系统抗震的优化参数研究[J]. 振动与冲击, 2001, 20(4): 8-11. SU Ronghua, LIANG Bing, SONG Weiyuan. Research on optimal parameters of structure-TMD system to suppress seismic response of structures[J]. Journal of vibration and shock, 2001, 20(4): 8-11. (  0) 0)
|
| [13] |
中国建筑科学研究院. GB 50011-2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010. China Academy of Building Research. GB 50011-2010, Code for seismic design of buildings[S]. Beijing: China Architecture & Building Press, 2010. (  0) 0)
|
| [14] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2013. WANG Xinmin. Numerical analysis of ANSYS engineering structure[M]. Beijing: China Communications Press, 2013. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


