对于在冰区航行的船舶,冰块容易随着船体外壳传递到船体尾部和螺旋桨产生相互干扰作用,这种相互干扰作用可以分为临近、阻塞、切削等。冰块阻塞不仅容易使螺旋桨产生强烈的空化[1-2],而且会对螺旋桨的轴承力产生较大的影响,早在20世纪60年代左右,国际上学者便提出了螺旋桨诱导轴承力的概念。叶金铭等[3]分别采用理论计算和经验方法计算了常规和非常规螺旋桨的轴承力,最终讨论出了经验方法的适用范围;谭廷寿等[4]采用扰动速度势面元法,由双曲四边形面元将桨叶、桨毂以及尾涡面进行离散,采用时间步进迭代的方法求解了时域内的非定常问题,最终计算出非定常螺旋桨轴承力;李亮等[5]采用混合网格技术,对计及自由液面的KCS船桨舵一体做非定常计算,得到螺旋桨激振力的时域变化曲线。Mer Z等[6]通过使用有限元方法,分析表明由于螺旋桨激振力导致的轴系动态响应会造成螺旋桨振动。Kornev等[7]使用URANS-LES混合方法,对KVLCC2的船艉伴流场开展计算,研究认为非常伴流中,轴向轴承力能够达到时均伴流中的两倍。因此伴流场不稳定性较大,计算时要重点考虑。Wei等[8]以模型潜艇和五叶桨为研究对象,对其进行非定常激振力计算。结果显示螺旋桨轴向力对潜艇水下噪声贡献最大,而且螺旋桨的横向激励力要大于垂向激励力,且单片桨叶的脉动力与整桨之间存在一定的相位差。
由于重叠网格方法在处理流场中多体间具有大幅度相互运动所引起非定常干扰问题时,具有很大的优势[9],因此本文在流场区域的网格生成过程中主要采用了重叠网格方法。该方法由Steger等[9]提出,其显著特点是可将复杂的流场区域按需要分成多个简单的子区域,在每个单独生成网格的子区域间网格的重叠进行数据交换来传递流场信息[10]。目前的研究大多是针对敞水螺旋桨或者是船桨一体,对于冰桨干扰下螺旋桨的轴承力很少有学者研究。本文针对冰阻塞条件下螺旋桨的激振力性能进行建模,采用重叠网格法并结合CFD计算软件,计算并分析了螺旋桨激振力的变化规律。
1 冰桨干扰计算模型 1.1 模型建立本文根据加拿大海岸警卫队R-CLASS系列破冰船的冰级螺旋桨进行适当改进,设计了一款螺旋桨。该螺旋桨的螺距比为0.78,毂径比为0.3,盘面比为0.67,纵倾角为10°。
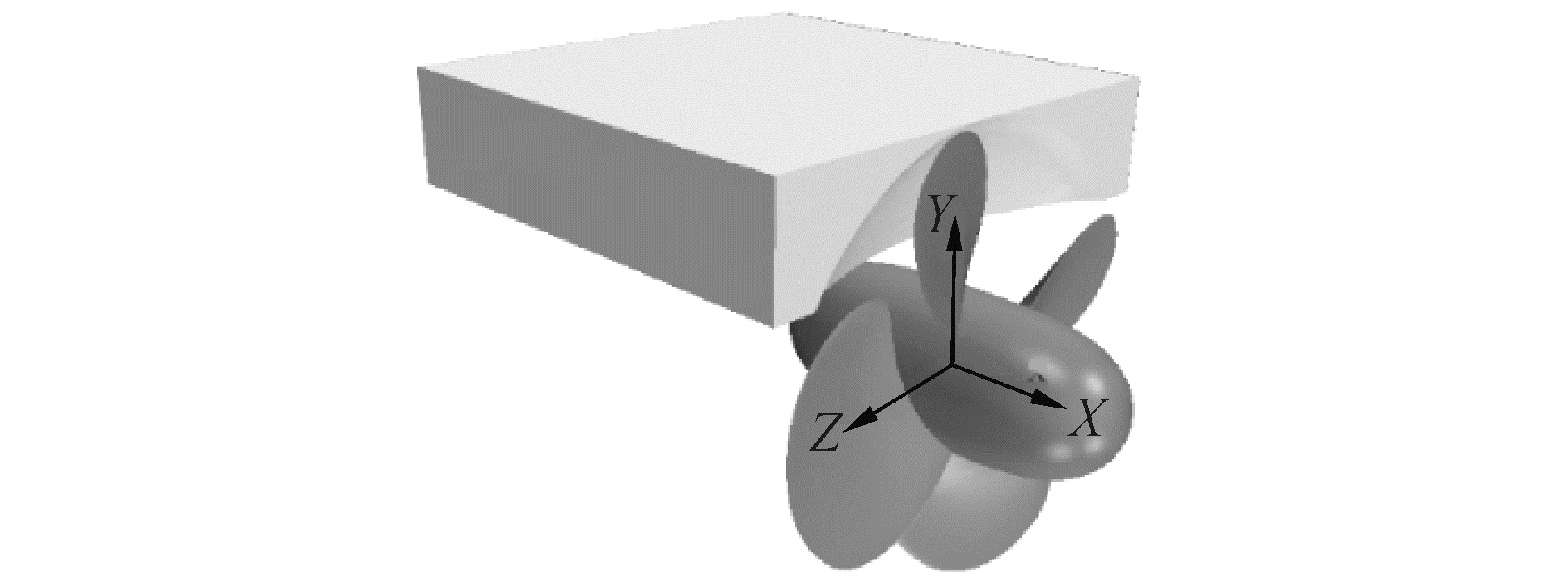
切削形状冰是指由于螺旋桨的切削而在长方体冰块前方产生了豁口的冰(见图 1),近桨叶一侧的冰面为桨叶导边旋转进入冰内切削形成的扫略轮廓,其余各侧表面均为矩形形状,将其置于螺旋桨前方流场中。冰与螺旋桨的相互作用模型参照了文献[11], 如图 1所示。
|
Download:
|
| 图 1 切削形状冰下螺旋桨 Fig. 1 Propeller after cutting shape ice | |
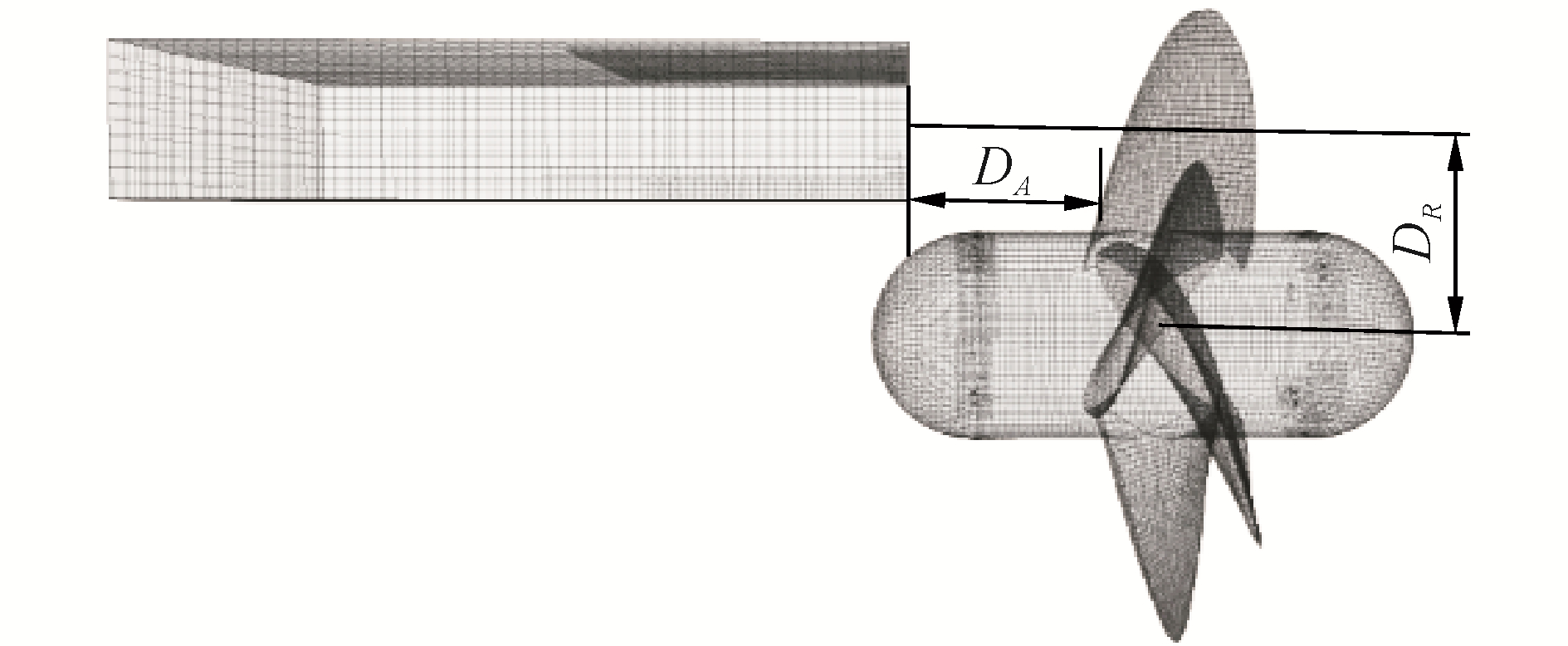
本文主要研究与“切削形状冰”紧密接触的螺旋桨的诱导轴承力的变化,由于本文的侧重点是水动力性能,因此此处的紧密接触定义为螺旋桨与切削形状冰的轴向间距很小(5 mm),希望借此工况来模拟切削状态下的轴承力。具体的冰桨轴向间距DA定义如图 2,DA表示近桨冰面距螺旋桨桨叶导边叶根位置的轴向距离,DR表示模型冰形心距螺旋桨轴线的距离。其中冰模型的长、宽和厚分别为D、D和0.2D,D为螺旋桨直径。
|
Download:
|
| 图 2 冰桨间距定义图 Fig. 2 Definition of spacing between ice and propeller | |
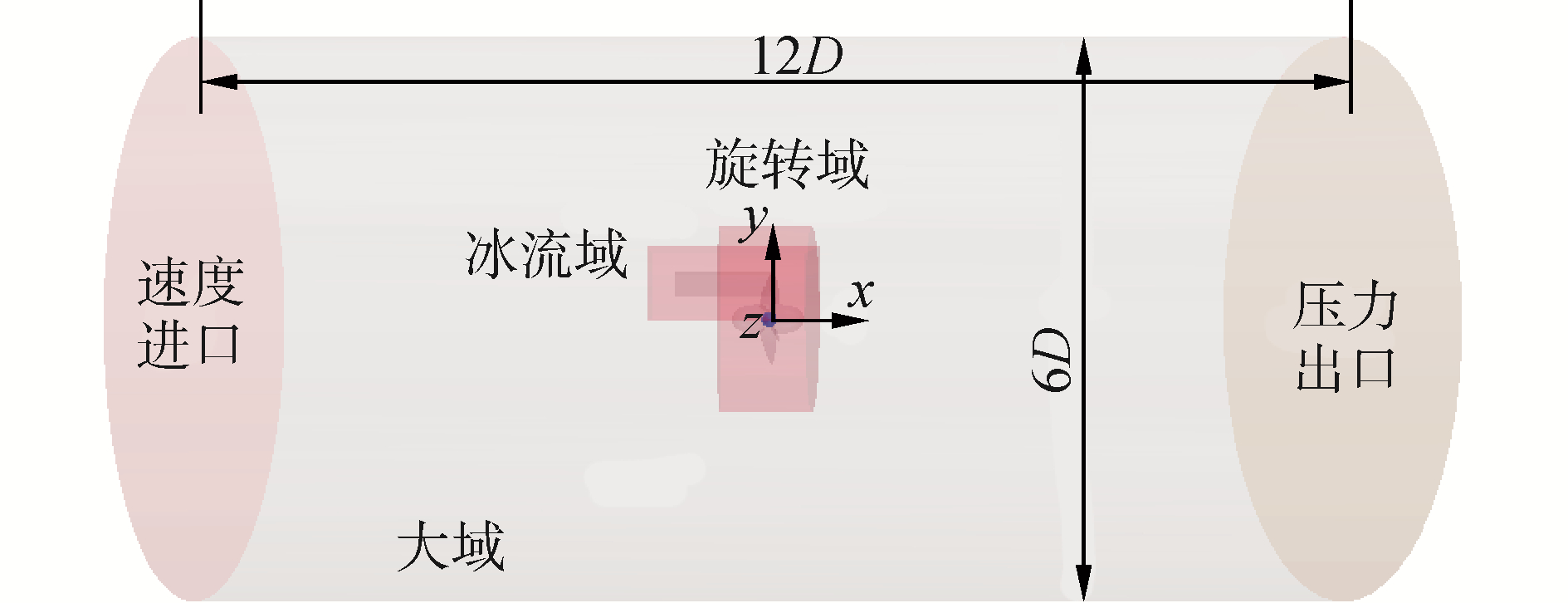
本文研究的水动力问题为外流场问题,所以建立了假定无限大的外流场区域,对整个流域的湍流模型采用SST k-ω模型。具体计算区域和边界定义情况如图 3所示,外流场计算域采用与螺旋桨同轴的圆柱体,且其中包含两个子计算区域:一个子区域采用六面体区域将模型冰包裹其中并将其定义为冰表面流场计算域(简称冰流域);另一个子区域采用与螺旋桨同轴的较小的圆柱域并定义为螺旋桨周围流场的旋转计算域(简称旋转域)。
|
Download:
|
| 图 3 计算域和边界条件 Fig. 3 Calculation domain and coordinate system | |
在CFD计算过程中,需要为螺旋桨表面和冰表面设置不可穿透的壁面条件;外域除了速度进口和压力出口之外,侧壁面也是壁面条件。外域边界壁面不考虑粘性作用,定义为滑移壁面。旋转域为较小的圆柱体与螺旋桨作布尔减运算得出的中间区域,需要在旋转域中建立一个局部坐标系,螺旋桨转速是600 r/min。在冰块区域和旋转域的外界面都会生成重叠网格。
1.3 网格收敛性分析为了开展计算模型的网格收敛性分析,本文在计算过程中选用了3种网格,网格数量分别为550万、1 380万、2 010万。为了便于和实验模型作对比,在计算过程中每种网格模型都将计算冰桨间距为1、5、10、20、30 mm的5个不同间距,为了简化分析过程,仅仅比较推力系数Kt这一项,将这3套网格的计算结果和模型实验的情况作对比,如表 1所示。
| 表 1 不同网格数Ktx的计算结果 Tab.1 Calculation results of Ktx with different mesh numbers |
由表 1可知,在网格数量为550万时,计算结果会与实验值存在较大的误差,当网格数量达到1 380万时,计算会趋近于实验结果,当网格数目达到2 010万时,计算的结果反而偏差过大。可见网格数量并不是越多越好,当能够验证实验结果并且不同网格之间的计算结果相差不大时,即可认为实验所采取的网格是具有收敛性的。因此,为了提高计算精度且不使计算时间过长,本文采取网格数量为1 380万来研究。
2 冰桨干扰计算分析 2.1 计算方法验证图 4为不同冰桨间距下螺旋桨推力系数Kt以及转矩系数10Kq的试验值与计算值的对比情况,其中试验值来自文献[12]。可以看出当冰桨间距较小时,螺旋桨的推力和转矩会变大,这是由于冰块后方会形成一个低速区,当桨叶经过低速区时叶元体攻角变大,使得推力和转矩明显增加。

|
Download:
|
| 图 4 不同冰桨间距下的螺旋桨转矩系数的变化 Fig. 4 Comparison of thrust and torque coefficient in the varying proximity | |
从图 4可以看出,当冰桨间距较小(小于3 mm)时试验值和计算值相差较大,这是由于在CFD计算过程中较小的间距对边界层网格的生成会产生影响,会影响该区域的计算精度。随着间距变大,试验值和计算值的误差会逐渐变小。当冰桨间距大于3 mm时,计算值和试验值的误差在5%左右,总体来说这种预报方法具有较好的预报精度。
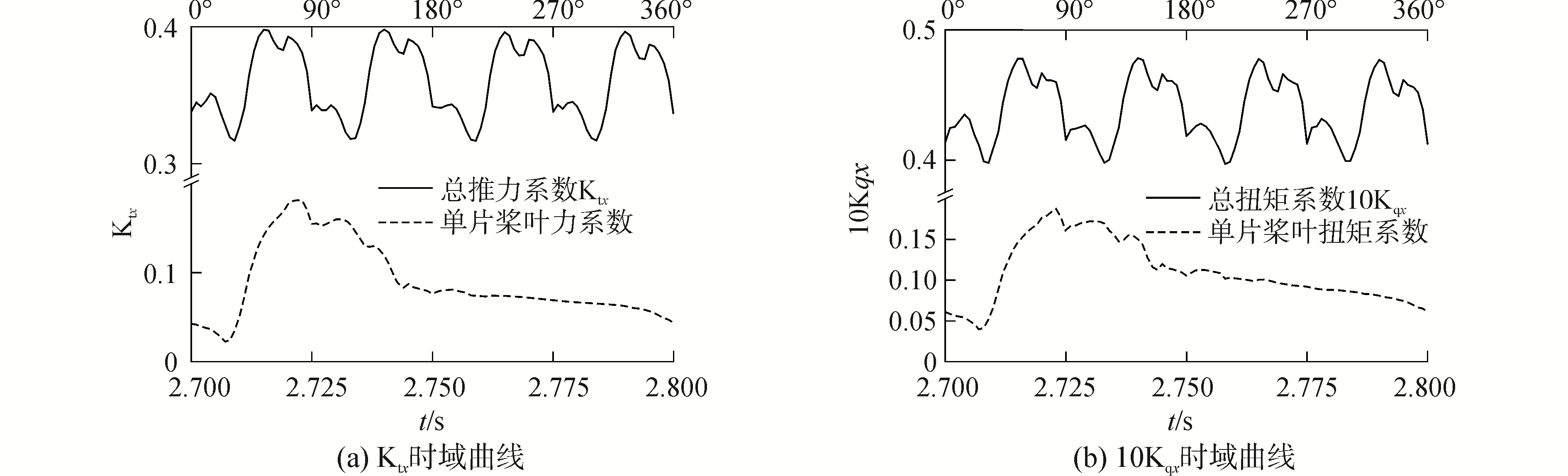
2.2 螺旋桨非定常轴承力由于本文旨在模仿冰桨切削瞬时状态下螺旋桨的轴承力,选定了3个工况进行计算,分别是进速系数J为0.2、0.4、0.6。对于非定常工况而言,本文主要计算螺旋桨6个轴承力分量Fx、Fy、Fz和Mx、My、Mz并对其进行无量纲化,发现沿Kty和Ktz相对于Ktx的是小量,所以重点分析Ktx和10Kqx的变化规律;又由于对不同的进速J为0.2、0.4和0.6来说,其推力系数Ktx和扭矩系数10Kqx随时间的变化规律是一致的,因此图 5仅列出了进速系数J=0.2的工况下的变化图像。
|
Download:
|
| 图 5 Ktx和10Kqx计算结果(J=0.2) Fig. 5 Unsteady calculation results of Ktx and 10Kqx(J=0.2) | |
由于模型所采用的是四叶桨模型,故主桨叶旋转的周期是整个螺旋桨旋转周期的4倍,这在图 5中也可看出。桨在旋转过程中,冰的阻塞效应较为明显,在周期性旋转过程中,任一桨叶经过冰块后方遮蔽区域时,螺旋桨的轴承力都会有明显的增加。从图 5可以看出,单片桨叶和总的螺旋桨产生的最大值力和力矩的时间基本相同,这说明在螺旋桨旋转一周的过程中,冰块后方的遮蔽区域能够对螺旋桨轴承力的增加产生明显的影响。
图 6为不同进速下Ktx、Ktz、10Kqx和10Kqz随时间的变化规律。参考螺旋桨水动力性能曲线可知,当进速变大时,Ktx和10Kqx都会减小;从r处(图 7)的速度三角形可以知道,当进速VA变大时,水流对桨盘面的攻角就会减小,升力在周向(Z方向)上的投影会变大,因此会导致Ktz和10Kqz的变大。从图 6中可以看出,10Kqz随着进速系数变化明显,这主要是由于进速变大后会导致桨盘面处的上下流场不对称加剧,从而使得沿Z方向的力矩变大。
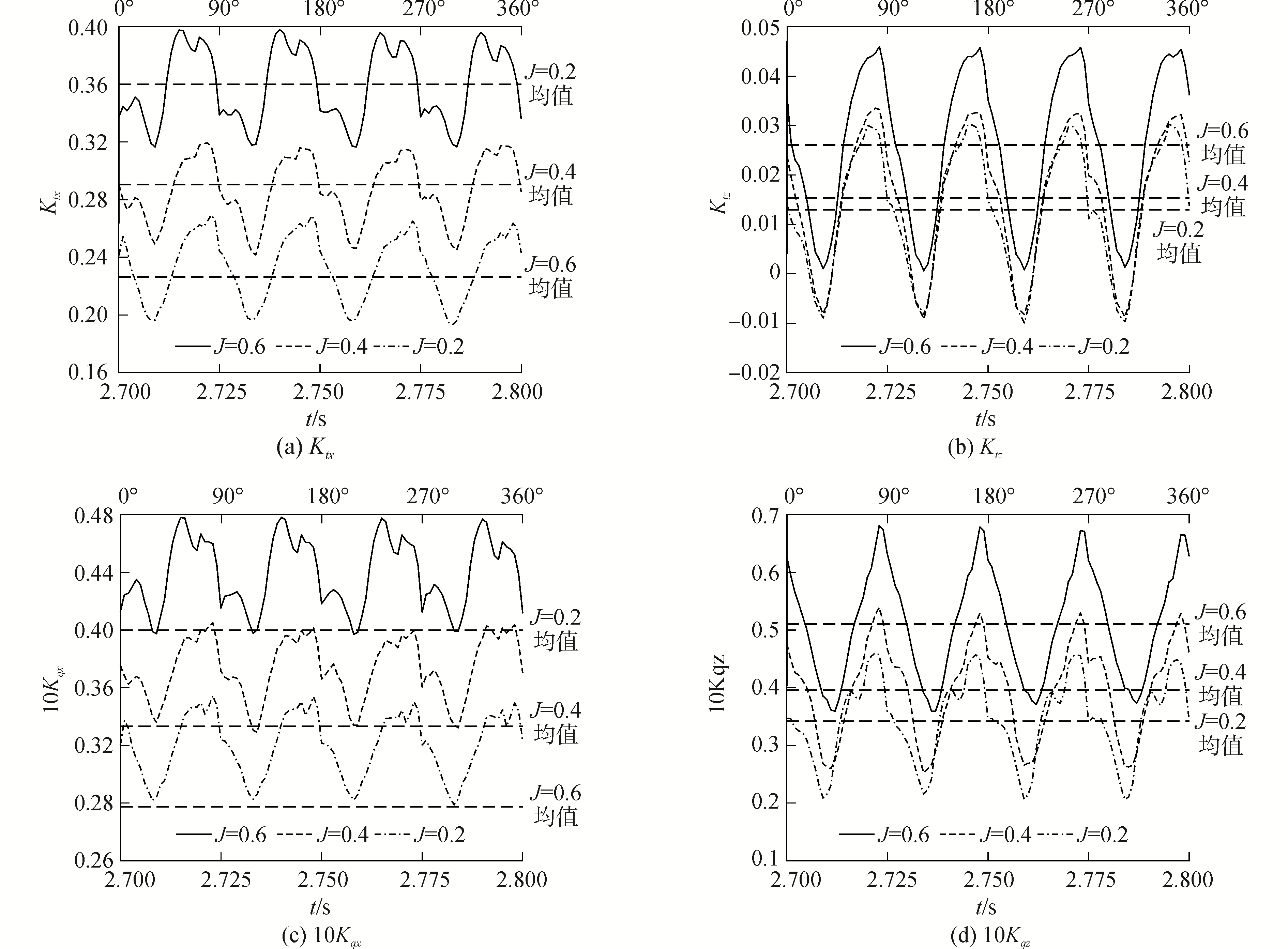
|
Download:
|
| 图 6 Ktx、Ktz、10Kqx和10Kqz时域变化图像 Fig. 6 The time domain change image of Ktx、Ktz、10Kqx and 10Kqz | |

|
Download:
|
| 图 7 叶剖面速度三角形图 Fig. 7 The velocity triangle diagram of leaf profile | |
图 8给出了主桨叶旋转一周的空间示意图,图 9为一个周期内主桨叶的推力和转矩变化规律。由图 9看出单个桨叶所受的推力和转矩变化趋势总体呈现先增大后减小的趋势。第一阶段,桨叶处于冰干扰区外,随着逐渐进入冰干扰区,推力转矩值急剧增加并达到一个极大值,处于冰干扰区内的这一桨叶的推力转矩值保持在这一极大值附近波动;第二阶段,桨叶逐渐旋出干扰区,推力转矩值急速下降,下降到一定程度时,下降速度突然放缓,这是因为此时其相邻桨叶刚好位于冰干扰区中,对流场产生了扰动,进而影响了此桨叶的推力转矩;第三阶段,桨叶逐渐远离冰块,推力转矩值继续迅速下降,直到到达极小值,桨叶转回起始点,继续循环往复。轴承力这样的“三阶段”下降变化,是敞水工况和冰桨干扰工况的一个重要区分点。
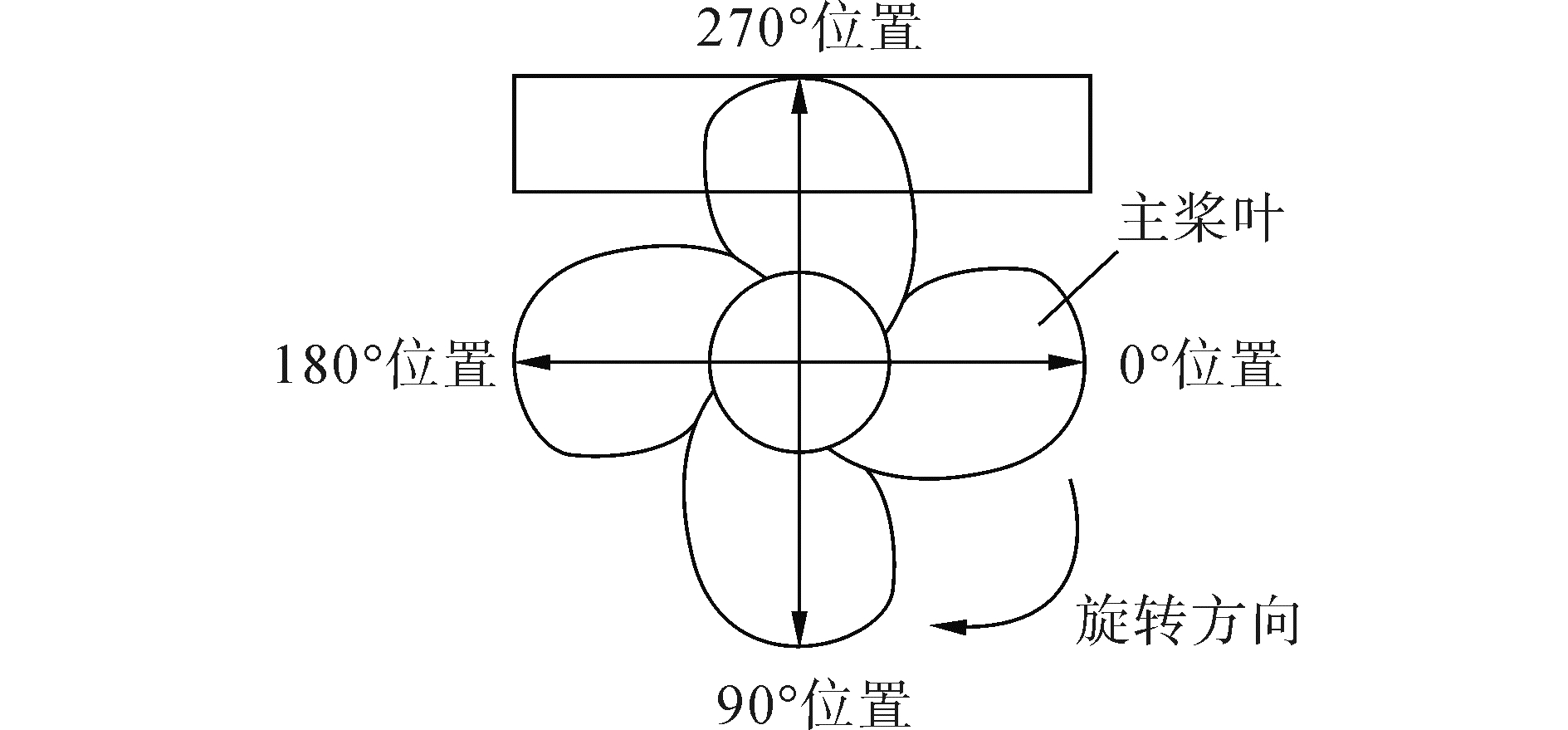
|
Download:
|
| 图 8 桨叶位置 Fig. 8 Key blade location | |

|
Download:
|
| 图 9 主桨叶Ktx和10Kqx的变化图 Fig. 9 The Ktx and 10Kqx change of main blade | |
在进速系数J=0.2的情况下,对三个推力系数分量Ktx、Kty和Ktz分别进行傅里叶变换,图 10(a)中是Ktx的傅里叶变换图,图 10(b)是10Kqx的傅里叶变换图,由变换得到的轴承力频域曲线可以看到,不再像冰桨间距较大时那样倍叶频处的峰值迅速衰减,切削形状冰后的螺旋桨的2 BPF(2倍叶频的脉动压力峰值)和3 BPF处频域峰值还会较大,因此高阶脉动峰值同样不可忽略。通过分析冰块后方桨盘面处Vx的分布进行谐调分析可大致知道流场的3阶脉动分量比2阶脉动分量大跃增,存在跃增现象,这与Ktx的频域曲线是对应的。

|
Download:
|
| 图 10 J=0.2,Ktx和10Kqx频域曲线图 Fig. 10 Frequency domain diagram of Ktxand 10Kqx, J=0.2 | |
对于所有的推力系数Ktx、Kty和Ktz以及转矩系数10Kqx、10Kqy和10Kqz在各个进速下都进行傅里叶变换,得出其各个叶频峰值,结果如表 2所示。
| 表 2 各进速下轴承力分量系数的叶频值 Tab.2 The value of the leaf frequency of the bearing force component coefficient at each advance |
由表 2可知,对于轴承力各个分量,侧向力分量(Y轴、Z轴)的脉动峰值相对于X方向都不再是小量,尤其是在高进速工况下这种脉动峰值增加现象更加明显,因此冰区桨的三个方向的强度要求都会比较高。此外,BPF处的脉动峰值是最大的,由于有冰块产生伴流场的特殊性,2BPF和3BPF仍然很大,同样不可忽略;当进速系数变大时,X方向叶频和倍叶频脉动峰值都会相应减小,Y和Z方向则会变大,这与推力系数和扭矩系数在时域上的变化是一致的,在频域上这样的变化同样可以用攻角来解释。
3 结论1) 本文采用的基于重叠网格的粘流计算方法与试验结果吻合较好,对求解冰桨干扰问题具有较好的适用性和可靠性。
2) 在桨与切削形状冰紧密“接触”的情况下,桨前流场中冰的存在,会对诱导速度场产生影响,使螺旋桨的推力和转矩均增大,在螺旋桨轴线方向(X轴)的推力和转矩脉动极值的主要成分是由旋入冰后干扰区的桨叶贡献的。
3) 在一定的变化周期内,由于螺旋桨旋转面上Y、Z方向是正交的,因此推力系数Kty和Ktz及扭矩系数10Kqy和10Kqz都会在某一时刻同时达到波峰和波谷。
4)“三阶段”变化是冰桨干扰下螺旋桨诱导轴承力的一个重要特征,这主要是桨叶旋入冰后干扰区的时间不同引起的。可以看出,本文的4叶螺旋桨表现的是“三阶段”变化,当螺旋桨叶变为5叶、6叶甚至更高时,轴承力将会表现出更为复杂的周期性变化,这也是以后的一个研究方向。
本文所计算的是冰桨切削的一个“瞬态过程”,这也为以后计算冰桨切削时螺旋桨的轴承力作一个铺垫。
| [1] |
DOUCET J M. Cavitation erosion experiments in blocked flow with two ice-class propeller models[D]. San Johns: Memorial University of Newfoundland, 1996: 160-197. https://core.ac.uk/display/20125378
(  0) 0)
|
| [2] |
SAMPSON R. Effect of cavitation during propeller ice interaction[D]. Newcastle: Newcastle University, 2009. https://core.ac.uk/display/38594340
(  0) 0)
|
| [3] |
叶金铭, 熊鹰, 贲友稳. 螺旋桨轴承力预报方法分析[J]. 船舶工程, 2003, 25(3): 16-18. YE Jinming, XIONG Ying, PEN Youwen. Analysis of prediction method of forces exerted on propeller bearing[J]. Ship engineering, 2003, 25(3): 16-18. DOI:10.3969/j.issn.1000-6982.2003.03.005 (  0) 0)
|
| [4] |
谭廷寿, 贺伟. 螺旋桨非定常轴承力计算[J]. 船海工程, 2006(2): 42-46. TAN Tingshou, HE Wei. Calculation of unsteady shaft forces of propeller[J]. Ship & ocean engineering, 2006(2): 42-46. DOI:10.3963/j.issn.1671-7953.2006.02.013 (  0) 0)
|
| [5] |
李亮, 王超, 孙盛夏, 等. 船桨舵一体的螺旋桨激振力数值预报分析[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(4): 768-772, 777. LI Liang, WANG Chao, SUN Shengxia, et al. Numerical prediction analysis of propeller exciting force for hull-propeller-rudder system[J]. Journal of Wuhan University of Technology (transportation science & engineering), 2015, 39(4): 768-772, 777. DOI:10.3963/j.issn.2095-3844.2015.04.021 (  0) 0)
|
| [6] |
MERZ S, KINNS R, KESSISSOGLOU N. Structural and acoustic responses of a submarine hull due to propeller forces[J]. Journal of sound and vibration, 2009, 325(1/2): 266-286. (  0) 0)
|
| [7] |
KORNEV N, TARANOV A, SHCHUKIN E, et al. Development of hybrid URANS-LES methods for flow simulation in the ship stern area[J]. Ocean engineering, 2011, 38(16): 1831-1838. DOI:10.1016/j.oceaneng.2011.09.024 (  0) 0)
|
| [8] |
WEI Yingsan, WANG Yongsheng. Unsteady hydrodynamics of blade forces and acoustic responses of a model scaled submarine excited by propeller's thrust and side-forces[J]. Journal of sound and vibration, 2013, 332(8): 2038-2056. DOI:10.1016/j.jsv.2012.12.001 (  0) 0)
|
| [9] |
STEGER J L, DOUGHERTY F C, BENEK J A. A chimera grid scheme[J]. Advances in grid generation ASME, 1983, 5: 59-69. (  0) 0)
|
| [10] |
田书玲.基于非结构网格方法的重叠网格算法研究[D].南京: 南京航空航天大学, 2008. TIAN Shuling. Investigation of overset unstructured grids algorithm[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. http://d.wanfangdata.com.cn/Thesis/D052041 (  0) 0)
|
| [11] |
常欣, 封振, 王超, 等. 冰临近过程中螺旋桨的水动力性能计算分析[J]. 武汉理工大学学报, 2016, 38(9): 43-50. CHANG Xin, FENG Zhen, WANG Chao, et al. Hydrodynamic performance calculation of a propeller under the action of an approaching ice block[J]. Journal of Wuhan University of Technology, 2016, 38(9): 43-50. DOI:10.3963/j.issn.1671-4431.2016.09.007 (  0) 0)
|
| [12] |
王超, 叶礼裕, 常欣, 等. 非接触工况下冰桨干扰水动力载荷试验[J]. 哈尔滨工程大学学报, 2017, 38(8): 1190-1196. WANG Chao, YE Liyu, CHANG Xin, et al. Test of hydrodynamic loads under non-contact propeller-ice interaction[J]. Journal of Harbin Engineering University, 2017, 38(8): 1190-1196. (  0) 0)
|
| [13] |
何友声, 王国强. 螺旋桨激振力[M]. 上海: 上海交通大学出版社, 1987: 7. HE Yousheng, WANG Guoqiang. Propeller exciting force[M]. Shanghai: Shanghai JiaoTong University press, 1987: 7. (  0) 0)
|
| [14] |
王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. WANG Fujun. Computational fluid dynamics analysis[M]. Beijing: Tsinghua University Press, 2004. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


