纤维增强复合材料比强度高、比模量高、热稳定性好,还有一定的阻尼减振能力,因此被广泛应用于航空、航天、汽车工业与兵器工业等重要领域[1-2]。目前,工程实际中存在大量通过该类型材料制成的典型复合薄板结构件,如太阳能帆板、航空发动机风扇叶片以及大型风力机叶片等,他们通常会受到基础激励载荷的作用,且随着它们的结构越来越复杂、工作环境越来越苛刻,其振动响应问题也越来越突出[3-4],由于振动响应超标而引发的碰撞、摩擦等问题也越来受到人们的关注。因此,研究基础激励下纤维复合薄板的振动响应问题具有重要的工程及学术意义。
长期以来,国内外学者在研究纤维复合薄板的振动响应方面做了很多的工作,已经取得了阶段性的研究成果。例如,Chow[5]基于Timoshenko梁理论推导获得简支边界条件下复合薄板的动力学方程,并且求解了冲击载荷下复合薄板的瞬态响应,但并未从实验角度验证该结果。Siu等[6]考虑材料阻尼的影响,采用Rayleigh-Ritz法求解获得了谐波激励下复合薄板的频域振动响应。Sun等[7]结合分离变量法和Mindlin-Goodman法研究了均布横向载荷作用下简支纤维复合薄板的时域振动响应问题。Reddy[8]研究了正弦分布载荷作用下,正交铺设和角铺设纤维复合薄板在自由和简支两种边界条件下的振动响应问题。Reddy[9]采用有限单元法研究了冲击载荷作用下四边简支和四边固支状态下复合薄板的瞬态响应问题,并通过Newmark直接积分法对振动响应进行了求解。Khdeir等[10]基于一阶剪切变形理论和经典层合板理论研究了正弦、三角等载荷作用下简支复合薄板的瞬态振动响应问题。Librescu等[11]基于高阶剪切变形理论对声震和冲击载荷下简支复合薄板的时域振动响应进行了研究。Ichinomiya等[12]考虑了弹性边界的影响,采用双重幂级数表示振型函数研究了单点正弦载荷激励时石墨/环氧复合薄板的振动响应问题。Khdeir[13]采用广义模态法,从时域角度研究了正弦脉冲和冲击载荷作用下四边简支、三边简支、对边简支以及简支和固支组合边界条件下复合薄板的瞬态响应问题。Wang等[14]考虑转动惯量的影响,采用样条单元法(SEM)求解了不同厚度和不同表层纤维方向的复合薄板振动响应问题。彭俊等[15]考虑了层间正应力和横向剪应力的影响,建立了冲击接触的有限元模型,采用Hertz接触定律和Newmark法求解获得了低速冲击作用下四边固支石墨/环氧复合薄板的时域响应。程起有等[16]采用有限元法对冲击载荷作用下四边固支碳纤维/环氧复合薄板的振动响应进行了研究。黄桥平等[17]考虑了应变率效应,研究了冲击载荷作用下四边固支T300/epoxy复合薄板的振动响应问题。
虽然人们已经对纤维复合薄板的振动响应进行了深入研究,但上述研究工作大多没有考虑基础激励载荷的影响,也未通过实验数据对响应分析结果进行修正。针对上述问题,本文采用了多层次修正技术,并研究了基础激励下该类型复合薄板振动响应的准确预测问题。
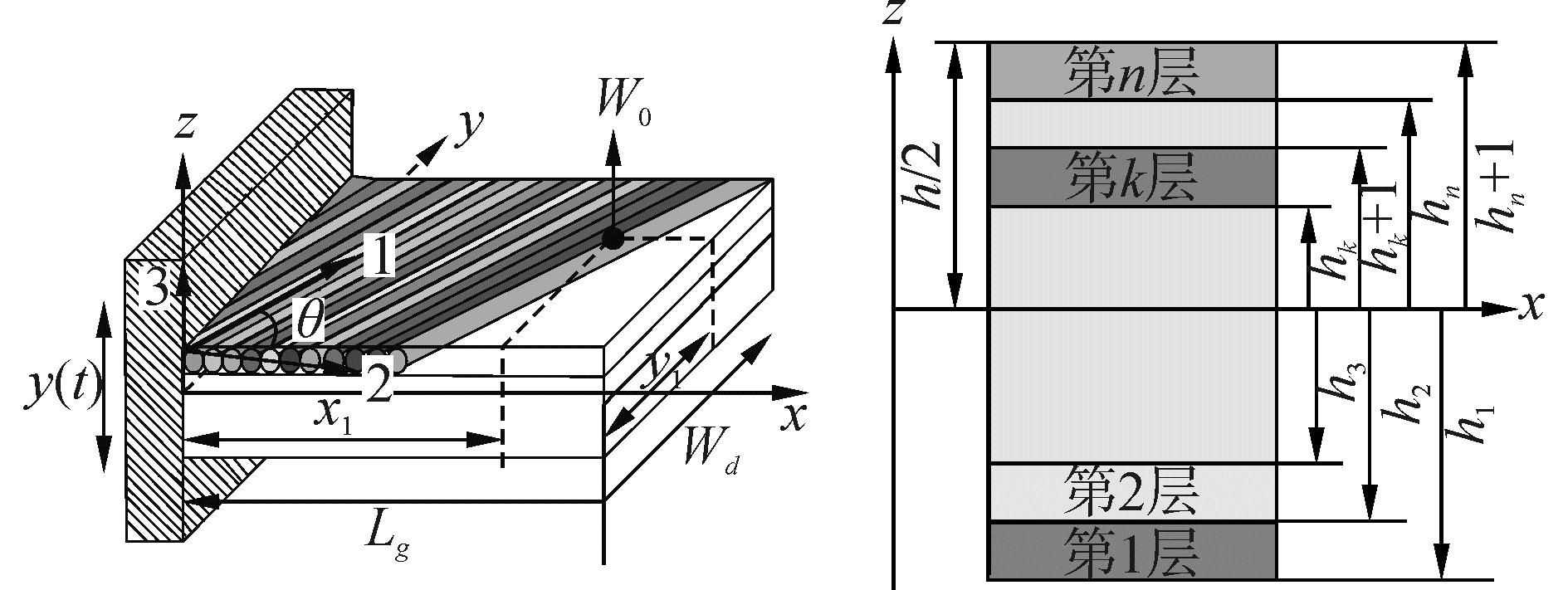
1 基础激励下纤维复合薄板振动响应求解所研究的复合薄板是由n层具有正交各向异性特点的纤维和基体材料组合而成的,如图 1所示。假设各层之间是牢固粘结的,层间无滑移,无相对位移,故可以不考虑层间耦合效应的影响。首先,将其中面作为参考平面,并建立xoy坐标系。假设纤维方向与整体坐标系x轴方向的夹角为θ,板长为Lg,板宽为Wd,板厚为h,每一层位于z坐标轴较低表面hk-1和较高表面hk之间,每层的厚度均相同。图中的1代表纤维纵向,2代表纤维横向,3代表垂直于1-2平面的方向。
|
Download:
|
| 图 1 基础激励下纤维复合薄板的理论模型 Fig. 1 Theoretical model of fiber composite plate under base excitation | |
假设复合薄板受到基础激励载荷的影响,且该基础激励的运动表达式为
| $ y\left( t \right) = Y{{\rm{e}}^{{\rm{i}}\omega t}} $ | (1) |
式中:Y为激励幅值,ω为激励频率。
考虑纤维方向的影响,将复合材料的弹性模量表示成如下形式
| $ E_1^ * = {{E'}_1}\left( {1 + {\rm{i}}{\eta _1}} \right),E_2^ * = {{E'}_2}\left( {1 + {\rm{i}}{\eta _2}} \right), $ |
| $ G_{12}^ * = {{G'}_{12}}\left( {1 + {\rm{i}}{\eta _{12}}} \right) $ |
式中:E1*、E2*分别代表平行纤维方向和垂直纤维方向的复弹性模量,G12*代表 1-2平面内的复剪切模量,E′1、E′2和G′12分别复弹性模量E1*、E2*和复剪切模量G12*的实部。并且1方向作用应力引起1、2方向应变的泊松比为ν12,2方向作用应力引起1、2方向应变的泊松比为ν21。
基于经典层合板理论,可将纤维复合薄板的位移场写为如下形式
| $ \left\{ \begin{array}{l} u\left( {x,y,z,t} \right) = {u_0}\left( {x,y,t} \right) - z\frac{{\partial {w_0}\left( {x,y,t} \right)}}{{\partial x}}\\ v\left( {x,y,z,t} \right) = {v_0}\left( {x,y,t} \right) - z\frac{{\partial {w_0}\left( {x,y,t} \right)}}{{\partial y}}\\ w\left( {x,y,z,t} \right) = {w_0}\left( {x,y,t} \right) \end{array} \right. $ | (2) |
式中:u、v、w代表板内任意一点的位移,u0、v0、w0代表板中面位移,h为复合薄板的厚度,t表示时间。
根据经典层合板理论的假设可知,正应变εz和剪应变γyz、γxz都为0,即εz=γyz=γxz=0,由应变和位移的关系,板内任意一点的应变可以表示为
| $ \left\{ \begin{array}{l} {\varepsilon _x} = \frac{{\partial u}}{{\partial x}} = - z\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\\ {\varepsilon _y} = \frac{{\partial v}}{{\partial y}} = - z\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}\\ {\gamma _{xy}} = \frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}} = - 2z\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} \end{array} \right. $ | (3) |
薄板中面弯曲挠曲率和扭曲率可表示为
| $ {\kappa _x} = - \frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}},{\kappa _y} = - \frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}},{\kappa _{xy}} = - 2\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} $ | (4) |
即
| $ {\varepsilon _x} = z{\kappa _x},{\varepsilon _y} = z{\kappa _y},{\gamma _{xy}} = z{\kappa _{xy}} $ |
对于正交各向异性材料,材料主轴方向的应力-应变关系为
| $ \left[ {\begin{array}{*{20}{c}} {{\sigma _1}}\\ {{\sigma _2}}\\ {{\sigma _6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {Q_{11}^ * }&{Q_{12}^ * }&0\\ {Q_{21}^ * }&{Q_{22}^ * }&0\\ 0&0&{Q_{66}^ * } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varepsilon _1}}\\ {{\varepsilon _2}}\\ {{\gamma _6}} \end{array}} \right] $ | (5) |
式中:
| $ \left\{ \begin{array}{l} Q_{11}^ * = \frac{{E_1^ * }}{{1 - \mathit{\boldsymbol{\nu }}_{12}^ * \mathit{\boldsymbol{\nu }}_{21}^ * }},Q_{12}^ * = Q_{21}^ * = \frac{{\mathit{\boldsymbol{\nu }}_{12}^ * E_2^ * }}{{1 - \mathit{\boldsymbol{\nu }}_{12}^ * \mathit{\boldsymbol{\nu }}_{21}^ * }}\\ Q_{22}^ * = \frac{{E_2^ * }}{{1 - \mathit{\boldsymbol{\nu }}_{12}^ * \mathit{\boldsymbol{\nu }}_{21}^ * }},Q_{66}^ * = G_{12}^ * ,{\mathit{\boldsymbol{v}}_{21}} = {\mathit{\boldsymbol{v}}_{12}}\frac{{{{E'}_2}}}{{{{E'}_1}}} \end{array} \right. $ | (6) |
当材料主轴方向与整体坐标系之间有一定夹角θ时,用应力-应变转轴公式计算得到第k层板在整体坐标系下的应力-应变关系如下
| $ {\left[ {\begin{array}{*{20}{c}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\sigma _{xy}}} \end{array}} \right]^{\left( k \right)}} = {\left[ {\begin{array}{*{20}{c}} {\bar Q_{11}^ * }&{\bar Q_{12}^ * }&{\bar Q_{16}^ * }\\ {\bar Q_{12}^ * }&{\bar Q_{22}^ * }&{\bar Q_{26}^ * }\\ {\bar Q_{16}^ * }&{\bar Q_{26}^ * }&{\bar Q_{66}^ * } \end{array}} \right]^{\left( k \right)}}\left[ {\begin{array}{*{20}{c}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\sigma _{xy}}} \end{array}} \right] $ | (7) |
式中:
薄板所受弯矩和扭矩为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{M_x}}\\ {{M_y}}\\ {{M_{xy}}} \end{array}} \right] = \sum\limits_{k = 1}^n {\int_{{z_k} - 1}^{{z_k}} {{{\left[ {\begin{array}{*{20}{c}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\sigma _{xy}}} \end{array}} \right]}^{\left( k \right)}}z{\rm{d}}z} } = }\\ {\left[ {\begin{array}{*{20}{c}} {D_{11}^ * }&{D_{12}^ * }&{D_{16}^ * }\\ {D_{12}^ * }&{D_{22}^ * }&{D_{26}^ * }\\ {D_{16}^ * }&{D_{26}^ * }&{D_{66}^ * } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\kappa _x}}\\ {{\kappa _y}}\\ {{\kappa _{xy}}} \end{array}} \right]} \end{array} $ | (8) |
式中:
为了便于理论分析建模,将复合薄板所受基础激励等效为均布惯性力外载
| $ q\left( t \right) = - \rho h\frac{{{{\rm{d}}^2}y\left( t \right)}}{{{\rm{d}}{t^2}}} = \rho hY{\omega ^2}{{\rm{e}}^{{\rm{i}}\omega t}} $ | (9) |
则薄板振动的动能可以用表示为
| $ T = \frac{{\rho h}}{2}\iint_R {{{\left( {\frac{{\partial {w_0}}}{{\partial t}}} \right)}^2}{\text{d}}x{\text{d}}y} $ | (10) |
式中:ρ为薄板的密度,h为薄板的厚度。
则薄板弯曲储存的应变能用下式表示
| $ U = \frac{1}{2}\iint_R {\left[ {{\mathit{\boldsymbol{M}}_x}{\mathit{\boldsymbol{\kappa }}_x} + {\mathit{\boldsymbol{M}}_y}{\mathit{\boldsymbol{\kappa }}_y} + {\mathit{\boldsymbol{M}}_{xy}}{\mathit{\boldsymbol{\kappa }}_{xy}}} \right]{\text{d}}x{\text{d}}y} $ | (11) |
薄板所受均布惯性力做功为
| $ {W_q} = \iint_R {q\left( t \right){w_0}{\text{d}}x{\text{d}}y} $ | (12) |
假设薄板横向振动的振动位移可以表示为
| $ {w_0}\left( {x,y,t} \right) = {{\text{e}}^{{\text{i}}\omega t}}W\left( {\xi ,\eta } \right) $ | (13) |
式中:ω为薄板振动的圆频率,与激励频率相同,Wij(ξ, η)为振型函数,形式如下
| $ W\left( {\xi ,\eta } \right) = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{a_{ij}}{p_i}\left( \xi \right){q_j}\left( \eta \right)} } $ | (14) |
式中:aij为待定系数,pi(ξ)(i=1, 2,…, M)和qj(η) (j=1, 2,…, N)为一系列的正交多项式。具体取值详见文献[18]。
将式(14)代入式(10)~(12)中,可以得到复合薄板振动的最大动能Tmax、最大应变能Umax和均布惯性力做功最大值Wqmax分别为
| $ {T_{\max }} = \frac{{\rho h{\omega ^2}}}{2}\iint_R {{W^2}{\text{d}}x{\text{d}}y} $ | (15) |
| $ \begin{array}{*{20}{c}} {{U_{\max }} = \frac{1}{2}\iint_A {\left[ {D_{11}^ * {{\left( {\frac{{{\partial ^2}W}}{{\partial {x^2}}}} \right)}^2} + 2D_{12}^ * \frac{{{\partial ^2}W}}{{\partial {x^2}}}\frac{{{\partial ^2}W}}{{\partial {y^2}}} + } \right.}} \\ {D_{22}^ * {{\left( {\frac{{{\partial ^2}W}}{{\partial {y^2}}}} \right)}^2} + 4s\left( {D_{16}^ * \frac{{{\partial ^2}W}}{{\partial {x^2}}} + D_{26}^ * \frac{{{\partial ^2}W}}{{\partial {y^2}}}} \right)\frac{{{\partial ^2}W}}{{\partial x\partial y}} + } \\ {\left. {4D_{66}^ * {{\left( {\frac{{{\partial ^2}W}}{{\partial x\partial y}}} \right)}^2}} \right]{\text{d}}A} \end{array} $ | (16) |
| $ {W_{q\max }} = \rho hY{\omega ^2}\iint_R {W{\text{d}}x{\text{d}}y} $ | (17) |
定义拉格朗日能量函数L的表达式为
| $ L = {T_{\max }} + {W_{q\max }} - {U_{\max }} $ | (18) |
通过使能量函数L对待定系数aij的偏导数等于零,即
| $ \frac{{\partial L}}{{\partial {a_{mn}}}} = 0,m = 1,2, \cdots ,M,n = 1,2, \cdots ,N $ | (19) |
可以获得M×N个非齐次线性代数方程,为了求解方便,将其写为矩阵形式为
| $ \left( {\mathit{\boldsymbol{K}} + i\mathit{\boldsymbol{C}} - {\omega ^2}\mathit{\boldsymbol{M}}} \right)\mathit{\boldsymbol{a}} = \mathit{\boldsymbol{F}} $ | (20) |
式中:K、C和M分别为结构刚度矩阵、材料阻尼矩阵和结构质量矩阵,广义位移向量a=(a11, a12, …aij)T,F为激振力向量。
对于复合薄板的自由振动问题,只需令材料阻尼矩阵C和激振力向量F为零,即
| $ \left( {\mathit{\boldsymbol{K}} - {\omega ^2}\mathit{\boldsymbol{M}}} \right)\mathit{\boldsymbol{a}} = 0 $ | (21) |
由式(21)即可求得复合薄板的固有频率和模态振型。进一步,假设纤维复合薄板受到基础激励载荷作用,并求解基础激励下其振动响应λ(x, y, t)的表达式。考虑到实验测试获得的是复合薄板绝对振动响应,即包括其自身的振动响应与基础激励位移之和。因此,可将基础激励下复合薄板的振动响应λ(x, y, t)表示为
| $ \lambda \left( {x,y,t} \right) = y\left( t \right) + {w_0}\left( {x,y,t} \right) $ | (22) |
式(22)即给出了复合薄板振动响应的求解表达式,可依据此式获得复合薄板任意一点的振动响应。
2 基于多层次修正的基础激励下复合薄板振动响应预测原理多层次建模[19]思想于2000年被提出,具有层次分明、建模准确等突出特点,本文借鉴了该修正思想的优点,将其应用于复合薄板振动响应的预测研究中。
由于复合薄板在制备过程中,其结构尺寸参数存在不均匀性问题。而且即使同一批次生产的复合薄板,其材料参数也存在一定的分散性,这都会影响振动响应计算结果的准确性。因此,准确确定损耗因子的取值是能否准确预测振动响应的关键。
首先,建立复合薄板的理论模型,计算获得复合薄板的固有频率和模态振型,并通过实验模态测试,获取复合薄板的频响函数,由频响函数辨识出各阶固有频率和模态振型结果。然后,在第1层次修正环节,对理论模型中复合薄板的长度、宽度和厚度等参数进行修正,使理论计算与测试获得的固有频率误差efreq处于允许范围内(例如10%~15%),即完成第一层次的修正;在第2层次修正环节,则对复合薄板纤维纵向、横向弹性模量、剪切模量、泊松比等参数进行修正,当迭代计算获得的固有频率与测试获得的误差efreq处于更小范围内(例如5%~10%),即完成第2层次修正;进一步,在第3层次修正环节,对复合材料纤维纵向损耗因子、纤维横向损耗因子以及面内损耗因子进行修正,直到理论计算获得的振动响应结果与测试结果的误差eres处于允许的范围内时(例如小于10%),即完成第3层次修正。利用该修正模型即对复合薄板的振动响应进行预测和分析。图 2给出了基于多层次修正的复合薄板振动响应预测原理图。

|
Download:
|
| 图 2 基于多层次修正的复合薄板振动响应预测原理图 Fig. 2 Prediction principle diagram of vibration response of composite plate based on multilevel correction technique | |
1) 建立复合薄板的理论模型。
首先,需要给出纤维复合薄板的几何参数,然后,输入材料参数,以建立复合薄板的理论模型。
2) 求解动能、应变能和外激励做功最大值。
考虑纤维方向的影响,推导获得纤维复合薄板的应力-应变关系式。同时,将振型函数式(14)代入复合薄板的动能、应变能和外激励做功的表达式中,并略去谐波分量,获得复合薄板的动能、应变能和外激励做功最大值的表达式Tmax、Umax和Wqmax。
3) 初步计算固有频率和振型。
将复合薄板的动能、应变能和外激励做功最大值的表达式Tmax、Umax和Wqmax代入式(18)中,化简获得频域响应方程(20),令其中的材料阻尼矩阵C和激振力向量F为零即可获得特征方程(21),求解特征方程得到复合薄板的固有频率和模态振型。
4) 基于第一层次修正复合薄板尺寸参数。
以实际测量获得的复合薄板尺寸参数为基准,考虑5%~10%的误差,选取合适的步长构造尺寸参数迭代向量Lg、Wd和h,随后进行尺寸参数修正,并以复合薄板的固有频率作为修正目标,当理论计算与测试获得的模态振型保持一致,且固有频率误差efreq处于允许范围内时(例如10%≤efreq≤15%),便可认为已经完成第一层次的修正。
5) 基于第二层次修正弹性模量和泊松比。
以厂商提供的材料参数均值E10、E20、G120、ν120为中心,考虑10%~20%误差,选取合适的步长构造材料参数向量E1、E2, G12、ν12,并以排列组合的方式对材料参数进行修正,仍然以复合薄板的固有频率和模态振型作为修正目标,当理论计算与测试获得的模态振型保持一致,且固有频率误差efreq处于更小范围内时(例如5%≤efreq≤10%),即视为第二层次修正成功。
6) 基于第三层次修正复合材料损耗因子。
选取合适的步长构造损耗因子迭代向量η1、η2和η12,通过对损耗因子不断迭代,并以扫频测试获得的复合薄板某阶固有频率附近的频域响应作为修正目标,当理论计算获得的频域曲线与测试曲线的误差处于允许范围内时(例如频域曲线的纵轴10%≤eres≤15%),便可认为完成第三层次的修正。图 3给出了采用多层次修正技术前、后获得的某复合薄板的第一阶频域响应曲线,从中可知应用该技术,确实可以较好地提高振动响应的预测精度。

|
Download:
|
| 图 3 采用多层次修正技术前、后获得的第一阶频域响应 Fig. 3 The 1st frequency domain responses obtained before and after using multilevel correction technique | |
7) 基于修正后模型预测关注的某阶振动响应。
基于修正后的复合薄板理论模型,求解获得复合薄板自身的振动响应w0(x, y, t),同时,考虑基础激励位移y(t)的影响,根据式(22)预测基础激励下关注的某阶振动响应。
4 实例研究本文以TC300碳纤维/树脂基复合薄板为研究对象。该复合薄板共有21层,为对称正交铺设,即[(0°/90°)5/0°/(90°/0°)5],其整体长、宽、厚尺寸分别为200 mm×130 mm×2.36 mm,纤维纵向弹性模量E1=136 GPa,纤维横向弹性模量E2=7.9 GPa,剪切模量G12=4 GPa,泊松比ν12=0.3,质量为109 g,密度ρ=1 780 kg/m3。
首先,对复合薄板进行模态测试,记录激励信号和测点的响应信号并生成频响函数,辨识出复合薄板的各阶固有频率和模态振型,相应的测试结果如表 1所示。然后,按照第3部分提出的预测流程,建立复合薄板的理论模型,并基于多层次修正技术对理论模型中的弹性模量和泊松比进行修正。为了方便比较,表 1也给出了通过修正后理论模型计算获得固有频率和振型结果。从中可以看出,分析获得的复合薄板前6阶振型与测试振型一致,且固有频率的误差最大不超过4.0%,可以利用该模型来开展下一步的振动响应预测工作。
| 表 1 预测和测试获得的纤维复合薄板前6阶固有频率和模态振形 Tab.1 The first 6 natural frequencies and modal shapes of FRCP obtained by prediction and experiment |
接下来,搭建基础激励下纤维复合薄板振动响应测试系统。采用电磁振动台对复合薄板进行基础激励,并使用Polytec PDV-100激光多普勒测振仪来测试其振动速度。同时,通过LMS数据采集前端控制器对激励信号和响应信号进行实时采集,进而通过DELL移动工作站上安装的控制软件,来提取复合薄板的频域振动响应(需通过Simpson积分处理操作来获得振动位移响应)。
以测试复合薄板第一、三、五阶频域响应为例,图 4给出了测试结果。同时,为了便于比较,在相同的基础激励幅度下,将基于多层次修正技术预测获得的第一、三、五阶频域响应结果一并给出。另外,表 2和表 3还分别给出了理论预测和扫频测试获得的共振响应和非共振响应结果及相应的误差。

|
Download:
|
| 图 4 理论预测和测试获得的复合薄板第一、三、五阶频域响应 Fig. 4 The 1st, 3rd and 5th frequency response of composite thin plate obtained by theoretical calculation and experiment test | |
| 表 2 预测和测试获得的纤维复合薄板共振响应 Tab.2 The resonance response of fiber composite thin plate obtained by prediction and experiment |
| 表 3 预测和测试获得的纤维复合薄板非共振响应 Tab.3 The non-resonance response of fiber composite thin plate obtained by prediction and experiment |
通过对比测试及预测的振动响应结果可知,基于多层次修正预测获得的基础激励下纤维复合薄板的共振响应与测试响应的误差最大不超过7.1%,且非共振响应的误差为11.8%~13.8%,处于误差允许的范围内,进而验证了理论预测方法的正确性,利用本文所提出的方法可以较好地实现基础激励下纤维复合薄板振动响应的预测。但仍有必要对上述误差原因进行分析,其可能来自于理论建模和实验测试两个方面。其中,理论误差包括在建模过程中没有考虑横向剪切应力、纤维排列不规则、界面缺陷、残余应力以及复合材料参数分散性的影响;而实验误差也客观存在,例如测试时边界条件(夹具夹紧程度)、仪器灵敏度漂移、实验方法等造成的影响。
5 结论1) 建立了该类型复合薄板的理论模型,明确了基于多层次修正的基础激励下复合薄板振动响应预测原理。
2) 提出了复合薄板振动响应预测流程,主要包括七个关键步骤。
3) 以TC300碳纤维/树脂基复合薄板为对象,进行了实验验证。结果表明,预测获得的共振及非共振响应结果与测试结果的误差最大不超过15%,处于误差允许的范围内,进而证明了所提出的响应预测方法的正确性。
| [1] |
MALLICK P K. Fiber-reinforced composites:materials, manufacturing, and design[M]. 3rd ed. Boca Raton: The Chemical Rubber Company Press, 2007.
(  0) 0)
|
| [2] |
沈观林, 胡更开. 复合材料力学[M]. 北京: 清华大学出版社, 2006. SHEN Guanlin, HU Gengkai. Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 2006. (  0) 0)
|
| [3] |
KAW A K. Mechanics of composite materials[M]. 2nd ed. Boca Raton: The Chemical Rubber Company Press, 2005.
(  0) 0)
|
| [4] |
WEAVER W J R, TIMOSHENKO S P, YOUNG D H. Vibration problems in engineering[M]. Hoboken: Wiley, 1990.
(  0) 0)
|
| [5] |
CHOW T S. On the propagation of flexural waves in an orthotropic laminated plate and its response to an impulsive load[J]. Journal of composite materials, 1971, 5(3): 306-319. DOI:10.1177/002199837100500302 (  0) 0)
|
| [6] |
SIU C C, BERT C W. Sinusoidal response of composite-material plates with material damping[J]. Journal of engineering for industry, 1973, 96(2): 603-610. (  0) 0)
|
| [7] |
SUN C T, WHITNEY J M. Forced vibrations of laminated composite plates in cylindrical bending[J]. Journal of the acoustical society of America, 1974, 55(5): 1003-1008. DOI:10.1121/1.1914639 (  0) 0)
|
| [8] |
REDDY J N. On the solutions to forced motions of rectangular composite plates[J]. Journal of applied mechanics, 1982, 49(2): 403-408. DOI:10.1115/1.3162101 (  0) 0)
|
| [9] |
REDDY J N. Dynamic (transient) analysis of layered anisotropic composite-material plates[J]. International journal for numerical methods in engineering, 1983, 19(2): 237-255. DOI:10.1002/(ISSN)1097-0207 (  0) 0)
|
| [10] |
KHDEIR A A, REDDY J N. Dynamic response of antisymmetric angle-ply laminated plates subjected to arbitrary loading[J]. Journal of sound and vibration, 1988, 126(3): 437-445. DOI:10.1016/0022-460X(88)90222-2 (  0) 0)
|
| [11] |
LIBRESCU L, NOSIER A. Response of laminated composite flat panels to sonic boom and explosive blast loadings[J]. AIAA journal, 1990, 28(2): 345-352. DOI:10.2514/3.10395 (  0) 0)
|
| [12] |
ICHINOMIYA O, NARITA Y, MARUYAMA K. Steady-state response analysis of elastically point-supported composite rectangular plates[J]. JSME international journal. ser. 3, vibration, control engineering, engineering for industry, 1990, 33(3): 304-309. DOI:10.1299/jsmec1988.33.304 (  0) 0)
|
| [13] |
KHDEIR A A. Forced vibration of antisymmetric angle-ply laminated plates with various boundary conditions[J]. Journal of sound and vibration, 1995, 188(2): 257-267. DOI:10.1006/jsvi.1995.0590 (  0) 0)
|
| [14] |
WANG Y Y, LAM K Y, LIU G R. The effect of rotatory inertia on the dynamic response of laminated composite plate[J]. Composite structures, 2000, 48(4): 265-273. DOI:10.1016/S0263-8223(99)00114-2 (  0) 0)
|
| [15] |
彭俊, 刘元镛. 低速冲击下复合材料层合板的响应过程模拟[J]. 力学季刊, 2001, 22(1): 138-142. PENG Jun, LIU Yuanyong. Response of composite laminated plate under low velocity impact[J]. Chinese quarterly of mechanics, 2001, 22(1): 138-142. DOI:10.3969/j.issn.0254-0053.2001.01.020 (  0) 0)
|
| [16] |
程起有, 童小燕, 姚磊江, 等. 复合材料层合板低速冲击响应的有限元分析[J]. 飞机设计, 2008, 28(1): 33-36. CHENG Qiyou, TONG Xiaoyan, YAO Leijiang, et al. Finite element analysis on response of composite laminated plate under low-velocity impact[J]. Aircraft design, 2008, 28(1): 33-36. DOI:10.3969/j.issn.1673-4599.2008.01.008 (  0) 0)
|
| [17] |
黄桥平, 赵桂平, 卢天健. 考虑应变率效应的复合材料层合板冲击动态响应[J]. 西安交通大学学报, 2009, 43(1): 72-76. HUANG Qiaoping, ZHAO Guiping, LU Tianjian. Dynamic response with strain rate dependence of composite laminates[J]. Journal of Xi'an Jiaotong University, 2009, 43(1): 72-76. DOI:10.3321/j.issn:0253-987X.2009.01.016 (  0) 0)
|
| [18] |
薛鹏程, 李晖, 常永乐, 等. 悬臂边界下纤维增强复合薄板固有频率计算及验证[J]. 航空动力学报, 2016, 31(7): 1754-1760. XUE Pengcheng, LI Hui, CHANG Yongle, et al. Natural frequency calculation and validation of fiber reinforced composite thin plate under cantilever boundary[J]. Journal of aerospace power, 2016, 31(7): 1754-1760. (  0) 0)
|
| [19] |
GREENLAND S. Principles of multilevel modelling[J]. International journal of epidemiology, 2000, 29(1): 158-167. DOI:10.1093/ije/29.1.158 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39














