2. 北京市遥感信息研究所, 北京 100192
2. Institute of Beijing Remote Sensing Information, Beijing 100192, China
随着我国高分辨率SAR投入使用,SAR图像目标检测与识别成为系统重要应用领域。其中,获取目标的散射特性是完成检测与识别的关键因素。由于SAR图像中目标散射特性随着目标物理特性、结构特性、雷达参数、成像关系等变化,获取完整的目标散射特性非常困难。因此,利用仿真计算得到目标的散射特性成为研究高精度SAR图像目标检测与识别的手段之一。
高精度SAR仿真精度的核心在于能否得到目标电磁特性,即如何通过获取在高分辨率条件下目标体各分辨单元随入射波的散射变化得到目标特性的描述。传统的SAR回波仿真算法往往采用后向散射系数赋值的方法得到,不能有效地模拟真实目标散射特性,无法满足当前高分辨率、高精度仿真的需求。计算电磁学是对麦克斯韦(Maxwell)方程计算上的有效近似[1-3],其中的时域有限差分(finite difference time domain, FDTD)算法是是目前应用最广泛的时域数值电磁计算方法,在一定程度上适用于任何形状目标的电磁散射。
传统的FDTD方法是Yee在1966年提出的将Maxwell旋度方程显式离散化,完成时间空间电磁场迭代的数值计算方法,并给出了以理想导体为截断边界下,电磁波在真空中传播情况[4-5]。虽然FDTD方法可以满足高分辨率SAR仿真中对目标电磁散射的高精度要求,但在大尺寸目标的计算过程中,经常会遇到极大的计算量和数据存储量等问题。在典型目标的电磁散射计算问题中,计算量和空间网格数成正比,网格数目和空间大小成正比、和波长成反比的关系,从而导致计算时间及所需资源在工程上实现困难。另一方面,对于庞大的数据迭代计算,单个处理单元的运算速度十分有限,导致计算过程时间漫长。因此,在保证计算精度不变或提高的前提下,减少计算时间、扩大计算规模成为能否实现高精度SAR目标回波仿真的关键[6-8]。
本文针对高分辨率SAR典型目标散射回波仿真需求,在研究了FDTD基本原理基础上,重点研究了典型目标在多机多线程条件下的并行时域快速电磁计算方法,并通过典型目标SAR回波成像对方法合理性进行了分析。
1 基于FDTD的典型目标电磁计算空间中的电磁行为可以用经典的描述宏观电磁运动规律的Maxwell方程组及描述媒质的本构关系的状态方程组描述。微分形式的Maxwell方程组:
| $ \left\{ \begin{array}{l} \nabla \times E = - \frac{{\partial B}}{{\partial t}} - {J_m}\\ \nabla \cdot D = \rho \\ \nabla \times H = \frac{{\partial D}}{{\partial t}} + J\\ \nabla \cdot B = 0 \end{array} \right. $ | (1) |
媒质的本构关系为
| $ \left\{ \begin{array}{l} \frac{{\partial {H_z}}}{{\partial y}} - \frac{{\partial {H_y}}}{{\partial z}} = \varepsilon \frac{{\partial {H_x}}}{{\partial t}} + \sigma {E_x}\\ \frac{{\partial {H_x}}}{{\partial z}} - \frac{{\partial {H_z}}}{{\partial x}} = \varepsilon \frac{{\partial {E_y}}}{{\partial t}} + \sigma {E_y}\\ \frac{{\partial {H_y}}}{{\partial x}} - \frac{{\partial {H_x}}}{{\partial y}} = \varepsilon \frac{{\partial {E_z}}}{{\partial t}} + \sigma {E_z} \end{array} \right. $ | (2) |
| $ \left\{ \begin{array}{l} \frac{{\partial {E_z}}}{{\partial y}} - \frac{{\partial {E_y}}}{{\partial z}} = - \mu \frac{{\partial {H_x}}}{{\partial t}} - {\sigma _m}{H_x}\\ \frac{{\partial {E_x}}}{{\partial z}} - \frac{{\partial {E_z}}}{{\partial x}} = - \mu \frac{{\partial {H_y}}}{{\partial t}} - {\sigma _m}{H_y}\\ \frac{{\partial {E_y}}}{{\partial x}} - \frac{{\partial {E_x}}}{{\partial y}} = - \mu \frac{{\partial {H_z}}}{{\partial t}} - {\sigma _m}{H_z} \end{array} \right. $ | (3) |
FDTD方法是对微分形式的Maxwell旋度方程进行离散。以一元函数为例,并假设函数在任意点处可导。将一元函数离散后,x轴上每隔Δx取点,那么在x点前半步长点(x-Δx/2)和后半步长点(x+Δx/2)处进行泰勒展开,分别为
| $ \begin{array}{*{20}{c}} {f\left( {x - \Delta x/2} \right) = f\left( x \right) - f'\left( x \right) \cdot \Delta x/2 + }\\ {\frac{{f''\left( x \right)}}{{2!}}{{\left( {\Delta x/2} \right)}^2} - \frac{{f'''\left( x \right)}}{{3!}}{{\left( {\Delta x/2} \right)}^3} + \cdots } \end{array} $ | (4) |
| $ \begin{array}{*{20}{c}} {f\left( {x + \Delta x/2} \right) = f\left( x \right) + f'\left( x \right) \cdot \Delta x/2 + }\\ {\frac{{f''\left( x \right)}}{{2!}}{{\left( {\Delta x/2} \right)}^2} + \frac{{f'''\left( x \right)}}{{3!}}{{\left( {\Delta x/2} \right)}^3} + \cdots } \end{array} $ | (5) |
其中式(4)和(5)中含有f′(x)项,可以在前半步长点(x-Δx/2)和后半步长点(x+Δx/2)分别表示为
| $ \begin{array}{*{20}{c}} {f'\left( x \right) = \frac{{f\left( x \right) - f\left( {x - \frac{{\Delta x}}{2}} \right)}}{{\Delta x}} + \frac{{f''\left( x \right)}}{{2!}}\left( {\Delta x/2} \right) - }\\ {\frac{{f'''\left( x \right)}}{{2 \cdot 3!}}{{\left( {\Delta x/2} \right)}^2} + \cdots } \end{array} $ | (6) |
| $ \begin{array}{*{20}{c}} {f'\left( x \right) = \frac{{f\left( {x + \frac{{\Delta x}}{2}} \right) - f\left( x \right)}}{{\Delta x}} - \frac{{f''\left( x \right)}}{{2!}}\left( {\Delta x/2} \right) - }\\ {\frac{{f'''\left( x \right)}}{{2 \cdot 3!}}{{\left( {\Delta x/2} \right)}^2} + \cdots } \end{array} $ | (7) |
将式(6)、(7)相加可以得到f′(x)为
| $ \begin{array}{*{20}{c}} {f'\left( x \right) = \frac{{f\left( {x + \frac{{\Delta x}}{2}} \right) - f\left( {x - \frac{{\Delta x}}{2}} \right)}}{{\Delta x}} - }\\ {\frac{{f'''\left( x \right)}}{{3!}}{{\left( {\Delta x/2} \right)}^2} + \cdots } \end{array} $ | (8) |
式(6)~(8)的三个等式都可以得到f′(x)项的近似,然而前两式的精度明显没有最后一式的精度高。
有限差分的中心思想是利用二阶中心差商近似Maxwell旋度方程组中的一阶偏微商,使得空间维、时间维都离散成计算机能够计算的形式:
| $ \begin{array}{l} \frac{{\partial f\left( {x,y,z,t} \right)}}{{\partial t}} \approx \frac{{{f^n}\left( {i + 1/2,j,k} \right) - {f^n}\left( {i - 1/2,j,k} \right)}}{{\Delta x}}\\ \frac{{\partial f\left( {x,y,z,t} \right)}}{{\partial t}} \approx \frac{{{f^{n + 1/2}}\left( {i,j,k} \right) - {f^{n - 1/2}}\left( {i,j,k} \right)}}{{\Delta t}} \end{array} $ | (9) |
传统FDTD方法在进行计算时需要消耗大量的时间和内存等资源,因此随着目标尺寸的增大及波长变小,其计算量会迅速增加甚至达到工程上无法应用的程度。为此,本文利用Pthread线程库,采用多机分布式的并行计算完成快速电磁散射计算,研究并行条件下的计算的精度及快速性,使该方法可应用于工程中解决关键问题[9-10]。
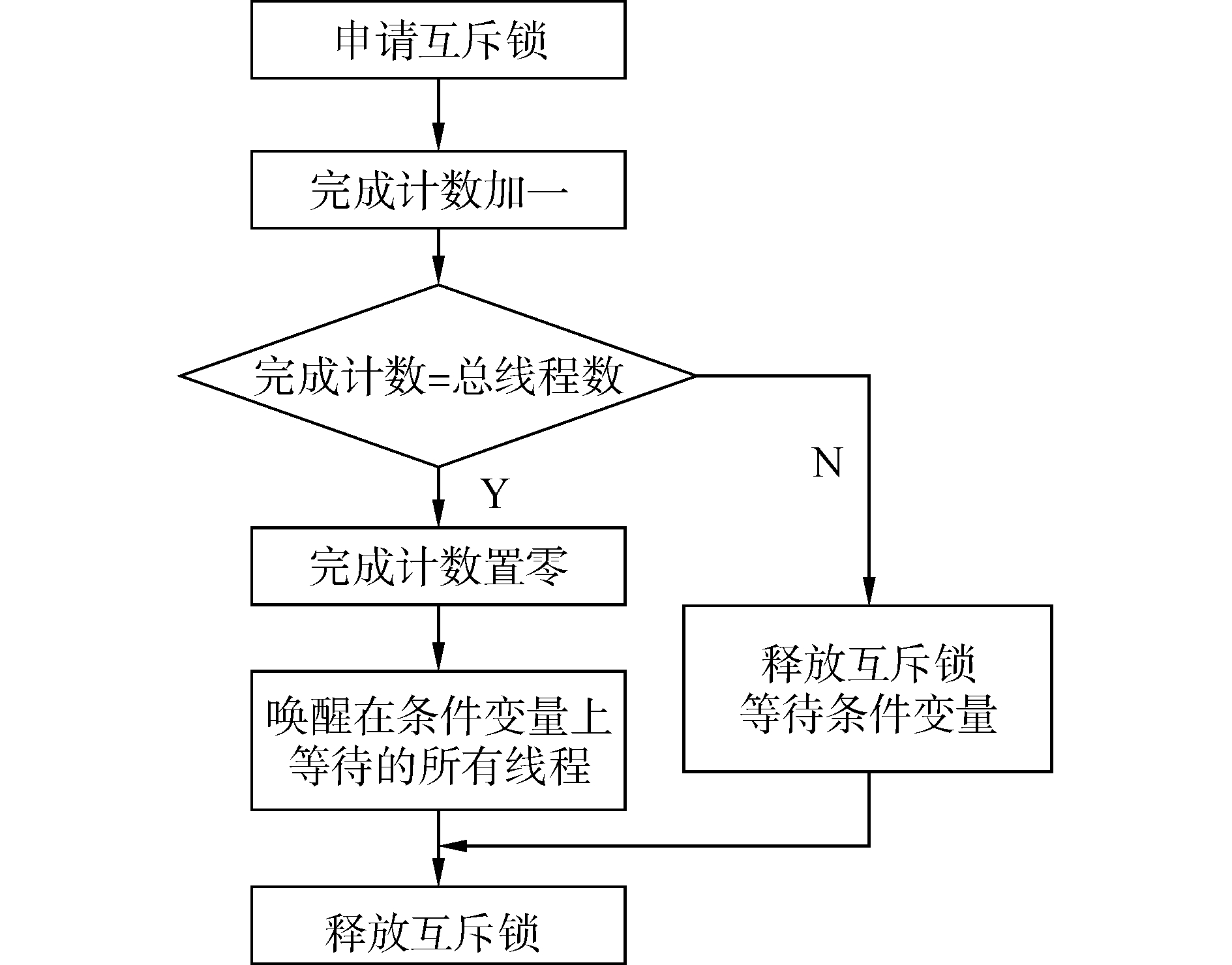
2.1 基于Pthread的多机并行FDTD方法POSIX标准定义了操作系统应该为应用程序提供创建和操纵线程的接口标准,Pthreads定义了一套C语言的类型、函数与常量,它以pthread.h头文件和一个线程库实现。利用Pthreads库可以实现POSIX定义的线程接口标准。与OpenMP不同的是,在利用Pthreads线程标准实现多线程并行处理时,需要在单线程的程序中显式地创建和销毁线程,并通过同步机制,保证各个线程按照预定方式协同工作。
|
Download:
|
| 图 1 基于Pthreads标准多线程并行计算模型 Fig. 1 Multi thread parallel computing model based on Pthreads standard | |
POSIX标准中,创建线程采用pthread_create函数,该函数创建一个新的线程执行传递给它的函数指针所指向的函数,同时可以传递给这个函数一个参数。此外还可以通过该函数指定所创建线程的优先级。使用Pthreads多线程标准完成并行计算可以实现各个线程之间的数据共享,且各个线程之间共享地址空间,无需特别的交换即可直接访问,因而只需要保证过程的同步,不用考虑数据的同步;缺点是这种方法要求操作系统能够提供很大的可用虚地址空间。
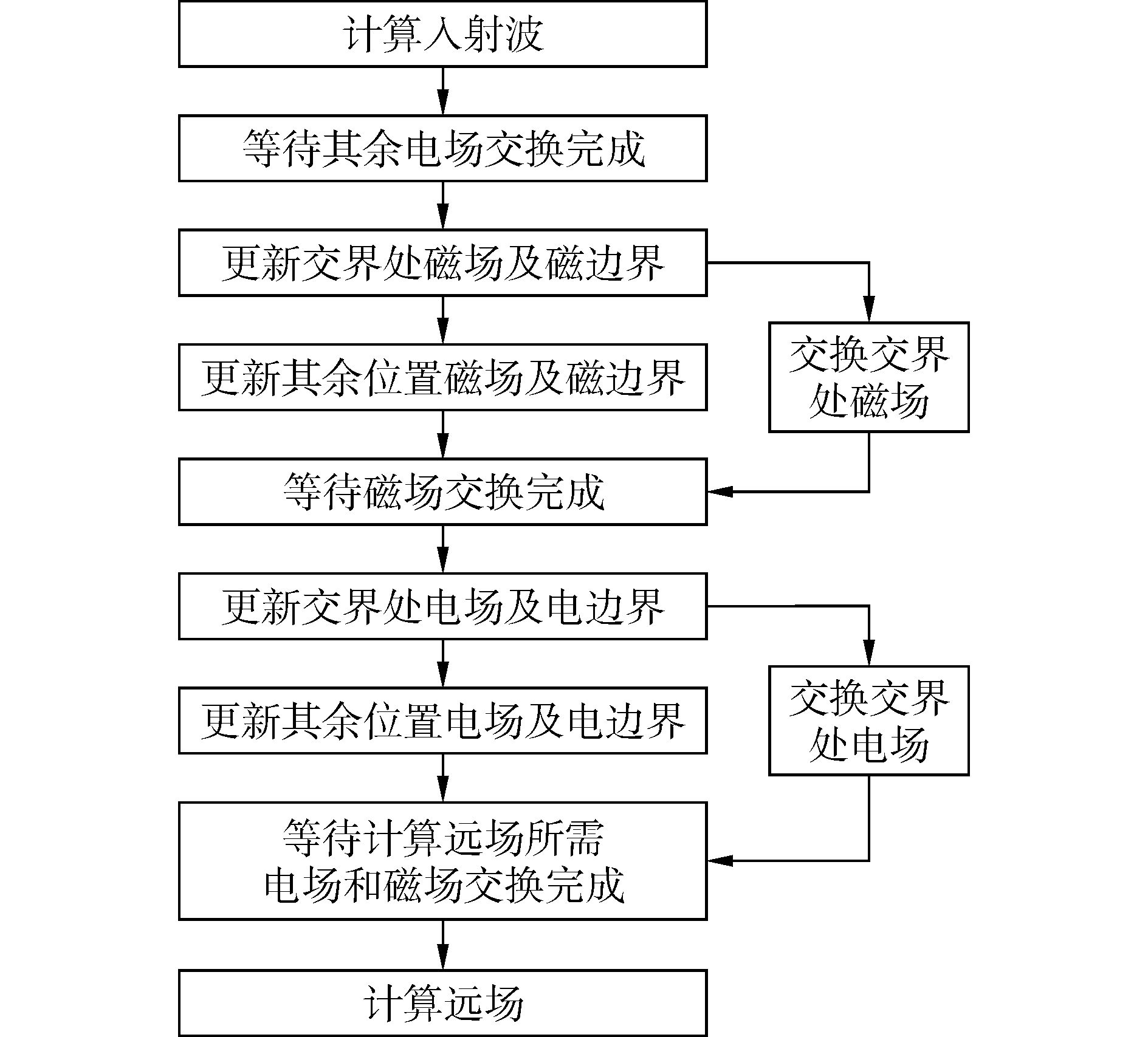
图 2是边交换边计算的并行计算迭代部分的流程图。过程采用非阻塞式的数据交换方式,每次更新过程中,首先计算需要交换的交界处的电(磁)场,计算完后立即发送给相邻节点,并立即从相邻节点接收。这里的发送和接收都是非阻塞式的,即开始发送和接收后立即返回,执行之后的程序,并不需要像阻塞式发送接收一样等待发送和接收完成才能返回。从而,程序可以马上继续更新非交界处的电(磁)场,实际上,与此同时数据的发送和接收还在继续。直到下一次更新磁(电)场之前,必须用到交界处电(磁)场值时,才检验数据是否交换完成。这时,如果数据交换尚未完成,不得不停下来等待,否则程序将无法保证计算的正确性。
|
Download:
|
| 图 2 边交换边计算的MPI并行FDTD方案 Fig. 2 Simultaneously exchanging computing scheme for MPI parallel FDTD | |
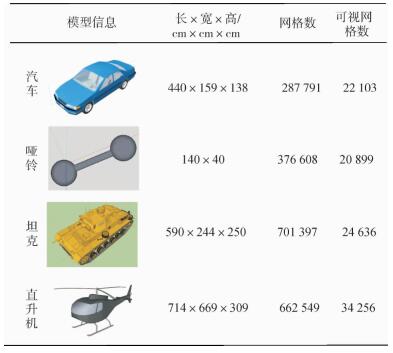
为了验证图 2方法的正确性及加速性能,仿真实验使用了多台HP工作站Z600和Z400,通过千兆交换机组成集群,按照前述方法进行配置,分别计算了4种不同尺寸的模型:汽车、哑铃、坦克、直升机。模型参数如表 1所示。
| 表 1 不同模型的大小及网格数 Tab.1 The size and mesh number of different models |
对于每个模型,分别使用1台Z600(作为对照组),2台Z600,3台Z600,4台Z600,6台Z400,以及4台Z600+6台Z400。均计算26 069步,0°照射角,观察每台计算机的CPU使用情况和内存使用情况,其中在Z400和Z600的混合仿真中,每台Z600使用2个线程,Z400使用1个线程。模型及计算结果如表 2所示。为了证明电磁计算结果的正确性,文中采用参考文献[11]中远场外推的方法形成SAR原始回波,并利用SAR成像算法对回波进行了成像,成像结果如表 3所示。
| 表 2 1 000 Mbit/s交换机不同模型计算时间比较 Tab.2 Calculation time comparison of different models of 1 000 Mbit/s switches |
| 表 3 仿真目标SAR成像结果 Tab.3 SAR imaging results of simulated models |
对于每个模型,分别使用1台Z600(作为对照组),2台Z600,3台Z600,4台Z600,6台Z400,以及4台Z600+6台Z400。均计算26 069步,0°照射角,观察每台计算机的CPU使用情况和内存使用情况,其中在Z400和Z600的混合仿真中,每台Z600使用2个线程,Z400使用1个线程。模型及计算结果如表 2所示。为了证明电磁计算结果的正确性,文中采用参考文献[11]中远场外推的方法形成SAR原始回波,并利用SAR成像算法对回波进行了成像,成像结果如表 3所示。
2.3 实验结果分析 2.3.1 计算资源消耗1) 使用1台机器仿真,CPU占用率为90%左右,分析认为是Windows操作系统的未知原因导致程序运行效率降低。
2) 两端节点(第一个和最后一个)的CPU占用率普遍较高,达到满负荷的90%左右,而中间节点占用率较低;内存占用也是如此。这是由于程序在分配每个节点的任务量时,没有考虑两端的节点需要额外进行吸收边界(CPML)的计算而导致负载分配不均,可以通过进一步改善各节点分配任务量的权重来平衡。
1) 各节点内存占用不均,CPU使用也不完全相同。除了各个机器的差异以及两端节点需要额外计算吸收边界外,各个节点计算区域可见的散射单元数也因模型结构而异,因此远场外推的任务量也有所不同,占用的计算机资源也不尽相同。
2) 对于一些模型,CPU使用率存在跳动现象。这种现象主要是由于交换时间大于计算时间导致的。通过调整坐标系方向,将模型最长方向定为X轴方向,就可以减小交换数据量。
3) 不同类型计算机组成的混合集群,一般无法通过现有程序实现负载平衡,需要修改程序中的分配权重,重新编译。但是本实验客观情况比较特殊,Z600计算机的计算速度接近Z400的2倍,Z600计算机的内存容量也是Z400计算机的2倍。因此,实验时在每台Z400上运行1个进程,Z600上运行2个进程。此时Z600上总线程数目过多,可以考虑适当调整每个进程建立的线程数目,和XYZ方向上的划分数目,以提高程序效率。实际实验也支持这一点,不同的线程数,或者不同的划分方式,CPU的使用率也不同。这点对相同计算机组成的集群也适用。
2.3.2 计算速度分析程序的计算效率(单机多线程假设为1)根据模型不同而不同,哑铃和汽车可以达到0.6左右。实验结果表明随着节点计算机数增加效率会下降,这主要是中间结点增加,而中间节点的CPU利用率通常偏低造成的。而坦克的效率只有0.4,其CPU使用率波动较大,应该是交换速度造成的瓶颈。直升机的单机无法计算,预计其需要的内存为8~9 GB,而两台Z600可以计算,这也显现出多机并行计算的优势——可以进行大规模运算。对于这种较大目标,多台机器的加速效果还是比较明显的,4台Z600+6台Z400的联合运算是使用两台Z600运算速度的5.3倍,如果两台Z600的效率是0.6,10台机器的效率大概是0.9,如果是0.4,10台的效率也为0.6,此外,效率还可以通过进一步平衡负载实现。
3 结论1) 本文提出了基于MPI和Pthreads方法的分布式共享内存并行时域电磁计算方法,仿真结果表明,所提出的方法能够在较短时间内实现典型目标的快速电磁计算。
2) 利用电磁仿真计算结果进行SAR仿真成像结果表明,所提出的电磁计算方法能够满足典型目标高分辨率SAR仿真需求。
论文结果对于高分辨、高精度SAR回波仿真系统仿真及应用具有重要的实用价值。
| [1] |
谢德馨, 唐任远. 计算电磁学近年来的若干重要成果——第15届COMPUMAG会议概述[J]. 电工技术学报, 2005, 20(9): 1-6. XIE Dexin, TANG Renyuan. Several key achievements of computational electromagnetics in recent years-summary of the 15th conference of COMPUMAG[J]. Transactions of china electrotechnical society, 2005, 20(9): 1-6. DOI:10.3321/j.issn:1000-6753.2005.09.001 (  0) 0)
|
| [2] |
文舸一. 计算电磁学的进展与展望[J]. 电子学报, 1995, 23(10): 62-68. WEN Geyi. Recent advances in computational electromagnetics[J]. Acta electronica sinica, 1995, 23(10): 62-68. DOI:10.3321/j.issn:0372-2112.1995.10.011 (  0) 0)
|
| [3] |
胡来平, 刘占军. 电磁学计算方法的比较[J]. 现代电子技术, 2003(10): 75-78. HU Laiping, LIU Zhanjun. Comparison among computational methods of electromagnetics[J]. Modern electronics technique, 2003(10): 75-78. DOI:10.3969/j.issn.1004-373X.2003.10.027 (  0) 0)
|
| [4] |
YEE K. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J]. IEEE transactions on antennas and propagation, 1966, 14(3): 302-307. DOI:10.1109/TAP.1966.1138693 (  0) 0)
|
| [5] |
YEE K S, INGHMA D, SHLAGER K. Time-domain extrapolation to the far field based on FDTD calculations[J]. IEEE Transactions on antennas and propagation, 1991, 39(3): 410-413. DOI:10.1109/8.76342 (  0) 0)
|
| [6] |
JIANG Shugang, LV Zhaofeng, ZHANG Yu, et al. Analysis of parallel performance of MPI based parallel FDTD on supercomputer[C]//Proceedings of 2013 IET International Radar Conference. Xi'an, China, 2013.
(  0) 0)
|
| [7] |
YU Wenhua, YANG Xiaoling, LIU Yongjun, et al. New development of parallel conformal FDTD method in computational electromagnetics engineering[J]. IEEE antennas and propagation magazine, 2011, 53(3): 15-41. DOI:10.1109/MAP.2011.6028417 (  0) 0)
|
| [8] |
潘鑫.典型目标时域电磁散射计算及快速算法的研究[D].哈尔滨: 哈尔滨工业大学, 2014. PAN Xin. Research on the electromagnetic scattering calculation of typical targets in time domain and the fast algorithm[D]. Harbin: Harbin Institute of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014082027.htm (  0) 0)
|
| [9] |
邴丕浩, 钟立俊, 严少虎, 等. 基于OpenMP的并行空间电磁分布计算[J]. 电子信息对抗计术, 2015, 30(2): 75-78. BING Pihao, ZHONG Lijun, YAN Shaohu, et al. Parallel space electromagnetic distribution computation on OpenMP[J]. Electronic information warfare technology, 2015, 30(2): 75-78. (  0) 0)
|
| [10] |
徐藻, 王毅, 李琳, 等. 基于MPI的FDTD并行算法及其优化策略[J]. 计算机仿真, 2009, 26(3): 121-124. XU Zao, WANG Yi, LI Lin, et al. A FDTD parallel algorithm based on mpi and its optimization strategy[J]. Computer simulation, 2009, 26(3): 121-124. DOI:10.3969/j.issn.1006-9348.2009.03.031 (  0) 0)
|
| [11] |
KANG Lihong, LU Jian, TIAN Jing, et al. Near-to-far-field transformation in FDTD for high resolution radar signal simulation[C]//IEEE International Conference on Electronic Information and Communication Technology. Harbin, China, 2016.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39