2. 黑龙江省农业科学院 遥感技术中心, 黑龙江 哈尔滨 150086
2. Remote Sensing Technology Center, Heilongjiang Academy of Agricultural Science, Harbin 150086, China
随着近年来的发展,高光谱遥感逐渐成为遥感发展的主干力量。通过获取的高光谱图像包含数百个窄而连续的波段,去识别和分类特征提供丰富而细腻的光谱信息。高光谱图像已被广泛应用于多个领域[1]。在高光谱图像处理过程中,相邻光谱间的相关性高并且训练样本数量有限[2-3],获得有标签的样本需要较高的成本和大量的时间,具有一定的困难,并且高光谱数据集维数较高,通常包含冗余信息,不仅增加了计算量还可能导致Hudges现象[4],因此高光谱图像的分类问题面临着巨大的挑战[5]。为了解决上述问题,Shahshahani等[6]提出了半监督学习的思想,利用少量难获取的有标记样本和大量易获取的未标记样本训练,不仅降低了成本,且能提高分类器的性能。一般情况下,半监督分类方法可分成几类:模型生成算法[7]、半监督支持向量机[8-9]、基于图的半监督分类[10]、自训练算法[11](Self-training)、协同训练分类[12](Co-training)、三重训练[13](Tri-training)及M训练算法[14](M-training)。其中M训练、三重训练以及协同训练都是通过两个或两个以上的分类器合作达到分类的目的,是目前研究的热点问题之一。Blum等[14]提出了协同训练算法,该算法证明了在充分冗余视图这一条件成立时,可以有效地利用未标记样本提升分类器的性能。但是在实际中很难满足充分冗余这一条件。基于此问题,Goldman等[15]对协同训练算法进行了改进,在协同训练过程中, 每个分类器通过统计技术来估计标记置信度, 并且把标记置信度最高的样本进行标记后提交给另一个分类器作为有标签样本,以便对方对有标签样本集进行更新,但是在对无标签样本进行预测以及标记的过程中,大量的使用了十倍交叉验证,不仅效率低,而且对置信度的估计不稳定。Zhou等[16]提出了Tri-training算法,该算法使预测无标签样本问题变得简单,使用三个分类器进行集成学习,提高了泛化能力。Zhang等[17]改进了Co-training半监督分类算法,利用空间与光谱信息对高光谱图像进行分类,并发现基分类器的选择对于Co-training算法的分类效果具有很大的影响。Huang等[18]提出了一种基于Tri-training的半监督算法,在该算法中,将输出结果与最终假设进行融合,引入自训练的方法,利用未标记样本不断扩大有标签样本集,对高光谱图像进行分类。Jia等[14]提出M-training算法,将M-training算法应用于气体分类,取得了很好的效果。研究发现在不增加训练样本的数量的情况下,使用四个分类器时,分类精度比Tri-training算法具有明显提高,然后不断增加分类器数量,分类精度不再发生改变。
本文将M-training算法应用于高光谱图像分类,并针对原始算法分类器差异性不足的问题加以改进,该改进方法采用两个SVM、一个K近邻(KNN)以及一个随机森林(RF)分类器进行组合。并且引入无标签样本错误率的概念,在每一次更新有标签样本集的过程中采用了有标签样本与无标签样本的错误率加权的形式对更新进行条件限制,从而更优地扩充有标签样本集,更好地初始化四个分类器,实现分类精度的提高。
1 M-training改进算法 1.1 传统的M-training算法在传统的M-training算法中,构建了四个完全相同的分类器,用来对未标记样本集进行分类[13]。可以设四个分类器分别是h1、h2、h3和h4。令L表示初始有标签样本集,|L|表示有标签样本集中所有的样本个数;令U表示初始的无标签样本集,则|U|表示无标签样本集中所有的样本个数。令L(t-1)以及L(t)分别表示第t-1次循环和第t次循环中辅助分类器为主分类器标记完成的样本集,那么在第t-1次循环和第t次循环中h1的训练样本集分别是L∪L(t-1)和L∪L(t)。令e(t)表示在第t次循环中h2、h3和h4分类误差的最大值,即h2、h3和h4对样本的联合预测中产生的误差率。如果满足式(1),正在被分类的无标签样本x将被允许加入h1中,从而扩大有标签样本集,为下次循环做准备[7]:
| $ 0 < \frac{{e\left( t \right)}}{{e\left( {t - 1} \right)}} < \frac{{\left| {L\left( {t - 1} \right)} \right|}}{{L\left( t \right)}} < 1 $ | (1) |
在这些样本中, h2、h3和h4都做了正确分类的个数为q,这样e(t)估计可以表示为
| $ e\left( t \right) = \frac{{p - q}}{p} $ | (2) |
其中,e(0)的初始值设定为0.5。如果不等式(1)成立,那么e(t)|L(t)| < e(t-1)|L(t-1)|。但当e(t) < e(t-1)且L(t)>L(t-1)时,并不能保证一定存在e(t)|L(t)| < e(t-1)|L(t-1)|。为了保证该情况下e(t)|L(t)| < e(t-1)|L(t-1)|仍然成立,在M-Training算法中采用的是对L(t)进行随机抽样的方法。令S代表抽样后L(t)的样本数量,若要满足e(t)|L(t)| < e(t-1)|L(t-1)|,只需:
| $ S = \left\lceil {\frac{{e\left( {t - 1} \right)\left| {L\left( {t - 1} \right)} \right|}}{{e\left( t \right)}} - 1} \right\rceil $ | (3) |
|L(t-1)|需要满足:
| $ \left| {L\left( {t - 1} \right)} \right| > \frac{{e\left( t \right)}}{{e\left( {t - 1} \right) - e\left( t \right)}} $ | (4) |
使得抽样后仍有|L(t)|>|L(t-1)|。根据以上条件的判定,可判断由h2、h3和h4给出相同标记的样本组成的样本集L(t)是否应该被加入到h1的新训练集中。
当h2、h3和h4分别为主分类器,其他分类器为辅助分类器时,分类方法与上述方法相同。
1.2 基分类器多样化由于传统的M-training算法中基分类器种类单一,不具有差异性,在文中采用差异性较大的三种分类器组合的形式实现高性能分类,该改进方法的原因如下:如图 1(a)所示,大量数据在二维空间无法区分,将其映射到三维空间里划分,因此SVM适用于高光谱图像分类。然而,SVM通常在边界位置无法获得良好的性能,而KNN算法对边界分类较为敏感,所以将SVM和KNN进行组合能够进行互补。当某空间中含有未知样本时,找出待分类样本最近邻的k个样本,并根据其类别确定待测样本的数据类型,即KNN算法的核心思想,如图 1(b)所示,当k=3时,待测样本与圆形数据类别相同。此外,RF在处理高光谱图像时,即使在小样本的情况下,也具有很强的泛化能力。决策树与决策树之间可以进行并行处理,算法效率较高,并且具有很好的抗噪声能力,在规模增加时不会出现过拟合现象,随机森林分类原理图如图 1(c)所示。从图中可以看到,随机森林是基于决策树的一个组合模型,同单一的决策树分类不同的是,随机森林通过多个决策树投票结果进行分类,适用于半监督分类。由于SVM分类速度比一般的分类器快很多,所以这时可以考虑使用2个SVM、1个KNN以及1个RF作为基分类器,与传统算法相比,基分类器之间具有较大的差异性,能够进行优势互补,使分类器性能提高。

|
Download:
|
| 图 1 算法原理图 Fig. 1 Schematic diagram | |
在传统的多重训练算法中,分类误差e(t)是采用h2、h3和h4在初始的有标记数据集L上的错误率近似的,忽略了训练样本中大量存在的无标签样本错误率的影响,基于此本文进行了改进,本文引入了无标签样本的错误率,将有标签样本分类错误率与无标签样本分类错误率进行加权。其中有标签样本的错误率用e-L表示为
| $ {e_ - }L = \left( {m - mm} \right)/m $ | (5) |
式中:m为h2、h3和h4对有标签样本标记相同的个数,mm为h2、h3和h4对有标签样本分类正确的个数。当只有少量有标记样本可用的情况下,在某次循环时如果对有标签样本的分类完全正确,那么这次循环的错误率e(x)为零,这种情况下将不能满足式(1),分类器的性能将不稳定或恶化[19]。这时可以充分利用训练集中大量的无标签样本,所以本文引入了无标签样本的错误率。由于无法确切地计算无标签样本的错误率的大小,可以根据各分类器对无标签样本的分类结果,采用投票机制将无标签样本的错误率e-U定义为
| $ {e_ - }U = ({n_ - }u - k)/{n_ - }u $ | (6) |
式中:n-u为h2、h3和h4进行分类的无标签样本的个数,k为h2、h3和h4对无标签样本标记相同的个数。然后将有标签样本的错误率与无标签样本的错误率赋予不同的权重,将加权后的值赋予e(t),则
| $ e\left( t \right) = \lambda *{e_ - }L + \left( {1 - \lambda } \right)*{e_ - }U $ | (7) |
式中:λ分别取值为0、0.1、0.2…0.9、1。与传统的M-training算法相比,充分考虑了所有的样本对错误率的影响,当有标签样本的数量一定时,一定存在某个特定的λ值,使分类性能达到最优,即λ在该值下总体分类精度与Kappa系数分别高于其他情况。以上过程一直循环,直到没有分类器再改变为止,最后的结果通过投票法进行决策融合,即最多数分类器分类结果一致的类别作为待分类样本的类别。
1.4 实验步骤及流程图1) 利用有标签样本集训练分类器h1、h2、h3和h4;
2) 对于分类器h1,对无标签样本集U中的样本进行分类时,由h2、h3和h4分类得到相同的结果,这时满足不等式(1)的有标签样本集L(t)得到了扩充(对于主分类器为h2、h3或h4时同理),即,L(t)={x|x∈U且h2(x)=h3(x)=h4(x)};
3) 若e(t)|L(t)| < e(t-1)|L(t-1)|,那么h1的训练集扩充为L(t)=L(t-1)∪L(t),否则将对L进行再次抽样得到训练集S,如果满足e(t)|L(t)| < e(t-1)|L(t-1)|,则L(t)=S;
4) 重复步骤1)~3)直到hi(i=1, 2, 3, 4)不再发生改变,得到所需分类器;
5) 输入测试样本,利用所得分类器进行多重训练,对无标签样本进行分类;
6) 最终结果由多数投票方式决定。
算法流程图如图 2所示。

|
Download:
|
| 图 2 算法流程图 Fig. 2 Flowchart of the proposed algorithm | |
印第安纳数据:该数据来源于AVIRIS传感器,是拍摄于美国西北部印第安纳州的一幅高光谱图像的一部分。图像大小为145×145(空间分辨率:200 m),在去除20个低信噪比波段以及水吸收波段后,参与实验的共有200个波段。本文使用样本数目较多的8个主要类别进行分类实验。
帕维亚大学数据:该数据是由ROSIS光学传感器在意大利帕维亚大学拍摄的高光谱遥感图像。图像大小为610×340(空间分辨率:1.3 m),去除12个噪声波段,实际参与实验的共103个波段。本文使用所有类别的所有样本进行分类实验。
2.2 实验设置应用本文提出的基于M-training改进算法对以上两种高光谱图像进行分类,为了确保实验的准确性,每种数据集进行10次独立实验,分别对所得的总体分类精度(overall accuracy,OA)、平均分类精度(average accuracy,AA)、Kappa系数取平均值。
在实验中,使用所有样本中均匀选择的25%的样本进行训练,其余75%的样本用于测试。从训练样本中选出30个样本,构成初始的有标签样本集,其余的被视为未标记的训练样本,其中改进1为基于分类器多样性的改进,改进2为基于错误率加权的改进。
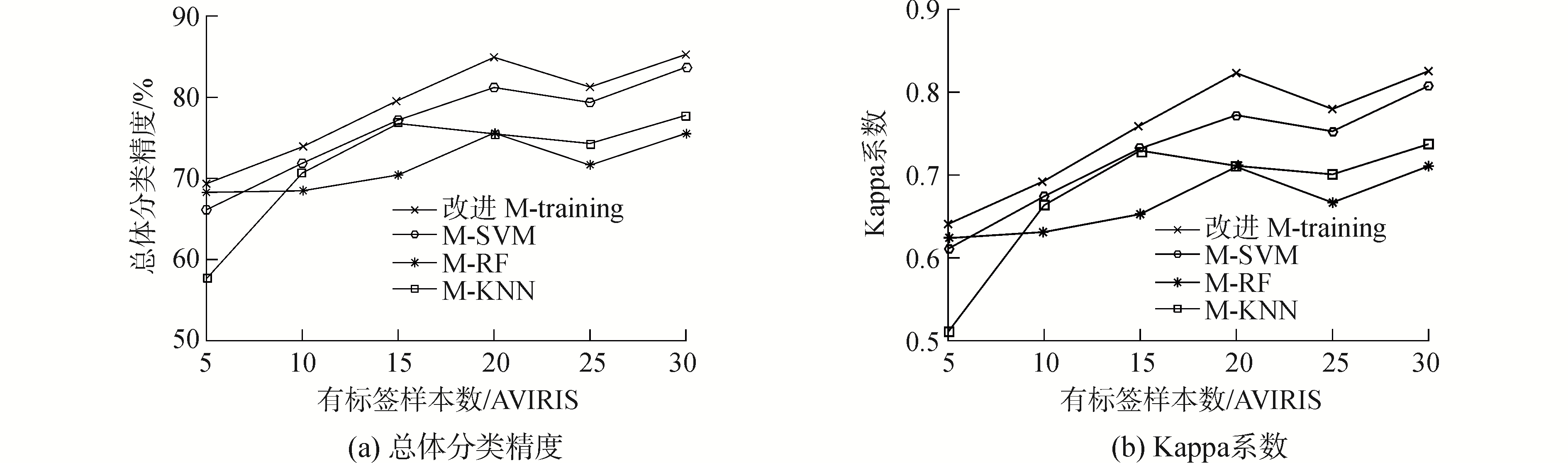
3 实验结果 3.1 AVIRIS数据的实验结果与分析改变基分类器的种类,与传统的M-training算法相比,各精度与Kappa系数均有不同程度的提高,在引入了无标签样本的错误率对更新有标签样本进行限制后,分类性能得到进一步的提高。如表 1所示,对于OA,改进算法比M-SVM提高1.85%,比M-RF提高了12.10%,比M-KNN提高8.75%。对于AA,改进算法比M-SVM提高1.17%,比M-RF提高9.93%,比M-KNN提高7.50%。对于Kappa系数,该进算法比M-SVM提高了0.0215,比M-RF提高了0.1413,比M-KNN提高0.1033。4种算法的某次分类结果示于图 3。AVIRIS数据在使用不同数量的有标签样本分类时,总体精度和Kappa系数曲线图分别如图 4(a)、(b)所示。
| 表 1 基于AVIRIS的5种算法的实验结果 Tab.1 Experimental results of 5 algorithms based on AVIRIS |

|
Download:
|
| 图 3 AVIRIS数据4种算法分类结果图 Fig. 3 Four algorithms classification result graph based on AVIRIS | |
|
Download:
|
| 图 4 初始有标签数不同时,4种算法的各评价指标曲线图(AVIPIS) Fig. 4 In the case of different number of labeled samples, evaluation index curves of four algorithms(AVIPIS) | |
通过图 4可以看出,由于该算法在训练过程中,不断扩充有标签样本集,该算法的优势逐渐明显。在有标签样本为20个左右时,改进算法的优势更加明显,但是在有标签样本的个数为25时,曲线出现下降趋势,这就说明了在半监督分类过程中,并不是有标签样本的个数越多越好,可能出现过拟合现象。当有标签样本数量在25~30,四条曲线趋于平行状态,即当有标签样本达到一定数量时,各个分类系统逐渐稳定,该算法比其他算法分类结果提高的程度也呈稳定趋势。改进算法相对于M-SVM、M-RF和M-KNN算法,在初始有标签样本的不同的情况下,性能都有一定的提高,这说明了该改进算法较其他几种算法具有一定的优势。
3.2 ROSIS数据的实验结果与分析从表 2可以看出,所提出的算法明显优于传统的M-training算法。对于OA,提出的算法比M-SVM提高了4.87%,比M-RF提高了10.33%,比M-KNN提高了9.68%。对于AA,算法比M-SVM提高了2.10%,比M-RF提高了6.75%,比M-KNN提高8.07%。对于Kappa系数,提出的算法比M-SVM提高0.0562,比M-RF提高0.1166,比M-KNN提高0.1182。4种算法的某次分类结果示于图 5,直观地体现了分类效果。
| 表 2 基于ROSIS的4种算法的实验结果 Tab.2 Experimental results of 4 algorithms based on ROSIS |

|
Download:
|
| 图 5 ROSIS数据4种算法分类结果图 Fig. 5 Four algorithms classification result graph based on ROSIS | |
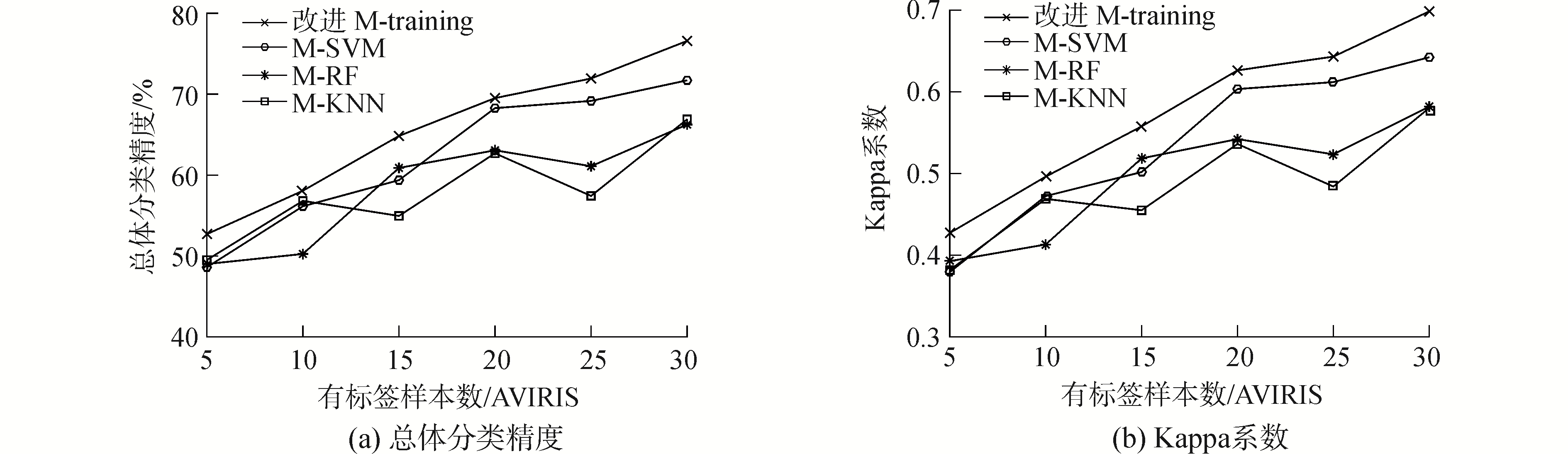
图 6 (a)和(b)分别描述了ROSIS数据的初始有标签样本数与OA和Kappa系数的关系曲线。
|
Download:
|
| 图 6 在初始有标签数不同时,4种算法的各评价指标曲线图(ROSIS) Fig. 6 In the case of different number of labeled samples, evaluation index curves of four algorithms(ROSIS) | |
通过观察图 6曲线可以看出,在有标签样本数为5~20时,随着有标签样本数量的增多,改进的M-training算法和M-SVM算法的分类精度和Kappa系数呈现逐渐升高的趋势,这是因为有标签的样本越多能获得的先验知识越多,使分类性能得以提升。和AVIRIS数据的实验结果类似,有标签样本数量为25时,M-RF与M-KNN算法的总体精度和Kappa系数略微下降,但是改进算法没有出现下降的现象,表明了该改进算法应用于ROSIS数据时,不易发生过拟合现象。在有标签样本数量为25~30时,各精度又逐渐升高。由于本文对ROSIS数据的所有种类的地物的所有样本进行分类,受地物种类多样性以及待分类样本数量的限制,导致所有方法的总体精度以及Kappa系数都偏低。但是当对改进的M-training算法与M-SVM、M-RF、M-KNN进行比较可以发现,在半监督分类方面还是具有明显的优势,证明了本文提出的改进算法的有效性。
4 结论1) 通过改变基分类器的种类,增加了分类器的多样性和差异性。
2) 通过少量的有标签样本以及大量的无标签样本进行分类器的训练,各个分类器协同作用不断丰富有标签样本集。
3) 在更新迭代实现有标签样本集扩充的过程中,引入了无标签样本的错误率,采用分类错误率加权值作为更新迭代的限制条件,从而在扩充有标签样本集的过程中减少噪声样本的引入,提高了半监督分类的精度。
4) 通过与传统M-SVM、M-KNN以及M-RF算法的实验结果比较,证明该改进方法的分类精度有很大的提高,充分利用了有标签样本,具有更好的性能。
此外,由于基分类器的选择具有很大的影响,今后在这方面可以做进一步的研究。
| [1] |
GUYON I M, GUNN S R, NIKRAVESH M, et al. Feature extraction: foundations and applications[C]//Studies in Fuzziness and Soft Computing. Heidelberg, 2006: 68-84.
(  0) 0)
|
| [2] |
TARABALKA Y, BENEDIKTSSON J A, CHANUSSOT J, et al. Multiple spectral-spatial classification approach for hyperspectral data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(11): 4122-4132. (  0) 0)
|
| [3] |
DOPIDO I, VILLA A, PLAZA A, et al. A quantitative and comparative assessment of unmixing-based feature extraction techniques for hyperspectral image classification[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2012, 5(2): 421-435. DOI:10.1109/JSTARS.2011.2176721 (  0) 0)
|
| [4] |
TAN Kun, HU Jun, LI Jun, et al. A novel semi-supervised hyperspectral image classification approach based on spatial neighborhood information and classifier combination[J]. ISPRS journal of photogrammetry and remote sensing, 2015, 105: 19-29. DOI:10.1016/j.isprsjprs.2015.03.006 (  0) 0)
|
| [5] |
XIA Junshi, CHANUSSOT J, DU Peijun, et al. (Semi-) supervised probabilistic principal component analysis for hyperspectral remote sensing image classification[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2014, 7(6): 2224-2236. DOI:10.1109/JSTARS.2013.2279693 (  0) 0)
|
| [6] |
SHAHSHAHANI B M, LANDGREBE D A. The effect of unlabeled samples in reducing the small sample size problem and mitigating the Hughes phenomenon[J]. IEEE transactions on geoscience and remote sensing, 1994, 32(5): 1087-1095. DOI:10.1109/36.312897 (  0) 0)
|
| [7] |
BARALDI A, BRUZZONE L, BLONDA P. A multiscale expectation-maximization semisupervised classifier suitable for badly posed image classification[J]. IEEE transactions on image processing, 2006, 15(8): 2208-2225. DOI:10.1109/TIP.2006.875220 (  0) 0)
|
| [8] |
YANG Lixia, YANG Shuyuan, JIN Penglei, et al. Semi-supervised hyperspectral image classification using spatio-spectral laplacian support vector machine[J]. IEEE geoscience and remote sensing letters, 2014, 11(3): 651-655. DOI:10.1109/LGRS.2013.2273792 (  0) 0)
|
| [9] |
TAN Kun, LI Erzhu, DU Qian, et al. An efficient semi-supervised classification approach for hyperspectral imagery[J]. ISPRS journal of photogrammetry and remote sensing, 2014, 97: 36-45. DOI:10.1016/j.isprsjprs.2014.08.003 (  0) 0)
|
| [10] |
MA Li, CRAWFORD M M, YANG Xiaoqian, et al. Local-manifold-learning-based graph construction for semisupervised hyperspectral image classification[J]. IEEE transactions on geoscience and remote sensing, 2015, 53(5): 2832-2844. DOI:10.1109/TGRS.2014.2365676 (  0) 0)
|
| [11] |
王俊淑, 江南, 张国明, 等. 高光谱遥感图像DE-self-training半监督分类算法[J]. 农业机械学报, 2015, 46(5): 239-244. WANG Junshu, JIANG Nan, ZHANG Guoming, et al. Semi-supervised classification algorithm for hyperspectral remote sensing image based on DE-self-training[J]. Transactions of the chinese society for agricultural machinery, 2015, 46(5): 239-244. (  0) 0)
|
| [12] |
BLUM A, MITCHELL T. Combining labeled and unlabeled data with co-training[C]//Proceedings of Eleventh Annual Conference on Computational Learning Theory. Madison, 1998: 92-100. http://dl.acm.org/citation.cfm?id=279962
(  0) 0)
|
| [13] |
王立国, 杨月霜, 刘丹凤. 基于改进三重训练算法的高光谱图像半监督分类[J]. 哈尔滨工程大学学报, 2016, 37(6): 849-854. WANG Liguo, YANG Yueshuang, LIU Danfeng. Semi-supervised classification for hyperspectral image based on improved tri-training method[J]. Journalof Harbin Engineering University, 2016, 37(6): 849-854. (  0) 0)
|
| [14] |
JIA Pengfei, HUANG Tailai, DUAN Shukai, et al. A novel semi-supervised electronic nose learning technique:M-training[J]. Sensors, 2016, 16(3): 370. DOI:10.3390/s16030370 (  0) 0)
|
| [15] |
GOLDMAN S A, ZHOU Yan. Enhancing supervised learning with unlabeled data[C]//Proceedings of the Seventeenth International Conference on Machine Learning. San Francisco, 2000: 327-334. http://dl.acm.org/citation.cfm?id=658273
(  0) 0)
|
| [16] |
ZHOU Zhihua, LI Ming. Tri-training:exploiting unlabeled data using three classifiers[J]. IEEE transactions on knowledge and data engineering, 2005, 17(11): 1529-1541. DOI:10.1109/TKDE.2005.186 (  0) 0)
|
| [17] |
ZHANG Xiangrong, SONG Qiang, LIU Ruochen, et al. Modified Co-training with spectral and spatial views for semisupervised hyperspectral image classification[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2014, 7(6): 2044-2055. DOI:10.1109/JSTARS.2014.2325741 (  0) 0)
|
| [18] |
HUANG Rui, ZHOU Li'na. Classification of hyperspectral data based on semi-supervised tri-training learning framework[C]//Proceedings of 2010 International Conference on Remote Sensing. 2010: 374-382. http://www.scientific.net/KEM.500.374
(  0) 0)
|
| [19] |
HUANG Rui, HE Wenyong. Using tri-training to exploit spectral and spatial information for hyperspectral data classification[C]//Proceedings of 2012 International Conference on Computer Vision in Remote Sensing. Xiamen, 2012: 30-33.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


