碰撞检测技术伴随着计算机技术的快速发展,已成为计算机科学的一个热门研究领域,特别是近几年碰撞检测技术占有越来越重要的地位。但是因为计算机技术的不断发展,所以人们对于碰撞检测技术在实时性和精确度方面的要求也越来越高了,针对碰撞检测效率和精确度方面的一些算法也相继被提出。在针对检测效率的提升方面, 于凌涛等[1]在传统包围盒的基础上提出了一种结合轴向包围盒和包围球的混合包围盒碰撞检测算法。Wong等[2]选择通过径向视图来剔除不必要的包围盒。Schvartzman等[3]提出了一种星级轮廓分层的自碰撞检测算法,通过对物体构建星级轮廓来分层检测。Tang等[4-5]也提出了一种分层控制的算法和一种剔除算法。Ouyang等[6]提出一种基于八叉树球面分层模型的碰撞检测算法。He等[7]也提出一种基于动态聚类的拓扑变化模型的连续碰撞检测算法。当然不止是从包围盒方向改进也有学者从其他方向进行了研究来提升检测效率,Pabst等[8]利用电脑硬件提出了一种的新型CPU/GPU混合碰撞检测技术。Wang[9]利用GPU和浮点进行优化来提升检测效率。Brochu等[10]利用几何计算的方法通过改进布尔运算来实现检测效率的提高。Tang等[11]也提出了一种通过伯恩斯坦符号分类来进行碰撞检测的算法。张智等[12]采用棱形投影来对多面体进行碰撞检测。林凌等[13]提出利用深度图形来进行实时的碰撞检测算法。Xing等[14]提出一种通过投影的方法把高纬度转换为低纬度的碰撞检测算法。虽然学者们从各个角度来对碰撞检测进行了研究,也确实提高了碰撞检测的效率,但是仍存在一定的局限性,检测效率也还有一定的提升空间。因此本文在前人算法的基础上进行改进,提出了一种基于质点转换和包围盒相结合的碰撞检测算法。
1 质点转换和包围盒混合法总体描述质点转换和包围盒混合算法的总体流程如图 1所示。

|
Download:
|
| 图 1 总体流程图 Fig. 1 Overall flow chart | |
从图 1中可以看出该算法首先利用区域中心法[15]构建改进的OBB(oriented bounding box)包围盒;然后通过二叉树原理建立一个树状结构的OBB层次包围盒;再利用质点转换公式,使其作用于外层包围盒把物体转换为一个点,并对这些点进行距离计算;接下来通过对计算结果与还原距离进行判定,对没有通过验证的点不作处理,而对通过验证的点则将其还原为包围盒;最后,对还原的OBB层次包围树进行遍历的相交测试。
2 质点转换和包围盒混合法原理 2.1 OBB层次包围盒的构建包围盒算法指的是通过对各种形状的物体在外围用一些简单的几何物体构建包围盒来进行碰撞检测的方法,它能简化碰撞检测的复杂度。具体的原理就是通过在复杂物体上构建一个包围盒,然后通过对包围盒进行相交测试来完成碰撞检测。因为只有当包围盒相交时物体才能相交,所以基于此,这类方法能够有效排除空间中所有不相交的物体,保留相交的物体。常用的包围盒有以下几类:轴向包围盒AABB(axis-aligned bounding boxes)、包围球(sphere)、方向包围盒OBB等,图 2所示为不同包围盒的二维构造效果图。

|
Download:
|
| 图 2 不同包围盒的构造 Fig. 2 The structure of the different bounding boxes | |
在图 2中,三角形代表物体,包围着三角形的各种图形代表包围盒,可以看出单个包围盒虽然可以起到替代复杂模型的效果,但是在包围盒和模型间还留有空隙,所以利用单个包围盒实现的碰撞检测算法一般不够精确。不同于单个包围盒,层次包围盒是在单个包围盒的基础上通过构造树状结构生成多个包围盒来进行相交测试的一种方法,该方法能够提高检测的精确度。
文中采用的是OBB包围盒来与质点转换法相结合,因为OBB包围盒是根据物体本身来决定盒子的大小和方向,能够随着物体的方向转动,这样就可以选择最合适最紧凑的包围盒。
传统的OBB包围盒构建方法根据物体表面的顶点,通过主成分分析(principal component analysis,PCA)获得特征向量,通过特征向量来确定OBB的主轴最后构建一个OBB包围盒。
首先构建一个协方差矩阵:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm cov}} \left( {x, x} \right)}&{{\mathop{\rm cov}} \left( {x, y} \right)}&{{\mathop{\rm cov}} \left( {x, z} \right)}\\ {{\mathop{\rm cov}} \left( {x, y} \right)}&{{\mathop{\rm cov}} \left( {y, y} \right)}&{{\mathop{\rm cov}} \left( {y, z} \right)}\\ {{\mathop{\rm cov}} \left( {x, z} \right)}&{{\mathop{\rm cov}} \left( {y, z} \right)}&{{\mathop{\rm cov}} \left( {z, z} \right)} \end{array}} \right] $ | (1) |
式中cov(xi, xj)=E[(xi-ui)(xj-uj)]为协方差计算公式。
在式(1)中协方差矩阵A的特征向量可以表示OBB包围盒的方向。而大的特征值对应大的方差,所以让OBB包围盒沿着最大特征值对应的特征向量的方向,这样就得到包围盒的坐标轴,然后再根据包围盒的中心点,构造出一个OBB包围盒。
然后在传统OBB包围盒法的基础上利用文献[15]中提出的区域中心法来构建包围盒,该方法把物体划分为表面积相似的数个区域,分别计算每个区域的中心坐标,再求这几个区域中心坐标的平均值,根据得到的中心坐标利用传统OBB包围盒构建方法就可以得到一个更加紧密的OBB包围盒。
通过上述方法能够构建一个完整的OBB包围盒,然后利用二叉树原理,采用自顶向下的方法构建一个OBB包围盒树,具体步骤:首先通过计算对物体构建整体的外层包围盒模型,然后再通过递归形式构建子包围盒,根据需求一层层建立,直到终端节点,形成一个树状结构。二叉树的原理如图 3所示。

|
Download:
|
| 图 3 二叉树原理图 Fig. 3 Binary tree | |
图 3中可以看出二叉树每个父节点最多有2个子节点,据此原理每层能够构建2个子包围盒,通过层层构建OBB包围盒使其成为OBB包围盒树,二维构建过程展示如图 4所示。

|
Download:
|
| 图 4 包围盒构建图 Fig. 4 The structure of hierarchical bounding box | |
图 4为通过二叉树原理在二维空间中展示的OBB包围盒树的构建原理,图 4(a)中1为外层整体包围盒,图 4(b)中2和3为第一层子包围盒,图 4(c)中4、5、6、7为第二层子包围盒,而根据物体的复杂度也可以构建不同层数的子包围盒,虽然构造的层数越多,检测精度就越准确,但是相应的检测效率就会降低。
2.2 质点转换在物理学中如果物体大小相对研究对象较小或影响不大,可以把物体看作质点。因此文中提出的质点转换也借用此概念,当两物体间隔一定距离,对包围盒的相交测试基本无影响时,利用质点转换的公式将包围盒看成是一个空间中的点来进行计算,只有两物体之间将要进行包围盒相交测试时才从点还原为包围盒。
首先根据上一节所述原理对物体构建OBB层次包围盒,然后选择空间中相同大小包围盒数相对较多的物体将其构建的包围盒定义为单位包围盒,并将类物体命名为单位物体,最后进行质点转换,设包围盒质点转换系数s为单位包围盒边长,o(xi, yi, zi)为包围盒中点坐标,根据包围盒质点转换公式就可以确定点的位置。
包围盒质点转换公式为
| $ {x_j} = \frac{{{x_i}}}{s} $ | (2) |
| $ {y_j} = \frac{{{y_i}}}{s} $ | (3) |
| $ {z_j} = \frac{{{z_i}}}{s} $ | (4) |
式中:xj为点在空间中x轴坐标,yj为点在空间中y轴坐标,zj为点在空间z轴坐标,所以物体包围盒转换为点后坐标为q(xj, yj, zj),三维空间也看成由V/s3个点构成的空间,其中V为三维空间的大小。
以上为三维空间中质点转换的原理,二维空间与三维空间原理相同,如图 5就是用二维平面来表示的质点转换图。

|
Download:
|
| 图 5 质点转换图 Fig. 5 Particle conversion | |
图 5中表示的在二维空间中截取的一个面的质点转换形式。而根据质点转换公式可知图中转换前空间大小是转换后空间大小的s2倍,如果把单位包围盒转换的点当作一个单位点,那么质点转换后的空间可以看作一个由16个单位点组成的面,图中一个格子代表一个点,其中白色的格子为假想的点,黑色的格子代表物体包围盒转换的真正的质点。
2.3 质点还原根据质点转换的思想可知,质点转换须在包围盒与包围盒间隔一定距离的情况下才能成立的。而这个距离则是两个物体包围盒不相交时的间距,所以只要保持两物体外层包围盒不相交,就能把包围盒转换为点。
质点还原成包围盒则是在两外层包围盒将要相交时的情况下进行的,所以只要确定两包围盒将要相交时的距离就能把点还原成包围盒继续碰撞检测。但是如果是在两外层包围盒刚要相交时还原质点则有可能出现一定的误差,此时包围盒之间可能已经产生了一定的穿透现象。所以要在两点间选定一个距离值,通过在该距离值上还原质点,既不会影响检测效率,也不会使包围盒间发生穿透现象,将这个距离定义为还原距离,还原距离的确定是通过还原距离计算公式来得到的,首先假设两物体外层包围盒的中点分别为o1(xi1, yi1, zi1),o2(xi2, yi2, zi2),顶点为a1(xia1, yia1, zia1)和a2(xia2, yia2, zia2)然后利用还原距离计算公式计算具体的还原距离。
还原距离计算公式为
| $ {L_{xi}} = \frac{{|{x_{{i_1}}} - {x_{i{a_1}}}{\rm{|}}}}{s} + \frac{{{\rm{|}}{x_{{i_2}}} - {x_{i{a_2}}}|}}{s} $ | (5) |
| $ {L_{yi}} = \frac{{|{y_{{i_1}}} - {y_{i{a_1}}}{\rm{|}}}}{s} + \frac{{{\rm{|}}{y_{{i_2}}} - {y_{i{a_2}}}|}}{s} $ | (6) |
| $ {L_{zi}} = \frac{{|{z_{{i_1}}} - {z_{i{a_1}}}{\rm{|}}}}{s} + \frac{{{\rm{|}}{z_{{i_2}}} - {z_{i{a_2}}}|}}{s} $ | (7) |
式中:Lxi、Lyi、Lzi分别为两物体在x轴、y轴、z轴方向上的还原距离,s为前文中所定义的转换系数。
通过上述理论能够确定还原距离,不过想要进行质点还原还需要知道两点之间的距离,通过下述方法计算两点间距离。
设两点分别为q1(xj1, yj1, zj1)、q2(xj2, yj2, zj2),那么两点间距离计算公式为
| $ {L_{xj}} = |{x_{{j_1}}} - {x_{{j_2}}}| $ | (8) |
| $ {L_{yj}} = |{y_{{j_1}}} - {y_{{j_2}}}| $ | (9) |
| $ {L_{zj}} = |{z_{{j_1}}} - {z_{{j_2}}}| $ | (10) |
式中:Lxj、Lyj、Lzj分别为两点在x轴、y轴、z轴方向上的间距。
根据得到的还原距离和质点间距离进行比较,可定义质点-包围盒还原定理:当质点在x轴、y轴、z轴方向上间距全都小于还原距离的时候,质点还原为包围盒,而当质点在x轴、y轴、z轴上距离不满足全小于还原距离时,质点不还原为包围盒,继续把包围盒看作质点进行计算。
从上述所说原理能够得出质点转换的具体步骤:
1) 选择空间中相同大小包围盒数目相对较多的物体将其包围盒定义为单位包围盒;
2) 根据选择好的单位包围盒,确定质点转换中所需的转换系数;
3) 根据确定好的转换系数,利用质点转换公式把空间中包围盒全部转换为空间中的一个点;
4) 对空间中运行的点进行还原距离的计算;
5) 对空间两点的间0距进行计算;
6) 最后通过对两点间还原距离和间距之间的比较判断该质点是否还原为包围盒。
2.4 OBB层次包围盒相交测试通过前面质点转换原理可知,质点转换只是对物体在一定距离时进行的浅层次的检测,而对于通过了质点还原的物体应该对其进行深层次的碰撞检测,对构建好的物体层次包围盒进行相交测试来精确判断是否发生碰撞。
因为文中构造的包围盒为OBB包围盒,所以选用分离轴定理来进行OBB包围盒的相交测试。该定理的定义为:如果能够有一条直线,使得包围盒A和包围盒B分别在直线的两边,则两包围盒不重叠,这条直线就被称为分离线且一定垂直于分离轴,此为二维空间中的叫法,而在三维空间中被称为分离面。以下为二维空间中OBB包围盒的分离轴定理演示,如图 6所示。

|
Download:
|
| 图 6 分离轴定理图 Fig. 6 Separation axis | |
图 6表示一个二维空间中存在A、B两个包围盒,X为分离轴,Y为分离线,T1为包围盒中点间间距,T2为T1在分离轴X上的投影,r1、r2分别为A、B包围盒在X上的投影,只要满足T2>r1+r2,则包围盒不相交。因为对于两包围盒来说只要存在一条分离轴就可判断两包围盒不相交,在三维空间中一对OBB包围盒之间最多有15条潜在的分离轴,所以最多进行15次判定,如果没有出现分离轴,那么两包围盒就是相交的,反之只要在15次判定中某一次出现分离轴,就可以直接结束判定,此时两包围盒一定不相交。
以上为两个单独OBB包围盒之间的碰撞检测原理,由于构建的是层次包围盒,所以要在单个包围盒检测的基础上,根据图 3、图 4所示的包围盒树进行遍历,即对整个包围盒树进行碰撞检测,检测图如图 7所示。

|
Download:
|
| 图 7 层次包围盒检测图 Fig. 7 Detection of hierarchical bounding boxes | |
从图 7可以看出:A1、B1分别为物体A,B的最外层包围盒,A2、A3、B2、B3分别为物体A、B的第1层子包围盒,A4、A5、A6、A7、B4、B5、B6、B7分别为物体A、B的第二层子包围盒,图 7中两物体进行层次包围盒的碰撞检测时具体步骤如下:
1) 对物体A的最外层包围盒A1和物体B的最外层包围盒B1进行分离轴定理相交测试,测试结果两包围盒相交。
2) 使A1和物体B的第一层子包围盒B2、B3进行相交测试,测试结果A1和B3相交。
3) 使A1和物体B的第一层子包围盒中的B3的子包围盒B6、B7进行相交测试,测试结果A1和B6相交,因为图中为两层子包围盒的层次包围盒所以经过三次测试确定本次碰撞的物体B的终端节点包围盒B6。
4) 根据确定的终端节点包围盒B6对物体A的层次包围盒进行遍历,首先使B6和物体A的第一层子包围盒A2、A3进行相交测试,测试结果B6和A2相交。
5) 使B6和物体A的第一层子包围盒中的A2的子包围盒A4,A5进行相交测试,测试结果B6与A5相交,那么可以确定本次碰撞的物体A的最终节点包围盒A5。
6) 通过前面相互遍历的相交测试能够知道两物体的最终节点包围盒B6和A5相交,那么就可以判定两物体发生了碰撞。
3 实验结果与分析为了验证质点转换和包围盒混合算法对检测效率的提升,选择一个一定大小的三维空间中放入一定量的四面体进行碰撞检测实验。具体的实验环境为Intel(R)Core(TM)i7-4700HQ,编译环境为VS2010,采用C++语言编写代码。
首先是碰撞检测的精度测试,通过在空间中构建两个四面体,然后利用文献[15]的区域中心法与文中改进的质点转换和包围盒混合算法分别进行碰撞检测,最后用物体显示包围盒的碰撞图与没有显示包围盒的碰撞图的对比来观察三维空间中进行的碰撞检测精度情况。
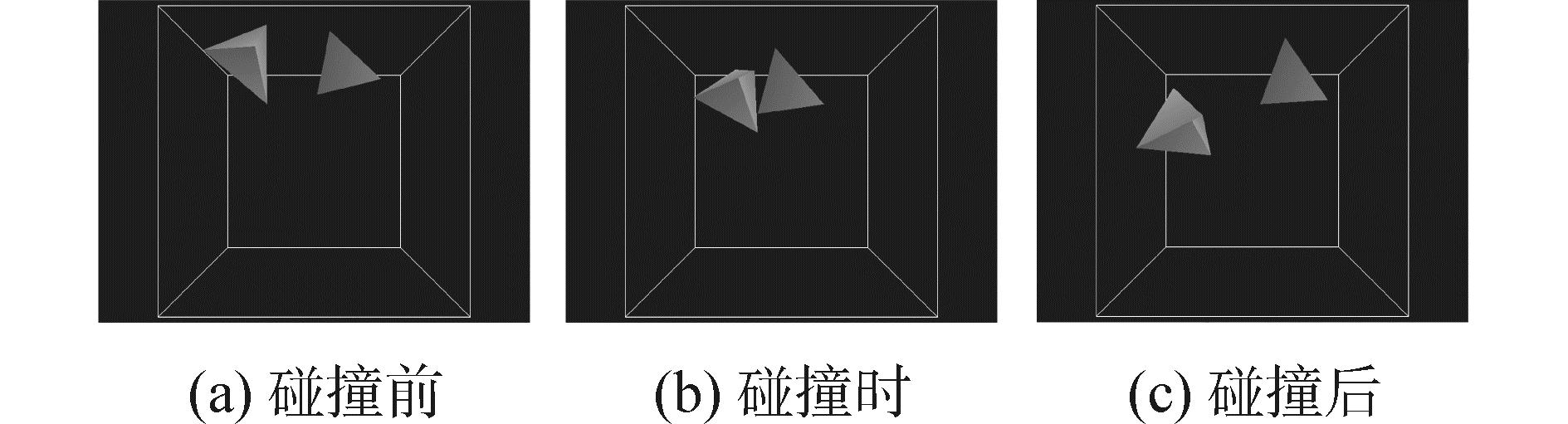
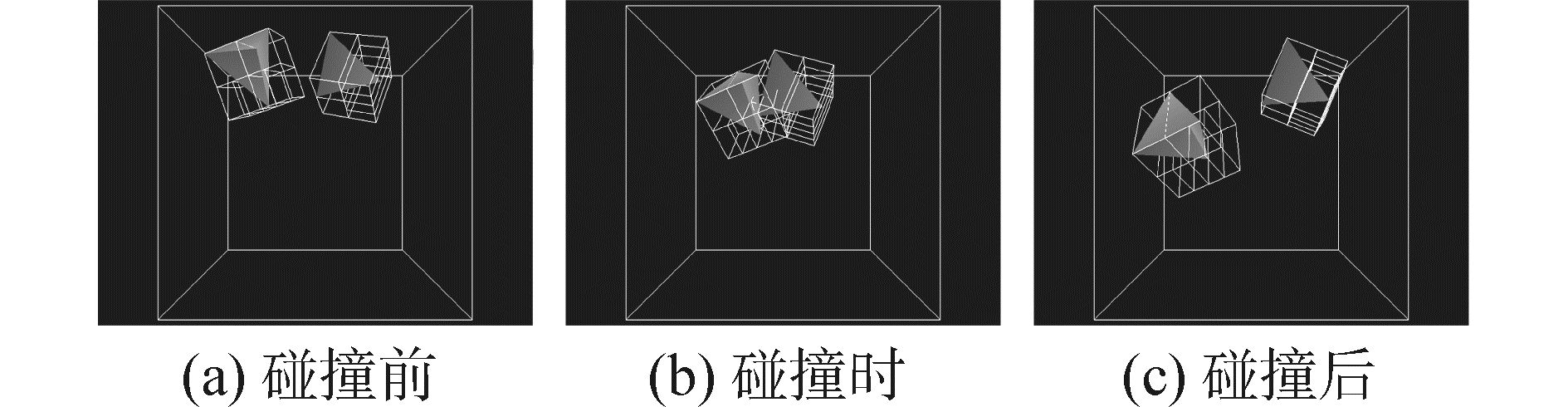
图 8与图 9分别为空间中两四面体的不显示包围盒的碰撞检测过程图和显示包围盒的碰撞检测过程图,其中图 8(a)和图 9(a)为碰撞之前的情况,图 8(b)和图 9(b)为物体碰撞时的状况,图 8(c)和图 9(c)为碰撞之后的状况。通过对两图进行对比可以清楚地看到碰撞检测的大致情况,在两物体间隔很小时碰撞检测才生效,物体根据检测结果改变运动方向,同时可以明显看出,利用文献[15]的区域中心法构建的包围盒结合改进的质点转换方法能够有效地保障碰撞检测的精度。
|
Download:
|
| 图 8 两物体碰撞图 Fig. 8 Two objects collide | |
|
Download:
|
| 图 9 显示包围盒的两物体碰撞图 Fig. 9 Two objects collide with bounding boxes | |
将两物体分别运行文献[15]的区域中心法与文中改进的质点转换和包围盒混合算法1 000步得到所花费的时间,如表 1所示。
| 表 1 两物体花费时间 Tab.1 The time consumption of two objects |
从表 1中可以看出在两物体的环境中质点转换和包围盒混合算法比文献[15]的区域中心包围盒法时间花费更少。
然后在前文两物体碰撞检测的基础上进行多物体碰撞实验,对两种算法在物体数目较多的环境中进行碰撞检测效率的对比。具体实验为:将文献[15]的区域中心法与改进的质点转换与包围盒相结合的碰撞检测算法在不同大小的三维空间中构建随机数量的四面体运行1 000步进行效率测试实验,测试出该算法花费的时间,即可知道该算法运行的效率,实验环境如图 10所示。

|
Download:
|
| 图 10 多物体碰撞图 Fig. 10 Multiple objects collide | |
图 10中的实验空间里存在30个四面体,根据前面单位包围盒的定义,定义单位包围盒边长的长度为单位长度m,那么此三维空间的体积为8 000 m3。
上述只是本文对比实验的其中一种环境条件,完整的多物体碰撞实验中存在8种不同的环境条件,即在1 000 m3空间中物体数目为10、20、30和50的环境条件和在8 000 m3空间中物体数目为10、20、30和50的环境条件,然后将两种算法在不同环境下运行1 000步得到检测花费时间来进行对比,结果如表 2和表 3所示。
| 表 2 区域中心包围盒法花费时间 Tab.2 The time consumption of region center bounding box method |
表 2为利用区域中心法生成的包围盒进行碰撞检测实验,通过对此算法在不同空间大小和不同物体数量的环境中进行多次实验,可以看出该算法在相同物体数目不同空间大小的环境下运行1 000步,花费的时间相差不大。
表 3为本文提出算法利用质点转换和包围盒混合来进行碰撞检测的实验结果,通过对该算法在不同空间大小和相同物体数目的环境下进行同样的实验,可以看出该算法随着空间大小的增加花费的时间将会减少,检测效率将会得到提高。
| 表 3 质点转换和包围盒混合算法花费时间 Tab.3 The time consumption of particle conversion and bounding box hybrid algorithm |
图 11(a)为区域中心包围盒法与质点转换和包围盒相结合的碰撞检测算法在1 000 m3空间,不同物体个数的实验环境中进行实验得到结果的对比曲线;图 11(b)为区域中心包围盒法与质点转换和包围盒相结合的碰撞检测算法在8 000 m3空间,不同物体个数的实验环境中进行实验得到结果的对比曲线。通过两算法的对比可以看出比起前人算法,在空间中物体数目较多时质点转换和包围盒相结合的碰撞检测算法花费的时间更少,检测效率更高。

|
Download:
|
| 图 11 花费时间对比曲线 Fig. 11 Curves of consumption time | |
1) 通过在传统OBB包围盒算法基础上利用区域中心法构建包围盒,然后在该包围盒的基础上与质点转换的方法相结合来进行碰撞检测,通过实验结果显示该方法能够保障检测的精度。
2) 在多物体环境中对两种算法进行了效率对比实验,通过实验结果可以看出,比起前人算法质点转换和包围盒相结合的方法能够有效地减少碰撞检测所花费的时间,检测效率更高,随着空间大小的增加检测效率还会进一步提高,特别适用于空间中存在大量物体的复杂环境。
对于质点转换和区域中心OBB包围盒法相结合来进行碰撞检测,虽然通过利用区域中心法来构建OBB包围盒能够满足一定的检测精度,但是因为质点转换的方法可以与任意包围盒相结合,所以在检测精度上还有提高的空间,下一步的工作是尝试着利用质点转换的方法与其他改进包围盒法相结合来继续提高检测的精度。
| [1] |
于凌涛, 王涛, 宋华建, 等. 面向虚拟手术的碰撞检测优化算法[J]. 哈尔滨工程大学学报, 2014, 35(9): 1164-1170. YU Lingtao, WANG Tao, SONG Huajian, et al. An optimization algorithm of collision detection applied to virtual surgery[J]. Journal of Harbin Engineering University, 2014, 35(9): 1164-1170. (  0) 0)
|
| [2] |
WONG S K, LIN W C, HUANG C H, et al. Radial view based culling for continuous self-collision detection of skeletal models[J]. ACM transactions on graphics, 2013, 32(4): Article No. 114. (  0) 0)
|
| [3] |
SCHVARTZMAN S C, PÉREZ Á G, OTADUY M A. Star-contours for efficient hierarchical self-collision detection[J]. ACM transactions on graphics, 2010, 29(4): 80. (  0) 0)
|
| [4] |
TANG Min, MANOCHA D, YOON S E, et al. VolCCD:fast continuous collision culling between deforming volume meshes[J]. ACM transactions on graphics, 2011, 30(5): 111. (  0) 0)
|
| [5] |
TANG Min, MANOCHA D, KIM Y J. Hierarchical and controlled advancement for continuous collision detection of rigid and articulated models[J]. IEEE transactions on visualization and computer graphics, 2014, 20(5): 755-766. DOI:10.1109/TVCG.2013.266 (  0) 0)
|
| [6] |
OUYANG Fan, ZHANG Tie. Octree-based spherical hierarchical model for collision detection[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation. Beijing, China, 2012: 3870-3875. http://ieeexplore.ieee.org/document/6359118/
(  0) 0)
|
| [7] |
HE Liang, ORTIZ R, ENQUOBAHRIE A, et al. Interactive continuous collision detection for topology changing models using dynamic clustering[C]//Proceedings of The 19th Symposium on Interactive 3D Graphics and Games. San Francisco, USA, 2015: 47-54. http://www.ncbi.nlm.nih.gov/pubmed/26191116
(  0) 0)
|
| [8] |
PABST S, KOCH A, STAßER W. Fast and scalable CPU/GPU collision detection for rigid and deformable surfaces[J]. Computer graphics forum, 2010, 29(5): 1605-1612. DOI:10.1111/cgf.2010.29.issue-5 (  0) 0)
|
| [9] |
WANG Huamin. Defending continuous collision detection against errors[J]. ACM transactions on graphics, 2014, 33(4): 122. (  0) 0)
|
| [10] |
BROCHU T, EDWARDS E, BRIDSON R. Efficient geometrically exact continuous collision detection[J]. ACM transactions on graphics, 2012, 31(4): 96. (  0) 0)
|
| [11] |
TANG Min, TONG Ruofeng, WANG Zhendong, et al. Fast and exact continuous collision detection with Bernstein sign classification[J]. ACM transactions on graphics, 2014, 33(6): 186. (  0) 0)
|
| [12] |
张智, 邹盛涛, 李佳桐, 等. 凸多面体碰撞检测的棱线投影分离算法[J]. 计算机辅助设计与图形学学报, 2015, 27(8): 1407-1415. ZHANG Zhi, ZOU Shengtao, LI Jiatong, et al. A collision detection algorithm between convex polyhedrons based on projection of edges[J]. Journal of computer-aided design & computer graphics, 2015, 27(8): 1407-1415. DOI:10.3969/j.issn.1003-9775.2015.08.007 (  0) 0)
|
| [13] |
林凌, 张明敏, 潘志庚, 等. 布料人体快速连续碰撞检测与响应[J]. 软件学报, 2015, 26(S2): 1-7. LIN Ling, ZHANG Mingmin, PAN Zhigeng, et al. Image based detection and response of continuous fast collision between cloth and human body[J]. Journal of software, 2015, 26(S2): 1-7. (  0) 0)
|
| [14] |
XING Dengpeng, XU De, LIU Fangfang. Collision detection for blocking cylindrical objects[C]//Proceedings of 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems. Hamburg, Germany, 2015: 4798-4803. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=7354051
(  0) 0)
|
| [15] |
史旭升, 乔立红, 朱作为. 基于改进OBB包围盒的碰撞检测算法[J]. 湖南大学学报(自然科学版), 2014, 41(5): 26-31. SHI Xusheng, QIAO Lihong, ZHU Zuowei. Algorithm of collision detection based on improved oriented bounding box[J]. Journal of Hunan University (natural sciences), 2014, 41(5): 26-31. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


