配准技术是当今数字化检测领域的一项关键技术,是实现零件检测、模型评估、误差分析以及数据拼合等的前提条件,最早出现于医疗诊断和图像处理领域[1],目前已广泛应用于逆向工程[2]、虚拟现实[3]、机器人[4]和柔性装配[5]等领域。配准技术已成为三维模型空间分析领域的研究热点问题之一。
模型配准分为刚性配准和非刚性配准。刚性配准是计算三维空间下的刚性变换(如旋转和平移),可以看成两个输入对象在三维刚性变换作用下的匹配问题。刚性配准需要求解的参数简单,相对而言比较容易计算,可用于零件的检验。而非刚性配准是一个非常复杂的问题,需要具体分析每个模型局部的姿态变化,是一种局部与局部之间的匹配问题。解决这一问题的关键:一方面如何准确区分开模型间姿态相同和不同的部分,以确保不对相同部分进行变换,对不相同的部分进行非刚性变形;另一方面,如何计算非刚性变形是复杂的非线性问题,这是因为该变形中的局部旋转变换的计算本身就是非线性的。此外,计算出的非刚性变形过程应该是自然的,不产生畸变,这样才能使得模拟变形过程与真实动态对象的演化过程相一致。
一直以来,国内外研究者不断尝试提出各种非刚性配准的方法。Gelfand等[6]从空间嵌入式变形框架中得到启发提出了一种对应关系优化引导变形的非刚性变形方法,在两模型间建立对应关系时,通过对应点对间的测地距离和法向量的差别赋予不同的权值,自动优化对应关系。算法以对应关系引导变形,在求解变形参数的同时更新对应关系,最终将源模型与目标模型完全对齐配准。文献[7]不用建立显式的对应关系,而是对每一帧模型的点云数据加入时间坐标,并将这些数据拼接在同一坐标系下。与两个模型间的配准不同,这种算法是将一组帧模型两两分别配准再统一在同一坐标系下,计算在时间维度下最终的配准结果。Sumner等[8]提出了基于单点仿射变换的非刚性配准方法,不需要计算显性的对应关系,但是该方法的解是一个病态问题,且要求模型表面变形较小。李俊等[9]提出了具有鲁棒性的面向大尺度变形的非刚性配准方法,但是这种方法需要设定标记点并计算模型间显性对应关系,由对应关系引导非刚性变形,对应关系的正确与否会直接影响两模型的配准结果,如果出现模型的对称性影响对应关系计算的问题,则会导致很大的配准误差。
此外,还有很多学者改进了迭代最近点(iterative closest point,ICP)算法并实现了非刚性配准。文献[10]介绍了一种针对变形的大脑皮层表面的配准方法。首先,将得到的大脑皮层表面信息进行手动分割,然后利用Hessian矩阵从表面信息中得到大脑皮层的脑沟分布指数(sulcal distribution index,SDI),根据SDI变形程度再采用ICP算法逐点移动,达到完全对齐配准大脑表面皮层的目标,实验证明这种方法对于新生儿的大脑皮层表面配准效果非常好。文献[11]提出了一种递归配准两个形状不同但数量相同的点云的方法,充分利用点云中每一个点的表面空间信息(如法向量和曲率),以及点云集合三维结构信息之间的关联确定两个点云集合之间的变形关系,即根据对应点对之间表面法向和曲率的变换确定需要变形的点,逐点移动调整实现对齐配准。文献[12]针对三维脸模型的非刚性配准问题,首先将源模型和目标模型都通过标记点跟踪的方式映射到平面上,在二维平面上利用图像的非刚性配准方法对二维空间中的模型进行非刚性配准,然后再通过标记点确定三维空间中变形后的模型,完成配准。文献[13]针对ICP算法对于初始值的敏感性以及整体与部分模型的配准精确度两方面进行了研究。首先采用PCA算法对模型进行初始配准;然后用KD-tree进行最近点搜索提高搜索速度;最后执行三维目标重合度检测算法进一步调整模型姿态。该算法利用自适应最优阈值优化ICP算法,提高模型配准的准确度。虽然ICP算法对于刚性配准效果好,但是用于非刚性配准只局限于小尺度变形的模型间的配准,比如面部不同表情间的配准,或者简单的曲面配准。当模型姿态差异较大时,尤其对于部分与整体模型间的配准,已有的基于ICP的算法只是对模型进行整体移动和旋转,没有对模型进行局部—局部的配准,导致配准误差较大,因此,对于较大尺度变形的模型配准不具有实用性。
综上所述,目前的方法大都是针对两个完整模型间的非刚性配准,对姿态不同的整体与部分模型间的配准精度不高;此外,能够配准较大尺度变形的模型的方法需要建立显式对应关系,否则无法完成配准。本文针对这些问题提出了一种基于骨架子空间变形和Laplace网格变形技术的、并且能够用于较大尺度变形的模型间的配准方法。该方法不需要建立显性的对应关系,同时适用于姿态不同的两个完整模型,或整体与部分模型间的配准。
1 模型配准算法 1.1 ICP算法迭代最近点算法[14]是Besl和Mckay在1992年提出来的,由于其操作简单和良好的配准效果而广泛应用于各领域的配准问题。ICP算法的基本原理是利用最小二乘的优化思想,计算当函数值最小时的旋转变换矩阵R和平移变换矩阵T,即源模型和目标模型点集之间的配准矩阵:
| $ g\left( {\mathit{\boldsymbol{R}}, \mathit{\boldsymbol{T}}} \right) = \mathop \sum \limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{Q}}_i} - (\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_i} + \mathit{\boldsymbol{T}})} \right\|^2} $ | (1) |
式中:Pi为源模型点集的初始坐标矩阵,Qi为目标模型点集中与Pi对应的最近点,R为3×3的旋转变换矩阵;T为3×1的平移变换矩阵。g(R, T)表示源模型经过旋转和平移变换之后,其点集中每一个顶点与目标模型点集中的对应顶点之间距离的平方和。当函数g(R, T)达到最小时,即满足了最小二乘的要求,得到了所需的矩阵R和T。
本文在经典ICP算法的基础上,加入了缩放变换,以便于配准大小不同的两个模型,缩放变换矩阵的计算参照文献[13];并且加入了自适应最优阈值来优化原始算法,即给定不同的阈值执行ICP算法,其中误差最小时对应的阈值为最优阈值,此阈值下的配准结果为最佳配准结果,提高了经典ICP算法的配准精确度,并且可用于整体与部分模型间的配准。
通过ICP算法的旋转和平移变换将两模型放置同一位置,使源模型与目标模型中姿态没有变化的部分能够最大程度地对齐,为下一步的Laplace网格变形过程提供必要的准备。
1.2 骨架子空间变形非刚性变形的方法主要分为两类:一类是基于插值重构思想的方法,如自由变形技术,骨架变形技术,多分辨技术等,这种方法方便高效且实用,但容易丢失模型细节;另一类是能量优化方法,如Laplace网格变形,泊松变形等,该方法能够保留模型表面信息,但需要人为设定控制点。
在执行ICP算法将两模型放置同一位置后,需要计算Laplace网格变形所需要的控制点在移动前和移动后的坐标。由于变形前的控制点坐标已知,因此本文采用骨架子空间变形技术(skeleton subspace deformation,SSD)[15]自动获取变形后的控制点坐标。
一般情况下,使用骨架子空间变形技术对模型进行变形前,需要简化网格模型得到变形所需的坐标点,然而本文算法对源模型表面网格变形的精度要求非常高,要与目标模型尽可能完全配准,而简化后的模型对齐性能反而更差,所以本文改进了骨架子空间变形技术,去掉了网格简化这一步骤。在执行ICP算法之后,直接扫描两模型间的对应点对,根据对应点对间的误差得到需要移动的控制点,这些点的移动方向即为源模型整体骨架的移动方向。
骨架子空间变形技术的基本过程为:选取适当的方法设定权值系数Wij,使
| $ - \mathit{\boldsymbol{L}}{w_j} + \mathit{\boldsymbol{D}}{w_j} = \mathit{\boldsymbol{D}}{p_j} $ | (2) |
| $ {D_{ii}} = 1/{d_i}^2 $ | (3) |
| $ {p_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1, }&{\left\| {{\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{s}}_j}} \right\| = \mathop {\min }\limits_{k \in \left[ {1, \cdots , m} \right]} (\left\| {{\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{s}}_k}} \right\|)}\\ {0, }&{其他} \end{array}} \right. $ | (4) |
式中:i∈[1, n],j∈[1, m],L为Laplace算子,di是源模型上需要移动的顶点vi到目标模型的最小距离,D为i×i的对角矩阵。
1.3 Laplace网格变形通过上述的方法可以将两模型通过刚性变形放置于同一位置,并通过骨架子空间变形技术计算非刚性变形所需要的控制点,接下来需要对模型进行非刚性变形,所以本文采用Laplace网格变形技术实现模型的最终精确匹配。
2004年,Sorkine等[16]将微分域坐标引入图像处理,由于其能够使变形后的图像保持内容的完整性、连贯性和光滑度,于是2005年,Igarash等[17]提出可以将微分域坐标推广到三维数据,用来处理三维模型,并从理论上论述了该想法的可行性。Sorkine等[18]受文献[17]算法的启发,成功将微分域融入模型表面的三角网格的处理中,这种算法可以保留模型的表面信息(如曲率,法向量等),使模型表面始终保持光滑,并逐渐成为常用的网格编辑算法,即Laplace网格变形。文中对源模型应用Laplace网格变形,并使其与目标模型完全对齐。
1.3.1 Laplace-Beltrami算子Laplace-Beltrami算子[19]是定义在黎曼流形上的二阶微分算子,是在欧式空间中的Laplace算子的一种推广,本质上描述了空间中某点坐标值与其邻域坐标均值差异这一特征。
在实际应用中,三维模型通常使用网格或者点云的形式进行离散化表示,相应地,常需要Laplace-Beltrami算子的离散化形式。假设S⊂R3是一个2D流形曲面,f:R2→R3是S的参数化形式,则等式Δsf=2Hn成立,此处H表示此流形曲面的平均曲率,n表示曲面法向量,那么对于一点p来说,此公式可写为
| $ {\mathit{\Delta }_s}p = 2{H_p}{\mathit{\boldsymbol{n}}_p} $ | (5) |
式中:Δsp表示点p处的Laplace-Beltrami算子,Hp表示点p处的平均曲率,np表示点p处的单位法向量,Hpnp即是平均曲率法向算子,所以Δs内蕴含了模型表面的几何特征信息。假定M=(V, E, F)表示给定的三角形网格模型,顶点个数为n,V表示顶点集合,E表示边集合,F表示曲面片集合,N(i)={j|(i, j)δiE}表示与第i个点相邻的顶点集合。于是,定义δi为vi的离散化Laplace算子:
| $ {\delta _i}(\delta _i^x, \delta _i^y, \delta _i^z) = \mathop \sum \limits_{j = N\left( i \right)} {\mathit{\boldsymbol{w}}_{ij}}({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}_j}) $ | (6) |
| $ {w_{ij}} = \frac{{{\omega _{ij}}}}{{\mathop \sum \limits_{\left( {i, k} \right) \in E} {\omega _{ik}}}} $ | (7) |
对于权重的设定,有以下两种选择:
1) ωij=1,表示均匀权重,则Laplace算子
| $ {\delta _i} = \frac{1}{{{d_i}}}\mathop \sum \limits_{j \in N\left( i \right)} ({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}_j}) $ | (8) |
一般称被为均匀Laplace算子[20],可以看作是曲线积分的离散化。在微分几何中有
| $ \mathop {\lim }\limits_{\left| \gamma \right| \to 0} \frac{1}{{\left| \gamma \right|}}{\smallint _{v \in \gamma }}({\mathit{\boldsymbol{v}}_i} - \mathit{\boldsymbol{v}}){\rm{d}}l\left( \mathit{\boldsymbol{v}} \right) = H({\mathit{\boldsymbol{v}}_i}){\mathit{\boldsymbol{n}}_i} $ | (9) |
式中:γ表示曲面上环绕vi的封闭曲线,|γ|表示γ的长度,H(vi)表示顶点vi的平均曲率,ni表示顶点vi处的曲面法向量。因此,δ的方向可以近似表征曲面法向量方向,微分坐标δ表示为vi的绝对坐标与其邻接点的中心之差
2) ωij=cotα+cotβ,表示余切权重。2003年Meyer等[21]提出了用余切权重代替均匀权重,产生了Cotangent Laplace算子:
| $ {\delta _i} = \mathop \sum \limits_{j \in N\left( i \right)} \left( {\cot \alpha + \cot \beta } \right)({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}_j}) $ | (10) |
Cotangent Laplace算子是Laplace-Beltrami算子与模型表面几何信息相结合的一种Laplace-Beltrami算子的离散化形式,能够更好地逼近曲面的局部特征。
1.3.2 Laplace网格变形Laplace网格变形技术[22]由Alexa提出的,已成为目前流行的能量优化类的网格变形算法。
定义M=(V, E, F)为有|V|个顶点的三角网格,其中V、E、F分别表示顶点、边、面的集合。由上述均匀Laplace算子可知,顶点vi的Laplace坐标(也称为δ坐标、微分坐标)可以表示为vi的绝对坐标与其邻接点的中心之差:
| $ {\delta _i} = (\delta _i^{\left( x \right)}, \delta _i^{\left( y \right)}, \delta _i^{\left( z \right)}) = {\mathit{\boldsymbol{v}}_i} - \frac{1}{d}\mathop \sum \limits_{j \in N\left( i \right)} {\mathit{\boldsymbol{v}}_j} $ | (11) |
式中:N(i)={j| (i, j)δE},di=|N(i)|为vi的度,即与vi相邻顶点的个数。
设V为模型顶点的笛卡尔坐标矩阵,δ为模型顶点的Laplace坐标矩阵,在变形前需要将模型的笛卡尔坐标矩阵转化为Laplace坐标矩阵。已知笛卡尔坐标系与Laplace坐标系之间的线性变换可以表示为矩阵形式:δ=LV,其中L为Laplace算子,是笛卡尔坐标与Laplace坐标之间的转换矩阵,可以表示为L=1-D-1A。式中I为单位矩阵,D为对角矩阵(Dii=di),A为连接矩阵。
| $ {A_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1, }&{\left( {i, j} \right) \in E}\\ {0, }&{其他} \end{array}} \right. $ | (12) |
设由k个控制点cj组成的控制点集合为C,即cj∈C, j∈[1, k],作为模型变形的参考点,同时也作为方程的约束条件。求解线性系统:
| $ \left( {\frac{\mathit{\boldsymbol{L}}}{{\omega {\mathit{\boldsymbol{I}}_{k \times k}}~|~0}}} \right)V = \left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\delta }}\\ {\omega {c_{1:k}}} \end{array}} \right) $ | (13) |
将式(13)中系统矩阵用
| $ \mathit{\boldsymbol{V}}' = \arg \min ({\left\| {\mathit{\boldsymbol{LV}} - \mathit{\boldsymbol{\delta }}} \right\|^2} + \mathop \sum \limits_{j \in C} {\omega ^2}|{v_j} - {c_j}{|^2}) $ | (14) |
V'是变形后网格上顶点的新的笛卡尔坐标值。此最小二乘解的解析解可以表示为:
| $ V' = {({\mathit{\boldsymbol{L}}^{'{\rm{T}}}}\mathit{\boldsymbol{L}}')^{ - 1}}{\mathit{\boldsymbol{L}}^{'{\rm{T}}}}\mathit{\boldsymbol{b}} $ | (15) |
式中b=[δ, ωc1, …, ωck]T。
1.4 模型配准针对非刚性变形的模型间配准问题,提出了一种结合骨架子空间变形技术和Laplace网格变形技术的配准方法。具体步骤如下:
1) 采用改进的ICP算法,将两模型放置于同一位置,使模型姿态相同的部分完全对齐。
2) 根据执行完ICP算法后对应点对的位置误差确定执行骨架子空间变形技术所需的顶点坐标vi,并计算这些顶点在变形后的坐标
3) 将vi作为执行Laplace网格变形的控制点,由于vi被移动后的坐标为,则式(13)方程组右边向量约束条件为ci=v'i。求解式(13),可得到变形后除控制点外其他顶点的笛卡尔坐标。
2 实验结果与分析本文算法采用Matlab编程实现。总共完成了6组实验,如图 1~6所示,其中图 1~3是姿态不同的两个完整模型间的配准,图 4~6是姿态不同的整体与部分模型间的配准。

|
Download:
|
| 图 1 两个人体模型的配准结果与迭代误差 Fig. 1 The registration results and iterative error of two human models | |
|
Download:
|
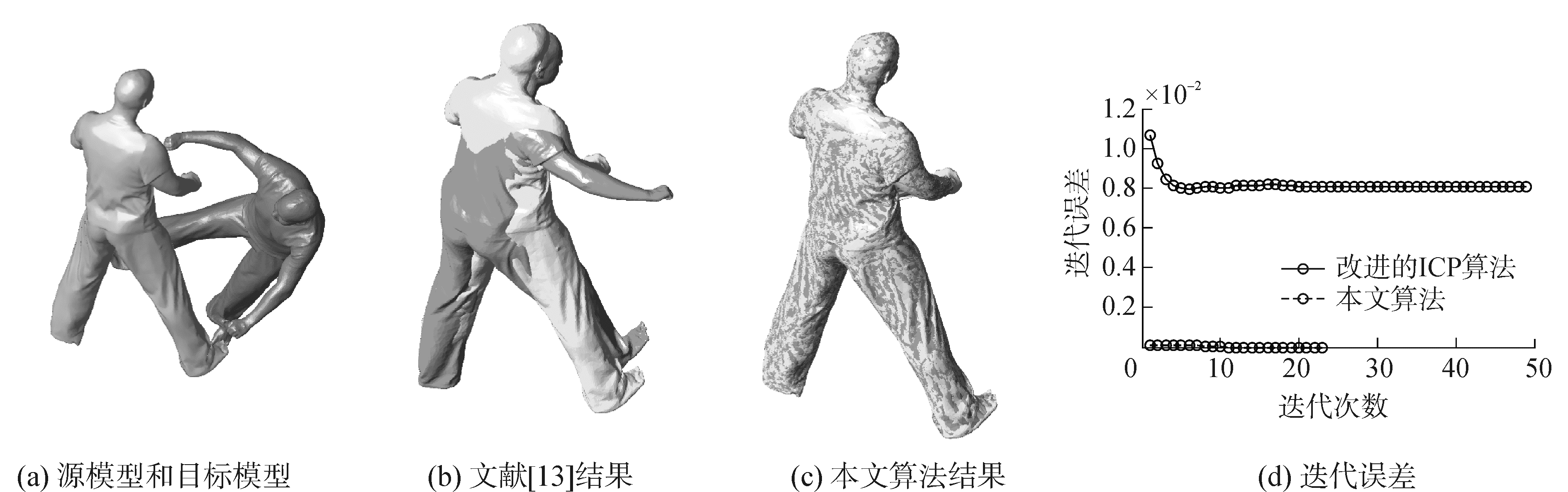
| 图 2 穿衣服的两个人体模型的配准结果和迭代误差 Fig. 2 The registration results and iterative error of two human models wearing clothes | |

|
Download:
|
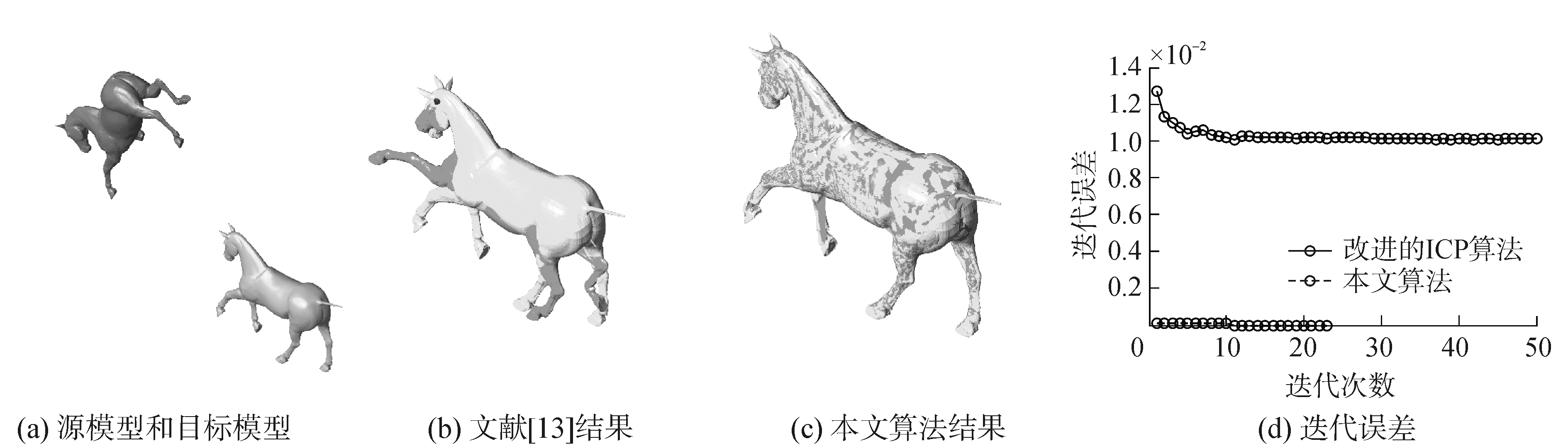
| 图 3 两个马模型的配准结果和迭代误差 Fig. 3 The registration results and iterative error of two horse models | |
|
Download:
|
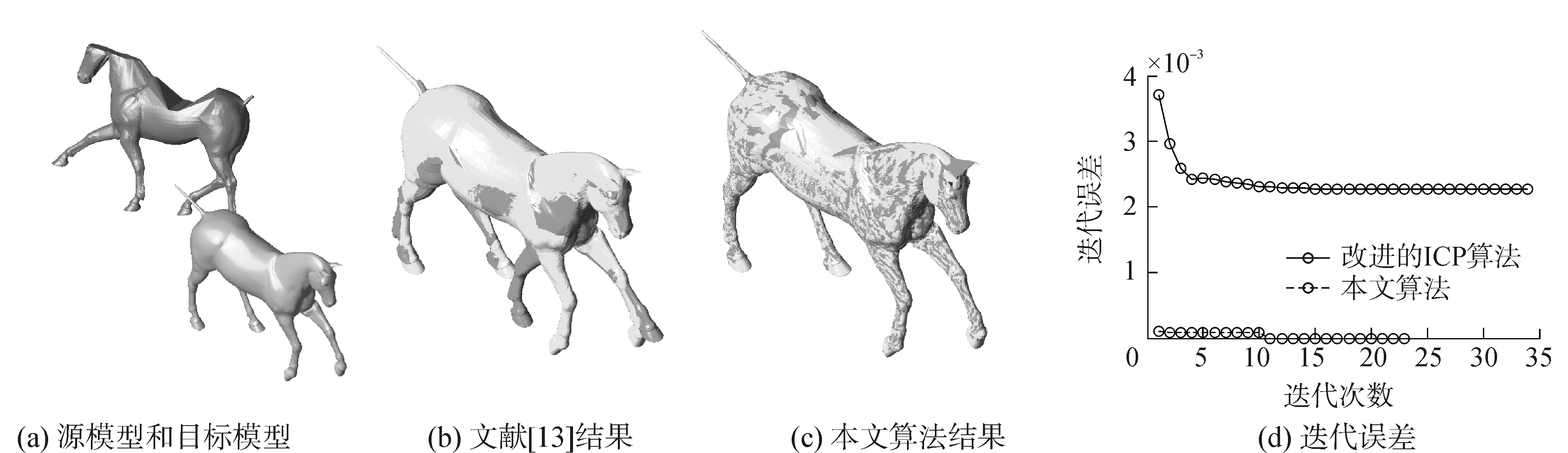
| 图 4 完整与部分(缺少一条腿)马模型的配准结果和迭代误差 Fig. 4 The registration results and iterative error of the horse models(complete horse model vs horse model lacking of right foreleg) | |
|
Download:
|
| 图 5 完整与部分(缺少部分背部)马模型的配准 Fig. 5 The registration results and iterative error of the horse models(complete horse model vs horse model lacking of partial back) | |

|
Download:
|
| 图 6 穿衣服的完整与部分(缺少右臂)人体模型的配准结果和迭代误差 Fig. 6 The registration results and iterative error of two human models wearing clothes(complete human model vs human model lacking of right arm) | |
图 1是两个完整的人体模型间的配准结果和迭代误差图,从文献[13]算法的配准结果图中很明显地观察到两模型在胳膊和腿部都有形变,如图 1(b)所示,而本文算法通过Laplace网格变形技术使源模型的胳膊和腿部发生形变,最终基本完全配准两模型,如图 1(c)所示。从迭代误差图中可以看出执行文献[13]算法后,由于两模型姿态不同导致误差始终较高,而执行本文算法后两模型间误差相对于文献[13]明显降低,如图 1(d)所示,主要是因为文献[13]的算法是对模型整体移动和旋转,属于刚性变形,没有对模型进行局部—局部的配准,而本文中所有的模型组别都是非刚性变形的,非刚性配准是一种局部—局部的匹配问题。图 2是两个姿态不同的穿衣服的完整人体模型的配准结果,从文献[13]算法的配准结果可以很明显地看出源模型与目标模型在整个上半身都有很大的形变,如图 2(b)所示,而本文算法先采用改进的ICP算法将两模型通过旋转和平移放置于同一位置,然后执行Laplace网格变形技术使源模型发生形变,并使源模型与目标模型接近完全重合,如图 2(c)所示。迭代误差实验结果表明,执行本文算法后,源模型与目标模型间的误差与文献[13]相比大大降低,如图 2(d)所示。然而,与图 1的配准结果相比,图 2人体模型的右胳膊处匹配结果仍然不够精准,这是因为这组模型有衣服的皱褶,模型点集数目的增加会使配准的速度和准确度受到影响,但是本文算法仍然基本配准了两模型。图 3是两个完整的马模型的配准结果,这组模型的变形主要在马的四肢,头部和背部,从配准结果图和迭代误差图可看出本文算法可以完全配准两模型。
图 4~6的三组实验是姿态不同的整体与部分模型的配准结果和迭代误差比较。图 4和图 5是两个马模型配准结果,其中图 4中的源模型比目标模型少了右前腿,在马的四肢和头部有形变。由配准结果可以看出,即使源模型相对于目标模型缺少某些部件,本文算法依然可以配准两模型,迭代误差相较于文献[13]较低。图 5中源模型背部缺少了很大一部分,并在前腿和背部有较大形变,实验结果表明本文算法完全可以配准两模型,配准后两模型间误差趋于0。图 6是两个穿衣服的人体模型的配准结果,源模型少了右胳膊,文献[13]的实验结果可以看出两人体模型的整个身体都有很大的形变,而本文算法有形变的部分能够基本配准,迭代误差比文献[13]的算法有明显降低。
3 结论1) 本文所提出的结合骨架子空间变形技术和Laplace网格变形的非刚性三维模型配准算法既可以配准姿态不同的两个完整模型,也可以配准姿态不同的整体与部分模型(缺少某个部件或带有孔洞的模型)。此外,本算法还可以构建两个模型间的稠密对应关系。
2) 在实验中发现如果只是简单地移动位置相差比较大的点,没有保留模型表面的信息(如法向量、曲率等),形变后模型表面会有毛刺现象,但通过骨架子空间变形技术得到控制点,结合Laplace网格变形算法可以保留模型表面的基本信息,确保模型表面的光滑性。然而,由于本算法对配准精度要求比较高,只能设置大量的控制点来克服弯曲、毛刺或者锯齿等缺陷,操作繁琐,运行时间比较长。能够把模型简化再进行非刚性配准以提高配准速度的同时还要确保配准的精确度是未来研究的方向。
| [1] |
ZHANG Jing, YAN C H, CHUI C K, et al. Multimodal image registration system for image-guided orthopaedic surgery[J]. Machine vision and applications, 2011, 22(5): 851-863. DOI:10.1007/s00138-010-0302-z (  0) 0)
|
| [2] |
KIM E, GORDONOV T, LIU Y, et al. Reverse engineering to suggest biologically relevant redox activities of phenolic materials[J]. ACS chemical biology, 2013, 8(4): 716-724. DOI:10.1021/cb300605s (  0) 0)
|
| [3] |
MOGLIA A, FERRAR V, MORELLI L, et al. A systematic review of virtual reality simulators for robot-assisted surgery[J]. European urology, 2016, 69(6): 1065-1080. DOI:10.1016/j.eururo.2015.09.021 (  0) 0)
|
| [4] |
ZHANG Dongwen, LI Zhicheng, CHEN Ken, et al. An optical tracker based robot registration and servoing method for ultrasound guided percutaneous renal access[J]. Biomedical engineering online, 2013, 12: 47. DOI:10.1186/1475-925X-12-47 (  0) 0)
|
| [5] |
FINETTO C, ROSATI G, FACCIO M, et al. Implementation framework for a fully flexible assembly system (F-FAS)[J]. Assembly automation, 2015, 35(1): 114-121. DOI:10.1108/AA-03-2014-022 (  0) 0)
|
| [6] |
GELFAND N, MITRA N J, GUIBAS L J, et al. Robust global registration[C]//Proceedings of the 3th Eurographics Symposium on Geometry Processing. Switzerland, 2005: 197-206. http://dl.acm.org/citation.cfm?id=1281953
(  0) 0)
|
| [7] |
MITRA N J, FLORY S, OVSJANIKOV M, et al. Dynamic geometry registration[C]//Proceedings of the 5th Eurographics Symposium on Geometry Processing. Switzerland, 2007: 172-182. http://dl.acm.org/citation.cfm?id=1281991.1282015
(  0) 0)
|
| [8] |
LI Hao, SUMNER R W, PAULY M. Global correspondence optimization for non-rigid registration of depth scans[J]. Computer graphics forum, 2008, 27(5): 1421-1430. DOI:10.1111/cgf.2008.27.issue-5 (  0) 0)
|
| [9] |
李俊, 程志全, 李宏华, 等. 一种面向大尺度变形的非刚性注册算法[J]. 计算机学报, 2011, 34(3): 539-547. LI Jun, CHENG Zhiquan, LI Honghua, et al. A non-rigid registration algorithm of large-scale deformable models[J]. Chinese journal of computers, 2011, 34(3): 539-547. (  0) 0)
|
| [10] |
MORITA K, KOBASHI S, WAKATA Y, et al. Non-rigid cerebral surface registration for neonates using ICP algorithm[J]. Transactions of the institute of systems, control and information engineers, 2016, 29(5): 195-201. DOI:10.5687/iscie.29.195 (  0) 0)
|
| [11] |
SERAFIN J, GRISETTI G. NICP: dense normal based point cloud registration[C]//Proceedings of 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems. Hamburg, Germany, 2015: 742-749. http://ieeexplore.ieee.org/document/7353455/
(  0) 0)
|
| [12] |
CHENG Shiyang, MARRAS I, ZAFEIRIOU S, et al. Active nonrigid ICP algorithm[C]//Proceedings of 2015 11th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition. Ljubljana, Slovenia, 2015: 1-8. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7163161
(  0) 0)
|
| [13] |
杨军, 张瑶, 黄亮. 改进的ICP算法在三维模型配准中的研究[J]. 计算机科学与探索, 2018, 12(1): 153-162. YANG Jun, ZHANG Yao, HUANG Liang. Research on 3D model registration by improved ICP algorithm[J]. Journal of frontiers of computer science and technology, 2018, 12(1): 153-162. (  0) 0)
|
| [14] |
BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE transactions on pattern analysis and machine intelligence, 1992, 14(2): 239-256. DOI:10.1109/34.121791 (  0) 0)
|
| [15] |
MURAI A, ENDO Y, TADA M. Anatomographic volumetric skin-musculoskeletal model and its kinematic deformation with surface-based SSD[J]. IEEE robotics and automation letters, 2016, 1(2): 1103-1109. DOI:10.1109/LRA.2016.2524069 (  0) 0)
|
| [16] |
TAUBIN G. A signal processing approach to fair surface design[C]//Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques. New York, 1995: 351-358. http://dl.acm.org/citation.cfm?id=218473
(  0) 0)
|
| [17] |
IGARASHI T, MOSCOVICH T, HUGHES J F. As-rigid-as-possible shape manipulation[J]. ACM transactions on graphics, 2005, 24(3): 1134-1141. DOI:10.1145/1073204 (  0) 0)
|
| [18] |
SORKINE O, ALEXA M. As-rigid-as-possible surface modeling[C]//Proceedings of the 5th Eurographics Symposium on Geometry Processing. Aire-la-Ville, Switzerland, 2007: 109-116. http://dl.acm.org/citation.cfm?doid=1281991.1282006
(  0) 0)
|
| [19] |
UMEHARA M, YAMADA K. Differential geometry of curves and surfaces[J]. Undergraduate texts in mathematics, 2016, 2(4): 273-275. (  0) 0)
|
| [20] |
VODEV G. Uniform estimates of the resolvent of the laplace-beltrami operator on infinite volume riemannian manifolds with cusps[J]. Communications in partial differential equations, 2002, 27(7/8): 1437-1465. (  0) 0)
|
| [21] |
MEYER M, DESBRUN M, SCHRODER P, et al. Discrete differential-geometry operators for triangulated 2-manifolds[M]//HEGE H C, POLTHIER K. Visualization and Mathematics Ⅲ. Berlin, Heidelberg: Springer, 2003: 35-57.
(  0) 0)
|
| [22] |
ALEXA M. Differential coordinates for local mesh morphing and deformation[J]. The visual computer, 2003, 19(2/3): 105-114. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


