船舶设计领域涉及众多学科知识,其中最为重要的水动力性能就包括快速性、耐波性、操纵性、稳性、浮性等多个学科,各个学科之间相互冲突、相互矛盾,单学科性能的提升会降低其他学科的性能[1]。随着船舶面临的海洋环境越来越复杂,以及承担的任务越来越全面,迫切需要船舶水动力性能的综合优化,从而达到船舶航行多学科综合兼优的目标[2]。
船舶水动力性能优化问题(ship hydrodynamic performance optimization, SHPO)是一个非线性、非凸的多目标优化问题,且包含众多等式和不等式约束条件[3]。早期的处理方法是根据先验知识将多目标优化问题转化为单目标优化问题,然后采用传统优化方法求解,但其很难在多个目标间取得权衡,且求解精度不高。近年来,进化算法因其并行性和分布式特点,以及不需要目标函数的可导性、连续性等梯度信息,很适合解决复杂的多目标优化问题。
胡腾飞等[4]将基于进化算法的多目标优化技术引入到船舶水动力性能综合优化当中,对多目标遗传算法NSGA-Ⅱ和多目标粒子群优化算法MOPSO进行分析,为寻求适用于船舶水动力性能优化的多目标进化算法及其参数配置提供参考。Guha等[5]建立了以艏加速度和摩擦阻力为2目标的多目标优化模型,利用多目标遗传算法MOGA对这一模型进行求解,在大量船体模型上进行的仿真实验表明优化后的船体性能有了很大提升。Diez等[6]以DTMB5415船型为研究对象,建立了以耐波性和快速性为2目标的多目标优化模型,并采用NSGA-Ⅱ进行求解,优化设计结果经模型试验验证总阻力减小10%和耐波性指标提高9%。以上文献,有两方面不足:一方面都只对水动力性能中的快速性和耐波性进行理论研究,缺少对操纵性的考虑,文献[7-8]虽综合考虑了船舶水动力性能中的耐波性、快速性和操纵性多个目标,但却是加权为单目标优化问题来求解,要求决策者具有足够的先验知识且易陷入局部极值;另一方面采用的NSGA-Ⅱ和MOPSO算法求解的解集质量不是很理想,且收敛速度较慢。
对于多目标优化问题,算法的求解速度和收敛能力,一直是多目标优化领域关注的焦点。Zhang等[9]将进化算法和数学规划方法有机结合,提出了基于分解技术的多目标进化算法MOEA/D。该算法将多目标优化问题分解成多个单目标子问题,子问题间信息互享、协同优化,在提高解集质量同时提高了计算效率。目前,该算法已被成功应用到电力环境经济调度[10]、无线网络优化[11]及船型参数设计[12]等众多领域。
为此,本文将采用MOEA/D算法用于求解SHPO问题,提出基于MOEA/D的船舶水动力性能多目标优化算法。以DTMB5415为母型船,建立以快速性、耐波性和操纵性为3目标的多目标优化模型,采用改进的MOEA/D算法对船舶水动力性能进行优化,并与其他基于多目标进化算法的设计方案对比。
1 船舶水动力性能优化问题的数学模型 1.1 设计变量选取以下与水动力性能重要相关的船型参数作为设计变量:船长L(m),船宽B(m),型深D(m),吃水T(m),方形系数Cb,水线面系数Cw,船中剖面系数Cm,浮心纵向位置Lcb,航速Vs(kn),舵高hR(m),舵宽bR(m),其向量表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}{{\left[ {{x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8},{x_9},{x_{10}},{x_{11}}} \right]}^{\rm{T}}} = }\\ {{{\left[ {L,B,D,T,{C_b},{C_{\rm{w}}},{C_{\rm{m}}},{L_{{\rm{cb}}}},{V_{\rm{s}}},{h_{\rm{R}}},{b_{\rm{R}}}} \right]}^{\rm{T}}}} \end{array} $ | (1) |
对于船舶快速性的评估,本文主要考虑船体所受总阻力,计算方法采用Holtrop经验公式[13],其表达式为
| $ {R_{\rm{T}}} = {R_{\rm{F}}}\left( {1 + {k_1}} \right) + {R_{{\rm{APP}}}} + {R_{\rm{W}}} + {R_{\rm{B}}} + {R_{{\rm{TR}}}} + {R_{\rm{A}}} $ | (2) |
式中:RF为摩擦阻力,依据ITTC-1957标准计算;1+k1为船体粘性阻力形状因子;RAPP为附体阻力;RW为兴波阻力;RB为球鼻首近水面附加压阻力;RTR为方尾浸水附加压阻力;RA为船模修正阻力。
1.2.2 耐波性指标采用文献[14]提出的耐波性品级指标SR对船舶耐波性进行定量评估。对于本文研究的DTMB5415船型,经验回归公式可表示为
| $ \begin{array}{*{20}{c}} {{S_{\rm{R}}} = 8.422 + 55.182{C_{\rm{w}}} + 378.465T/L + }\\ {1.273{C_{\rm{w}}}/L - 39.3885{C_{{\rm{vp}}}}} \end{array} $ | (3) |
式中:垂向菱形系数Cvp=Cb/Cw;SR越大,耐波性越好。
1.2.3 操纵性指标传统的船舶水动力性能优化主要根据快速性和耐波性的要求设计船型参数,很少考虑操纵性指标,但其与航行的安全性密切相关[15]。因此船舶优化设计中考虑操纵性变得尤为重要,有利于进一步提高船舶的综合性能。选取回转性和直线稳定性两个指标,并参照文献[8]的权重分配将两者聚合为操纵性指标的目标函数,表达式为
| $ {M_V} = - aC' + bD' $ | (4) |
式中:a、b的取值分别为0.7和0.3;C′为直线稳定性指数,其值越大直线稳定性越好;D′为相对回转直径,其值越小则回转性越好,从而MV越小,船舶操纵性越好。
直线稳定性衡准数表达式为
| $ C' = {{N'}_{\rm{v}}}\left[ {{{Y'}_{\rm{r}}} - \left( {m' + {{\lambda '}_{11}}} \right)} \right] - {{Y'}_{\rm{v}}}{{N'}_{\rm{r}}} $ | (5) |
式中:
相对回转直径的计算采用Lyster回归公式:
| $ \begin{array}{*{20}{c}} {D' = 4.19 - 203\frac{{{C_{\rm{b}}}}}{{\left| \delta \right|}} + 47.4\frac{{{T_{{\rm{rim}}}}}}{L} - 13.0\frac{B}{L} + }\\ {\frac{{194}}{\delta } - 3.82\frac{{{h_{\rm{R}}}{b_{\rm{R}}}}}{{LT}} + 7.79\frac{{{A_{\rm{b}}}}}{{LT}}} \end{array} $ | (6) |
式中:δ为舵角,Ab为艏部浸湿面积,Trim为船舶纵倾。已知Ab=15 m2,并且不考虑纵倾。
1.3 约束条件 1.3.1 设计变量约束条件设计变量的上界和下界如表 1所示。
| 表 1 设计变量上界和下界 Tab.1 Lower and upper bound of design variables |
此外,设计变量之间还应该满足
1) 浮性约束条件:重量W等于排水量Δ,但在实际优化过程中,允许两者的相对误差ε在5%以内。
2) 初稳性约束条件:
| $ {\rm{GM}} > 0.04B $ |
| $ {\rm{GM}} = {\rm{KB}} + {\rm{BM}} - {\rm{KG}} $ |
| $ {\rm{KB}} = 0.53T $ |
| $ {\rm{BM}} = \left( {0.085{C_b} - 0.002} \right){B^2}/T{C_b} $ |
| $ {\rm{KG}} = 1 + 0.52D $ |
式中:KB为浮心高度,BM为初稳心半径,KG为重心高度。
3) 耐波性约束条件:
| $ {T_s} = 0.58\sqrt {\frac{{{B^2} + 4{\rm{K}}{{\rm{G}}^2}}}{{{\rm{GM}}}}} > 8.5\;{\rm{s}} $ |
式中Ts为横摇周期。
4) 操纵性约束条件:根据操纵性衡准规范,参照实船操纵性试验资料,对直线稳定性指数C′、相对回转直径D′约束为0.002 < C′ < 0.02,0 < D′ < 4。
2 多目标优化问题综合以上目标函数和约束条件,船舶水动力性能多目标优化模型可以描绘如下:
| $ \begin{array}{*{20}{c}} {\min \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) = {{\left( {{f_1}\left( \mathit{\boldsymbol{x}} \right),{f_2}\left( \mathit{\boldsymbol{x}} \right),{f_3}\left( \mathit{\boldsymbol{x}} \right)} \right)}^{\rm{T}}} = }\\ {{{\left( {{R_T},1/{S_{\rm{R}}},{M_{\rm{V}}}} \right)}^{\rm{T}}}}\\ {{\rm{subjectto}}{g_j}\left( \mathit{\boldsymbol{x}} \right) \ge 0,j = 1, \cdots ,J}\\ {{h_k}\left( x \right) = 0,k = 1, \cdots ,K} \end{array} $ | (7) |
式中:x=(x1, x2, …, xn)T称为决策向量;F(x)=(RT, 1/SR, MV)T称为目标向量,由于耐波性品级SR是越大越好,本文通过求其倒数转化为最小化问题。gj(x)为第j个不等式约束条件,J为不等式约束条件的个数,hk(x)为第k个等式约束条件,K为等式约束条件的个数。如果解x满足式(10)中的所有约束条件,则称x为可行解;x不完全满足式(10)中的约束条件,则称x为不可行解。
将约束条件转化成约束违反度函数,其大小称为约束违反度:
| $ {\rm{CV}}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{j = 1}^J {\left\langle {{g_j}\left( \mathit{\boldsymbol{x}} \right)} \right\rangle } + \sum\limits_{k = 1}^K {| {{h_k}\left( \mathit{\boldsymbol{x}} \right)} | } $ | (8) |
其中当α < 0时,〈α〉返回α的绝对值;当α≥0时,〈α〉返回0。值得注意的是,可行解的约束违反度CV=0,可行解的约束违反度CV=0。
以最小化问题为例,给定两个决策变量x、y∈Ω,称x Pareto支配y(
| $ \left\{ \begin{array}{l} \forall i \in \left\{ {1,2, \cdots ,m} \right\}:{f_i}\left( \mathit{\boldsymbol{x}} \right) \le {f_i}\left( \mathit{\boldsymbol{y}} \right)\\ \exists i \in \left\{ {1,2, \cdots ,m} \right\}:{f_i}\left( \mathit{\boldsymbol{x}} \right) < {f_i}\left( \mathit{\boldsymbol{y}} \right) \end{array} \right. $ | (9) |
式中m为目标函数个数。
如果不存在x∈Ω使x
MOEA/D算法通过预设一组均匀分布的权重向量并结合聚合函数方法,将多目标优化问题分解为一系列单目标子问题。每个子问题有且仅有一个不同的权重向量,在进化过程中维持相应权重向量的一个最优解,MOEA/D算法利用相邻子问题相似解间的信息对各子问题进行协同进化,这使得算法具有更低的计算复杂度和更强的搜索能力。同时,由于有均匀分布的权重向量来引导种群进化,使得解集能够均匀分布在整个目标空间。
MOEA/D算法中最核心的是分解策略,文献[9]给出了3种分解方法:加权和法、切比雪夫法和边界交集法。由于切比雪夫法对前沿面形状不敏感,且计算简单,本文采用此方法,其表达式为
| $ \min {g^{te}}\left( {\mathit{\boldsymbol{x}}\left| {\mathit{\boldsymbol{w}},{\mathit{\boldsymbol{z}}^ * }} \right.} \right) = \mathop {\max }\limits_{1 \le i \le m} \left\{ {\left| {{f_i}\left( \mathit{\boldsymbol{x}} \right) - {z_i}^ * } \right|/{\mathit{\boldsymbol{w}}_i}} \right\} $ | (10) |
式中:
MOEA/D最早提出是用以解决无约束多目标优化问题,而本文建立的优化模型包含众多非线性约束条件,使得设计空间可行域的拓扑结构异常复杂,需在MOEA/D算法中引入约束处理技术,获得位于可行域的Pareto最优解。
可行性准则[17]是目前比较行之有效的一种约束处理方法,其规则定义如下:1)两个比较的个体中一个是可行解另一个是不可行解时,可行解获胜;2)两个都是可行解时,目标函数值较优的个体获胜;3)两个都是不可行解时,约束违反度较小的个体获胜。
然而,可行性准则过分强调可行解,没有充分利用不可行解的优良信息,压缩了搜索范围,使得算法易陷入局部收敛。船舶水动力性能优化目标由于约束条件的存在而变得不连续,且约束条件将导致可行区域变得非常狭小,在进化前期大部分解都是不可行的,而可行性准则过分强调可行解,会使算法陷入局部最优,找不到更多的可行解;而在进化后期,当大部分解都是可行解时,这时则需要使种群向着可行域中的Pareto最优前沿逼近。为此,本文基于可行性准则,根据不同的进化阶段对可行解与不可行解进行自适应地评价,设计了一个动态变化的不可行度阈值ε:
| $ \begin{array}{l} \varepsilon = {\rm{C}}{{\rm{V}}_{{\rm{mean}}}} \cdot {\rm{FR}}\\ {\rm{C}}{{\rm{V}}_{{\rm{mean}}}} = \frac{1}{N}\sum\limits_{j = 1}^N {\left( {{\rm{C}}{{\rm{V}}_j}} \right)} \end{array} $ | (11) |
式中:CVmean为平均违反度,可行解比率FR=NF/N,N为种群规模。
某个体的不可行度CV只需满足小于等于阈值ε就表明个体为可行解,在进化前期由于大部分解为不可行解,CVmean值比较大,较大的ε阈值可以让优秀的不可行解参与进化,充分探索搜索空间,寻找到更多的可行解;在进化后期,大部分解为可行解时,CVmean值接近0,FR接近1,导致阈值ε接近0,加强对可行解的开发。这样就可达到对可行解与不可行解的自适应评价,使种群先在整个解空间搜索再逐步向着可行域中的Paret最优前沿逼近。
3.2.2 目标值归一化MOEA/D将多目标优化问题分解为一系列单目标子问题,在子问题对应的权重向量方向上,通过计算目标值与理想值之间的差,优化具有最大差值的那一维目标,从而在这一方向上靠近理想值,不同方向上的最优解组合成所求问题的PF。然而,SHPO问题的目标函数具有不同量纲,当采用MOEA/D算法时,目标函数总是在总阻力的方向上进化,导致最终获得的Pareto前沿并不能给决策者提供分布均匀、具有代表性的最优解。
为了消除目标函数量纲不同导致的优化效果不佳,本文对各个目标函数值进行归一化操作,计算公式如下
| $ f_i^n\left( x \right) = \frac{{{f_i}\left( x \right) - f_i^{\min }}}{{f_i^{\max } - f_i^{\min }}},i = 1,2, \cdots ,m $ | (12) |
式中:fi(x)、fin(x)分别为目标函数的原始值和归一化值,fimax、fimin分别为第i维目标函数上的最大值和最小值。值得注意的是,在本文中只对可行解集进行归一化操作,其最大最小值也是在可行解集中计算。
3.3 船舶水动力性能优化设计实现流程基于MOEA/D算法的船舶水动力性能多目标优化的具体步骤如下:
1) 初始化
① 设置实验参数,包括算法种群规模N,权重向量的邻域大小T,最大迭代次数Gmax;确定船型参数的上下限;令迭代次数t=0。
② 在决策空间里随机生成产生N个体,构成初始种群P0;计算种群P0中每个个体对应的目标函数值RT, 1/SR, MV;初始化参考点z*=[z1*, z2*, z3*]T,其中
③ 初始化权重向量{w1, w2, …, wN}。计算与第i个权重向量欧氏距离最近的T个权重向量,记其邻域为B(i)={i1, i2, …, iT},则wi1, wi2, …, wiT分别对应wi的T个相邻权重向量。
2) 进化
对种群中每一个个体,进行以下操作:
① 从B(i)中随机选取个体与xi经过遗传算子生成新解y;
② 若y的某一维分量超出船型参数的上下限,则对该分量重新赋值;
③ 计算新解的目标函数值
3) 更新
① 更新参考点:如果CV(y)=0,z=min(z, F(y));
② 目标值归一化:计算种群中可行解集每一维的最大最小值,对可行解的目标值进行归一化;
③ 更新相邻问题的解:对于每一个j∈B(i),如果y和xj均为不可行解,即CV(y)>ε, CV(xj)>ε,且CV(y) < CV(xj),则xj=y,F(xj)=F(y);如果y为可行解,xj为不可行解,即CV(y) < ε, CV(xj)>ε,则xj=y,F(xj)=F(y);如果y和xj均为可行解,即CV(y)≤ε, CV(xj)≤ε,则比较y和xj的切比雪夫聚合函数值,如果
4) 停止判据
如果t=Gmax,则停止计算。否则t=t+1,转至步骤2)。
5) 输出
输出目标值集合{F(x1), F(x2), …, F(xN)},对应的最优解集{x1, x2, …, xN}。
4 优化结果分析为验证本文提出的优化模型合理性及改进MOEA/D算法的有效性,以DTMB5415为母船型,对其进行船舶水动力性能的多目标优化。同时,在文献[4]中已验证,对船舶水动力性能优化效果较好的2种算法分别是NSGA-Ⅱ和MOPSO算法,本文将与之进行对比。所有算法程序采用MatlabR2016b编写,测试环境为:Intel Pentium、4G内存、2.6 GHz主频,win7 64位操作系统。
4.1 参数设置及评价指标MOEA/D算法的种群规模等于权重向量个数,其设置受限于分段参数H,由于每个权重向量的每一维权重都是从{0/H, 1/H, …, H/H}中不重复选取,则种群规模即权重向量的个数为N=CH+m-1m-1。设置MOEA/D算法种群规模为91(H=12),邻域大小T=20。为了保证结果的可比性,NSGA-Ⅱ和MOPSO算法的种群规模与MOEA/D算法相等。交叉算子采用模拟二进制交叉,ηc=20,交叉率为pc=1.0;变异算子采用多项式变异ηm=20,pm=1/V。算法在SHPO问题上独立运行30次,最大迭代次数Gmax=1 000。
与单目标优化问题不同,多目标优化算法得到的是一组Pareto最优解集,而不是单一的最优解。在此,采用文献[16]提出的模糊集理论定量评估Pareto解集中的每个解,并挑选最好折中解。首先,对Pareto解集中的每个解在每维目标上的满意度用模糊隶属度函数表示:
| $ {\mu _i} = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_i} \le f_i^{\min }\\ \frac{{f_i^{\max } - {f_i}}}{{f_i^{\max } - f_i^{\min }}},\;\;\;\;f_i^{\min } < {f_i} < f_i^{\max }\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_i} \ge f_i^{\max } \end{array} \right. $ | (13) |
式中:fi为解第i维目标上的函数值,fmax i、fmin i分别为解集中第i维目标上的最大和最小值。
在此基础上定义隶属函数μk表征第k个Pareto最优解最终的满意度,计算公式如下
| $ {\mu ^k} = \sum\limits_{i = 1}^m {\mu _i^k} /\sum\limits_{k = 1}^{{N_{{\rm{PF}}}}} {\sum\limits_{i = 1}^m {\mu _i^k} } $ | (14) |
式中:μik为第k个Pareto最优解在第i维目标上的满意度,NPF为Pareto最优解的数量。可以看出,μk越大Pareto最优解的质量越高,选取μk最大的解作为最好折中解。
为了反映3种算法最后求得的Pareto最优解集质量优劣,本文采用多目标优化领域通用的超体积(hyper volume, HV)综合评价解集的收敛性和分布性[17],其定义如下
| $ {\rm{HV}}\left( {P,{\rm{r}}} \right) = {\rm{Volume}}\left( {\bigcup\limits_{F \in \mathit{\boldsymbol{P}}} {\left[ {{f_1},{r_1}} \right] \times \cdots \left[ {{f_m},{r_m}} \right]} } \right) $ | (15) |
式中:P为算法在目标空间获得的最终解集;r=[r1, r2, …, rm]为参考点,其被解集P中所有个体支配。本文根据SHPO问题的实际情况,设置r=[5×105, 0.1, 15]。HV越大表明算法求得的Pareto最优解集质量越好。
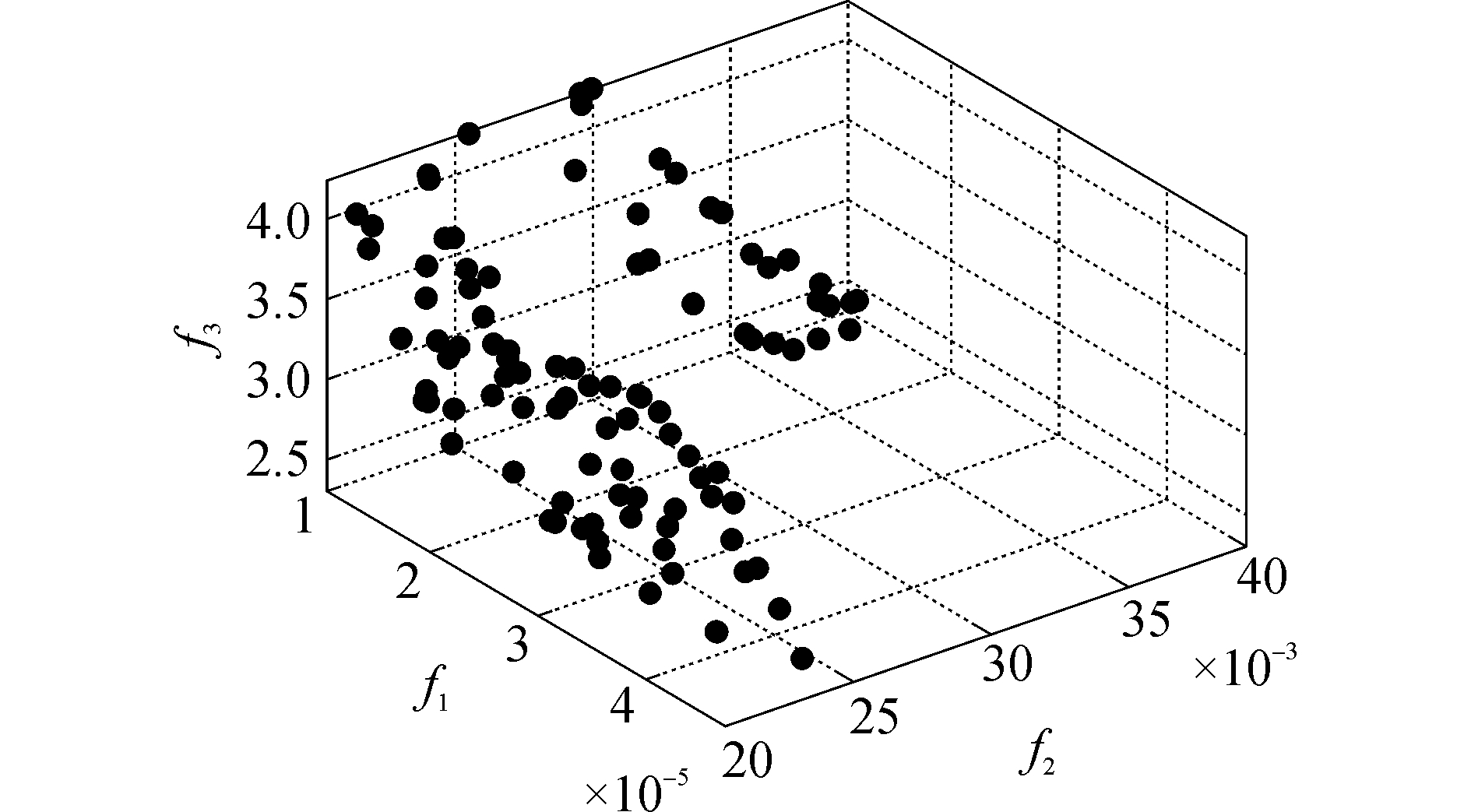
4.2 Pareto最优解集分析MOEA/D算法求得的优化结果分别如图 1和图 2所示,图 1为3维空间的SPHO问题的Pareto前沿,图 2为Pareto最优前沿的散点图,其中数据来源于30次独立运行中HV值最接近平均值的那一组数据。从图 1中可以看出,SHPO问题的Pareto最优前沿形状为凹面,呈非线性,表明3个目标之间是相互冲突的。
|
Download:
|
| 图 1 SPHO问题的Pareto最优前沿 Fig. 1 PF of SPHO problem | |

|
Download:
|
| 图 2 3个目标函数的散点图 Fig. 2 Scatter plots for 3 objectives | |
从图 2(a)中可以看出,在Pareto解集中,耐波性品级SR的提高会导致总阻力RT的增加,也就是说耐波性提高会导致快速性恶化,在耐波性为50的附近区域,存在总阻力增加但耐波性品级增加不明显的区域,这部分Pareto解对设计人员是有价值的,它表明不是一味牺牲快速性就能换取耐波性的提高。从总阻力为(1.37~1.45)×105 N可以看出,即使牺牲快速性能反而会有损耐波性能。从图 2(b)中可以看出,在Pareto解集中,MV的减小会导致总阻力RT的增加,也就是说操纵性的提高会导致快速性的恶化,但存在(1.24~1.32)×105 N这段区域,即使总阻力增加也没能换来操纵性的提高,反而在(1.33~1.45)×105 N,牺牲快速性能反而会有损操纵性能。从图 2(c)中可以看出,在Pareto解集中,耐波性品级SR的增大会导致操纵性MV的增加,也就是说耐波性的提高会导致操纵性的恶化,与图 2(a)、(b)中类似,在SR为50的附近区域,即使MV增加也没换取耐波性的增加。
4.3 对比结果分析为了验证本文算法的有效性,同时采用NSGA-Ⅱ和MOPSO算法对DTMB5415船型的SHPO问题进行求解,3种算法求得的极端解分别列于表 2、表 3和表 4,最优折中解列于表 5。
| 表 2 最优总阻力比较 Tab.2 Comparison of best total resistance |
| 表 3 最优耐波性品级比较 Tab.3 Comparison of best seakeeping rank |
| 表 4 最优操纵性比较 Tab.4 Comparison of best maneuverability |
| 表 5 最优折中解比较 Tab.5 Comparison of best compromise solution |
由表 2~表 4可以看出,在极端解方面,MOEA/D均能取得总阻力、耐波性品级和操纵性3个目标上最好的结果,其中最优船舶总阻力比较时,尽管NSGA-Ⅱ在SR和MV上取得了同MOEA/D相同的结果,但RT稍大于MOEA/D,说明MOEA/D求得的阻力目标上的极端解Pareto支配NSGA-Ⅱ求得的解;最优耐波性品级比较时,尽管MOEA/D和NSGA-Ⅱ求得的耐波性品级上的极端解是互不支配的,但MOEA/D在RT和SR两目标上是优于NSGA-Ⅱ,另外MOPSO求得的耐波性品级与NSGA-Ⅱ一样,但另外两个目标上明显劣于NSGA-Ⅱ;最优操纵性比较时,NSGA-Ⅱ虽然在SR上优于MOEA/D,但在另外两个目标劣于MOEA/D,MOPSO虽然在SR上获得了最好结果,但在另外两个目标上明显劣于MOEA/D和NSGA-Ⅱ。综上所示,MOEA/D能在一个目标上取得最好收敛精度的同时,保证另外两个目标不占劣势。
由表 5最优折中解可以看出,MOEA/D具有最小的RT和MV值,尤其是在RT上,明显好于另外两种算法,在SR上稍差于NSGA-Ⅱ,由此可以得出MOEA/D获得的最优折中解质量是优于NSGA-Ⅱ和MOPSO。
为了综合评价3种算法求得的整个Pareto最优解集的性能,采用HV指标定量评价。MOEA/D,NSGA-Ⅱ和MOPSO在IGD值上的比较统计结果如表 6所示,分别为30次独立运行结果的平均值与标准差,其中最好的结果用黑色加粗表示。同时,为了比较3种算法的计算效率,表 7给出了3种算法30次独立运行的平均时间。从表 6和表 7中得出,MOEA/D在解集质量和运行时间上均优于NSGA-Ⅱ和MOPSO。在解集质量方面,MOEA/D采用了分解机制和邻域思想,具有很好的收敛能力,加上有预设的均匀分布的权重向量引导个体进化,使得解集具有更好的分布性,因此在综合性能指标HV上具有更好结果;在运行时间方面,由于采用多个单目标子问题同时优化,不需要NSGA-Ⅱ和MOPSO中耗时的Pareto非支配比较,因而具有更快的求解速度。
| 表 6 3种算法在SHPO问题上获得的HV平均值与标准差 Tab.6 Average and standard deviation of the HV values by the three algorithms on SHPO problem |
| 表 7 3种算法运行时间比较 Tab.7 Average time required for three algorithmss |
1) 通过对船舶快速性、耐波性和操纵性3个目标同时优化,发现三者是相互冲突、相互制约的,一个目标性能的提高会导致其他目标性能的降低。因此,寻求三者的同时最优是不可能的,这为船舶水动力性能的综合优化提供了一定的理论意义。
2) 将多目标进化算法MOEA/D用于DTMB5415船型的优化设计,与NSGA-Ⅱ和MOPSO算法在极端解、最优折中解、Pareto最优解集综合性能和运行时间上进行了对比。结果表明,本文算法具有很好的收敛速度和求解精度,可以为决策者提供更具代表性的选择方案。
| [1] |
李冬琴, 蒋志勇, 杨永祥. 基于自适应加权的船舶多目标协同优化[J]. 中国造船, 2012, 53(4): 75-83. LI Dongqin, JIANG Zhiyong, YANG Yongxiang. Multidisciplinary and multi-objective design optimization based on adaptive weighted-sum method[J]. Shipbuilding of China, 2012, 53(4): 75-83. DOI:10.3969/j.issn.1000-4882.2012.04.011 (  0) 0)
|
| [2] |
周奇, 蒋平, 许辉, 等. 基于动态罚因子的多学科协同优化算法及其在船舶设计中的应用[J]. 船舶力学, 2016, 20(10): 1269-1280. ZHOU Qi, JIANG Ping, XU Hui, et al. Application of improved multi-discipline collaborative optimization in ship conceptual design based on dynamic penalty factors[J]. Journal of ship mechanics, 2016, 20(10): 1269-1280. DOI:10.3969/j.issn.1007-7294.2016.10.007 (  0) 0)
|
| [3] |
胡翩. 船舶概念设计阶段的多目标优化与决策[J]. 计算机与数字工程, 2014, 42(3): 390-394. HU Pian. Multi-objective optimization and decision making of conceptual ship design[J]. Computer & digital engineering, 2014, 42(3): 390-394. DOI:10.3969/j.issn.1672-9722.2014.03.010 (  0) 0)
|
| [4] |
胡腾飞, 王先洲, 刘平, 等. 船舶水动力性能的多目标优化方法[J]. 舰船科学技术, 2014, 36(6): 14-19. HU Tengfei, WANG Xianzhou, LIU Ping, et al. Investigation of multi-objective optimization on ship hydrodynamic performance[J]. Ship science and technology, 2014, 36(6): 14-19. DOI:10.3404/j.issn.1672-7649.2014.06.003 (  0) 0)
|
| [5] |
GUHA A, FALZARANOA J. Application of multi objective genetic algorithm in ship hull optimization[J]. Ocean systems engineering, 2015, 5(2): 91-107. DOI:10.12989/ose.2015.5.2.091 (  0) 0)
|
| [6] |
DIEZ M, SERANI A, CAMPANA E F, et al. Multi-objective hydrodynamic optimization of the DTMB 5415 for resistance and seakeeping[C]//Proceedings of the 13th International Conference on Fast Sea Transportation. Washington DC, 2015.
(  0) 0)
|
| [7] |
周玉龙, 杨松林, 奚炜, 等. 基于遗传-混沌算法的船舶动力学性能综合优化研究[J]. 舰船科学技术, 2005, 27(4): 18-21. ZHOU Yulong, YANG Songlin, XI Wei, et al. Study on synthetical optimization of performance of ship dynamics based on GA-chaos[J]. Ship science and technology, 2005, 27(4): 18-21. (  0) 0)
|
| [8] |
李密, 刘江波, 杨松林. 高速单体船航行性能综合优化的遗传混沌算法[J]. 中国舰船研究, 2008, 3(1): 23-27. LI Mi, LIU Jiangbo, YANG Songlin. Genetic-chaos algorithm on the overall optimization of navigational performances for high-speed ships[J]. Chinese journal of ship research, 2008, 3(1): 23-27. DOI:10.3969/j.issn.1673-3185.2008.01.006 (  0) 0)
|
| [9] |
ZHANG Qingfu, LI Hui. MOEA/D:a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 (  0) 0)
|
| [10] |
朱永胜, 王杰, 瞿博阳, 等. 采用基于分解的多目标进化算法的电力环境经济调度[J]. 电网技术, 2014, 38(6): 1577-1584. ZHU Yongsheng, WANG Jie, QU Boyang, et al. Environmental economic dispatch adopting multi-objective evolutionary algorithm based on decomposition[J]. Power system technology, 2014, 38(6): 1577-1584. (  0) 0)
|
| [11] |
KONSTANTINIDIS A, YANG Kun. Multi-objective energy-efficient dense deployment in wireless sensor networks using a hybrid problem-specific MOEA/D[J]. Applied soft computing, 2011, 11(6): 4117-4134. DOI:10.1016/j.asoc.2011.02.031 (  0) 0)
|
| [12] |
杨路春, 杨晨俊, 汪志强, 等. 基于分解的进化算法和多变量分析技术在船型参数设计中应用[J]. 上海交通大学学报, 2016, 50(8): 1200-1206. YANG Luchun, YANG Chenjun, WANG Zhiqiang, et al. Application of decomposition-based evolutionary algorithm and multivariate analysis in ship form parameter research[J]. Journal of Shanghai Jiao Tong University, 2016, 50(8): 1200-1206. (  0) 0)
|
| [13] |
HOLTROP J, MENNEN G G J. A statistical power prediction method[J]. International shipbuilding progress, 1978, 25(290): 253-256. DOI:10.3233/ISP-1978-2529001 (  0) 0)
|
| [14] |
BALES N K, CUMMINS W E. The influence of hull form on seakeeping[J]. Water waves, 1970: 00007480. (  0) 0)
|
| [15] |
周奇, 陈立, 周猛猛, 等. 基于自适应加权的船舶操纵性能多目标优化[J]. 舰船电子工程, 2014, 34(2): 37-40. ZHOU Qi, CHEN Li, ZHOU Mengmeng, et al. Application of adaptive weighted-sum method in ship maneuverability[J]. Ship electronic engineering, 2014, 34(2): 37-40. (  0) 0)
|
| [16] |
PAL S, QU B, DAS S, et al. Linear antenna array synthesis with constrained multi-objective differential evolution[J]. Progress in electromagnetics research B, 2010, 21: 87-111. (  0) 0)
|
| [17] |
BADER J, ZITZLER E. HypE:an algorithm for fast hypervolume-based many-objective optimization[J]. Evolutionary computation, 2011, 19(1): 45-76. DOI:10.1162/EVCO_a_00009 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


