随着高光谱遥感技术日新月异的发展, 高光谱图像相关处理技术的应用领域也不断拓宽。其中高光谱图像的分类和聚类技术愈发吸引学术界的关注。高光谱图像有标签数据的数量是十分稀缺的, 人们经常在先验知识极其匮乏的情况下进行高光谱影像的分析和研究, 所以高光谱图像的聚类学习往往是分类学习的前提, 是高光谱图像分析研究中的重点[1]。流形学习在机器学习领域的热度越来越高, 其在高光谱数据分析领域具有较高的研究价值。以ISOMAP[2]为代表的全局特性保持的流形学习方法中的测地距离概念能够更为客观地反映样本之间的距离, 并能在一定程度上抑制局部最优的情况出现, 在高光谱数据处理上具有广泛的应用研究前景。
在众多经典聚类算法中, 基于目标函数的分割聚类算法因其形式简洁、实现方便等优势, 得到了极为广泛的应用, 其中K_Medoids算法是基于这一思想的最为经典的算法之一。近年来学术界对于传统聚类算法K_Medoids进行了多种改进。Yue等[3]提出了一种基于MapReduce的K_Medoids算法, 能够有效抑制传统K_Medoids算法运算量较大的问题;Aghaee等[4]提出一种利用三角不等式来计算未知距离上限的方法, 能够显著降低K_Medoids算法的运算量;曹丹阳等[5]提出了一种基于CF树的K_Medoids算法, 可以显著提高收敛速度。马箐等[6]提出了一种基于粒计算的K_Medoids算法, 通过定义新的相似度函数来寻找更可靠的聚类初始位置;王常武等[7]提出了一种基于初始中心微调与增量中心候选集的改进K_Medoids算法, 能够在一定程度上提高聚类质量;赵烨等[8]提出了结合蚁群算法和K_Medoids的聚类算法(AKCA), 能够融合蚁群算法和K_Medoids算法各自在聚类上的优点。上述文献虽然能够在一定程度上抑制聚类算法初值敏感的弊端, 但在多维模式下未能选用更合适的样本距离度量方法来完成聚类。
针对传统方法的上述不足, 本文提出一种基于流形的K_Medoids聚类算法, 并且将其应用于高光谱图像的聚类处理上。该算法通过基于“最小最大”原则的改进Canopy算法的预处理结果来确定K值和聚类中心的初始位置, 在此基础上执行K_Medoids算法进行聚类。聚类时, 通过构建基于测地距离的像元距离矩阵为K_Medoids算法提供支持。
1 理论基础 1.1 K_Medoids算法K_Means算法是最为经典的聚类算法之一, 其基本实现思想为:首先随机选定K个原始聚类中心的位置, 计算其余样本目标与聚类中心的欧氏距离, 并把样本赋予到最近的聚类之中;然后计算每个类内部各样本的平均值进而得到新的聚类中心。反复迭代以上步骤, 直到目标函数收敛为止。其均值的平方误差目标函数为
| $ J = \sum\limits_{n = 1}^N {\sum\limits_{k = 1}^K {{{\left\| {{x_n} - {\mu _k}} \right\|}^2}} } $ | (1) |
式中:J是误差的平方和, xn表示对样本目标的遍历, μk表示聚类簇的中心位置。
K_Medoids算法是在K_Means算法的基础上改进而来, 不同之处在于K_Medoids的初始聚类中心是选择当前簇内的中值点, 也就是到其他簇内各样本点的距离之和最小的样本点。这样做有两大好处:1)削弱了离群点的负面影响;2)能够把K_Means的应用领域拓展到离散样本空间。基于K_Medoids的典型算法是Kaufman和Rousseeuw提出的PAM(partitioning around medoid)算法[9], 以及他们之后提出的基于抽样的CLARA(clustering LARge applications)算法[10]。K_Medoids的基本算法流程为
1) 为每个簇随机选择一个初始聚类中心, 剩余对象根据其距离中心的距离分给最近的指定簇;
2) 用非中心点来代替中心点, 重新计算其到簇内各个样本点的距离, 如果满足条件则替换聚类中心。
传统的K_Medodids使用欧氏距离计算样本点之间的距离, 两个n维向量a=(x11, x12, …, x1n)与b=(x21, x22, …, x2n)间的欧氏距离为
| $ {d_{\mathit{\boldsymbol{ab}}}} = \sqrt {\sum\limits_{k = 1}^n {{{({x_{1k}} - {x_{2k}})}^2}} } $ | (2) |
3) 聚类结果的质量用目标函数来评估, 该函数评估了对象与其聚类中心的相似程度。当聚类中心的变化小于某阈值时, 计算过程结束。其误差的平方和为
| $ J = \sum\limits_{j = 1}^K {\mathop \sum \limits_{p \in {c_j}} ({{\left\| {p - {o_i}} \right\|}^2})} $ | (3) |
式中:p为当前隶属于某类簇的一个点, oi为某类簇的代表对象。
虽然, K_Medoids相较于K_Means算法对于离群点有一定抑制作用, 但其两种经典形式PAM和CLARA算法都无法解决初值敏感和局部最优的问题, 说明该算法依然有较大的改进空间。
1.2 Canopy算法Canopy算法是一种“粗”聚类算法, 快速简单。该算法最大的优势是不用预先设定K的取值, 因此非常适合作为K_Means或K_Medoids算法的预处理算法, 能够在一定程度上解决K值选择的盲目性。在Canopy算法的基础上在选择出来的局部Canopy里进行K_Means或K_Medoids算法, 能够有效减少相似计算的数量。
Canopy算法基本实现步骤如下:
1) 将数据集经过向量化处理为一个list, 预先设定两个阈值:T1和T2, 其中T1>T2;
2) 在list中随机取一点P, 计算点P与所有Canopy之间的距离(首次计算时把点P设置为第一个Canopy), 将点P归属到与其距离在T1以内的Canopy内;
3) 如果点P距离某个Canopy在T2以内, 此时需在list中移除点P。
4) 重复步骤2)、3), 直到list为空结束。
算法类聚过程见图 1。

|
Download:
|
| 图 1 Canopy算法的聚类过程 Fig. 1 process of Canopy algorithm clustering | |
经过以上步骤, 理论上可获得K的参考值, 降低人为随机选择的盲目性。并且经过Canopy算法的预处理后将获得一个“粗”聚类结果, 其中某些样本可能同时属于多个Canopy, 在此基础上再进行K_Medoids聚类算法, 理论上可以抑制初值敏感的弊端。对于某些样本点较少的Canopy, 通过合理的设定阈值可以排除一些离群点, 这对于某些脏数据有一定的抑制作用。文献[11]提出了一种基于Hadoop的Canopy_KMeans算法, 该算法使用Canopy取得了良好的“预聚类”效果, 在此基础上再使用K_Means算法进行聚类。但Canopy算法也存在着很严重的缺陷, 首先, T1和T2的取值对个人经验的依赖较大, 目前还没有通用的取值准则, 不合适的取值会对算法效果产生较大的不利影响;其次, Canopy算法同传统K_Means和K_Medoids算法一样, 都是随机选定初始聚类中心位置, 容易造成聚类结果时好时坏。所以, 对于Canopy算法的改进思路主要是提出初值选定准则, 克服凭经验确定初值T1和T2的问题。
1.3 ISOMAP与测地距离在聚类算法中选用合适的方法度量样本之间的距离是十分重要的。对于常见的UCI数据(如机器学习中常使用的鸢尾花数据集iris), 直接使用欧氏距离作为度量标准在大多数情况下是合适的, 但也极容易产生局部最优的问题。高光谱数据的维度一般较大, 数据整体呈非线, 如果不考虑数据的流形结构, 直接使用欧氏距离往往不能真实反应样本点之间的关系。所以对于多维度非线性数据欲达到全局最优, 更适合使用等距离映射(ISOMAP)中提出的测地距离作为度量方法。ISOMAP是由Tenenbaum等提出的一种基于流形非迭代的全局优化算法[12], 本质是一种非线性的降维算法。算法流程如图 2所示[2]。

|
Download:
|
| 图 2 ISOMAP算法流程图 Fig. 2 Algorithm flowchart of ISOMAP | |
“等距映射”主要体现在降维之后样本点之间的距离不变, 此时的距离即为测地距离。通俗地说, 从A城市到B城市的欧氏距离是两城市的直线长度, 而测地距离是经过沿途各城镇距离之和中的最短距离。测地距离与欧氏距离的对比如图 3。

|
Download:
|
| 图 3 测地距离与欧氏距离对比示意图 Fig. 3 Comparison of geodesic distance and Euclidean distance | |
测地距离在宏观上看是基于图论的最短路径, 从起点出发沿着流形一步一步到达终点的最短距离。测地距离从微观上看可以使用的度量标准有欧氏距离、曼哈顿距离、切比雪夫距离、马氏距离等。其中马氏距离表示数据的协方差距离, 不受纲量影响, 而欧氏距离、曼哈顿距离、切比雪夫距离都统称闵氏距离, 本质上都是闵氏距离的不同变形。文献[13-14]在高光谱图像的特征分析中应用马氏距离(Mahalanobis distance)降维取得了很好的效果。但马氏距离在处理高光谱数据时有其局限性:1)马氏距离对微小的变化有敏感的反应, 可能会夸大微小变量(如噪声)的作用;2)如果要使用马氏距离, 空间内的每一个样本点都要计算协方差矩阵, 这是一个十分庞大的工程, 会大大降低运算效率。所以, 对于局部近似线性空间内较近的两个样本点(近邻点), 适合使用简易的欧氏距离直接计算;对于相隔较远的点(非近邻点), 则使用基于图论的最短路径法度量。在K_Medoids算法中引入基于流形的测地距离取代直接使用欧氏距离构建像元距离矩阵, 能够保持嵌入在高维观测空间中的低维流形模型的局部的非线性特征, 能够有效避免局部最优对聚类效果的不利影响。
2 基于流形的Canopy-K_Medoids联合算法Canopy算法和K_Medoids算法是用来聚类的常用算法, Canopy算法的主要功能是预先划分聚类区域, 为其后的聚类算法提供参考;K_Medoids算法是以簇内中值点位聚类中心, 利用簇内各点距离作为衡量标准进行聚类的算法。文献[11]运用Canopy算法对K_Means算法进行改进, 应用在多类UCI数据集上取得了很好的效果, 借鉴其算法思想并进行改进, 将改进的Canopy和K_Medoids的联合算法应用在高光谱图像的无监督聚类上。首先使用基于“最大最小”原则的Canopy改进算法对整个数据集进行预处理, 在此基础上再应用基于测地距离的K_Medoids算法进行聚类。
2.1 Canopy算法进行预处理过程描述基于Canopy预处理的K_Medoids算法中, Canopy算法进行预处理的步骤描述如下:
1) 初始化。
加载等待预处理的高光谱图像数据P, 为了降低运算开销, 需截取实验所需的图像范围W。
2) Canopy算法的聚类中心点位置设定。
如1.2节所述, Canopy算法的T1与T2值的设定十分重要, 关系到其后进行K_Medoids聚类的效果好坏。其中T2的值对聚类中心点的位置影响较大。当T2过大时, 会使算法容易陷入局部最优;当T2过小时, 会显著增加算法的运算开销。大多数学者认为T1与T2的值需要根据具体的数据环境进行反复的测试和观测, 即通过交叉检验的方法最终调试出适合的T1与T2组合。文献[15]提出了一种基于“最小距离最大”原则的广义最佳鉴别矢量集求解方法, 并成功应用到模式分类。借鉴这一思想, 将“最小最大”原则应用到Canopy算法中。最小最大原则的主要目的是尽量使初始聚类中心尽量间隔较远, 其基本步骤如下:1)假设存在一个数据集D随机选择点D1作为第一个初始聚类中心;2)计算D中各点到D1的距离, 选取距离最大的点D2为第二个初始聚类中心;3)计算D中其余各点到D1和D2的距离, 取这些距离的最小值的点min(d1, d2), 选取其中的最大值所在的点max(min(d1, d2))作为下个聚类中心, 其迭代条件满足:
| $ \left\{ \begin{array}{l} {\rm{Dist}}D = \max (\min ({d_1}, {d_2}))\\ {\rm{Dist}}D = \max (\min ({d_1}, {d_2}, \cdots , {d_M})) \end{array} \right. $ | (4) |
式中:d1, d2, …, dM是到各个数据点的距离, 以此类推, 直到找到所有聚类中心。借鉴这一思想运用到Canopy的初始聚类中心选择上。这样就无需再考虑T2的取值, 只需要斟酌T1的取值即可完成对Canopy的参数设定。
3) Canopy算法的聚类中心个数K的设定。
通过第2步运用“最小最大准则”设定初始聚类中心, 虽然有效避免了聚类陷入局部最优的问题, 而且得出了若干聚类中心的备选位置, 但并不能确定初始聚类中心的实际应取个数。如果T1值设定的过小, 会使Canopy算法产生过多的初始聚类中心点, 即造成过度聚类的情况;如果T1值设定过大, 会使Canopy算法提前结束, 造成聚类的不彻底。文献[16]中提出了一种确定K_Means初值K的方法, 其主旨思想是观测某种合适的类簇指标, 当K值远离真实值时, 该指标变化较缓慢。当接近真实值时, 指标变化十分显著。借鉴这一思想并进行相应细化和改进, 对Canopy算法改进如下:
① 通过上个步骤确定M个聚类中心备选点, 在一定合理区间内逐步增加聚类中心点的个数C, 调整T1的值, 当D内数据被全部囊括在Canopies中后停止调整T1值的大小;
② 记录每次C值变动后各Canopy内各样本点到聚类中心的平均距离ds;
③ 选取适当的突变点并保存此时的C值, 将此数计为K值;
④ 终止。设置终止条件为最大迭代次数N1。
2.2 基于测地距离的K_Medoids聚类算法过程描述通过Canopy算法对数据集的预处理, 在此基础上再进行K_Medoids改进算法对数据集进行聚类分析。在计算样本点到中心点距离时, 使用基于流形的测地距离替换直接使用欧氏距离来构建像元之间的距离矩阵。
1) 初始化。
加载2.1节Canopy算法产生的K值和聚类中心位置, 并加载等待处理的高光谱图像数据, 其具体过程同2.1节中的初始化步骤。然后构造一个包含所有样本点的图G, 如果样本点Di和Dj的欧氏距离d(Di, Dj)小于一个阈值ε或二者是近邻点, 那么Di与Dj有边连接, 边长为d(Di, Dj)。
2) 计算数据样本数据D内各样本间的最短路径矩阵。
近邻图构造完成后, 以此基础计算各样本之间的最短距离。如果两个Di和Dj有边连接, 则设置其最短路径是dG(Di, Dj)=d(Di, Dj), 否则dG(Di, Dj)=∞。计算样本点之间的最短路径时, Dijkstra算法的计算复杂度较低, 而且更适合权值非负的情况, 所以计算dG(Di, Dj)时采用Dijkstra算法[12]。
3) 应用K_Medoids算法对数据点进行聚类。
Canopy粗聚类提供了K参考值和初始聚类中心位置, 同时加载上一步生成的最短路径矩阵HG, 在此基础上可以进行K_Medoids聚类运算。其算法步骤如下:
① 按照Canopy算法的运算结果, 设置K个初始聚类中心D1, D2, …, Dk;
② 通过最短路径矩阵HG找到其他样本点距离最短的聚类中心, 为样本点寻找所应归属的簇O1, O2, …, Ok;
③ 在每个簇Oi内, 顺序选取各点Di, 计算Di到其余簇内各点的距离之和
④ 重复执行②~③直到聚类中心的位置不再变化为止。
4) 终止条件。
设置终止条件为最大迭代次数N2。
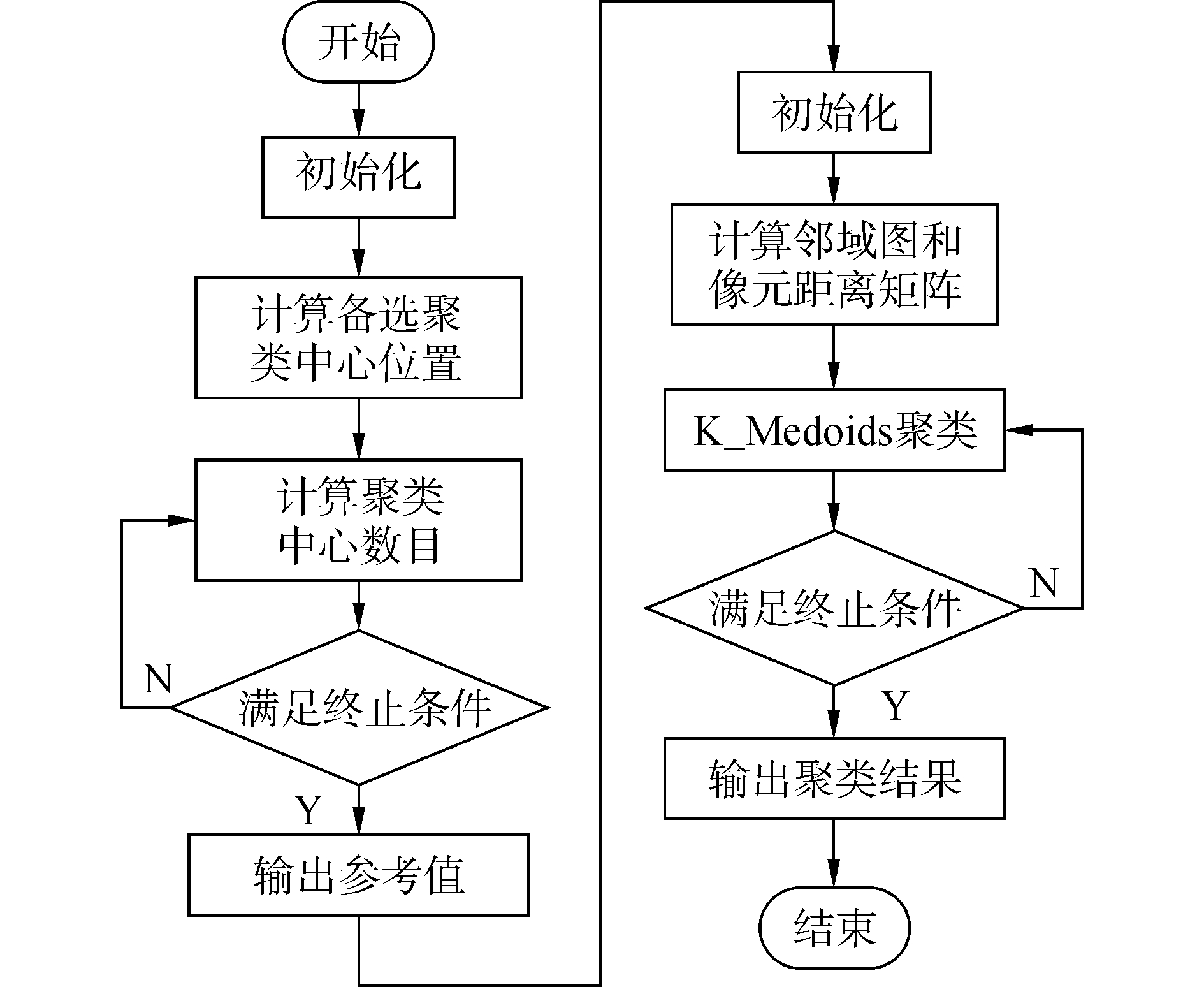
2.3 基于流形的Canopy-K_Medoids算法在高光谱图像聚类上的应用依据2.1节描述的改进型Canopy算法对高光谱数据进行预处理, 通过对最小最大准则确定初始聚类中心的备选位置M, 通过目标函数davg确定聚类中心的时间数目K。经过N1次迭代, 选取出最合适的初值组合。利用改进的Canopy算法获取初值不仅简单高效, 而且能够克服人为选择初值的盲目性, 有利于更好地完成下一步的聚类任务。然后依据2.2节描述的基于流形的K_Medoids算法进行更详细地聚类运算, 首先对高光谱数据求解邻域图G, 在此基础上求解基于测地距离的最短路径矩阵HG。将结果代入K_Medoids之中, 迭代N2次输出最终的聚类结果。该算法的具体流程如图 4所示。
|
Download:
|
| 图 4 本文算法整体流程图 Fig. 4 The overall flow chart of this algorithm | |
实验环境CPU为Intel(R) Xeon(R) E5-1620, 3.60 GHz, 内存8 GB的PC机。使用MATLAB 2014a对高光谱图像的聚类算法进行实验。实验所采取的高光谱AVIRIS数据是美国加利福尼亚州萨利纳斯山谷和美国印第安纳州农林混合实验场两种高光谱图像。其中萨利纳斯山谷图像大小为512×217像素, 空间分辨率为3.7 m, 光谱范围为400~2 500 nm, 原始波段数为224个, 去除20个水吸收波段, 共有204个波段参与实验, 其参考地物如图 5所示。印第安纳州农林混合实验场图像的光谱范围为0.41~2.45 μm, 空间分辨率为25 m, 光谱分辨率为10 nm, 图像大小为144×144像素, 共包含220个波段, 由于噪声和水吸收等因素除去其中的20个波段, 其参考地物如图 6所示。

|
Download:
|
| 图 5 萨利纳斯山谷图像参考地物 Fig. 5 Salinas valley image reference feature | |

|
Download:
|
| 图 6 印第安纳州农林混合实验场图像参考地物 Fig. 6 Indiana agriculture and forestry mixed test site image reference | |
本文算法中参数设置为:M=16, T1=7 000~12 000, ε=500, K=8(对照实验组), N1=50, N2=50。
为了证明本文算法是既可以保留分割聚类算法简单易实现的优点, 又能够抑制其初值敏感和局部最优问题的有效无监督聚类方法。将K_Means、K_Medoids算法与本文算法进行对比。同时, 也将其他类别的聚类算法:模糊聚类算法(fuzzy c_means algorithm, FCM)和基于核函数kernel_Kmeans算法与本文算法对比。FCM算法在运算后生成的概率矩阵中, 每个样本点选取概率值最大的作为其类簇, 在kernel_Kmeans算法中的核函数使用径向基函数(radial basis function, RBF), 所有对照算法的K值均人工设定为正确值。
不同于有监督分类使用OA和Kappa系数衡量分类效果, 在无监督聚类算法之间的比较标准选择上, 文献[17]提出使用内部度量和外部度量相结合的方法作为聚类效果检验的准则函数, 文献[18]提出使用Jaccard系数作为文档聚类效果检验的标准。参考以上文献的思想, 本文算法选择的聚类效果检验准则为:类内距离D, 类间距离L, Jaccard系数J'和Rand指数R。类内距离又称为类内误差平方和, 是类簇内所有样本点到类簇中心的距离和, 计算公式为
| $ D = \sum\limits_{i = 1}^K {\sum\limits_{{x_{ik}} \in {\varphi _j}, k = 1}^{N({\varphi _j})} {|{x_{ik}} - {{\bar x}_i}|} } $ | (6) |
式中:φ={φi}是第i类的样本数据的集合φi, i={1, 2, …, K}, N(φi)是第i个簇类的样本容量, xik是第i个簇类的第k个样本点, xi是第i个簇类的所有数据的均值。类内距离越小, 说明类别凝聚力越强, 聚类效果越好。
类间距离是指每个类的类簇中心xi到全域中心x'的距离, 类间距离越大, 说明其各类之间差别越大, 聚类效果越好。类间距离的计算公式为
| $ L = \sum\limits_{i = 1}^K {|{x_i} - x'|} $ | (7) |
Jaccard系数和Rand指数是常用于评价聚类效果好坏的标准, 其取值越大说明聚类效果越好。设数据集X的一个聚类结构为C={C1, C2, …, Cm}, 数据集已知的划分为P={P1, P2, …, Ps}, 可通过比较C和P的比较来评价聚类的质量。遍历所有数据点, 对数据集中任一对点, 计算下列项:
1) 两个点同属C, 且同属P, 则a++;
2) 两个点同属C, 但不同属P, 则b++;
3) 两个点不属于同一个C, 但同属P, 则c++;
4) 两个点既不属于同一个C, 也不同属P, 则d++。
则Rand指数为
| $ R = \left( {a + b} \right)/\left( {a + b + c + d} \right) $ | (8) |
Jaccard系数为
| $ J' = a/\left( {a + b + c} \right) $ | (9) |
从表 1、2的数据对比中可以发现, 5种算法的类内距离D、类间距离L比较接近, 本文算法的数值略好于其他算法。而Jaccard系数J'和Rand指数R更本文算法则明显优于其他算法。出现这种情况主要原因为参与实验的图像规模较小, 所以类内和类间距离不会有太大差异。在这种小规模图像下, Jaccard系数J'和Rand指数R更能体现聚类的准确程度。所以通过以上四个客观指数分析, 本文算法具有一定的实用性和优越性。另外, 由于本文的对照算法均人为设定了正确的K值, 而本文算法皆为Canopy算法计算出来的参考值。所以如果在完全无监督的条件下, 随机设定对照算法的初值K和初始聚类中心位置, 本文算法的数据指标在理论上应更为优越。
| 表 1 萨利纳斯山谷图像8种地物类别下的5种算法比较 Tab.1 Comparison of 5 kinds of algorithms in 8 species of Salinas valley images |
| 表 2 印第安纳州农林混合实验场图像8种地物类别下的5种算法比较 Tab.2 Comparison of 5 kinds of algorithms in 8 kinds of artifacts in the Indiana agriculture and forestry mixed test site |
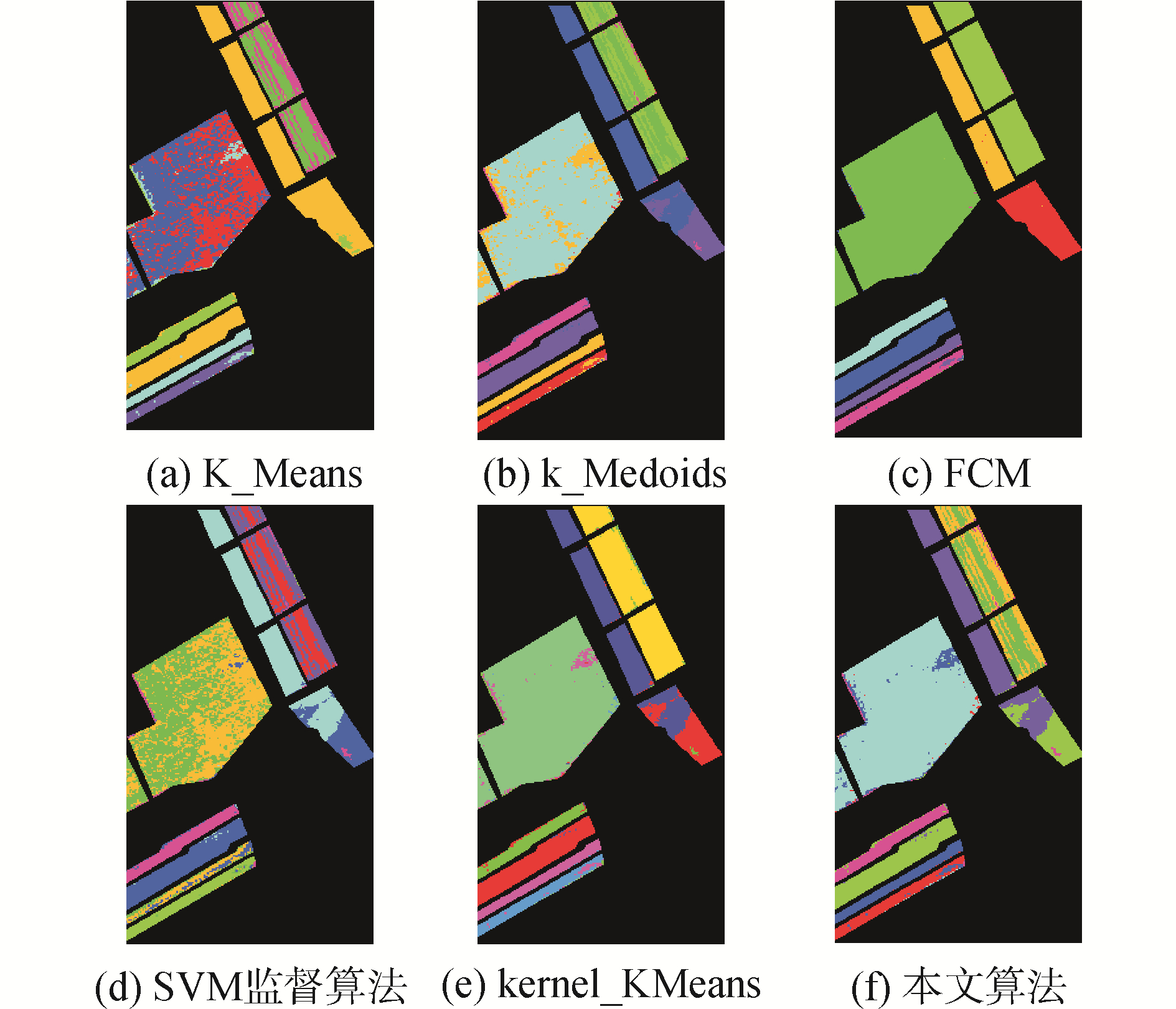
为了更加直观地反映不同聚类方法的实际效果差异, 图 7和8分别反映了两种高光谱图像在不同方法中的聚类效果图, 为了直观比较, 加入了SVM监督算法进行对照。
|
Download:
|
| 图 7 萨利纳斯山谷8种地物下6种算法的效果对比图 Fig. 7 Comparsion of 6 algorthms for 8 classes in Salinas valley images | |

|
Download:
|
| 图 8 印第安纳州农林混合实验场8种地物下6种算法的效果对比图 Fig. 8 Comparsion of 6 algorithms for 8 classes in the Indiams agriculture and forestry mixed text site | |
由于无监督聚类算法存在着缺乏监督数据指导的先天缺陷, 所以聚类效果明显不如SVM监督算法, 各种无监督聚类算法都存在着明显的错分情况。其中萨利纳斯山谷图像由于其光谱值之间差异较大, 不同类簇之间区别明显, 所以各种无监督聚类算法的聚类效果都很好, 其中本文算法甚至可以媲美SVM监督分类算法的效果。而印第安纳州农林混合实验场图像则更为复杂, 所以聚类效果明显不如前者。但由图像直观显示和四个客观指标对比, 本文算法的聚类效果均明显优于传统的K_Means、K_Medoids和FCM算法, 相较于核K_Means虽然4个准则指标的数值接近, 但本文算法实际聚类效果要明显要好于核K_Means。以上实验可以证明, 本文算法具有一定程度的优越性和可行性。
4 结论1) 通过对照实验, 证明了提出算法所使用的改进的Canopy算法预聚类算法有效地克服了传统聚类算法所具有的初值敏感的问题;使用测地距离改进样本距离度量标准有效的克服了传统聚类算法所具有的离群点敏感、初值敏感、易陷入局部最优的问题, 获得了较为理想的聚类效果。与其他主流聚类算法的对比实验证明了本文算法的有效性和优越性。
2) 高光谱图像数据因其匮乏有标签数据, 所以其聚类分析往往是分类的前提。在合理的聚类结果基础上再进行分类分析, 往往更加方便可靠。本文所提出的改进聚类算法对于高光谱图像的聚类分析有一定的应用价值, 所提出的聚类效果判定标准对于聚类分析有一定的指导意义。
3) 在实验中发现提出算法需要计算所有样本点之间的距离, 而测地距离作为一种图论距离本身也十分庞大。这就导致本文算法在运行时间上要远远长于其他传统算法, 对实验设备的性能要求也比较高, 这一点目前尚没有较好的解决途径。
由于本文所提出的聚类算法优于传统的聚类算法, 所以后续研究中可以考虑以本文提出算法为基础, 引入少量有标签进行分类分析, 有望得到更精确的分类结果。在这一方面值得更为深入地研究和探讨。
| [1] |
李翔.高光谱影像的聚类分析及应用[D].北京: 北京交通大学, 2015. LI Xiang. Clustering analysis of hyperspectral image and its application[D]. Beijing: Beijing Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015594115.htm (  0) 0)
|
| [2] |
李波. 高维数据的流形学习分析方法[M]. 武汉: 武汉大学出版社, 2016. LI Bo. Manifold learning analysis method for high dimensional data[M]. Wuhan: Wuhan University, 2016. (  0) 0)
|
| [3] |
YUE Xia, WANG Man, YUE Jun, et al. Parallel K-Medoids++ spatial clustering algorithm based on MapReduce[J]. arXiv preprint arXiv: 1608.06861, 2016. http://cn.arxiv.org/abs/1608.06861
(  0) 0)
|
| [4] |
AGHAEE A, GHADIRI M, BAGHSHAH M S. Active distance-based clustering using K-Medoids[M]//BAILEY J, KHAN L, WASHIO T, et al. Advances in Knowledge Discovery and Data Mining. Cham: Springer International Publishing, 2016.
(  0) 0)
|
| [5] |
曹丹阳, 杨炳儒, 李广原, 等. 一种基于CF树的K-Medoids聚类算法[J]. 计算机应用研究, 2011, 28(9): 3260-3263. CAO Danyang, YANG Bingru, LI Guangyuan, et al. K-Medoids clustering algorithm based on CF tree[J]. Application research of computers, 2011, 28(9): 3260-3263. DOI:10.3969/j.issn.1001-3695.2011.09.015 (  0) 0)
|
| [6] |
马箐, 谢娟英. 基于粒计算的K-Medoids聚类算法[J]. 计算机应用, 2012, 32(7): 1973-1977. MA Qing, XIE Juanying. New K-Medoids clustering algorithm based on granular computing[J]. Journal of computer applications, 2012, 32(7): 1973-1977. (  0) 0)
|
| [7] |
王常武, 刘小凤, 王宝文, 等. IC-Kmedoids:适用于RNA二级结构预测的聚类算法[J]. 生物医学工程学杂志, 2015, 32(1): 99-103. WANG Changwu, LIU Xiaofeng, WANG Baowen, et al. IC-Kmedoids:a clustering algorithm for RNA secondary structure prediction[J]. Journal of biomedical engineering, 2015, 32(1): 99-103. (  0) 0)
|
| [8] |
赵烨, 黄泽君. 蚁群K-Medoids融合的聚类算法[J]. 电子测量与仪器学报, 2012, 26(9): 800-804. ZHAO Ye, HUANG Zejun. Clustering algorithm based on fusion of ant colony algorithm and K-Medoids[J]. Journal of electronic measurement and instrument, 2012, 26(9): 800-804. (  0) 0)
|
| [9] |
KAUFMAN L, ROUSSEEUW P J. Partitioning around medoids (Program PAM)[M]//KAUFMAN L, ROUSSEEUW P J. Finding groups in Data: An Introduction to Cluster Analysis. Hoboken: John Wiley & Sons, Inc., 2008: 68-125.
(  0) 0)
|
| [10] |
KAUFMAN L, ROUSSEEUW P J. Clustering large applications (Program CLARA)[M]//KAUFMAN L, ROUSSEEUW P J. Finding Groups in Data: An Introduction to Cluster Analysis. Hoboken: John Wiley & Sons, Inc., 2008: 126-163.
(  0) 0)
|
| [11] |
赵庆. 基于Hadoop平台下的Canopy-Kmeans高效算法[J]. 电子科技, 2014, 27(2): 29-31. ZHAO Qing. Efficient algorithm of Canopy-Kmeans based on Hadoop platform[J]. Electronic science & technology, 2014, 27(2): 29-31. (  0) 0)
|
| [12] |
TENENBAUM J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319-2323. DOI:10.1126/science.290.5500.2319 (  0) 0)
|
| [13] |
孙岩.湿地植物高光谱特征分析与物种识别模型构建[D].北京: 清华大学, 2008. SUN Yan. Hyperspectral characters and species identification model for wetland plants[D]. Beijing: Tsinghua University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10003-2009083317.htm (  0) 0)
|
| [14] |
XIANG Shiming, NIE Feiping, ZHANG Changshui. Learning a mahalanobis distance metric for data clustering and classification[J]. Pattern recognition, 2008, 41(12): 3600-3612. DOI:10.1016/j.patcog.2008.05.018 (  0) 0)
|
| [15] |
KEERTHI S S, SHEVADE S K, BHATTACHARYYA C, et al. A fast iterative nearest point algorithm for support vector machine classifier design[J]. IEEE transactions on neural networks archive, 2000, 11(1): 124-136. (  0) 0)
|
| [16] |
MO Jiahui, KIANG M Y, ZOU Peng, et al. A two-stage clustering approach for multi-region segmentation[J]. Expert systems with applications, 2010, 37(10): 7120-7131. DOI:10.1016/j.eswa.2010.03.003 (  0) 0)
|
| [17] |
李荟娆. K-means聚类方法的改进及其应用[D].哈尔滨: 东北农业大学, 2014. LI Huirao. Improved K-means clustering method and its application[D]. Harbin: Northeast Agricultural University, 2014. http://d.wanfangdata.com.cn/Thesis_Y2621098.aspx (  0) 0)
|
| [18] |
张人.一种新的动态XML文档聚类方法[D].长春: 吉林大学, 2012. ZHANG Ren. A novel clustering method for dynamic XML documents[D]. Changchun: Jilin University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013118753.htm (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


