2. 晋西集团技术中心五所, 山西 太原 030000
2. The Fifth Research Institute of Jinxi Group Technology Center, Taiyuan 030000, China
在火箭炮组成系统中,闭锁机构是设计中常采用的重要部件,其主要作用有两个:行军时起挡弹作用可靠约束火箭弹,发射时提供一定的闭锁力,为火箭弹“齐步走”提供保障[1-3]。除了具备上述两个正常功能,闭锁机构还必须具有发射时的被强制解脱能力,即火箭弹必须在不破坏火箭炮的前提下,借助推力作用强制冲破闭锁机构的约束而被发射出去(本文称之为“闭锁机构的撞击失效”)。按照火箭炮的设计原则,闭锁力通常为火箭弹重力的2~5倍[1],其设计值选取时的基本依据首先是行军时的各种惯性,所选的闭锁力值必须保证火箭弹即使在惯性载荷作用下也不致滑落出定向器;其次需要考虑闭锁解脱时引起的振动对火箭炮射击效果的影响。综合来讲,在满足上述功能的前提下,选取的闭锁力越小,越有利于减小火箭炮的振动和推力损失。
对于小质量火箭弹(例如122 mm火箭弹),2~3倍重力的闭锁力值为200 kg,仅是发动机推力的1/10、发射系统重量的1/100。而对于中大质量(大于1 000 kg)火箭弹而言,该比例分别达1/3和1/5,此时,若继续沿用传统的设计原则,所设计的闭锁机构在解脱时必定给火箭炮带来巨大的冲击振动,严重影响发射稳定性和射击密集度。近年来,一些可实现平时“大闭锁”、发射“零闭锁”的新型闭锁机构应运而生。这些闭锁机构由“大闭锁”向“零闭锁”的转化,通常借助于燃气射流的能量或气动机构的动作来实现,而当出现不可靠转化时,将出现发射事故。因此,必须通过结构设计保证这类闭锁机构的失效性能——能被强制解脱。闭锁机构正常解脱性能的优劣仅仅关系到射击的精度和密集度,但失效性能“失灵”则会造成炮毁人亡。
火箭炮的闭锁机构在发挥闭锁功能时,与火箭弹之间会产生力的相互作用,这种作用的本质是构件间的接触和撞击作用,而强制解脱过程就是闭锁机构在撞击中产生失效的过程。对撞击失效的研究可分为两类:1)利用失效进行防护,如文献[4-6],通过研究能量吸收机理设计了合理的缓冲装置来起到防护措施;2)避免失效破坏、增强抗撞击能力,文献[7-8]研究了桥梁、建筑物等倒塌机理,文献[9-14]研究了撞击过程中的破坏损伤问题。经过分析可以发现,这些研究主要关注的是构件在撞击破坏损伤后的特性,少见对撞击失效过程的影响因素及作用规律进行深入分析,更未见对火箭弹闭锁机构撞击失效的研究。而已有的关于闭锁机构的研究,又多是关注正常解脱状态下的闭锁性能,如文献[15-16]对正常解脱过程中的闭锁机构动态特性进行了研究。此外,在闭锁机构的实验研究中,曾采用静态水压或液压机构动态施压等方法对闭锁力进行测量[17-18],这种类似于材料性能测量的准静态实验,并不能准确定量模拟发射过程火箭发动机的推力加载,因而,其测试结果难以提供精确验证和评价火箭系统安全性和可靠性。
本文结合闭锁机构的特点,通过一般力学原理理论推导,建立闭锁机构撞击失效过程的理论模型,寻找撞击失效过程的影响因素及其作用规律,为撞击失效过程的理论和实验研究,尤其对火箭弹闭锁机构等产品的撞击失效过程研究提供帮助,并初步确立闭锁机构产品性能验证的方法。
1 闭锁机构撞击失效模型建立 1.1 模型简化某型闭锁机构的结构模型如图 1所示。在行军过程中,保险环固连于火箭弹上,闭锁机构通过保险环约束闭锁钩转动,起到闭锁作用;在正常发射过程中,保险环在燃气射流作用下率先脱落,此时闭锁钩可以自由转动,实现发射时“零闭锁”。

|
Download:
|
| 图 1 闭锁机构示意图 Fig. 1 Locking mechanism diagram | |
若发射时出现意外情况导致保险环不能正常脱落,闭锁钩将无法自由转动,这时火箭弹在燃气作用下向前运动,与闭锁机构发生撞击。随着燃气推力的迅速增大,闭锁钩与保险环在火箭弹的撞击下产生塑性变形,甚至是断裂破坏。该过程与两构件相撞的情形类似,可以认为,闭锁机构在此过程中所遵循的规律,应与冲击构件撞击固定构件时的规律相同,因此,将闭锁机构失效过程简化为图 2所示模型。图 2虚线部分为闭锁机构撞击前的位置,实线部分为撞击失效过程完成时刻,即完成强制解脱时刻的位置。

|
Download:
|
| 图 2 闭锁机构失效过程原理图 Fig. 2 Locking mechanism failure process schematic diagram | |
在撞击过程中,考虑到闭锁机构无法自由转动,火箭弹的刚度远大于闭锁机构,能量耗散主要在塑性变形上,因此对图 2模型作如下假设:1)受冲击体(闭锁机构)不能自由运动;2)冲击载荷量级相同时,受冲击体变形相同;3)冲击体(弹体)为刚体,不发生变形; 4)不考虑声、热等的能量消耗。
根据冲量定理和能量守恒定理有
| $ \smallint \left( {F - f} \right){\rm{d}}t = M({v_1} - {v_0}) $ | (1) |
| $ \smallint F{\rm{d}}s = \frac{1}{2}M(v_1^2 - v_0^2) + \frac{1}{2}{\rm{ }}m{(a{v_1})^2} + U $ | (2) |
| $ \smallint f{\rm{d}}s = \frac{1}{2}m{(a{v_1})^2} + U $ | (3) |
式中:F为冲击体所受推力,f为冲击体所受阻力,M为冲击体质量,v1为受冲击体失效时冲击体速度,v0为开始撞击时冲击体速度,s为受冲击体失效时冲击体运行位移,m为受冲击体质量,a为受冲击体失效时受冲击体质心等效速度与v1的比值(考虑到在撞击过程中,冲击体与受冲击体保持相互接触,故a小于1),U为受冲击体失效或者破坏时的变形能。为了方便求解,将初始计算时刻前移至冲击体速度为零时刻,同时假设Fc为该过程中平均推力,fc为平均阻力,于是式(1)~(3)可转化为
| $ \frac{1}{2}({F_{\rm{c}}} - {f_{\rm{c}}}){t^2} = Ms $ | (4) |
| $ {F_{\rm{c}}}s = \frac{1}{2}Mv_1^2 + \frac{1}{2}m{(a{v_1})^2} + U $ | (5) |
| $ {f_{\rm{c}}}s = \frac{1}{2}m{(a{v_1})^2} + U $ | (6) |
从式(4)~(6)中,可以看出,当s一定时,fc随Fc的增大而增大,随M的增大而减小,时间t与
| $ ({F_{\rm{c}}} - F{{'}_{\rm{c}}})s = \frac{1}{2}(M + {a^2}m)(v_1^2 - v{'}_1^2) $ | (7) |
| $ ({f_{\rm{c}}} - f{{'}_{\rm{c}}})s = \frac{1}{2}{a^2}m(v_1^2 - v{'}_1^2) $ | (8) |
由式(7)、(8)可得
| $ {f_{\rm{c}}} - f{{'}_{\rm{c}}} = \frac{{{a^2}m}}{{M + {a^2}m}}({F_{\rm{c}}} - F{{'}_{\rm{c}}}) $ | (9) |
对于闭锁机构,有a2m≪M,则
| $ {f_{\rm{c}}} - f{{'}_{\rm{c}}} = 0 $ | (10) |
可见,对于不同推力载荷,当a2m≪M时,平均阻力大小近似相等。当任意选取两个不同质量M和M',保持其他参数不变时,则由式(5)~(6)可得
| $ (M + {a^2}m)v_1^2 = (M' + {a^2}m)v{'}_1^2 $ | (11) |
| $ ({f_{\rm{c}}} - f{{'}_{\rm{c}}})s = \frac{1}{2}(M'v{'}_1^2 - Mv_1^2) $ | (12) |
当a2m≪M,M'时,则
| $ {f_{\rm{c}}} - f{{'}_{\rm{c}}} = 0 $ | (13) |
可见,对于不同质量M和M',当a2m与其相差很大时,平均阻力大小近似相等。
由此,可以认为闭锁机构在失效过程中产生的平均阻力保持恒定,撞击作用时间与冲击体质量的平方根成正比,与平均推力跟平均阻力之差的平方根成反比。
2 有限元验证与等效实验验证 2.1 有限元仿真验证 2.1.1 闭锁机构强制解脱过程有限元模型建立根据1.1节的撞击失效简化模型,建立如图 3所示有限元模型。图 3中板1代表冲击体,质量为M,板2代表闭锁机构,质量mbs=1 kg。1、2之间设置接触关系,对板1施加作用力Fc,板2左侧设置固定边界条件。

|
Download:
|
| 图 3 闭锁机构作用有限元模型示意图 Fig. 3 Finite element model of locking mechanism | |
考虑到火箭弹推力平均值约70 kN,受冲击体质量需满足M≫a2m的条件,同时考虑到后续实验中受冲击体质量的合理性,选取Fc=60 kN、M=70 kg,Fc=80 kN、M=70 kg以及采用推力曲线(如图 4)、M=700 kg,进行三组有限元仿真,仿真结果如图 5及表 1所示。

|
Download:
|
| 图 4 推力载荷曲线 Fig. 4 Thrust load curve | |

|
Download:
|
| 图 5 不同参数下位移-时间仿真曲线 Fig. 5 Displacement-time simulation curves under different parameters | |
| 表 1 不同参数下的解脱时间 Tab.1 Time of unlock process under different parameters |
根据式(4)由前两组的结果可以求出平均阻力fc=4 615 N。对于采用推力曲线、质量M=700 kg的模型,进行理论计算求解其失效所需时间,分别对推力及平均阻力进行两次时间积分,获得动力曲线(即∫∫Fdtdt-Ms)与阻滞曲线(即∫∫fcdtdt),则动力曲线与阻滞曲线的交点就是该模型解脱的理论计算时刻,如图 6所示。

|
Download:
|
| 图 6 解脱时间求解曲线 Fig. 6 Time of unlock process solving curve | |
从图 6中曲线可以看出,在冲击体质量700 kg、采用推力曲线的情况下,理论解脱时间为37.3 ms,仿真结果36.6 ms。由于理论计算中,平均阻力被近似为恒定,而仿真中其值是变化的,因此二者有误差。工程经验表明,1.91%的误差基本可以说明理论与仿真的一致性,因此认为闭锁机构在撞击失效过程中的特性规律与理论推导相符。
2.2 等效实验设计及验证根据前述结果,设计实验测量闭锁机构的平均阻力,评估真实环境下闭锁机构的撞击失效性能。
2.2.1 实验设计实验原理如图 7所示。实验装置主要由落锤、橡胶垫、压头和闭锁机构组成,各部分作用如下:

|
Download:
|
| 图 7 原理图 Fig. 7 Schematic diagram | |
1) 落锤:给装置施加冲击载荷;
2) 橡胶垫:起缓冲作用,以延长冲击作用时间;
3) 压头:将载荷传递至闭锁机构。
2.2.2 落锤冲击力作用分析由前文分析可知,通过改变平均推力或冲击体质量均可获取计算闭锁机构平均阻力所需的2组实验数据。由于改变冲击体质量不易操作,因此,实验中主要通过改变推力特性来获取计算所需参数。
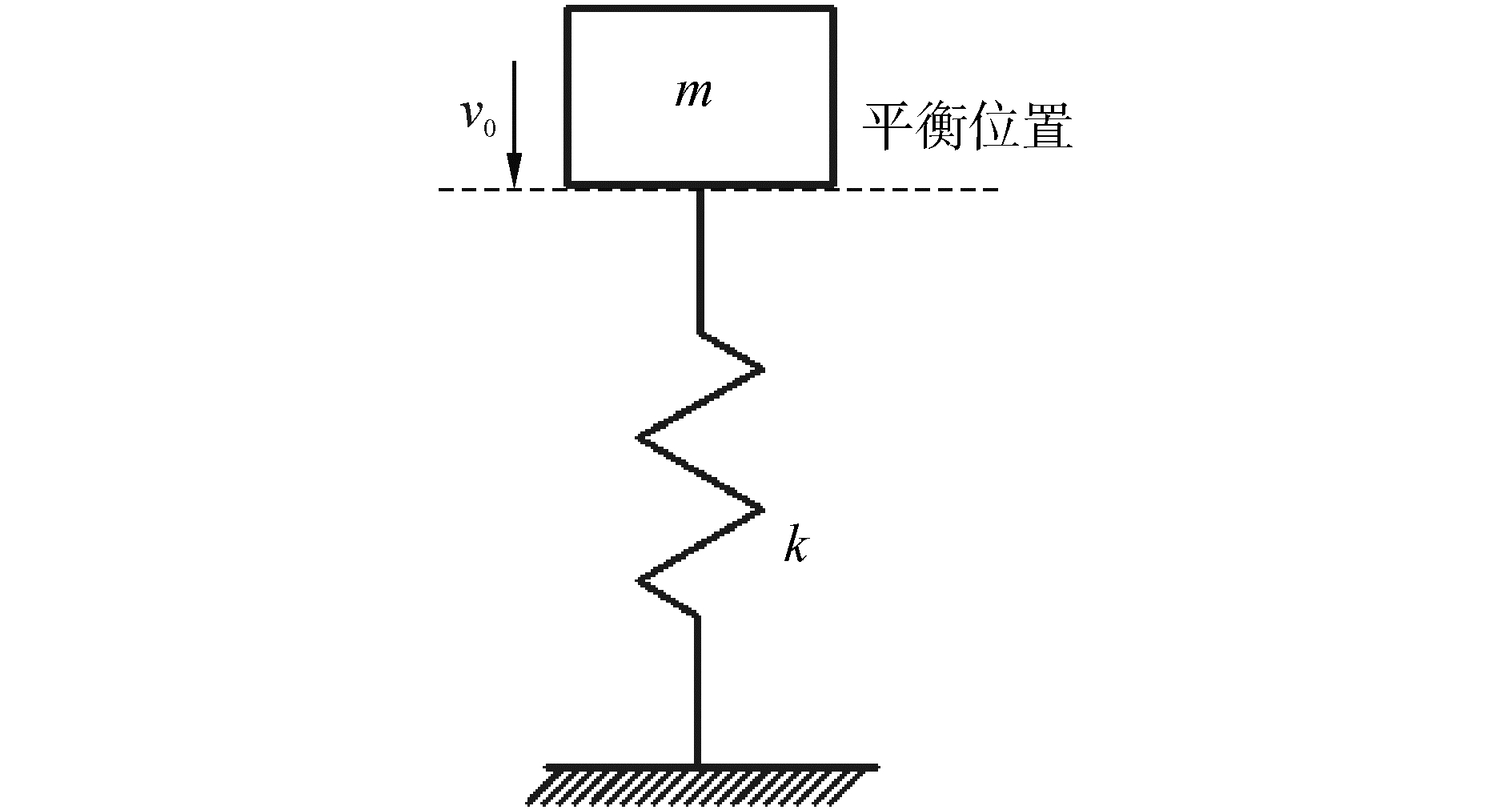
实验中通过落锤冲击橡胶垫产生推力,当落锤锤开始与橡胶垫接触时,二者可简化成一个单自由度弹簧振子系统[19],如图 8所示。
|
Download:
|
| 图 8 弹簧振子系统图 Fig. 8 Spring vibration subsystem diagram | |
其运动学特性即可视为单自由度系统的自由振动,故有
| $ x\left( t \right) = A\sin ({\omega _{\rm{n}}}t + \varphi ) $ | (14) |
| $ {\omega _{\rm{n}}} = \sqrt {k/m} $ | (15) |
| $ {T_{\rm{n}}} = 2{\rm{ \mathsf{ π} }}/{\omega _{\rm{n}}} $ | (16) |
| $ F = kx\left( t \right) $ | (17) |
| $ A = \sqrt {2ghm/k} $ | (18) |
式中:x(t)为弹簧振子系统振子的位移,A为振幅,ωn为系统的固有频率,φ为相角,Tn为系统的周期,k为系统刚度系数(即橡胶垫的等效刚度系数),m为振子质量(即落锤质量),h为落锤初始高度。
由式(15)~(18)可以看出,影响推力特性的因素主要有振子质量m,落锤初始高度h和系统刚度系数k。振子质量m和系统刚度系数k可分别通过改变落锤质量和橡胶垫等效刚度系数实现。对于橡胶垫,有如下关系:
| $ $ | (19) |
式中:S为受力面积,E为橡胶垫弹性模量,l为橡胶垫原始厚度,Δl为橡胶垫变形量。根据式(19)可以知道橡胶垫的等效刚度系数为ES/l,因此,通过改变橡胶垫的厚度、受力面积以及橡胶垫弹性模量,可以改变橡胶垫的等效刚度系数。
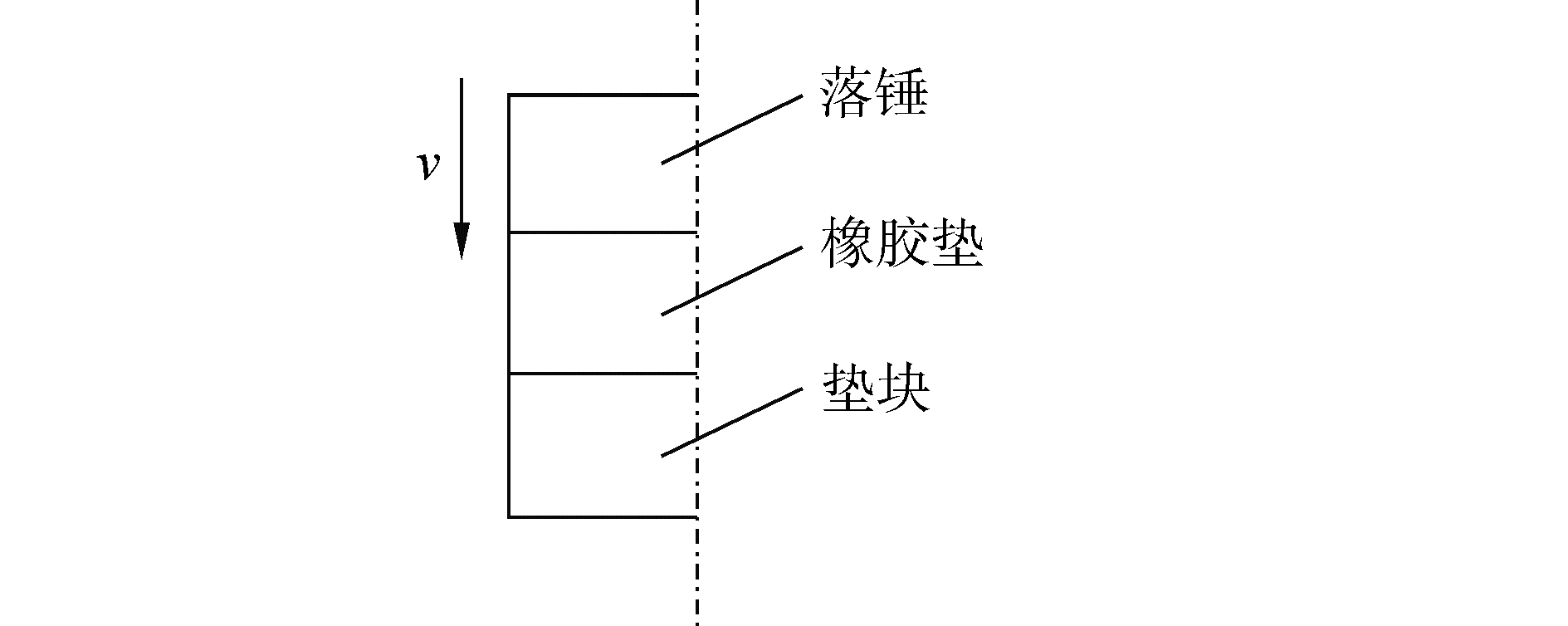
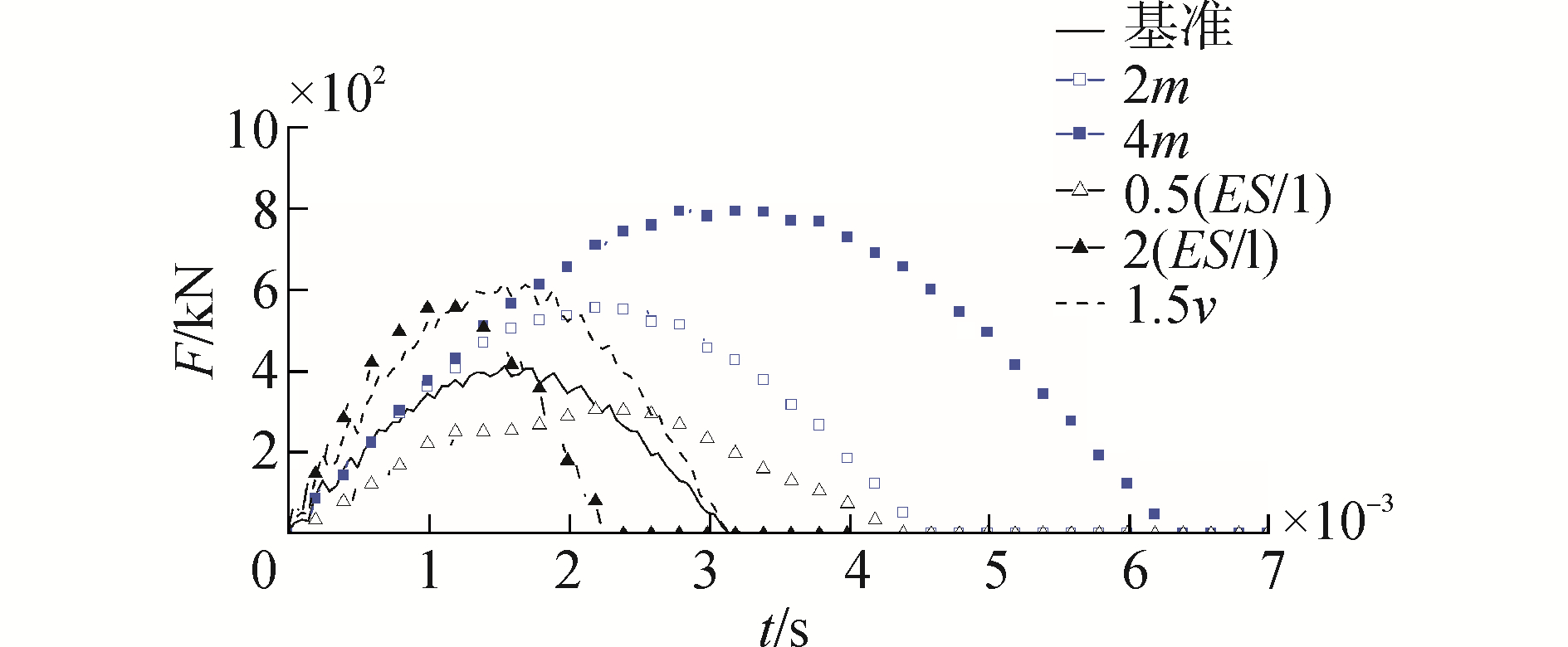
2.2.3 落锤冲击力作用仿真分析验证为进一步仿真验证落锤冲击力的作用规律,建立如图 9所示的有限元模型,模型自上而下由落锤、橡胶垫和垫块组成,橡胶垫上下表面分别与落锤和垫块产生接触关系,垫块下表面设置为固定边界条件,赋予落锤初始速度v。选取基准参数:落锤质量m=200 kg,橡胶垫半径100 mm,厚度l=75 mm,弹性模量E=500 MPa,初始速度v=2 000 mm/s。分别改变落锤的质量m、橡胶垫的等效刚度系数ES/l和落锤初始速度v,得到如图 10和表 2所示结果。
|
Download:
|
| 图 9 落锤冲击有限元模型示意图 Fig. 9 Finite element model of drop hammer impact | |
|
Download:
|
| 图 10 不同参数下冲击力曲线 Fig. 10 Impact force curves under different parameters | |
| 表 2 不同参数下冲击力最大值及撞击时间 Tab.2 Maximum impact force and impact time under different parameters in the table |
从图 10和表 2中可以看出,通过改变落锤质量、落锤高度和橡胶垫等效刚度系数,可以改变冲击力作用特性。
2.2.4 撞击失效过程规律实验验证根据图 7原理,采用真实的闭锁机构设计实验装置。在落锤与橡胶垫之间设置力传感器来获取冲击力,在闭锁机构上添加应变片,将所测应力等效转换为闭锁机构的受力,根据受力情况判断其解脱作用时间。根据2.2.3节结论,改变落锤高度获取实验数据,并选取3次实验数据进行分析,结果如图 11所示。

|
Download:
|
| 图 11 3次实验冲击力及闭锁机构受力 Fig. 11 Impact force and locking mechanism stress in 3 experiments | |
3次实验的解脱所用时间由各自闭锁机构受力曲线获得,将冲击力曲线进行两次时间积分,结果如表 3所示。
| 表 3 3次冲击实验结果 Tab.3 Results of 3 impact experiments in the table |
由实验1及实验2结果,根据式(4)可求得平均阻力fc=4.44 kN, 进而求得在实验3冲击载荷下解脱所需的理论时间(20.46 ms),与实验结果(20.7 ms)的误差为1.16%。分析误差原因,可能由理论计算中近似平均阻力不变和实验的系统误差造成。
3 结论1) 通过理论推导建立的闭锁机构撞击失效模型及由此获得的撞击失效规律,可为闭锁机构撞击失效过程的理论和实验研究提供基础参考。
2) 当闭锁机构撞击失效过程的应变率不变时,即使冲击载荷和冲击体质量发生变化,闭锁机构提供的平均阻力依然恒定。
3) 依据本文定义的闭锁机构平均阻力,可以评估真实环境条件下火箭弹强制解脱过程中的闭锁机构失效性能,研究结果可初步为闭锁机构的设计及其可靠性和安全性评价提供一种途径。
| [1] |
李军, 马大为, 曹听荣, 等. 火箭发射系统设计[M]. 北京: 国防工业出版社, 2008: 83-85.
(  0) 0)
|
| [2] |
于存贵, 李志刚. 火箭发射系统分析[M]. 北京: 国防工业出版社, 2012.
(  0) 0)
|
| [3] |
贺北斗, 林永明, 曹听荣, 等. 火箭发射装置结构分析[M]. 北京: 国防工业出版社, 1997.
(  0) 0)
|
| [4] |
万志敏, 王莉, 杜星文. 层合圆柱壳轴向撞击失效行为的试验研究[J]. 哈尔滨工业大学学报, 2001, 33(3): 304-308. WAN Zhimin, WANG Li, DU Xingwen. Failure behavior of laminated composite cylindrical shells under axial impact loading[J]. Journal of Harbin Institute of Technology, 2001, 33(3): 304-308. DOI:10.3321/j.issn:0367-6234.2001.03.009 (  0) 0)
|
| [5] |
王彪, 刘军, 杨帅. 桥墩柔性防撞装置设计及数值分析[J]. 机电工程, 2016, 33(1): 30-36. WANG Biao, LIU Jun, YANG Shuai. Flexible anti-collision device design and numerical analysis on viaduct pier[J]. Journal of mechanical & electrical engineering, 2016, 33(1): 30-36. (  0) 0)
|
| [6] |
张在中, 姚曙光. 城市轨道车辆吸能结构设计[J]. 铁道科学与工程学报, 2013, 10(3): 94-98. ZHANG Zaizhong, YAO Shuguang. Design of energy absorption structure for urban track vehicle[J]. Journal of railway science and engineering, 2013, 10(3): 94-98. DOI:10.3969/j.issn.1672-7029.2013.03.019 (  0) 0)
|
| [7] |
姜华, 王君杰, 贺拴海. 钢筋混凝土梁桥船舶撞击连续倒塌数值模拟[J]. 振动与冲击, 2012, 31(10): 68-73. JIANG Hua, WANG Junjie, HE Shuanhai. Numerical simulation on continuous collapse of reinforced concrete girder bridge subjected to vessel collision[J]. Journal of vibration and shock, 2012, 31(10): 68-73. (  0) 0)
|
| [8] |
崔铁军, 马云东. 超高层建筑受大型高速飞行物撞击所致非连续性坍塌模拟与研究[J]. 计算力学学报, 2016, 33(1): 66-72. CUI Tiejun, MA Yundong. Numerical simulation for the impact of induced discontinuity collapse of high-rise buildings with large high-speed flying object[J]. Chinese journal of computational mechanics, 2016, 33(1): 66-72. (  0) 0)
|
| [9] |
管公顺, 毕强, 张羽. 铝球弹丸高速撞击表面陶瓷化铝板防护结构实验研究[J]. 振动与冲击, 2015, 34(18): 63-68, 93. GUAN Gongshun, BI Qiang, ZHANG Yu. Experimental investigation on aluminum bumper with ceramic surface coating impacted by an aluminum sphere[J]. Journal of vibration and shock, 2015, 34(18): 63-68, 93. (  0) 0)
|
| [10] |
HUANG Jie, MA Zhaoxia, REN Leisheng, et al. A new engineering model of debris cloud produced by hypervelocity impact[J]. International journal of impact engineering, 2013, 56: 32-39. DOI:10.1016/j.ijimpeng.2012.07.003 (  0) 0)
|
| [11] |
GONGSHUN G, BAOJUN P, WEI Z, et al. Crater distribution on the rear wall of AL-Whipple shield by hypervelocity impacts of AL-spheres[J]. International journal of impact engineering, 2008, 35(12): 1541-1546. DOI:10.1016/j.ijimpeng.2008.07.028 (  0) 0)
|
| [12] |
葛庆子, 翁大根, 张瑞甫. 飞机撞击特大型LNG储罐全过程仿真分析[J]. 振动与冲击, 2016, 35(4): 1-7, 21. GE Qingzi, WENG Dagen, ZHANG Ruifu. Whole process simulation analysis of aircraft's crashing into an extra-large LNG storage tank[J]. Journal of vibration and shock, 2016, 35(4): 1-7, 21. (  0) 0)
|
| [13] |
WILT T, CHOWDHURY A, COX P A. Response of reinforced concrete structures to aircraft crash impact[R]. San Antonio, Texas: Southwest Research Institute, 2011.
(  0) 0)
|
| [14] |
HUO Jin, HU Zirong, SUN Yuping. Modeling and analysis of concrete-filled steel structure under aircraft impact[C]//ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Washington: The American Society of Mechanical Engineers, 2011: 961-965.
(  0) 0)
|
| [15] |
陈四春, 李军, 张伟, 等. 火箭炮闭锁机构工作过程瞬态动力学分析[J]. 南京理工大学学报, 2014, 38(5): 608-614. CHEN Sichun, LI Jun, ZHANG Wei, et al. Transient dynamics analysis on working process of rocket lock mechanism[J]. Journal of Nanjing University of Science and Technology, 2014, 38(5): 608-614. DOI:10.3969/j.issn.1005-9830.2014.05.006 (  0) 0)
|
| [16] |
李彦君.发射装置与火箭弹间相互作用非线性动力学分析[D].南京: 南京理工大学, 2012. LI Yanjun. Nonlinear dynamic analysis of the interaction between the launcher and the rocket[D]. Nanjing: Nanjing University of Science and Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10288-1013165674.htm (  0) 0)
|
| [17] |
周彦江, 袁占杰, 刘广生. 某型火箭炮闭锁装置检测研究[J]. 火炮发射与控制学报, 2010(4): 106-109. ZHOU Yanjiang, YUAN Zhanjie, LIU Guangsheng. Study on lock mechanism test in a type of rocket launcher[J]. Journal of gun launch & control, 2010(4): 106-109. DOI:10.3969/j.issn.1673-6524.2010.04.026 (  0) 0)
|
| [18] |
陈国虎, 陈祥龙, 应跃明, 等. 火箭发射装置闭锁力自动检测装置研究[J]. 机电工程, 2015, 32(9): 1210-1213. CHEN Guohu, CHEN Xianglong, YING Yueming, et al. Automatic detecting device for locking force of rocket launcher[J]. Journal of mechanical & electrical engineering, 2015, 32(9): 1210-1213. (  0) 0)
|
| [19] |
张义民. 机械振动[M]. 北京: 清华大学出版社, 2007. ZHANG Yimin. Mechanical vibration[M]. Beijing: Tsinghua University Press, 2007. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


