2. 中南大学 高性能复杂制造国家重点实验室, 湖南 长沙 410083;
3. 中铁十四局集团有限公司, 山东 济南 250014
2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China;
3. China Railway 14 th Construction Bureau Co. Ltd., Ji'nan 250014, China
断面岩石隧道掘进机(full-face rock tunnel boring machine, TBM)凭借其安全、高效、稳定等优点被广泛应用于水利工程等岩石环境隧道的开发建设[1]。TBM掘进时,滚刀破碎岩石形成的岩碴通过出碴槽、刮碴板、溜碴板和皮带输送机等出碴系统排出[2]。在刀盘上如何布置出碴槽,设计其结构形状,避免岩碴卡死滚刀和对滚刀产生二次磨损是TBM刀盘设计的重要环节,也是影响TBM掘进效率的关键[3-4]。在盾构刀盘开口特征方面,王洪新[5]通过理论计算得到不同开口率刀盘在地层中产生的额外应力,提出开口率定量选型方法,并成功应用于上海地铁工程;Shi等[6]通过试验研究获得了刀盘扭矩随开口率的增加而减小;刘建琴等[7-8]应用流体力学方法模拟了土体-盾构刀盘系统流场静压力和流场速度分布,探究了刀盘开口率对刀盘前后压差的影响规律;郭伟等[9]基于CFD理论,研究不同开口分布特征对盾构机刀盘前后支护压力、渣土流量以及压力传递函数的影响;Xu等[10]通过盾构相似试验台对比分析了2种不同开口率的刀盘其推力、扭矩以及土舱压力的变化;武力等[11-12]建立了盾构土舱压力离散元数值模型,研究了不同刀盘开口率下密封舱隔板压力分布规律。关于TBM刀盘开口方面的研究相对较少:霍军周等[13-14]以引洮工程为研究对象,基于岩碴流动性仿真研究了TBM刀盘出碴槽口的优化选型;陈巍等[15]利用PFC3D对出碴过程进行仿真,确定了5.55 m直径刀盘的合理开口面积。上述研究分别从不同角度采用不同理论模型、数值方法和实验研究探究刀盘开口特征对刀盘载荷特性的影响,但是还没有关于利用数值方法真实模拟刀盘出碴过程的文献。
本文以引松供水隧道工程为研究背景,基于离散元方法,并考虑掘进过程中岩碴产生、下落以及与滚刀的碰撞等因素,建立了TBM排碴过程的数值计算模型,探究出碴槽开口特征参数对出碴效率的影响规律。
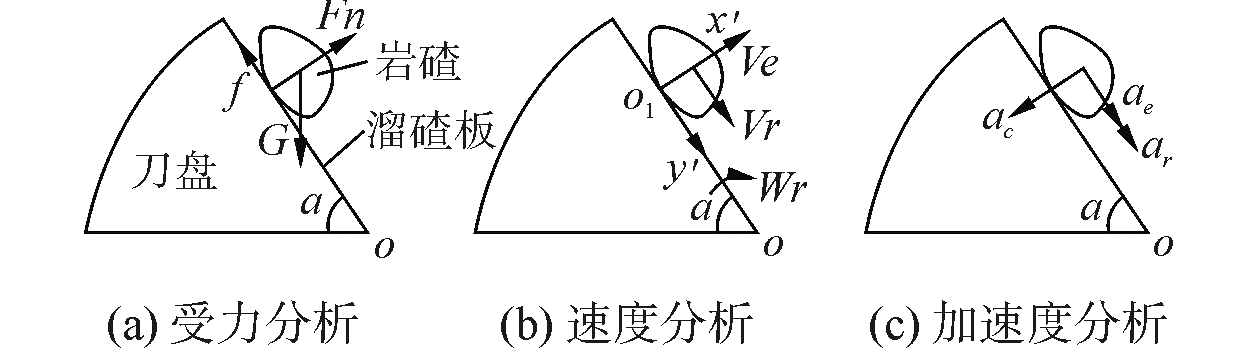
1 TBM出碴过程数值计算建模 1.1 TBM出碴过程分析岩碴相对溜碴板的运动为沿着溜碴板向下滑动,相对速度为Vr,动参考系O1x′y′固定在溜碴板上,溜碴板绕刀盘中心轴匀速转动,因此岩碴的牵连运动Ve沿切向运动,相对加速度为ar。刀盘从水平位置逆时针旋转α角度时,岩碴在溜碴板上承受重力、来自溜碴板的支持力和摩擦力,如图 1(a)所示。岩碴的速度和加速度分析如图 1(b)、(c)所示。
|
Download:
|
| 图 1 岩碴的受力和运动分析 Fig. 1 The load and motion of rock analysis | |
| $ m({a_r} + {a_e}) = mg\sin \alpha - {\mu _d}{F_N} $ | (1) |
| $ m{a_c} = mg\cos \alpha - {F_N} $ | (2) |
式中:科氏加速度ac=2ωe×vr,方向垂直于溜碴板向下;相对加速度ae为向心加速度,指向刀盘中心O, ae=ωe2r;相对速度vr=∫stardt;径向位移Sr=∫stvrdt;径向距离r=Rmax-Sr;刀盘转角α=ωet。
岩碴脱离溜碴板时,支持力为0,即FN(te)=0。g=9.81 m/s2,当ω=8 r/min,μd=0.45,r=3.965 m时,得到αs=69.3°,即当刀盘从水平位置逆时针旋转69.3°时,岩碴脱离溜碴板。
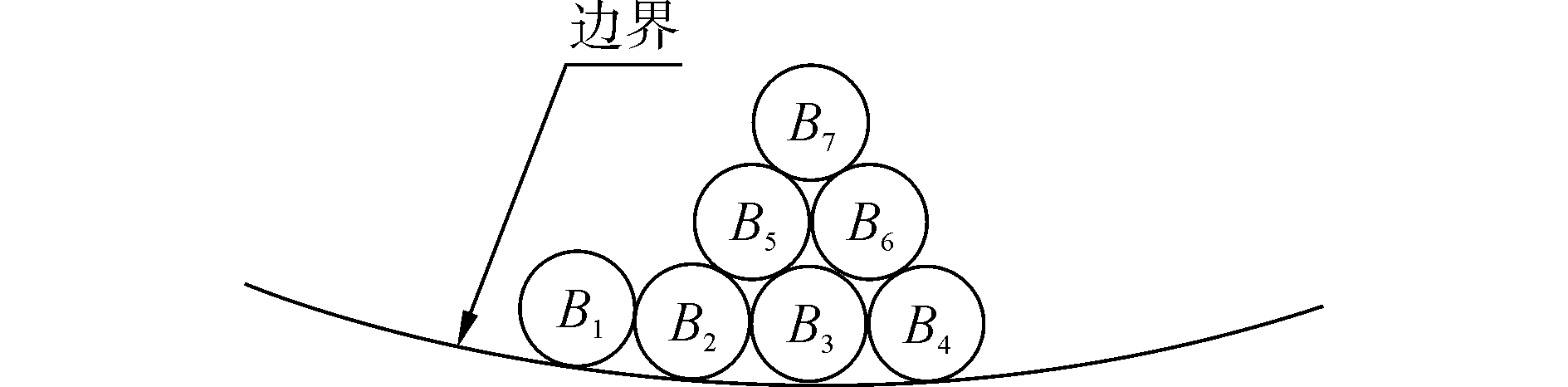
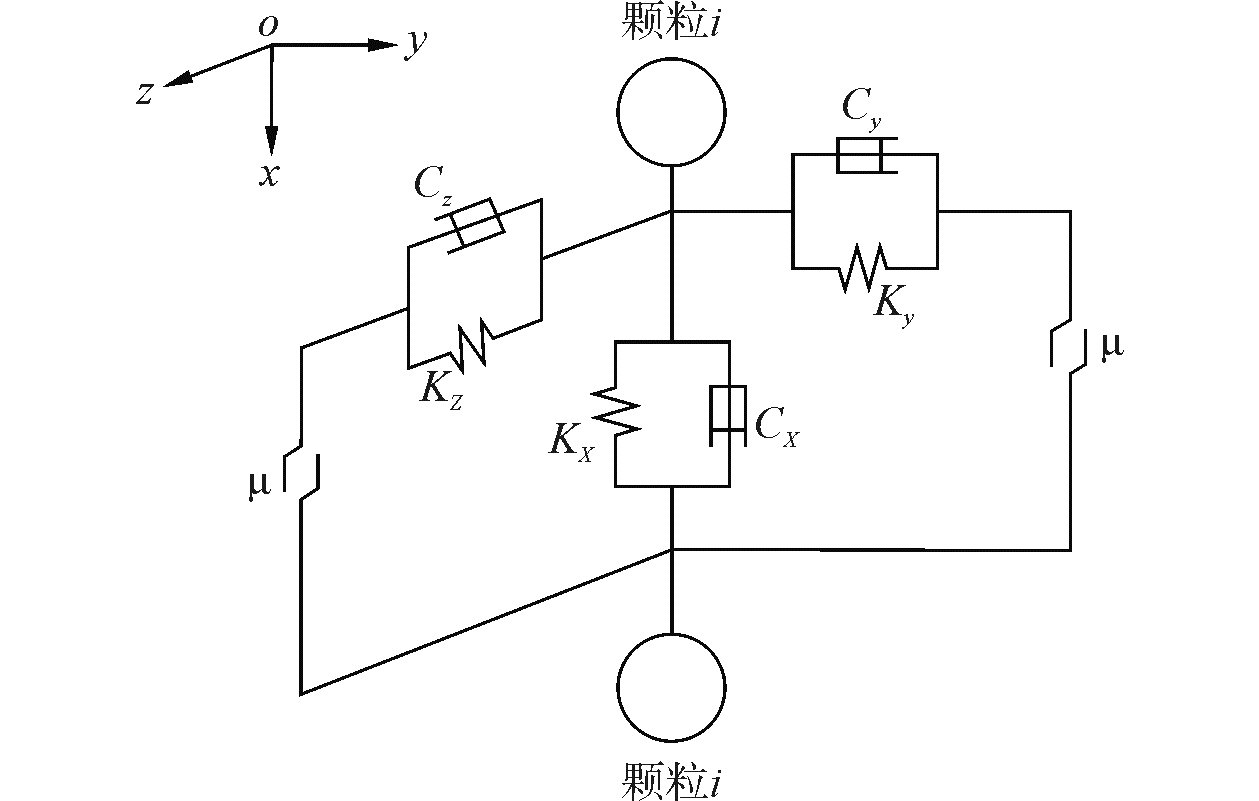
1.2 离散元岩碴颗粒模型的建立隧道地层岩石是脆性材料,其破坏过程是内部裂纹产生、扩展、合并直至贯通的过程。由于复杂的地质条件和TBM工作性能的不稳定性,切削下来的岩块性状具有随机性、不规则性,但是切削下来的岩碴总体积不变,因此采用离散元球形颗粒模拟TBM在掘进过程中产生的岩碴。岩碴颗粒之间的碰撞是瞬时的,且在碰撞过程中不会产生显著的塑性变形。如图 2所示,离散元方法中用振动运动方程来模拟岩碴颗粒与岩碴颗粒以及岩碴颗粒与地质边界的接触。如图 3所示,建立局部坐标系,x为法向方向,法线方向的振动可以通过弹簧阻尼器来体现;y、z为切向方向,切向振动表现为切向滑动和岩碴颗粒的滚动,简化为弹簧阻尼器和摩擦元件。当切向力大于摩擦力时两岩碴颗粒产生相对运动,滑动摩擦元件才起作用。运动方程为
|
Download:
|
| 图 2 岩碴颗粒相互接触及岩碴颗粒与边界的接触 Fig. 2 Contact between rock particles and boundary | |
|
Download:
|
| 图 3 岩碴颗粒之间的接触模型 Fig. 3 Contact model between rock particles | |
| $ m{{\ddot U}_x} + {C_x}{{\dot U}_x} + {K_x}{U_x} = {F_x} $ | (3) |
| $ m{{\ddot U}_{y, z}} + {C_{y, z}}{{\dot U}_{y, z}} + {K_{y, z}}{U_{y, z}} = {F_{y, z}} $ | (4) |
| $ I\ddot \varphi + ({C_{y, z}}\dot \varphi + {K_{y, z}}\varphi )r = {M_{y, z}} $ | (5) |
式中:m为岩碴的等效质量,I为岩碴的等效转动惯量,r为旋转半径,U为岩碴的相对位移,φ为岩碴自身的旋转角度,F为岩碴所受外力,M为岩碴所受外力矩,K为接触模型中的弹性系数,C为阻尼系数。
根据岩碴颗粒单元间的相互作用和牛顿运动定律采用动态松弛法进行循环迭代计算,确定每一个时间步长所有单元的受力和位移,并更新所有单元的位置。通过对每个单元的微观运动进行跟踪计算,即可得到整个研究对象的宏观运动规律。
1.3 TBM出碴仿真模型的建立以某工程的TBM刀盘为研究对象,假设刀盘作纯转动且刀盘上所有滚刀的贯入度一致,在TBM掘进的过程中,单位时间内产生的岩碴量是由实际的掘进速度决定的。由于TBM掘进过程中刀盘整体向前推进,掌子面表面积与刀盘盘面面积基本相同,则刀盘转动一周掌子面产生的岩碴体积VK与颗粒单元数量N分别为
| $ {V_K} = \lambda AH = \lambda \frac{{{\rm{ \mathsf{ π} }}{D^2}}}{4}H $ | (6) |
| $ N = \frac{{{V_K}}}{{4/3{\rm{ \mathsf{ π} }}{r^3}}} $ | (7) |
式中:根据该工程的地质条件确定岩石的孔隙率λ=1.5;刀盘直径D=7.93 m;滚刀的贯入度H=6 mm/r;可得N=1 132,因此设置刀盘旋转一周产生颗粒单元为1 132个。
根据实际TBM出碴过程,固定岩壁的所有自由度;刀盘转速为6 r/min;掌子面上产生的岩碴设置水平向后0.8 mm/s的速度来模拟刀盘向前掘进的速度;整个系统赋予竖直向下的重力加速度。
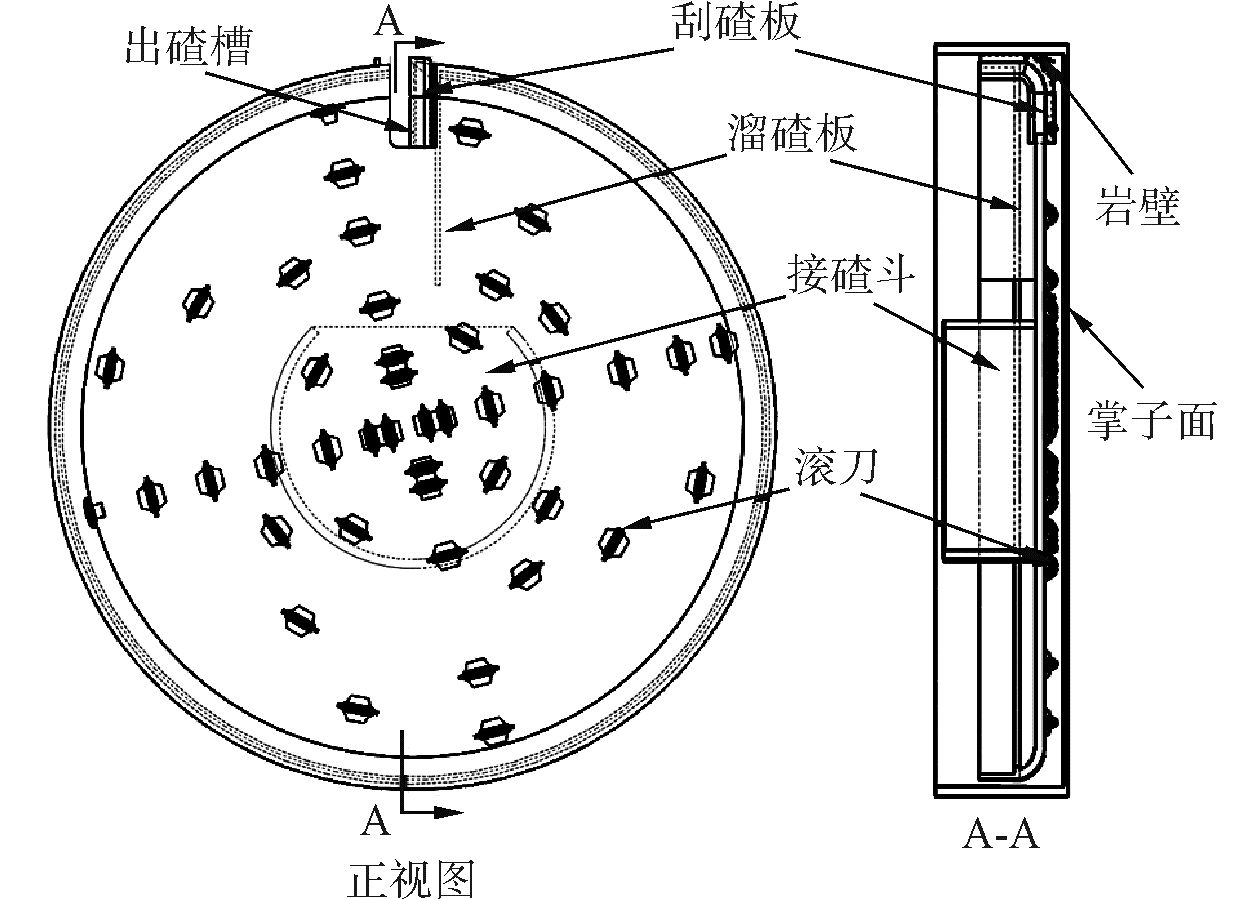
初步确定总开口面积为3.4 m2,由于每个出碴槽的结构都为长条铲斗型,并且出碴原理相同,以单个出碴槽为研究对象,其开口面积为0.425 m2。岩碴在刀盘与掌子面之间下落过程会不断与盘面上的滚刀发生碰撞,因此保留滚刀突出刀盘盘面的部分。由于滚刀距刀盘正面板0.15 m,因此在刀盘前方0.15 m建立一个与刀盘等直径的圆面来模拟掌子面,在圆面上随机产生一定数量的球形颗粒单元,来模拟TBM掘进过程中产生的岩碴,在刀盘后方布置溜碴板和集碴斗,用以统计岩碴数量,简化后的模型如图 4所示。
|
Download:
|
| 图 4 刀盘简化模型 Fig. 4 The simplified model of cutterhead | |
刮碴板以刀盘最上方为起始位置,刀盘逆时针旋转,岩碴颗粒单元在掌子面上随机位置产生,在重力场的作用下竖直向下运动,可能与多把滚刀发生碰撞,如图 5所示,该岩碴颗粒与滚刀发生了两次碰撞。随后落入掌子面与刀盘盘面之间的底部,当t=5.8 s时,即出碴槽从底部旋转29°,岩碴进入刀盘内部。随着刀盘的旋转被刮碴板带着旋转。当t=8 s时,即溜碴板与x轴正方向呈18°,岩碴颗粒单元开始在溜碴板上向下滑动;当t=9.4 s时,即溜碴板与x轴正方向呈68°,岩碴颗粒单元脱离溜碴板,随皮带输送机排出洞外,完成一次排碴过程,如图 6所示。

|
Download:
|
| 图 5 单个岩碴颗粒的运动轨迹 Fig. 5 The motion trajectory of the rock particle | |

|
Download:
|
| 图 6 TBM出碴过程 Fig. 6 TBM mucking process | |
为了研究单个出碴槽长度以及宽度尺寸对出碴性能的影响规律,控制出碴槽开口面积一定,改变出碴槽的开口长度和宽度的比值,受刀盘布置滚刀的限制,出碴槽长宽比值从1逐渐增加至2.6,设计了16组仿真方案,如表 1所示。
| 表 1 出碴槽不同长宽比仿真方案 Tab.1 Simulation scheme of mucking slots with different aspect ratio |
当出碴槽长宽比为1时, 通过的岩碴颗粒数随时间的变化曲线如图 7所示。当t=8.4 s时,即溜碴板与x轴正方向呈32°,接碴斗中开始出现颗粒单元;8.4~9.2 s时,即溜碴板与x轴正方向的角度从32°转动到61°,接碴斗内颗粒数量增长速度呈现先增大后趋于平缓;在9.2~9.8 s时,即溜碴板与x轴正方向的角度从61°转动到83°,颗粒数保持最大的增长速度急剧增加,在9.8 s之后,颗粒数基本保持不变,完成一个排碴过程。对比出碴槽长宽比分别为1、2、2.6时排碴颗粒数随时间的变化曲线,可知:出碴槽长宽比从1增加至2.6,出碴槽明显变窄了,排碴颗粒数的增长速度明显减慢,颗粒数达到稳定的时间基本相同,排碴颗粒数的增长速度降低,排碴效率大大下降。

|
Download:
|
| 图 7 不同长宽比的出碴槽排碴数量随时间的变化曲线 Fig. 7 Variation of rock quantity with different aspect ratios | |
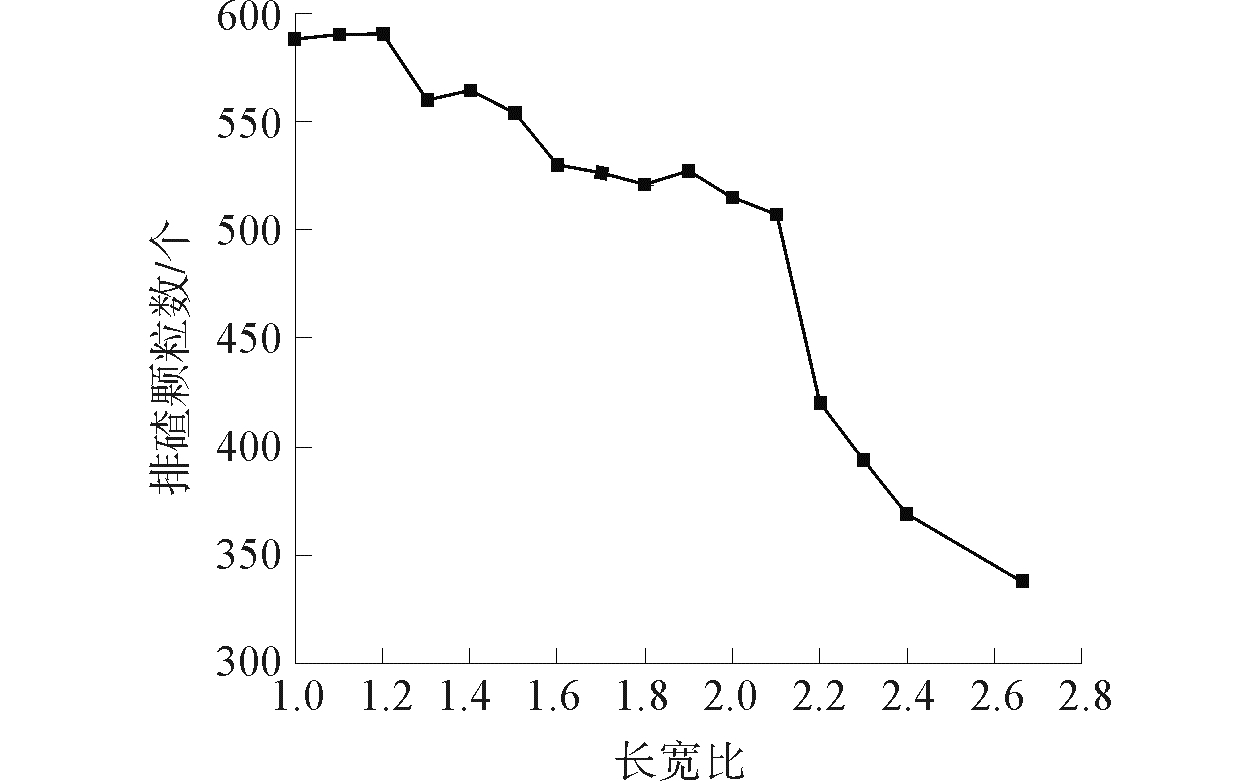
经过仿真模拟,得到出碴颗粒数随出碴槽长宽比值的变化曲线,如图 8所示。随着出碴槽长宽比值的增大,排碴颗粒数呈现总体下降的趋势。当出碴槽长宽比值为1~1.2时,排碴颗粒数基本保持不变;出碴槽长宽比值为1.2~2.1时,随着长宽比值的不断增大,排碴颗粒数缓慢减少,长宽比为2.1时的排碴量比长宽比为1时的排碴量下降了14%;当长宽比值从2.1增加至2.6,排碴量急剧减少,长宽比为2.6时,排碴量较长宽比为1时的排碴量下降了4 3%。因此在设计出碴槽的时候应优先考虑出碴槽的开口宽度。
|
Download:
|
| 图 8 出碴颗粒数随出碴槽长宽比的变化曲线 Fig. 8 Relationship between aspect ratio and rock quantity | |
控制开口面积不变,开口宽度为600 mm,改变出碴槽的开口角度,从0°逐渐增加到45°分别设计10组仿真方案,如图 9(a)所示。控制开口面积和开口长度708 mm不变,改变出碴槽的开口角度,从0°逐渐增加到45°分别设计10组仿真方案,如图 9(b)所示。

|
Download:
|
| 图 9 不同开口角度出碴槽设计方案 Fig. 9 Desin scheme of mucking slot with different angles | |
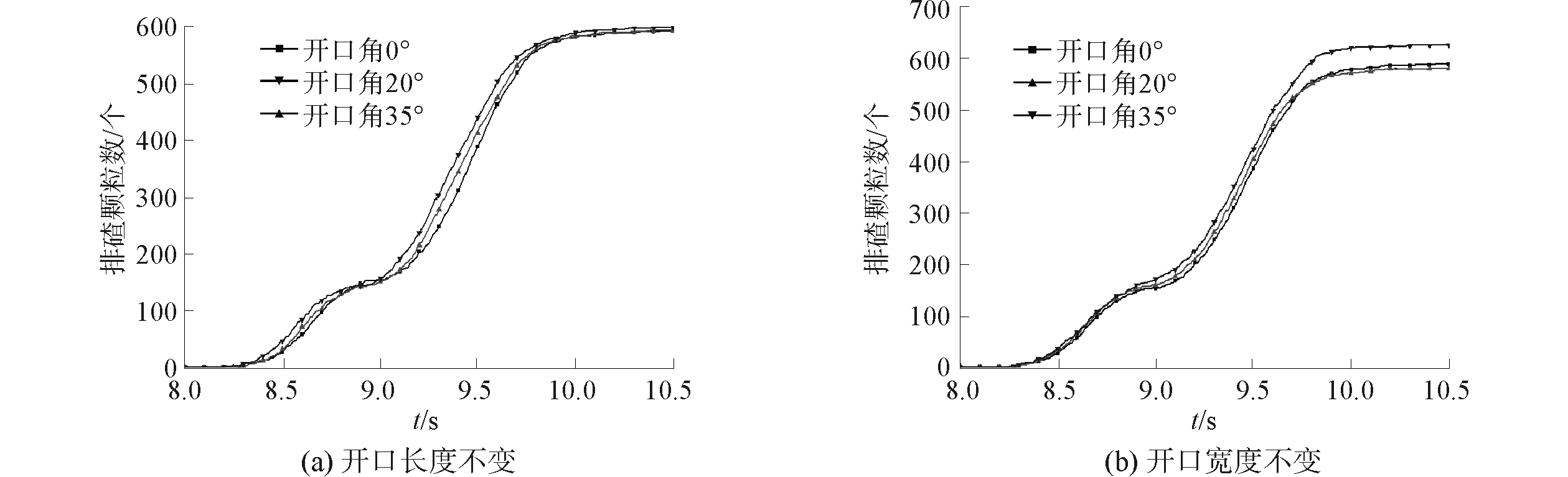
控制出碴槽的开口长度不变,设置不同的开口角度,排碴颗粒数随时间的变化曲线如图 10(a)所示。在出碴过程前期,开口角度越大,排碴速度越慢;在出碴过程中期,开口角度越大,排碴速度越快;在出碴过程后期,颗粒数均逐渐趋于稳定,完成出碴过程;控制出碴槽的开口宽度不变,设置不同的开口角度,排碴颗粒数随时间的变化曲线如图 10(b)所示。在出碴过程的前期,开口角度对排碴过程基本影响不大;在出碴过程中期,开口角度越大,排碴速度越快;在出碴过程后期,颗粒数均逐渐趋于稳定,完成出碴过程。
|
Download:
|
| 图 10 不同开口角度排碴数量曲线 Fig. 10 Variation of rock quantity with different angles | |
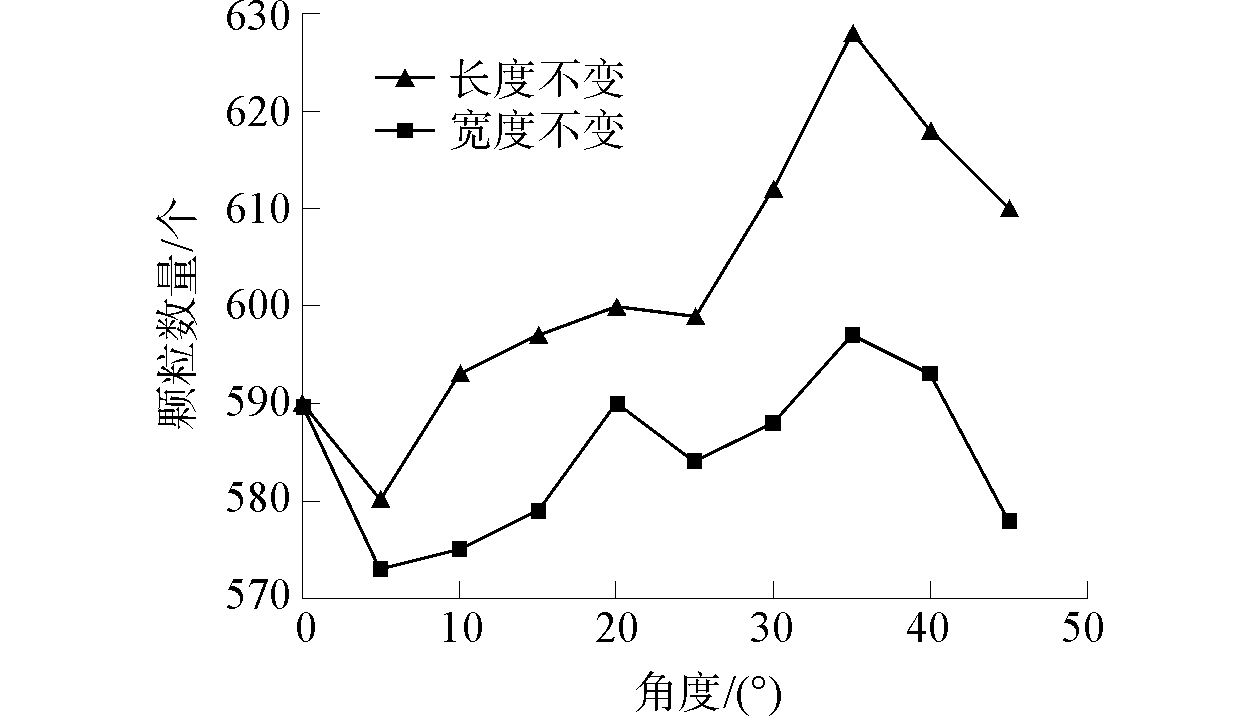
通过仿真数值模拟,得到出碴效率随开口角度的变化规律,如图 11所示。随着出碴槽开口角度的增大,无论是控制开口长度不变还是开口宽度不变,排碴量随开口角度变化趋势相似,都呈现先增加后减少的趋势;控制开口宽度不变时,出碴效率明显高于控制长度不变的出碴效率,说明开口宽度的影响因子高于开口长度;当开口角度从5°增长到20°时,排碴量呈平缓增长趋势,当开口角度从25°增加至35°时,排碴量呈现急剧增长趋势,在开口角度为35°时达到最大值。控制开口宽度不变时,开口角度为35°时排碴量相比于开口角度为5°时增长了8%;控制开口长度不变时,开口角度为35°时排碴量相比于开口角度为5°时增长了4%。因此在设计出碴槽时,在控制宽度尽量大的前提下,优先设置开口角度范围为20°~35°。
|
Download:
|
| 图 11 出碴颗粒数随出碴槽开口角度的变化曲线 Fig. 11 Relationship between opening angle and rock quantity | |
采用离散元方法,建立TBM出碴过程数值模拟模型,得到出碴槽长宽比和出碴槽开口角度对出碴性能的影响规律,结果表明出碴槽长宽比越接近于1,出碴效率越高,在设计出碴槽时,应优先考虑出碴槽宽度;当出碴槽开口角度为20°~35°时,出碴效率较高,因此在保证出碴槽宽度的前提下,可设置出碴槽的开口角度为20°~35°。
3 工程应用某供水隧道沿线的岩石地层主要以凝灰岩和花岗岩为主,根据仿真结果该工程的刀盘开口进行设计。布置出碴槽时由于刀盘空间的局限性,只能布置8个出碴槽,宽度最大设置为500 mm;由于刀盘是由一个中心块和四个边块组成,位于边块中间位置的出碴槽长度设置为1 000 mm,鉴于空间有限,没有设置出碴槽开口角度;处于边块边缘位置的出碴槽长度只能设置为700 mm。由于靠近边块装配位置,设置有一个20°的开口角度。该工程刀盘的出碴槽布局如图 12所示。

|
Download:
|
| 图 12 TBM刀盘出碴槽布局 Fig. 12 Layout of TBM cutterhead mucking slot | |
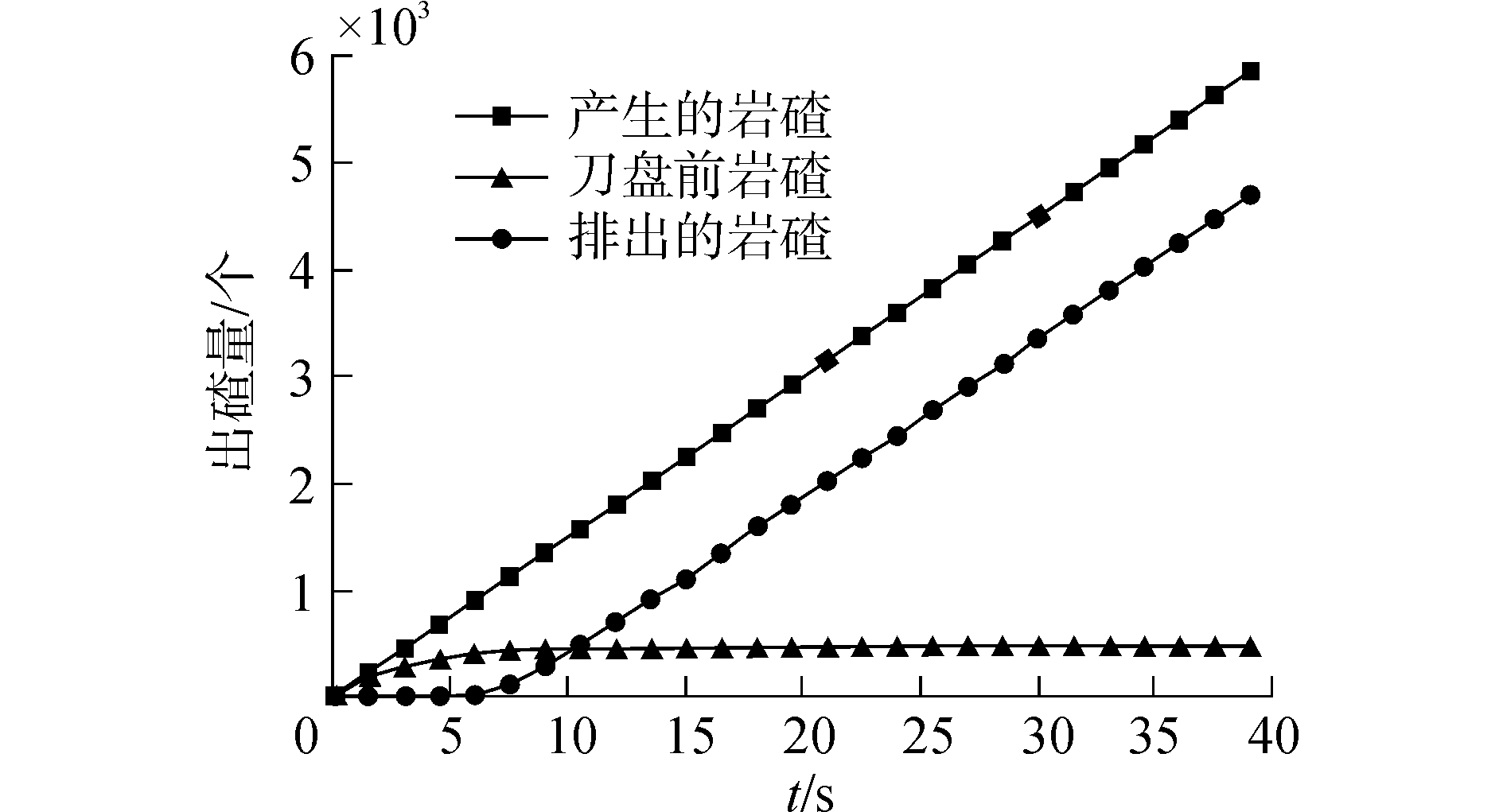
对该供水工程的最终刀盘方案进行出碴过程仿真模拟,得到该TBM的出碴特性如图 13所示。掌子面均匀产生岩碴量,刀盘排碴速率随着刀盘的旋转逐渐增大,最后趋于与产碴速率相等,因此留在刀盘与掌子面底部的岩碴趋于稳定,达到一个平衡状态。刀盘旋转四圈后出碴效率高达到80.4%。
|
Download:
|
| 图 13 供水工程刀盘出碴量随时间变化曲线 Fig. 13 Variation of rock quantity in water supply project | |
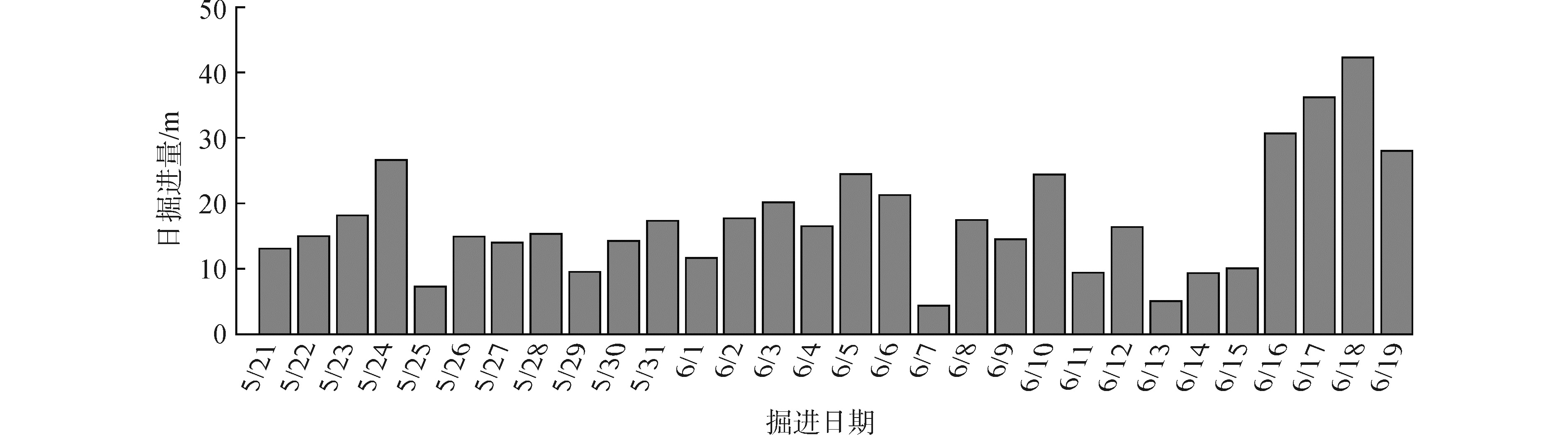
图 14所示为统计的该隧道工程TBM正常施工时的掘进量。该月的总掘进里程为544 m,最高日掘进量为42.26 m。结合现场观测结果,刀盘前的残余岩碴很少,几乎所有的岩碴都顺利地被铲斗铲起,排出洞外。目前该TBM还在施工,且设备状态良好,排碴效率高。结果表明该刀盘的开口结构设计较为合理,基于离散元理论的刀盘出碴过程仿真模拟能有效指导实际应用,为TBM刀盘出碴槽结构设计和优化提供参考价值。
|
Download:
|
| 图 14 隧道工程TBM的掘进量 Fig. 14 The tunneling speed of TBM tunnel project | |
1) 当出碴槽开口面积一定时,出碴槽长宽比越大,排碴速率越低,排碴量越少;出碴槽长宽比为2.1时,其排碴量比长宽比为1时下降了14%;当出碴槽长宽比达到2.6时与长宽比为1时相比下降了43%,设计出碴槽时应优先考虑开口宽度。
2) 随着出碴槽开口角度增大,出碴颗粒数总体呈现先增多后减少的趋势;控制宽度不变时出碴槽出碴效率明显高于控制长度不变时;当开口角度为35°时,出碴槽出碴效率最高。因此在设计出碴槽时,在保证开口宽度尽量大的前提下,应尽量将开口角度设置为20°~35°。
3) 根据仿真结果对某供水隧道工程的刀盘开口进行设计,模拟预测刀盘出碴效率较高,通过在实际工程中近两年的掘进,出碴效率良好。
| [1] |
韩美东, 曲传咏, 蔡宗熙, 等. 刀盘掘进过程动态仿真[J]. 哈尔滨工程大学学报, 2015, 36(8): 1098-1102. HAN Meidong, QU Chuanyong, CAI Zongxi, et al. Dynamic numerical simulation of tunneling by the TBM cutter head[J]. Journal of Harbin Engineering University, 2015, 36(8): 1098-1102. (  0) 0)
|
| [2] |
XIA Yimin, TANG Lu, JI Zhiyong, et al. Optimal design of structural parameters for shield cutterhead based on fuzzy mathematics and multi-objective genetic algorithm[J]. Journal of Central South University, 2015, 22(3): 937-945. DOI:10.1007/s11771-015-2604-9 (  0) 0)
|
| [3] |
ROSTAMI J, OZDEMIR L. Computer modeling of mechanical excavators cutterhead[C]//Proceedings of the World Rock Boring Association Conference. Ontario, 1996.
(  0) 0)
|
| [4] |
ROSTAMI J. Geomechanics and tunnelling, 2008, 1(1): 18-28. DOI:10.1002/(ISSN)1865-7389 (  0) 0)
|
| [5] |
王洪新. 土压平衡盾构刀盘开口率对土舱压力的影响[J]. 地下空间与工程学报, 2012, 8(1): 89-93, 104. WANG Hongxin. Influence of aperture ratio of cutterhead of EPB Shield on earth pressure in the chamber[J]. Chinese journal of underground space and engineering, 2012, 8(1): 89-93, 104. (  0) 0)
|
| [6] |
SHI Hu, YANG Huayong, GONG Guofang, et al. Determination of the cutterhead torque for EPB shield tunneling machine[J]. Automation in construction, 2011, 20(8): 1087-1095. DOI:10.1016/j.autcon.2011.04.010 (  0) 0)
|
| [7] |
刘建琴, 刘蒙蒙, 郭伟, 等. 隧道掘进机刀盘结构性能评价研究关键问题分析[J]. 现代隧道技术, 2014, 51(2): 5-10. LIU Jianqin, LIU Mengmeng, GUO Wei, et al. Analysis of key problems in the structural performance evaluation for TBM cutter heads[J]. Modern tunnelling technology, 2014, 51(2): 5-10. DOI:10.3969/j.issn.1009-6582.2014.02.002 (  0) 0)
|
| [8] |
刘建琴, 郭伟, 黄丙庆, 等. 土压平衡盾构刀盘开口率与刀盘前后压差的关系[J]. 天津大学学报, 2011, 44(8): 659-664. LIU Jianqin, GUO Wei, HUANG Bingqing, et al. Relationship between aperture ratio and fore-and-back pressure of EPB shield cutter head[J]. Journal of Tianjin University, 2011, 44(8): 659-664. DOI:10.3969/j.issn.0493-2137.2011.08.001 (  0) 0)
|
| [9] |
郭伟, 胡竟, 王磊, 等. 基于CFD的土压平衡盾构刀盘开口分布特征研究[J]. 机械工程学报, 2012, 48(17): 144-151. GUO Wei, HU Jing, WANG Lei, et al. Study on the opening distribution characteristics of earth pressure balance shield cutter head based on CFD[J]. Journal of mechanical engineering, 2012, 48(17): 144-151. (  0) 0)
|
| [10] |
XU Qianwei, ZHU Hehua, DING Wenqi, et al. Laboratory model tests and field investigations of EPB shield machine tunnelling in soft ground in Shanghai[J]. Tunnelling and underground space technology, 2011, 26(1): 1-14. DOI:10.1016/j.tust.2010.09.005 (  0) 0)
|
| [11] |
武力, 屈福政, 孙伟, 等. 基于离散元的土压平衡盾构密封舱压力分析[J]. 岩土工程学报, 2011, 32(1): 18-23. WU Li, QU Fuzheng, SUN Wei, et al. Discrete numerical model for analysis of chamber pressure of earth pressure balance shield machine[J]. Chinese journal of geotechnical engineering, 2011, 32(1): 18-23. (  0) 0)
|
| [12] |
WU Li, GUAN Tianmin, LEI Lei. Discrete element model for performance analysis of cutterhead excavation system of EPB machine[J]. Tunnelling and underground space technology, 2013, 37: 37-44. DOI:10.1016/j.tust.2013.03.003 (  0) 0)
|
| [13] |
霍军周, 杨静, 孙伟, 等. TBM刀盘支撑筋结构设计及静动态特性分析[J]. 哈尔滨工程大学学报, 2014, 35(7): 883-888. HUO Junzhou, YANG Jing, SUN Wei, et al. Structure design and static/dynamic analysis of TBM cutterhead supporting ribs[J]. Journal of Harbin Engineering University, 2014, 35(7): 883-888. (  0) 0)
|
| [14] |
霍军周, 孙伟, 欧阳湘宇, 等. 隧道掘进机刀群与盘体支撑筋耦合布置设计[J]. 机械工程学报, 2014, 50(21): 23-30. HUO Junzhou, SUN Wei, OUYANG Xiangyu, et al. Coupling layout design of disc cutters group and cutterhead supporting structure[J]. Journal of mechanical engineering, 2014, 50(21): 23-30. (  0) 0)
|
| [15] |
陈巍, 孙伟, 霍军周. TBM刀盘开口面积的确定[J]. 机械设计与制造, 2015(5): 29-31, 35. CHEN Wei, SUN Wei, HUO Junzhou. The open area determination of TBM cutterhead[J]. Machinery design and manufacture, 2015(5): 29-31, 35. DOI:10.3969/j.issn.1001-3997.2015.05.008 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


