随着云计算、物联网以及移动互联网的普及和推广,促使了大量数据的产生。如何从这些数据中快速挖掘和发现知识,成为学者和企业关注的焦点。聚类作为一种数据分析工具,已广泛应用于模式识别、数据挖掘等领域,其中基于目标函数的聚类方法是人们研究的热点, 例如K均值聚类和模糊c均值聚类FCM(Fuzzy C-Means)。研究表明该聚类算法却存在许多缺陷[1-8]。为此,学者提出了不同的改进算法,它们主要基于K均值聚类且对特征赋予权值,以此表明不同特征在聚类中的作用[9-12]。为了解决复杂数据的聚类,学者将核引入到K均值聚类中,提出了自动修正特征权值的硬聚类算法[13-14]。另外,李洁等[15]将特征权值引入到模糊聚类中,提出了特征加权的模糊聚类算法。然而,该方法聚类前需要事先使用ReliefF方法计算特征的权值,且这些值在聚类过程中是保持不变的。为了解决数据中噪声的干扰,一些学者通过引入样本的权重,提出了样本加权的聚类算法[16-18]。由于模糊聚类算法的重要性,最近,学者们采取不同方法对模糊c均值聚类进行研究[19-23]。通过深入研究特征权值或样本权值的聚类算法,在FCM聚类的目标函数中,同时考虑不同特征和样本对聚类的影响,通过引入特征权值和样本权值,研究了特征和样本权值动态修正的模糊聚类,从理论上导出了模糊隶属度、聚类中心、特征权值和样本权值的迭代公式,给出了相应的模糊聚类算法。
1 样本与特征加权的模糊聚类给定数据集X={x1, x2, …, xn},其中xi∈Rs,uij为第j个样本隶属于第i个簇的程度,U为隶属度构成的矩阵,vi为聚类中心,V为聚类中心构成的矩阵,m为加权指数,n为数据样本的个数,rj是第j个样本的权值,wk是第k个特征的权值,c是聚类数,p和q分别为不等于1的整数,则样本与特征加权的模糊c均值聚类对应的优化问题为
| $ \begin{array}{l} \mathop {\min }\limits_{U, V} J\left( {\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{V}}} \right) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {r_j^p\mathit{\boldsymbol{u}}_{ij}^m\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2}} } } \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} \sum\limits_{i = 1}^c {{\mathit{\boldsymbol{u}}_{ij}} = 1, } \;\;\;j = 1, 2, \cdots , n\\ \sum\limits_{j = 1}^n {{\mathit{\boldsymbol{r}}_j} = 1} \\ \sum\limits_{k = 1}^s {{\mathit{\boldsymbol{w}}_k} = 1} \end{array} \right. \end{array} $ | (1) |
为了获得隶属度和簇中心,使用拉格朗日方法对式(1)求解,则优化的拉格朗日函数为
| $ \begin{array}{l} L\left( {\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{V}};\mathit{\boldsymbol{\alpha }}, \lambda , \beta } \right) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {r_j^p\mathit{\boldsymbol{u}}_{ij}^m\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2}} } } - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^n {{\mathit{\boldsymbol{\alpha }}_j}(\sum\limits_{i = 1}^c {{\mathit{\boldsymbol{u}}_{ij}} - 1} ) - } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \left( {\sum\limits_{j = 1}^n {{\mathit{\boldsymbol{r}}_j} - 1} } \right) - \beta \left( {\sum\limits_{k = 1}^s {{\mathit{\boldsymbol{w}}_k} - 1} } \right) \end{array} $ | (2) |
式中:λ和β分别是拉格朗日乘子,α是由拉格朗日乘子α1, α2, …, αn构成的向量,即α=(α1, α2, …, αn)。
将拉格朗日函数L(U, V; α, λ, β)分别对uij和αj求偏导数,并令其等于0,即∂L/∂uij=0和∂L/∂αj=0,由此得到
| $ m\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^{m - 1}\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2} - {\mathit{\boldsymbol{\alpha }}_j} = 0} $ | (3) |
| $ \sum\limits_{i = 1}^c {{\mathit{\boldsymbol{u}}_{ij}} = 1} $ | (4) |
由式(3)进一步得到
| $ {\mathit{\boldsymbol{u}}_{ij}} = {\left( {{\alpha _j}/m\mathit{\boldsymbol{r}}_j^p\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2}} } \right)^{\frac{1}{{m - 1}}}} $ | (5) |
将式(5)代入式(4),则有
| $ \alpha _j^{\frac{1}{{m - 1}}} = \frac{1}{{{{\sum\limits_{i = 1}^c {\left( {1/m\mathit{\boldsymbol{r}}_j^p\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2}} } \right)} }^{\frac{1}{{m - 1}}}}}} $ | (6) |
将式(6)代入式(5),从而得到模糊隶属度
| $ {u_{ij}} = \frac{1}{{\sum\limits_{l = 1}^c {{{\left( {\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2}/\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{lk}})}^2}} } } \right)}^{\frac{1}{{m - 1}}}}} }} $ | (7) |
同理,由∂L/∂vik=0,∂L/∂rj=0与∂L/∂wk=0分别得到聚类中心vik、样本权值rj和特征权值wk,即
| $ \begin{array}{l} \;\;{\mathit{\boldsymbol{v}}_{ik}} = \frac{{\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m{\mathit{\boldsymbol{x}}_{jk}}} }}{{\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m} }}, \\ i = 1, 2, \cdots , c;k = 1, 2, \cdots , s \end{array} $ | (8) |
| $ \begin{array}{l} {\mathit{\boldsymbol{r}}_j} = \frac{1}{{\sum\limits_{l = 1}^n {{{\left( {\sum\limits_{i = 1}^c {\mathit{\boldsymbol{u}}_{ij}^m\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2}/\sum\limits_{i = 1}^c {\mathit{\boldsymbol{u}}_{il}^m\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{({\mathit{\boldsymbol{x}}_{lk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2}} } } } } \right)}^{\frac{1}{{p - 1}}}}} }}, \\ j = 1, 2, \cdots , n \end{array} $ | (9) |
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}_k} = \frac{1}{{\sum\limits_{l = 1}^s {{{\left( {\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m{{({\mathit{\boldsymbol{x}}_{jk}} - {\mathit{\boldsymbol{v}}_{ik}})}^2}/\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m{{({\mathit{\boldsymbol{x}}_{jl}} - {\mathit{\boldsymbol{v}}_{il}})}^2}} } } } } \right)}^{\frac{1}{{q - 1}}}}} }}, \\ k = 1, 2, \cdots , s \end{array} $ | (10) |
通过上述推导,获得了样本和特征权值自动更新的模糊聚类算法,将其记为SFWFCM。该算法首先固定m、p、q,最大迭代次数maxIter,精度ε,并初始化聚类中心vi(i=1, 2, …, c),rj(j=1, 2, …, n)和wk(k=1, 2, …, s),然后分别使用式(7)~(10)更新隶属度、聚类中心、样本权值和特征权值,直至满足‖v(l)-v(l-1)‖ < ε为止,其中l为当前迭代次数。
2 样本和特征加权的核模糊聚类为了解决较复杂数据的聚类,使用核方法将原空间的数据样本映射到特征空间,然后在此空间聚类。假设φ是一个从原空间到特征空间的映射,则样本与特征加权的核模糊c均值聚类对应的优化问题如下:
| $ \begin{array}{l} \mathop {\min }\limits_{U, V} J\left( {\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{V}}} \right) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2}} } } \\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\left\{ \begin{array}{l} \sum\limits_{i = 1}^c {{\mathit{\boldsymbol{u}}_{ij}} = 1, \;\;\;j = 1, 2, \cdots , n} \\ \sum\limits_{j = 1}^n {{\mathit{\boldsymbol{r}}_j} = 1} \\ \sum\limits_{k = 1}^s {{\mathit{\boldsymbol{w}}_k} = 1} \end{array} \right. \end{array} $ | (11) |
为了求解优化问题式(11),构造拉格朗日函数
| $ \begin{array}{l} L\left( {\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{V}};\mathit{\boldsymbol{\alpha }}, \lambda , \beta } \right) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q||\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - } } } \\ {\mathit{\boldsymbol{v}}_{ik}}|{|^2} - \sum\limits_{j = 1}^n {{\alpha _j}\left( {\sum\limits_{i = 1}^c {{\mathit{\boldsymbol{u}}_{ij}} - 1} } \right) - } \\ \lambda \left( {\sum\limits_{j = 1}^n {{\mathit{\boldsymbol{r}}_j} - 1} } \right) - \beta \left( {\sum\limits_{k = 1}^s {{\mathit{\boldsymbol{w}}_k} - 1} } \right) \end{array} $ | (12) |
式中:λ和β分别是拉格朗日乘子,α是由拉格朗日乘子α1, α2, …, αn构成的向量,即α=(α1, α2, …, αn)。
由式(11)和(12)看到,函数中含有未知映射φ,可以通过如下方法将其转换为核函数K的函数关系,即
| $ \begin{array}{*{20}{c}} {{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2} = {{(\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}})}^{\rm{T}}}(\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}) = }\\ {\varphi {{({\mathit{\boldsymbol{x}}_{jk}})}^{\rm{T}}}\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - 2\varphi {{({\mathit{\boldsymbol{x}}_{jk}})}^{\rm{T}}}{\mathit{\boldsymbol{v}}_{ik}} + {\mathit{\boldsymbol{v}}_{ik}}^{\rm{T}}{\mathit{\boldsymbol{v}}_{ik}} = }\\ {K({\mathit{\boldsymbol{x}}_{jk}}, {\mathit{\boldsymbol{x}}_{jk}}) - 2\frac{{\sum\limits_{b = 1}^n {\mathit{\boldsymbol{u}}_{ib}^mK({\mathit{\boldsymbol{x}}_{jk}}, {\mathit{\boldsymbol{x}}_{bk}})} }}{{\sum\limits_{b = 1}^n {\mathit{\boldsymbol{u}}_{ib}^m} }} + }\\ {\frac{{\sum\limits_{b = 1}^n {\sum\limits_{t = 1}^n {\mathit{\boldsymbol{u}}_{ib}^m\mathit{\boldsymbol{u}}_{it}^mK({\mathit{\boldsymbol{x}}_{bk}}, {\mathit{\boldsymbol{x}}_{tk}})} } }}{{{{\left( {\sum\limits_{t = 1}^n {\mathit{\boldsymbol{u}}_{it}^m} } \right)}^2}}}} \end{array} $ |
由∂L/∂uij=0和∂L/∂αj=0得到:
| $ m\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^{m - 1}\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2} - {\alpha _j} = 0} $ | (13) |
| $ \sum\limits_{i = 1}^c {{\mathit{\boldsymbol{u}}_{ij}} = 1} $ | (14) |
由式(13)进一步得到
| $ {\mathit{\boldsymbol{u}}_{ij}} = {\left( {\frac{{{\alpha _j}}}{{mr_j^p\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2}} }}} \right)^{\frac{1}{{m - 1}}}} $ | (15) |
将式(15)代入式(14)得到
| $ \sum\limits_{i = 1}^c {{{\left( {\frac{{{\alpha _j}}}{{mr_j^p\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2}} }}} \right)}^{\frac{1}{{m - 1}}}} = 1} {\rm{ }} $ |
从而有
| $ \alpha _j^{\frac{1}{{m - 1}}} = \frac{1}{{\sum\limits_{i = 1}^c {{{\left( {1/m\mathit{\boldsymbol{r}}_j^p\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2}} } \right)}^{\frac{1}{{m - 1}}}}} }}, $ |
进一步得到隶属度
| $ \begin{array}{*{20}{c}} {{u_{ij}} = }\\ {\frac{1}{{\sum\limits_{l = 1}^c {{{\left( {\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2}/\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{lk}}} \right\|}^2}} } } \right)}^{\frac{1}{{m - 1}}}}} }}} \end{array} $ | (16) |
同理,由∂L/∂vik=0,∂L/∂rj=0与∂L/∂wk=0分别得到聚类中心vik、样本权值rj和特征权值wk,即
| $ \begin{array}{l} {\mathit{\boldsymbol{v}}_{ik}} = \frac{{\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m\varphi ({\mathit{\boldsymbol{x}}_{jk}})} }}{{\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m} }}, \\ i = 1, 2, \cdots , c;k = 1, 2, \cdots , s \end{array} $ | (17) |
| $ \begin{array}{l} {\mathit{\boldsymbol{r}}_j} = \frac{1}{{{{\sum\limits_{l = 1}^n {\left( {\sum\limits_{i = 1}^c {\mathit{\boldsymbol{u}}_{ij}^m\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2}/\sum\limits_{i = 1}^c {\mathit{\boldsymbol{u}}_{il}^m\sum\limits_{k = 1}^s {\mathit{\boldsymbol{w}}_k^q{{\left\| {\varphi ({x_{lk}}) - {v_{ik}}} \right\|}^2}} } } } } \right)} }^{\frac{1}{{p - 1}}}}}}, \\ j = 1, 2, \cdots , n \end{array} $ | (18) |
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}_k} = \frac{1}{{\sum\limits_{l = 1}^s {{{\left( {\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jk}}) - {\mathit{\boldsymbol{v}}_{ik}}} \right\|}^2}/\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_j^p\mathit{\boldsymbol{u}}_{ij}^m{{\left\| {\varphi ({\mathit{\boldsymbol{x}}_{jl}}) - {\mathit{\boldsymbol{v}}_{il}}} \right\|}^2}} } } } } \right)}^{\frac{1}{{q - 1}}}}} }}, \\ k = 1, 2, \cdots , s \end{array} $ | (19) |
由上述推导,获得了样本和特征权值自动更新的核模糊聚类算法,将其记为SFWKFCM。该算法首先固定m、p、q,最大迭代次数maxIter,精度ε,并初始化rj(j=1, 2, …, n)和wk(k=1, 2, …, s),然后分别使用式(16)、(18)和(19)更新隶属度、样本权值和特征权值,直至满足‖U(l)-U(l-1)‖ < ε为止。
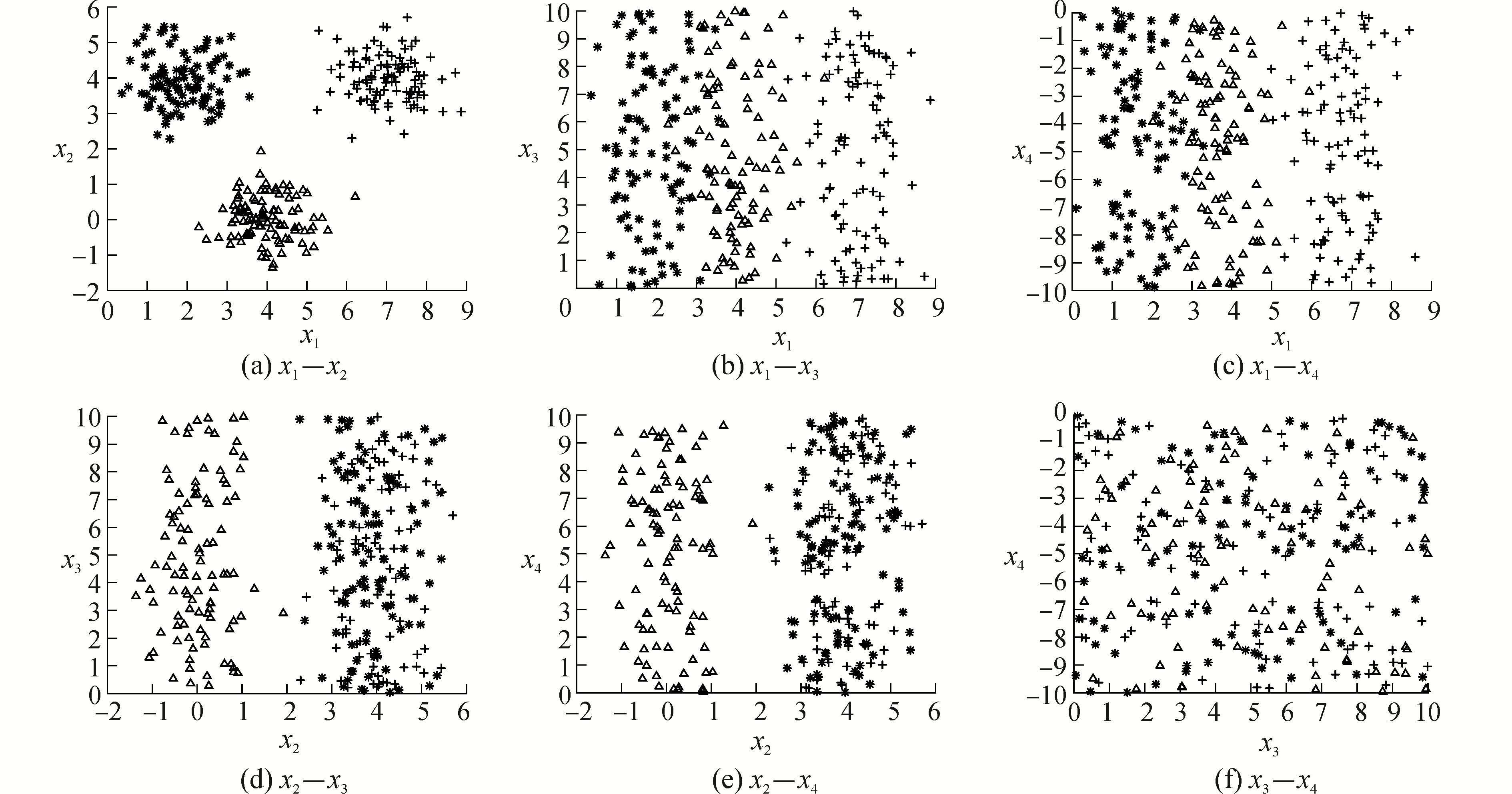
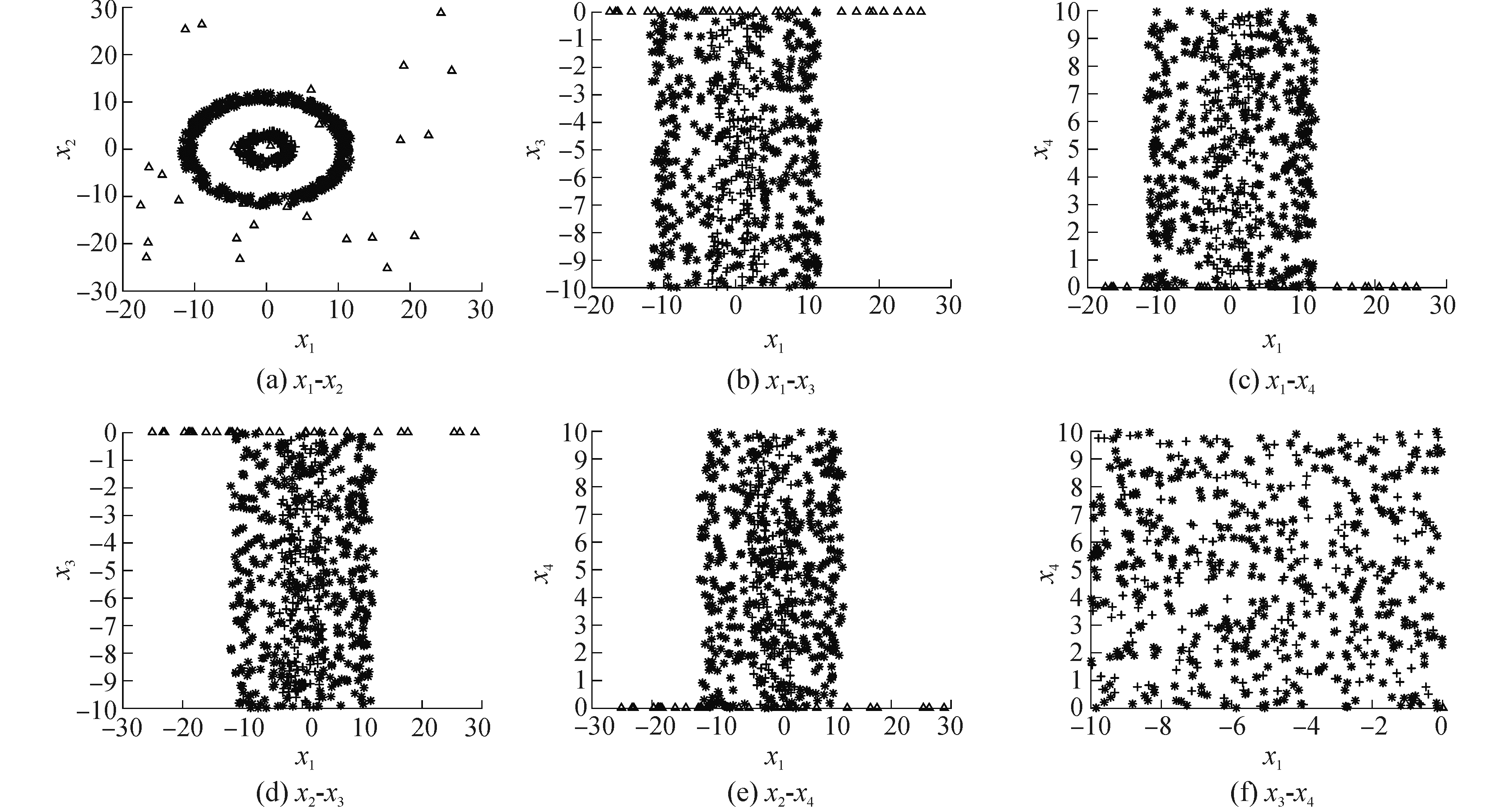
3 实验结果与分析 3.1 实验数据与性能指标为了验证提出算法的性能,选择了人工生成的数据集和UCI标准数据集进行了实验,其中人工生成数据集包括Data3和Ring。Data3数据集是由300个2维数据样本点组成,每组为100个样本点,共分为3组,分别按照均值为[2,4],[7,4]和[4,0],方差为[0.5 0,0 0.5]生成。为了测试算法的抗噪特性,在范围(0, 10)和(-10, 0)随机生成了2个符合均匀分布的特征噪声,以及在范围(-10, 10)随机生成符合均匀分布的数据样本噪声,如图 1所示。Ring数据集是由两个圆环构成,共600个样本点且分为两类,其中外圆环有400个点,内圆环有200个点,另外,在Ring中按照均匀分布随机产生了(-30, 30)的噪声样本,以及随机产生的(-10, 10)范围的2维特征噪声,如图 2所示。实验中选择的UCI数据集[24]包括wine,haberman,glass,sonar,machine,heart_scale,heart_statlog和iris,聚类前对所有数据集中的数据进行了标准化处理,且使用的核函数为高斯核。在实验中,评价聚类算法的性能指标为聚类正确率Accuracy和Jaccard系数,实验结果为10次运行的平均值。为了更好地体现本文提出算法的有效性和一般性,对提出算法的部分参数提供了一些特殊值,从而获得样本加权的模糊聚类和特征加权的模糊聚类。实验时,对这些特殊取值的聚类算法与提出的聚类算法进行了聚类性能比较。
|
Download:
|
| 图 1 Data3数据集的二维分布 Fig. 1 Two-dimensional distribution with data set Data3 | |
|
Download:
|
| 图 2 Ring数据集的二维分布 Fig. 2 Two-dimensional distribution with data set Ring | |
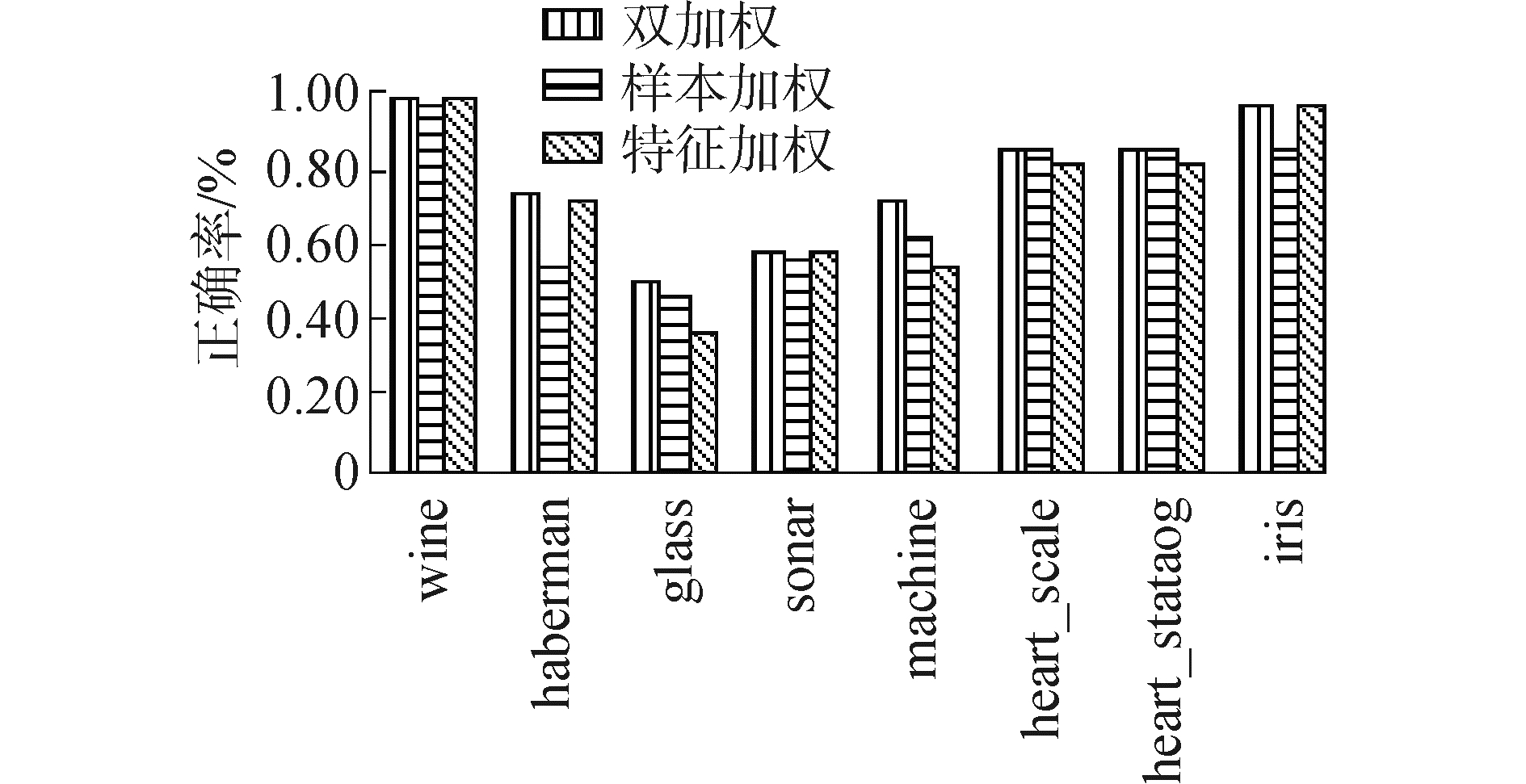
针对选择的8个标准数据集,分别使用样本加权、特征加权以及样本与特征加权(简记为双加权)的聚类算法进行了实验,如图 3、4所示,其中图 3为未使用核函数的聚类结果,图 4为使用高斯核的聚类结果。

|
Download:
|
| 图 3 不同算法在数据集的聚类正确率 Fig. 3 Clustering accuracies for different algorithms with data sets | |
|
Download:
|
| 图 4 基于核的算法在不同数据集的聚类正确率 Fig. 4 Clustering accuracies for different kernel-based algorithms with data sets | |
可以看到,样本和特征双加权的模糊聚类算法在选择的8个数据集上,其聚类正确率都优于特征加权或样本加权的模糊聚类算法。
3.3 有噪声数据的聚类为了更好地表明双加权模糊聚类算法的优势,针对Data3、Ring和iris数据集分别加入比例为5%、10%、15%和20%的噪声(包括特征噪声和样本噪声)进行了实验,实验结果如表 1~3所示。
| 表 1 不同算法在Data3数据集加入噪声后的聚类性能 Tab.1 Clustering performance of different algorithms with additional noisy for data set Data3 |
| 表 2 不同算法在Ring数据集加入噪声后的聚类性能 Tab.2 Clustering performance of different algorithms with additional noisy for data set Ring |
| 表 3 不同算法在iris数据集加入噪声后的聚类性能 Tab.3 Clustering performance of different algorithms with additional noisy for data set iris |
同时,针对Data3、Ring和iris加入不同比例的噪声数据对样本和特征双加权的核模糊聚类算法进行了实验,其中核函数为高斯核,实验结果如表 4~表 6所示。
| 表 4 不同核聚类算法在Data3数据集加入噪声后的聚类性能 Tab.4 Clustering performance of kernel-based algorith-ms with additional noisy for data set Data3 |
| 表 5 核聚类算法在Ring数据集加入噪声后的聚类性能 Tab.5 Clustering performance of kernel-based algorithms with additional noisy for data set Ring |
| 表 6 核聚类算法在iris数据集加入噪声后的聚类性能 Tab.6 Clustering performance of kernel-based algorithms with additional noisy for data set Ring |
由表 1~6可知,样本加权和特征双加权的模糊聚类算法的抗噪性能优于样本加权或特征加权的模糊聚类算法,例如,当在Data3数据集中加入10%的噪声数据,双加权的模糊聚类算法的聚类正确率为94%,而样本或特征加权的模糊聚类算法的聚类正确率分别为88.33%和51.41%。同样的,对于该数据集,当使用相应的核模糊聚类算法时,其聚类正确率分别为100%、91.67%和65.03%,可见双加权的核模糊聚类算法并未出现聚类错误,而样本加权或特征加权的核模糊聚类算法的聚类性能明显低于双加权的模糊聚类算法。
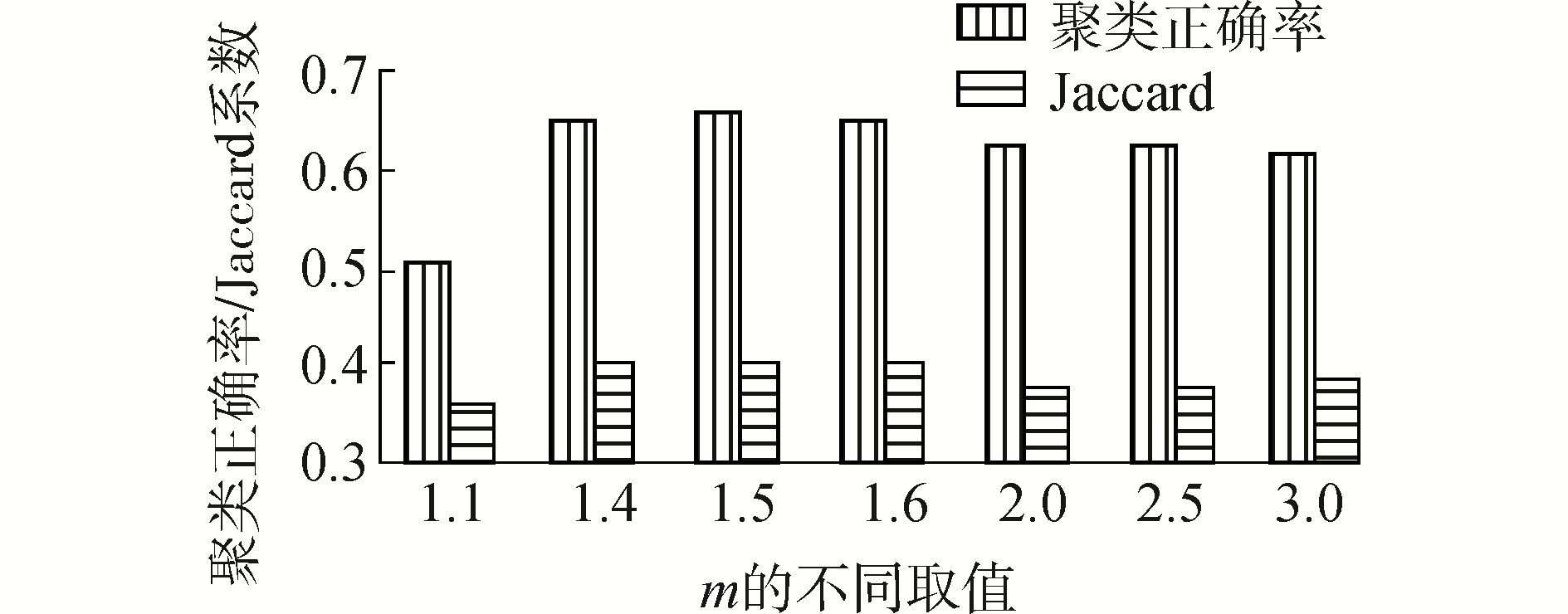
另外,针对噪声比例为10%的iris数据集,对提出的样本与特征双加权的模糊聚类算法中的参数取值进行了实验研究。此时,固定p=-2和q=2,m分别取值为1.1,1.4,1.5,1.6,2,2.5和3,实验结果如图 5所示;类似的,固定m=1.5和q=2,p分别取值为-2,-3,-4,-5和-8时,实验结果如图 6所示。
|
Download:
|
| 图 5 算法使用不同m值在iris数据集的聚类正确率和Jaccard系数 Fig. 5 Clustering accuracy and Jaccard index of algorithm in data set iris using the different value of m | |

|
Download:
|
| 图 6 算法使用不同p值在iris数据集的聚类正确率和Jaccard系数 Fig. 6 Clustering accuracy and Jaccard index of algorithm in data set iris using the different value of p | |
由图 5、6知,当固定p=-2和q=2时,则m取值在1.5附近时,样本和特征双加权模糊聚类算法的聚类性能优于m的其他值;当固定m=1.5和q=2,则p分别取值为-2、-3、-4、-5和-8时,其聚类性能并没有明显的差异。
4 结论提出的模糊聚类算法优于样本加权或特征加权的模糊聚类算法,较好地解决了含有特征噪声与样本噪声数据的聚类,以及样本和特征权值的动态调整方法。
提出的算法并未考虑不同特征对簇的影响,且该算法涉及参数选择问题。因此,下一步的工作是研究不同特征对簇的影响,对参数选择问题进行探索研究。
| [1] |
李衡, 康维新. 基于EMD与模糊聚类的桩缺陷特征提取与识别[J]. 应用科技. LI Heng, KANG Weixin. Pile defect feature extraction and identification based on Empirical Mode Decomposition (EMD) and fuzzy clustering[J]. Applied science and technology. DOI:10.11991/yykj.201803015 (  0) 0)
|
| [2] |
卞则康, 王士同. 基于混合距离学习的鲁棒的模糊C均值聚类算法[J]. 智能系统学报, 2017, 12(4): 450-458. BIAN Zekang, WANG Shitong. Robust FCM clustering algorithm based on hybrid-distance learning[J]. CAAI transactions on intelligent systems, 2017, 12(4): 450-458. (  0) 0)
|
| [3] |
ZHOU Jin, CHEN Long, CHEN C L P, et al. Fuzzy clustering with the entropy of attribute weights[J]. Neurocomputing, 2016, 198: 125-134. DOI:10.1016/j.neucom.2015.09.127 (  0) 0)
|
| [4] |
FAHAD A, ALSHATRI N, TARI Z, et al. A survey of clustering algorithms for big data:taxonomy and empirical analysis[J]. IEEE transactions on emerging topics in computing, 2014, 2(3): 267-279. DOI:10.1109/TETC.2014.2330519 (  0) 0)
|
| [5] |
TIMOTHY C H, JAMES C B, CHRISTOPHER L, et al. Fuzzy c-means algorithms for very large data[J]. IEEE transactions on fuzzy systems, 2012, 20(6): 1130-1146. DOI:10.1109/TFUZZ.2012.2201485 (  0) 0)
|
| [6] |
朱林, 王士同, 邓赵红. 改进模糊划分的FCM聚类算法的一般化研究[J]. 计算机研究与发展, 2009, 46(5): 814-822. ZHU Lin, WANG Shitong, DENG Zhaohong. Research on generalized fuzzy c-means clustering algorithm with improved fuzzy partitions[J]. Journal of computer research and development, 2009, 46(5): 814-822. (  0) 0)
|
| [7] |
WU L, STEVEN C H, JIN R, et al. Learning bregman distance functions for semi-supervised clustering[J]. IEEE transactions on knowledge and data engineering, 2012, 24(3): 478-491. DOI:10.1109/TKDE.2010.215 (  0) 0)
|
| [8] |
STEFAN F, FRIEDHELM S. Semi-supervised clustering of large data sets with kernel methods[J]. Pattern recognition letters, 2014, 37: 78-84. DOI:10.1016/j.patrec.2013.01.007 (  0) 0)
|
| [9] |
DESARBO W S, CARROLL J D, CLARK L A, et al. Synthesized clustering:a method for amalgamating alternative clustering bases with differential weighting of variables[J]. Psychometrika, 1984, 49(1): 57-78. DOI:10.1007/BF02294206 (  0) 0)
|
| [10] |
MAKARENKOV V, LEGENDRE P. Optimal variable weighting for ultrametric and additive trees and k-means partitioning:methods and software[J]. Journal of classification, 2001, 18(2): 245-271. (  0) 0)
|
| [11] |
MODHA D S, SPANGLER W. S.. Feature weighting in k-means clustering[J]. Machine learning, 2003, 52(3): 217-237. DOI:10.1023/A:1024016609528 (  0) 0)
|
| [12] |
HUANG J Z, NG M K, RONG Hongqiang, et al. Automated variable weighting in K-means type clustering[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(5): 657-668. DOI:10.1109/TPAMI.2005.95 (  0) 0)
|
| [13] |
FERREIRA M R P, DE A T D, CARVALHO F. Kernel-based hard clustering methods in the feature space with automatic variable weighting[J]. Pattern recognition, 2014, 47(9): 3082-3095. DOI:10.1016/j.patcog.2014.03.026 (  0) 0)
|
| [14] |
FERREIRA M R P, DE A T, DE CARVALHO F, SIM? ES E C. Kernel-based hard clustering methods with kernelization of the metric and automatic weighting of the variables[J]. Pattern recognition, 2016, 51: 310-321. DOI:10.1016/j.patcog.2015.09.025 (  0) 0)
|
| [15] |
李洁, 高新波, 焦李成. 基于特征加权的模糊聚类新算法[J]. 电子学报, 2006, 34(1): 89-92. LI Jie, GAO Xinbo, JIAO Licheng. A new feature weighted fuzzy clustering algorithm[J]. Acta electronica sinica, 2006, 34(1): 89-92. DOI:10.3321/j.issn:0372-2112.2006.01.017 (  0) 0)
|
| [16] |
LI Jie, GAO Xinbo, JIAO Licheng. A novel typical-sample-weighted clustering algorithm for large data sets[C]//Computational Intelligence and Security. Heidelberg, 2005, 3801: 696-703. http://link.springer.com/10.1007/11596448_103
(  0) 0)
|
| [17] |
YU Jian, YANG Miinshen, LEE E S. Sample-weighted clustering methods[J]. Computers & mathematics with applications, 2011, 62(5): 2200-2208. (  0) 0)
|
| [18] |
刘兵, 夏士雄, 周勇, 等. 基于样本加权的可能性模糊聚类算法[J]. 电子学报, 2012, 40(2): 371-375. LIU Bing, XIA Shixiong, ZHOU Yong, et al. A sample-weighted possibilistic fuzzy clustering algorithm[J]. Acta electronica sinica, 2012, 40(2): 371-375. (  0) 0)
|
| [19] |
WEN Wudi, LIU Zhongle, LI Hua. A method to ascertain parameters of samples and their feature weights in the weighted fuzzy clustering[J]. Applied mechanics and materials, 2013, 300-301: 653-658. DOI:10.4028/www.scientific.net/AMM.300-301 (  0) 0)
|
| [20] |
PIMENTEL B A, DE SOUZA R M C R. Multivariate fuzzy c-means algorithms with weighting[J]. Neurocomputing, 2016, 174: 946-965. DOI:10.1016/j.neucom.2015.10.011 (  0) 0)
|
| [21] |
SIMINSKI K. Fuzzy weighted c-ordered means clustering algorithm[J]. Fuzzy sets and systems, 2017, 318: 1-33. DOI:10.1016/j.fss.2017.01.001 (  0) 0)
|
| [22] |
ZHU Xiubin, PEDRYCZ W, LI Zhiwu. Fuzzy clustering with nonlinearly transformed data[J]. Applied soft computing, 2017, 61: 364-376. DOI:10.1016/j.asoc.2017.07.026 (  0) 0)
|
| [23] |
CHAGHARI A, FEIZI-DERAKHSHI M R, BALAFAR M A. Fuzzy clustering based on Forest optimization algorithm[J]. Journal of King Saud university-computer and information sciences, 2018, 30(1): 25-32. DOI:10.1016/j.jksuci.2016.09.005 (  0) 0)
|
| [24] |
DUA D, KARRA E. UCI Machine Learning Repository[EB/OL]. Irvine, CA: University of California. Department of Information and Computer Science, 2017. http://archive.ics.uci.edu/ml.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


