突破障碍物环境下的无碰撞轨迹规划技术是提高机器人对复杂环境适应性的关键[1]。由于同时具备灵活的移动和操作能力,移动机械臂更加有助于实现障碍物环境下友好、紧密的人机交互。但是移动机械的避障行为除了受到障碍物环境的约束,还受到当前机器人位置的影响。
常用的无碰撞路径规划大致可以分为局部算法[2]和全局算法[3],前者的不足是容易陷入局部最优解,而后者难以获得完整、高维的构型空间模型。基于采样法[4]可以避免对构型空间的完整建模,但由于其采样或路径搜索过程具有一定的随机性,因此容易造成机械臂末端轨迹的突变。上述避障方法多基于障碍物环境的几何特征,如障碍物质心,尺寸和最危险点(离机器人最近点)等,主要存在如下两个问题:1)从传感器信息中提取障碍物环境模型的过程十分复杂[5];2)基于上述方法生成的轨迹无法进行在线修正和调整。Wrede等[6]提出将工作空间中静态的环境约束通过示教学习[7-8]的方式融合到训练数据中,以避免对环境信息的准确建模。Steil[9]证明通过示教学习可显著减小障碍物环境下操作者对冗余机械臂位形的控制负担。由于友好的人机交互方式可以帮助操作者更好的理解其控制行为并有效的提高人机合作的质量[10],刘维惠等[11]针对第二个问题设计了一种人机交互界面,提出利用操作者的直观感觉(视觉感知和避障能力)辅助操作者完成障碍物环境下的轨迹修正。
为避免对机械臂末端轨迹的重复修正和提高机器人的环境适应能力,本文基于示教学习思想,融合机器学习算法,通过操作者在线示教轨迹修正过程,学习机器人在当前位置下的障碍物环境信息和机器人避障决策。
1 基于DMP模型的轨迹生成DMP[12-13]通过加有外部干扰项的线性弹簧阻尼系统实现对任意形状轨迹的动作表达。每个独立自由度上的动力学表达式如下
| $ \tau \dot v = K\left( {g - x} \right) - Dv + f\left( s \right) $ | (1) |
| $ \tau \dot x = v $ | (2) |
式中:K是弹簧系数;D是阻尼系数;g是目标位置;x、v、
| $ f\left( s \right) = \frac{{\mathop \sum \limits_i {\omega _i}{\psi _i}\left( s \right)s}}{{\mathop \sum \limits_i {\psi _i}\left( s \right)}} $ | (3) |
式中:ψi(s)=exp(-hi(s-ci)2)是高斯基函数,以ci为中心,hi为宽度;权值ωi是可调节参数,用来控制轨迹的形状;s是相参数,初值为1并在动作执行过程中单调收敛于0。
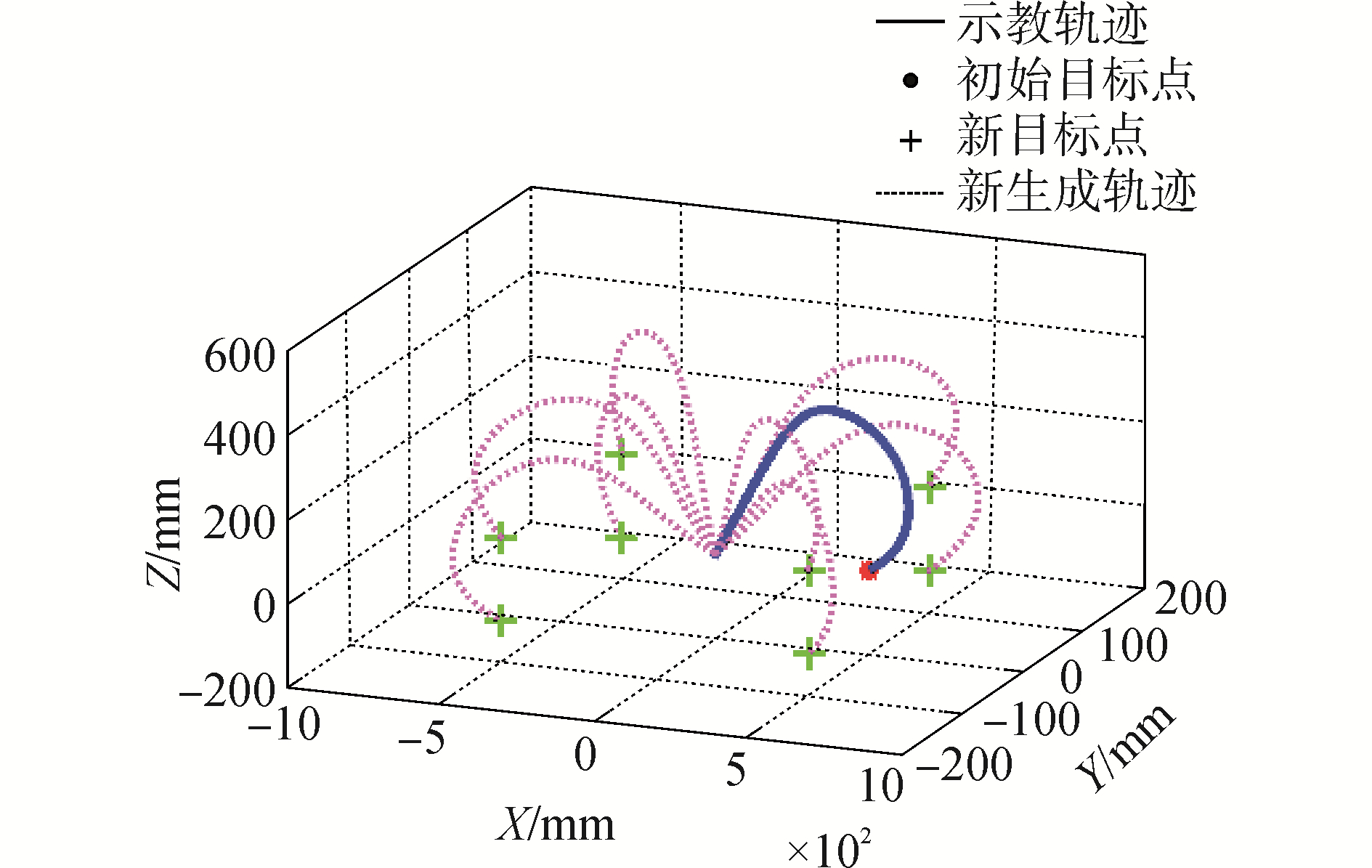
通过式(3)可知,该DMP模型中干扰外力f的权值ωi可通过示教学习来生成任意指定形状的轨迹。由于f随着相参数s单调收敛于零,所以生成轨迹总是收敛于目标点g,使系统具有较好的鲁棒性。其生成轨迹效果如图 1所示,生成轨迹能够在各个方向稳定的保持示教轨迹的形状特征。
|
Download:
|
| 图 1 基于DMP模型的轨迹生成方法 Fig. 1 Trajectory generation based on DMP model | |
面对有障碍物的工作环境,机器人需要具备灵活的轨迹修正和避障能力来保证操作的高效、安全。文献[14-15]在原DMP模型上添加耦合项实现轨迹避障,使得模型复杂化,从而增加了示教和计算难度。文献[11]采用双抛物线插值算法,实现对整条轨迹的全局修正,但是调整的灵活性受限,如图 2所示。图 2(a)为初始轨迹,分别与障碍物左右两侧发生碰撞,通过调整交互点位置实现其中一侧的轨迹避障,如图 2(b)、(c)。但是对任一区域的轨迹修正都会影响另一侧的轨迹形状,从而加剧碰撞或导致新碰撞。

|
Download:
|
| 图 2 基于双抛物线插值法的轨迹修正方法 Fig. 2 Trajectory adjustment based on dual parabolic interpolation | |
为避免对环境的准确建模和障碍物几何信息的提取,本文提出基于距离加权k-近邻(k-Nearest Neighbor,k-NN)[16]的局部轨迹修正算法以实现障碍物环境下机械臂末端轨迹修正能力的推广,从而避免操作者的重复调整,减轻其控制负担。
2.1 基于距离加权k-NN的轨迹修正算法为保证DMP模型的简化,本文并不采取在DMP模型中添加耦合项的轨迹避障方法,而是直接以轨迹的修正量作为学习对象,所以修正后的轨迹T如下
| $ T = {T_{{\rm{original}}}} + \Delta T $ | (4) |
学习过程通常分为训练和执行两个阶段,图 3分别阐述了上述不同阶段中基于距离加权k-近邻算法求取轨迹修正量ΔT主要过程。其中,预处理过程用来调整基于DMP模型生成的轨迹点布局,使其分布均匀,并得到轨迹Toriginal={P1, P2, …, PN},N是轨迹上点的个数。学习机训练过程中,在轨迹Toriginal上提取离交互点最近的轨迹点作为调整点pnew,并计算该调整点与交互点间的距离dnew,将其作为新的训练数据{pnew, dnew}并更新训练数据库。最后,基于距离加权k-NN算法,可依次求得该轨迹上点Pi(测试点)的修正值ΔPi,i=1, 2, …, N。

|
Download:
|
| 图 3 轨迹修正过程 Fig. 3 Trajectory adjustment process | |
距离加权k-NN算法主要包括以下几个步骤[17]:
1) 计算轨迹点Pi到每一个训练数据Pk的距离。本文采用欧式距离‖Pi-Pk‖;
2) 按照距离由小到大对训练数据进行排序;
3) 确定最近邻域个数K,本文暂定为10;
4) 按照反距离加权法计算轨迹点Pi的修正值ΔPi。其中,每个训练数据的权值与到该轨迹点的距离成反比。
本文采训练数据的样本权重表示为
| $ {\omega _k} = {{\rm{e}}^{ - \lambda \left\| {{P_i} - {P_k}} \right\|}}/\left( {\sum\limits_{k = 1}^K {{{\rm{e}}^{ - \lambda \left\| {{P_i} - {P_k}} \right\|}}} } \right) $ | (5) |
轨迹修正值表示为
| $ \Delta {P_i} = \sum\limits_{k = 1}^K {({\omega _k}{d_k})} $ | (6) |
式中:ωk是训练数据{Pk, dk}的权值,‖Pi-Pk‖是测试数据Pi到训练数据Pk的欧式距离,λ是缩放因子,控制训练数据的收敛强度,如图 4,λ越大,函数y=exp(-λx)越陡峭。由式(5)可知离轨迹点(测试点)较近的训练点,对修正值ΔPi的影响大于远离该轨迹点的训练点。

|
Download:
|
| 图 4 y=exp(-λx)的函数关系曲线图 Fig. 4 The functional relationship graphic of y=exp(-λx) | |
但上述的k-NN算法用于对轨迹修正值的学习和生成具有以下三点不足:1)当轨迹点Pi距离障碍物较远时,并不需要对该点进行修正。但由式(5)中的归一化表达式可知,当点Pi距所有训练点的距离都较远时,其修正值仍受训练点的影响,且相对越近的训练点影响越大;2)当机器人与障碍物环境发生相对运动时,轨迹点Pi的修正值还受到当前机器人与障碍物环境相对位置的影响,从而确定避障决策;3)轨迹的起始点和目标点由任务给定,不应该受交互点位置的影响。
通过对距离加权k-NN算法的改进来解决上述不足。针对不足1),需要在式(6)中添加一项影响因子用来表示训练点Pk对该轨迹点修正值的影响力,满足当轨迹点Pi距离训练点较远时,训练点影响力近似于0,则轨迹点的修正值不受此训练点影响。反之,当轨迹点Pi距离训练点较近时,其影响力近似于1,此训练点对轨迹点的修正效果近似于式(6)。影响力取值范围是(0, 1)。基于上述函数特征,采用S型函数作为该影响因子项,用来表达训练点到轨迹点距离与该训练点对轨迹修正值影响力的关系,并与距离加权k-NN结合:
| $ \Delta {P_i} = \sum\limits_{k = 1}^K {\left( {\frac{1}{{1 + {{\rm{e}}^{\alpha (\left\| {{P_i} - {P_k}} \right\| - {P_{{\rm{threshold}}}})}}}}{\omega _k}{d_k}} \right)} $ | (7) |
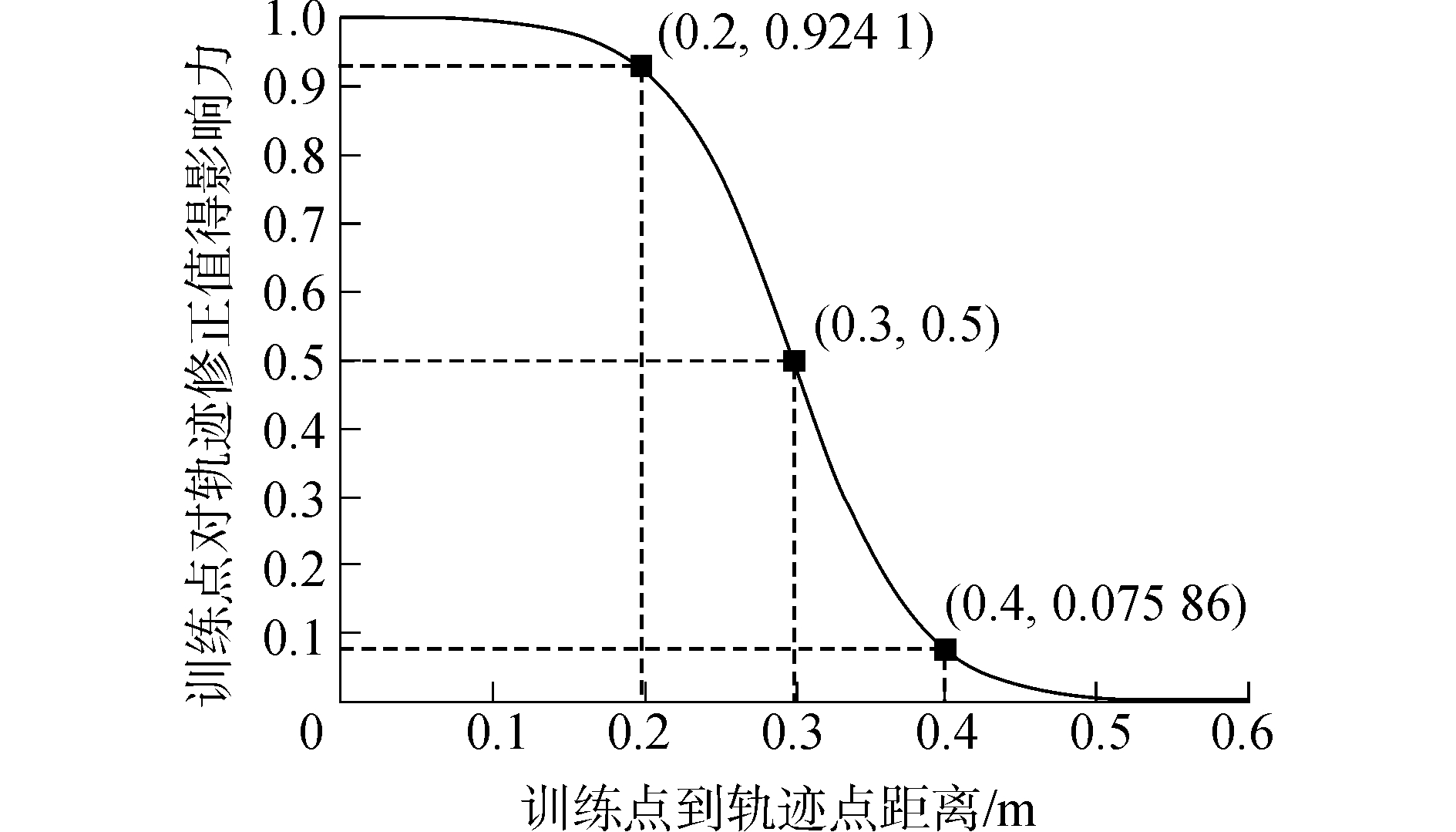
其中,1/(1+eα(‖Pi-Pk‖-Pthreshold))是变形的Sigmoid函数;α为倾斜系数,其值越大,曲线越陡峭;Pthreshold是欧氏距离阈值。若以轨迹点与训练点欧氏距离x=‖Pi-Pk‖为自变量,该训练点pk对轨迹修正值的影响力y=1/(1+eα(‖Pi-Pk‖-Pthreshold))为因变量,则其关系曲线如图 5所示。
|
Download:
|
| 图 5 训练点到轨迹点距离与该训练点对轨迹修正值影响力的关系 Fig. 5 The relationship between the distance from training data to the trajectory point and the influence of the training data on the adjustment | |
由图 5可知,阈值点的影响力为0.5。当轨迹点与训练点的距离小于阈值时,S型函数值大于0.5,该轨迹点修正值受附近训练点的影响;反之,其距离越大,其修正值受到该训练点的影响力越小。为保证到轨迹点距离小于0.2 m的训练值的影响力不被削减,而距离大于0.4 m的训练值对其几乎没有影响,所以选取α=25,Pthreshold=0.3 m。
同样,为解决机器人相对障碍物不同位置Ri下,轨迹修正值的决策问题,用S型函数表示训练数据中机器人位置与该训练点对轨迹点修正值影响力的关系,所以轨迹点Pi的修正值如式(8)表示为
| $ \begin{array}{*{20}{c}} {\Delta {P_i} = }\\ {\sum\limits_{k = 1}^K {\left( {\frac{1}{{1 + {{\rm{e}}^{\beta (\left\| {{R_i} - {r_k}} \right\| - {R_{{\rm{threshold}}}})}}}}\frac{1}{{1 + {{\rm{e}}^{\alpha (\left\| {{P_i} - {P_k}} \right\| - {P_{{\rm{threshold}}}})}}}}{\omega _k}{d_k}} \right)} } \end{array} $ | (8) |
其参数的定义类似于式(7),‖Ri-rk‖是机器人当前位置Ri到训练数据rk的欧式距离。需要注意的是,此时训练数据为{(pk, rk), dk},其中修正值dk作为k-NN算法的输出,调整点和相应的机器人位置(pk, rk)共同作为其输入,以提高系统的决策能力和对新环境的适应能力。
为解决轨迹的起始点和目标点位置受附近训练数据的影响,在用上述方法进行轨迹修正前,需要临时添加两组关于当前起始点和目标点的训练值,{(Pstart, Rstart), dstart}和{(Pend, Rend), dend},且保证这两组训练数据优先级最高。其中,在三维空间下,dstart=dend=[0, 0, 0]T,则起始点和目标点附近的轨迹修正值近似于零。其轨迹修正效果,如图 6所示。

|
Download:
|
| 图 6 基于k-NN的轨迹修正方法 Fig. 6 Trajectory adjustment based on k-NN | |
不同于双抛物线全局修正方法,即每次只能根据当前的交互点位置对轨迹进行调整,k-近邻局部轨迹修正算法能够每次根据附近多个训练点对轨迹形状进行调整,修正过程更加灵活且更适于对复杂障碍物环境信息的学习。除此之外,k-NN算法能够利用其学习机制的泛化能力对训练数据的避障性能进行拓展,从而避免了大量的重复训练和轨迹调整工作。
3 训练数据的更新操作者可以通过调整界面上的交互点位置来改变当前轨迹形状,并计算轨迹修正值,将其存储为新的训练实例。因为k-近邻是基于实例的机器学习算法,所以训练实例的质量会直接影响其学习效果,进而训练数据的更新和筛选过程显得尤为重要,在保证轨迹的在线修正能力的同时,需要避免对有效数据的覆盖。
为保证轨迹修正过程中系统的在线更新能力,即轨迹形状跟随当前交互点的位置进行调整,通常将任意两组训练数据间的最小距离定义为更新阈值δupdate,用来实现训练数据的在线更新和存储,以提高机器人的适应性和灵活性[18]。
所以,当新训练数据与相邻数据间的距离小于更新阈值时,则相邻数据被新训练数据所替代。本文实验部分中,更新阈值为0.2 m。在式(7)、(8)中,为保证在当前交互点处受到附近其他训练点的影响不显著,即修正后的轨迹紧密跟随当前交互点(最新训练点)位置,取λ=12。
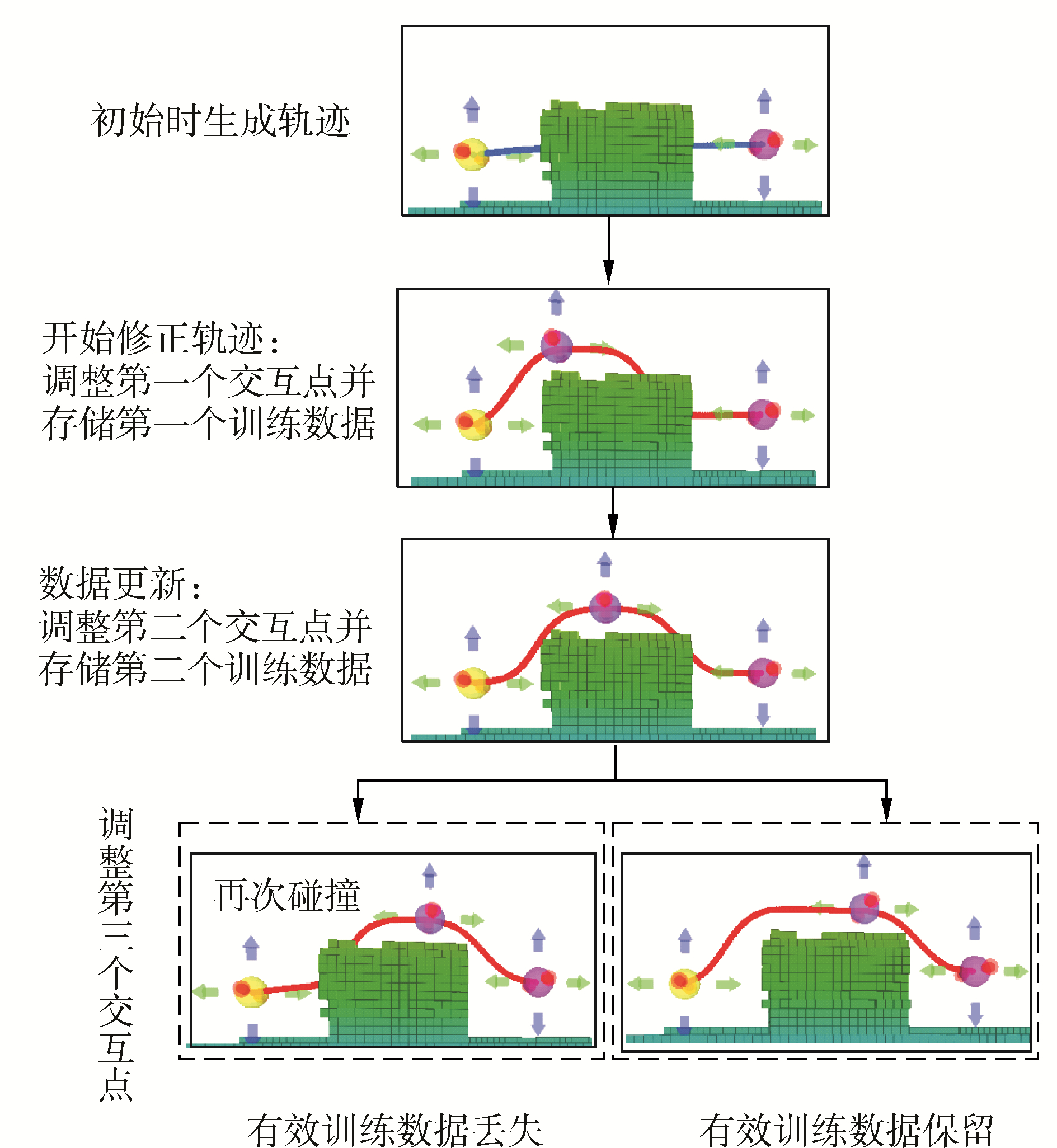
但是在上述更新算法中,当相邻训练点距离均小于δupdate时,新训练数据总会覆盖前一个训练数据,造成先前的有效训练数据丢失。如图 7所示,当生成轨迹与障碍物碰撞时,从左至右依次调整交互点位置进行轨迹形状的修正。当保存第二个交互点作为系统新训练点时,由于与第一个训练点距离小于更新阈值,覆盖第一个训练点。当保存第三个交互点作为新训练点时,第二个训练点被覆盖。此时,系统只留有第三个训练数据的信息,第一个有效训练数据丢失,因此左侧轨迹再次与障碍物发生碰撞,如图 7左图。
|
Download:
|
| 图 7 训练数据的更新 Fig. 7 Training data updating and selection | |
因此,在保存第三个交互点作为新训练数据时,应该无效化第二个训练数据并恢复第一个训练点作为系统的有效训练数据。所以,本文提出了如下训练数据更新方法以避免直接删除到当前交互点距离小于更新阈值的潜在有效训练点。
输入:所有训练数据data={(pm,rm),dm}, m=1, 2, …, M,M为当前训练点个数;
更新阈值δupdate。
输出:用于轨迹修正的训练数据data_new
将训练数据反向排列\\新训练数据优先级高于先前数据
FOR k=1:1:M
data_new(k)=data(M-k+1);
ENDFOR
num=M; \\需要具有两个或两个以上训练数据
FOR i=1:1:num-1
FOR j=i+1:1:num
IF (‖ pj- pi‖ < δupdate )& (‖rj- ri‖ < δupdate )
DELETE data_new(j) \\删除该训练数据
ENDIF
ENDFOR
ENDFOR
经过上述更新方法,其实验效果如图 7右侧所示,证明了该数据选取算法可以避免有效数据的丢失,更好的对轨迹进行避障修正。
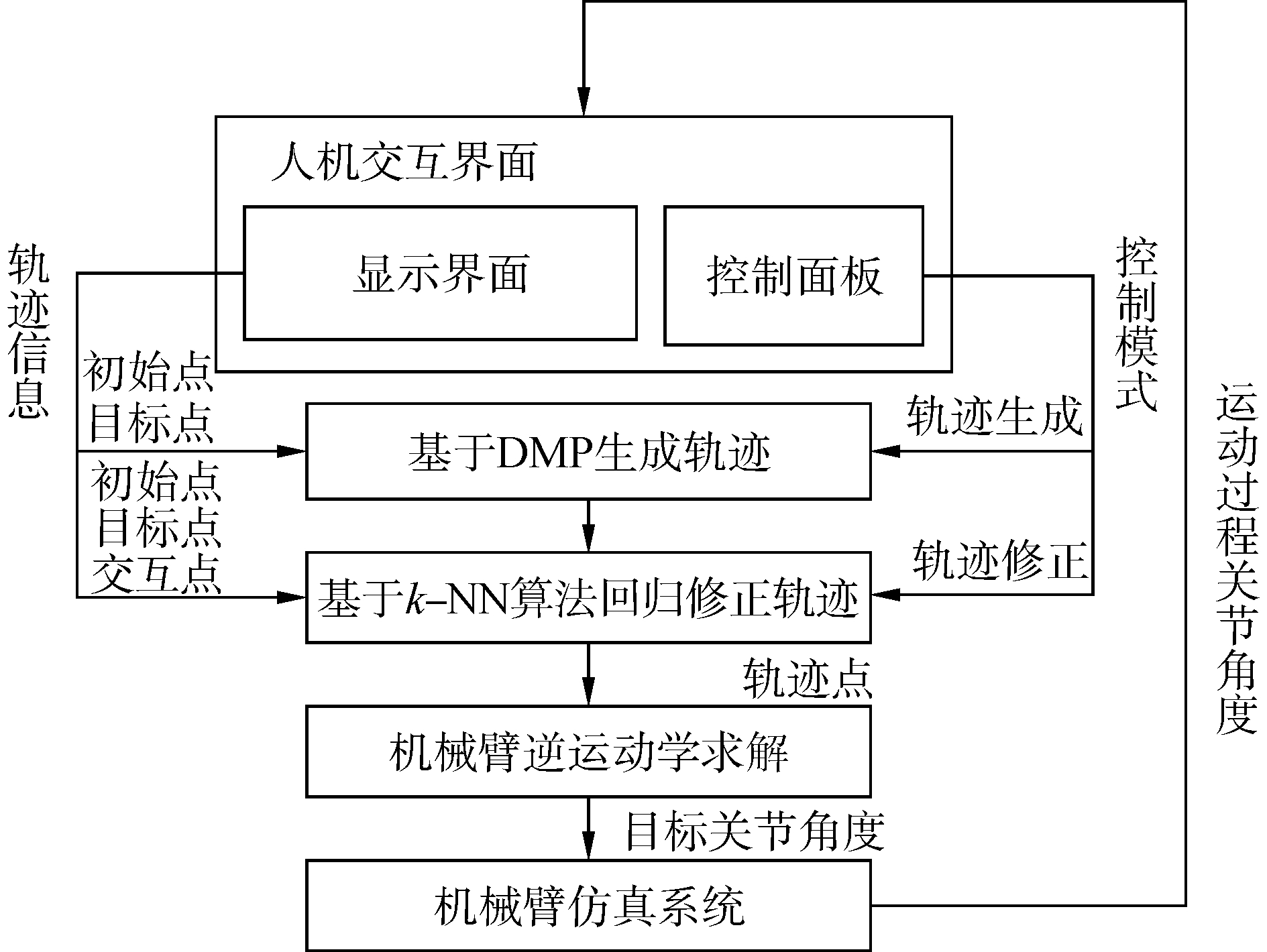
4 避障能力实验 4.1 实验平台本文以7自由度Schunk模块化机械臂为实验平台,通过Kinect的人体骨架跟踪或数据手套[19]实现对示教轨迹的采集。基于ROS(robot operating system)机器人操作系统设计可视化交互界面。通过轨迹修正过程的示教学习,提高机械臂末端轨迹对障碍物环境的适应性。该实验平台模块间通信机制如图 8所示。上述控制模块均集成于一台笔记本电脑上,采用理i5双核2.4 GHz处理器,内存为4 GB。
|
Download:
|
| 图 8 模块间通信体制 Fig. 8 Communication Scheme between modules | |
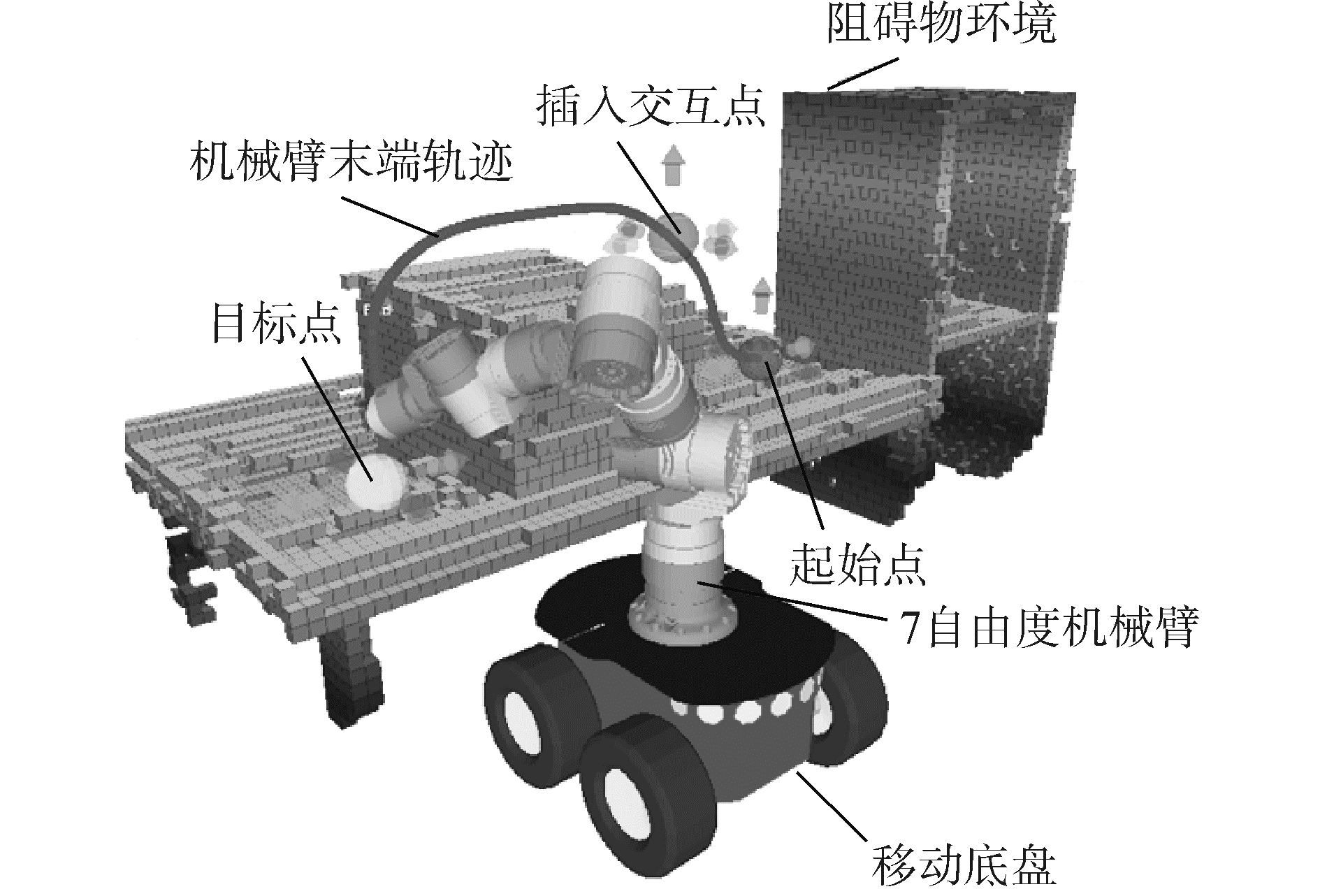
友好的人机交互界面能够辅助操作者直观的对机械臂进行控制,如图 9所示。其中,初始点、插入交互点和目标点可沿选中的箭头方向移动。
|
Download:
|
| 图 9 人机交互界面 Fig. 9 Interface for human robot interaction | |
基于上述实验平台及人机交互界面,分别以机械臂与障碍物环境间未发生和发生相对运动情况下的末端轨迹修正实验,验证本文算法对新任务的适应性和避障能力。并结合已有的逆运动学求解算法,在仿真环境下执行该运动过程。
图 10为当机器人与障碍物环境相对静止时的避障实验。基于上述人机交互界面,操作者可以通过对插入交互点位置的调整逐步对轨迹进行修正,并以修正后轨迹为示教轨迹。当新目标点在距离示教轨迹目标点[±0.1, ±0.1, ±0.1]m的范围内移动时,新生成的轨迹仍具有良好的避障能力。上述结果不仅证明了距离加权k-近邻学习算法具有较好的泛化能力,提高了机器人系统对新任务的适应性。还可以证明通过人机交互界面,能够将障碍物环境信息和操作者的避障决策融合于示教信息中。

|
Download:
|
| 图 10 机器人相对障碍物环境静止时,轨迹避障实验 Fig. 10 Obstacle avoidance experiment of the trajectory in the case that robot is relative static to the obstacle environment | |
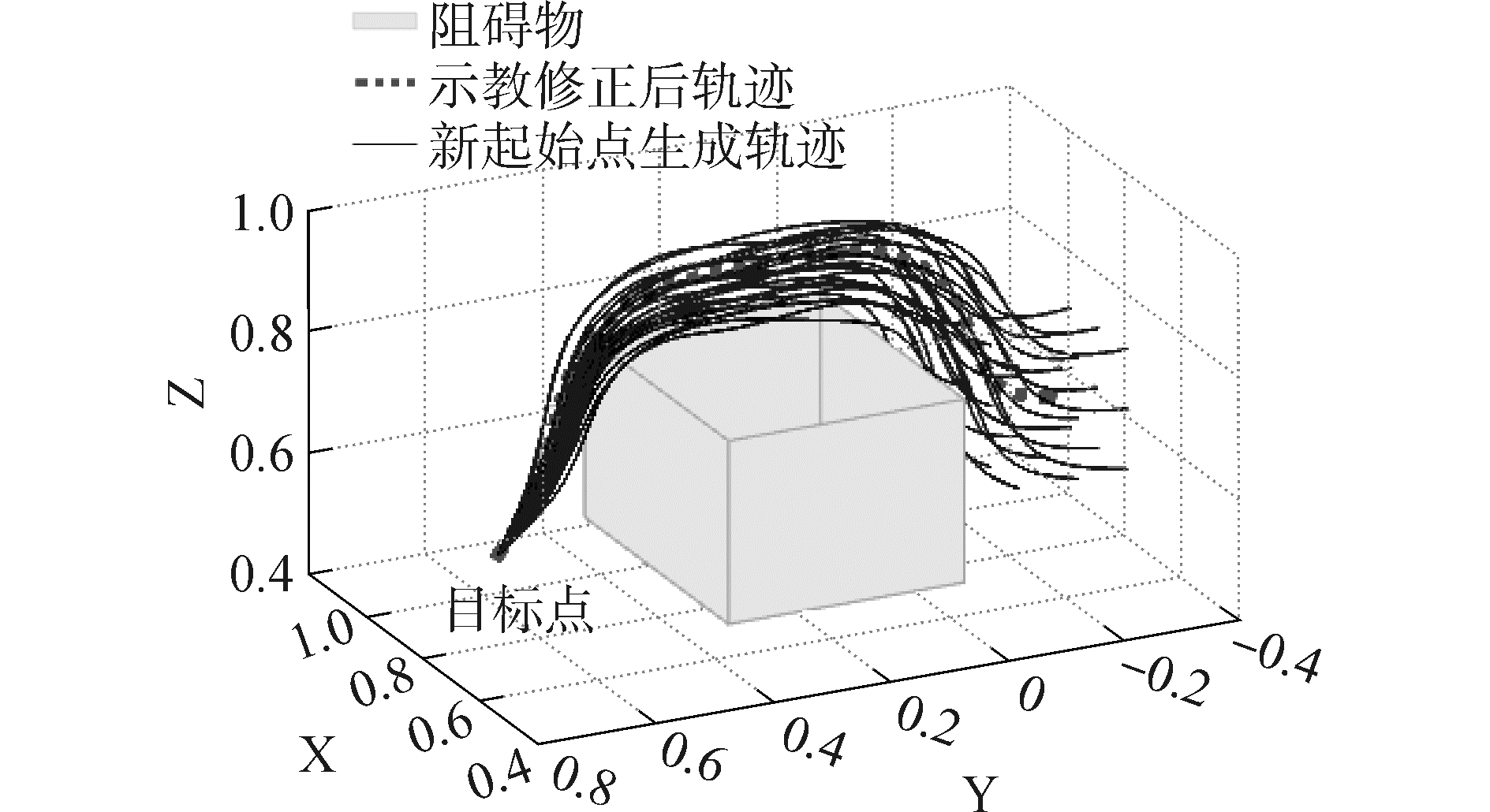
为保证机器人最佳抓取位置,服务机器人通常需要根据目标物的初始位置来调整当前姿态。基于图 10中的示教轨迹,图 11验证了当移动平台跟随目标物初始位置在[±0.1, ±0.1, ±0.1]m的范围内进行调整时,新生成的轨迹仍保持示教轨迹的避障能力和形状特征。
|
Download:
|
| 图 11 机器人跟随初始点移动时,轨迹避障实验 Fig. 11 Obstacle avoidance experiment of the trajectory in the case that robot is following the position of start point | |
在实际应用中,针对给定目标物位置,因为导航误差、规划算法和障碍物环境等因素,移动平台难以重复到达同一最佳抓取位置。图 12阐述了当机器人由位置[0.05, 0.1, 0.0]m逐渐移动到[0.45, 0.1, 0.0]m时的轨迹修正过程。当机器人离障碍物较近时,将轨迹向上调整以实现避障,如图 12(a)。然而,当机器人离障碍物较远时,将轨迹向靠近机械臂的方向调整,如图 12(b)。以上述两种情况下的修正轨迹作为示教轨迹,图 12(c)验证了当机器人在这个范围内移动时,新生成的轨迹仍具有一定的避障能力,且避障决策受距离当前位置较近的训练点影响较大,说明系统具有较好的鲁棒性和避障决策能力。

|
Download:
|
| 图 12 避障决策实验 Fig. 12 Experiment of making obstacle avoidance decision | |
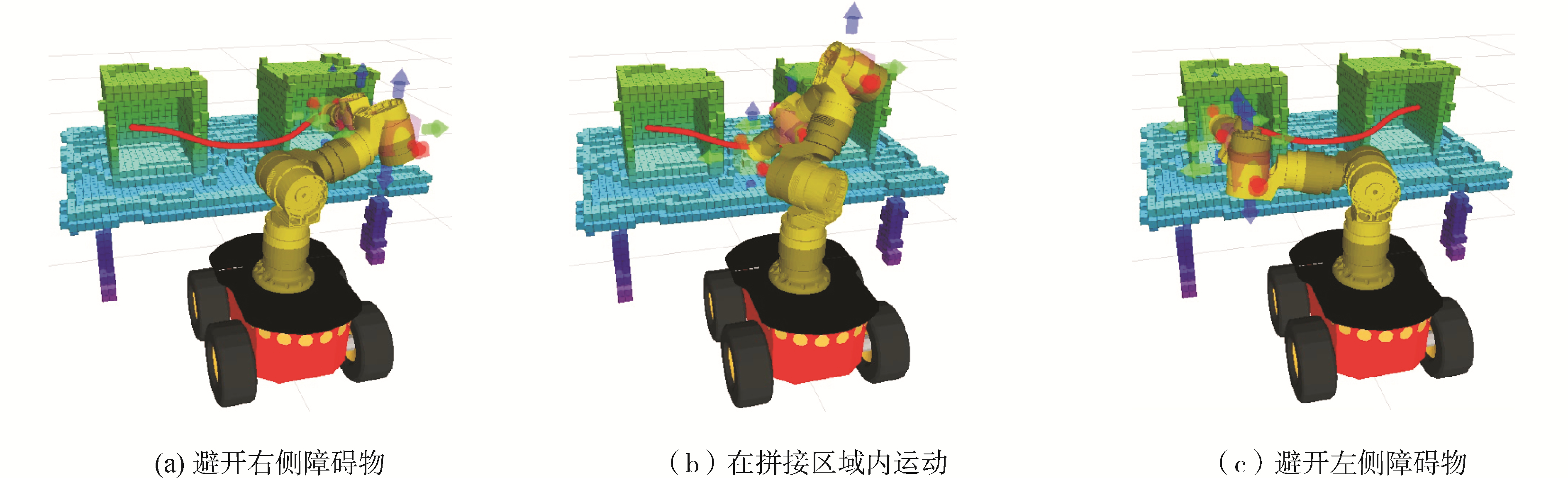
用Kinect等机器视觉所感知到的障碍物环境通常是局部有限的,当目标物与机器人位置均产生较大变动时,为了减少操作者的示教训练任务,实现相邻障碍物环境的拼接和避障能力的扩展显得尤为重要。如图 13(a)所示,初始时机器人位于左右两个障碍物中间,生成轨迹与两侧障碍物均发生碰撞。通过机器人分别在靠近右侧障碍物(图 13(b))和靠近左侧障碍物(图 13(c))场景下的轨迹修正训练,在这两个场景间的新生成轨迹具有同时避免与左、右两侧障碍物碰撞的能力,如图 13(d)。经过逆运动学求解,沿该无碰撞轨迹的机械臂运动过程如图 14所示。

|
Download:
|
| 图 13 多障碍物场景的信息融合 Fig. 13 Information fusion of multiple obstacle scenarios | |
|
Download:
|
| 图 14 机械臂沿轨迹运动 Fig. 14 Manipulator moves along the trajectory | |
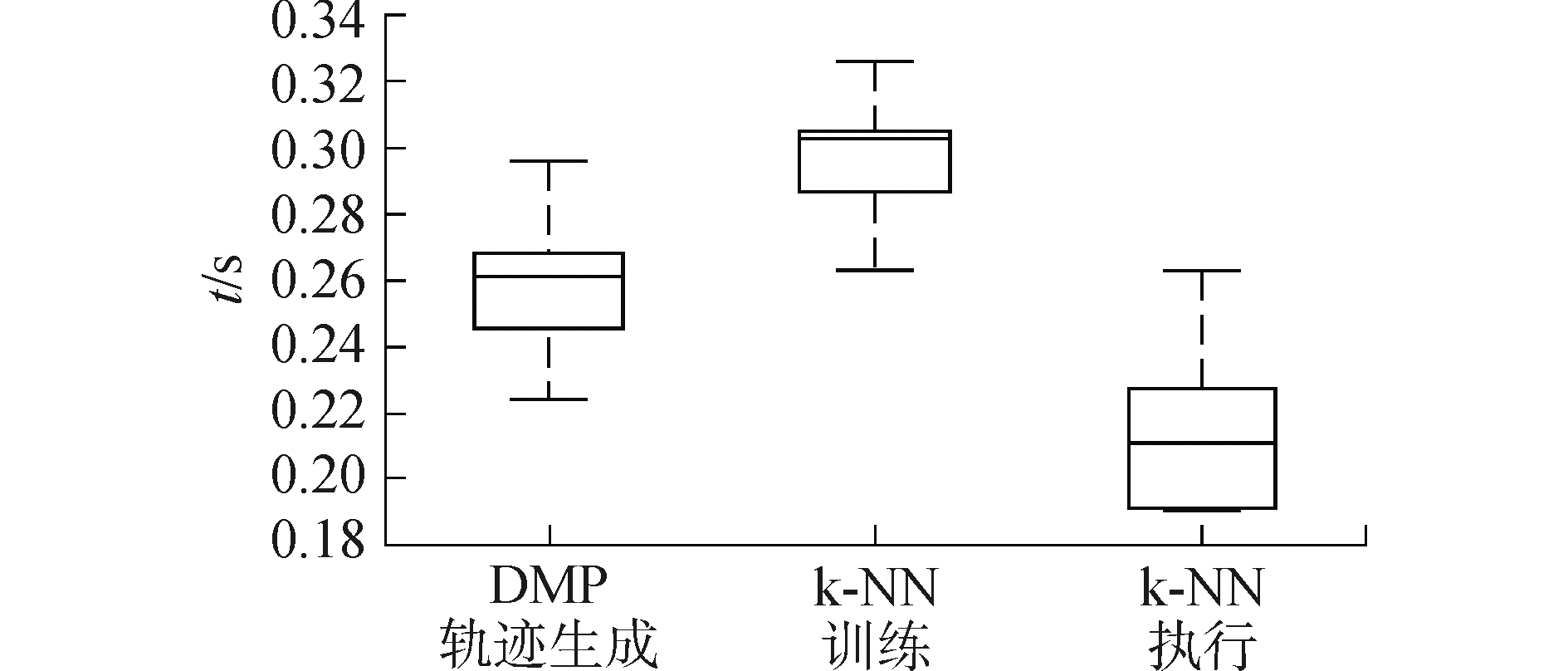
通过分析基于距离加权k-近邻算法的训练和执行过程的实时性,验证其在线轨迹修正能力。由于有效训练数据的个数可能会影响系统的响应时间。因此,记录了有效训练数据个数由1~10逐渐增加时,学习算法的训练过程与执行过程所用时间,以及目标位置发生改变时,基于DMP模型的轨迹生成时间,测试数据如表 1,其数据分布如图 15所示。
| 表 1 实时性测试数据 Tab.1 Real-time performance |
|
Download:
|
| 图 15 实时性测试的箱形图 Fig. 15 Box-plot of the real-time performance | |
无论是基于DMP的轨迹生成时间还是k-近邻学习算法所需要的训练和执行时间,其十组实验数据的平均值都小于0.3 s,满足系统的实时性要求。由于训练过程相较于执行过程需要在轨迹上寻找和计算新训练点并更新训练数据库,所以训练过程略慢于执行过程。当有效训练数据由1逐渐增加到10时,训练数据的个数对系统的实时性无显著影响。
6 结论1) 通过友好的人机交互界面,操作者可以利用其视觉感知和避障能力向机器人系统示教轨迹修正过程。不仅提高了系统的控制直观性,而且障碍物的环境信息和操作者轨迹修正策略的倾向性均隐性的融合于示教信息中,避免了对该障碍物环境的准确建模和信息提取。
2) 结合Sigmoid函数提出改进的距离加权k-近邻算法用于障碍物环境下的轨迹修正。解决与距离相关的训练点影响力问题和不同机器人位置下的避障决策问题。与全局的双抛物线插值算法相比,该算法不仅具有更好的灵活性,而且可通过学习将训练点的避障能力拓展到新工作空间,从而避免大量的重复性训练工作,减轻操作者的使用负担,并通过算法的实时性分析验证了该算法的在线修正能力。
3) 提出新的训练数据在线更新方法,一方面保证了系统的在线更新能力,另一方面避免了潜在有效训练点的丢失。从而提高训练数据的质量,保证隐含环境信息的准确性,使系统的应用灵活性和适应性得以提高。
| [1] |
WREDE S, BEYER O, DREYER C, et al. Vertical integration and service orchestration for modular production systems using business process models[J]. Procedia technology, 2016, 26: 259-266. DOI:10.1016/j.protcy.2016.08.035 (  0) 0)
|
| [2] |
PARK D H, HOFFMANN H, PASTOR P, et al. Movement reproduction and obstacle avoidance with dynamic movement primitives and potential fields[C]//Humanoids 2008-8th IEEE-RAS International Conference on Humanoid Robots. Daejeon, South Korea, 2008: 91-98. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4755937
(  0) 0)
|
| [3] |
LOZANO-PEREZ T. A simple motion-planning algorithm for general robot manipulators[J]. IEEE journal on robotics and automation, 1987, 3(3): 224-238. DOI:10.1109/JRA.1987.1087095 (  0) 0)
|
| [4] |
LOPEZ A S, ZAPATA R, LAMA M A O. Sampling-based motion planning:a survey[J]. Computación Y sistemas, 2008, 12(1): 5-24. (  0) 0)
|
| [5] |
PAN J, SUCAN I A, CHITTA S, et al. Real-time collision detection and distance computation on point cloud sensor data[C]//2013 IEEE International Conference on Robotics and Automation. Karlsruhe, Germany, 2013: 3593-3599. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6631081
(  0) 0)
|
| [6] |
WREDE S, EMMERICH C, GRVNBERG R, et al. A user study on kinesthetic teaching of redundant robots in task and configuration space[J]. Journal of human-robot interaction, 2013, 2(1): 56-81. DOI:10.5898/JHRI.1.2 (  0) 0)
|
| [7] |
CALINON S, GUENTER F, BILLARD A. On learning, representing, and generalizing a task in a humanoid robot[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2007, 37(2): 286-298. DOI:10.1109/TSMCB.2006.886952 (  0) 0)
|
| [8] |
BILLARD A, GROLLMAN D H. Robot learning by demonstration[J]. Scholarpedia, 2013, 8(12): 3824. DOI:10.4249/scholarpedia.3824 (  0) 0)
|
| [9] |
STEIL J J, EMMERICH C, SWADZBA A, et al. Kinesthetic teaching using assisted gravity compensation for model-free trajectory generation in confined spaces[M]//RÖHRBEIN F, VEIGA G, NATALE C. Gearing Up and Accelerating Cross-Fertilization Between Academic and Industrial Robotics Research in Europe. Cham: Springer, 2014: 107-127.
(  0) 0)
|
| [10] |
FISCHER K, KIRSTEIN F, JENSEN L C, et al. A comparison of types of robot control for programming by Demonstration[C]//2016 11th ACM/IEEE International Conference on Human-Robot Interaction. Karlsruhe, Germany, 2016: 213-220. http://dl.acm.org/citation.cfm?id=2906868
(  0) 0)
|
| [11] |
刘维惠, 陈殿生, 张立志. 人机协作下的机械臂轨迹生成与修正方法[J]. 机器人, 2016, 38(4): 504-512. LIU Weihui, CHEN Diansheng, ZHANG Lizhi. Trajectory generation and adjustment method for robot manipulators in human-robot collaboration[J]. Robot, 2016, 38(4): 504-512. (  0) 0)
|
| [12] |
UDE A, GAMS A, ASFOUR T, et al. Task-specific generalization of discrete and periodic dynamic movement primitives[J]. IEEE transactions on robotics, 2010, 26(5): 800-815. DOI:10.1109/TRO.2010.2065430 (  0) 0)
|
| [13] |
KULVICIUS T, NING K J, TAMOSIUNAITE M, et al. Joining movement sequences:modified dynamic movement primitives for robotics applications exemplified on handwriting[J]. IEEE transactions on robotics, 2012, 28(1): 145-157. DOI:10.1109/TRO.2011.2163863 (  0) 0)
|
| [14] |
RAI A, MEIER F, IJSPEERT A, et al. Learning coupling terms for obstacle avoidance[C]//2014 14th IEEE-Ras International Conference on Humanoid Robots. Madrid, Spain: IEEE, 2014: 512-518. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7041410
(  0) 0)
|
| [15] |
RAI A, SUTANTO G, SCHAAL S, et al. Learning feedback terms for reactive planning and control[C]//2017 IEEE International Conference on Robotics and Automation. Singapore, Singapore, 2017: 2184-2191. http://ieeexplore.ieee.org/document/7989252/
(  0) 0)
|
| [16] |
KPOTUFE S. k-NN regression adapts to local intrinsic dimension[C]//Advances in Neural Information Processing system.Granda, spain, 2011: 729-737. http://cn.arxiv.org/abs/1110.4300
(  0) 0)
|
| [17] |
DUDANI S A. The distance-weighted k-Nearest-Neighbor rule[J]. IEEE transactions on systems, man, and cybernetics, 1976, SMC-6(4): 325-327. DOI:10.1109/TSMC.1976.5408784 (  0) 0)
|
| [18] |
CHA E, KRONANDER K, BILLARD A. Combined kinesthetic and simulated interface for teaching robot motion models[C]//2015 24th IEEE International Symposium on Robot and Human Interactive Communication. Kobe, Japan, 2015: 83-88. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7333655
(  0) 0)
|
| [19] |
FANG B, GUO D, SUN F C, et al. A robotic hand-arm teleoperation system using human arm/hand with a novel data glove[C]//2015 IEEE International Conference on Robotics and Biomimetics. Zhuhai, China, 2015: 2483-2488.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


