船舶在海上航行时,受到海洋环境的干扰会产生纵荡、横荡、垂荡、横摇、纵摇和艏摇六个自由度上的运动[1]。相比于其他五个自由度的运动,较小的横摇阻尼使得横摇运动尤为剧烈。剧烈的横摇运动会降低乘员的舒适度,干扰舰载仪器设备的正常工作,增加航行阻力和燃料消耗[2-3]。严重时还会引起货物损失,甚至导致船舶倾覆。为了减小船舶横摇,工程师设计制造了多达数百种类型的减摇装置,而减摇鳍是其中最为常用、减摇效果最好的主动式减摇装置[4]。
随着陆上资源的消耗,海洋资源开发愈来愈受到各国的重视。许多海洋工程船舶需要在航速接近于零的情况下进行工作,同时要求船在海浪中尽可能保持平稳;而在正常航行时也需要有较为稳定的工作和生活环境。常规减摇鳍依靠来流速度产生升力,仅在较高航速下才具有较好的减摇效果,而在低航速和零航速下几乎没有减摇能力[5-6]。为解决这一问题,荷兰Maritime研究院和美国Quantum Control公司对减摇鳍零航速减摇的问题进行研究,证明其减摇效果可达63%~75%,明显高于被动式减摇水舱,但其研究多以试验为主[7-10]。国内对零航速减摇鳍的研究最早是由哈尔滨工程大学船舶减摇与控制技术研究所于2005年开始进行的,在多项自然基金和项目的支持下,完成了从理论模型、仿真及实验的一整套研究[11-16]。
针对零航速减摇鳍的控制问题,张晓飞[11-12]设计了基于改进遗传算法的模糊控制器实现了最小能量消耗下的减摇控制。王帆[13-14]利用数值迭代反演控制解决了零航速下稳定力矩的非线性问题,但鳍上升力限制和特殊工作方式使该方法的减摇效果不高。宋吉广[6, 15]考虑了航速的影响,建立了零低航速下减摇鳍上水动力模型,并基于RBF网络和广义回归神经网络设计了零航速减摇鳍主从控制器。苏晓宇[17]设计了模糊控制器来解决鳍运动与鳍上水动力的非线性问题。本文通过分析海浪干扰力矩、船舶横摇运动、鳍的运动和鳍上产生的水动力之间的相位匹配关系,从扰动(海浪干扰力矩)和补偿(鳍控制力矩)的角度,对零航速减摇鳍在两种模式下的控制策略进行了研究。
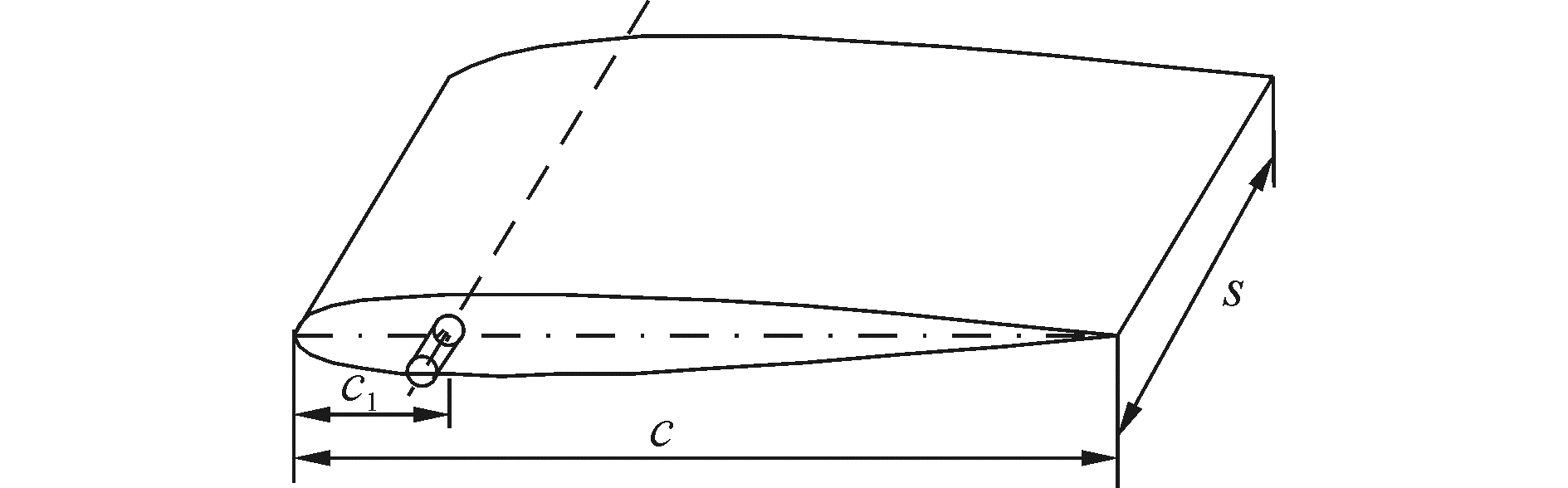
1 零航速减摇鳍水动力特性分析零航速减摇鳍的模型如图 1所示,其中c1是鳍轴中线距鳍前缘的距离,c为鳍的弦长,s为鳍的展长。为了满足零航速下减摇要求,零航速减摇鳍的展弦比较常规减摇鳍更小,通常取0.38~0.5,且鳍轴位置更加靠近前缘[18]。
|
Download:
|
| 图 1 零航速减摇鳍模型 Fig. 1 Model of zero-speed fin stabilizer | |
常规减摇模式下,零航速减摇鳍的水动力特性与常规减摇鳍相似,均是利用水流过鳍面时上下表面压力差来产生升力,其升力可表示为[19]
| $ L = \frac{1}{2}\rho A{V^2}{C_L}\left( \alpha \right) $ | (1) |
式中:ρ为流体密度,A为减摇鳍鳍面积,V为来流速度,CL(α)为减摇鳍的升力系数。升力系数一般通过水池实验获得,在未达到失速角之前,其升力特性基本随鳍攻角呈线性增大。通常,升力系数可由以下半经验公式计算[3]:
| $ {C_L}\left( \alpha \right) = {C_{L0}}\alpha + \frac{{{C_{DC}}}}{\Lambda }{\left( {\frac{\alpha }{{57.3}}} \right)^2} $ | (2) |
式中:α为鳍的攻角;CDC为鳍的横流阻力系数,取决于叶梢形状和斜率比,可通过查阅系数图谱获得;Λ为鳍的展弦比;CL0为升力系数曲线在α=0处的斜率,可由下式进行估算:
| $ {C_{L0}} = \frac{{0.9\left( {2{\rm{ \mathsf{ π} }}} \right)\Lambda }}{{57.3[\sqrt {{\mathit{\Lambda }^2} + 4{e_0}} + 1.8]}} $ | (3) |
式中e0是与鳍后掠角有关的修正系数。
1.2 零航速模式零航速模式下减摇鳍上产生的水动力主要由形状阻力、旋涡阻力和附加质量力构成。
1.2.1 形状阻力减摇鳍转动时,鳍排开的流体会对鳍产生一个反作用力,该力垂直于鳍表面并且与单位时间排开流体的量成正比,取决于鳍几何形状的力即为形状阻力[15]:
| $ {F_{{\rm{fd}}}} = \frac{1}{6}{C_D}\rho s{\omega ^2}[{(c - {c_1})^3} - {c_1}^3] $ | (4) |
式中:CD为阻力系数,一般由实验测定,文献[10]推荐CD取3~5;ρ为流体密度;ω为鳍转动的角速度。
1.2.2 旋涡阻力鳍转动时,在鳍的前缘和艉缘与鳍运动方向相反的一侧会产生诱导速度,在鳍上下两侧产生压力差,进而使鳍受到漩涡阻力的作用。考虑到零航速减摇鳍鳍轴非常靠近鳍的前缘,导致鳍前缘涡几乎不会出现,鳍受到的漩涡阻力可为[17]:
| $ \begin{array}{l} {F_{vd}} = \frac{1}{6}\rho s{\omega ^2}[3{k_2}{(c - {c_1})^2} - 3k_2^2(c - {c_1}) + \\ \;\;\;\;\;\;\;(k_2^3 - c_1^3)] \end{array} $ | (5) |
式中k2为后缘涡在沿弦长方向的长度。
1.2.3 附加质量力鳍在流体中作加速或减速运动时,会迫使鳍面周围流体的运动状态随之改变,而流体质点具有的惯性会阻碍其自身状态的改变,其效果相当于增加了鳍的转动惯量,被加速或减速的流体质点对鳍面形成的反向作用力即为附加质量力为[18]:
| $ {F_{{\rm{ad}}}} = \frac{1}{8}{k_a}{\rm{ \mathsf{ π} }}\rho s{c^2}(c - 2{c_1})\dot \omega $ | (6) |
式中:ka为附加质量力系数,与转鳍角加速度有关,近似为常数;
将上述三种力进行叠加,即得到零航速时减摇鳍拍动产生的总的水动力:
| $ F = {F_{{\rm{fd}}}} + {F_{{\rm{vd}}}} + {F_{{\rm{ad}}}} $ | (7) |
考虑到鳍转动时产生的升力与角速度的方向,式(4)~(6)中的ω2均由ω|ω|代替。由式(4)和式(5)可知,鳍受到的形状阻力和漩涡阻力均与转鳍角速度的平方成正比,为了简化分析,将形状阻力和漩涡阻力项进行合并,合称为阻力,则式(7)可改写为
| $ F = {K_1}\omega |\omega | + {K_2}\dot \omega $ | (8) |
式中:K1和K2为常数,可由下式计算得到:
| $ \left\{ \begin{array}{l} {K_1} = \frac{1}{6}{C_D}\rho s[{(c - {c_1})^3} - c_1^3] + \frac{1}{6}\rho s[3{k_2}(c - \\ \;\;\;\;\;\;\;\;{c_1}{)^2} - 3k_2^2(c - {c_1}) + (k_2^3 - c_1^3)]\\ {K_2} = \frac{1}{8}{k_a}{\rm{ \mathsf{ π} }}\rho s{c^2}(c - 2{c_1}) \end{array} \right. $ | (9) |
其结果通常要根据CFD仿真或者水池实验的结果进行修正。
2 相位匹配分析 2.1 未减摇时船舶横摇运动根据Conolly横摇理论,小角度横摇时,船舶横摇运动为[20]
| $ ({I_{xx}} + \delta {I_{xx}})\ddot \phi + 2{N_u}\dot \phi + Dh\phi = W $ | (10) |
式中:ϕ、
根据线性横摇理论,若设海浪的横摇干扰力矩W=Wuexp(iωet),则船舶的开环横摇角ϕ可表示为
| $ \phi = {\phi _u}\exp [{\rm{i}}({\omega _e}t + {\gamma _u})] $ | (11) |
式中:ϕu为横摇幅值;ωe为海浪遭遇频率;γu为横摇角ϕ较海浪干扰力矩W的滞后相角,其相位关系可如图 2所示。

|
Download:
|
| 图 2 未减摇时船舶横摇运动相位矢量图 Fig. 2 Phase vector diagram of ship roll motion without control | |
装备减摇鳍的船舶横摇运动为[19]
| $ W + {K_C} = ({I_{xx}} + \delta {I_{xx}})\ddot \phi + 2{N_u}\dot \phi + Dh\phi $ | (12) |
式中KC为减摇鳍上产生的减摇控制力矩。
当鳍产生的减摇力矩完全补偿海浪干扰力矩,即W+KC=0时,船舶将停止横摇。因此,减摇的关键就是使减摇鳍产生的控制力矩尽量的补偿海浪引起的干扰力矩。而减摇鳍一般是成对安装在船舯舭部两侧,则左右鳍产生的减摇力对船舶横摇轴力矩,得到:
| $ {K_C} = 2{F_c}{l_f}\cos {\varepsilon _f} \approx 2{F_c}{l_f} $ | (13) |
式中:Fc为单鳍产生的减摇力;lf为鳍上水动力压力中心至船舶横摇轴之间的距离;εf为鳍轴轴线与自鳍中心至穿过船中心的纵轴垂直线之间的夹角,通常很小,可忽略。
考虑到零航速减摇鳍在两种减摇模式下生力机理不同,下面分别进行讨论。
2.2.1 常规减摇模式由1.1节可知,常规减摇模式下,在鳍攻角未达到失速角时,减摇鳍的升力系数与鳍攻角成正比,由式(1)和(13)可知,减摇鳍产生的控制力矩也与鳍角成正比关系。而海浪干扰很难直接测量,但可通过船舶的横摇信息间接获得。因此,对减摇控制力矩与海浪干扰力矩之间相位关系的分析就可以转化为对鳍运动与船舶横摇之间的相位关系的分析,而对减摇鳍的控制最终体现在鳍角上,故着重分析鳍角和船舶横摇的相位匹配关系。
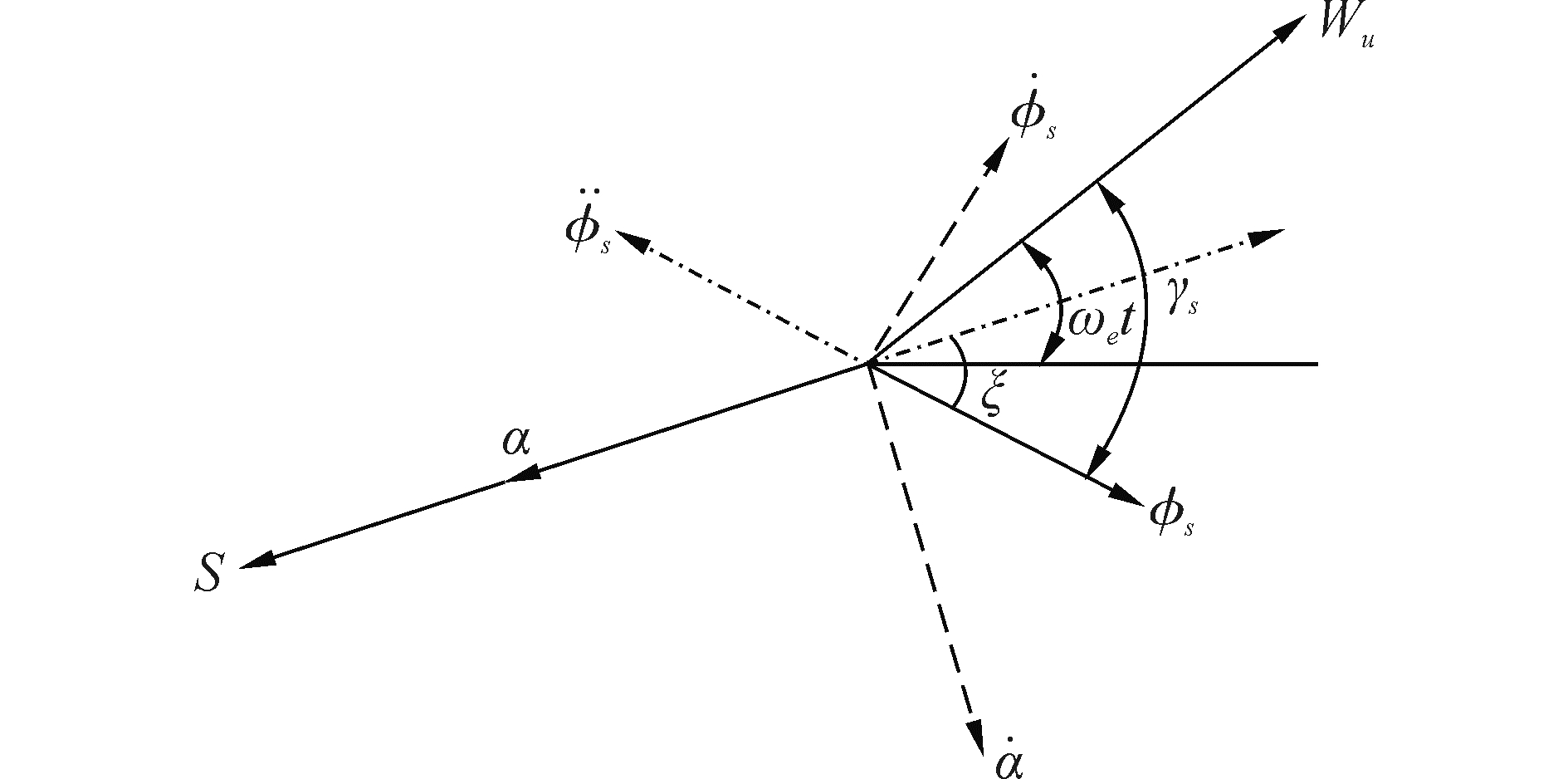
常规减摇模式下船舶横摇运动的相位矢量图如图 3所示。图中,Wu表示海浪干扰力矩; ϕs、
|
Download:
|
| 图 3 常规减摇模式下船舶横摇运动相位矢量图 Fig. 3 Phase vector diagram of ship roll motion under NAM | |
| $ {K_C} = S\exp [{\rm{i}}({\omega _e}t - {\gamma _s} + \xi )] $ | (14) |
式中:减摇控制力矩相位超前船舶横摇角(ξ+π),而γs为横摇角滞后海浪干扰力矩的相位。
常规减摇模式下,鳍上产生的减摇控制力矩与鳍攻角相位相同,故若想减小船舶的横摇,则需根据船舶横摇实时调整鳍的攻角。分析图 3中各量之间的相位关系,以鳍角为最终控制输入,易得:
1) 若采用单一信号反馈控制,则应使鳍角按横摇角速度负反馈进行控制,即
| $ {K_{{\rm{C}}{{\rm{C}}_{\rm{1}}}}} = {K_{{\rm{Cvel}}}}\dot \phi $ | (15) |
式中KCvel>0为横摇角速度反馈控制增益。
2) 若采用多用信号反馈的复合控制,考虑到横摇角速度的微分和积分即为横摇角加速度和横摇角度,分别对应于PID控制中的P、D和I,则应将横摇角速度作为主反馈控制信号,横摇角和横摇角加速度作为辅助反馈控制信号,即
| $ {K_{{\rm{C}}{{\rm{C}}_{\rm{2}}}}} = {K_{{\rm{Cang}}}}\phi + {K_{{\rm{Cvel}}}}\dot \phi + {K_{{\rm{Cacc}}}}\ddot \phi $ | (16) |
式中:KCang>0、KCvel>0和KCacc>0分别为横摇角、角速度和角加速度反馈控制增益。
根据文献[19],按横摇角速度的控制产生一个正比于横摇角速度的控制力矩,考虑到控制力矩与海浪干扰力矩反相,则式(12)变为
| $ W = ({I_{xx}} + \delta {I_{xx}})\ddot \phi + (2{N_u} + {K_{{\rm{Cvel}}}})\dot \phi + Dh\phi $ | (17) |
由上式可见,横摇角速度反馈控制的减摇原理是增加了船舶横摇阻尼,可大大减小船舶在谐摇区内的横摇。而式(16)表示的以横摇角速度作为主反馈信号,横摇角和横摇角加速度的综合控制,即为目前大多数减摇鳍控制系统采用的按力矩控制,其具有最好的减摇效果。而按横摇角度和横摇角加速度控制基本没有减摇效果。
通过与文献[19]中给出的常规减摇鳍的控制方法对比,可知本文通过分析海浪干扰、船舶横摇、鳍动作及鳍上产生的减摇力之间的相位匹配关系得到的常规模式下减摇鳍的控制策略是有效的,并且也说明了按照扰动和补偿的相位匹配方法的有效性。
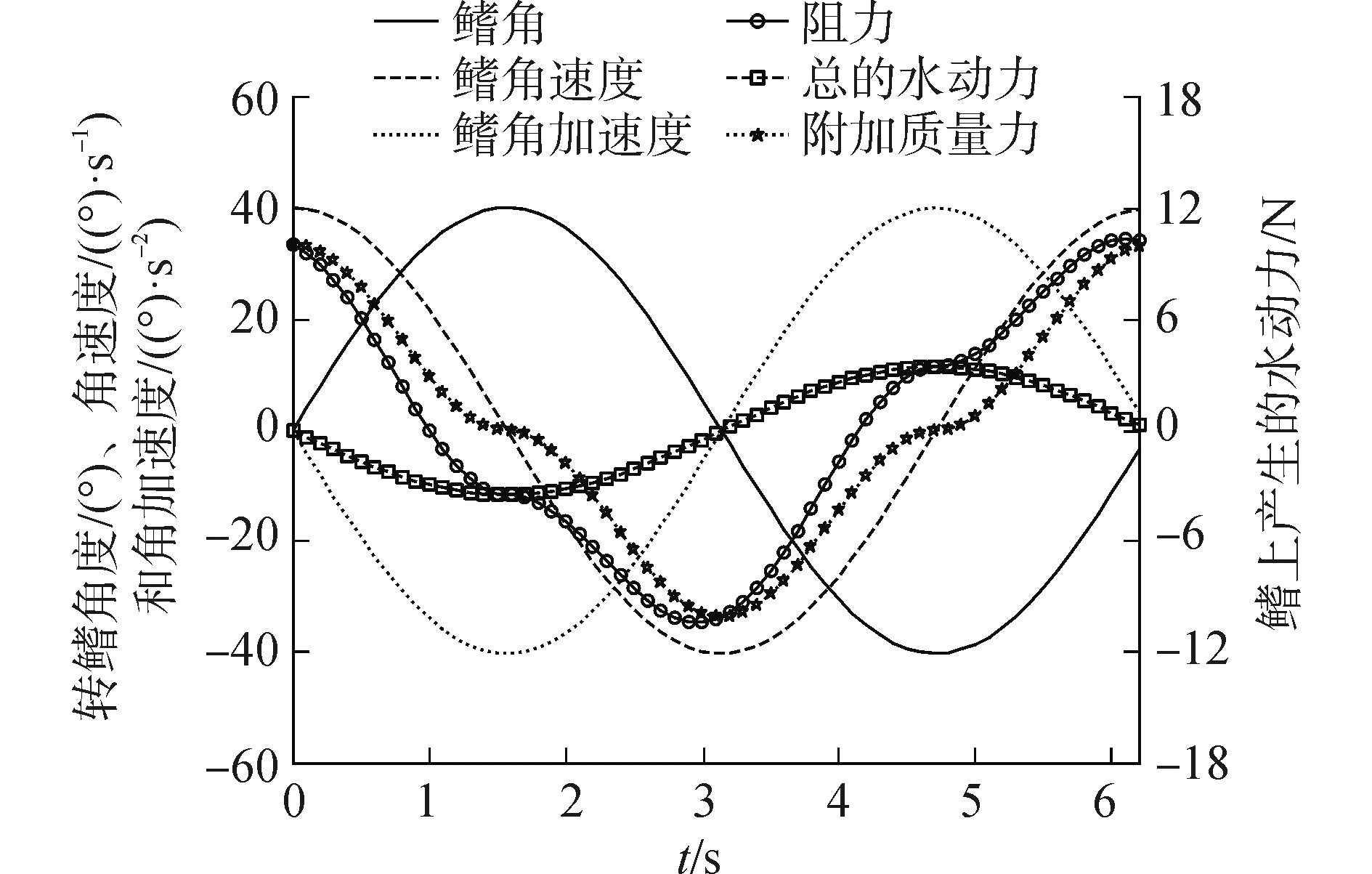
2.2.2 零航速模式由1.2节分析可知,零航速减摇模式下,鳍上产生的水动力由与转鳍角速度的平方成正比的阻力以及与转鳍角加速度成正比的附加质量力组成。为了便于讨论且不失一般性,选定鳍面积4 m2、展弦比0.5的某型鳍作为分析对象,并对该型鳍进行了大量的流体力学仿真[16, 21-22],所获得的数据按式(8)进行拟合,得到K1=20 580,K2=4 974。设减摇鳍按正弦规律α=αmaxsin(ω0t)进行转动,取ω0=1,αmax=40°,可得如图 4所示的鳍上产生的水动力曲线。
|
Download:
|
| 图 4 鳍的运动以及鳍上产生的水动力 Fig. 4 Fin′s movement and the hydrodynamic forces | |
由图 4可知,鳍上产生的阻力与转鳍角速度同相位,而附加质量力与转鳍角加速度同相位,且鳍上产生的阻力相比于附加质量力对总的水动力贡献更大。鳍上产生的总的水动力的相位仅略超前转鳍角速度的相位。不失一般性,设海浪的干扰力矩W=Wuexp(iωet),则船舶在海浪干扰下的横摇运动为
| $ \phi = {\phi _s}\exp [{\rm{i}}({\omega _e}t - {\gamma _s})] $ | (18) |
式中:ϕs和γs分别为船舶横摇运动的幅值和滞后海浪干扰力矩的相角,为了补偿海浪干扰,减摇鳍应以相同的频率进行转动,即为
| $ \alpha = {\alpha _a}\exp [{\rm{i}}({\omega _e}t - {\gamma _s} + \varepsilon )] $ | (19) |
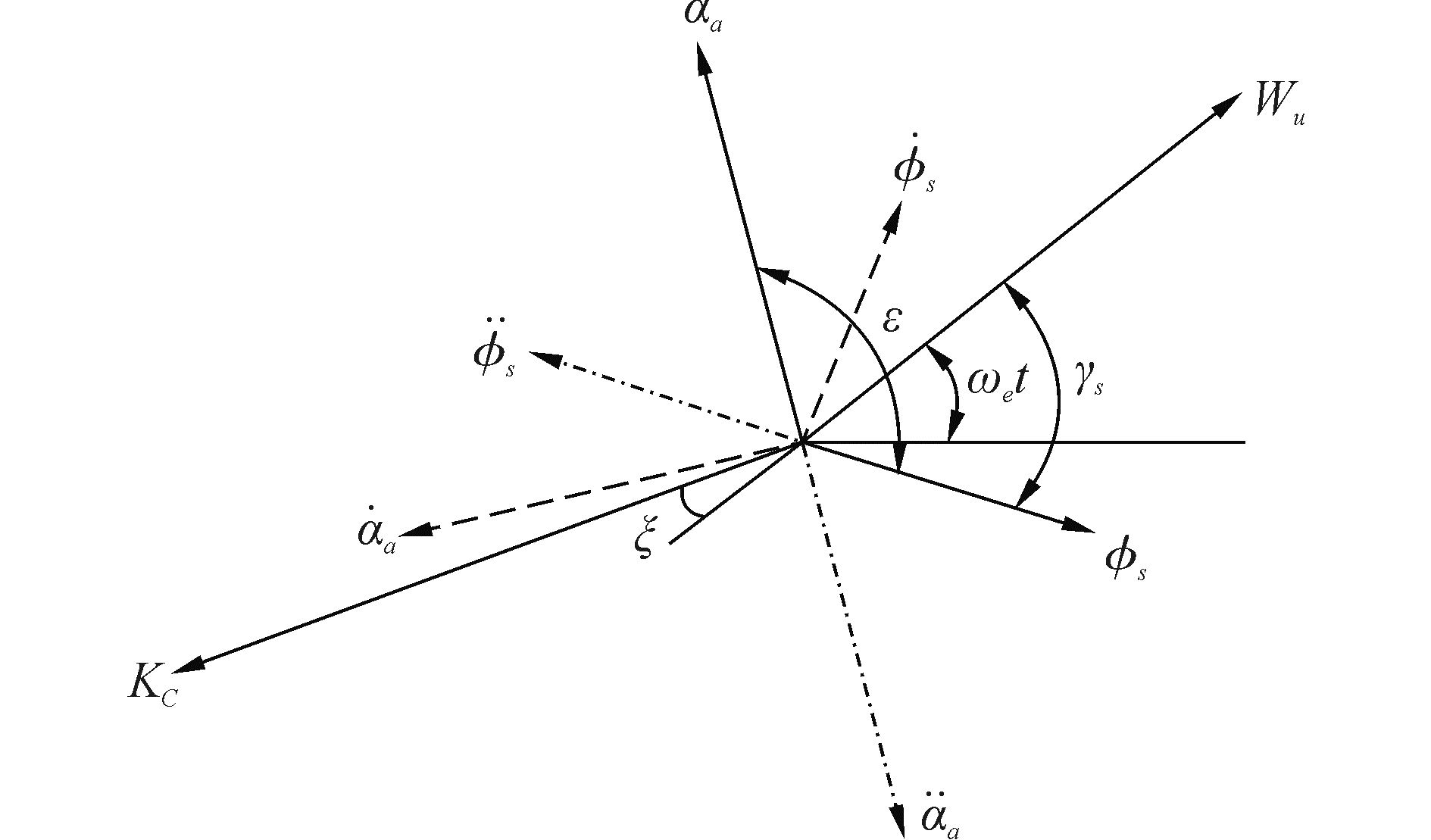
式中ε是鳍角超前横摇角的相角。此时,船舶横摇运动各量之间的相位矢量图如图 5所示。
|
Download:
|
| 图 5 零航速模式下船舶横摇运动相位矢量图 Fig. 5 Phase vector diagram of ship roll motion under ZSAM | |
通过分析图 5中海浪干扰、船舶横摇、鳍动作以及鳍上产生的减摇力之间的相位关系,在以鳍角为最终表现,可得
1) 若采用单一信号反馈控制,则应使鳍角按照横摇角负反馈进行控制,对应于PID控制中的P控制,即
| $ {K_{{\rm{Z}}{{\rm{C}}_{\rm{1}}}}} = {K_{{\rm{Zang}}}}\phi $ | (20) |
式中KZang>0为横摇角反馈控制增益。
2) 若采用多信号反馈的复合控制,考虑到以横摇角度为主反馈信号,对应于PID控制中的P控制,其微分为横摇角速度,而积分无实际意义,故在以鳍角为最终表现,且仅考虑船舶横摇角和角速度信号作为反馈控制量时,对应于PD控制,即
| $ {K_{{\rm{Z}}{{\rm{C}}_{\rm{2}}}}} = {K_{{\rm{Zang}}}}\phi + {K_{{\rm{Zvel}}}}\dot \phi $ | (21) |
式中KZang>0和KZvel>0分别为横摇角和横摇角速度反馈控制增益。
为了验证根据相位匹配分析方法得到的零航速模式下控制策略的有效性,下面通过仿真和水池实验进行验证。
3 仿真及实验 3.1 仿真分析 3.1.1 系统建模海浪干扰以波倾角的形式作用于船体,船舶在其干扰下产生绕其长轴的横摇运动,安装在船体中部的角速度陀螺检测船舶的横摇信息,将之转换成电信号并发送至控制器,控制器接收到船舶的横摇信息后对其进行解算,得到鳍角的控制信号并发送至随动控制系统,随动系统控制减摇鳍转动,产生抵抗海浪干扰的控制力矩,以减小船舶的横摇。船舶减摇控制系统结构如图 6所示。

|
Download:
|
| 图 6 船舶减摇控制系统结构图 Fig. 6 Structure diagram of ship roll reduction control system | |
1) 船舶横摇运动模型
在2.2.2节中所讨论的零航速减摇鳍是针对某型船舶设计的,该船的主要参数为:船长L=84 m,船宽B=10 m,吃水d=3.2 m,排水量D=1 300 t,横稳心高h=1.1 m,横摇周期Tϕ=8 s,横摇无因次衰减系数nu=0.12。
对式(10)在零初始条件下进行拉式变换,并带入船舶参数,可得该船横摇运动传递函数为
| $ {W_\phi }\left( s \right) = \frac{1}{{1.82{s^2} + 0.33s + 1}} $ | (22) |
2) 海浪干扰模型
海浪干扰采用ITTC单参数谱进行描述,其功率谱密度函数为[19]
| $ {S_\zeta }\left( \omega \right) = \frac{{0.0081{g^2}}}{{{\omega ^5}}}\exp \left( { - \frac{{3.11}}{{h_{1/3}^2{\omega ^4}}}} \right) $ | (23) |
式中:h1/3是有义波高,ω为海浪频率,g为重力加速度。下标ζ表示式(23)描述的是波高谱,而海浪是以波倾角的形式作用于船体的,因此需要将波高谱转换成波倾角谱,转换公式为
| $ {S_\alpha }\left( \omega \right) = {k^2}{S_\zeta }\left( \omega \right) $ | (24) |
式中:k=ω2/g是波数,下标α表示式(24)所示Sα(ω)为波倾角谱。作用于船体的波倾角可由下式计算得到:
| $ \alpha \left( t \right) = \sum \sqrt {2{S_\alpha }\left( \omega \right)\Delta \omega } \cos ({\omega _i}t + {\varepsilon _i}) $ | (25) |
式中ωi和εi分别为第i个规则波的波频和随机相角。
3) 角速度陀螺
仿真所采用的角速度陀螺仪的传递函数为
| $ {G_{{\rm{rrg}}}}\left( s \right) = \frac{{400s}}{{{s^2} + 80s + 4000}} $ | (26) |
4) 随动系统
零航速减摇鳍采用泵控液压缸系统[23],随动系统的传递函数为
| $ {G_{{\rm{ss}}}}\left( s \right) = \frac{1}{{s\left( {0.0063\;s + 1} \right)\left( {\frac{{{s^2}}}{{{{33.4}^2}}} + \frac{{0.6\;s}}{{33.4}} + 1} \right)}} $ | (27) |
仿真条件为如下:有义波高h1/3为2 m,浪向角为90°, 图 7和8分别采用基于横摇角度反馈控制以及横摇角度/角速度综合反馈控制下减摇前后船舶的横摇角、横摇角速度以及鳍角曲线。

|
Download:
|
| 图 7 基于横摇角反馈控制的船舶横摇运动 Fig. 7 Ship roll with roll angle based feedback control | |

|
Download:
|
| 图 8 基于横摇角/角速度的综合反馈控制的船舶横摇运动 Fig. 8 Ship roll with roll angle/rate integrated feedback control | |
为了更加直观的比较,两种控制策略下减摇前后的横摇角有义值在表 1中给出,根据文献[5]中给出的方法来计算减摇效果,表中“RA”代表基于横摇角的反馈控制,“RA/R”表示基于横摇角/角速度的综合反馈控制。
| 表 1 减摇效果统计 Tab.1 Summary of anti-rolling effects |
由图 7、8以及表 1可知,采用横摇角反馈控制的减摇效果为75%,而采用横摇角/角速度综合反馈控制的减摇效果达到80.4%。结果说明:零航速模式下,当鳍角按横摇角反馈进行控制时,鳍上产生的减摇力与海浪干扰之间的相位已接近180°,因此通过微分环节进行相位补偿之后,虽进一步提高了减摇效果,但增加幅度相对较小。仿真结果表明,本文基于干扰和补偿的相位匹配分析得到的控制策略是有效的。
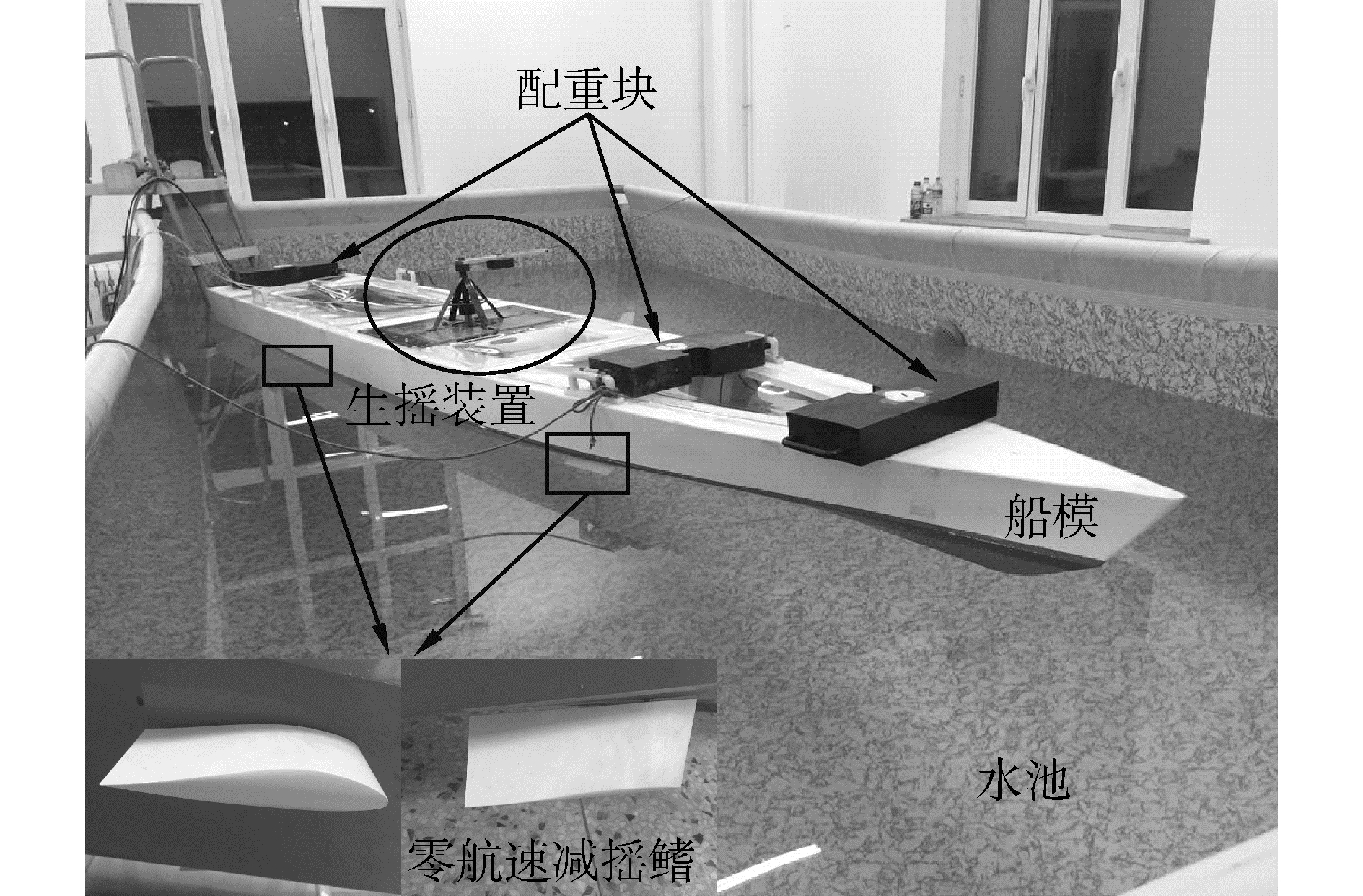
3.2 水池试验为了进一步研究基于相位匹配分析所得零航速模式下控制策略在实际环境中的适用性,利用哈尔滨工程大学船舶减摇与控制技术研究所自行设计构建的零航速船模减摇控制系统(图 9),对所得控制策略进行验证。
|
Download:
|
| 图 9 零航速船模减摇控制系统 Fig. 9 Zero-speed ship model roll stabilization control system | |
两种控制策略下船模水池试验结果如表 2所示。可知,采用横摇角反馈控制的减摇效果为66.93%,基于横摇角/角速度的反馈控制减摇效果为71.7%,水池试验结果与表 1仿真试验结果具有一致性,进一步验证了所得零航速模式减摇控制策略的有效性和实用性。
| 表 2 水池试验结果 Tab.2 Water tank experiment results |
1) 常规减摇模式下减摇鳍的控制与常规减摇鳍相同,应以横摇角速度为主反馈信号。
2) 零航速减摇模式下减摇鳍的控制则应以横摇角为主反馈信号,辅以横摇角速度反馈。
今后应进一步研究两航速减摇鳍在两种模式下的切换控制,以实现最优减摇控制。
| [1] |
PEREZ T, BLANKE M. Ship roll damping control[J]. Annual reviews in control, 2012, 36(1): 129-147. DOI:10.1016/j.arcontrol.2012.03.010 (  0) 0)
|
| [2] |
LIANG Lihua, ZHAO Peng, ZHANG Songtao. Research on hydrodynamic characteristics of Magnus rotor wing at medium/low speed[C]//2016 IEEE International Conference on Mechatronics and Automation. Harbin, China, 2016: 2547-2552. http://ieeexplore.ieee.org/document/7558944/
(  0) 0)
|
| [3] |
LIANG Lihua, ZHAO Peng, ZHANG Songtao, et al. Simulation analysis of fin stabilizer on ship roll control during turning motion[J]. Ocean Engineering, 2018(164): 733-748. (  0) 0)
|
| [4] |
LIANG Lihua, ZHAO Peng, ZHANG Songtao. Research and simulation of ship roll control in turning motion[C]//Proceedings of the 37th Chinese Control Conference. Wuhan, China, 2018. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-KZLL201807003073.htm
(  0) 0)
|
| [5] |
LIANG Lihua, ZHAO Peng, ZHANG Songtao, et al. Simulation and analysis of Magnus rotating roll stabilizer at low speed[J]. Ocean engineering, 2017, 142: 491-500. DOI:10.1016/j.oceaneng.2017.07.012 (  0) 0)
|
| [6] |
宋吉广, 梁利华, 金鸿章, 等. 零航速减摇鳍自适应主从控制器设计[J]. 控制理论与应用, 2015, 32(5): 703-708. SONG Jiguang, LIANG Lihua, JIN Hongzhang, et al. Adaptive master-slave controller for zero-speed fin stabilizer[J]. Control theory & applications, 2015, 32(5): 703-708. (  0) 0)
|
| [7] |
DALLINGA R P. Roll stabilization of motor yacht: use of fin stabilizers in anchored conditions[R]. Amsterdam, Netherlands: Maritime Research Institute, 1999.
(  0) 0)
|
| [8] |
OOMS J. The Use of Roll Stabilization fins at zero speed[R]. Amsterdam, Netherlands: Maritime Research Institute, 2002.
(  0) 0)
|
| [9] |
SEBASTIANI L, RUSCELLI D, PEVERERO M, et al. The design of at-anchor stabilization systems for mega yachts based on calculations and models tests[R]. CETENA, Fincantieri Group, 2006.
(  0) 0)
|
| [10] |
DALLINGA R P, RAPUC S. Merits of flapping roll stabilizer fins[R]. MARIN, The Netherlands, 2008.
(  0) 0)
|
| [11] |
张晓飞.船舶零航速减摇鳍建模与控制策略研究[D].哈尔滨: 哈尔滨工程大学, 2008. ZHANG Xiaofei. Research on modeling and control of fin stabilizer at zero speed[D]. Harbin: Harbin Engineering University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1489316 (  0) 0)
|
| [12] |
金鸿章, 张晓飞, 綦志刚, 等. 零航速减摇鳍升力特性分析[J]. 武汉理工大学学报, 2008, 30(2): 136-139. JIN Hongzhang, ZHANG Xiaofei, QI Zhigang, et al. Analysis on lift characteristics of fin stabilizer at zero speed[J]. Journal of Wuhan University of Technology, 2008, 30(2): 136-139. (  0) 0)
|
| [13] |
WANG Fan, JIN Hongzhang, QI Zhigang. Modeling for active fin stabilizers at zero speed[J]. Ocean engineering, 2009, 36(17/18): 1425-1437. (  0) 0)
|
| [14] |
王帆.零航速减摇鳍仿生机理及控制关键技术[D].哈尔滨: 哈尔滨工程大学, 2010. WANG Fan. Key technologies of bionic mechanism and control for zero speed fin stabilizers[D]. Harbin: Harbin Engineering University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012264996.htm (  0) 0)
|
| [15] |
宋吉广.基于升力反馈的全航速减摇鳍研究[D].哈尔滨: 哈尔滨工程大学, 2012. SONG Jiguang. Study on fin stabilizer of all speed based on lift feedback[D]. Harbin: Harbin engineering university, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10217-1013172101.htm (  0) 0)
|
| [16] |
JI Ming, YE Qingyun, AN Na, et al. The dynamic lift formula fitting for low speed fin[C]//Proceedings of 2014 IEEE International Conference on Mechatronics and Automation. Tianjing, China, 2014: 1757-1761. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6885966
(  0) 0)
|
| [17] |
SU Xiaoyu, GAO Yannan, ZHAO Ruihan. Roll attitude controller design for ships at zero speed[J]. International journal of fuzzy systems, 2018, 20(2): 611-620. DOI:10.1007/s40815-017-0402-2 (  0) 0)
|
| [18] |
金鸿章, 綦志刚, 宋吉广, 等. 船舶零航速减摇控制装置与系统[M]. 北京: 国防工业出版社, 2015. JIN Hongzhang, QI Zhigang, SONG Jiguang, et al. Ship anti-rolling control device and system at zero speed[M]. Beijing: National Defense Industry Press, 2015. (  0) 0)
|
| [19] |
金鸿章, 姚绪梁. 船舶控制原理[M]. 2版. 哈尔滨: 哈尔滨工程大学出版社, 2013. JIN Hongzhang, YAO Xuliang. Ship control theory[M]. 2nd ed. Harbin: Harbin Engineering University Press, 2013. (  0) 0)
|
| [20] |
CONOLLY J. E.. Rolling and its stabilization by active fins[J]. Transaction of the Royal Institution of Naval Architects, 1969(111): 21-48. (  0) 0)
|
| [21] |
叶青云.鳍-船体适配性及其低航速控制策略研究[D].哈尔滨: 哈尔滨工程大学, 2014. YE Qingyun. Fin-hull adaptation and low speed control strategy research[D]. Harbin: Harbin Engineering University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D750383 (  0) 0)
|
| [22] |
孔祥建.基于多模态技术的减摇鳍全航速减摇控制策略研究[D].哈尔滨: 哈尔滨工程大学, 2017. KONG Xiangjian. Research on anti-rolling control strategy of fin stabilizer at full speed based on multi-mode technology[D]. Harbin: Harbin Engineering University, 2017. (  0) 0)
|
| [23] |
梁利华. 液压传动与电液伺服系统[M]. 哈尔滨: 哈尔滨工程大学出版社, 2005. LIANG Lihua. Hydraulic transmission and electro-hydraulic servo system[M]. Harbin: Harbin Engineering University Press, 2005. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


