高光谱遥感图像具有空间维度信息与丰富的光谱维度信息,可以对极其相似的物质进行细微地光谱差异性区分,为目标检测提供优势[1-3]。因此,目标检测技术在高光谱遥感图像领域受到广泛关注,并已经成功运用到地质中稀有矿物、环境中油类污染问题的研究以及人造机器的侦察与监控等多个实际应用中[4-6]。目标检测技术着力于利用目标的先验知识从复杂的背景中区分特定的目标像元,其本质上是二分类问题[7-8]。现有的目标检测方法大部分是利用从高光谱遥感图像数据中得到丰富光谱信息来实现目标与背景的区分。根据不同的假设模型,近年来大量的目标检测算法被提出,如约束能量最小化(constrained energy minimization,CEM)[9],自适应子空间检测(adaptive subspace detector,ASD)[10],光谱匹配滤波(spectral matched filter, SMF)[11]与匹配子空间(matched subspace detector, MSD)[12]等。与上述算法相比,稀疏模型能够更加全面的表示目标光谱特征所构成的子空间,无需对待检测数据的统计分布进行假设,因此稀疏表示模型引入到目标检测领域中,如传统基于稀疏表示的目标检测算法(sparse representation method, SR)[13]、基于稀疏表示的二元假设模型检测(sparse representation-based binary hypothesis, SRB)[14]等。但是在过完备字典构造过程中,需要从待检测图像中获取先验光谱信息,存在很多不确定因素易导致检测效果不理想,并且传统基于稀疏表示的目标检测算法无法实现对亚像元目标的准确检测识别。针对上述不足,本文利用非监督方法对过完备字典进行构造并引入二元对立假设模型,提出了基于字典重构的高光谱图像亚像元目标检测算法,在过完备字典的构造阶段,实现目标与背景像元的可区分选取,提高目标检测精度。
1 稀疏表示目标检测原理稀疏表示理论的提出使高维图像数据得到更好地解决,其中心思想是原始信号可以被过完备字典中极少量原子线性表示。随着信号稀疏表示理论的快速发展,在检测过程中字典的构造尤为重要。在实际应用中需要按照实际情况选择相对应的方法进行字典的构造,通常情况下,字典的构造可以分为三种情况:1)没有训练样本数据的情况下,使用变换方法得到字典,例如分析类字典;2)当待检测图像中的数据含量较少时,可以利用图像中包含的部分数据直接构造过完备字典;3)当待检测图像中包含大量样本时,需要采用学习类字典。本文中待检测图像的数据量不大,选用待检测图像左侧十分之一的像素点进行字典的构造,然而由于此种构造字典的方法随机性大,导致极有可能过完备字典中不包含目标像元的光谱特征信息,影响其检测精度,由此提出对目标像元与背景像元进行预处理区分的方法。
稀疏表示基础模型中,假设x为背景像元,它的光谱特征可以由背景训练样本aib,i=1, 2, …, Nb的线性组合形式表示为
| $ \begin{array}{l} \mathit{\boldsymbol{x}} \approx {\mathit{\boldsymbol{\alpha }}_1}\mathit{\boldsymbol{a}}_1^b + {\mathit{\boldsymbol{\alpha }}_2}\mathit{\boldsymbol{a}}_2^b + \cdots + {\mathit{\boldsymbol{\alpha }}_{{N_b}}}\mathit{\boldsymbol{a}}_{{N_b}}^b = \\ \;\;\;\;\;[\mathit{\boldsymbol{a}}_1^b\;\;\mathit{\boldsymbol{a}}_2^b \cdots \mathit{\boldsymbol{a}}_{{N_b}}^b]{[{\mathit{\boldsymbol{a}}_1}{\mathit{\boldsymbol{a}}_2} \cdots {\mathit{\boldsymbol{a}}_{{N_b}}}]^{\rm{T}}} = {\mathit{\boldsymbol{A}}_b}\mathit{\boldsymbol{\alpha }} \end{array} $ | (1) |
式中:Nb表示背景训练样本的数目,Ab为N×Nb维的背景字典,α为背景字典所对应的稀疏向量,该向量中只有很少量的非零值。
相似地,一个目标像元x的光谱特征便可以由目标训练样本ait,i=1, 2, …, Nt的线性组合进行稀疏表示,形式如下
| $ \begin{array}{l} \mathit{\boldsymbol{x}} \approx {\mathit{\boldsymbol{\beta }}_1}\mathit{\boldsymbol{a}}_1^t + {\mathit{\boldsymbol{\beta }}_2}\mathit{\boldsymbol{a}}_2^t + \cdots + {\mathit{\boldsymbol{\beta }}_{{N_t}}}\mathit{\boldsymbol{a}}_{{N_t}}^t = \\ \;\;\;\;\;\;[\mathit{\boldsymbol{a}}_1^t\mathit{\boldsymbol{a}}_2^t \cdots \mathit{\boldsymbol{a}}_{{N_t}}^t]{[{\mathit{\boldsymbol{\beta }}_1}{\mathit{\boldsymbol{\beta }}_2} \cdots {\beta _{{N_i}}}]^{\rm{T}}} = {\mathit{\boldsymbol{A}}_t}\mathit{\boldsymbol{\beta }} \end{array} $ | (2) |
式中:Nt表示目标训练样本的数目,At表示N×Nt维的目标字典,β为目标字典所对应的稀疏向量,其中只有很少量原子是非零值。因此,待检测样本中的像元可以被看作是目标子空间与背景子空间的线性组合,可以通过将目标字典与背景字典相结合,实现对待检测样本的稀疏表示:
| $ \mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{A}}_b}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{A}}_t}\mathit{\boldsymbol{\beta }} = \underbrace {[{\mathit{\boldsymbol{A}}_b}\;\;{\mathit{\boldsymbol{A}}_t}]}_\mathit{\boldsymbol{A}}\underbrace {\left[ \begin{array}{l} \mathit{\boldsymbol{\alpha }}\\ \mathit{\boldsymbol{\beta }} \end{array} \right]}_\gamma = \mathit{\boldsymbol{A\gamma }} $ | (3) |
式中:A是由背景字典Ab与目标字典At组合而成的过完备字典,α与β是背影字典与目标字典所对应的稀疏系数。稀疏矩阵γ可以通过下式进行求解:
| $ \mathit{\boldsymbol{\hat \gamma }} = \arg \min {\left\| \mathit{\boldsymbol{\gamma }} \right\|_0}\;\;\;{\rm{subject}}\;{\rm{to}}\;\;\;\mathit{\boldsymbol{x}} = \mathit{\boldsymbol{A\gamma }} $ | (4) |
式中:l0范数表示稀疏向量的稀疏度即其非零元素的个数。
| $ {\left\| \mathit{\boldsymbol{s}} \right\|_0} = \mathop {\lim }\limits_{p \to 0} \left\| \mathit{\boldsymbol{s}} \right\|_p^p = \mathop {\lim }\limits_{p \to 0} \sum\limits_{k = 1}^m {|{\mathit{\boldsymbol{s}}_k}{|^p}} $ | (5) |
式中:l0范数的最小化是NP-hard问题,难以求解,因此将其限制条件松弛化,得到如下表示:
| $ \mathit{\boldsymbol{\hat \gamma }} = \arg \min {\left\| \mathit{\boldsymbol{\gamma }} \right\|_0}\;\;\;{\rm{subject}}\;{\rm{to}}\;\;\;{\left\| {\mathit{\boldsymbol{A\gamma }} - \mathit{\boldsymbol{x}}} \right\|_2} \le \sigma $ | (6) |
式中:σ表示其误差容限,可以将上式进一步化简,转化为在固定稀疏条件下的误差最小化问题。式(7)可以通过凸优化技术或者贪婪算法进行求解,本文使用正交匹配追踪(OMP)算法实现稀疏向量的求解:
| $ \mathit{\boldsymbol{\hat \gamma }} = \arg \min {\left\| {\mathit{\boldsymbol{A\gamma }} - \mathit{\boldsymbol{x}}} \right\|_2}\;\;\;{\rm{subject}}\;{\rm{to}}\;\;\;{\left\| \mathit{\boldsymbol{\gamma }} \right\|_0} \le K $ | (7) |
式中K表示其稀疏条件限制。
求得稀疏向量后,进行背景残差rb(x)与目标残差rt(x)的构建并进行比较:
| $ {r_b}\left( \mathit{\boldsymbol{x}} \right) = {\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{A}}_b}\mathit{\boldsymbol{\hat \alpha }}} \right\|_2} $ | (8) |
| $ {r_t}\left( \mathit{\boldsymbol{x}} \right) = {\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{A}}_t}\mathit{\boldsymbol{\hat \beta }}} \right\|_2} $ | (9) |
| $ R\left( \mathit{\boldsymbol{x}} \right) = {r_b}\left( \mathit{\boldsymbol{x}} \right) - {r_t}\left( \mathit{\boldsymbol{x}} \right) $ | (10) |
检测器对目标像元或者背景像元的输出由上式进行判断,δ为选取的阈值,当R(x)>δ时,待检测像元x被定义为目标像元,当R(x) < δ时,待检测像元x被定义为背景像元。对整幅图像的待检测像元进行遍历,实现目标与背景的区分,检测过程结束。
2 字典重构亚像元检测算法 2.1 字典重构在传统基于稀疏表示的目标检测算法中,过完备字典的构造尤为重要,由于本文实验部分所选用的检测图的尺寸不大,因此直接从待检测高光谱遥感图像中的一部分数据直接进行光谱信息的获取来构造过完备字典[13],如图 1所示。

|
Download:
|
| 图 1 直接构造法 Fig. 1 Construction method of overcompleted dictionary | |
图 1中包含三架飞机,过完备字典中包含的光谱信息从高光谱遥感图像数据的左侧直接提取,字典中样本数为360,其中目标训练样本数为28,背景训练样本数为332。字典仅包含待检测图像中小部分光谱信息,其光谱特征信息不丰富。直接从图像数据中进行过完备字典的构造也存在许多不确定因素,当待检测图像的左侧恰好不包含目标像元或者目标像元极少时,就会出现过完备字典中不包含或只包含极少量的目标像元的光谱信息,给目标检测的结果带来了影响。在高光谱遥感图像中,背景像元的个数要远高于目标像元的个数,目标出现的概率低,因此可以利用无监督方法[14]进行字典重构以确保字典中包含目标像元的光谱信息。
首先构造全局正交投影算子,需要对待检测图像进行互相关矩阵的求解:
| $ \mathit{\boldsymbol{R}} = \frac{1}{N}\sum\limits_{i = 1}^N {{\mathit{\boldsymbol{r}}_i}\mathit{\boldsymbol{r}}_i^{\rm{T}}} $ | (11) |
式中:N表示像元数目,ri表示待检测高光谱图像中的像元。接下来,对互相关矩阵R进行特征值与特征向量的求解,将特征值按照由大到小顺序进行排列,即λ1>λ2>…>λL,L表示高光谱遥感图像的波段数,选择前q个特征值对应的特征向量,构成背景光谱矩阵U=[e1, e2, …, eq], q < L,其中每一列都代表着一种地物光谱信号,正交投影算子P的构造可表示为
| $ \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{U}}{({\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}})^{ - 1}}{\mathit{\boldsymbol{U}}^{\rm{T}}} = \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{U}}^\# } $ | (12) |
式中:U#=(UTU)-1 UT表示背景光谱矩阵U的伪逆。一般情况下,待检测图像中,目标像元所占的比重小,信息量不丰富,其通常分布于互相关矩阵中小特征值所对应的特征向量,背景像元在待检测图像中所占的比重大,通常分布于互相关矩阵中大特征值所对应的特征向量。由此可知,通过大特征值对应的特征向量构建的矩阵U可以近似被看作真实的背景矩阵,利用背景矩阵U构造的正交投影算子P能够抑制背景地物信息,使目标像素更突出。字典D的计算公式:
| $ \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{Ipx}} $ | (13) |
式中:I是一个q维的行向量,其元素均为1。由于采用了背景抑制方法,因此待检测高光谱图像中的背景像元所对应的值接近于0,目标像元所对应的值则远大于0,通过选取合适的阈值T,可以完成字典的构造。当其运算值D>T则判断为目标字典中的元素,相反则为背景字典中的元素。通过上述方法得到字典D可以将待检测信号进行稀疏表示:
| $ \mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{D}}_b}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{D}}_t}\mathit{\boldsymbol{\beta }} = \underbrace {[{\mathit{\boldsymbol{D}}_b}\;\;{\mathit{\boldsymbol{D}}_t}]}_\mathit{\boldsymbol{D}}\underbrace {\left[ \begin{array}{l} \mathit{\boldsymbol{\alpha }}\\ \mathit{\boldsymbol{\beta }} \end{array} \right]}_\mathit{\boldsymbol{\gamma }} = \mathit{\boldsymbol{D\gamma }} $ | (14) |
假设x为包含N个波段的待检测光谱向量,根据二元对立假设模型[15],背景像元的光谱向量位于由背景字典Db中原子张成的背景子空间中,而目标像元的光谱向量,尤其是亚像元的目标光谱则会位于由背景字典Db与目标字典Dt中原子张成的联合子空间中。当待检测光谱为背景光谱时,仅依赖于少量的背景光谱信息就可以实现背景像元的重建,因此对于背景像元x,它能够被背景字典中的训练样本表示为
| $ \begin{array}{l} \mathit{\boldsymbol{x}} \approx {\mathit{\boldsymbol{\alpha }}_1}\mathit{\boldsymbol{d}}_1^b + {\mathit{\boldsymbol{\alpha }}_2}\mathit{\boldsymbol{d}}_2^b + \cdots + {\mathit{\boldsymbol{\alpha }}_{{N_b}}}\mathit{\boldsymbol{d}}_{{N_b}}^b = \\ \;\;\;\;\;[\mathit{\boldsymbol{d}}_1^b\;\;\mathit{\boldsymbol{d}}_2^b \cdots \mathit{\boldsymbol{d}}_{{N_b}}^b]{[{\mathit{\boldsymbol{\alpha }}_1}{\mathit{\boldsymbol{\alpha }}_2} \cdots {\mathit{\boldsymbol{\alpha }}_{{N_b}}}]^{\rm{T}}} = {\mathit{\boldsymbol{D}}_b}\mathit{\boldsymbol{\alpha }} \end{array} $ | (15) |
式中:α为稀疏向量,表示背景字典中的原子所对应的比重。相似地,如果待检测像元x为目标像元,那么它可以被由目标字典以及背景字典所张成的联合低维子空间中包含的训练样本线性表示,其形式如下
| $ \begin{array}{l} \mathit{\boldsymbol{x}} \approx ({\mathit{\boldsymbol{\alpha }}_1}\mathit{\boldsymbol{d}}_1^b + {\mathit{\boldsymbol{\alpha }}_2}\mathit{\boldsymbol{d}}_2^b + \cdots + {\mathit{\boldsymbol{\alpha }}_{{N_b}}}\mathit{\boldsymbol{d}}_{{N_b}}^b) + \\ \;\;\;\;\;\;({\mathit{\boldsymbol{\beta }}_1}\;\mathit{\boldsymbol{d}}_1^t + {\mathit{\boldsymbol{\beta }}_2}\mathit{\boldsymbol{d}}_2^t + \cdots + {\mathit{\boldsymbol{\beta }}_{{N_t}}}\mathit{\boldsymbol{d}}_{{N_t}}^t) = \\ \;\;\;\;\;\;[\mathit{\boldsymbol{d}}_1^b\;\mathit{\boldsymbol{d}}_2^b \cdots \mathit{\boldsymbol{d}}_{{N_b}}^b]{[{\mathit{\boldsymbol{\alpha }}_1}\;{\mathit{\boldsymbol{\alpha }}_2} \cdots {\mathit{\boldsymbol{\alpha }}_{{N_b}}}]^{\rm{T}}} + \\ \;\;\;\;\;\;[\mathit{\boldsymbol{d}}_1^t\;\mathit{\boldsymbol{d}}_2^t \cdots \mathit{\boldsymbol{d}}_{{N_t}}^t]{[{\mathit{\boldsymbol{\beta }}_1}\;{\mathit{\boldsymbol{\beta }}_2} \cdots {\mathit{\boldsymbol{\beta }}_{{N_t}}}]^{\rm{T}}} = \\ \;\;\;\;\;{\mathit{\boldsymbol{D}}_b}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{D}}_t}\mathit{\boldsymbol{\beta }} = \mathit{\boldsymbol{D\gamma }} \end{array} $ | (16) |
式中:D=[Db, Dt]表示背景字典与目标字典所构成的联合字典,γ表示联合字典所对应的稀疏向量。因此,待检测光谱向量x可以通过二元假设检测模型表示为
| $ \mathit{\boldsymbol{x}} = \left\{ \begin{array}{l} {\mathit{\boldsymbol{D}}_b}\mathit{\boldsymbol{\alpha }}, \;\;{H_0}\\ {\mathit{\boldsymbol{D}}_b}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{D}}_t}\mathit{\boldsymbol{\beta }} = \mathit{\boldsymbol{D\gamma }}, \;\;{H_1} \end{array} \right. $ | (17) |
式中:H0表示不存在目标的情况,H1表示目标存在的情况。D=[Db, Dt]表示由目标字典和背景字典构成的联合字典,γ=[α, β]表示线性组合中各原子所占的比重。由于目标像元的光谱向量位于由目标和背景字典中原子共同张成的低维子空间中,因此可由背景字典与目标字典所构成的联合字典有效表示。而背景像元位于由背景光谱张成的低维子空间中,因此可以由背景字典进行有效表示。与单纯利用目标字典对目标像元进行稀疏表示相比,利用联合字典方法对目标像元进行表示可以在有效进行纯像元目标检测的基础上对亚像元目标也进行有效检测。利用正交匹配追踪算法对稀疏向量进行求解,最终通过构造残差实现目标检测。
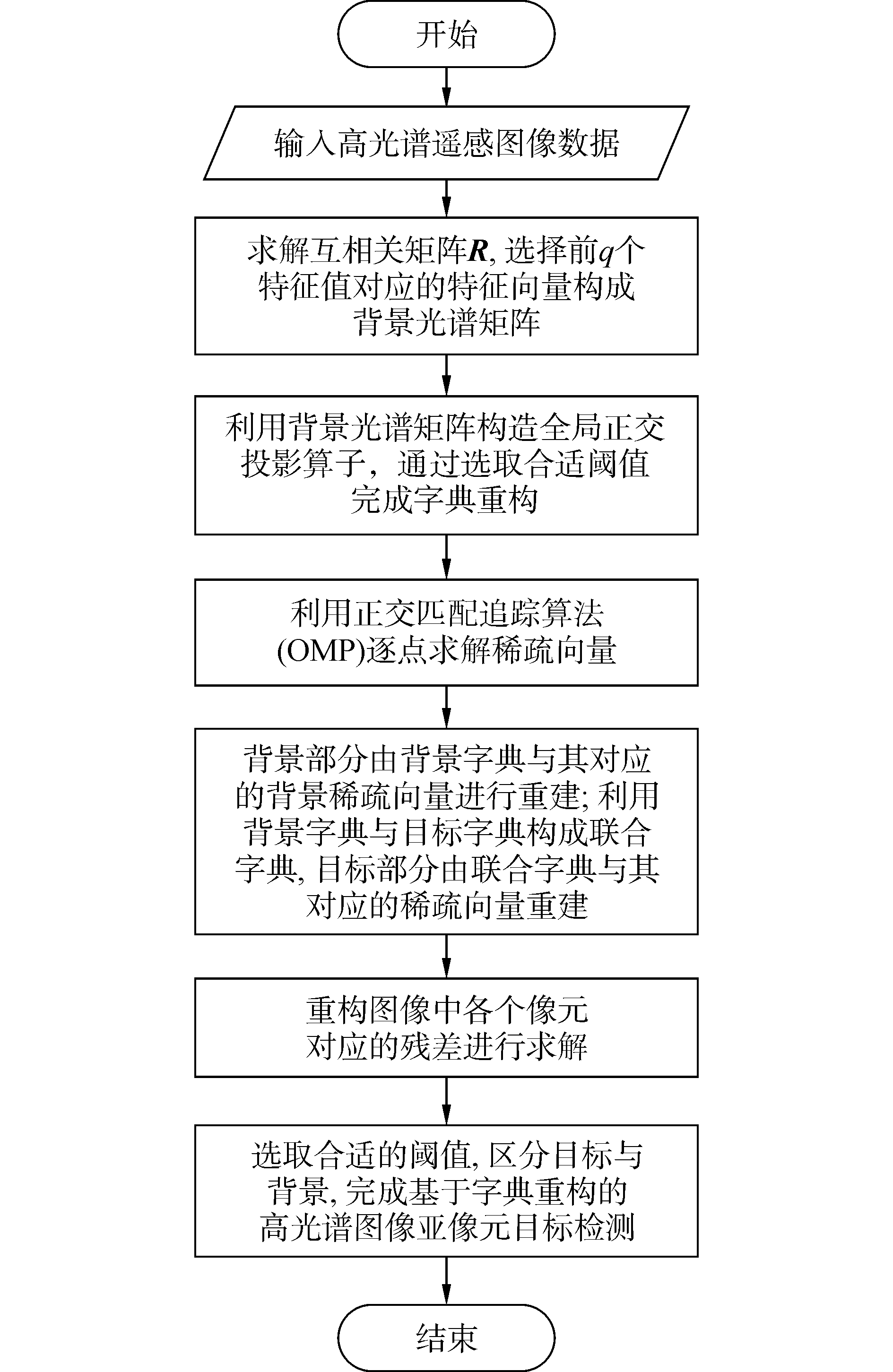
2.3 算法流程图基于字典重构的高光谱图像亚像元目标检测算法的处理流程图如图 2所示。
|
Download:
|
| 图 2 算法流程图 Fig. 2 Algorithm flowchart | |
为了验证本文提出方法的有效性,共使用两幅高光谱遥感图像数据进行仿真实验。其中一幅为模拟数据。该数据的背景光谱信息满足于高斯分布,在背景数据的基础上增添了四种物质(G、H、T、P)作为目标,每行目标由同种物质构成,每个目标都是3×3大小的像元。其中第一列由纯像元构成; 第二列包含了75%目标像元光谱特性和25%背景光谱特性;第三列包含了50%目标像元光谱特性和50%背景光谱特性;第四列包含了25%目标像元光谱特性和75%背景光谱特性,图 3为模拟数据集第50波段的灰度图像与目标分布二值图。

|
Download:
|
| 图 3 模拟数据 Fig. 3 Synthetic dataset | |
第二组数据是在美国圣地亚哥机场由机载可见光成像光谱仪(AVIRIS)获取的真实高光谱数据。每个像元的空间分辨率可以达到20 m2,在可见光波长以及红外波长的范围内获取图像信息,相邻波段的间隔为10 nm,将图像中水汽吸收带以及信噪比略低的波段除去,该高光谱遥感实验数据含有126个波段,像元数目为60×60,数据中包含三架飞机,其中目标像元数目为89,背景像元数目为271。图 4为此高光谱数据集第50波段的灰度图像以及真实地物分布的二值图。

|
Download:
|
| 图 4 真实数据 Fig. 4 Real dataset | |
将本文所提出的基于字典重构的高光谱图像亚像元目标检测算法定义为LSRB。为了验证该方法的有效性,在进行实验仿真过程中,与其他三种算法进行对比,这三种算法依次为传统的基于稀疏表示的目标检测算法(SR)、基于稀疏表示的二元假设模型目标检测算法(SRB)以及利用非监督方法进行字典重构的稀疏表示目标检测算法(LSR)。接收机工作性能(ROC)曲线是衡量算法检测性能优劣的标准[16],曲线越靠近左上角说明此种方法能够在较小的虚警概率下达到较大的检测概率,检测性能更优。ROC曲线下方面积值(area under the curve,AUC)越大,说明ROC曲线越快速向左上角逼近,检测效果越好。上述四种算法的仿真结果三维图像如图 5。

|
Download:
|
| 图 5 模拟数据实验结果三维图 Fig. 5 Experimental results for synthetic dataset in 3-D version | |
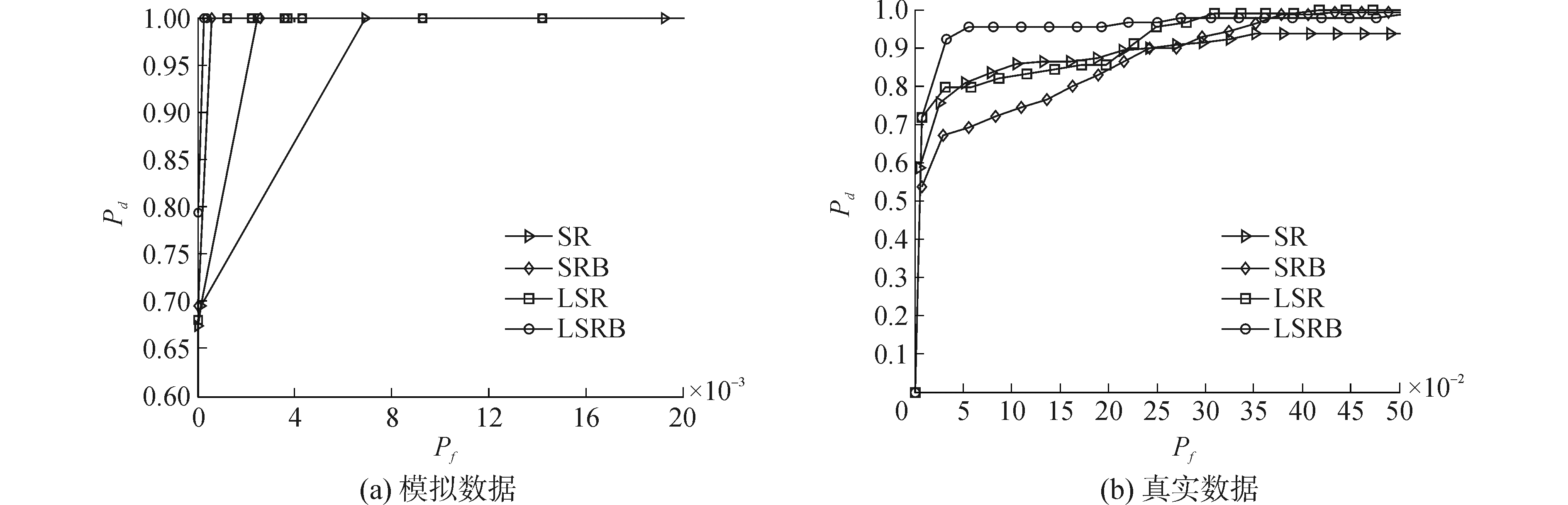
通过对模拟数据以及真实飞机场数据进行仿真实验,上述四种算法的ROC曲线如图 7所示,AUC值的对比情况如图 8所示。

|
Download:
|
| 图 6 真实数据实验结果三维图 Fig. 6 Experimental results for real dataset in 3-D version | |
|
Download:
|
| 图 7 接收机工作特性(ROC)曲线 Fig. 7 Curves of receiver operating characteristics (ROC) | |

|
Download:
|
| 图 8 两幅数据AUC柱状图 Fig. 8 Bars of AUC of two datasets | |
由模拟数据三维结果图可以看出,本文所提出的算法LSRB与对比算法均可以有效地对模拟数据中目标与背景进行区分,但LSRB对待检测数据中的目标像元检测更为突出,说明此算法的检测效果更优。从真实高光谱遥感图像的仿真三维图中同样可以看出,LSRB可以更加有效地实现对三架飞机的检测,且在字典重构的过程中突出目标像元的光谱信息,有较强的背景抑制效果。从ROC曲线可以看出,对于两种类型的检测图像来说,LSRB的ROC曲线均为最靠近左上角,说明其能在较低虚警概率时达到较高的检测概率。通过分析AUC柱状图可以看出LSRB均具有最大的数值,同样说明LSRB对实现高光谱图像的目标检测有最佳的有效性和准确性。
4 结论1) 本文针对传统基于稀疏表示的目标检测算法中字典构造的不确定性,提出利用非监督方法进行字典的重构,与传统目标检测算法相比,二元假设检验模型相结合,能够实现对亚像元目标的有效检测。
2) 对模拟高光谱遥感图像数据以及真实高光谱遥感图像数据进行实验仿真,通过对实验结果三维图、ROC曲线以及AUC值的对比分析得出本文所提出的基于字典重构的高光谱图像亚像元目标检测算法不仅提高了检测精度而且更好地抑制了背景噪声。
| [1] |
赵春晖, 王立国, 齐滨. 高光谱遥感图像处理方法及应用[M]. 北京: 电子工业出版社, 2016. ZHAO Chunhui, WANG Liguo, QIN Bin. Hyperspectral remote sensing images processing methods and applications[M]. Beijing: Publishing House of Electronics Industry, 2016. (  0) 0)
|
| [2] |
MASIA F, KARUNA A, BORRI P, et al. Hyperspectral image analysis for CARS, SRS, and raman data[J]. Journal of raman spectroscopy, 2015, 46(8): 727-734. DOI:10.1002/jrs.4729 (  0) 0)
|
| [3] |
DU Qian, ZHANG Liangpei, ZHANG Bing, et al. Foreword to the special issue on hyperspectral remote sensing:Theory, methods, and applications[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2013, 6(2): 459-465. DOI:10.1109/JSTARS.2013.2257422 (  0) 0)
|
| [4] |
STEFANOU M S, KEREKES J P. Image-derived prediction of spectral image utility for target detection applications[J]. IEEE transactions on geoscience and remote sensing, 2010, 48(4): 1827-1833. DOI:10.1109/TGRS.2009.2034295 (  0) 0)
|
| [5] |
KUMAR G V S, SIVAMURUGESAN V, SHARMILA N. MF based spectral unmixing for subpixel target detection in hyperspectral images[J]. International journal of applied engineering research, 2015, 10(55): 292-296. (  0) 0)
|
| [6] |
EISMANN M T, STOCKER A D, NASRABADI N M. Automated hyperspectral cueing for civilian search and rescue[J]. Proceedings of the IEEE, 2009, 97(6): 1031-1055. DOI:10.1109/JPROC.2009.2013561 (  0) 0)
|
| [7] |
MANOLAKIS D, TRUSLOW E, PIEPER M, et al. Detection algorithms in hyperspectral imaging systems:An overview of practical algorithms[J]. IEEE signal processing magazine, 2014, 31(1): 24-33. DOI:10.1109/MSP.2013.2278915 (  0) 0)
|
| [8] |
NASRABADI N M. Hyperspectral target detection:an overview of current and future challenges[J]. IEEE signal processing magazine, 2014, 31(1): 34-44. DOI:10.1109/MSP.2013.2278992 (  0) 0)
|
| [9] |
GENG Xiurui, JI Luyan, SUN Kang, et al. CEM:more bands, better performance[J]. IEEE geoscience and remote sensing letters, 2014, 11(11): 1876-1880. DOI:10.1109/LGRS.2014.2312319 (  0) 0)
|
| [10] |
KWON H, NASRABADI N M. Kernel adaptive subspace detector for hyperspectral imagery[J]. IEEE geoscience and remote sensing letters, 2006, 3(2): 271-275. DOI:10.1109/LGRS.2006.869985 (  0) 0)
|
| [11] |
KWON H, NASRABADI N M. A comparative study of kernel spectral matched signal detectors for hyperspectral target detection[C]//Proceedings Volume 5806, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI. Orlando, Florida, United States: SPIE, 2005: 371-383.
(  0) 0)
|
| [12] |
SCHARF L L, FRIEDLANDER B. Matched subspace detectors[J]. IEEE transactions on signal processing, 1994, 42(8): 2146-2157. DOI:10.1109/78.301849 (  0) 0)
|
| [13] |
CHEN Yi, NASRABADI N M, TRAN T D. Sparse representation for target detection in hyperspectral imagery[J]. IEEE journal of selected topics in signal processing, 2011, 5(3): 629-640. DOI:10.1109/JSTSP.2011.2113170 (  0) 0)
|
| [14] |
JIMENEZ L O, MORALES-MORELL A, CREUS A. Classification of hyperdimensional data based on feature and decision fusion approaches using projection pursuit, majority voting, and neural networks[J]. IEEE transactions on geoscience and remote sensing, 1999, 37(3): 1360-1366. DOI:10.1109/36.763300 (  0) 0)
|
| [15] |
ZHANG Yuxiang, ZHANG Liangpei, DU Bo, et al. A nonlinear sparse representation-based binary hypothesis model for hyperspectral target detection[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2015, 8(6): 2513-2522. DOI:10.1109/JSTARS.2014.2368173 (  0) 0)
|
| [16] |
韦修喜, 周永权. 基于ROC曲线的两类分类问题性能评估方法[J]. 计算机技术与发展, 2010, 20(11): 47-50. WEI Xiuxi, ZHOU Yongquan. A new performance categories evaluation method based on ROC curve[J]. Computer technology and development, 2010, 20(11): 47-50. DOI:10.3969/j.issn.1673-629X.2010.11.012 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


