2. 哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨 150001
2. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China
水声换能器是声呐设备中实现声波产生、发射和接收的装置,其性能的优劣一直是声呐系统以及水声技术发展的关键。新型功能材料技术与性能的突破是换能器技术长足发展的根本,新型结构的设计也影响着换能器的性能[1]。弛豫铁电单晶材料做为新型功能材料中性能较为突出的一种,d33是压电陶瓷的6~8倍,纵向机电耦合系数k33可达0.9,杨氏模量大概为压电陶瓷材料的1/3,从而有利于换能器实现小尺寸、大功率、宽带发射的性能指标[2-4]。自压电单晶材料问世以来,其优越的压电性能和多方面应用一直是声学换能器的研究热点。Richard等[5]分别采用压电单晶和PZT8陶瓷做为换能器驱动部分,在保证工作频率和发射性能基本不变下,纵向尺寸可减少30%。Kim等[6]制作了PMNT单晶换能器、PZT基1-3复合材料换能器和块体PZT材料换能器,结果显示压电单晶换能器的频率响应比PZT复合材料换能器高2.4 dB、比块体PZT换能器高7 dB。Hyun-Taek等[7]的研究结果显示Mn掺杂单晶更适合大功率换能器的研制,与PZT4陶瓷相比损耗更低,尺寸更小。可见,新型压电单晶材料的应用可大幅提高换能器的各方面性能,是新一代换能器理想的功能材料。
纵向换能器以其结构坚固、效率高、性能稳定、制作工艺成熟等优点,应用较为广泛。其宽带性能的实现方式有很多,包括匹配层技术、纵弯耦合技术、单端激励、混合激励、多激励等[8-11]。双激励纵向换能器是将传统单晶堆结构改变成尺寸不同的两组晶堆,通过所能够激励出的前两阶纵振模态的耦合实现宽带发射[12-13]。
为了从根本上提高纵向换能器的发射性能和拓宽工作带宽,本文采用新型压电单晶PMNT(pb(Mgy3Nb2/3)O3-xPbTiO3)做为有源材料,双晶堆结构驱动的方式,以激励出耦合较好的前两阶纵振模态,从而实现宽带发射性能,并通过试验样机的制作与测试验证本文分析与计算的可靠性。
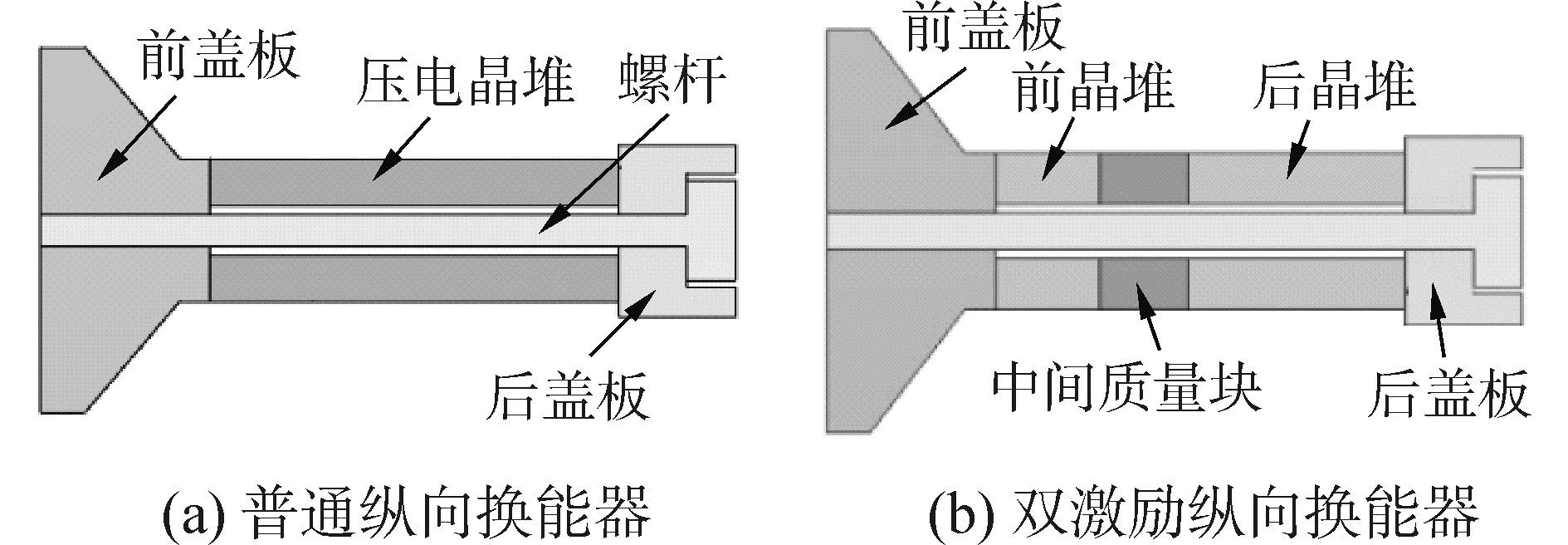
1 双激励纵向换能器结构模型普通的纵向换能器结构如图 1(a)所示,由一段压电晶堆驱动前盖板和后盖板,中间由螺杆连接结构整体,提供一定预应力以保证换能器的安全工作状态。双激励纵向换能器结构如图 1(b)所示,由机械串联的两个晶堆组成,前晶堆尺寸较小、后晶堆尺寸较大,中间由金属质量块分开,其他部分与普通纵向换能器结构类似。
|
Download:
|
| 图 1 普通纵向换能器和双激励纵向换能器 Fig. 1 The structure of the ordinary and dual-excited longitudinal transducer | |
晶堆作为换能器的核心部分,其结构形式和激励方式对性能影响最大,关系到各阶纵向谐振模态是否可以被成功激励出来。基频纵向谐振一般很容易被激发,比如纵弯模态耦合利用的一阶纵振与辐射端弯曲模态,单端激励利用的一阶纵振与二、三阶纵振模态,Janus-Helmholtz换能器利用的液腔振动和结构的一阶纵振模态等。双晶堆结构采用的是一阶纵振与二阶纵振模态耦合实现宽带性能,如果辐射面尺寸够大,也可以利用前两阶纵振模态与辐射面弯曲模态作用,实现更宽带宽、响应起伏更小的效果。
2 晶堆激励方式分析为了便于分析,只对4片晶片组成的晶堆施加不同相位的电压,以此来分析晶堆激励方式对纵振模态的影响。如图 2所示,图中箭头方向表示晶片的极化方向,晶堆激励方式包括同相激励、同尺寸反相激励及不同尺寸反相激励。同相激励是指4片晶片均施加相同相位电压,晶堆各部分振动形式一样,即同时扩张或同时收缩;同尺寸反相激励是指相邻的2片晶片与另外相邻的2片晶片施加反相电压,晶堆振动形式为一半扩张,另一半收缩;不同尺寸反相激励是指3片相邻的晶片与另1片施加反相电压,晶堆振动形式为小部分扩张时,其余部分收缩。

|
Download:
|
| 图 2 压电晶堆不同的激励形式 Fig. 2 Various excitations of the piezoelectric stacks | |
图 3给出了晶堆的一、二阶纵振模态和形变形式,一阶纵振模态有一个位移节点,两端面位移反相,形变形式为两端同时扩张同时收缩;二阶纵振模态有两个位移节点,两端面位移同相,形变形式为一端扩张,另一端收缩。可见,晶堆的纵振模态和形变形式符合两端自由状态细棒的振动特征。

|
Download:
|
| 图 3 晶堆的一、二阶纵振模态和形变形式 Fig. 3 The first and second order resonant modes and deformed shapes of the stack | |
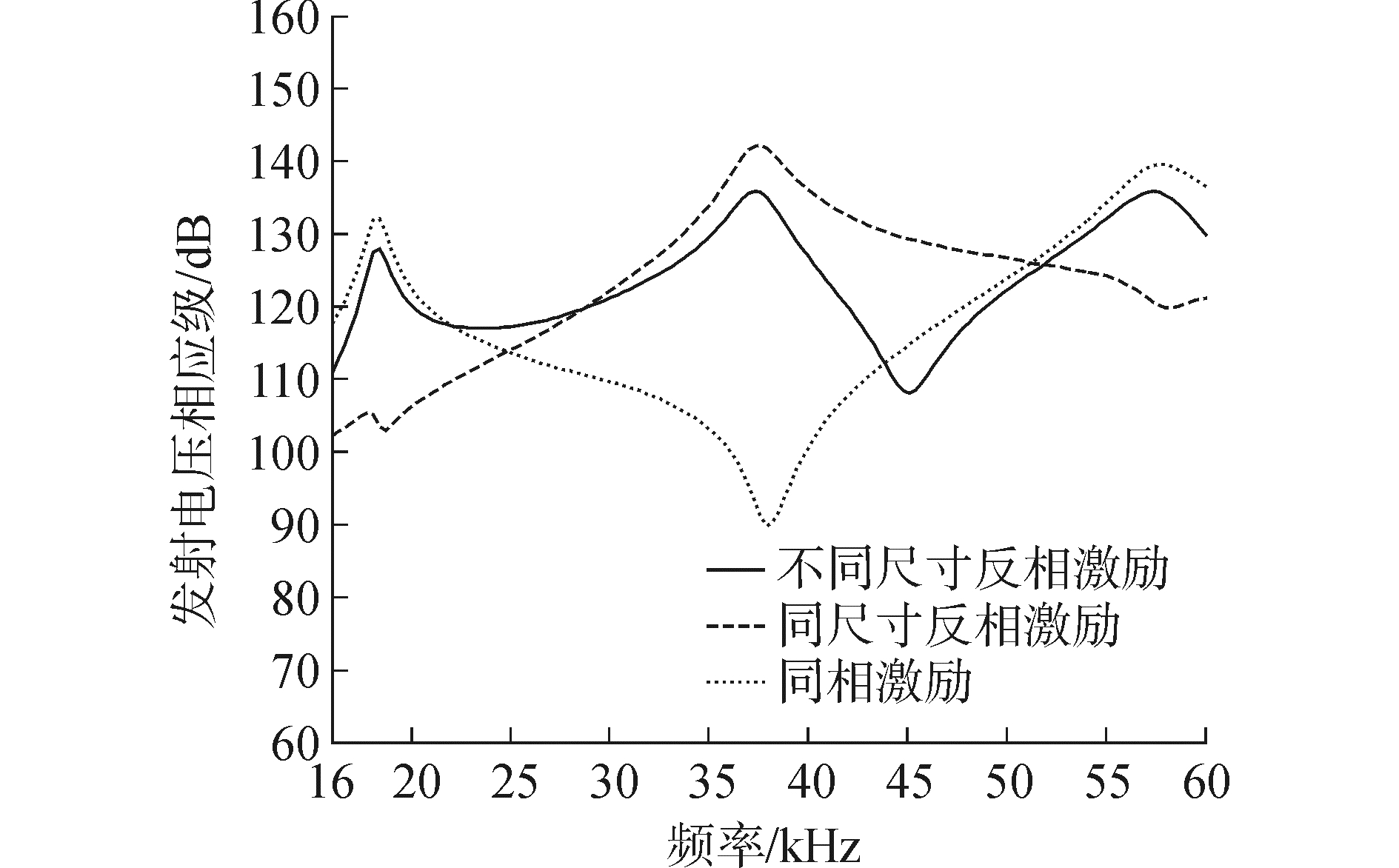
三种不同激励方式下,晶堆的水中发射电压响应如图 4所示。一阶纵向谐振在18 kHz附近,二阶纵向谐振在37 kHz附近,三阶纵向谐振在57 kHz附近。同相激励可以激发出一、三阶谐振但不能激发出二阶谐振,同尺寸反相激励只能激发出二阶谐振但不能激发一、三阶谐振,而不同尺寸反相激励则可以同时激发一、二、三阶纵向谐振[9],其中一、二阶纵向谐振的有效耦合可实现宽带效果。
|
Download:
|
| 图 4 不同激励形式下的发射电压响应曲线 Fig. 4 The transmitting voltage response using different incentives | |
纵振模态能否被激发出来与图 3中谐振处晶堆的形变形式密切相关。在一阶谐振频率处,如果晶堆的激励方式能够使晶堆两端同时扩张同时收缩,则可激发一阶纵振模态,如图 2(a)的同相激励方式;同理,在二阶谐振频率处,如果晶堆的激励方式能够使晶堆一端收缩一端扩张,则可激发二阶纵振模态,如图 2(b)的同尺寸反相激励方式;若想同时激励出一、二阶纵振模态,则要符合图 2(c)中的不同尺寸反相激励方式。首先,不同尺寸反相激励形变形式符合二阶纵振模态,即一端收缩一端扩张,因而可激发二阶纵振模态; 其次,在一阶谐振频率处,不同尺寸反相激励虽会抵消一部分形变,仍满足两端同时扩张同时收缩的形变形式,因而可以激发一阶纵振模态。这样,不同尺寸反相激励可以同时激励出前两阶纵振模态,实现宽频带工作。
3 换能器的等效电路纵向换能器结构不复杂,如果不涉及复杂的振动模态可以采用解析法计算,自由棒的一、二阶纵振均属于经典的振动形式,利用一、二阶纵振模态耦合实现宽带工作的双激励纵向换能器可以采用解析法计算。
首先给出换能器的非集中参数等效电路。图 1(b)所示各部分结构均是空心圆柱及圆台形,每个组成结构都可以表示为一个T型网络[15],T型网络两端传递着力与振速,在各组成部分理想的刚性连接条件下,接触面力与振速相等,因此T型网络可以直接连接,得到的换能器完整的等效电路如图 5所示。编号为1、3、5的T型网络分别代表后盖板、中间质量和前盖板,虚线框中编号为2和4的机电耦合网络则代表后晶堆和前晶堆,Zb和Zf分别表示后端和前端的辐射阻抗[17],n2和n4为后晶堆与前晶堆的机电转换系数,ZE2和ZE4为晶堆电端并联阻抗[15]。

|
Download:
|
| 图 5 换能器完整的等效电路 Fig. 5 Complete equivalent circuit of the transducer | |
电路中各部分阻抗Zai、Zbi和Zci表达式为
| $ \begin{array}{l} {Z_{ai}} = \frac{{{z_2}\left( i \right)F}}{{{\rm{j}}\left( {F + 1} \right){\rm{sin}}\left( {{k_i}{l_i}} \right)}}\\ \;\;\;\;\;\;\;\;\left\{ {\frac{{{z_1}\left( i \right)\left( {F + 1} \right)}}{{{z_2}\left( i \right)F}}\left[{\frac{{{\rm{sin}}\left( {{k_i}{l_i}} \right)}}{{F{k_i}{l_i}}} + {\rm{cos}}\left( {{k_i}{l_i}} \right)} \right] -1} \right\} \end{array} $ |
| $ \begin{array}{l} {Z_{bi}} = \frac{{{\rm{j}}{z_2}\left( i \right)F}}{{\left( {F + 1} \right){\rm{sin}}\left( {{k_i}{l_i}} \right)}}\\ \;\;\;\;\;\;\;\;\left\{ {\frac{{\left( {F + 1} \right)}}{F}\left[{\frac{{{\rm{sin}}\left( {{k_i}{l_i}} \right)}}{{\left( {F + 1} \right){k_i}{l_i}}} + {\rm{cos}}\left( {{k_i}{l_i}} \right)} \right] + 1} \right\} \end{array} $ |
| $ {Z_{ci}} = \frac{{{z_2}\left( i \right)}}{{\rm{j}}}\frac{F}{{\left( {F + 1} \right){\rm{sin}}\left( {{k_i}{l_i}} \right)}} $ |
式中:z1(i)=ρiciS1,z2(i)=ρiciS2,ρi、ci、ki、li分别为第i部分密度、声速、波数及厚度,S1与S2为第i部分两端截面积,F=R1/(R2-R1),R1与R2为第i部分两端截面等效半径。
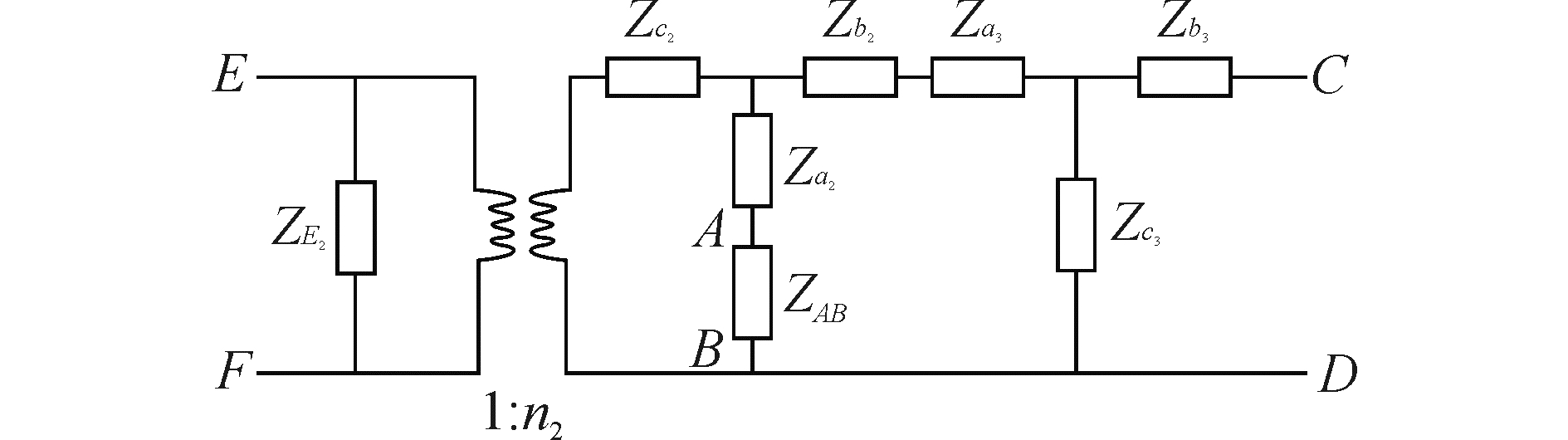
图 5中CD左端电路代表后盖板、后晶堆和中间质量块,先对这一部分化简。后辐射阻抗Zb很小近似为0,后端可看成短路状态,在这一特殊条件下,后盖板部可等效的转化为阻抗ZAB如图 6所示,EF为后晶堆电激励端,与前晶堆电激励端EF施加相同的电压。EF与CD端之间包含后晶堆机电耦合部以及两个T型网络,均可转化为相应的四端网络形式[14]。四端网络可以通过2×2矩阵来表征,与T型网络一样,两端传递着各部分力与振速,因此,相邻的四端网络可通过矩阵相乘的方式进行简化计算,简化后EF与CD间用四个参数A1、A2、A3、A4表示,如图 7所示。
|
Download:
|
| 图 6 CD左端部分的等效电路 Fig. 6 Partial equivalent circuit of CD left side | |
|
Download:
|
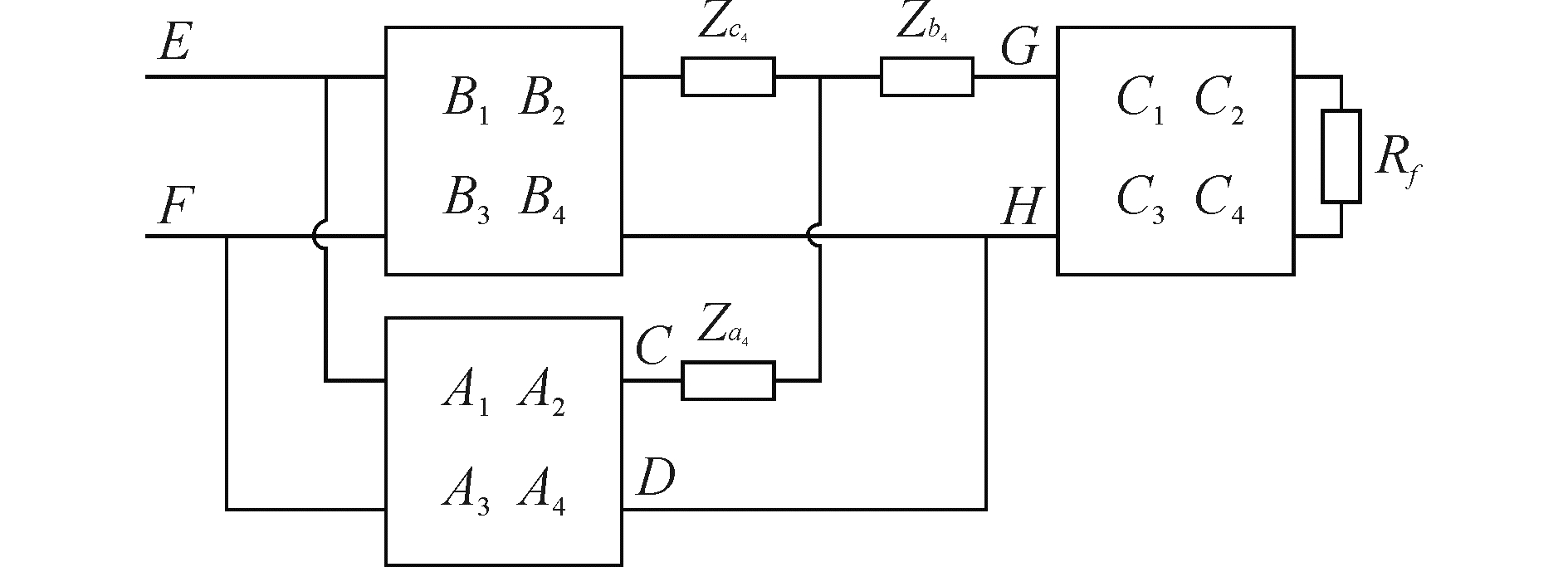
| 图 7 换能器完整的四端网络 Fig. 7 Complete four terminal circuit of the transducer | |
图 5中CD与GH之间这部分为前晶堆的等效电路,电端耦合部分转化为相应的四端网络形式后以B1、B2、B3、B4表示。GH右端为前盖板部分,将其T型网络转化为四端网络后以C1、C2、C3、C4表示,完整电路的四端网络形式如图 7所示。将Zc4和Za4化简掉之后会得到两个并联的四端网络,根据两端电压电流、力与振速相互关系可列出四个方程,计算出并联电路简化后的四个等效参数[12],并与前盖板部分进行矩阵相乘化简得到最终的四个参数D1、D2、D3、D4。
最简化的电路形式如图 8所示,可根据最后的四个参数D1、D2、D3、D4计算发射电压响应、导纳曲线等。计算过程涉及的辐射阻抗、指向性指数均采用理论公式[17]计算,机械损耗是一个随频率变化的量, 不同类型换能器机械损耗差别也很大且不易测得,本文机械损耗采用恒定数值计算,根据谐振频率处测得的电导值大小确定。

|
Download:
|
| 图 8 四端网络最简化形式 Fig. 8 The simplest form of the four terminal circuit | |
有限元软件ANSYS可以分析结构振动较复杂的换能器,具有解析法计算无法比拟的优势,计算结果一般较准确。本文采用双晶堆不同尺寸反相激励的方式,设计了双激励纵向换能器,并优化换能器结构尺寸。
4.1 换能器模态分析利用有限元软件建立换能器的有限元模型,忽略对性能影响不大的电极片、胶层及密封外壳等结构。换能器属于轴对称结构,只建立二维模型可以满足计算要求。前盖板选用密度与特性阻抗都较小的铝合金材料,后盖板选用密度较大的黄铜,中间质量块和螺杆选用韧性较好的45#钢。压电材料、各部分金属结构需要设置特定单元类型和材料参数[16]。
模态分析可以预报出结构可能出现的振动模态和谐振频率。有限元模型和模态分析结果如图 9所示,一阶纵振模态出现在31 kHz附近,只有一个位移节点;二阶模态出现在58 kHz附近,有两个位移节点,符合自由棒振动模态特征。

|
Download:
|
| 图 9 换能器有限元模型和振动模态 Fig. 9 Finite element model and vibration pattern of the transducer | |
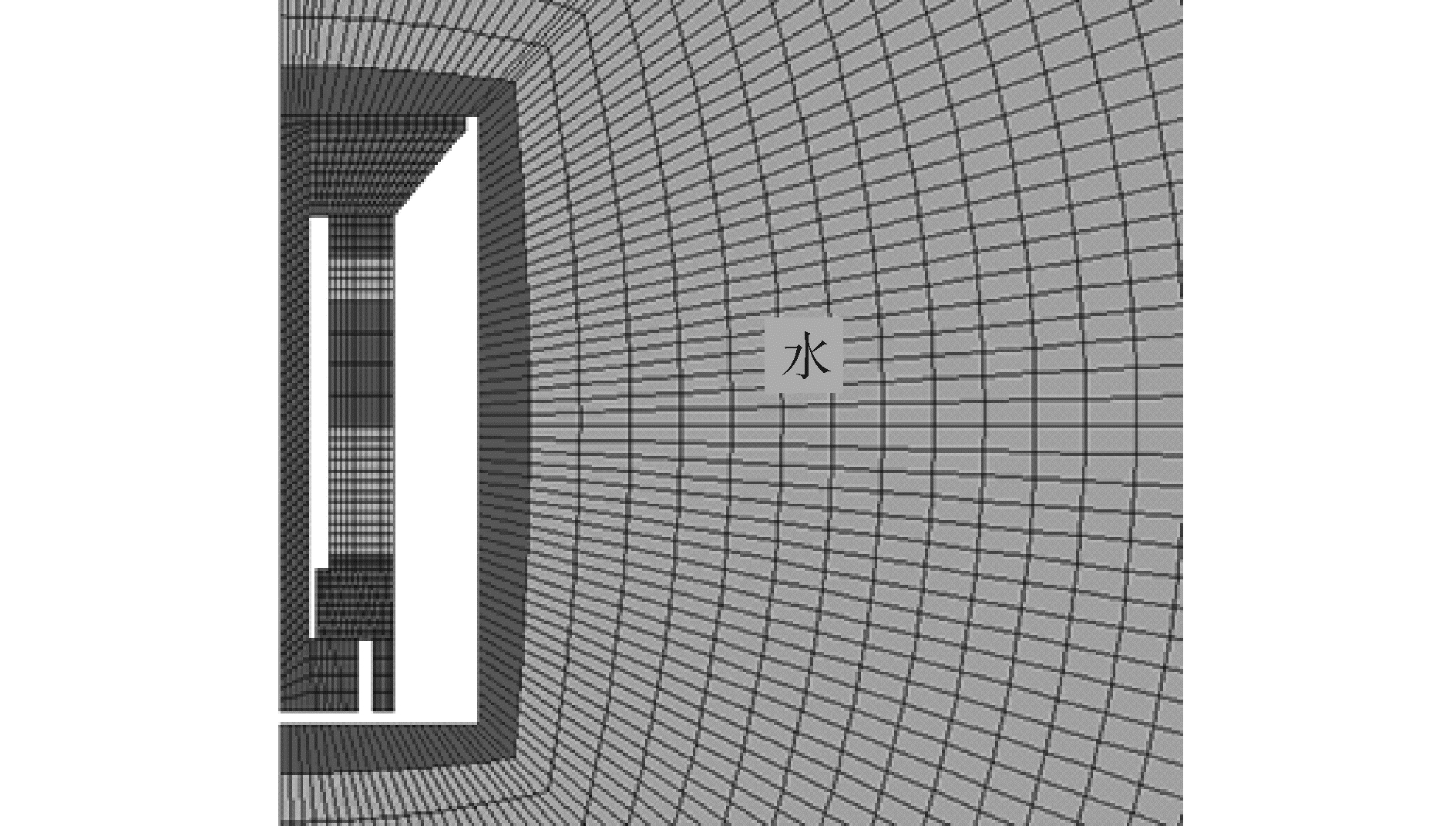
双激励换能器水中有限元模型如图 10所示,外部为换能器工作的水域环境,内部为纵向换能器的轴对称模型,内部白颜色区域为空气,与空气接触的水域默认为刚性边界。
|
Download:
|
| 图 10 换能器水中有限元模型 Fig. 10 Finite element model of the transducer in water | |
经过大量的优化设计,最终确定了最优结构尺寸:压电晶片材料为单晶PMNT,内径7 mm,外径16 mm,厚度为3 mm,前晶堆采用1片晶片,后晶堆采用3片晶片;前辐射端半径13 mm,厚度10 mm,中间质量厚度为9 mm,横向尺寸与压电晶片相同;后辐射端厚度为11 mm,横向尺寸同样与压电晶片相同。最终计算出双激励纵向换能器水中导纳曲线如图 11所示,一阶谐振频率31.3 kHz,二阶谐振频率57.8 kHz。

|
Download:
|
| 图 11 水中电导纳仿真结果 Fig. 11 The simulation result of the admittance curves in water | |
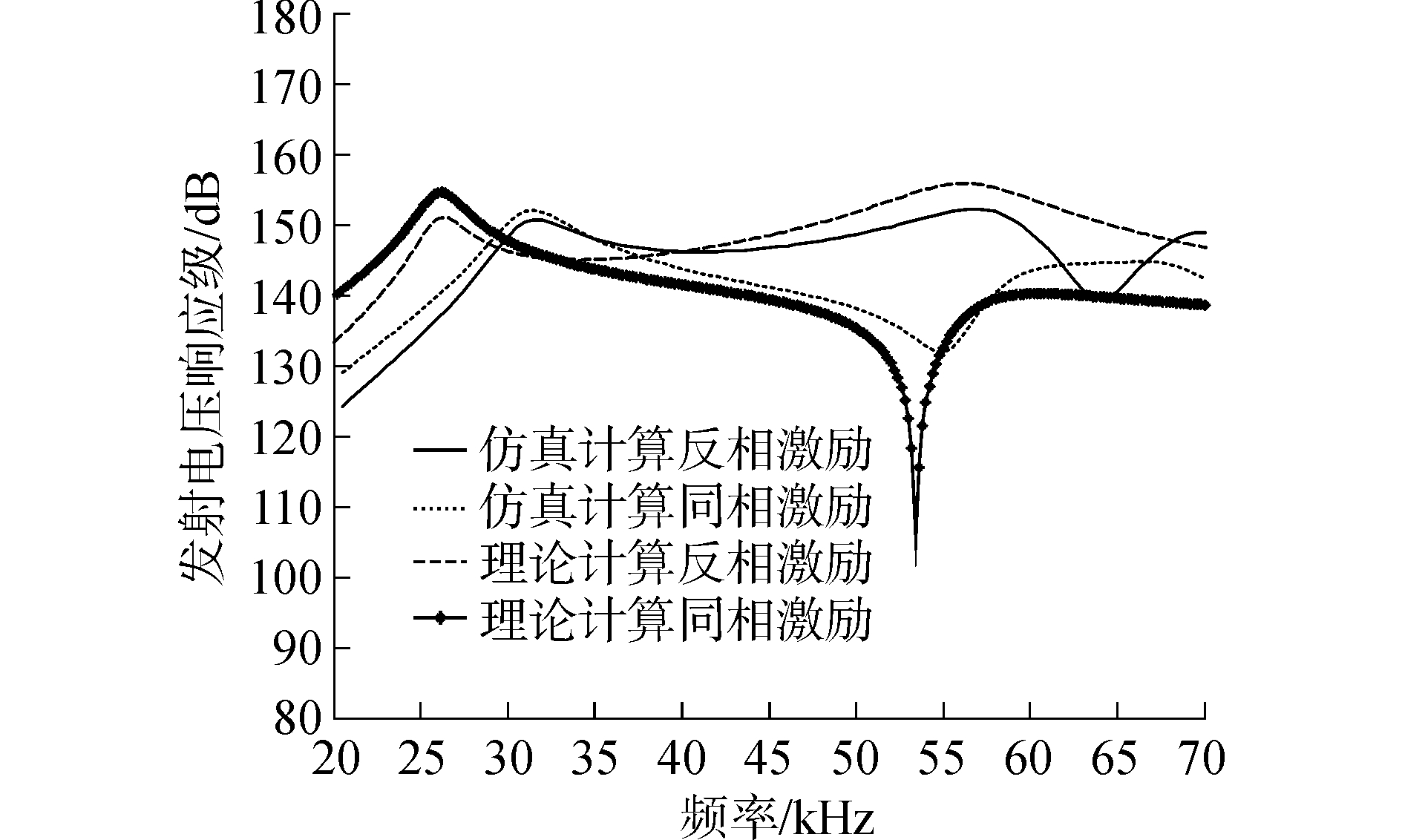
双激励纵向换能器发射电压响应曲线如图 12所示,同时列举出了不同激励情况时ANSYS仿真计算与理论计算结果。仿真与理论计算结果显示:同相激励无法激发结构的二阶纵振模态,会在频带内产生较深的响应凹坑;晶堆不同尺寸反相激励可激发出二阶纵振模态,有效拓展工作带宽。两种方法计算的响应随频率变化趋势基本一致,可对换能器的设计进行有效预报。最终仿真设计换能器的工作频带为29.3~61.3 kHz,最大发射电压响应值可达152.1 dB,带内起伏6 dB。
|
Download:
|
| 图 12 发射电压响应的理论与仿真计算结果 Fig. 12 The simulation and theory calculation results of the transmitting voltage response in water | |
依据前文有限元分析与优化所确定的结构尺寸,制作了一支压电单晶PMNT驱动的双激励纵向换能器试验样机,制作灌封完成后的换能器以及测试现场如图 13所示,样机最大外径49 mm,长度95 mm。

|
Download:
|
| 图 13 制作完成的换能器与测试现场 Fig. 13 The final complete transducer and testing scene | |
在哈尔滨工程大学水声技术重点实验室消声水池进行了换能器发射性能的测试,吊放深度为3 m,换能器与标准水听器距离1.2 m(满足远场条件)。测试的水中电导纳曲线如图 14所示,一阶谐振频率31.1 kHz,二阶谐振频率54.6 kHz,谐振处导纳峰值与仿真计算结果基本一致。测得的换能器发射电压响应曲线与ANSYS仿真计算、理论计算结果对比如图 15所示,最后测得的工作频带为27~65 kHz,最大发射电压响应150.7 dB,带内起伏约11 dB。

|
Download:
|
| 图 14 水中电导纳测试曲线 Fig. 14 The testing result of the admittance curves in water | |

|
Download:
|
| 图 15 发射电压响应的实测结果与仿真计算和理论计算对比 Fig. 15 The comparison of the testing result with simulation and theory calculations | |
各曲线具体的谐振频率、响应峰值列于表 1中,测试结果与理论计算、仿真计算结果略有差距。首先,理论计算没有考虑结构较大的横向耦合;辐射阻抗以及指向性指数均是理论公式计算的结果,而换能器实际的工作状态会与理想情况略有差距;机械损耗的大小及随频率的变化规律尚不确定,计算时采用恒定的数值;计算时还忽略了预应力螺杆的影响。其次,在仿真计算过程中,单晶材料PMNT的各项性能参数采用恒定值,而实际的性能参数随频率、温度、压力等的变化而变化,材料一致性差。最后,在换能器制作过程中,零件尺寸与设计尺寸存在的小差别,表面的不平整,粘接后各部分可能存在的非刚性连接,换能器在灌封外壳内的装配略有倾斜等均会造成一定能量损失,因此实测结果不可避免与理论计算、仿真计算结果存在一定差别。
| 表 1 测试结果与理论、仿真计算结果的对比 Tab.1 The comparison between testing result and simulation, theory calculations |
值得注意的是,测试结果显示在二阶谐振峰之后响应曲线依旧保持平坦。从图 14中可观察到附近存在其他谐振模态,高阶模态的再次耦合使得响应曲线在二阶谐振之后没有明显下降。高阶模态可能为非对称模态,本文所采用的轴对称模型并不能计算出高阶非对称模态。关于高阶模态的影响与合理应用将会在今后的工作中作进一步研究。
6 结论1) 基于四端网络法的纵向换能器设计理论可以用来计算较复杂的双激励纵向换能器。
2) 双晶堆同相激励无法激发二阶纵振模态,采用不同尺寸反相激励的方式可有效激发出一、二阶纵振模态,拓宽换能器的工作带宽。
3) 测试结果显示,理论计算与仿真计算均可为此种类型换能器性能进行有效预测,为换能器的设计制作提供可靠依据。
| [1] |
莫喜平. 功能材料及其应用于换能器技术的研究进展[J]. 物理, 2009, 38(3): 149-156. MO Xiping. Functional materials and their applications in acoustic transducers[J]. Physics, 2009, 38(3): 149-156. (  0) 0)
|
| [2] |
SHERLOCK N P, MEYER R J. Modified single crystals for high-power underwater projectors[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2012, 59(6): 1285-1291. DOI:10.1109/TUFFC.2012.2319 (  0) 0)
|
| [3] |
OAKLEY C G, ZIPPARO M J. Single crystal piezoelectrics: a revolutionary development for transducers[C]//Proceedings of 2000 IEEE Ultrasonics Symposium. San Juan, Puerto Rico, USA, 2002, 2(2): 1157-1167.
(  0) 0)
|
| [4] |
陈思, 蓝宇, 顾郑强. 压电单晶弯张换能器研究[J]. 哈尔滨工程大学学报, 2010, 31(9): 1167-1171. CHEN Si, LAN Yu, GU Zhengqiang. Analysis of a single crystal piezoelectric flextensional transducer[J]. Journal of Harbin Engineering University, 2010, 31(9): 1167-1171. DOI:10.3969/j.issn.1006-7043.2010.09.006 (  0) 0)
|
| [5] |
MEYER R J, MONTGOMERY T C, HUGHES W J. Tonpilz transducers designed using single crystal piezoelectric[C]//OCEANS'02 MTS/IEEE. Biloxi, MI, USA, 2002, 4: 2328-2333.
(  0) 0)
|
| [6] |
KIM K B, HSU D K, AHN B, et al. Fabrication and comparison of PMN-PT single crystal, PZT and PZT-based 1-3 composite ultrasonic transducers for NDE applications[J]. Ultrasonics, 2010, 50(8): 790-797. DOI:10.1016/j.ultras.2010.04.001 (  0) 0)
|
| [7] |
OH H T, LEE J Y, LEE H Y. Mn-modified PMN-PZT[Pb(Mg1/3Nb2/3)O3-Pb(Zr, Ti)O3] single crystals for high power piezoelectric transducers[J]. Journal of the Korean ceramic society, 2017, 54(2): 150-157. DOI:10.4191/kcers.2017.54.2.03 (  0) 0)
|
| [8] |
BUTLER S C. Triple-resonant transducers[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2012, 59(6): 1292-1300. DOI:10.1109/TUFFC.2012.2320 (  0) 0)
|
| [9] |
BUTLER J L, BUTLER A L. Ultra wideband multiple resonant transducer[C]//Proceedings of Oceans 2003. San Diego, USA, 2003, 5: 2381-2387.
(  0) 0)
|
| [10] |
BUTLER S C, TITO F A. A broadband hybrid magnetostrictive/piezoelectric transducer array[C]//OCEANS 2000 MTS/IEEE Conference and Exhibition. Providence, RI, USA, 2000, 3: 1469-1475.
(  0) 0)
|
| [11] |
周天放, 蓝宇, 桑永杰. 空腔式前盖板宽带纵向换能器研究[J]. 哈尔滨工程大学学报, 2016, 37(9): 1215-1219, 1226. ZHOU Tianfang, LAN Yu, SANG Yongjie. Research on longitudinal broadband transducer with cavity-type front cover[J]. Journal of Harbin Engineering University, 2016, 37(9): 1215-1219, 1226. (  0) 0)
|
| [12] |
俞宏沛, 潘先松, 赵颂阳, 等. 双激励源振子的初步理论分析与实验研究[J]. 声学与电子工程, 1997, 48(4): 24-27. YU Hongpei, PAN Xiansong, ZHAO Songyang, et al. Preliminary theoretical analysis and experimental study of transducer with double excitation[J]. Acoustics and electronics engineering, 1997, 48(4): 24-27. (  0) 0)
|
| [13] |
BUTLER S C. Development of a high power broadband doubly resonant transducer (DRT)[C]//UDT Conference Proceedings. Waikiki, Hawaii, USA, 2001.
(  0) 0)
|
| [14] |
俞宏沛. 纵向振动换能器工程设计理论[J]. 水声通讯, 1984(3): 17-58. YU Hongpei. Engineering design theory of longitudinal vibrating transducer[J]. Underwater communication, 1984(3): 17-58. (  0) 0)
|
| [15] |
栾桂冬, 张金铎, 王仁乾. 压电换能器和换能器阵[M]. 北京: 北京大学出版社, 2005: 147-155.
(  0) 0)
|
| [16] |
莫喜平. ANSYS软件在模拟分析声学换能器中的应用[J]. 声学技术, 2007, 26(6): 1279-1290. MO Xiping. Simulation and analysis of acoustics transducers using the ANSYS software[J]. Technical acoustics, 2007, 26(6): 1279-1290. DOI:10.3969/j.issn.1000-3630.2007.06.042 (  0) 0)
|
| [17] |
何祚镛, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1981: 245-247, 238.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


