目前，主流的自由表面追踪方法有流体体积(volume of fluid，VOF)方法^[1-3]和水平集(level set)方法^[4-6]两种。虽然VOF方法可保持局部质量守恒，但其重构的自由表面往往不光滑甚至是不连续，降低了自由表面几何信息(法向和曲率)的准确性^[7]。Level set方法无法保证质量守恒，但可通过重新初始化^[8]以及采用高精度格式(如时间上采用3阶TVD格式，空间上采用5阶WENO格式)来减少数值耗散^[7]。近年来，一些学者提出了改进的level set方法以提高计算的精度，其中有代表性的两类方法是CLSVOF(coupled level set and volume of fluid)方法^[9-12]和粒子level set方法^{[7, 13-18]}。在捕捉细丝状界面时粒子level set方法比CLSVOF方法更有效。除了计算精度外，界面追踪方法计算效率提升也是研究者追求的目标。Enright等^[13]提出的快速粒子level set(FPLS)方法采用一阶精度的半拉格朗日方法求解对流方程，利用一阶精度的快速步进法进行重新初始化，在保持原有计算精度同时有效地减少了计算时间。事实上，提高level set方法效率最直接的办法是并行化^[19-20]。但到目前为止，有关快速粒子level set方法并行化的文献不多见。本文将基于计算区域分解以及粒子分解思想，提出一种FPLS方法的并行化策略。并行化的FPLS方法将采用OpenMP技术实现，所建立的数值模型将通过Zalesak圆盘、单涡、三维变形等典型算例来检验。

1 快速粒子level set方法的基本原理

Level set方法是将运动的交界面看作一个高阶符号距离函数的零等值面，其控制方程如下

$ {\varphi _t} + \mathit{\boldsymbol{u}} \cdot \nabla \varphi = 0 $

(1)

式中：$φ$_t表示level set函数对时间求偏导，u为速度矢量。然而，数值求解对流方程式(1)会造成level set函数丧失符号距离的属性，即无法满足

$ \left| {\nabla \varphi } \right| = 1 $

(2)

因此，需要对方程(1)的解进行重新初始化。

1.1 半拉格朗日方法

从对流方程式(1)可以看出，特征曲线上的level set函数值保持不变。在一个时空变化的二维流场区域(网格尺寸为Δh，时间步长为Δt)中，新时刻网格节点的level set函数值等于特征曲线起始点的值。在一个时间步长内，可假定特征曲线为一直线，这样新时刻的level set可通过式(3)获得:

$ \begin{array}{l} \varphi _{i,j}^{n + 1} = \alpha \beta \varphi _{r + 1,s + 1}^n + \left( {1 - \alpha } \right)\beta \varphi _{r,s + 1}^n + \\ \;\;\;\;\;\;\;\;\;\;\alpha \left( {1 - \beta } \right)\varphi _{r + 1,s}^n + \left( {1 - \alpha } \right)\left( {1 - \beta } \right)\varphi _{r,s}^n \end{array} $

(3)

其中

$ r = i - \left[ {{u_{i,j}}\Delta t/\Delta h} \right],\alpha = \left[ {\left( {j - r} \right)\Delta h - {u_{i,j}}\Delta t} \right]/\Delta h $

$ s = j - \left[ {{v_{i,j}}\Delta t/\Delta h} \right],\beta = \left[ {\left( {j - s} \right)\Delta h - {v_{i,j}}\Delta t} \right]/\Delta h $

由于半拉格朗日方法是无条件稳定的，故时间步长的大小不受稳定性CFL条件限制，计算时间开销将减少。

1.2 快速步进法

式(2)可离散为

$ \begin{array}{l} \left| {\nabla {\varphi _{i,j}}} \right| = \left( {\max {{\left( {D_{ij}^{ - x}\varphi , - \varphi ,0} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {\max {{\left( {D_{ij}^{ - y}\varphi , - \varphi ,0} \right)}^2}} \right)^{1/2}} = 1 \end{array} $

(4)

其中

$ D_{ij}^{ - x}\varphi = \left( {{\varphi _{i,j}} - {\varphi _{i - 1,j}}} \right)/\Delta h $

$ D_{ij}^{ + x}\varphi = \left( {{\varphi _{i + 1,j}} - {\varphi _{i,j}}} \right)/\Delta h $

$ D_{ij}^{ - y}\varphi = \left( {{\varphi _{i,j}} - {\varphi _{i,j - 1}}} \right)/\Delta h $

$ D_{ij}^{ + y}\varphi = \left( {{\varphi _{i,j + 1}} - {\varphi _{i,j}}} \right)/\Delta h $

从式(4)可以看出，在$φ$为正值的区域内，节点上$φ$的空间导数离散会选择$φ$值更小的相邻节点。当节点上$φ$值梯度的模固定时，节点的$φ$值可由这些$φ$值更小的相邻节点来确定。这样，当紧邻界面的网格节点的$φ$值确定后，其他节点的值即可从界面开始逐渐向外构造出来。$φ$为负值的区域亦然。具体操作过程中，最小堆数据结构将保证值重新初始化严格按照从小到大的顺序执行。

1.3 误差校正

初始时刻在交界面附近的网格内布置一定数量粒子，本文中，距交界面3倍网格尺寸内的每个网格将布置正负粒子数各16个(2D)或64个(3D)；接着，将正负粒子迁移到相应的区域，即正粒子在正值区域，负粒子在负值区域；然后，确定粒子半径，保证每个粒子的圆周或球面均与交界面相切。

计算过程中，若粒子穿越交界面达一个半径的距离，则意味着对流方程的解存在误差，而这种粒子被称为逃逸粒子。由于每个粒子与交界面相切，逃逸粒子周围节点上$φ$的校正值为

$ {\varphi _p}\left( {{\mathit{\boldsymbol{x}}_{i,j}}} \right) = {s_p}\left( {{\mathit{\boldsymbol{r}}_p} - \left| {{\mathit{\boldsymbol{x}}_{i,j}} - {\mathit{\boldsymbol{x}}_p}} \right|} \right) $

(5)

一个网格节点周围可能存在多个逃逸粒子，需要对校正值进行比较筛选。对于正粒子，选取最大值为

$ {\varphi ^ + } = \mathop {\max }\limits_{\forall p \in {E^ + }} \left( {{\varphi _p},{\varphi ^ + }} \right) $

(6)

对于负粒子，选取最小值为

$ {\varphi ^ - } = \mathop {\min }\limits_{\forall p \in {E^ + }} \left( {{\varphi _p},{\varphi ^ - }} \right) $

(7)

比较前，$φ$⁺和$φ$^-取节点$φ$值。最终校正结果为

$ \varphi = \left\{ \begin{array}{l} {\varphi ^ + },\;\;\;\;\left| {{\varphi ^ + }} \right| \le \left| {{\varphi ^ - }} \right|\\ {\varphi ^ - },\;\;\;\;\left| {{\varphi ^ + }} \right| > \left| {{\varphi ^ - }} \right| \end{array} \right. $

(8)

除了对流方程的解需要校正外，重新初始化的结果也需要校正。

2 快速粒子level set方法的并行 2.1 计算区域分解与粒子分解

固定网格下的欧拉运算，如对流方程求解和重新初始化，可通过区域分解的方式来平分总的计算开销。分解后的子块将分配给相应的处理单元，每个处理单元负责该子块上的相关运算。粒子也可以按照所在子块进行分解。由于粒子可能在一个时间步长内迁移到另一个子块，其处理单元在检测其离开所在子块后，将处理权限移交给其他处理单元^[21]。然而，这种粒子分解很难保证其运算，包括粒子时程积分和误差校正，能在处理单元间获得荷载平衡。

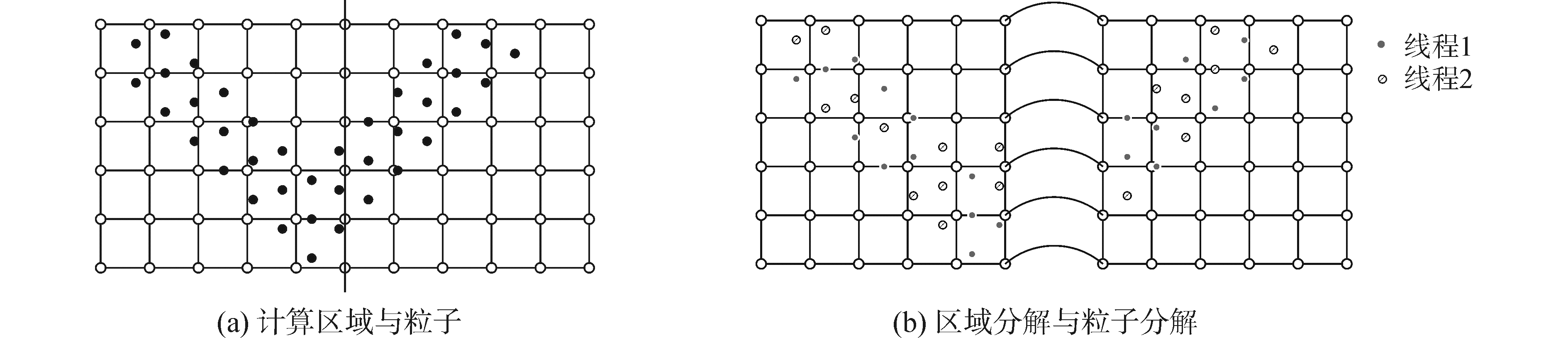
若要获得完美的荷载平衡，每个处理单元控制的网格数和粒子数都应该相同。在PIC(particle in cell)模拟中，Qiang等^[22-23]提出了一种粒子-区域分解(particle-field decomposition)策略，不仅将计算区域分成尺寸大小相等的子块，也将粒子分成数目相等的子集。图 1为粒子-区域分解的示意图。在该策略中，粒子的处理单元与所在子块的处理单元不一定相同，粒子时程积分要求这两个单元之间进行信息交换。不过，由于本文采用基于共享内存的OpenMP来实现并行，粒子的处理单元可以直接获得粒子所在网格的速度信息，无需通过信息传递来获得。

2.2 对流方程与重新初始化

基于区域分解，每个子块将独立完成对流方程的时间步进。尽管某些节点(如边界节点)的推算始点可能出现在别的区域内，但由于采用了共享内存的OpenMP技术，子块的处理单元仍可直接获得推算始点的信息。

比较而言，快速步进重新初始化的并行化要复杂得多。当每个子块完成重新初始化后，除了要通过信息交换以保证与相邻子块在边界节点上的统一，还要通过节点重演^[24-25]确保各子区域内level set函数单调性。事实上，共享内存下信息传递开销非常小，故可以在每个边界节点完成重置后立即将其值传递给相邻区域，这样将大大减少节点重演的数目和次数^[25]。

并行的快速步进重新初始化的步骤如下：

1) 确定紧邻交界面网格节点(下面称之为交界面节点)的$φ$值，将其他节点初始化；

2) 最小堆的初始化，即试算与交界面节点相邻节点，并放置到最小堆中；

3) 若最小堆非空，取出$φ$值最小的节点，对其相邻的节点进行更新，并将相邻节点放置在最小堆中；若取出的节点为边界节点，则将该节点的信息传递给相邻区域；否则，前往6)；

4) 根据接收的信息，排查需要重演的节点，并将这些节点重新放回至最小堆中；

5) 返回步骤3)；

6) 等待其他线程的最小堆为空；若接受到新的节点信息，返回4)。

快速粒子level set方法只需在交界面周围一定带宽内执行对流运算(6倍网格尺寸)和重新初始化(12倍网格尺寸)，区域分解无法保持欧拉运算的荷载平衡。尽管如此，由于欧拉运算的计算开销比重小，其对总体计算效率的提升影响不大。

2.3 粒子计算

在FPLS中，粒子的运算开销会超过总体计算的60%。若处理单元所控制的粒子数相等，粒子时程积分开销将平均到各处理单元，计算效率将得到大幅提升。在误差校正过程中，网格节点的$φ$值校正将由节点周围逃逸粒子的处理单元来执行，而非节点的处理单元。在串行算法中，所有正负粒子根据网格编号顺序构成两组粒子队列，同一网格内粒子根据粒子产生顺序进行排列。在并行过程中，若按粒子队列顺序依次将粒子分配给各处理单元，每个处理单元中逃逸粒子的数目应相差不大，误差校正也将在单元间获得荷载平衡。由于网格节点逃逸粒子可能属于不同处理单元，对节点进行校正时会出现处理单元竞争的情况，本文将OpenMP函数库中的锁函数加以解决。

所有子区域完成误差校正后，需要通过数据交换以保证相邻子区域在区域边界上$φ$值相等。由于网格节点上最终校正值是取决于距离最近的逃逸粒子，故传递来的$φ$值将与对应的边界节点φ值进行比较，取绝对值较小者作为同步的结果。

3 算例及结果讨论 3.1 Zalesak圆盘

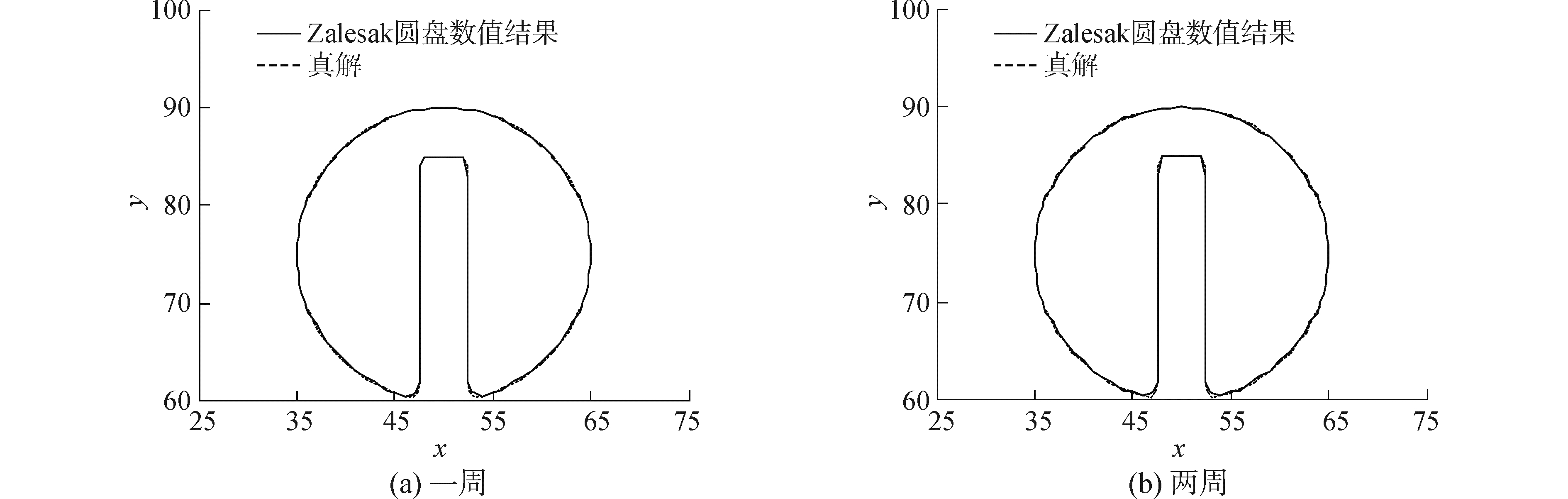
计算区域为100×100×100，圆盘的半径为15，缺口的长度和宽度分别为25和5，面积为582.2，如图 2(a)所示。定流场为

$ \left\{ \begin{array}{l} u = \left( {{\rm{ \mathsf{ π} /314}}} \right)\left( {{\rm{50}} - y} \right)\\ v = \left( {{\rm{ \mathsf{ π} /314}}} \right)\left( {x - 50} \right) \end{array} \right. $

(9)

在式(9)给定流场下，Zalesak圆盘每628个单位时间旋转一周。除非特别说明，本算例以及后面算例的CFL数均取4.9。计算中，整个计算区域分成4个大小相同的子区域，粒子集也将分成数目相同的4组。

图 2给出了Zalesak圆盘分别旋转一周和两周之后的形状，并行的FPLS方法能够使圆盘旋转两周以后缺口保持尖锐。表 1为并行算法的计算误差精度和计算时间，其误差精度保持在1阶左右。

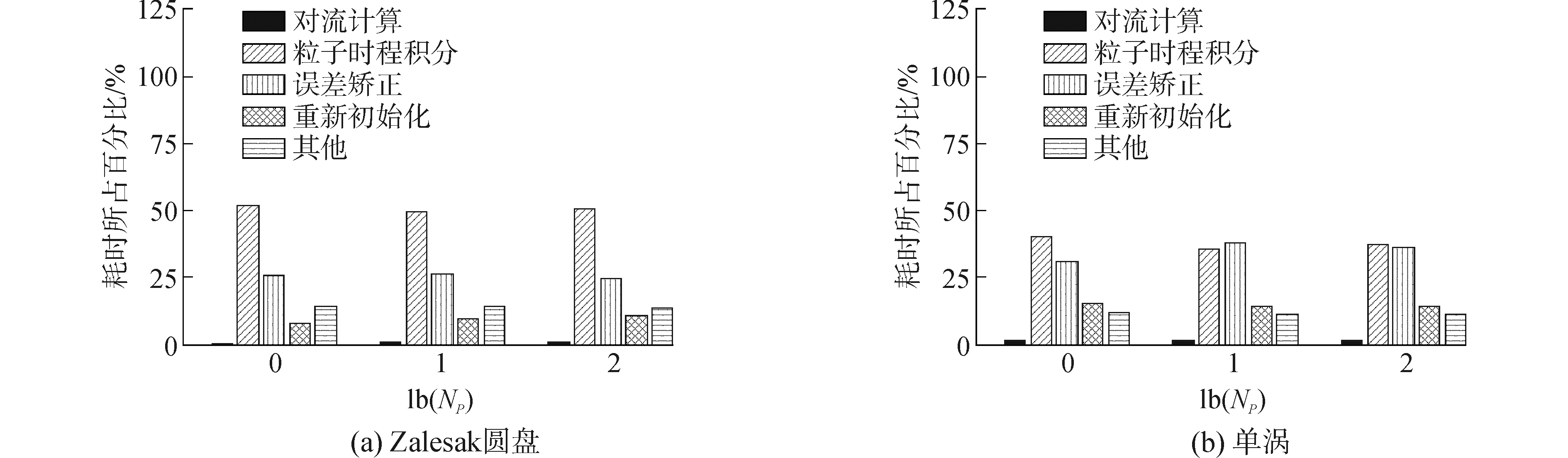
并行环境下，FPLS方法的主要步骤计算耗时的比较如图 3(a)所示，N_p表示线程数目，可以看出，粒子相关计算耗时占到整个计算的75%，而欧拉运算所占比例较小，对流计算的比例几乎可忽略不计。由于快速步进重新初始化仅在界面附近一定区域内进行，当采用区域分解的并行模式时，并非全部线程参与执行。故本算例中，重新初始化占比会随线程增加而有所扩大。不同线程数目下各计算环节以及总体计算的加速比(t₁/t_N)见图 4(a)。各计算环节与总体计算的加速比并未随线程数增加呈线性递增；误差校正以及总体计算的加速比增长趋势基本与粒子时程积分保持一致，而对流计算和重新初始化因无法在多线程下达到荷载平衡，其加速比增加的幅度将小于粒子计算。最终，4线程下的总体计算的加速比将达2.3。

3.2 单涡

二维单涡模拟用于测试level set方法捕捉拉伸剪切流场下细丝状界面的能力。

$ \left\{ \begin{array}{l} u = - {\sin ^2}\left( {{\rm{ \mathsf{ π} }}x} \right)\sin \left( {2{\rm{ \mathsf{ π} }}y} \right)\cos \left( {{\rm{ \mathsf{ π} }}t/T} \right)\\ v = \sin \left( {{\rm{2 \mathsf{ π} }}x} \right){\sin ^2}\left( {{\rm{ \mathsf{ π} }}y} \right)\cos \left( {{\rm{ \mathsf{ π} }}t/T} \right) \end{array} \right. $

(10)

式中：T为界面拉伸到最大再恢复初始形状的总时间。本算例中，计算区域大小为1×1，半径为0.15的圆初始时刻放置在(0.5, 0.75)处，网格分辨率取为128×128，最大线程数为4。

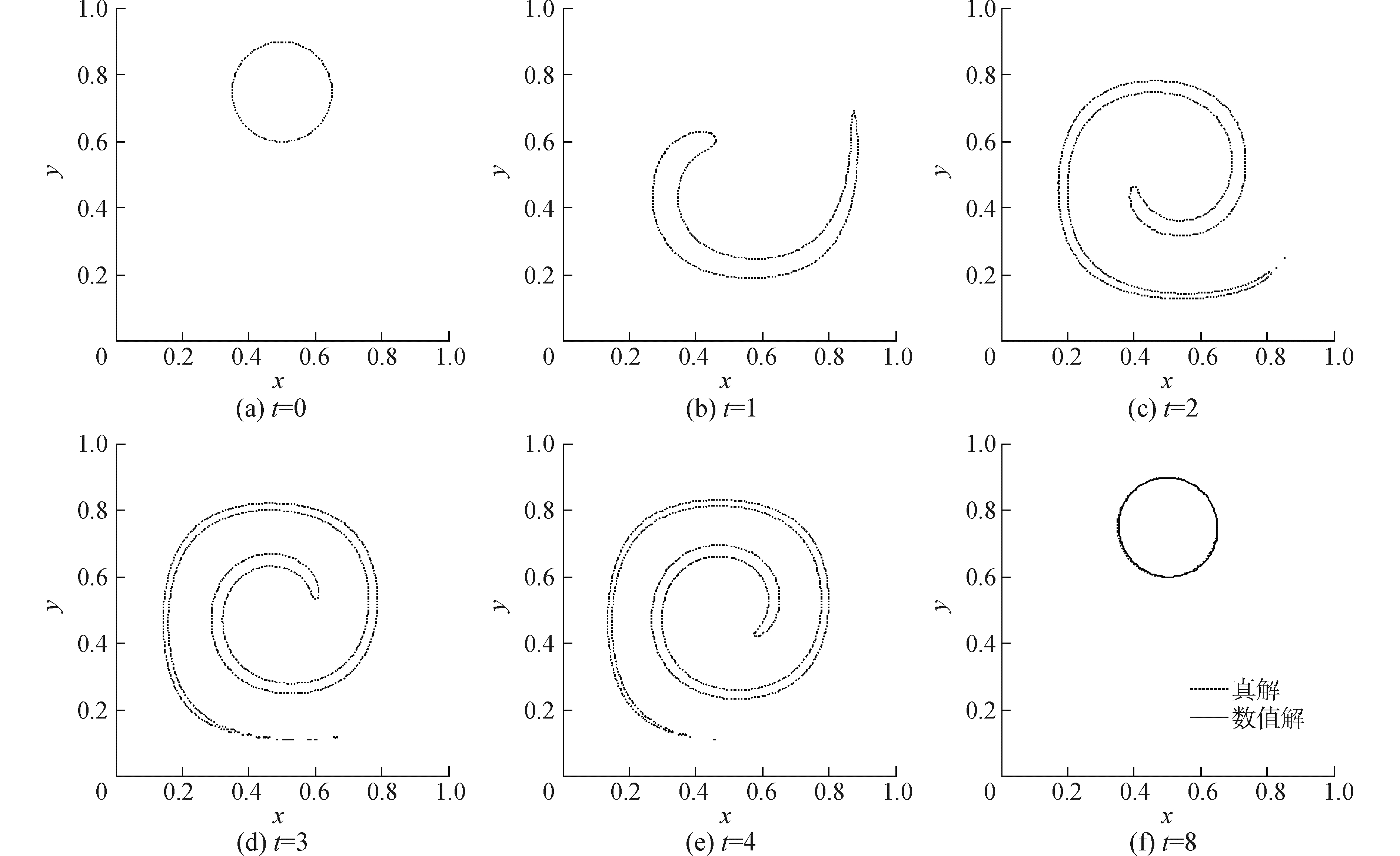
图 5为不同时刻界面的形状，可以看出，前半段时间内，界面呈螺旋式向涡中心运动，而且逐渐变细，到t＝4时界面拉伸到最大。当t＝8时，界面恢复到原状，从图 5(f)看出，最终的界面形状基本与初始形状吻合。计算误差精度以及时间开销见表 2，不同分辨率下的CFL数同取2.5。图 3(b)给出各计算环节耗时占比。当多线程计算时，因避免线程竞争，误差校正耗时比重明显上升。由于拉伸的界面分布在整个区域，计算区域分解后重新初始化过程在线程间能保证较好的荷载平衡，故耗时比重并未增加。而从图 4(b)可以看出，在2个线程下，总计算的加速达1.6，而4线程可获得的加速比接近2.2。

3.3 Zalesak圆球

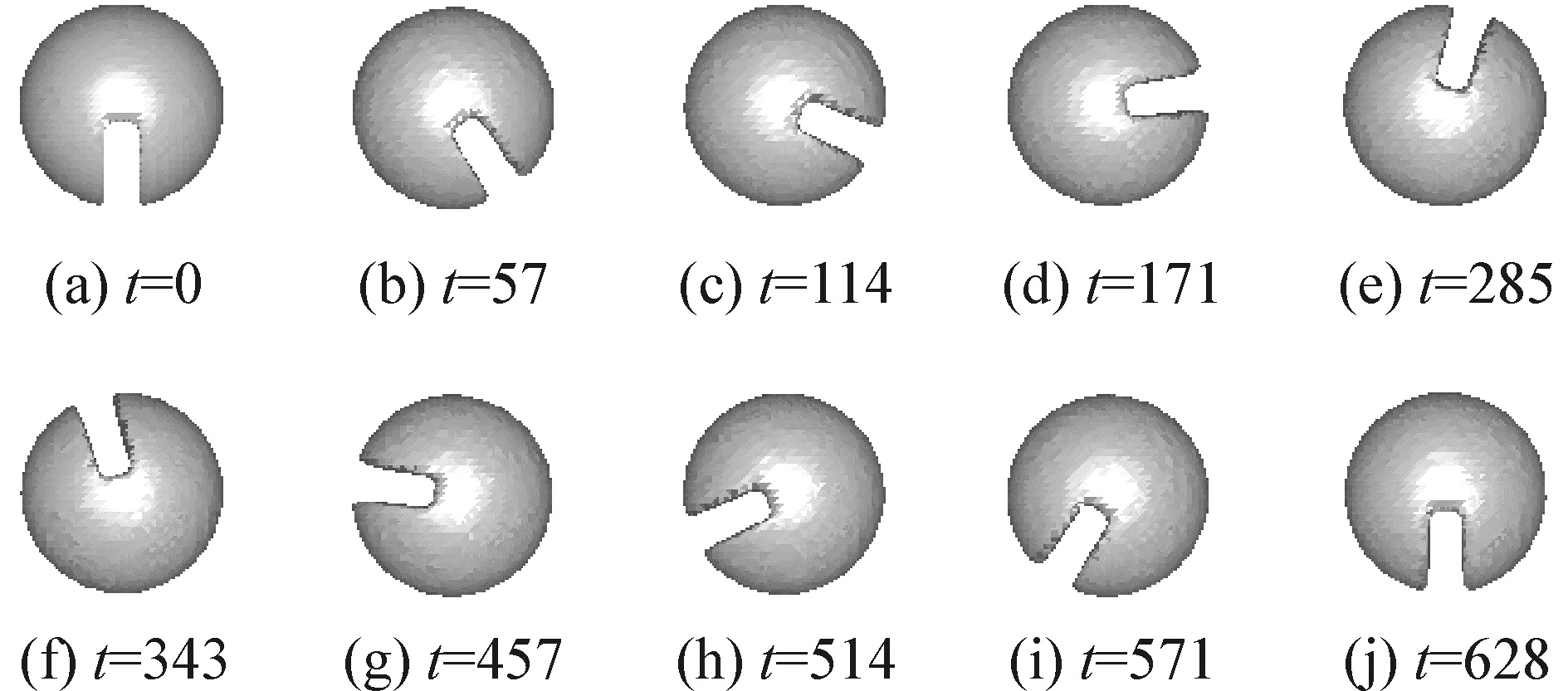
Zalesak圆球追踪是为了检验FPLS方法在三维条件下的耗散性。本算例中，半径为15的Zalesak球Zalesak圆球布置在尺寸大小为100×100×100的计算区域内，缺口的深度和宽度分别为12.5和5。在式(9)给定的流场作用下，圆球在z＝50的平面上从初始位置(50, 75, 50)开始，绕区域中心作圆周运动。旋转一周同样需628个单位时间。三维算例所采用的最大线程数为8。图 6给出了8线程下FPLS方法的计算结果，最终的体积损失小于1%。不同线程数下各主要计算环节加速比及总加速比见图 4(c)，当线程数增加时，加速比也随之增加，8线程所获得总加速比能达到4.0。

3.4 三维变形

在有关Level set方法的文献中，一个在x-y和x-z平面上均出现变形的三维算例常用于分析其精确捕捉界面的能力。该算例的计算区域为一单位长度的立方体，网格分辨率为128×128×128，半径为0.15的球体放置在(0.35, 0.35, 0.35)处，速度场的表达式为

$ \left\{ \begin{array}{l} u = 2{\sin ^2}\left( {{\rm{ \mathsf{ π} }}x} \right)\sin \left( {{\rm{2 \mathsf{ π} }}y} \right)\sin \left( {{\rm{2 \mathsf{ π} }}z} \right)\cos \left( {{\rm{ \mathsf{ π} }}t/T} \right)\\ v = - \sin \left( {{\rm{2 \mathsf{ π} }}x} \right){\sin ^2}\left( {{\rm{ \mathsf{ π} }}y} \right)\sin \left( {{\rm{2 \mathsf{ π} }}z} \right)\cos \left( {{\rm{ \mathsf{ π} }}t/T} \right)\\ w = - \sin \left( {{\rm{2 \mathsf{ π} }}x} \right)\sin \left( {{\rm{ \mathsf{ π} }}y} \right){\sin ^2}\left( {{\rm{2 \mathsf{ π} }}z} \right)\cos \left( {{\rm{ \mathsf{ π} }}t/T} \right) \end{array} \right. $

(10)

反转周期T=3。图 6为不同时刻的计算结果，最终体积损失为4.3%。并行获得的加速比如图 4(d)所示，其中，8线程下总加速比约为3.6。

4 结论

1) 并行的粒子Level set方法保留了原有串行算法的精度和守恒性，而计算时间大大缩减，在二维算例中，4线程能够达到的加速比超过2，而在三维算例中，8线程的加速比也接近4。

2) 粒子Level set方法中，粒子时程积分和误差校正的计算开销比重占总计算开销的7成以上，将粒子计算开销在线程间平均，能够显著提高计算效率。

3) 快速粒子Level set方法的对流计算和重新初始化只在界面附近区域进行，区域分解无法保证这两步计算在线程间保持荷载平衡。但由于其计算开销比重较低，对整体并行计算效率影响较小。