自然循环蒸汽发生器由于“收缩”与“膨胀”引起的逆动力学效应,存在“虚假水位”现象,使得单参量的控制不能获得良好的过渡过程特性[1],所以对蒸汽发生器汽水系统进行模拟,并进行虚假水位分析具有十分重要的意义[2]。目前针对蒸汽发生器水位控制的研究大多是依据热工水力实验或电站实际数据辨识出的传递函数模型[2-4],并不包含热工水力过程,因此不能准确反映出核电站蒸汽发生器的运行状态。为了能更好的实现对蒸汽发生器水位的控制,可以利用蒸汽发生器的运行机理进行建模研究,利用模型反映相关参数变化时蒸发器的水位变化趋势,同时该模型也可为水位控制系统设计提供被控对象的特性。国际上有很多根据机理建模能够模拟真实系统的瞬态过程的软件程序[5],然而这些程序不适合于设计复杂控制系统。本文参考自然循环锅炉汽水系统[6-10],以大亚湾核电站蒸汽发生器为研究对象, 通过合理假设化简,基于蒸发与冷凝原理,建立了一种既能反映一定热工特性又便于控制系统设计的自然循环蒸汽发生器四阶动态水位机理模型,对不同工况点负荷扰动及热量扰动的情况下,水位及影响水位的参数的变化过程进行了分析与验证,并对水位系统设计了串级PID控制器,对不同工况下的控制效果进行了分析。
1 SG四阶动态水位模型的建立研究蒸汽发生器的动态水位特性、对其进行建模仿真与控制系统设计,首先要确定蒸汽发生器的输入输出参数之间的关系。
考虑到核电站自然循环蒸汽发生器的复杂程度,建模时应对系统进行一定程度的简化,并做出合理的假设。这是建立自然循环蒸汽发生器动态水位模型的前提,对系统作如下假设:1)给水进入蒸汽发生器后吸收来自一次侧的热量即变为饱和水(仅对时间常数有微小的影响,可以忽略),整个系统给定状态为饱和态;2)忽略上升通道工质流动的阻力和重力压头变化的影响,各处工质压力同步变化,与汽腔压力相同,工质饱和状态的密度、焓值、温度等参数都是汽腔压力的函数;3)传热管壁温度与饱和温度相同;4)升通道横截面上汽液均匀,水和蒸汽的流速相同。
整个系统的质量守恒方程为
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\rho _{\rm{s}}}{V_{{\rm{st}}}} + {\rho _{\rm{w}}}{V_{{\rm{wt}}}}} \right) = {W_{{\rm{fw}}}} - {W_{\rm{s}}} $ | (1) |
式中:ρ代表密度,V代表体积,W代表质量流量,下标s代表蒸汽,t代表总量,w代表水,fw代表给水。
整个系统的能量守恒方程为
| $ \frac{{{\rm{d}}\left( {{\rho _{\rm{s}}}{V_{{\rm{st}}}}{u_{\rm{s}}} + {\rho _{\rm{w}}}{V_{{\rm{wt}}}}{u_{\rm{w}}} + {m_{\rm{t}}}{C_{\rm{p}}}T} \right)}}{{{\rm{d}}t}} = Q + {W_{{\rm{fw}}}}{h_{{\rm{fw}}}} - {W_{\rm{s}}}{h_{\rm{s}}} $ | (2) |
式中:u代表内能,m代表质量,Cp代表金属比热容,T代表温度,Q代表系统换热量,h代表比焓。
由于内能为
| $ u = h - \frac{P}{\rho } $ | (3) |
式中P代表系统压力。
则整个系统的能量守恒方程变为
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}\left( {{\rho _{\rm{s}}}{V_{{\rm{st}}}}{u_{\rm{s}}} + {\rho _{\rm{w}}}{V_{{\rm{wt}}}}{h_{\rm{w}}} - {V_{\rm{t}}}P + {m_{\rm{t}}}{C_{\rm{p}}}T} \right)}}{{{\rm{d}}t}} = }\\ {Q + {W_{{\rm{fw}}}}{h_{{\rm{fw}}}} - {W_{\rm{s}}}{h_{\rm{s}}}} \end{array} $ | (4) |
整个系统总体积为
| $ {V_{\rm{t}}} = {V_{{\rm{st}}}} + {V_{{\rm{wt}}}} $ | (5) |
式中:ξ(0≤ξ≤1)是经过归一化的沿长度分布的因子,x是沸腾段的出口质量含气率,则沿长度的质量含气率为
| $ {x_{\rm{m}}}\left( \xi \right) = x\xi $ | (6) |
式中下标m代表汽水混合量。
体积含气率βv与质量含气率xm的关系是
| $ {\beta _{\rm{v}}} = \frac{{{\rho _{\rm{w}}}{x_{\rm{m}}}}}{{{\rho _{\rm{s}}} + \left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right){x_{\rm{m}}}}} $ | (7) |
则预热段与沸腾段的平均体积含气率为
| $ \begin{array}{*{20}{c}} {{{\bar \beta }_{\rm{v}}} = \int\limits_0^1 {{\beta _{\rm{v}}}\left( \xi \right){\rm{d}}\xi } = \frac{1}{x}\int\limits_0^x {{\beta _{\rm{v}}}\left( \xi \right){\rm{d}}\xi } = }\\ {\frac{{{\rho _{\rm{w}}}}}{{{\rho _{\rm{w}}} - {\rho _{\rm{s}}}}}\left( {1 - \frac{{{\rho _{\rm{s}}}}}{{\left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right)x}}\ln \left( {1 + \frac{{{\rho _{\rm{w}}} - {\rho _{\rm{s}}}}}{{{\rho _{\rm{s}}}}}x} \right)} \right)} \end{array} $ | (8) |
预热段与沸腾段的质量守恒方程为
| $ \frac{d}{{{\rm{d}}t}}\left( {{\rho _{\rm{s}}}{{\bar \beta }_{\rm{v}}}{V_{\rm{b}}} + {\rho _{\rm{w}}}\left( {1 - {{\bar \beta }_{\rm{v}}}} \right){V_{\rm{b}}}} \right) = {W_{{\rm{dc}}}} - {W_{\rm{b}}} $ | (9) |
式中:下标b代表预热段与沸腾段,dc代表下降通道。
沸腾段出口的汽液混合焓值为
| $ {h_{\rm{m}}} = x{h_{\rm{s}}} + \left( {1 - x} \right){h_{\rm{w}}} $ | (10) |
预热段与沸腾段的能量守恒方程为
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}\left( {{\rho _{\rm{s}}}{{\bar \beta }_{\rm{v}}}{V_{\rm{b}}}{h_{\rm{s}}} + {\rho _{\rm{w}}}\left( {1 - {{\bar \beta }_{\rm{v}}}} \right){V_{\rm{b}}}{h_{\rm{w}}} - {V_{\rm{b}}}P + {m_{\rm{b}}}{C_{\rm{p}}}T} \right)}}{{{\rm{d}}t}} = }\\ {Q + {W_{{\rm{dc}}}}{h_{\rm{w}}} - {W_{\rm{b}}}{h_{\rm{m}}}} \end{array} $ | (11) |
上升段水位高度为
| $ {L_{\rm{r}}} = {L_{{\rm{dc}}}} - {L_{\rm{b}}} $ | (12) |
式中:L代表水位高度,下标r代表上升段。
根据下降通道上升通道动量守恒方程可得
| $ \begin{array}{*{20}{c}} {\frac{1}{2}k\frac{{{W_{{\rm{dc}}}}^2}}{{{A_{{\rm{dc}}}}^2{\rho _{\rm{w}}}}} = }\\ {{\rho _{\rm{w}}}g{L_{{\rm{dc}}}} - \left( {{{\hat \beta }_{\rm{v}}}{\rho _{\rm{s}}} + \left( {1 - {{\hat \beta }_{\rm{v}}}} \right){\rho _{\rm{w}}}} \right)g{L_{\rm{b}}} - {\rho _{\rm{w}}}g{L_{\rm{r}}}} \end{array} $ | (13) |
式中:k代表摩擦系数,A代表横截面积,g代表重力加速度。
蒸汽发生器汽水界面处于上升段,上升段主要的物理过程是汽水的分离和冷凝。上升段液面下气体的质量守恒方程为
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\rho _{\rm{s}}}{V_{{\rm{sr}}}}} \right) = x{W_{\rm{b}}} - {W_{{\rm{sr}}}} - {W_{{\rm{cr}}}} $ | (14) |
其中
| $ {W_{{\rm{sr}}}} = x{W_{\rm{b}}} - \frac{{{\rho _{\rm{s}}}}}{{{t_{\rm{r}}}}}\left( {{V_{{\rm{sr0}}}} - {V_{{\rm{sr}}}}} \right) $ | (15) |
| $ \begin{array}{*{20}{c}} {{W_{{\rm{cr}}}} = \frac{1}{{{h_{\rm{s}}} - {h_{\rm{w}}}}}\left[ {{\rho _{\rm{s}}}{V_{{\rm{sr}}}}\frac{{{\rm{d}}{h_{\rm{s}}}}}{{{\rm{d}}t}} + {\rho _{\rm{w}}}{V_{{\rm{wr}}}}\frac{{{\rm{d}}{h_{\rm{w}}}}}{{{\rm{d}}t}} - } \right.}\\ {\left. {\left( {{V_{{\rm{sr}}}} - {V_{{\rm{wr}}}}} \right)\frac{{{\rm{d}}P}}{{{\rm{d}}t}} + {m_{\rm{r}}}{C_{\rm{p}}}\frac{{{\rm{d}}T}}{{{\rm{d}}t}}} \right]} \end{array} $ | (16) |
| $ {V_{{\rm{wr}}}} = {V_{{\rm{wt}}}} - {V_{{\rm{dc}}}} - \left( {1 - {{\bar \beta }_{\rm{v}}}} \right){V_{\rm{b}}} $ | (17) |
式中:Wcr代表冷凝量,tr代表蒸汽在上升段停留的时间,Vsr0代表没有冷凝时上升段液位下蒸汽体积。
最终水位可以表示为
| $ L = \frac{{{V_{{\rm{sr}}}} + {V_{{\rm{wr}}}}}}{{{A_{\rm{r}}}}} + {L_{\rm{b}}} $ | (18) |
通过变形整理,以上的时域方程可以转换成如下状态空间方程:
| $ \left\{ \begin{array}{l} {a_{11}}\frac{{{\rm{d}}{V_{{\rm{wt}}}}}}{{{\rm{d}}t}} + {a_{12}}\frac{{{\rm{d}}P}}{{{\rm{d}}t}} = {W_{{\rm{fw}}}} - {W_{\rm{s}}}\\ {a_{21}}\frac{{{\rm{d}}{V_{{\rm{wt}}}}}}{{{\rm{d}}t}} + {a_{22}}\frac{{{\rm{d}}P}}{{{\rm{d}}t}} = Q + {W_{{\rm{fw}}}}{h_{{\rm{fw}}}} - {W_{\rm{s}}}{h_{\rm{s}}}\\ {a_{32}}\frac{{{\rm{d}}P}}{{{\rm{d}}t}} + {a_{33}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = Q - x{W_{{\rm{sc}}}}\left( {{h_{\rm{s}}} - {h_{\rm{w}}}} \right)\\ {a_{42}}\frac{{{\rm{d}}P}}{{{\rm{d}}t}} + {a_{44}}\frac{{{\rm{d}}{V_{{\rm{sr}}}}}}{{{\rm{d}}t}} = \frac{{{\rho _{\rm{s}}}}}{{{t_{\rm{r}}}}}\left( {{V_{{\rm{sr0}}}} - {V_{{\rm{sr}}}}} \right) \end{array} \right. $ | (19) |
其中:
| $ {a_{11}} = {\rho _{\rm{w}}} - {\rho _{\rm{s}}} $ |
| $ {a_{12}} = {V_{{\rm{wt}}}}\frac{{\partial {\rho _{\rm{w}}}}}{{\partial P}} - {V_{{\rm{st}}}}\frac{{\partial {\rho _{\rm{s}}}}}{{\partial P}} $ |
| $ {a_{21}} = {\rho _{\rm{w}}}{h_{\rm{w}}} - {\rho _{\rm{s}}}{h_{\rm{s}}} $ |
| $ \begin{array}{l} {a_{22}} = {V_{{\rm{wt}}}}\left( {{h_{\rm{w}}}\frac{{\partial {\rho _{\rm{w}}}}}{{\partial P}} + {\rho _{\rm{w}}}\frac{{\partial {h_{\rm{w}}}}}{{\partial P}}} \right) + \\ \;\;\;\;\;\;\;\;{V_{{\rm{st}}}}\left( {{h_{\rm{s}}}\frac{{\partial {\rho _{\rm{s}}}}}{{\partial P}} + {\rho _{\rm{s}}}\frac{{\partial {h_{\rm{s}}}}}{{\partial P}}} \right) - {V_{\rm{t}}} + {m_{\rm{t}}}{C_{\rm{p}}}\frac{{\partial T}}{{\partial P}} \end{array} $ |
| $ \begin{array}{l} {a_{32}} = \left( {{\rho _{\rm{w}}}\frac{{\partial {h_{\rm{w}}}}}{{\partial P}} - x\left( {{h_{\rm{s}}} - {h_{\rm{w}}}} \right)\frac{{\partial {\rho _{\rm{w}}}}}{{\partial P}}} \right)\left( {1 - {{\bar \beta }_{\rm{v}}}} \right){V_{\rm{b}}} + \\ \;\;\;\;\;\;\;\;\left( {{\rho _{\rm{s}}}\frac{{\partial {h_{\rm{s}}}}}{{\partial P}} - \left( {1 - x} \right)\left( {{h_{\rm{s}}} - {h_{\rm{w}}}} \right)\frac{{\partial {\rho _{\rm{s}}}}}{{\partial P}}} \right){{\bar \beta }_{\rm{v}}}{V_{\rm{b}}} + \\ \;\;\;\;\;\;\;\;\left( {{\rho _{\rm{s}}} + x\left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right)} \right)\left( {{h_{\rm{s}}} - {h_{\rm{w}}}} \right)\frac{{\partial {{\bar \beta }_{\rm{v}}}}}{{\partial P}}{V_{\rm{b}}} - {V_{\rm{b}}} + \\ \;\;\;\;\;\;\;\;{m_{\rm{r}}}{C_{\rm{p}}}\frac{{{\rm{d}}T}}{{{\rm{d}}P}} \end{array} $ |
| $ {a_{33}} = \left( {\left( {1 - x} \right){\rho _{\rm{s}}} + x{\rho _{\rm{w}}}} \right)\left( {{h_{\rm{s}}} - {h_{\rm{w}}}} \right){V_{\rm{b}}}\frac{{\partial {{\bar \beta }_{\rm{v}}}}}{{\partial x}} $ |
| $ \begin{array}{l} {a_{42}} = {V_{{\rm{sr}}}}\frac{{\partial {\rho _{\rm{s}}}}}{{\partial P}} + \frac{1}{{{h_{\rm{s}}} - {h_{\rm{w}}}}}\left( {{\rho _{\rm{s}}}{V_{{\rm{sr}}}}\frac{{{\rm{d}}{h_{\rm{s}}}}}{{{\rm{d}}P}} + {\rho _{\rm{w}}}{V_{{\rm{wr}}}}\frac{{{\rm{d}}{h_{\rm{w}}}}}{{{\rm{d}}P}} - } \right.\\ \;\;\;\;\;\;\;\;\left. {\left( {{V_{{\rm{sr}}}} + {V_{{\rm{wr}}}}} \right) + {m_{\rm{r}}}{C_{\rm{p}}}\frac{{{\rm{d}}T}}{{{\rm{d}}P}}} \right) \end{array} $ |
| $ {a_{44}} = {\rho _{\rm{s}}} $ |
| $ \begin{array}{*{20}{c}} {\frac{{\partial {{\bar \beta }_{\rm{v}}}}}{{\partial P}} = \frac{{\left( {{\rho _{\rm{w}}}\frac{{{\rm{d}}{\rho _{\rm{s}}}}}{{{\rm{d}}P}} - {\rho _{\rm{s}}}\frac{{{\rm{d}}{\rho _{\rm{w}}}}}{{{\rm{d}}P}}} \right)}}{{{{\left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right)}^2}}} \cdot \left( {1 + \frac{{{\rho _{\rm{w}}}}}{{x{\rho _{\rm{w}}} + \left( {1 - x} \right){\rho _{\rm{s}}}}} - } \right.}\\ {\left. {\frac{{{\rho _{\rm{w}}} + {\rho _{\rm{s}}}}}{{x\left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right)}}\ln \left( {x{p_{\rm{w}}} + \frac{{\left( {1 - x} \right){p_s}}}{{{\rho _{\rm{s}}}}}} \right)} \right)} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\frac{{\partial {{\bar \beta }_{\rm{v}}}}}{{\partial x}} = {\rho _{\rm{w}}}\left[ {\frac{{{\rho _{\rm{s}}}}}{{x\left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right)}}\ln \left( {\frac{{x{\rho _{\rm{w}}} + \left( {1 - x} \right){\rho _{\rm{s}}}}}{{{\rho _{\rm{s}}}}}} \right) - } \right.}\\ {\left. {\frac{{{\rho _{\rm{s}}}}}{{x{\rho _{\rm{w}}} + \left( {1 - x} \right){\rho _{\rm{s}}}}}} \right]/x\left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right)} \end{array} $ |
| $ \begin{array}{l} {W_{\rm{b}}} = {W_{{\rm{dc}}}} - {V_{\rm{b}}}\left[ {{{\bar \beta }_{\rm{v}}}\frac{{{\rm{d}}{\rho _{\rm{s}}}}}{{{\rm{d}}P}} + \left( {1 - {{\bar \beta }_{\rm{v}}}} \right)\frac{{{\rm{d}}{\rho _{\rm{w}}}}}{{{\rm{d}}P}} + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right)\frac{{\partial {{\bar \beta }_{\rm{v}}}}}{{\partial P}}} \right]\frac{{{\rm{d}}P}}{{{\rm{d}}t}} + {V_{\rm{b}}}\left( {{\rho _{\rm{w}}} - {\rho _{\rm{s}}}} \right)\frac{{\partial {{\bar \beta }_{\rm{v}}}}}{{\partial x}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} \end{array} $ |
以
本文所建模型中,所求四个状态变量分别为:Vwt、P、x、Vsr。这四个状态变量能够反映系统总的质量和能量的变化,描述整个上升通道中蒸汽的分布,这样就可以从内部完整地描述整个系统中蒸汽和水以及质量和能量的动态变化。本文建立的四阶水位模型机理方程中共有26个未知数,12个微分代数方程,再加上10个分别关于饱和压力的状态关系式,输入4个独立变量后,系统可求得唯一解输出。
2 仿真结果分析当蒸汽流量和换热量分别扰动时,对蒸汽发生器进行仿真实验,整个仿真过程中假设给水流量不变,得到蒸汽发生器各个参数的动态响应曲线。
2.1 蒸汽流量扰动以30%工况为例,保持其他量不变,蒸汽流量在第40 s增加30 kg/s,蒸汽发生器各参量动态响应特性如图 1所示。

|
Download:
|
| 图 1 蒸汽流量扰动时各参量动态响应曲线 Fig. 1 Dynamic response curve of each parameter with steam flow diaturbance | |
在其他量保持不变时,出口蒸汽流量的增加导致了压力下降、再循环流量增加。压力下降引起蒸发增强,因此水的总体积下降。质量含气率一开始先增加是因为压力减小,之后下降是因为再循环流量的增加。由于一开始液面下的气泡迅速增多,导致水位一开始先上升,即“虚假水位”,之后由于出口蒸汽流量大于入口给水流量,水位开始下降。
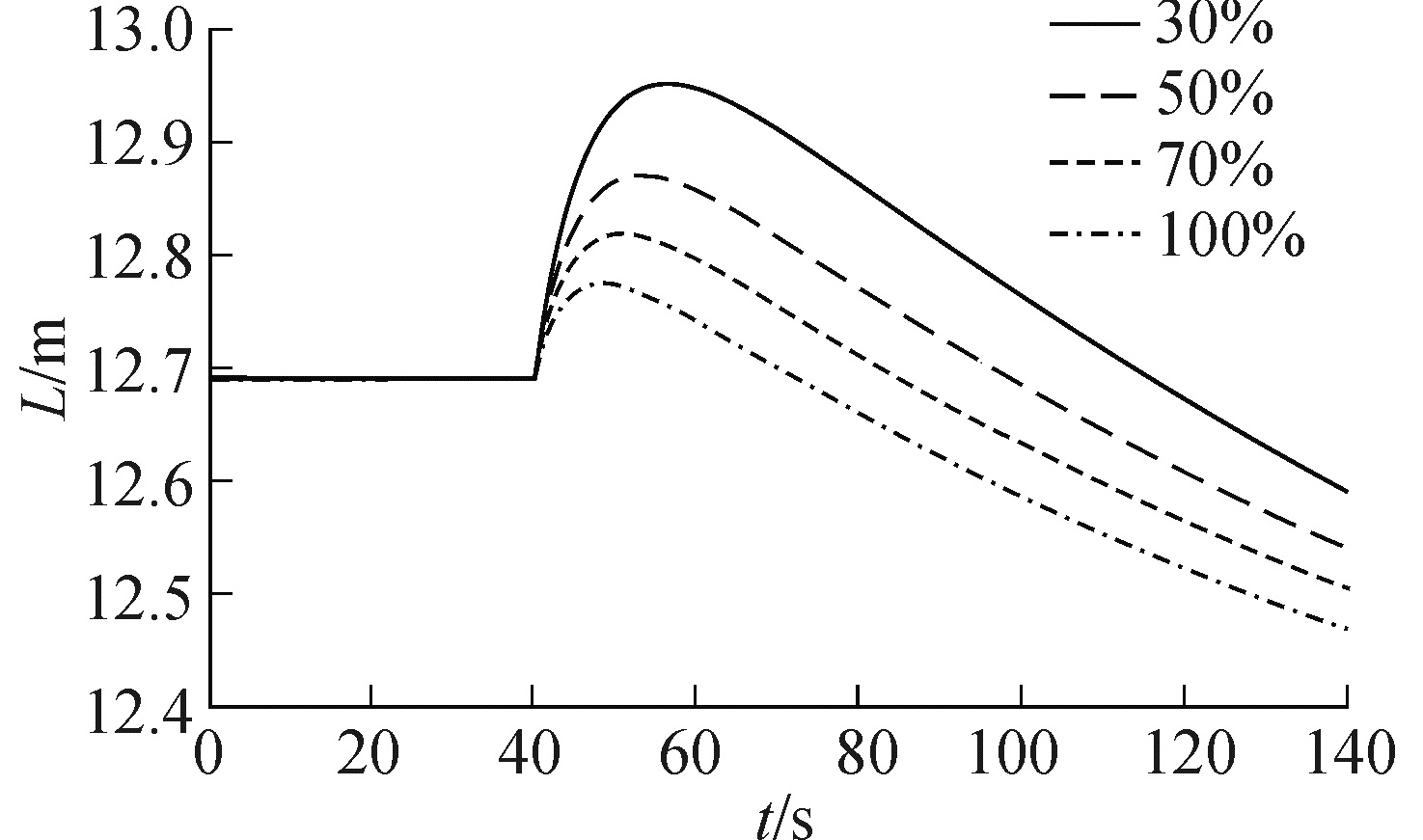
在不同工况下,保持其他量不变,蒸汽流量在第40 s增加30 kg/s,水位动态响应特性对比结果如图 2所示。
|
Download:
|
| 图 2 不同工况水位响应对比曲线 Fig. 2 The water level response contrast curves in different conditions | |
根据图 2所显示,对于不同的工况点,相同的蒸汽流量扰动产生的虚假水位不同。低工况比高工况的虚假水位过渡时间更长,这也是低工况水位更难控制的原因。这与根据实验数据拟合所建立的经典欧文模型[11]趋势完全一致,验证了所建立的动态水位模型的合理性。
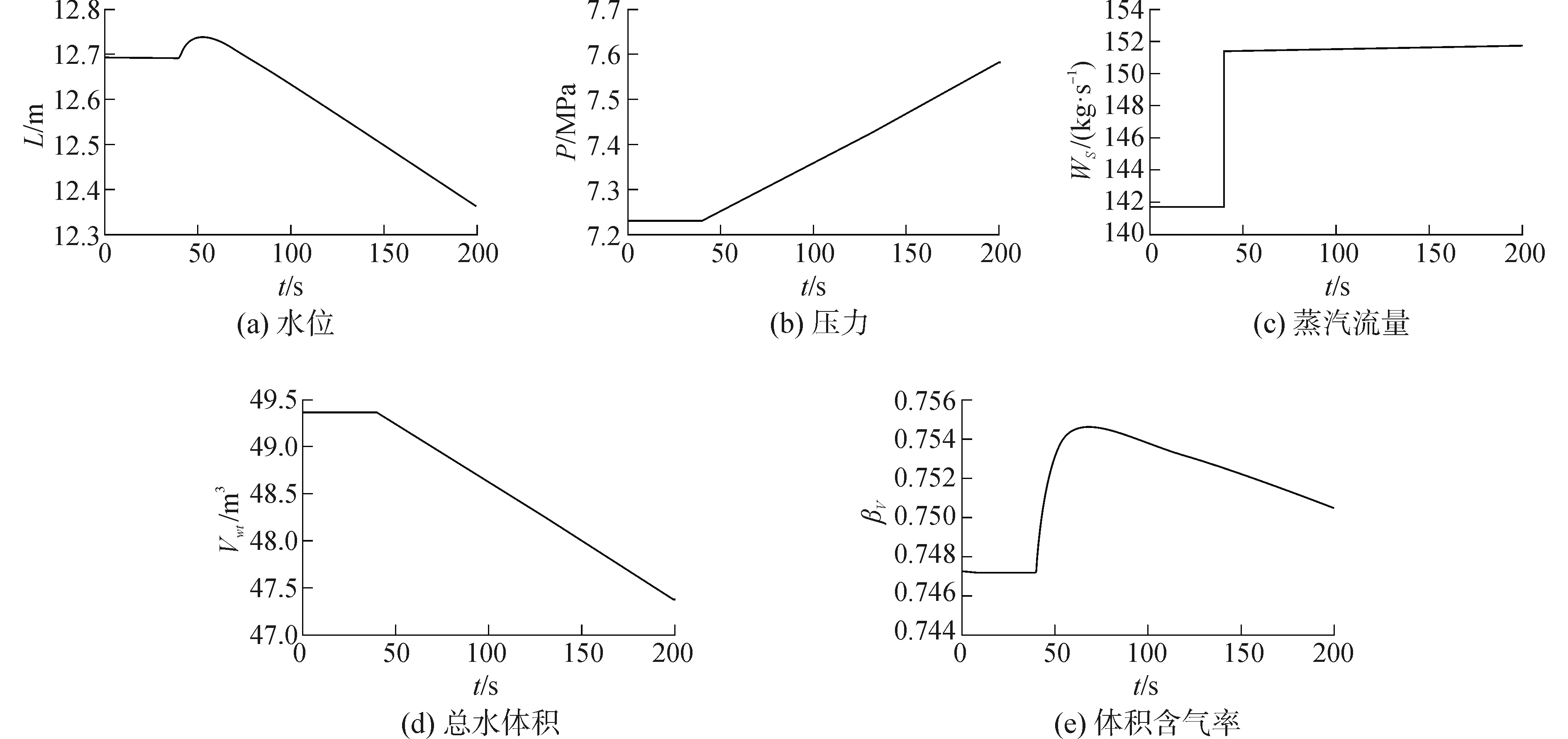
2.2 换热量扰动同样以30%工况为例,保持其他量不变,换热量在第40 s增大20 MW,蒸汽发生器各参量动态响应特性如图 3所示。
|
Download:
|
| 图 3 换热量扰动时各参量动态响应曲线 Fig. 3 Dynamic response curve of each parameter with heat exchange diaturbance | |
在其他量保持不变时,换热量增大引起压力增加,上升通道沸腾强度也增大,出口蒸汽流量增加,导致水的总体积下降,一开始上升通道出口的汽水混合物中蒸汽所占比重迅速增加,之后压力的增大使得水位下汽泡体积收缩,因此水位会先增加,即“虚假水位”,之后由于水的总体积下降,水位开始下降。
在不同工况下,保持其他量不变,换热量在第40 s增大20 MW,水位动态响应特性对比结果如图 4所示。

|
Download:
|
| 图 4 不同工况相同换热量水位响应对比曲线 Fig. 4 The water level response contrast curves of the same heat exchange in different conditions | |
如图 4所示,对于不同的工况点,相同的换热量扰动产生的虚假水位不同。低工况比高工况的虚假水位过渡时间更长,因此低工况水位更难控制。仿真结果与理论分析趋势一致,所建立的动态水位模型合理。
3 SG串级PID控制与仿真结果 3.1 控制系统结构与原理目前,大多数核电厂对于蒸汽发生器水位波动均采用串级PID控制[12-13]。结构图如图 5所示。

|
Download:
|
| 图 5 SG串级PID控制结构图 Fig. 5 The cascade PID control structure diagram of SG | |
将蒸汽发生器水位的偏差值作为系统给水流量补偿控制的调节依据,并且应用蒸汽流量前馈的方式来构建系统。由于系统的蒸汽流量应用前馈的方式与系统的控制输入相加,当蒸汽流量扰动时,系统的给水补偿量也施加了与其相对应的信号以抵消“虚假水位”的影响,这种串级PID控制系统能够抑制干扰。
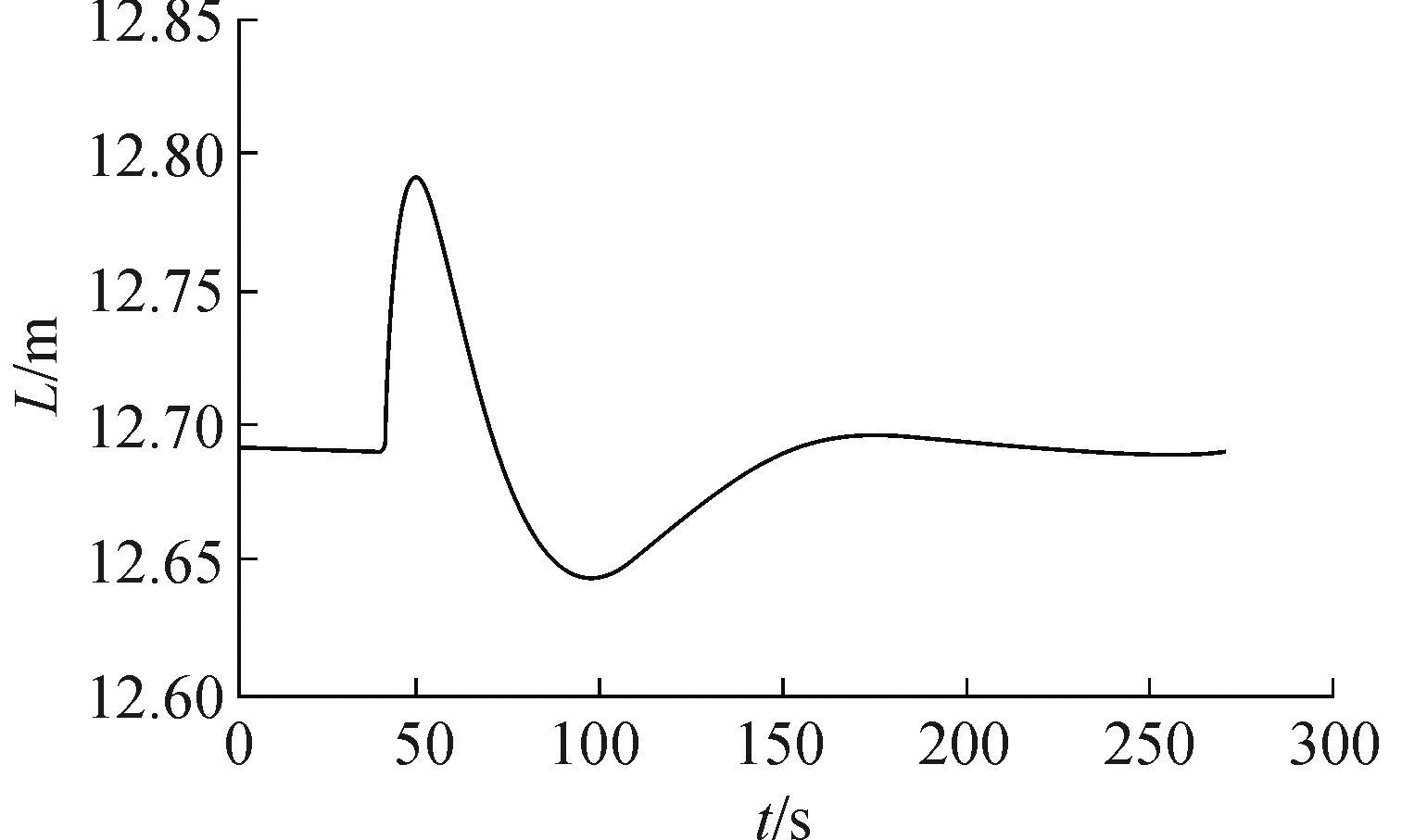
3.2 控制系统仿真结果 3.2.1 蒸汽流量扰动保持其他量不变,在40 s时,加入蒸汽流量10%的正阶跃扰动,引入串级PID控制器,对30%工况进行仿真,蒸汽发生器水位动态响应过程如图 6所示。
|
Download:
|
| 图 6 蒸汽流量扰动水位响应曲线 Fig. 6 The water level response curve with steam flow disturbance | |
从仿真结果可以看出,在串级PID控制调节下,蒸汽发生器水位的调节时间约为200 s,水位值最终稳定在稳态值,超调量约为0.09 m,振荡次数为2次。蒸汽发生器水位控制系统的一般技术要求是水位控制系统能承受蒸汽流量10%的正阶跃变化,水位最大超调量在正负300 mm之内,可见控制系统能满足蒸汽发生器液位控制系统的一般技术要求。
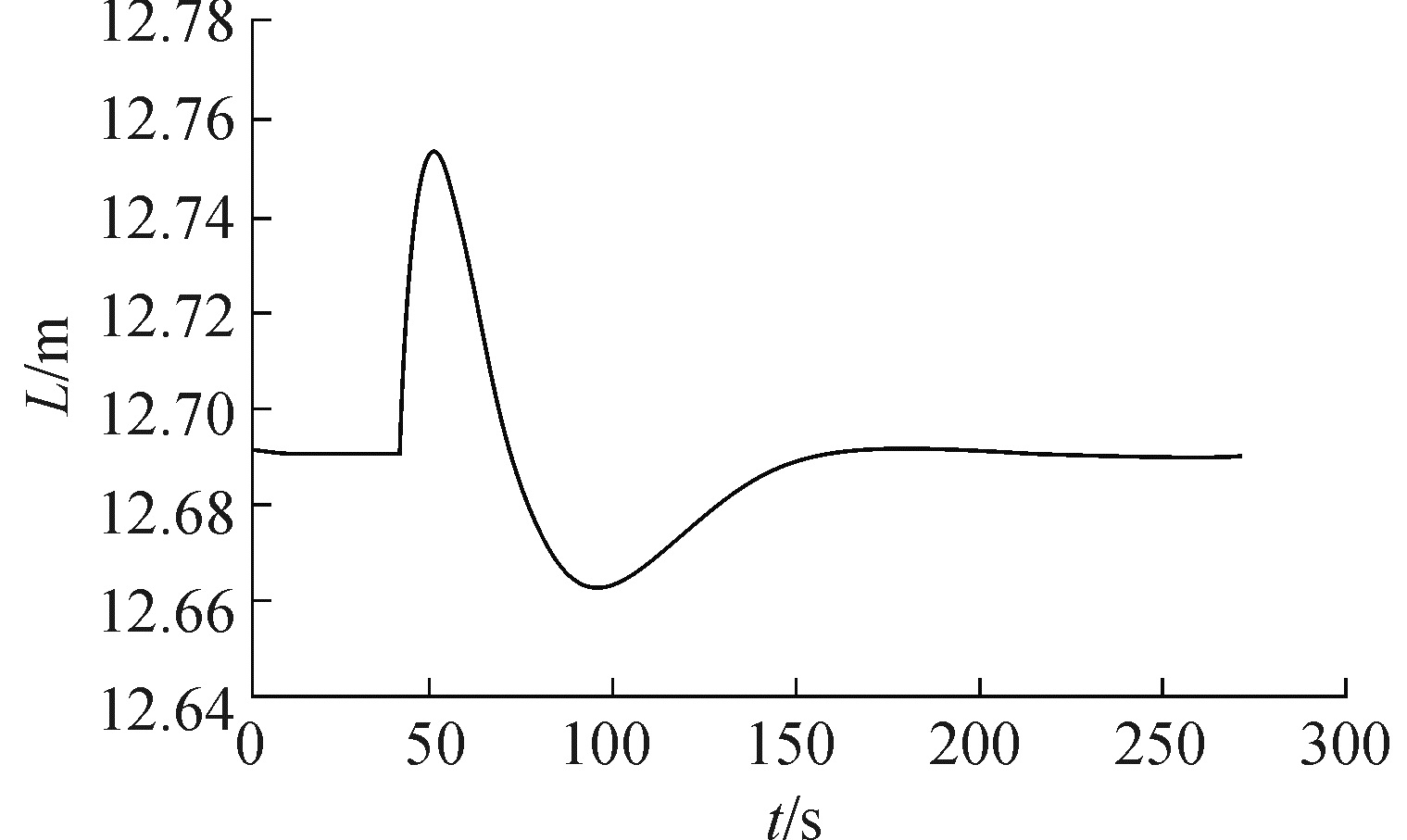
3.2.2 换热量扰动保持其他量不变,在40 s时,加入换热量20 MW的正阶跃扰动,采用串级PID控制器,对30%工况进行仿真,蒸汽发生器水位动态响应过程如图 7所示。
|
Download:
|
| 图 7 换热量扰动水位响应曲线 Fig. 7 The water level response curve with heat exchange diaturbance | |
从仿真结果可以看出,在串级PID控制调节下,蒸汽发生器水位的调节时间约为250 s,超调量约为0.08 m, 振荡次数为2次,没有稳态误差。
4 结论1) 本文成功建立了一种既能反映一定热工特性又便于控制系统设计的自然循环蒸汽发生器四阶动态水位机理模型,为后期控制系统设计提供了很大便利。
2) 当引入负荷扰动及热量扰动时,蒸汽发生器主要参数都表现出合理的变化趋势,准确的模拟出了虚假水位现象。
3) 验证了串级PID控制系统基本上能满足蒸汽发生器水位控制的要求。
4) 由于计算机技术和信息技术的迅猛发展,导致控制理论与控制技术不断向前推进,一些尖端的控制策略不断被提出,在低工况、大扰动下,水位特性参数变化大,控制效果不佳,控制器参数难以整定,因此本文对后期研究更为先进的控制方法有重要的指导意义。
| [1] |
彭敏俊. 船舶核动力装置[M]. 哈尔滨: 原子能出版社, 2011. PENG Minjun. Marine nuclear power plant[M]. Harbin: Atomic Energy Press, 2011. (  0) 0)
|
| [2] |
BAO Jie, SUN Baozhi, ZHANG Guolei. Simulation and analysis of steam generator water level based on nonlinear level model[C]//2012 Asia-Pacific Power and Energy Engineering Conference. Shanghai, China, 2012: 1-4.
(  0) 0)
|
| [3] |
ZHAO Futao, OU Jing, DU Wei. Simulation modeling of nuclear steam generator water level process-a case study[J]. ISA transactions, 2000, 39(2): 143-151. DOI:10.1016/S0019-0578(00)00015-X (  0) 0)
|
| [4] |
BASHER A M H. Development of a robust model-based water level controller for U-tube steam generator[R]. ORNL Oak Ridge National Laboratory (US), 2001.
(  0) 0)
|
| [5] |
ZHOU Gang, ZHANG Dafa, YANG Shiben. Simulation and analysis on dynamics characteristic for nuclear steam generator water level process[J]. Journal of system simulation, 2006, 18(12): 3383-3386. (  0) 0)
|
| [6] |
蒸汽发生器编写组. 蒸汽发生器[M]. 北京: 原子能出版社, 1982.
(  0) 0)
|
| [7] |
ÅSTRÖM K J, BELL R D. Drum-boiler dynamics[J]. Automatic, 2000, 36(3): 363-378. DOI:10.1016/S0005-1098(99)00171-5 (  0) 0)
|
| [8] |
KIM H, CHOI S. A model on water level dynamics in natural circulation drum-type boilers[J]. International communications in heat and mass transfer, 2005, 32(6): 786-796. DOI:10.1016/j.icheatmasstransfer.2004.10.010 (  0) 0)
|
| [9] |
史达明, 马文智. 自然循环锅炉蒸发区动态数学模型[J]. 中国电机工程学报, 1990, 10(1): 68-72. SHI Daming, MA Wenzhi. The mathematical model of evaporation zone of nature circulation boiler[J]. Proceedings of the CSEE, 1990, 10(1): 68-72. (  0) 0)
|
| [10] |
郭广跃, 袁景淇, 袁嘉婧, 等. 自然循环锅炉汽水系统动态模型的建立[J]. 控制工程, 2010, 17(S2): 39-41. GUO Guangyue, YUAN Jingqi, YUAN Jiajing, et al. Modeling for the steam-water system of the natural circulation boilers in the power plant[J]. Control engineering of China, 2010, 17(S2): 39-41. (  0) 0)
|
| [11] |
王卓, 付冬梅, 刘德军. 锅炉汽包水位控制系统的研究[J]. 自动化仪表, 2006, 27(11): 51-52, 56. WANG Zhuo, FU Dongmei, LIU Dejun. The study on drum water level control system for boiler[J]. Process automation instrumentation, 2006, 27(11): 51-52, 56. DOI:10.3969/j.issn.1000-0380.2006.11.016 (  0) 0)
|
| [12] |
IRVING E, MIOSSEC C, TASSART J. Towards efficient full automatic operation of the PWR steam generator with water level adaptive control[C]//Proceedings of the 2nd International Conference on Boiler Dynamics and Control in Nuclear Power Stations 2. London: British Nuclear Energy Society, 1980.
(  0) 0)
|
| [13] |
刘金琨. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2004.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


