2. 武汉理工大学 国家水运安全工程技术研究中心, 湖北 武汉 430063
2. National Engineering Research Center for water Transport Safety, Wuhan University of Technology, Wuhan 430063, China
超大型船舶的富裕水深[1]是船舶航行时船底以下必须保留的水深余量,是防止船舶拖底、触底和搁浅的水深保留量,主要由波浪、船舶倾斜等水深余量、净富余水深[2]组成。近年来随着我国沿海水域超大型船舶流量的增加,船舶事故风险不断加大,尤其是在受限水域[3]超大型船舶富裕水深预留不足导致的搁浅事故较为突出,如2005年“阿提哥”触礁溢油事故,造成了极其严重的海洋生态环境破坏和经济社会影响。
目前国内外有关UKC的计算和取值方法主要有经验取值法[4-5]、理论计算方法[6-8]和实船或船模试验方法[9-10]三大类别。其中,经验取值法主要是利用常年航行在某一水域的不同类型船舶不同天气条件下积累的航行经验及良好船艺的要求确定船舶UKC的方法,如比值法、比值-固定值混合法、分类取值法等。理论计算方法主要包括基于解析式、半经验数学公式的计算方法[11-13],主要将船舶参数、通航环境参数代入解析式、半经验数学公式,从而求取结果,如Hooft公式、Huuska公式、Eryuzlu公式等。试验方法主要是将GPS系统安装于船舶,精确测定船舶航行时的下沉量,如加拿大海岸警卫队采用的GPS-OTF技术(GPS- on the fly)、德国学者采用的SHIPS方法(shore independent precise squat observation)。国内外现有UKC求取方法与船舶大型化发展的趋势不同步,普遍存在求解复杂、精确度不高、试验成本高的共性问题,没有考虑和解决受限水域UKC动态变化及经验取值的边界问题。本文采集了曹妃甸港2009—2016年超大型船舶进出港统计数据,提出了一种基于数据驱动的高斯混合分布模型(gaussian mixture model, GMM)和期望最大算法(expectation-maximization, EM)的UKC计算方法,为船型大型化和航运效益与安全的最优化提供理论和技术参考。
1 超大型船舶富裕水深/船舶吃水计算方法通过对大量超大型船舶进出港数据统计分析,超大型船舶的富裕水深/船舶吃水(UKC/T)不符合常用的高斯分布和泊松分布,为准确统计分析超大型船舶的UKC/T值数据的分布特征,采用GMM模型对UKC/T值的分布进行拟合以得到最佳统计分布结果,并运用EM算法计算得到GMM模型各参数值,推导得到受限水域下不同船舶类别下的取值区间。令y表示UKC/T值,用于拟合真实概率分布的GMM模型为
| $ p\left( y \right) = \sum\limits_{c = 1}^C {{w_c}p\left( {y\left| {{\mu _c},{\sigma _c}} \right.} \right)} $ | (1) |
式中:C为单一高斯模型的个数,w、μ和σ分别为相应单一高斯模型的权重、均值和标准差。同时,采用的GMM模型还满足如下的约束条件:
| $ \sum\limits_{c = 1}^C {{w_c} = 1} $ | (2) |
由于高斯模型个数C可事先假设,则可简化成对权重、期望和方差的估计。在实际应用过程中,参数C的选取无需太大即可满足拟合精度的要求。为保证最终参数估计结果的准确性,采用期望最大算法来对GMM模型进行参数估计。令“集核” Θ=(μ, σ),则有
| $ \begin{array}{*{20}{c}} {p\left( {{y_i}\left| \mathit{\Theta } \right.} \right) = \sum\limits_{c = 1}^C {{w_c}{p_c}\left( {{x_i}\left| {{\theta _c}} \right.} \right)} }\\ {i = 1,2, \cdots ,N} \end{array} $ | (3) |
式中N为数据样本量的大小。此时,可推导得到式(4)中不完全数据y的对数似然函数(log-likelihood expression)的表达形式为
| $ \begin{array}{*{20}{c}} {\ln \left( {L\left( {\mathit{\Theta }\left| y \right.} \right)} \right) = \ln \prod\limits_{i = 1}^N {p\left( {{y_i}\left| {{\mathit{\Theta }_c}} \right.} \right)} = }\\ {\sum\limits_{i = 1}^N {\ln \left( {\sum\limits_{c = 1}^C {{w_c}{p_c}\left( {{y_i}\left| {{\mathit{\Theta }_c}} \right.} \right)} } \right)} } \end{array} $ | (4) |
式中:“子集核”Θc⊂Θ。从数值计算角度考虑,为便于问题求解,通过引入一组指示函数z={z1, z2, …, zN},可将式(5)转化成如下问题的优化求解:
| $ \begin{array}{*{20}{c}} {\ln \left( {L\left( {\mathit{\Theta }\left| {y,z} \right.} \right)} \right. = \ln \left( {p\left( {y,z\left| \mathit{\Theta } \right.} \right)} \right) = }\\ {\sum\limits_{i = 1}^N {\ln \left( {p\left( {{y_i}\left| {{z_i}} \right.} \right)p\left( z \right)} \right)} = }\\ {\sum\limits_{i = 1}^N {\ln \left( {{w_{pi}}{p_{{z_i}}}\left( {{y_i}\left| {{\theta _{{z_i}}}} \right.} \right)} \right)} } \end{array} $ | (5) |
根据常用的贝叶斯公式,可得到
| $ \begin{array}{*{20}{c}} {p\left( {{z_i}\left| {{y_i},{\mathit{\Theta }^{{\rm{old}}}}} \right.} \right) = \frac{{w_{{z_i}}^{{\rm{old}}}{p_{{z_i}}}\left( {{y_i}\left| {\theta _{{z_i}}^{{\rm{old}}}} \right.} \right)}}{{p\left( {{y_i}\left| {{\mathit{\Theta }^{{\rm{old}}}}} \right.} \right)}} = }\\ {\frac{{w_{{z_i}}^{{\rm{old}}}{p_{{z_i}}}\left( {{y_i}\left| {\theta _{{z_i}}^{{\rm{old}}}} \right.} \right.}}{{\sum\nolimits_{c = 1}^C {w_c^{{\rm{old}}}{p_c}\left( {{y_c}\left| {\theta _c^{{\rm{old}}}} \right.} \right)} }}} \end{array} $ | (6) |
且
| $ p\left( {z\left| {y,{\mathit{\Theta }^{{\rm{old}}}}} \right.} \right) = \prod\limits_{i = 1}^N {p\left( {{z_i}\left| {{\mathit{y}_i},{\mathit{\Theta }^{{\rm{old}}}}} \right.} \right.} $ | (7) |
可通过求解完全数据问题ln(L(Θ|y, z))来逼近原有的不完全数据问题ln(L(Θ|y))的解,此时可得到高斯混合模型(GMM)中各项参数的估计值为
| $ w_c^t = \frac{1}{N}\sum\limits_{i = 1}^N {p\left( {c\left| {{y_i},{\mathit{\Theta }^{t - 1}}} \right.} \right)} $ | (8) |
| $ \mu _c^t = \frac{{\sum\limits_{i = 1}^N {{y_i}p\left( {c\left| {{y_i},{\mathit{\Theta }^{t - 1}}} \right.} \right)} }}{{\sum\nolimits_{i = 1}^N {p\left( {c\left| {{y_i},{\mathit{\Theta }^{t - 1}}} \right.} \right)} }} $ | (9) |
| $ \sigma _c^t = \sqrt {\frac{{\sum\limits_{i = 1}^N {p\left( {c\left| {{y_i},{\mathit{\Theta }^{t - 1}}} \right.} \right)\left( {{y_i} - \mu _c^t} \right)\left( {{y_i} - \mu _c^t} \right)} }}{{\sum\limits_{i = 1}^N {p\left( {c\left| {{y_i},{\mathit{\Theta }^{t - 1}}} \right.} \right)} }}} $ | (10) |
式中:t为EM算法执行过程中的迭代次数。一旦w、μ和σ满足预先设定的精度要求,即可终止EM算法得到最优估计值。
在保证预先设定的可接受概率p的前提下,UKC/T需满足一定的范围[ymin, ymax],其具体的计算公式为
| $ \begin{array}{*{20}{c}} {p\left( {{y_{\min }} \le y \le {y_{\max }} = } \right.}\\ {\left. {\int\limits_{{y_{\min }}}^{{y_{\max }}} {\sum\limits_{c = 1}^C {{w_c}p\left( {y\left| {{\mu _c},{\sigma _c}} \right.} \right)} } } \right){\rm{d}}y \le \bar p} \end{array} $ | (11) |
本文研究的超大型船舶是指进出曹妃甸港150 000 t级及以上(且满载吃水16.5 m以上)的船舶,船型尺度见表 1。通过在曹妃甸港设置观测站,委托唐山港引航站、唐山曹妃甸海事处收集了2009—2016年进出曹妃甸港超大型船舶动态数据。
| 表 1 超大型船舶尺度表 Tab.1 The scale of ultra large-scale ships |
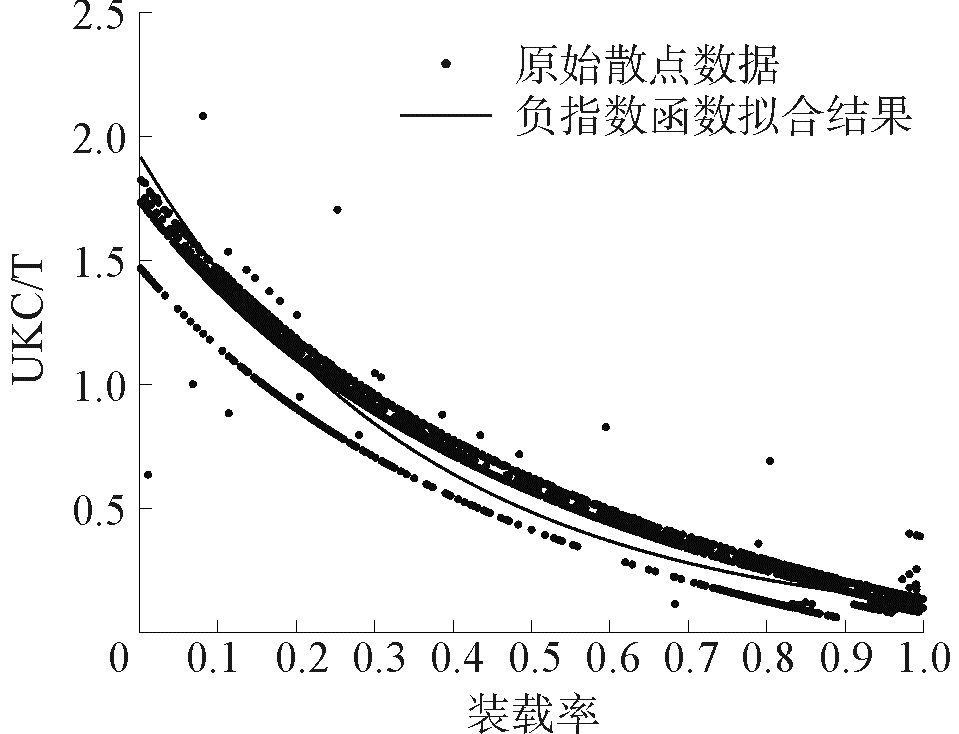
通过曹妃甸港2009—2016年超大型船舶进出港吃水数据,考虑进出港时间、潮汐、水深、气候等实际因素,将船舶装载率对应UKC/T值进行升序排列,通过Matlab进行数据拟合可以发现,两者之间存在负指数函数关系,见图 1所示。
|
Download:
|
| 图 1 装载率与UKC/T的函数关系图 Fig. 1 The function relationship between loading rate and UKC/T | |
进一步将2009—2016年超大型船舶数据按不同吨位、不同载重率进行分类,运用GMM模型和EM算法得出不同超大型船舶的UKC取值区间。
2.1 基于GMM的不同超大型船舶UKC/T拟合不分吨位不分装载率的UKC/T值分布及拟合如图 2。

|
Download:
|
| 图 2 不分吨位不分装载率的UKC/T分布及GMM拟合图 Fig. 2 The GMM fitting of UKC/T probability distribution in terms of tonnage and loading rate | |
从图 2可见,概率分布图呈现大小两个波峰,分别表示超大型船舶满载、空载进出港时UKC/T的分布。根据数据统计分布规律,拟采用3个单高斯分布模型组成GMM模型对图 3中的数据进行拟合。理论上假设的单高斯分布模型数量越多,计算拟合精度越高。但由此产生的高计算量无法满足实际问题的需求,易引起过拟合问题。由式(8)~(10)得出GMM模型各参数值如表 2所示。
| 表 2 GMM模型各参数值 Tab.2 The parameters of GMM model |
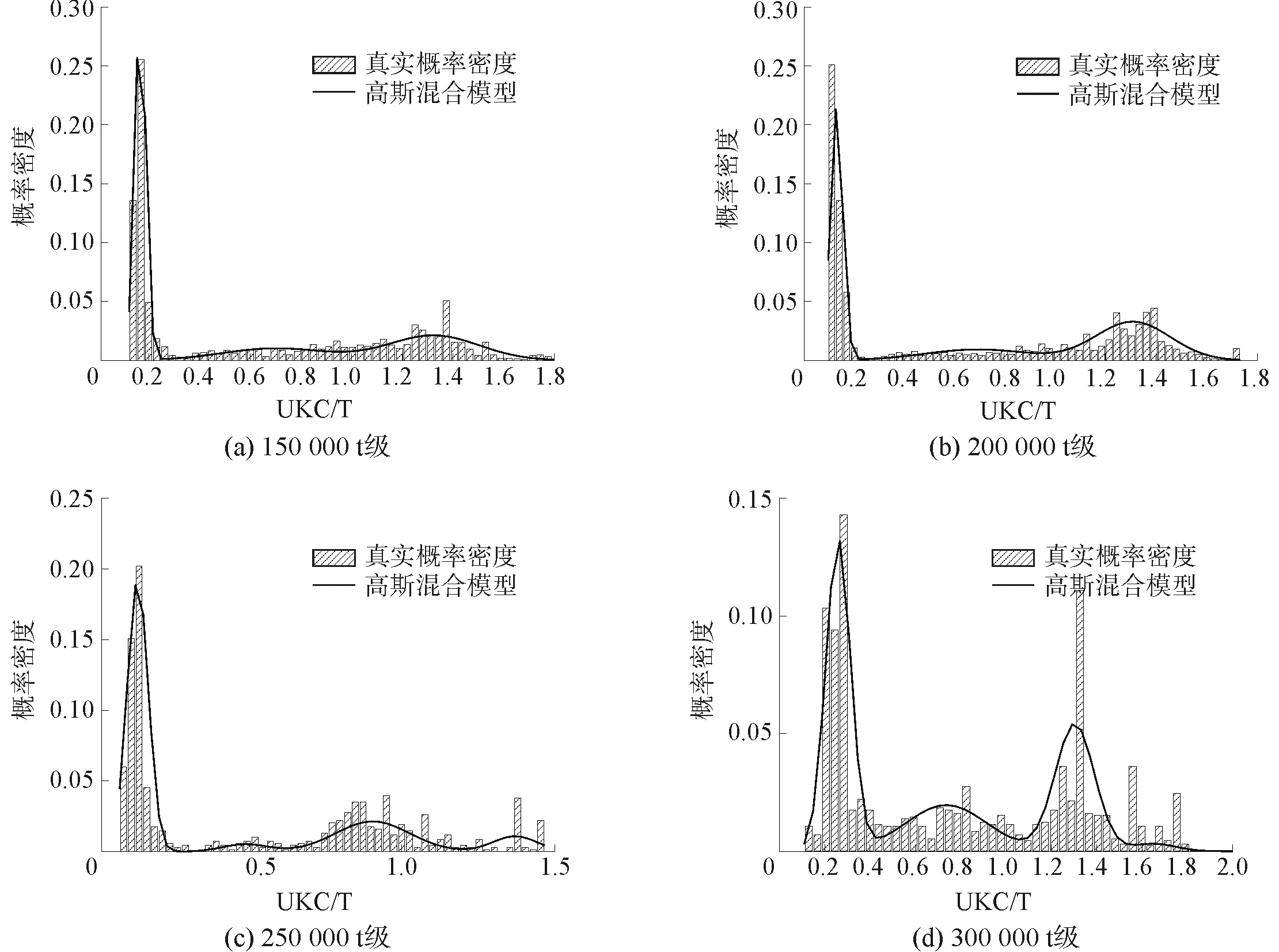
150 000、200 000、250 000和300 000 t级超大型船舶的UKC/T拟合见图 3。不同吨位下GMM拟合模型参数如表 3所示。
|
Download:
|
| 图 3 超大型船舶不同吨位下UKC/T值GMM拟合图 Fig. 3 The GMM fitting of UKC/T under different tonnages for ultra large-scale ships | |
| 表 3 不同吨位下超大型船舶的GMM模型参数计算表 Tab.3 The parameters of GMM model under different tonnage |
超大型船舶在满载、半载、轻载、空载状态下UKC/T拟合如图 4所示。不同装载率下GMM拟合模型参数如表 4所示。

|
Download:
|
| 图 4 超大型船舶不同装载率下UKC/T值GMM拟合图 Fig. 4 The GMM fitting of UKC/T with different loading rates | |
| 表 4 不同装载率下GMM模型参数计算表 Tab.4 The parameters of GMM model with different loading rates |
根据式(11),可接受概率下的总数据(不分吨位和载重率)及不同吨位超大型船舶的UKC/T取值区间如表 5所示。不同装载率下超大型船舶的UKC/T取值区间如表 6所示。
| 表 5 可接受概率下总数据及不同吨位的UKC/T取值区间表 Tab.5 The value range of total data and different tonnage under acceptable probability |
| 表 6 可接受概率下不同装载率的UKC/T取值区间表 Tab.6 The value range of different loading rate under acceptable probability |
根据表 5、6,得出不同类别下超大型船舶的UKC/T取值区间如表 7所示。由表 7可见,受限水域不同超大型船舶UKC/T应采取不同的区间。其中,总数据(不分吨位和装载率)UKC/T的取值区间为[0.059, 0.330]。在不同吨位情况下,150 000 t级船舶的UKC/T的取值区间为[0.112, 0.347];200 000 t级船舶的UKC/T的取值区间为[0.096, 0.323];250 000 t级船舶的UKC/T的取值区间为[0.059, 0.158];300 000 t级船舶的UKC/T的取值区间为[0.109, 0.362]。在不同装载率下,满载情况下的UKC/T的取值区间为[0.091, 0.256];半载、轻载、空载情况下UKC/T的取值区间无实际参考价值。
| 表 7 不同类别下UKC/T取值区间 Tab.7 The value range of UKC/T with different category |
为验证不同超大型船舶取值区间的可靠性,开展缩尺船摸试验、实船模拟试验,对取值区间的有效性进行验证。
3.2.1 缩尺船模试验两个位移传感器分别安装在艏柱及艉柱位置,分别测量艏艉位置的下沉量。通过试验测量各工况下超大型船舶艏、艉给定位置的下沉量,计算得到船体下沉和纵倾随航速、水深的变化规律如图 5所示。缩尺船模参数见表 8。

|
Download:
|
| 图 5 缩尺船模试验现场 Fig. 5 The test site of scaled model test | |
| 表 8 试验船舶船型参数 Tab.8 The parameters of test ship form |
试验工况中,其中船舶吃水及船速参数见表 9。
| 表 9 试验船舶吃水、船速参数 Tab.9 The parameters of test ship draught and speed |
试验水池尺度为90 m×15 m×2.0 m(长×宽×高),水深变化范围为0~1.8 m,车架车速为0~2.0 m/s。
3.2.2 实船试验选取满载的利比亚籍超大型油轮“M.T.NEW PARADISE”作为实船试验对象,尺度为:全长330 m,宽度60 m,满载吃水19.8 m。
主要作业技术指标为同步观测健康卫星数不小于4颗,点位几何图形强度因子(PDOP)小于6,数据采样率为30 s,天线对中精度为地面标志为±0.5 mm。
试验测量方法为:在试验船舶的船头和船尾分别安放GPS接收机,在码头的调控中心楼顶上的固定点上安放基准站GPS接收机进行长时间的观测,同时进行后处理差分测量(PPK)和实时动态差分测量(RTK),每个试验时,记录下该试验的开始和结束时间,然后根据该时间直接选取相关的定位数据。试验现场见图 6。

|
Download:
|
| 图 6 实船实验现场图 Fig. 6 The test site of full-scale sea trial | |
缩尺船模试验及实船试验结果与不同超大型船舶的UKC/T取值区间对比如表 10所示。
| 表 10 试验验证与理论计算对比表 Tab.10 The comparisons of experimental and theoretic results |
由表 10可分析,通过大量数据样本得出的理论计算区间范围较大,船模试验和实船试验验证可视为单样本验证,若单样本得出的区间值在理论计算区间内,则验证结论可判断为“一致”。由计算结果可知,船模试验、实船试验得出的取值范围均在理论计算区间内,因此可验证理论计算区间的有效性。在实际运用中,可根据港口通航环境状况对UKC/T进行取值。例如,超大型船舶的UKC/T取9.1%,较进出曹妃甸港UKC/T值10%的要求降低了9%。
4 结论1) 受限水域不同超大型船舶UKC应采取不同的取值范围,可实现对超大型船舶的UKC的个性化取值参考。
2) 船模试验、实船试验验证得出的结论可验证理论计算区间的有效性,存在的数据误差主要是由单样本验证产生。
3) 本文提出的UKC计算方法和优化取值方法,充分依托了2009-2016年曹妃甸港实测数据,为研究超大型船舶UKC取值提供了新的方法。
4) 对150 000~300 000 t超大型船舶UKC取值具有一定的普适性,在未来成果运用时,可考虑拓展到长江中下游及珠江水域。
同时随着船舶更大型化发展,对于近年新出现的400 000 t级大型船舶需进一步深入研究。
| [1] |
戴涛, 何志水. VLOC船舶航行在浅水域中的富余水深[J]. 航海技术, 2014(2): 8-11. DAI Tao, HE Zhishui. The study on the UKC of VLOC in shallow waterways[J]. Marine technology, 2014(2): 8-11. (  0) 0)
|
| [2] |
邹海峰. 横倾对满载VLCC安全富余水深的影响及对策[J]. 航海技术, 2017(3): 13-17. ZOU Haifeng. Influence and measures of heeling on the safe under keel clearance of full load VLCC[J]. Marine technology, 2017(3): 13-17. (  0) 0)
|
| [3] |
王春久. 超大型船舶在浅水域中下沉量与富余水深的探讨[J]. 航海技术, 2012(1): 2-7. WANG Chunjiu. The study on the squat and UKC of VLCC in shallow waterways[J]. Marine technology, 2012(1): 2-7. DOI:10.3969/j.issn.1006-1738.2012.01.001 (  0) 0)
|
| [4] |
HOWELL R. A port's perspective of evaluation and implementation of development opportunities with predicted under keel clearance. Implications for ports using predicted under keel clearance[C]//30th PIANC-AIPCN Congress, 2002: 1280-1292.
(  0) 0)
|
| [5] |
晏林.渤海海域VLCC安全富余水深研究[D].武汉: 武汉理工大学, 2013: 10-12. YAN Lin. Study on under keel clearance for VLCC in Bohai Sea[D]. Wuhan. Wuhan University of Technology, 2013: 10-12. (  0) 0)
|
| [6] |
张云鹏, 张吉平. 大型船舶沿岸航行富余水深的研究[J]. 大连海事大学学报, 2014, 40(3): 33-36, 41. ZHANG Yunpeng, ZHANG Jiping. Study on the under keel clearance of the ships sailing along the coast[J]. Journal of Dalian Maritime University, 2014, 40(3): 33-36, 41. DOI:10.3969/j.issn.1006-7736.2014.03.007 (  0) 0)
|
| [7] |
徐言民, 晏林, 许鹏, 等. 渤海海域超大型船舶安全航速限定标准研究[J]. 中国安全科学学报, 2013(1): 95-100. XU Yanmin, YAN Lin, XU Peng, et al. Study on safe speed model for ultra-large scale vessel navigating at Bohai Sea[J]. China safety science journal, 2013(1): 95-100. (  0) 0)
|
| [8] |
张云鹏.基于水动力数学理论及统计的船舶航行富余水深的研究[D].大连: 大连海事大学, 2013. ZHANG Yunpeng. Research on the theory of hydrodynamic mathematical and statistical for the Under Keel Clearance of sailing vessels[D]. Dalian: Dalian Maritime University, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2299908 (  0) 0)
|
| [9] |
Dynamic under-keel clearance. Information booklet. Australia: OMC International Marine Service Department, 2003.
(  0) 0)
|
| [10] |
GALOR W. Optimization of under-keel clearance during ship's manoeuvring in port water areas[C]. European Safety and Reliability Conference (ESREL 2007), July 2007, 1(6): 2681-2688.
(  0) 0)
|
| [11] |
PEDERSEN P, ZHANG S. Absorbed energy in ship collisions and grounding[J]. Journal of ship research, 2000, 44. (  0) 0)
|
| [12] |
SZYCA G. Comprehensive methods of the minimum safe under keel clearance valuation to the restricted tidal waters[J]. Transnav the international journal on marine navigation and safety of sea transportation, 2012, 6(1): 63-68. (  0) 0)
|
| [13] |
BRIGGS M J, SILVER A L, KOPP P J. Probabilistic model for predicting ship underkeel clearance:field and laboratory validation[J]. Coastal engineering journal, 2014, 56(2): 107-108. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


