陆地油气资源的减少与能源消耗的增加,促使石油工程行业陆续展开了对海洋油气的勘探开采。海洋隔水管作为海洋油气田开发中钻井工程系统的关键组成部分,其内部主要承受钻井液的循环流通,外部主要承受海流、波浪和内波的作用。涡激振动(vortex-induced vibration,VIV)作为隔水管的一种流固耦合响应形式,其周期性的振动会大大缩短隔水管系统的疲劳寿命,且“频率锁定”现象的出现会使振动加剧,甚至直接导致结构破坏[1]。
海洋内波是一种在密度稳定层化的海水内部所产生的波动,其波动频率在惯性频率与浮力频率两者之间,且最大振幅在海面以下。海洋内波在世界各海域中很常见,有大量的国内外实际观测资料表明我国南海海域为内波多发地。大振幅内波会在海洋结构物的局部区域上产生巨大的荷载和弯矩,使海洋结构物发生过载破坏[2]。
针对内波与海洋结构物之间的相互作用,Cai等[3]首次引用Morison经验公式计算孤立子内波对小尺度圆柱体的作用力和弯矩。叶春生等[4]借助Morison方程,在不同的水深及圆频率下,求得内波对圆柱体作用荷载的垂向分布特征,并与表面波和流作用下的圆柱荷载作了比对。Du等[5]也应用了这种方法求得内孤立波作用于海洋石油平台上的力,发现因内孤子立波所产生的流速大小为2.1 m/s剪切流,其作用于平台上的力与一个波长为300 m、波高18 m的表面波载荷相当。Cai等[6]研究了存在背景剪切流时内孤立波对圆柱体所产生的力和弯矩,发现圆柱体所受的作用力和弯矩会因背景流存在而大幅度增加。目前国内外针对内波导致的立管涡激振动研究较少,蒋武杰等[7]借助两层流体中内孤立波的mKdV理论与Morison公式,探究了立管在内孤立波及非均匀海流作用下的非线性动力响应。陈伟民等[8]探究了在内波导致的剪切流作用下大长径比海洋立管的涡激振动响应,开发出一种基于模态能量理论的多模态锁频的计算方法,并结合改进的尾流振子模型,对立管涡激振动响应进行了预测。
目前多数研究集中在内孤立波[9-11],并将内波致剪切流视为恒定流,没有考虑其波动性质,而实际内波场比较复杂,流场不是恒定不变的。本文利用一般意义上内波控制方程与刚盖边界条件求得存在背景流时的内波垂向结构及其水平往复剪切流分布情况,引入尾流振子模型模拟涡激振动时内波流场与隔水管的耦合作用,通过数值模拟求得了隔水管在背景流存在时的内波场中的涡激振动响应。
1 内波与隔水管理论模型 1.1 内波理论 1.1.1 内波控制方程在二维笛卡尔坐标系XOZ平面中,引入Boussinesq近似和线性近似条件,内波函数W(z)满足:
| $ W''\left( z \right) + k_3^2W\left( z \right) = 0 $ | (1) |
式中:k3为垂向波数,z轴取向上为正。当存在背景流时,垂向波数k3由下式定义:
| $ k_3^2 = k_h^2\frac{{{N^2} - {{\left( {w - {U_0}{k_h}} \right)}^2} + \left( {w - {U_0}{k_h}} \right){{U''}_0}/{k_h}}}{{{{\left( {w - {U_0}{k_h}} \right)}^2}}} $ | (2) |
式中:kh为内波水平波数;ω为内波圆频率;U0为背景流流速;U″0为背景流流速对z的二阶微分;N为内波浮频率,其定义为
| $ {N^2} = - \frac{{\rm{g}}}{{\rho \left( z \right)}}\frac{{{\rm{d}}\rho \left( z \right)}}{{{\rm{d}}z}} $ | (3) |
式中:g为重力加速度,ρ为海水密度。
联立方程(1)~(3)可以得到内波的波函数,然而,通常很难获得解析解,一般采用Thomson-Haskell数值方法获得其频散关系和波函数。考虑刚盖与固壁边界条件时,海面及海床处有W(0)=W(-H)=0。
采用Thomson-Haskell法求解内波控制方程时,假定内波浮频率为关于海水深度的连续函数,并根据浮频率特性将海水分层,各分层间的浮频率为定值,从而得到对应各分层方程的解析解,由边界条件及各层间界面的连续性特征,解出所有分层中内波方程的特征值,进而求得各特征函数的数值解。
1.1.2 内波速度根据微幅波理论,内波水质点的垂向速度可表示成以下形式:
| $ {\rm{w}} = AW\left( z \right)\cos \left( {{k_h}x - \omega t} \right) $ | (4) |
式中:A为海洋内波水质点垂向速度最大幅值,W(z)为垂向速度归一化的无量纲幅值在整个水深范围内的分布。依据海洋内波水质点的垂向位移η和垂向速度w的关系可得:
| $ \eta = \int {w{\rm{d}}t} = - \frac{{AW\left( z \right)}}{\omega }\sin \left( {{k_h}x - \omega t} \right) $ | (5) |
式中:AW(z)/ω表示内波水质点在整个水深范围内的最大垂向振动位移分布情况,即是内波振幅。则一旦内波最大振幅由测量得知,即可求得内波整个速度场分布情况。
根据二维不可压缩流体的连续性方程,得到内波水质点的水平速度:
| $ {u_h} = - \frac{A}{{{k_h}}}\varphi \left( z \right)\sin \left( {{k_h}x - \omega t} \right) $ | (6) |
式中
本文在分析隔水管的横向(YOZ平面内)运动时,考虑隔水管顶部张力、内外流体压力的影响,由参考文献[12-13]可得到隔水管振动方程:
| $ \begin{array}{*{20}{c}} {m\ddot v + \left( {c + c'} \right)s'\dot v + 2{m_i}V\frac{{\dot v'}}{{s'}} + {m_i}\dot v\frac{{v'}}{{s'}} + }\\ {\left( {{m_i}\frac{{{V^2}}}{{{{s'}^2}}} - {T_e}} \right)v'' + EI\frac{{{v^{\left( 4 \right)}}}}{{{{s'}^5}}} = {F_l}s'} \end{array} $ | (7) |
式中:m=mr+mi+ma,mr为单位长度上的隔水管质量,mi为单位长度管内流体的质量,ma=CaπρeD2/4为单位长度上流体附加质量,Ca为附加质量系数,ρe为管外流体的密度,D为隔水管外径;c为结构阻尼,c′为流体附加阻尼;
| $ {T_e} = EA\varepsilon + 2\upsilon \left[ {{P_e}{A_e}{\mathop{\rm sgn}} \left( {H - z} \right) - {P_i}{A_i}} \right] $ | (8) |
式中:A为隔水管横截面面积,P为流体静压力,下标i、e分别代表隔水管内、外截面,E为弹性模量,I是隔水管截面惯性矩,υ为泊松比,sgn为符号函数,涡激升力Fl=
假设隔水管的两端铰支,边界条件为
| $ \left\{ \begin{array}{l} u\left( {0,t} \right) = u\left( {L,t} \right) = 0\\ u''\left( {0,t} \right) = u''\left( {0,t} \right) = 0 \end{array} \right. $ | (9) |
非线性尾流振子在满足VanderPor方程时,可用于模拟旋涡脱落对圆柱体产生的作用力,其中Matteo Luca Facchinetti尾流振子模型[14]被广泛使用于圆柱体涡激振动。此模型考虑与结构运动方程的耦合作用及结构与流体之间的线性耦合作用,采用模拟振子运动的VanderPor方程来展示旋涡脱落的特征。该尾流振子的振动方程为
| $ \ddot q + \varepsilon {w_s}\left( {{q^2} - 1} \right)\dot q + w_s^2q = F $ | (10) |
式中:q=2CL/CL0为升力振子系数,CL0为固定圆柱体在流体中的横向升力系数的幅值,ε是一个与非线性相关的小参数,ωs=2πStU/D为旋涡脱落频率;St=0.2为Strouhal数,主要取决于结构物剖面的形状的雷诺数Re,当300 < Re < 3×105时处于亚临界状态St=0.2;F=A
| $ \begin{array}{*{20}{c}} {q\left( t \right) = }\\ {2\left[ {1 + \frac{{AR}}{\varepsilon }\frac{{\left( {2\xi \delta + \gamma /\mu } \right){\kappa ^2}}}{{{{\left( {{\delta ^2} - {\kappa ^2}} \right)}^2} + {{\left( {2\xi \delta + \gamma /\mu } \right)}^2}{\kappa ^2}}}} \right]\cos \left( {{\omega _v}t} \right)} \end{array} $ | (11) |
式中:
| $ \xi = \frac{c}{{2m{\omega _n}}}\int_0^L {{\phi ^2}s'{\rm{d}}z} /\int_0^L {{\phi ^2}{\rm{d}}z} + \frac{{{m_i}V}}{{m{\omega _n}}}\int_0^L {\phi \phi '{\rm{d}}z} /\int_0^L {{\phi ^2}{\rm{d}}z} $ |
δ=ωn/ωs为频率比,κ=ωv/ωs为失谐比,其中ωn为隔水管固有频率,ωv为振动频率。κ可以表示为
| $ \begin{array}{*{20}{c}} {{\kappa ^6} - \left[ {1 + 2{\delta ^2} - {{\left( {2\xi \delta + \gamma /\mu } \right)}^2}} \right]{\kappa ^4} + AR\left( {{\kappa ^2} - {\delta ^2}} \right){\kappa ^2} - }\\ {\left[ { - 2{\delta ^2} + {{\left( {2\xi \delta + \gamma /\mu } \right)}^2} - {\delta ^4}} \right]{\kappa ^4} - {\delta ^4} = 0} \end{array} $ | (12) |
对隔水管振动方程和尾流振子方程进行集成,得到隔水管振动方程和尾流振子方程的有限元形式为
| $ \mathit{\boldsymbol{M\ddot u}} + \mathit{\boldsymbol{C\dot u}} + \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{Fq}} $ | (13) |
| $ \mathit{\boldsymbol{\bar M\ddot q}} + \mathit{\boldsymbol{C\dot q}} + \mathit{\boldsymbol{\bar Kq}} = \mathit{\boldsymbol{\bar F\ddot u}} $ | (14) |
式中:M、C、K、F分别为隔水管总体质量矩阵、阻尼矩阵、刚度矩阵以及外载荷矩阵,M、C、K、F分别为尾流振子模型拟质量矩阵、拟阻尼矩阵、拟刚度矩阵以及拟外载荷矩阵。
式(13)、(14)代表了隔水管涡激振动的自激特性,尾流振子的振动会引发管道的振动,同时管道的振动又会对尾流产生影响。在求解方程(13)、(14)时,可采用Newmark时程分析方法直接积分。
2.2 模型验证本节计算作为存在背景流的内波场中隔水管涡激振动分析的对比基础,并用于检验有限元计算方法和程序的正确性。在水深300 m海域中存在流速为0.12 m/s的均匀流,海水平均密度为1 025 kg/m3,该隔水管长320 m,外径0.26 m,壁厚0.03 m,材料密度7 850 kg/m3,弹性模量2.07×1011 Pa,泊松比0.3,顶端张力476.198 kN,内流速度0 m/s。根据均匀背景流流速以及隔水管参数,计算了隔水管前5阶自振频率(fn=ωn/2π),并得出在此海流中的涡激泄放频率为0.092 3,隔水管自振频率及约化速度如表 1所示。
| 表 1 涡激振动相关参数 Tab.1 Parameters of drilling riser VIV |
约化速度Vr=U/fnD是一个无因次参数,主要影响结构物的涡激振动响应幅值,试验研究表明[15],当约化速度位于4.0~8.0,易出现隔水管的锁定现象,此时其振幅会出现大幅度的增加。从表 2中可以看出,隔水管在此海流中的涡激泄放频率处于隔水管的第1阶和第2阶自振频率之间,当取第1阶隔水管自振频率计算时,其约化速度为6.72,位于4.0~8.0;而当取第2阶自振频率以上计算时,其约化速度均小于4.0,这说明隔水管在此背景流中会与流体在第1阶模态频率处发生涡激振动的“频率锁定”现象,这时其振动频率大致等同于第1阶自振频率。
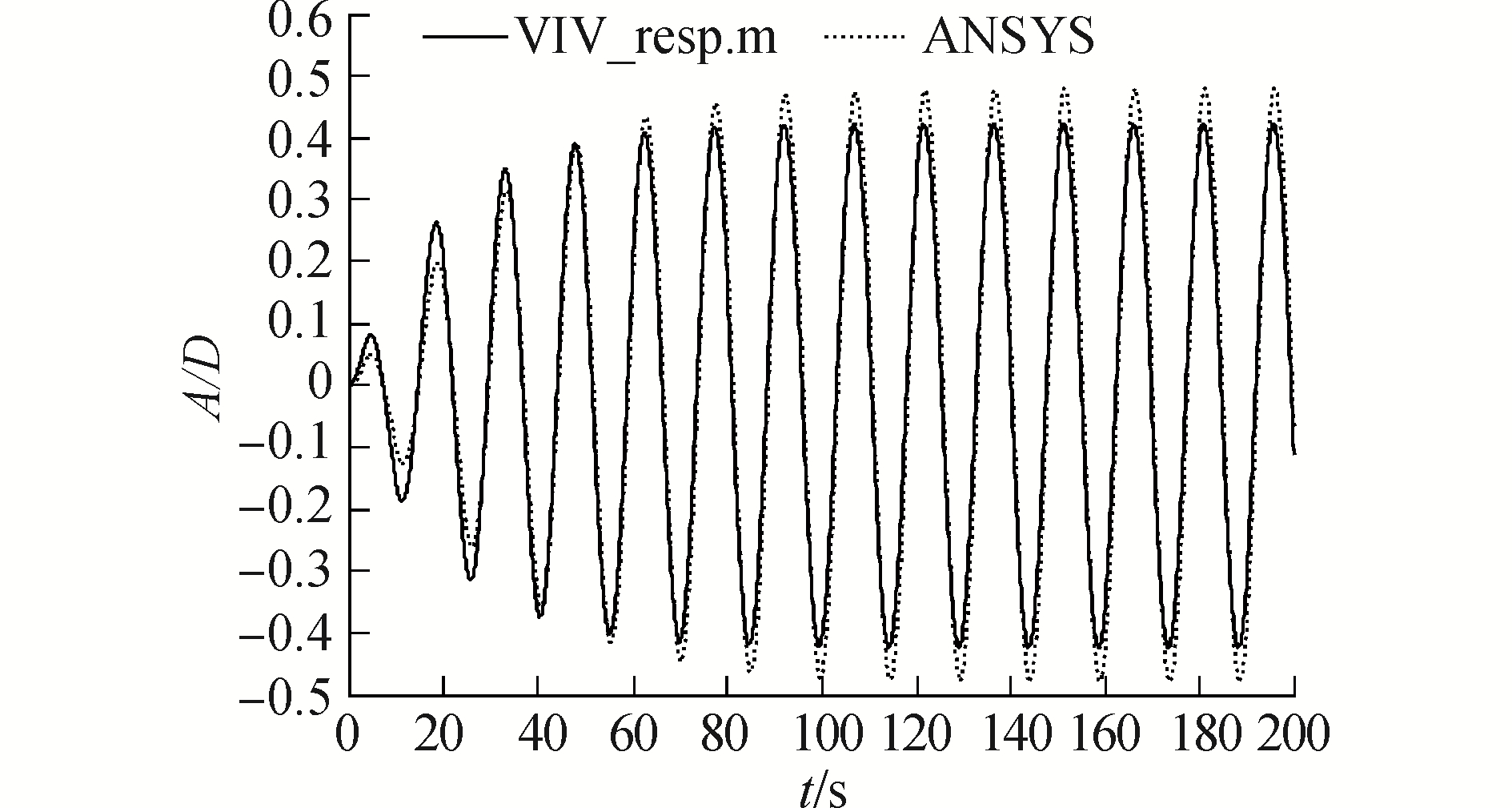
根据隔水管和流体参数,直接带入到涡激振动计算自编VIV_resp.m程序中,即可得到隔水管在均匀流中的涡激振动情况。同时采用ANSYS有限元软件的瞬态动力学计算模块,求解隔水管涡激振动的响应情况,以此验证涡激振动计算程序的正确性。取得两种计算工具中隔水管的无量纲最大相应幅值(A/D,响应幅值与隔水管外径比值,也称约化振幅,最大值一般位于隔水管中段)的时间历程曲线如图 1所示,图 2为位移功率谱分析(PSD)分析结果。
|
Download:
|
| 图 1 均匀流中的隔水管涡激振动约化振幅时程曲线 Fig. 1 Time histories of reduced displacement A/D of VIV in mean current | |

|
Download:
|
| 图 2 均匀流中隔水管涡激振动频率 Fig. 2 PSD distribution of drilling riser displacement amplitude of VIV in mean current | |
从ANSYS软件结果与自编程序(VIV_resp.m)计算结果对比来看,两者计算得到的约化位移时间历程曲线较为吻合,说明涡激振动方程是正确的并且自编涡激振动程序是可靠的。从图 2中可以看出,自编程序以及ANSYS软件得到的隔水管位移功率谱分析结果相同,隔水管的涡激振动频率都为f=0.070 Hz,和隔水管的自振频率f1=0.069 Hz非常接近,说明隔水管在此背景流中发生了流体与隔水管第1阶模态耦合的共振现象。
根据上述的分析可知,当流速为0.12 m/s的均匀流经过隔水管时,隔水管会在横向上产生第1阶模态的涡激共振现象,出现大位移响应,其无量纲振动幅值约为0.42,振动频率大约与隔水管第1阶自振频率相等。
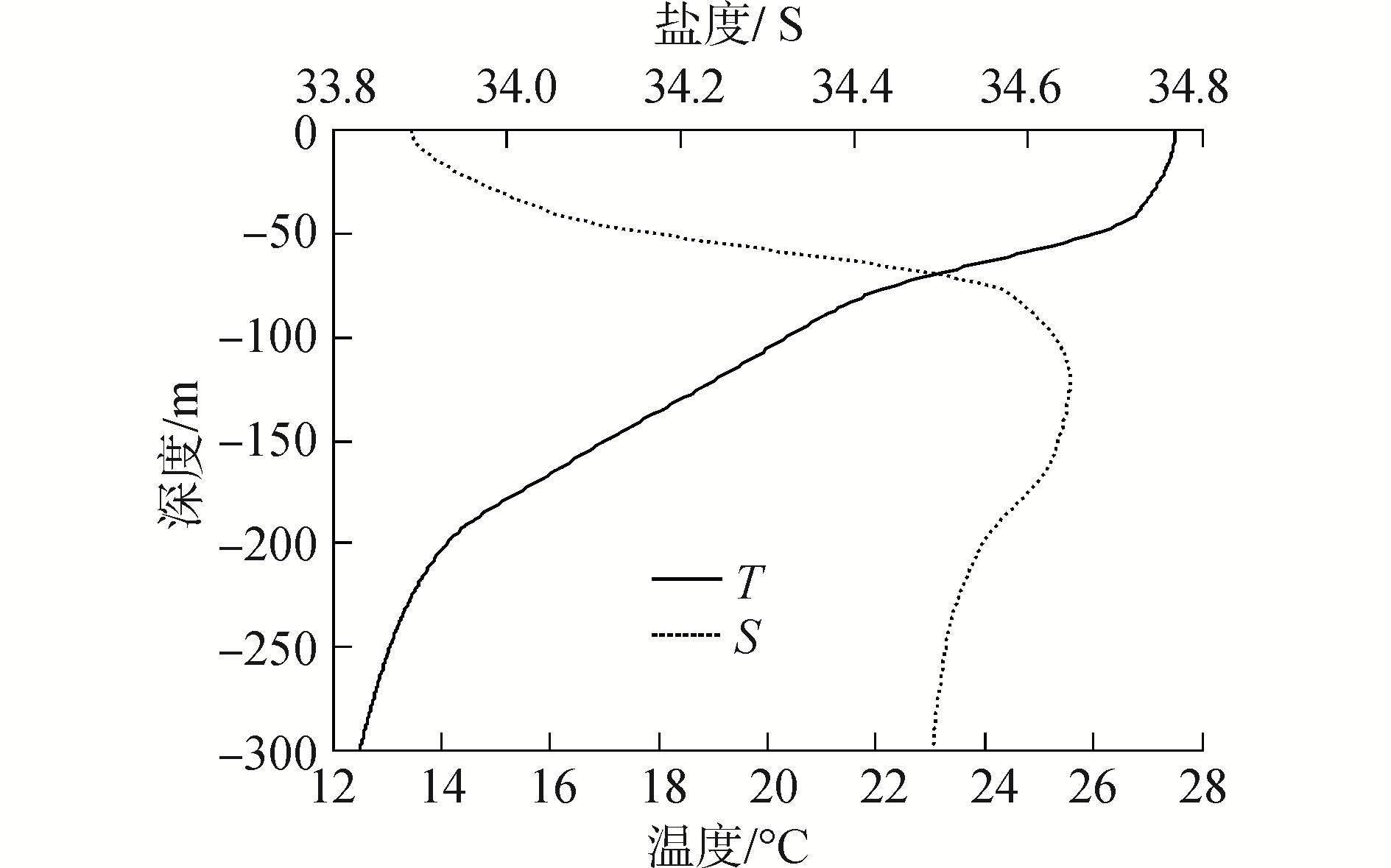
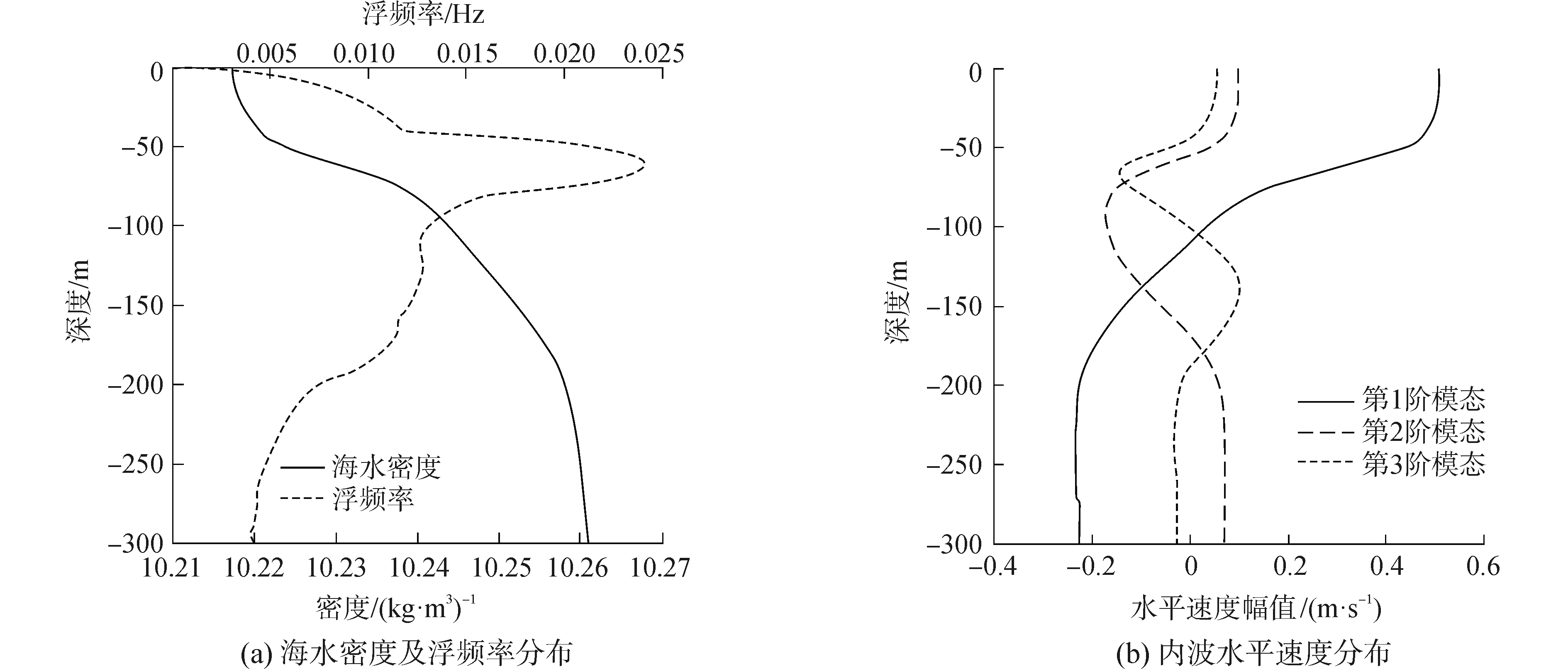
3 内波场中隔水管涡激振动分析 3.1 内波特性本文中所使用海洋数据来源于南海海洋科学数据库,选取2005年9月在南海北部开放航次中“试验3”号科考船在南海E502站(112°15.421′N;18°44.937′E)测量的温盐数据(conductivity-temperature-depth,CTD),如图 3所示,对CTD温盐数据进行处理计算后得到海水的密度和浮频率分布,结果如图 4(a)所示,可以看出存在海水密度沿水深变化梯度较大且稳定的密跃层。
|
Download:
|
| 图 3 南海E502站温、盐剖面 Fig. 3 Temperature and salinity profile on Station E502 | |
|
Download:
|
| 图 4 实际海水密度和浮频率分布情况及内波前三阶模态水平速度幅值 Fig. 4 Distribution of density, buoyancy frequency and the amplitude of internal waves corresponding to the first three modes | |
本文选取振幅为30 m,周期为20 min的内波,通过Thomson-Haskell法可以求得内波的前三阶模态的水平波数分别为0.003 449 4、0.011 142、0.015 815。海洋内波在传播过程中,不同模态的内波可同时存在,由于反射及其他因素对内波的影响下,高阶模态内波的能量必然会减小,相应振幅也会降低。本文中为了讨论不同模态内波对海洋隔水管的作用,在这里假设认为第2、3阶模态内波振幅只有第1阶的1/2和1/3大小。基于此便可以计算内波前三阶模态的水平速度幅值。内波的水平速度如图 4(b)所示,从图中我们可以看出,内波水平速度方向在不同海水层中是不同的,即内波在水平方向上生成剪切流。
Richardson数可表征流体流动的稳定性,用于判断背景流中内波是否稳定存在,其中Richardson数为Ri(z)=[N(z)/U′0(z)]2。海水中浮频率N越大,并且背景流在垂直方向上的流速梯度U′0越小,则流场越稳定,一般来说当有Ri>1/4时,内波就能在背景流场中稳定存在。本文中选用均匀背景流,由于均匀流中流速沿深度变化为零,此时Richardson数为无穷大,则可知内波在该背景流中始终能稳定存在。
本文考察了前3阶模态内波对隔水管在存在背景流的内波场中涡激振动的影响情况,背景流仍为流速为0.12 m/s的均匀流。根据不同模态内波场中内波水质点水平速度分布情况计算了整个流场的叠加速度及隔水管在5个内波周期内的涡激振动响应情况,提取隔水管在1/4、1/2及3/4管长位置处的位移-时间历程曲线并对其做位移功率谱分析。
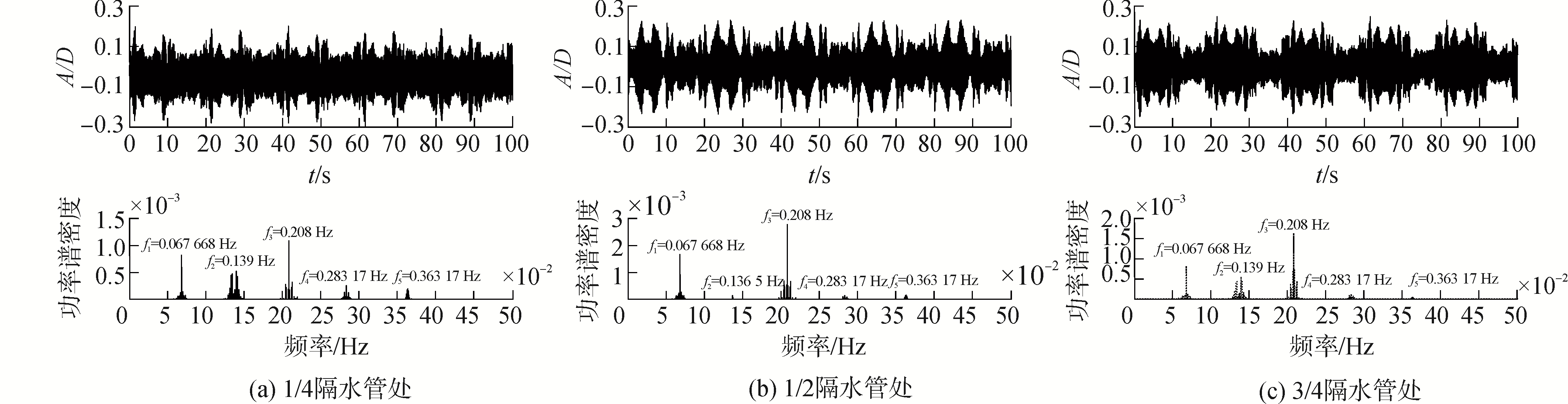
3.2 不同模态内波场中隔水管涡激振动情况图 5为第1阶模态内波场中隔水管涡激振动响应时不同位置处的位移时程曲线及功率谱密度分布情况。从隔水管涡激振动时程曲线来看,在大尺度时间范围内,具有一定的周期性,其循环周期与内波周期相同;另外,在隔水管1/4、1/2以及3/4长度位置处,其最大约化振动幅值均约为0.25,与单纯均匀流相比,隔水管最大振动幅值减小,且不再稳定振动。这一方面是由于内波致水平剪切流与背景流叠加后引起锁振区间的变化,隔水管与流体不再发生稳定频率锁定造成的;另一方面由于隔水管振动从低阶模态发展至复合高阶模态,与主振型相比,复合模态呈现局部振动,而最大振动幅值不一定发生在隔水管中间位置。
|
Download:
|
| 图 5 第1模态内波场中隔水管不同位置处涡激振动位移时程曲线及其功率谱密度 Fig. 5 Time histories and PSD of VIV displacement under the 1st mode internal waves and currents | |
从隔水管响应位移功率谱来看,隔水管在第1模态内波和背景流共同作用下,其涡激振动频率主要集中在0.067 7、0.139、0.208以及0.283 Hz左右,基本与隔水管前4阶自振频率相同,这进一步说明与单纯在均匀流场中相比,隔水管发生了多模态的共振。隔水管涡激共振发展到了第4阶模态自振频率处,其涡激振动不仅产生了多种模态共振情况,同时内波致水平剪切流也使得立管的振动扩展到了高阶模态,导致立管发生高频振动,加速了立管的疲劳破坏。另外,在隔水管不同位置处,其振动情况也是不同的,如隔水管中间位置处,以第1、3阶模态为主;而在1/4、3/4长度位置处,前3阶模态振动更为显著。
图 6为第2阶模态内波场中隔水管不同位置处的位移时程曲线及功率谱密度分布情况。与第1阶模态内波场中隔水管振动相似,在大时间尺度上存在与内波周期相同的循环,但振动曲线大不相同,并且在隔水管1/4、3/4位置处,最大约化振动幅值要比第1阶内波模态时稍小,约为0.2;而在隔水管中间位置处,其最大约化振动幅值约为0.25,变化不大。从频谱图可以看出,振动主要集中在前3阶模态,并且第1、3阶模态振动更为显著。

|
Download:
|
| 图 6 第2模态内波场中隔水管不同位置处涡激振动位移时程曲线及其功率谱密度 Fig. 6 Time histories and PSD of VIV displacement under the 2nd mode internal waves and currents | |
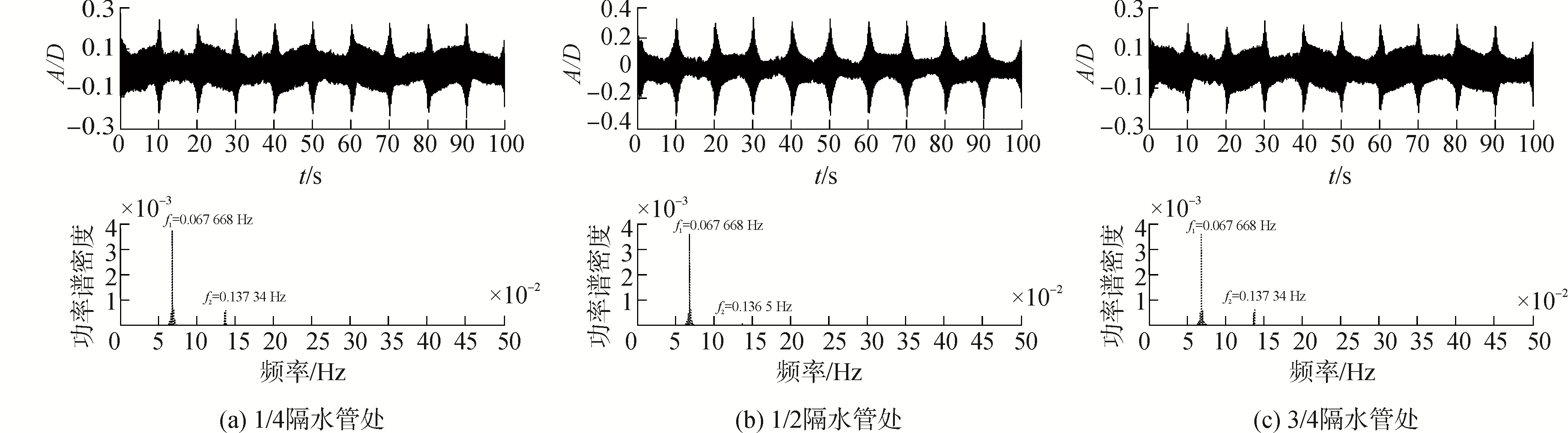
图 7为第3阶模态内波场中隔水管不同位置处的位移时程曲线及功率谱密度分布情况。从隔水管振动时程曲线来看,更为明显的出现与内波周期一致的循环周期。从最大振动幅值来看,在隔水管1/4、3/4位置处,其最大约化振动幅值约为0.25;在隔水管中间位置处,最大约化振动幅值约为0.35,已经趋近于均匀流中隔水管最大涡激振动幅值。从频谱图可以看出,振动主要集中在1阶自振频率处,此时隔水管以低阶振动模态为主,主要是由于高阶内波的能量大部分集中在密跃层中,隔水管涡激振动影响已经很小了。
|
Download:
|
| 图 7 第3模态内波场中隔水管不同位置处涡激振动位移时程曲线及其功率谱密度 Fig. 7 Time histories and PSD of VIV displacement under the 3rd mode internal waves and currents | |
1) 内波致水平剪切流与背景流叠加后引起锁振区间的变化,流场波动致使隔水管与流体共振不再锁定在固定频率范围,涡激振动难以充分发展,隔水管响应幅值减小。
2) 高阶模态内波能量主要集中在密跃层中且能量较小,对隔水管涡激振动影响较小,低模态内波对隔水管涡激振动影响更为显著。
3) 内波致水平剪切流虽然一定程度上抑制了隔水管整体涡激振动,但促发了隔水管的多模态涡激共振现象,导致隔水管发生复合模态振动,其影响更为复杂。
| [1] |
宋磊建, 付世晓, 任铁, 等. 均匀流下柔性立管涡激振动响应及涡激力载荷特性研究[J]. 振动与冲击, 2017, 36(22): 14-21. SONG Leijian, FU Shixiao, REN Tie, et al. Structural responses and vortex-induced force of flexible risersundergoing vortex-induced vibration in uniform flow[J]. Journal of vibration and shock, 2017, 36(22): 14-21. (  0) 0)
|
| [2] |
CHAKRABARTI S K. Handbook of offshore engineering[M]. Plainfield, Illinois, USA: Offshore Structure Analysis, Inc., 2005: 105-106.
(  0) 0)
|
| [3] |
CAI Shuqun, LONG Xiaomin, GAN Zijun. A method to estimate the forces exerted by internal solitons on cylindrical piles[J]. Ocean engineering, 2003, 30(5): 673-689. DOI:10.1016/S0029-8018(02)00038-0 (  0) 0)
|
| [4] |
叶春生, 沈国光. 海洋内波对小尺度圆柱体作用力的分析与计算[J]. 天津大学学报, 2005, 38(2): 102-108. YE Chunsheng, SHEN Guoguang. Numerical calculation and analysis about internal wave's force on small-scale cylinder[J]. Journal of Tianjin University, 2005, 38(2): 102-108. (  0) 0)
|
| [5] |
DU Tao, SUN Li, ZHANG Yijun, et al. An estimation of internal soliton forces on a pile in the ocean[J]. Journal of ocean university of China, 2007, 6(2): 101-106. DOI:10.1007/s11802-007-0101-y (  0) 0)
|
| [6] |
CAI Shuqun, LONG Xiaomin, WANG Shengan. Forces and torques exerted by internal solitons in shear flows on cylindrical piles[J]. Applied ocean research, 2008, 30(1): 72-77. DOI:10.1016/j.apor.2008.03.001 (  0) 0)
|
| [7] |
蒋武杰, 林忠义, 尤云祥, 等. 内孤立波与非均匀海流共同作用下顶张立管动力特性[J]. 水动力学研究与进展, 2012, 27A(4): 424-435. JIANG Wujie, LIN Zhongyi, YOU Yunxiang, et al. Dynamic characteristics of a top tension riser under combined internal solitary wave and non-uniform current[J]. Chinese journal of hydrodynamics, 2012, 27A(4): 424-435. DOI:10.3969/j.issn.1000-4874.2012.04.009 (  0) 0)
|
| [8] |
陈伟民, 郑仲钦, 张立武, 等. 内波致剪切流作用下深海立管的涡激振动[J]. 工程力学, 2011, 28(12): 250-256. CHEN Weimin, ZHENG Zhongqin, ZHANG Liwu, et al. Vortex-induced vibration of deepwater flexible riser experencing internal-wave-induced shera flow[J]. Engineering mechanics, 2011, 28(12): 250-256. (  0) 0)
|
| [9] |
XIE Jieshuo, JIAN Yongjun, YANG Liangui. Strongly nonlinear internal soliton load on a small vertical circular cylinder in two-layer fluids[J]. Applied mathematical modelling, 2010, 34(8): 2089-2101. DOI:10.1016/j.apm.2009.10.021 (  0) 0)
|
| [10] |
SONG Z J, TENG B, GOU Y, et al. Comparisons of internal solitary wave and surface wave actions on marine structures and their responses[J]. Applied ocean research, 2011, 33(2): 120-129. DOI:10.1016/j.apor.2011.01.003 (  0) 0)
|
| [11] |
刘碧涛, 李巍, 尤云祥, 等. 内孤立波与深海立管相互作用数值模拟[J]. 海洋工程, 2011, 29(4): 1-7. LIU Bitao, LI Wei, YOU Yunxiang, et al. Numerical simulation of interaction of internal solitary waves with deep-sea risers[J]. The ocean engineering, 2011, 29(4): 1-7. (  0) 0)
|
| [12] |
GUO Haiyan, WANG Shuqing, WU Jining, et al. Dynamic characteristics of marine risers conveying fluid[J]. China ocean engineering, 2000, 14(2): 153-160. (  0) 0)
|
| [13] |
GUO Haiyan, WANG Yuanbin, FU Qiang. The effect of internal fluid on the response of vortex-induced vibration of marine riser[J]. China ocean engineering, 2004, 18(1): 11-20. (  0) 0)
|
| [14] |
FACCHINETTI M L, DE LANGRE E, BIOLLEY F. Coupling of structure and wake oscillators in vortex-induced vibrations[J]. Journal of fluids and structures, 2004, 19(2): 123-140. DOI:10.1016/j.jfluidstructs.2003.12.004 (  0) 0)
|
| [15] |
KHALAK A, WILLIAMSON C H K. Dynamics of a hydroelastic cylinder with very low mass and damping[J]. Journal of fluids and structures, 1996, 10(5): 455-472. DOI:10.1006/jfls.1996.0031 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


