多波束测深系统集声呐系统、计算机技术、导航定位技术、姿态补偿技术和后期数据处理技术于一体[1]。其作业过程在测量平台不断运动的状态下进行,测量平台在海浪、海流、风等复杂海洋环境影响下使得多波束测深系统采集的数据中难免出现假信号,其存在将使测量的海底产生虚假地形,使得绘制的海图地形图与实际的海底地形存在差异,影响航行安全。在进行水深数据处理时,必须进行相应的异常值检测与滤波处理来获取真实的深度数据。
现有的水深数据滤波方法主要有交互式滤波和自动滤波两种[2]。针对交互式滤波方法耗时长、效率低(内外业工作量比例大约为3:1),无法满足大量数据处理情况,专家们提出许多自动滤波方法。黄谟涛等[3]将原来用于检验异常值的推值比较法与抗差估计结合起来,提出一种基于抗差估计的选权迭代插值比较检验法,对异常数据的剔除取得了较好的效果;黄贤源等[4]基于最小二乘支持向量机算法构造海底趋势面,通过调整LS-SVM的参数可以构造合理的海底趋势面达到较好的异常值探测效果,但是其对训练样本的选取依赖较强,训练样本选取不好的情况下,剔除效果并不理想;黄辰虎等[5]将CUBE算法应用于大批量多波束测深粗差剔除工作中,证明了CUBE算法在多波束粗差剔除中的高效性,但是该算法对船配置文件中的各个参数设置要求较高,在使用过程中需要反复调整,才能达到较好的效果;阳凡林等[6]提出了一种基于中值滤波、局部方差检测和小波分析相结合的方法来探测异常数据,很好地定位异常数据过滤噪声,但是小波阈值及中值滤波窗口的选择是不确定性的,不同海底地形不尽相同;董江等[7]将趋势面滤波方法应用于多波束粗差剔除中,取得了较好的效果,但是趋势面滤波在复杂海底地形情况下去噪效果并不理想。
Huang等[8]提出一种新的数据处理方法,即经验模态分解法,该方法能够保留数据本身的特点,将信号中不同尺度的波动或趋势逐级分解开来,产生一系列本征模态函数。关于经验模态分解方法的研究,专家们做了大量的工作[9-14],但是该方法在海洋测深数据处理方面的应用较少。
本文将二维经验模态分解方法引入多波束水深数据异常值探测工作中,试图构建合理的海底地形趋势面达到较好的异常数据探测效果,并在原有经验模态分解方法的基础上,采用径向基函数插值方法进行上、下包络面插值,同时利用小波分析方法对提取的本征模态函数分析提取有用信号。
1 二维经验模态方法 1.1 方法原理从本质上讲,经验模态分解方法是对一个信号进行平稳化处理,其结果是将信号中不同尺度的波动或趋势逐级分解开来,产生一系列具有不同特征尺度的数据序列,每一个序列称为一个本征模态函数(intrinsic mode function, IMF)[14]。其总体思路是通过上、下包络面的平均值去确定“瞬时平衡位置”,从而提取出本征模态函数。其具体数据处理过程如下:
1) 提取原始信号f(x, y)的极大值和极小值点,并对其进行插值拟合计算上、下包络面max(x, y)和min(x, y);计算上、下包络面均值m(x, y)=[min(x, y)+max(x, y)]/2。
2) 原始数据f(x, y)减去计算得到的包络面均值得到H1(x, y)=f-m。判断H1(x, y)是否为本征模态函数,若是则作为第一阶本征模态函数,若不是则令f(x, y)=H1(x, y),重复前步过程直至满足条件。最终得到第一阶本征模态函数:IMF1=H1(x, y)。
3) 将得到的IMF1从原始信号中分离出去,得到残余量R1=f(x, y)-IMF1,将R1作为新的数据,重复循环上述过程,直至满足筛分终止条件[10]。
1.2 关键问题研究 1.2.1 局部极值点提取二维经验模态分解过程受到很多因素影响,其中局部极值点的提取是非常重要的问题。本文在原有经验模态方法的基础上采用邻近窗口法提取局部极值点。
假设有样本数据X代表待处理的某区域数据,包含数据量m×n,表示成矩阵形式如下
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1n}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2n}}}\\ \cdots&\cdots&\cdots&\cdots \\ {{x_{m1}}}&{{x_{m2}}}&{}&{{x_{mn}}} \end{array}} \right] $ | (1) |
假设邻近窗口法窗口大小为s×s(s≠1),xij为待判断点,xpq为其窗口范围内的邻近点,极值点判断准则如下
| $ {x_{ij}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \max \left( {x,y} \right)\\ \min \left( {x,y} \right) \end{array}&\begin{array}{l} {x_{ij}} \ge {x_{pq}}\\ {x_{ij}} < {x_{pq}} \end{array} \end{array}} \right., $ |
其中
经验模态分解方法的关键在于,能否拟合出精确的上下包络面。Huang等[8]提出采用三次样条插值来拟合非均匀取样数据,三次样条插值方法虽然速度快,但是其局部数据插值误差较大,影响拟合的包络面精度。
径向基函数是一个取值仅仅依赖离原点距离的实值函数,能够逼近任意的非线性曲线,处理系统内的难以解析的规律,具有良好的泛化能力,成功应用于非线性函数逼近、图像处理、信息处理等。为了提高包络面插值精度,改进原有经验模态方法,采用径向基函数插值算法进行上下包络面插值。
径向基函数插值法属于完全内插方法,其插值表面经过每一个已知样点,同时使表面曲率最小。其插值公式如下
| $ S\left( x \right) = {p_m}\left( x \right) + \sum\limits_{i = 1}^N {{\lambda _i}\phi \left( {\left\| {x - {x_i}} \right\|} \right)} $ | (2) |
式中:S(x)是插值结果,pm是低阶线性多项式,λi是径向基函数系数,ϕ是核函数,常用的核函数有:线性函数(Linear)、三次样条函数(Cubic)、复二次函数(Multiquadric)、高斯函数(Gaussian)等,将其函数表达式列于表 1。
| 表 1 径向基函数的不同核函数及表达式 Tab.1 Different kernel functions of radial basis interpolation and its expression |
为了比较不同核函数对于径向基插值结果的影响,选取若干离散点进行不同核函数径向基插值计算,计算结果如表 2所示。
| 表 2 几种核函数对径向基插值结果的比较 Tab.2 Comparison results of several kernel functions of radial basis interpolationm |
比较表 1~2发现,总体上径向基函数插值方法插值精度较高,几种核函数中,三次样条核函数插值精度处于分米级;复二次核函数和线性核函数插值精度处于厘米级;而高斯核函数插值精度处于毫米级。本文径向基函数插值方法中选取高斯函数作为核函数以提高插值精度。
式(2)的矩阵形式表示如下
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{B}}&\mathit{\boldsymbol{P}}\\ {{\mathit{\boldsymbol{P}}^{\rm{T}}}}&{\bf{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\lambda }}\\ \mathit{\boldsymbol{C}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{H}}\\ {\bf{0}} \end{array}} \right] $ | (3) |
其中,
bij表示不同核函数对应系数,
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{H}}\\ {\bf{0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&\mathit{\boldsymbol{P}}\\ {{\mathit{\boldsymbol{P}}^{\rm{T}}}}&{\bf{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\lambda }}_0}}\\ {{\mathit{\boldsymbol{C}}_0}} \end{array}} \right] $ | (4) |
采用反距离加权插值法、克里格插值法、径向基函数插值法、三角剖分插值法和自然邻点插值法分别对待插值点进行实验比对,值得说明的是待插值点是依据前文方法从原始数据中提取得到的局部极大值点,各个方法的插值结果如图 1所示。
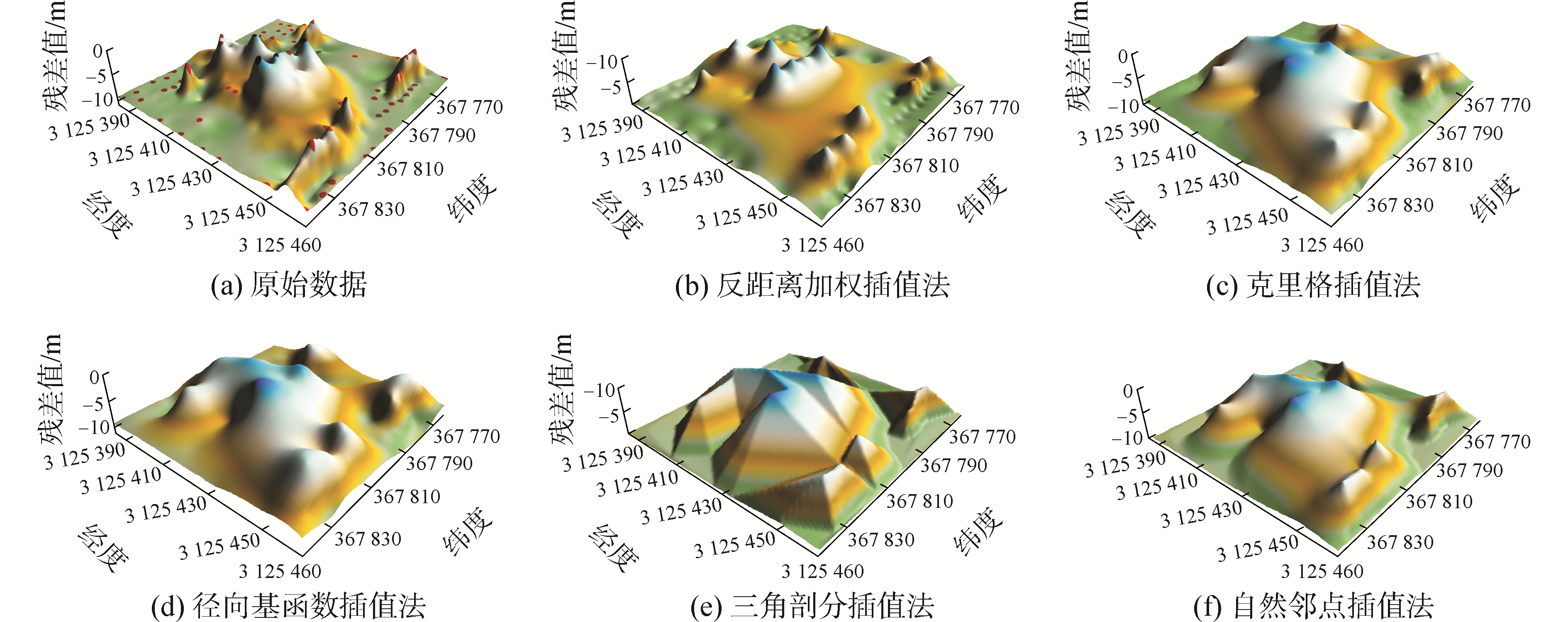
|
Download:
|
| 图 1 包络面插值方法比较 Fig. 1 Comparison of interpolation method of envelope surface | |
插值过程中的格网为100×100,图 1展示了不同插值方法的插值结果。其中,图 1(e)三角剖分插值方法构建的曲面不够光滑;图 1(f)虽然能够构建光滑曲面,但是其插值精度相对较差。为进一步比较不同插值方法的插值效果,将不同方法的插值精度列于表 3。表 3可以看出,不同插值方法对曲面插值精度影响很大:克里格、三角剖分、自然邻点插值法的插值精度相近,处在分米量级;反距离加权和径向基函数插值法的插值精度最高,处在厘米量级。径向基函数插值法是在种插值方法中插值精度最高。
| 表 3 不同插值方法插值精度比较 Tab.3 Comparison of interpolation precision of several interpolation methodsm |
为了进一步比较不同方法之间的插值结果,以原始插值点作为参考,绘制差值三维图如图 2所示。

|
Download:
|
| 图 2 差值三维图 Fig. 2 Three-dimensional diagram of difference value | |
多波束测深数据自动滤波方法的关键是如何合理设置算法及调整参数来最大限度的探测和剔除异常数据。本文利用二维经验模态分解方法探测异常数据,实质上是基于原始数据本身构建合理精确的海底地形趋势面,并利用残差中误差进行异常值的筛选。
利用经验模态分解方法将信号中不同尺度的趋势逐级分解开来的特点,对多波束水深数据进行二维经验模态分解,通过筛分过程产生有限个本征模态函数以及残余量表示为
| $ D\left( t \right) = \sum\limits_{i = 1}^n {{\rm{IM}}{{\rm{F}}_i}} + R $ | (5) |
式中R为残余量。
经验模态分解能够将信号中不同频率的趋势逐级分解开来,分解产生的IMF代表水深数据的不同频率特征,由高频至低频依次为IMF1、IMF2、IMF3等,残余量R中的频率最低。通常认为,噪声处于高频部分的第一、二级本征模态函数中,很多基于经验模态的去噪方法中直接将第一、二级本征模态函数去除。事实上,剥离出来的IMF仍然包含有用信号,直接去除会导致有用信号缺失影响趋势面构造效果。本文尝试利用小波变换方法对IMF进行分析分离出IMF中的有用信号,重新建立更加精确合理的海底地形趋势面。与其他方法相比较,小波变换具有自适应性强、快速灵活的特点,其提取有用信号的基本思路如图 3所示。

|
Download:
|
| 图 3 小波变换提取信号 Fig. 3 Signal extracted by wavelet transform | |
假设分解产生的本征模态函数为f(t),其小波变换表达式为
| $ {W_f}\left( {a,b} \right) = < f,{\psi _{a,b}}\left( t \right) \ge {\left| a \right|^{ - \frac{1}{2}}}\int_{ - \infty }^{ + \infty } {f\left( t \right)\bar \psi \left( {\frac{{t - b}}{a}} \right){\rm{d}}t} $ | (6) |
| $ {\psi _{a,b}}\left( t \right) = {\left| a \right|^{ - \frac{1}{2}}}\psi \left( {\frac{{t - b}}{a}} \right) $ | (7) |
式中:a∈R, a≠0,b∈R,ψa, b(t)为小波函数,它是由函数ψ(t)经过不同的时间尺度伸缩与不同时间平移所得,a为尺度参数,b为平移参数,Wf(a, b)为小波变换得到的小波系数。本文中采用的小波函数是Discrete Meyer小波函数,通过实验数据比较不同小波函数的信号提取效果,最终选择该小波函数。
通过小波变换方法进行信噪分离,应先设置一个阈值,比阈值大的小波系数认为是由信号产生,而比阈值的小波系数则认为是由噪声产生。采用文献[13]中的软阈值函数,进行信噪分离:
| $ F' = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\rm{sign}}\left( F \right)\left( {\left| F \right| - t} \right),\\ 0, \end{array}&\begin{array}{l} \left| F \right| \ge t\\ \left| F \right| < t \end{array} \end{array}} \right. $ | (8) |
式中:t为阈值, t=
将得到的有用信号与剩余的IMF及残余量R进行累加重构,构造海底地形趋势面Q=IMF′+IMFi+R, (i=3, 4, 5…),与原始水深数据作差得到水深数据残差值Zi=Di-Qi,并以其两倍或三倍标准差σ作为阈值标定异常数据,如下:
| $ \left\{ \begin{array}{l} {Z_i} \le k\sigma ,k = 2\;或\;3,第\;i\;个水深点为正常\\ {Z_i} > k\sigma ,k = 2\;或\;3,第\;i\;个水深点为异常值 \end{array} \right. $ | (9) |
实验数据来源于多波束实测水深数据,采用丹麦Reson公司生产的Seabat8101浅水多波束系统,后期数据处理软件采用Caris Hips 7.1以及Surfer 8.0软件,测区测线分布如图 4。实验截取其中一区域水深数据进行异常数据剔除工作,数据未剔除异常值之前,包含的测深数据量为10 000,最大水深为2 642.4 m,最小水深为1 480.4 m,地形起伏较大,如图 5所示。为了验证本文提出的方法,设计以下四种方案:1)对该区域水深数据进行手工编辑处理,剔除测深异常值;2)采用趋势面滤波方法构造海底趋势面剔除测深异常值;3)采用二维经验模态方法构造海底趋势面剔除测深异常值;4)采用二维经验模态方法结合小波分析构造海底趋势面剔除测深异常值。海底地形图如图 6所示。

|
Download:
|
| 图 4 测区多波束测深条带布设 Fig. 4 Measure area of mult-beam strip layout | |
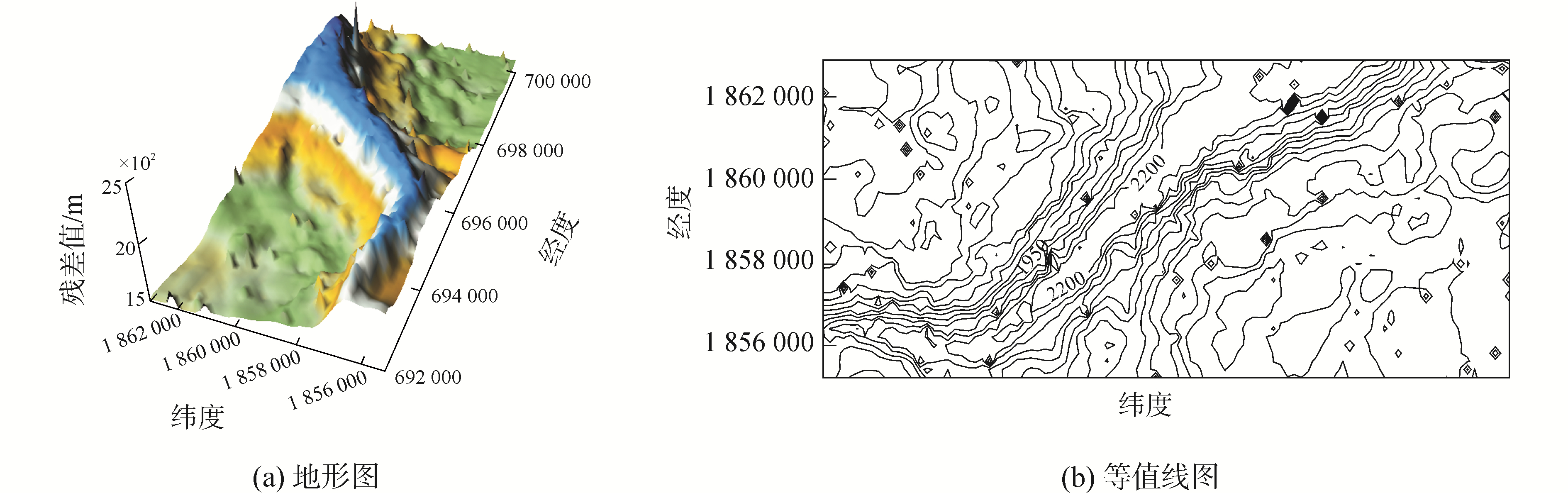
|
Download:
|
| 图 5 原始含异常值的水深数据 Fig. 5 Original water depth data containing outliers | |

|
Download:
|
| 图 6 基于Surfer 8.0软件显示的海底地形图 Fig. 6 Seabed topographic map based on Surfer 8.0 | |
通过上述四种方案的实验结果可以看出:1)在复杂海底地形情况下,趋势面滤波方法只能探测到部分异常值,而且会剔除真实水深数据导致地形被抬高。因为趋势面滤波方法基于多项式拟合构造海底地形趋势面的原理[4],在复杂海底地形情况下构造的趋势面不能反映海底实际,导致其异常值探测及剔除效果并不理想;2)单纯依靠二维经验模态方法构造海底趋势面剔除测深异常值的方法比趋势面滤波方法异常值剔除效果好,但仍然存在不能剔除的异常数据。因为其构造的趋势面仅依靠剥离IMF后的残余分量,剥离的IMP中仍然包含有用信号,使得该方法构造的趋势面不够精确,影响异常数据剔除。
为了说明IMP中包含的信号部分对构建海底地形趋势面的影响,将方案3、方案4中构造的海底地形趋势面展现如图 7。

|
Download:
|
| 图 7 方案3与方案4构建的海底地形趋势面比较 Fig. 7 Comparison of seabed contour map of plan 3 and plan 4 | |
方案4构造的海底地形趋势面包含更多细节信息,更接近真实海底情况,所以其异常值剔除效果更加理想,而方案3中的趋势面仅依靠经验模态分解产生的残余分量构建,不够精确。由此可见,本征模态函数中包含的信号对于构建精确海底地形趋势面有重要作用,不可忽视。
为更加直观的展现异常值剔除情况,将不同方案的异常值剔除情况列于表 4。
| 表 4 几种方案数据剔除效果比较 Tab.4 Statics of comparison of several plans gross error elimination |
1) 虽然水深数据中的异常值出现约仅占整体数据的1%~5%,但是在精确海底地形,确保航行安全的过程中,异常值的影响不容忽视,必须进行剔除工作。
2) 趋势面滤波法采用多项式拟合海底地形进行相应水深点的精度评定,其优点是算法简单易于编程实现,并且当海底地形较为品平缓的情况下该方法的异常值探测效果较好;其缺点是当海底地形较为复杂的情况下,异常值剔除效果较差且会剔除大量真实水深数据导致地形被人为改变。
3) 仅依靠二维经验模态分解的异常值剔除方法,其优点是可以依据数据本身特点,构建海底地形趋势面并探测出异常数据;其缺点是海底地形趋势面是由分解得到的残余量构建,仅包含原始数据中低频成分,不能精确反映海底地形特点,仍然存在部分未能探测到的异常数据,需要结合其他方法或者考虑分块处理。
4) 二维经验模态分解产生的本征模态函数中包含信号细节信息,经过小波分析方法可以提取出其有用信号,经过有用信号与经验模态分解得到的残余量构建的海底地形趋势面可精确反应海底真实情况,其异常值剔除效果好于单一经验模态分解方法。
| [1] |
李家彪. 多波束勘测原理技术与方法[M]. 北京: 海洋出版社, 1999.
(  0) 0)
|
| [2] |
赵建虎, 刘经南. 多波束测深及图像数据处理[M]. 武汉: 武汉大学出版社, 2008.
(  0) 0)
|
| [3] |
黄谟涛, 翟国君, 王瑞, 等. 海洋测量异常数据的检测[J]. 测绘学报, 1999, 28(3): 269-277. HUANG Motao, ZHAI Guojun, WANG Rui, et al. The Detection of abnormal data in marine survey[J]. Acta geodaetica et cartographica sinica, 1999, 28(3): 269-277. DOI:10.3321/j.issn:1001-1595.1999.03.015 (  0) 0)
|
| [4] |
黄贤源, 翟国君, 隋立芬, 等. LS-SVM算法中优化训练样本对测深异常值剔除的影响[J]. 测绘学报, 2011, 40(1): 22-27. HUANG Xianyuan, ZHAI Guojun, SUI Lifen, et al. The Influence of optimized train samples on elimination of sounding outliers in the LS-SVM arithmetic[J]. Acta geodaetica et cartographica sinica, 2011, 40(1): 22-27. (  0) 0)
|
| [5] |
黄辰虎, 陆秀平, 侯世喜, 等. 利用CUBE算法剔除多波束测深粗差研究[J]. 海洋测绘, 2010, 30(3): 1-5. HUANG Chenhu, LU Xiuping, HOU Shixi, et al. Study on detecting outlier of multibeam sounding based on CUBE algorithm[J]. Hydrographic surveying and charting, 2010, 30(3): 1-5. DOI:10.3969/j.issn.1671-3044.2010.03.001 (  0) 0)
|
| [6] |
阳凡林, 刘经南, 赵建虎. 多波束测深数据的异常检测和滤波[J]. 武汉大学学报(信息科学版), 2004, 29(1): 80-83. YANG Fanlin, LIU Jingnan, ZHAO Jianhu. Detecting outliers and filtering noises in multi-beam data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(1): 80-83. (  0) 0)
|
| [7] |
董江, 任立生. 基于趋势面的多波束测深数据滤波方法[J]. 海洋测绘, 2007, 27(6): 25-28. DONG Jiang, REN Lisheng. Filter of MBS sounding data based on trend surface[J]. Hydrographic surveying and charting, 2007, 27(6): 25-28. DOI:10.3969/j.issn.1671-3044.2007.06.007 (  0) 0)
|
| [8] |
HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the royal society A:mathematical, physical and engineering sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 (  0) 0)
|
| [9] |
NUNES J C, BOUAOUNE Y, DELECHELLE E, et al. Image analysis by bidimensional empirical mode decomposition[J]. Image and vision computing, 2003, 21(12): 1019-1026. (  0) 0)
|
| [10] |
陈建国, 肖凡, 常韬. 基于二维经验模态分解的重磁异常分离[J]. 地球科学——中国地质大学学报, 2011, 36(2): 327-335. CHEN Jianguo, XIAO Fan, CHANG Tao. Gravity and magnetic anomaly separation based on bidimensional empirical mode decomposition[J]. (Earth science)——Journal of China University of Geosciences, 2011, 36(2): 327-335. (  0) 0)
|
| [11] |
张彦铎, 汪敏敏, 鲁统伟. 改进的二维经验模式分解方法[J]. 武汉工程大学学报, 2013, 35(4): 61-65. ZHANG Yanduo, WANG Minmin, LU Tongwei. Decomposition method of improved two-dimensional empirical mode[J]. Journal of Wuhan Institute of Technology, 2013, 35(4): 61-65. DOI:10.3969/j.issn.1674-2869.2013.04.014 (  0) 0)
|
| [12] |
李翠芸, 曹潇男, 姬红兵, 等. 基于偏微分方程的快速二维经验模态分解方法及其应用[J]. 计算机辅助设计与图形学学报, 2014, 26(7): 1143-1150, 1158. LI Cuiyun, CAO Xiaonan, JI Hongbing, et al. A Fast Bidimensional empirical mode decomposition based on partial differential equation and its application on image processing[J]. Journal of computer-aided design & computer graphics, 2014, 26(7): 1143-1150, 1158. (  0) 0)
|
| [13] |
舒忠平, 杨智春. 抑制经验模分解边缘效应的极值点对称延拓法[J]. 西北工业大学学报, 2006, 24(5): 639-643. SHU Zhongping, YANG Zhichun. A better method for effectively suppressing end effect of empirical mode decomposition (EMD)[J]. Journal of Northwestern Polytechnical University, 2006, 24(5): 639-643. DOI:10.3969/j.issn.1000-2758.2006.05.023 (  0) 0)
|
| [14] |
刘慧婷, 张旻, 程家兴. 基于多项式拟合算法的EMD端点问题的处理[J]. 计算机工程与应用, 2004, 40(16): 84-86, 100. LIU Huiting, ZHANG Min, CHENG Jiaxing. Dealing with the end issue of EMD based on polynomial fitting algorithm[J]. Computer engineering and applications, 2004, 40(16): 84-86, 100. DOI:10.3321/j.issn:1002-8331.2004.16.028 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


