钢悬链线立管(steel catenary riser, SCR)是连接海上浮式平台和海底管道的重要系统[1],由悬垂段、触地段和海底流线段组成,在海流波浪等海洋环境的作用下,立管与海床相互作用的区域为触地段(touchdown zone, TDZ)。触地段管道与土体的相互作用是一个复杂的过程,是评价管道动力响应的关键要素,国内外学者基于不同的管土相互作用的模型对立管的动力响应进行分析。Palmer[2]提出了刚塑性海床假设研究触地段管道在海床中的沉陷过程。郭海燕等[3]利用接触单元模拟分析了钢悬链线立管与海床土体的接触问题。黄维平等[4]基于大挠度曲线梁模型和弹性地基梁理论,研究了管土相互作用的模拟方法。Hawlader[5]运用ANSYS有限元软件重点模拟了管道在海床上提升及浸入的过程中的土体抗力、土吸力、以及海床沟槽的形成过程。杜金新等[6]利用等效弹簧单元引入包含土体吸力效应的简化土体模型,建立了立管与海床的有限元接触模型。Pesce等[7]考虑立管触地段管道抗弯刚度以及管土相互作用,分析了触地段管道动力响应的非线性特征值问题。Bai等[8]在弹性地基梁的理论上建立了钢悬链线立管整体的动力学模型。白兴兰等[9]基于大挠度柔性索理论研究了海床土刚度对钢悬链线立管触地点动力响应的影响。
国内外学者针对触地段所做的大量研究基本立足于完好管道,对触地段损伤海底管道的分析较少, 无法考虑触地段管道所受内压、外压等压力荷载对动力响应的影响。目前还没有一个合适的作用模型来模拟触地段损伤管道在复杂载荷下的动力响应。针对不足,本文对Winkler弹性地基模型[10]进行改进,提出了改进的Winkler弹性地基模型。通过室内模型试验,验证了该模型的可靠性;并将该模型应用于全尺寸的具有体积损伤的管道模型中,分析对比了损伤管道不同节点处的位移响应和有效应力响应。
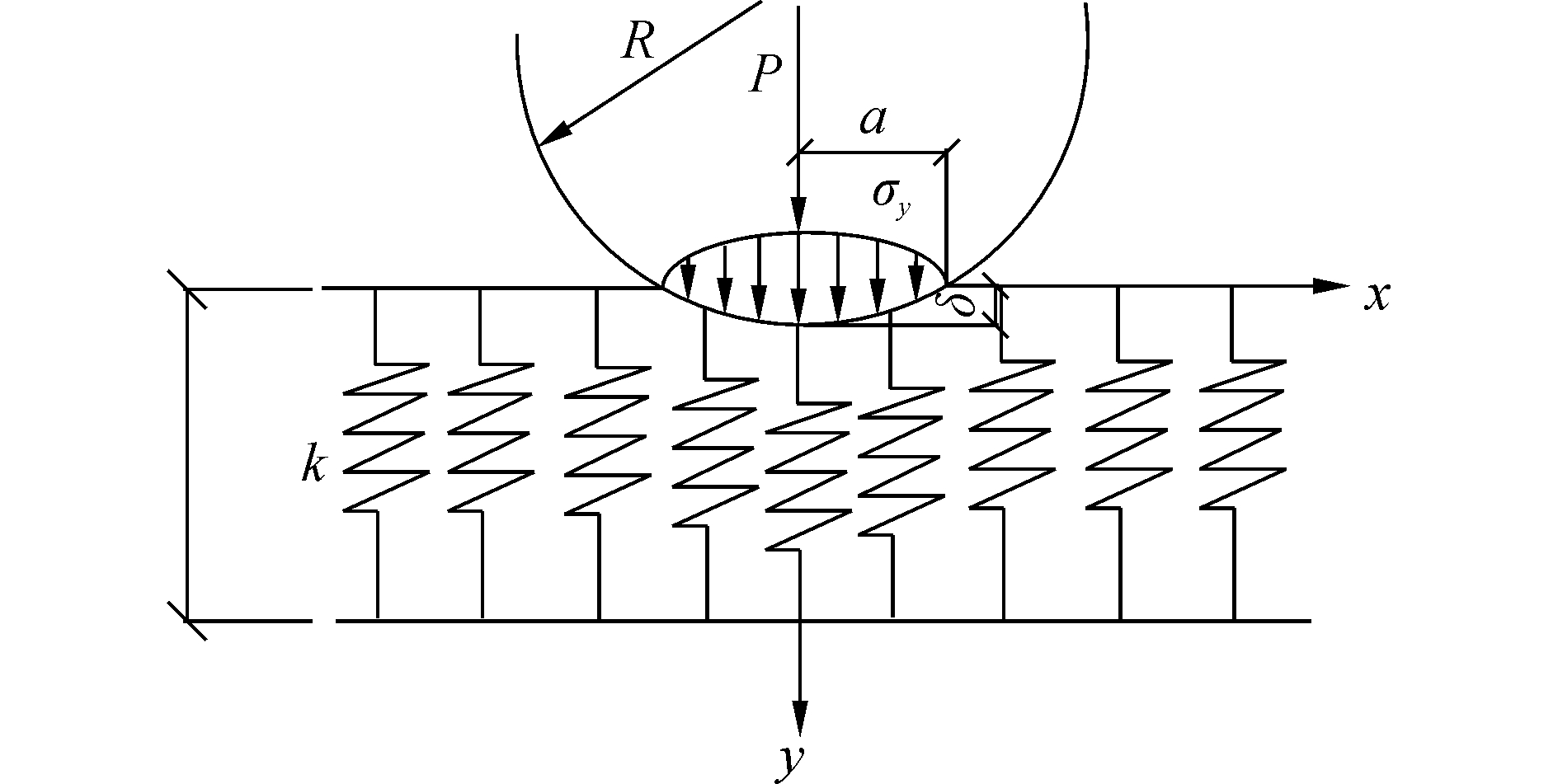
1 改进的Winkler弹性地基模型根据Johnson的Hertz理论[11],当海底管道铺设在海床上时,二者发生接触,在接触的初始时刻只有一条接触线,在重力等外载作用下,管土接触线附近发生变形,发展为有限面积上的接触。由于管道的形状是一个圆柱,海床表面是一个平面,相对于海床土体,海底管道的刚度非常大,可以近似为刚体,因此管土相互作用过程可以等效为刚性圆柱面压入弹性平面中的过程。设管道和海床的弹性模量分别为E1和E2,二者的曲率半径和泊松比分别为R1、R2和υ1、υ2。以Winkler弹性地基来模拟海床,模型的横截面图如图 1所示,在弹性系数为k,高度为h的弹性地基上放置半径为R的管道,其中k和h与海床的刚度E2相关。
|
Download:
|
| 图 1 管道压入Winkler弹性地基模型 Fig. 1 The model of pipeline on Winkler elastic foundation | |
为计算海床土体对管道施加的土体反力,提出以下简化和假设:1)两个接触面光滑,只有法向应力,没有摩擦应力;2)接触体是各向同性且有弹性;3)钢管的刚度远大于海床土体的刚度,E1
基于以上假设,根据Hertz理论进行相应的弹性分析得出,当管道与海床在力P(P < Pmax)作用下发生接触,由于轴对称情况,海床土体在压力P作用下压缩凹陷,接触区将发展成半接触宽度为a的矩形区域,a的表达式为
| $ a = \sqrt {\frac{{4P{R^ * }}}{{{\rm{ \mathsf{ π} }}{E^ * }}}} $ | (1) |
式中:E*和R*分别为管土接触作用中的等效弹性模量和等效半径,且
| $ \left\{ \begin{array}{l} {E^ * } = \left( {\frac{{1 - v_1^2}}{{{E_1}}} + \frac{{1 - v_2^2}}{{{E_2}}}} \right) - 1\\ {R^ * } = {\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)^{ - 1}} \end{array} \right. $ | (2) |
当海床土体的泊松比为υ2=0.3时,基于第3个假设和第4个假设,可得等效刚度和等效半径分别为
| $ \left\{ \begin{array}{l} {E^ * } = {E_2}/\left( {1 - \nu _2^2} \right) = 1.10{E_2}\\ {R^ * } = {R_1} = R \end{array} \right. $ | (3) |
二者的接触压力P和土体最大变形δ分别为
| $ P = \frac{2}{3}\left( {\frac{{ka}}{h}} \right)\frac{{{a^2}}}{R} $ | (4) |
| $ \delta = {a^2}/2R $ | (5) |
接触应力σy(x)分布在半接触宽度为a的矩形内,呈半椭圆状分布,最大接触压力发生在接触矩形的中心线上。在接触宽度内,接触应力分布为
| $ {\sigma _y}\left( x \right) = {\sigma _0}{\left[ {1 - {{\left( {\frac{x}{a}} \right)}^2}} \right]^{1/2}} $ | (6) |
以上提供了作用力和接触区域大小之间的关系,利用Hertz理论,对于轴对称情况,存在
| $ k/h = 1.18{E^ * }/a $ | (7) |
将式(7)代入式(4)得
| $ P = \frac{2}{3}\left( {1.18{E^ * }} \right)\frac{{{a^2}}}{R} $ | (8) |
对于海底管道触地段,当管道与海床相互作用达到稳定状态时候,管道与海床的接触状态可以归纳为3种沟槽形状[12],对应于管土接触宽度为D/3、2D/3和D,如图 2所示。D/3模型是最常见的一种沟渠形状,本文选择D/3模型重点研究,管土接触面的宽度为D/3,因此可得接触面的最大半宽度amax为
| $ {a_{\max }} = D/3/2 = R/3 $ | (9) |

|
Download:
|
| 图 2 不同的管土接触状态 Fig. 2 Pipe-soil contact status | |
当a取最大值的时候,土体抗力达到最大。将式(9)代入式(8),可得最大土体抗力Pmax和R的关系为
| $ {P_{\max }} = \frac{2}{3}\left( {1.18{E^ * }} \right)\frac{R}{9} $ | (10) |
地基的最大弹性抗力由Winkler弹性地基模型确定,考虑管土相互作用和动力荷载作用下土体性能的退化,即土体的非线性特性,其非线性抗力根据管土相互作用的最大接触面积(如图 2(a)所示),采用土体抗力的弹塑性模型。在管土相互作用之前,二者的作用力始终为零;当管土的接触面积达到最大时,土体抗力P达到抗力极限Pmax;当管道继续下压,二者接触面积不再增加,土体抗力P也不再增加,而保持Pmax不变。当管土作用力P由Pmax减小时,土体抗力线性回弹,因此海床土体的抗力模型简化为理想弹塑性模型,如图 3所示。

|
Download:
|
| 图 3 等效海床竖向土弹簧的P-y曲线 Fig. 3 Equivalent P-y curves of seabed soil spring | |
对应的弹簧刚度根据式(6)中管土相互作用的应力分布的解析解通过数值积分析得到:
| $ {P_{\max ,n}} = \int_{{x_n} - 1}^{{x_n}} {{\sigma _y}\left( x \right){\rm{d}}x} $ | (11) |
式中:Pmax,n表示第n种弹簧的屈服极限,n=1,2,…,N,N为管道截面内土弹簧的种类数,xn-1和xn分别表示土弹簧的等效土体抗力的始末范围。不同土弹簧所受的土壤阻力随管道竖向位移的变化而变化,即P-y曲线,如图 3所示,Pmax,1、Pmax,2、…、Pmax,n分别表示相应位置上土弹簧在受压过程中的屈服极限,ys表示土弹簧屈服极限所对应的最大弹性变形,三种弹簧的最大弹性变形相同,同时达到屈服。
1.2 建立改进的Winkler弹性地基模型基于本文分析,将作用于管道截面上的土体抗力离散为有限个土弹簧,建立改进的Winkler弹性地基模型。该模型首先将管道离散成实体单元,在管土作用区域的每个节点上连接土弹簧,用土弹簧来模拟海床对管道的约束。土弹簧的数量根据管道剖分网格的密度以及管-土作用过程中的接触面积(如图 2(a)所示)而确定,其弹簧刚度根据海床土体所能承受的最大弹性抗力及最大弹性变形而确定的,其表达式为
| $ {k_n} = \frac{{{P_{\max ,n}}}}{{{y_s}}} $ | (12) |
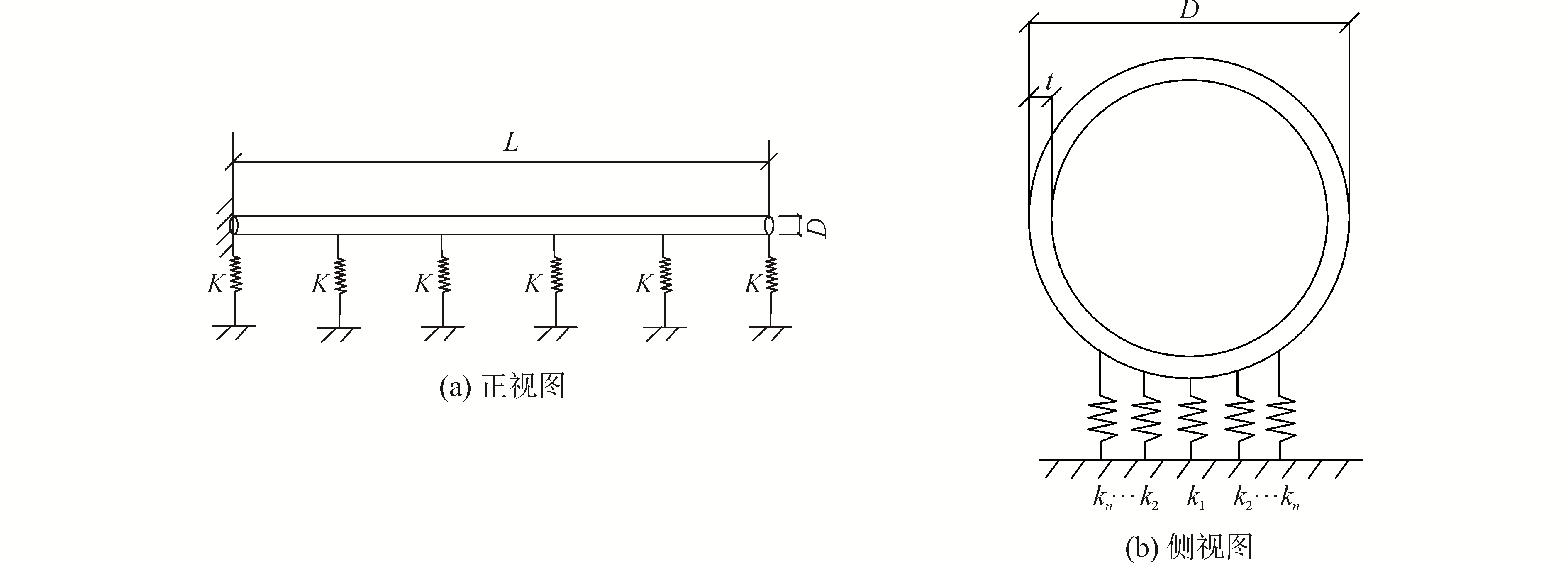
改进的Winkler弹性地基模型的立面图如图 4所示,长度为L、外径为D的管道放置在一系列刚度为K的土弹簧上,其中K的刚度为此截面上所有土弹簧的等效刚度。L的单位为m,D和t的单位均mm。其截面图如图 4(b)所示,在管土作用区域内的每一个节点上连接着对称分布的土弹簧,每一种土弹簧的刚度kn根据式(11)计算得出。在笛卡尔直角坐标系中,取管道的轴向为z方向,管道横截面的水平方向为x方向,竖直方向为y方向。管道流线端采用固定约束,悬垂端采用竖向和水平向约束。
|
Download:
|
| 图 4 改进的Winkler弹性地基模型改进的Winkler弹性地基模型 Fig. 4 Sketch of improved Winkler elastic foundation model | |
该模型在数值计算过程中能够考虑管材和海床在相互作用过程中的材料非线性、几何非线性以及接触非线性,不仅可以模拟损伤管道,还可以模拟管壁所受的内压、外压等载荷,从而获得不同节点处的动力响应。
2 改进模型的试验验证 2.1 试验装置为了验证改进的Winkler弹性地基模型的准确性,在大连理工大学开展了室内模型试验,试验系统如图 5所示,该系统由固结的海床土样、PVC模型管道、传感器和测量设备以及相关的约束设备组成。

|
Download:
|
| 图 5 大尺寸管土相互作用的模型试验 Fig. 5 The large scale pipe-soil system | |
固结海床的模型箱的大小为3 m×1 m×0.6 m。海床模型的土样来自大连市甘井子区某基坑中的红色软黏土,为了保证海床模型的均匀性以及与南海土体的一致性,海床模型由软黏土加水搅拌,水中过筛去除杂质后重新固结而成。基于一系列的土体材料试验,包括液塑限联合测定实验、含水率测定实验、T-bar触探试验等,得到软黏土和模型海床的一些关键地质参数。其中,土体的液限为41.3%,塑限为17.7%,塑性指数(PI)为23.6。固结海床的液性指数为2.34,含水率为43.6,孔隙比为1.43,天然密度为1.94 g/cm3,容重为18.99 kN/m3,压缩模量为0.528 MPa,不排水抗剪强度为4.58 kPa,均与南海土体的特性很接近[13],因此,该模型海床可以表示南海土体的主要特性。
2.1.2 管道模型受试验条件限制,模型立管的尺寸没有严格按照缩尺比选取。由于截断模型能够更准确的显示触地段海底管道的动力特性,且便于试验操作,同时,PVC管径相对较大,利于布置传感器。因此本文试验了钢悬链线立管在触地段附近的一个截断模型,包括立管的流线段、触地段及悬垂段的一部分,如图 5所示。管道模型的长为6 m,外径为75 mm,壁厚为2.3 mm的PVC管材,其动弹模为3.12 GPa,密度为1 420 kg/m3。为保证管道在触地段的变形,PVC管道内置了适当的配重铅块,由于PVC材料的弹性模量较低,铅块配重使管道的密度增大,从而使管道能够自然地垂落到海床上,满足流线段到触地段到悬垂段的变形要求。单位管长模型管道均匀配置6块铅环,每块铅环的高度为65 mm,外径为70.2 mm,内径为15.8 mm。管道悬垂端采用铰支约束,流线端采用固定约束。
2.1.3 传感器的布置加速度计采用防水型压阻式加速度计,型号有两种,分别为单向加速度计AR-5F(量程5 g)和三向加速度计ARF-100 A-T(量程10 g),频率响应范围均为0~120 Hz。加速度计以全桥的桥路的连接方法与MDR采集仪连接,试验过程中的采样频率为512 Hz。加速度计的布置位置如图 5所示。悬垂段和触地段附近布置的加速度计较密,在流线段,加速度计布置较疏。
2.2 模型验证对于结构物而言,模态参数(振型、固有频率等)是结构物的“指纹”,每一个结构都有其固有的模态参数,它是一系列独特的数据,可以通过比较结构的模态参数与结构数值模拟的模态参数结果验证数值模型的正确性。本试验通过一系列的敲击试验代表伪白噪声激励,来测试管道的震动模态,通过加速度传感器记录管道在敲击载荷下的振动响应,从而获得管道的振动模态,对比模型实验所测得的管道振型与数值模拟所得的振型来验证改进模型的正确性。
结构的模态参数主要由结构的质量阵、刚度阵及边界条件决定,如图 6所示。对于本模型试验中的触地段海底管道,管道的刚度阵和质量阵由钢管本身的材料及结构构型决定的,管道材料属性不受模型的影响,而管道在触地段的结构构型不仅与管道的材料属性相关,还与海床约束相关。边界条件主要包括管端的约束和海床的约束,流线端与悬垂端的约束是确定的,自流线段到触地段,其约束由海床提供。因此该模型的正确性在于真实的海床约束作用能否由土体抗力离散后的等效土弹簧代替。通过运用该改进的模型模拟试验中PVC管道的振型,并与模型试验的模态结果对比,来验证土弹簧对管道约束作用的合理性,从而验证该模型的合理性。

|
Download:
|
| 图 6 模型的验证过程 Fig. 6 Validation procedure of the improved model | |
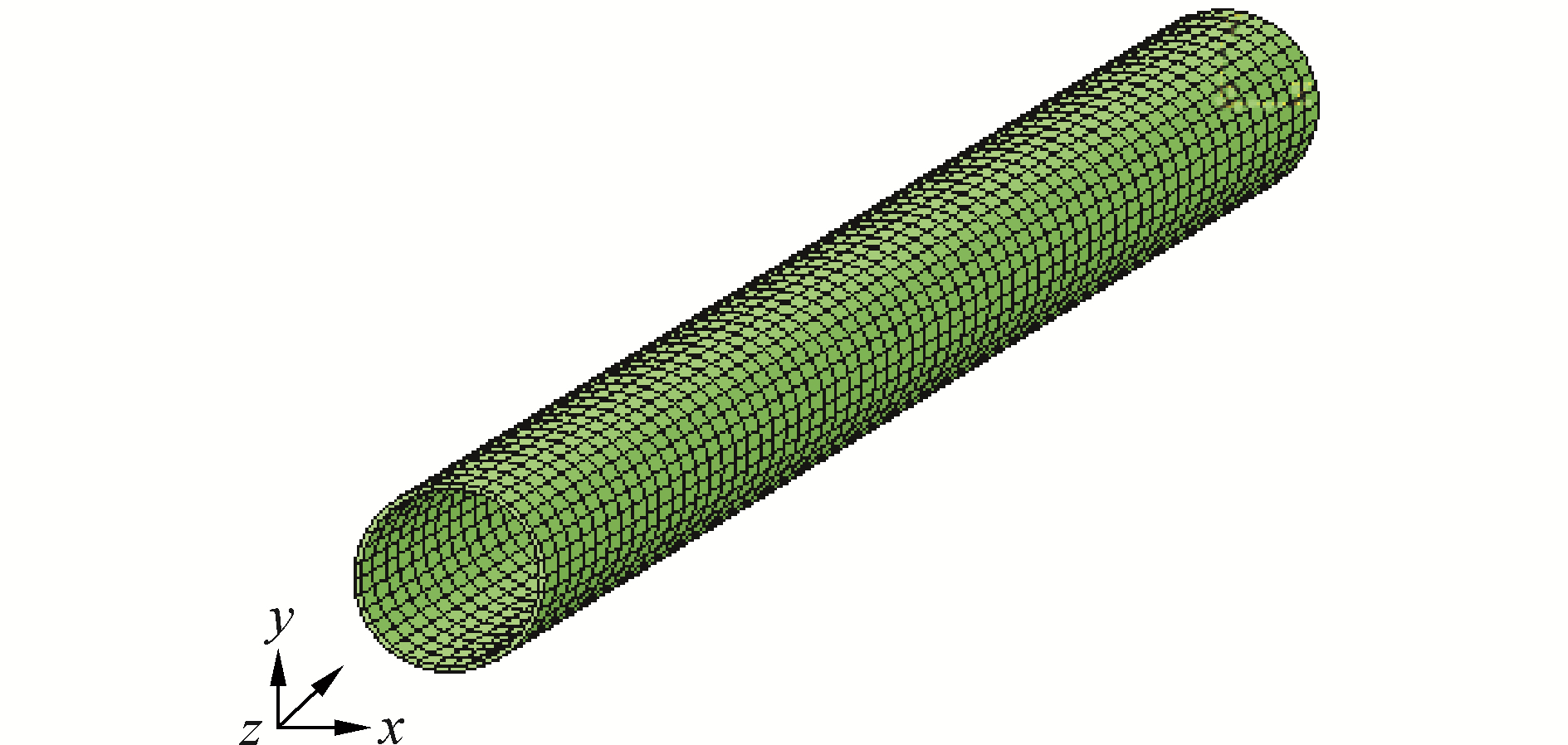
多数学者用梁单元模拟触地段管道,无法模拟作用于管壁上的压力荷载,也无法模拟在役管道可能存在的体积损伤。本模型将管道离散成实体单元,因为实体单元能够在保证计算精度的情况下抵御不规则变形,可以模拟具有体积缺陷的损伤管道,并且实体单元能够模拟作用在管壁上的内压和外压等载荷,进而对管道的不同部位进行深度分析。本文采用大型有限元软件ABAQUS建立了相应的动力学模型,管道采用三自由度八节点的实体单元C3D8I。如图 7所示,每个节点都有三个自由度。土体抗力由土弹簧模拟,连接在管土作用区域的每个节点上,相应土弹簧的P-y曲线由式(11)计算可得。
|
Download:
|
| 图 7 PVC管道的有限元模型 Fig. 7 View of finite element model of PVC pipeline | |
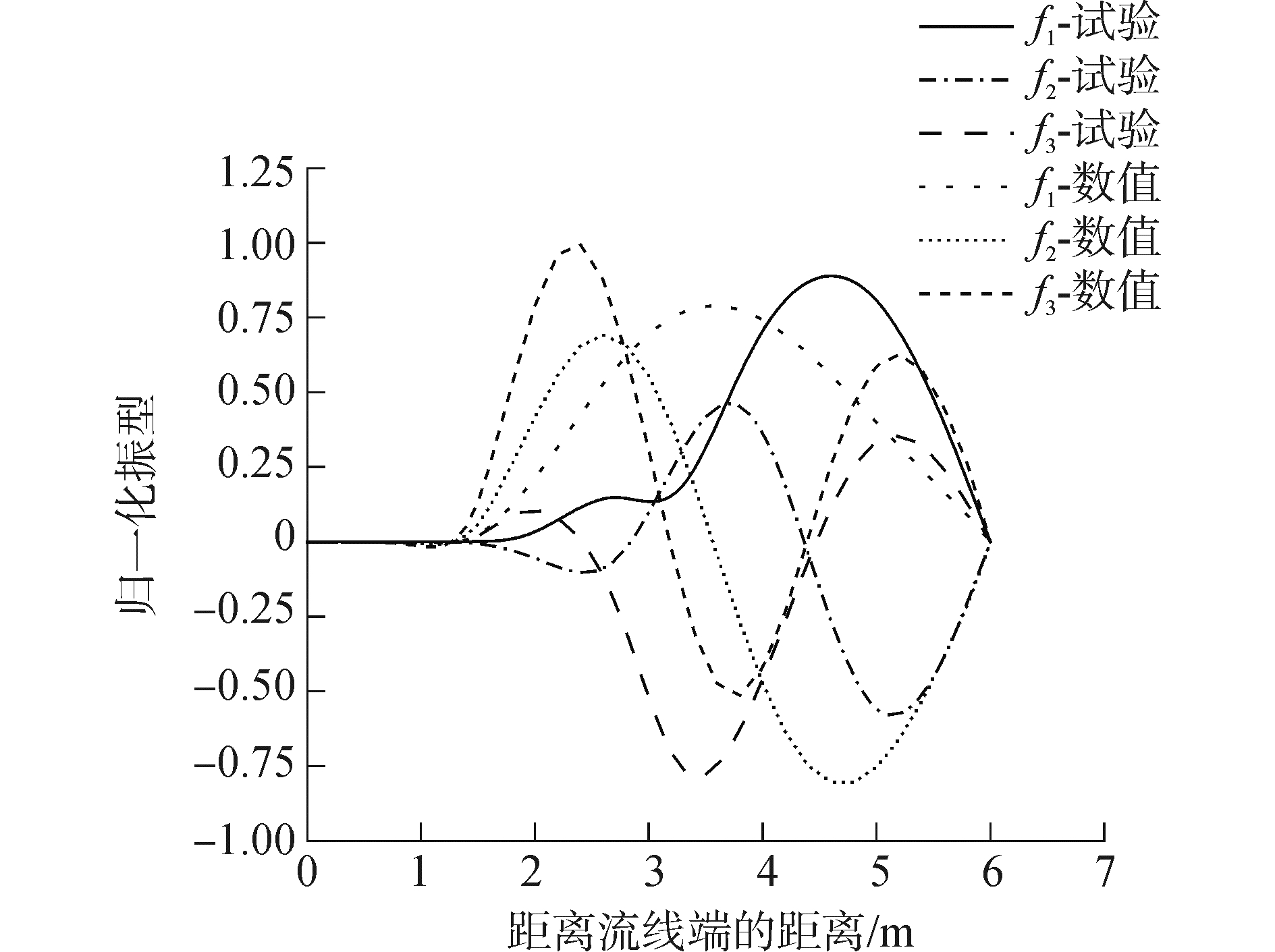
图 8给出PVC管道结构前三阶振型的试验结果与数值结果的对比图,结果表明:改进模型计算的振型形状与实验测量结果基本一致,波动形状吻合较好;但是数值模拟的结果整体上比较光滑,而试验结果在管土作用的临界点呈现出较明显的微小波动的特性,其主要原因是由于敲击试验会引起管道震动,从而导致与海床的接触与分离,在接触与分离的不同状态下,海床对管道的约束状态发生变化,因而会出现微小波动的现象。而在数值计算过程中,结构的模态是根据当前状态的边界条件,由结构的刚度矩阵和质量矩阵计算得出的。在模态分析步中,模拟土体的压缩弹簧已经被默认为线性的拉压弹簧,未考虑管土作用过程中的非线性作用,因而计算值与实验测量值存在一定差异。而在动力响应的计算分析中,会考虑到土弹簧的非线性效应,采用增量法根据每一个计算步的状态通过迭代的方法计算管道的动力响应,因此本文提出的改进的Winkler弹性地基模型能够对立管触地段进行较准确的数值模拟。
|
Download:
|
| 图 8 基于模型试验与数值模拟的振型对比图 Fig. 8 Comparison of mode shapes vertically based on test and numerical simulation | |
以上分析可知,该模型考虑了管材和海床在相互作用过程中的材料非线性、几何非线性及接触非线性,有效的模拟触地段管道较大的变形,更加符合立管质量和土体抗力的连续分布性。将管道离散成实体单元,不仅可以模拟体积缺陷,还可以施加内压、外压等载荷。因此将该模型应用于全尺寸损伤海底管线的动力响应分析中以探究其实用价值。
全尺寸管道采用X65型号钢,管道的计算长度为24 m,外径为171 mm,壁厚为5.7 mm。钢材的弹性模量为206 GPa,密度为7 850 kg/m3,泊松比为0.3,阻尼比为1%。管道的体积缺陷为管道外环形体积缺陷,其缺陷长度为100 mm,缺陷深度为1.71 mm。
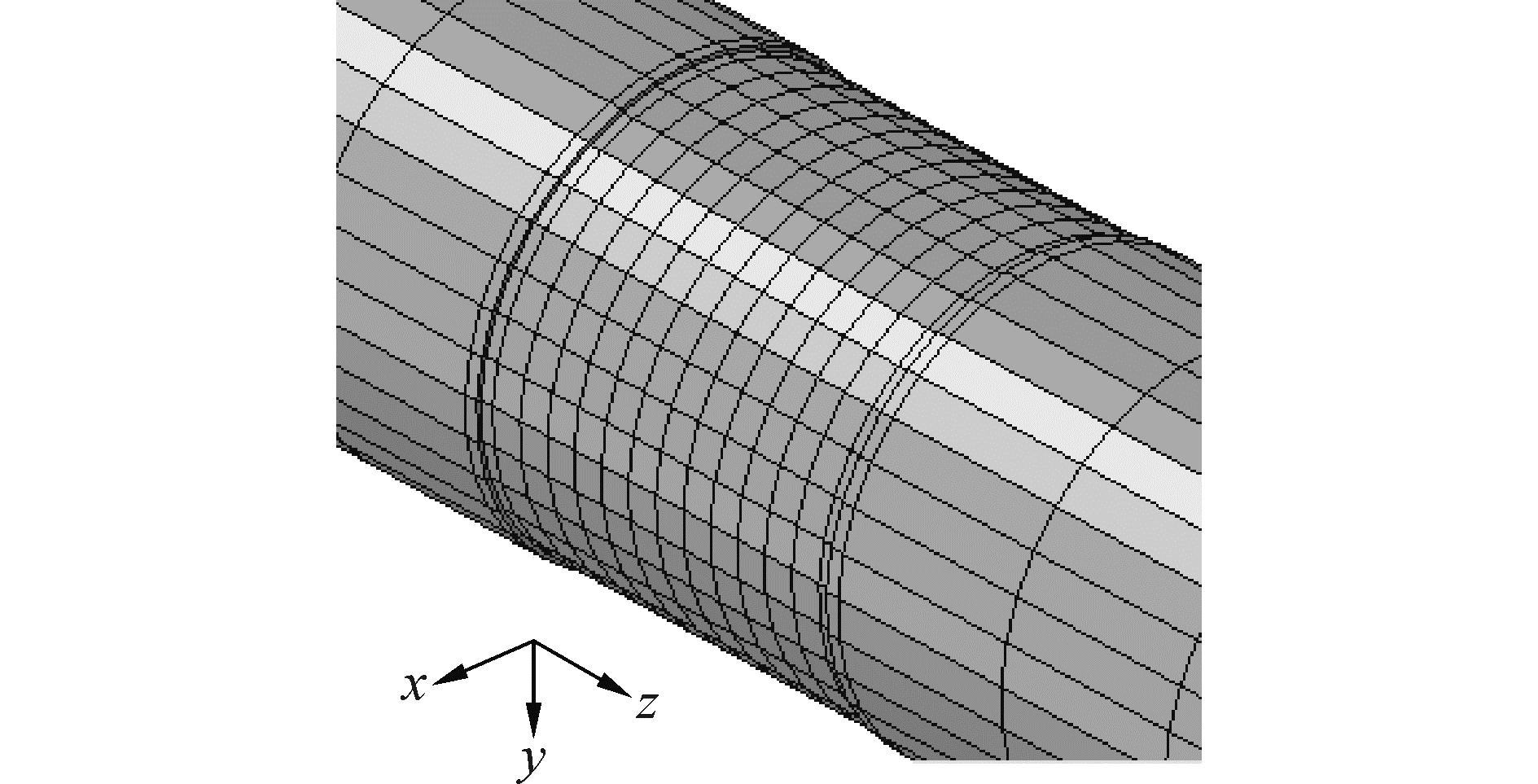
3.1 建立损伤管道与海床相互作用的模型体积损伤管道的单元类型为实体单元,基于管道结构的对称性,首先建立1/2的损伤管道的有限元计算模型,在体积缺陷处,网格进行细化,减小软件在求解过程中的应力集中效应。海底管道损伤部位的有限元模型在笛卡尔坐标系中如图 9所示。
|
Download:
|
| 图 9 海底管道体积损伤部位的完整模型 Fig. 9 Finite element model of pipeline in damaged zone | |
在役的触地段管道会受到重力、环境外压、工作内压,以及由海洋平台的牵引而导致的位移循环载荷。研究表明,在触地段管道悬垂端施加10周的位移循环载荷后,动力响应趋于稳定[8],因此在静载达到稳定状态后,在管道悬垂端施加10次垂向位移循环载荷进行隐式动力分析,载荷幅值A=0.1 m,频率f=0.5 Hz。其加载及分析过程如下:1)加载重力g=9.8 m/s2;2)加载外压Pe=5 MPa;3)加载竖向位移载荷u=0.12 m;4)加载内压Pi=5 MPa;5)加载动力循环载荷Xu=Asin(2πft)。
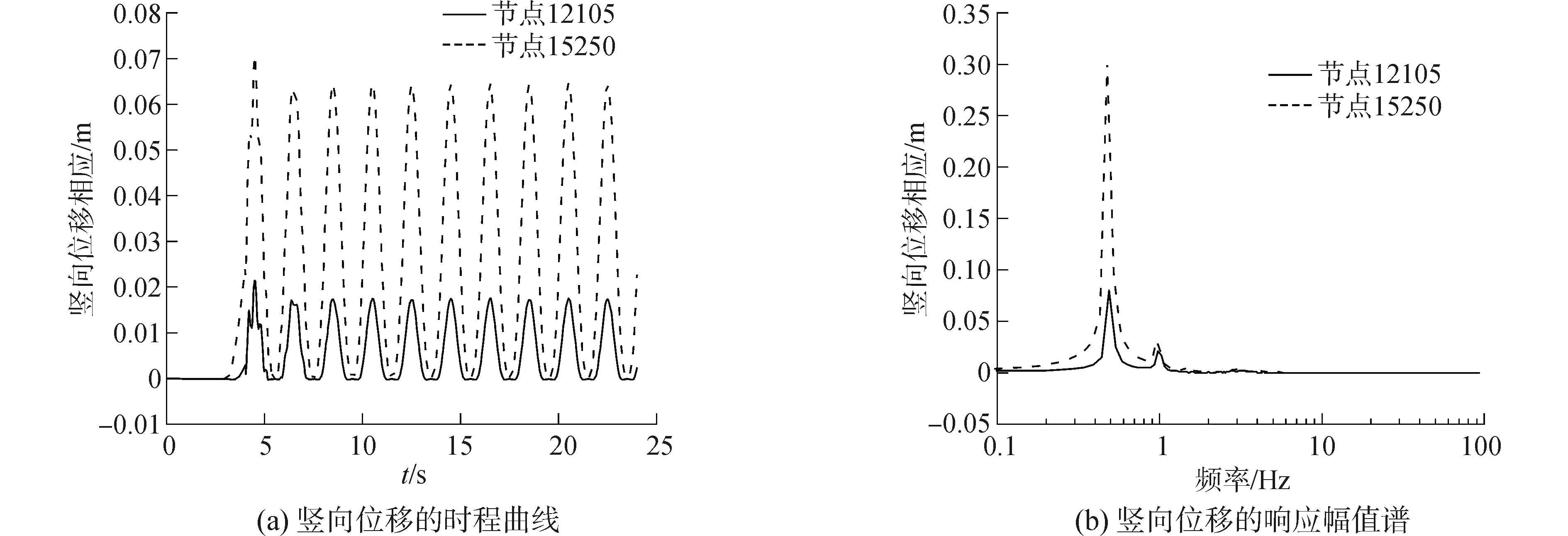
3.2 结果分析 3.2.1 位移响应绘制体积损伤部位的节点12105以及悬垂段节点15205的竖向位移时程曲线(图 10(a))。由图可知,在4 s时刻,突然加载竖向动力载荷,导致管道产生较剧烈的抖动,位移响应达到最大,节点12105与节点15205的峰值响应分别达到0.021 4、0.070 6 m。随着动力载荷的继续,结构位移响应趋于平稳,动力响应进入稳态,两点的最大响应分别稳定在0.017 2、0.064 3 m,且位移响应存在明显的不对称性,体现了海床对管道的非线性约束效应。位移响应的频谱图(图 10(b))显示,两节点的位移响应在其平衡位置附近根据载荷频率以一定的幅值振动。当节点由触地点越靠近管道的提升端,节点振幅越大,位移响应越强烈。
|
Download:
|
| 图 10 节点12105和15250的位移响应 Fig. 10 Displacement response of node 12105 and node 15250 | |
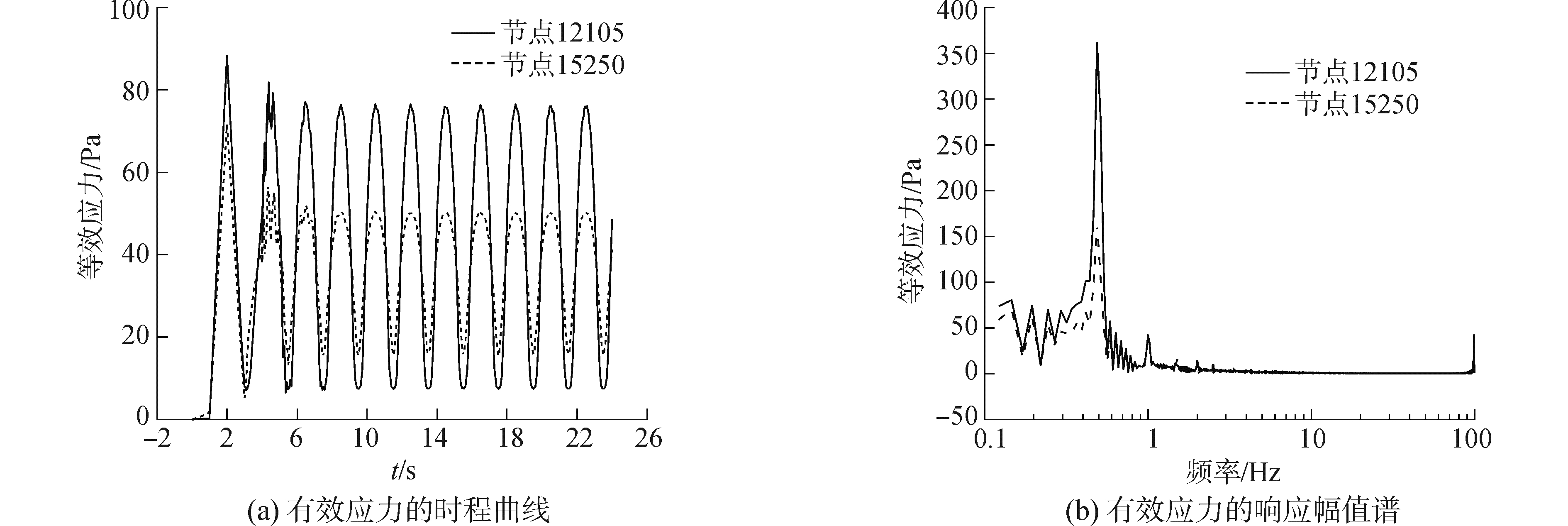
图 11为两节点等效应力的时程曲线及其位移响应的幅值谱,节点应力时程曲线的变化规律与位移响应的变化规律类似,两节点的应力在加载动力载荷的初始阶段达到最大值,分别为81.811 MPa和56.619 MPa,在后续的响应中,逐渐进入到稳态响应阶段,最大应力响应分别稳定于76.069 MPa和50.396 MPa,同样,不同节点的有效应力也存在一定程度的不对称性。
|
Download:
|
| 图 11 节点12105和15250的有效应力响应 Fig. 11 Stress response of node 12105 and node 15250 | |
结果表明:虽然损伤区节点12105的位移响应较小,但是其最大应力响应幅值远大于节点15205,说明管道的体积损伤不仅降低了管道损伤区的承载力,而且损伤区的应力响应幅值较大,响应剧烈,成为管结构的薄弱部位,这与工程实际是吻合的。
4 结论1) 改进模型在数值计算过程中考虑管材和海床在相互作用过程中的材料非线性、几何非线性以及接触非线性,使计算结果更加符合工程实际。
2) 改进模型充分考虑了触地段管道较大的位移载荷和弯曲变形,更加符合立管质量和海床约束力的连续分布的特点。
3) 改进模型不仅可以模拟体积缺陷等损伤管道,还可以模拟管道所受的内压、外压等载荷,进而对管道进行深度分析。
此模型应用于全尺寸损伤海底管线在复杂载荷作用下的动力分析,研究触地段损伤管道不同节点的动力响应,结果符合实际情况,表明该模型对处理实际的问题是有价值的,随着针对触地段管道研究的深入,这种价值也必然会得到越来越多的体现。
| [1] |
XIA Jie, DAS P K, KARUNAKARAN D. A parametric design study for a semi/SCR system in Northern North Sea[J]. Ocean engineering, 2008, 35(17/18): 1686-1699. (  0) 0)
|
| [2] |
PALMER A. Touchdown indentation of the seabed[J]. Applied ocean research, 2008, 30(3): 235-238. DOI:10.1016/j.apor.2008.09.004 (  0) 0)
|
| [3] |
郭海燕, 高秦岭, 王小东. 钢悬链线立管与海床土体接触问题的ANSYS有限元分析[J]. 中国海洋大学学报, 2009, 39(3): 521-525. GUO Haiyan, GAO Qinling, WANG Xiaodong. Finite element analysis of steel catenary riser/soil contact problem by ANSYS[J]. Periodical of Ocean University of China, 2009, 39(3): 521-525. (  0) 0)
|
| [4] |
黄维平, 孟庆飞, 白兴兰. 钢悬链式立管与海床相互作用模拟方法研究[J]. 工程力学, 2013, 30(2): 14-18. HUANG Weiping, MENG Qingfei, BAI Xinglan. The simulation methods of the interaction of steel catenary risers and soil in touchdown down zone[J]. Engineering mechanics, 2013, 30(2): 14-18. (  0) 0)
|
| [5] |
HAWLADER B, FOUZDER A, DUTTA S. Numerical modeling of suction and trench formation at the touchdown zone of steel catenary riser[J]. International journal of geomechanics, 2016, 16(1): 04015033. DOI:10.1061/(ASCE)GM.1943-5622.0000497 (  0) 0)
|
| [6] |
杜金新, LOW Y M. 海洋立管-海床土体接触作用数值分析[J]. 工程地质计算机应用, 2008(4): 6-11. DU Jinxin, LOW Y M. Numerical analysis the interaction of risers and seabed[J]. Calculating machine application on engineering and geology, 2008(4): 6-11. (  0) 0)
|
| [7] |
PESCE C P, MARTINS C A. Riser-soil interaction: Local dynamics at TDP and a discussion on the eigenvalue and the VIV problem[C]//Proceedings of the 23rd International Conference on Offshore Mechanics and Arctic Engineering. Vancouver: ASME, 2004: 583-594.
(  0) 0)
|
| [8] |
BAI Xinglan, HUANG Weiping, VAZ M A, et al. Riser-soil interaction model effects on the dynamic behavior of a steel catenary riser[J]. Marine structures, 2015, 41: 53-76. DOI:10.1016/j.marstruc.2014.12.003 (  0) 0)
|
| [9] |
白兴兰, 黄维平, 高若沉. 海床土刚度对钢悬链线立管触地点动力响应的影响分析[J]. 工程力学, 2011, 28(S1): 211-216. BAI Xinglan, HUANG Weiping, GAO Ruochen. Effect of seabed soil stiffness on dynamic response of a steel catenary riser at touchdown point[J]. Engineering mechanics, 2011, 28(S1): 211-216. (  0) 0)
|
| [10] |
余同希, 邱信明. 冲击动力学[M]. 北京: 清华大学出版社, 2011. YU Tongxi, QIU Xinming. Dynamic in shock[M]. Beijing: Tsinghua University Press, 2011. (  0) 0)
|
| [11] |
JOHNSON K L. Contact mechanics[M]. Cambridge: University Press, 1985.
(  0) 0)
|
| [12] |
毛海英, 郭海燕, 赵伟. 钢悬链线立管触地点区域管土动力相互作用分析[J]. 厦门大学学报(自然科学版), 2015, 54(1): 133-137. MAO Haiying, GUO Haiyan, ZHAO Wei. Analysis of steel catenary riser/seafloor interaction in the touch down zone[J]. Journal of Xiamen University (natural science), 2015, 54(1): 133-137. (  0) 0)
|
| [13] |
郑志昌, 陈俊仁, 朱照宇. 南海海底土体物理力学特征及其地质环境初步研究[J]. 水文地质工程地质, 2004, 31(4): 50-53, 65. ZHENG Zhichang, CHEN Junren, ZHU Zhaoyu. Physical and mechanical characteristics of seabed soils and its geological environment in South China Sea[J]. Hydrogeology and engineering geology, 2004, 31(4): 50-53, 65. DOI:10.3969/j.issn.1000-3665.2004.04.008 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


