港口作业或水产养殖等人类活动需要在相对平稳的水域中进行,易受海上波浪的影响,因此消波防浪成为部分海洋设施正常运作的重要保障。在波浪传播过程中,水质点动能沿垂向指数衰减,仅安装于波面附近的透空式防波堤应运而生。相较于传统坐底式防波堤,透空式结构有着建造成本低、不影响水体交换、对地质条件要求低等特点[1],这也为离岸式波能转换装置等的安装试验提供了切实可行的支撑基础。
针对板状结构,学者们已进行详实的研究[2-6]。Ursell[2]对无限水深中部分淹没的垂向薄板进行研究,并根据修正的贝塞尔函数计算出透射系数。Stoker[3]通过物理试验研究了固定于水体表面的单块水平板,主要考察长波作用下的反射和透射系数。为提高消波性能并联系工程实际,学者们不断探究更为复杂的防波堤结构及其应用环境。Günaydün等[7]提出了П型半潜式防波堤,并通过物理试验研究结构物的消波性能。顾倩等[8]通过物理试验研究了斜向波浪作用下双层水平板式防波堤的消波性能,并对不同影响因素下的波浪形态及反、透射系数进行比较和分析。Cho[9]对装有多孔垂板的П型浮式防波堤进行了理论研究,发现调整垂板的长度和孔隙率能显著影响波浪透射系数。Duan等[10]提出一种F型浮式防波堤,并通过数值模拟及物理实验对防波堤的消波性能进行了研究。Zhan等[11]通过数值模拟研究了规则波及非规则波与倒T型防波堤的相互作用,分析结构物的运动响应及消波性能。对T型防波堤的研究始于Neelamani等[12]的物理试验。何军等[13]通过数值模拟分析入射波高、防波堤尺寸对结构物附近流场和紊动动能等的影响。王国玉等[1]采用匹配特征函数展开法对T型结构的消波性能进行理论分析,发现水平板潜深和竖直板高度对其消波性能影响较大。刘宏霄等[14]基于有限体积法对T型开孔式防波堤的进行了研究。
目前理论和数模上对变形较大的结构物(如薄板结构)仍较难处理,因此关于波浪与板式透空结构相互作用的研究仍以物理实验为主。同时,分析防波堤所受波浪荷载能为结构物的安全建造和正常工作提供指导。本文应用匹配特征函数展开法对线性波与T型结构相互作用的问题进行求解,并通过引入切比雪夫多项式和盖根堡多项式分别表示出结构物尖角附近流体运动的奇异性特征。忽略垂板厚度,重点讨论T型结构各几何参数对波浪荷载及其消波性能的影响。
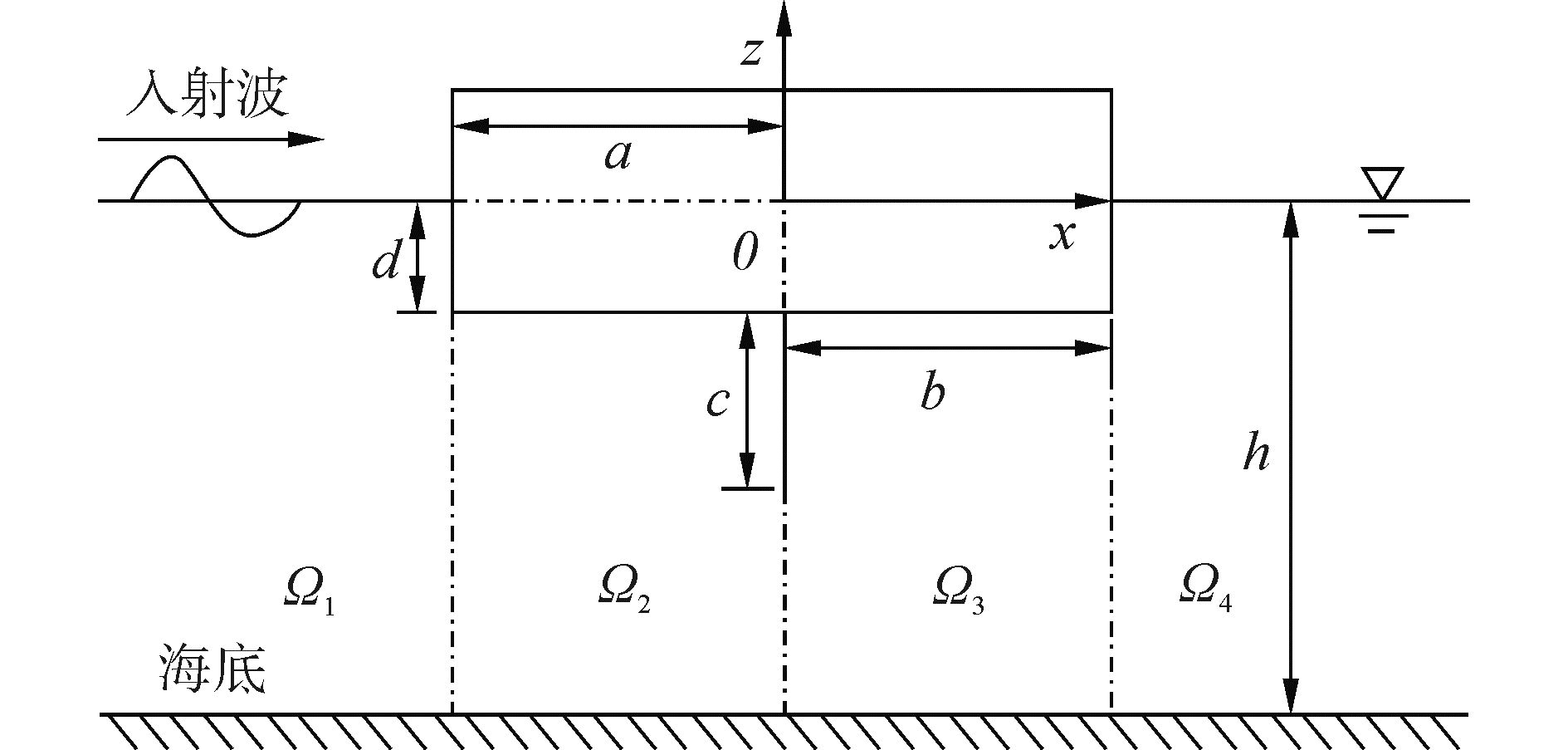
1 控制方程和边界条件如图 1所示,T型透空式防波堤分别由一块有厚度的水平板和可忽略厚度的垂向薄板组成。静水深为h;水平板的长度为a+b,吃水深度为d;垂向薄板的长度为c;整个结构物的吃水深度为H,即H=c+d。以垂向薄板与静水面的交点为原点,水平板位于x轴负值部分的长度为a,正值部分为b,波浪沿x轴正向传播。根据边界条件的差异,将整个流场分为四个区域(Ω1、Ω2、Ω3和Ω4)。
|
Download:
|
| 图 1 固定T型结构示意图 Fig. 1 Schematic diagram of a T-type breakwater | |
对于频率为ω的单色波,速度势Ф为
| $ \mathit{\Phi }\left( {x,z,t} \right) = {\mathop{\rm Re}\nolimits} \left[ {\phi \left( {x,z} \right){{\rm{e}}^{ - {\rm{i}}\omega t}}} \right] $ | (1) |
基于无旋无粘的理想流体假定,势函数复振幅ϕ(x, z)满足拉普拉斯方程:
| $ \frac{{{\partial ^2}\phi \left( {x,z} \right)}}{{\partial {x^2}}} + \frac{{{\partial ^2}\phi \left( {x,z} \right)}}{{\partial {z^2}}} = 0 $ | (2) |
自由表面边界条件为
| $ \frac{{\partial \phi \left( {x,z} \right)}}{{\partial x}} = \frac{{{\omega ^2}}}{g}\phi \left( {x,z} \right),z = 0 $ | (3) |
结构物处于固定状态,物面边界条件为
| $ \frac{{\partial \phi }}{{\partial n}} = 0 $ | (4) |
式中包含海底边界条件,n表示物面法向量,指向流体区域外。同时,ϕ(x, z)还需满足Sommerfeld辐射边界条件。
2 速度势展开式及辅助函数区域Ω1中的势函数包含入射波与反射波,区域Ω4中仅包含透射波,区域Ω2和Ω3中为振荡流。
2.1 区域Ω1和Ω4中的速度势区域Ω1和Ω4的底部为不可穿透的固壁边界,顶部为自由表面。根据分离变量法,其速度势在垂向上可展开为特征函数Zm(kmz)的线性叠加:
| $ \left\{ \begin{array}{l} {Z_0}\left( {kz} \right) = N_0^{ - 1/2}\cosh \left[ {k\left( {z + h} \right)} \right]\\ {Z_m}\left( {{k_m}z} \right) = N_m^{ - 1/2}\cos \left[ {{k_m}\left( {z + h} \right)} \right],\;\;\;\;m = 1,2,3, \cdots \end{array} \right. $ | (5) |
其中
| $ \left\{ \begin{array}{l} {N_0} = \frac{{2kh + \sinh \left( {2kh} \right)}}{{4k}}\\ {N_m} = \frac{{2{k_m}h + \sinh \left( {2{k_m}h} \right)}}{{4{k_m}}} \end{array} \right. $ | (6) |
应用自由表面边界条件可求得色散方程:
| $ {\omega ^2} = gk\tanh \left( {kh} \right) $ | (7) |
| $ {\omega ^2} = - g{k_m}\tan \left( {{k_m}h} \right),\;\;\;m = 1,2,3, \cdots $ | (8) |
式中:k为波数,是式(7)的实根; km是方程(8)的实根。为方便计算,取k0=-ik。在区间z∈[-h, 0]上,特征函数Zm(kmz)满足正交关系:
| $ \int_{ - h}^0 {{Z_m}\left( {{k_m}z} \right){Z_n}\left( {{k_n}z} \right){\rm{d}}z} = {\delta _{mn}},\;\;\;\;m,n = 0,1,2, \cdots $ | (9) |
其中
| $ {\delta _{mn}} = \left\{ \begin{array}{l} 1,m = n\\ 0,m \ne n \end{array} \right. $ | (10) |
入射势为
| $ {\phi _i}\left( {x,z} \right) = - \frac{{{\rm{i}}gA}}{\omega }\frac{{\cosh \left[ {k\left( {z + h} \right)} \right]}}{{\cosh \left( {kh} \right)}}{{\rm{e}}^{{\rm{i}}k\left( {x + a} \right)}} $ | (11) |
式中A为波幅。可将区域Ω1和Ω4中的速度势分别展开为
| $ {\phi _1}\left( {x,z} \right) = {\phi _i} - \frac{{{\rm{i}}gA}}{\omega }\sum\limits_{m = 0}^\infty {{A_m}{{\rm{e}}^{{k_m}\left( {x + a} \right)}}{Z_m}\left( {{k_m}z} \right)} $ | (12) |
| $ {\phi _4}\left( {x,z} \right) = - \frac{{{\rm{i}}gA}}{\omega }\sum\limits_{j = 0}^\infty {{F_j}{{\rm{e}}^{ - {k_j}\left( {x - b} \right)}}{Z_j}\left( {{k_j}z} \right)} $ | (13) |
式中Am和Fj (m, j=0, 1, 2, …)为待定系数。
2.2 区域Ω2和Ω3中的速度势区域Ω2和Ω3的底部和顶部均为不可穿透的固壁边界,由此可得特征函数Yn(λnz):
| $ \left\{ \begin{array}{l} {Y_0}\left( {{\lambda _0}z} \right) = M_0^{ - 1/2}\\ {Y_n}\left( {{\lambda _n}z} \right) = M_n^{ - 1/2}\cos \left[ {{\lambda _n}\left( {z + h} \right)} \right],\;\;\;\;n = 1,2,3, \cdots \end{array} \right. $ | (14) |
其中
| $ \left\{ \begin{array}{l} {M_0} = h - d\\ {M_n} = \left( {h - d} \right)/2 \end{array} \right. $ | (15) |
| $ {\lambda _n} = n{\rm{ \mathsf{ π} }}/\left( {h - d} \right) $ | (16) |
同样,Yn(λnz)在区间z∈[-h, -d]上相互正交。可将区域Ω2和Ω3中的速度势分别展开为
| $ \begin{array}{l} {\phi _2}\left( {x,z} \right) = - \frac{{{\rm{i}}gA}}{\omega }\left[ {\left( {{B_0} - {C_0}\frac{x}{a}} \right){Y_0}\left( {{\lambda _0}z} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\sum\limits_{n = 1}^\infty {\left( {{B_n}{{\rm{e}}^{{\lambda _n}x}} + {C_n}{{\rm{e}}^{ - {\lambda _n}x}}} \right){Y_n}\left( {{\lambda _n}z} \right)} } \right] \end{array} $ | (17) |
| $ \begin{array}{l} {\phi _3}\left( {x,z} \right) = - \frac{{{\rm{i}}gA}}{\omega }\left[ {\left( {{D_0} + {E_0}\frac{x}{b}} \right){Y_0}\left( {{\lambda _0}z} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\sum\limits_{l = 1}^\infty {\left( {{D_l}{{\rm{e}}^{{\lambda _l}x}} + {E_l}{{\rm{e}}^{ - {\lambda _l}x}}} \right){Y_l}\left( {{\lambda _l}z} \right)} } \right] \end{array} $ | (18) |
式中:Bn、Cn、Dl和El (n, l=0, 1, 2, …)均为待定系数。
2.3 结构物尖角附近的奇异性问题流场中尖角的存在易使数值计算中出现奇异性病态矩阵,致使计算难以收敛甚至无法获得结果。根据Porter等[15-18]的方法,垂向薄板处流体界面上的速度分布表现出|z+H|-1/2的特征。记x=0处界面上的速度分布函数为U0(z),可将其以z=-h为对称轴展开为区间z∈[-2h+H, -H]上的偶函数:
| $ {U_0}\left( z \right) = - \frac{{{\rm{i}}gA}}{\omega }\sum\limits_{s = 0}^\infty {{\beta _s}{u_{2s}}\left( z \right)} $ | (19) |
式中:βs为待定系数;其中,u2s(z)表达式如下
| $ {u_{2s}}\left( z \right) = \frac{{{\rm{2}}{{\left( {{\rm{ - 1}}} \right)}^{\rm{s}}}}}{{{\rm{ \mathsf{ π} }}\sqrt {{{\left( {h - H} \right)}^2} - {{\left( {z + h} \right)}^2}} }}{T_{2s}}\left( {\frac{{z + h}}{{h - H}}} \right) $ | (20) |
式中:T2s表示第一类切比雪夫多项式的偶数项。在x=-a, b处的公共界面上,流体运动表现出|z+d|-1/3的分布特征。分别将相应的速度分布函数记为U-a(z)和Ub(z),可得
| $ {U_{ - a}}\left( z \right) = - \frac{{{\rm{i}}gA}}{\omega }\sum\limits_{r = 0}^\infty {{\alpha _r}{u_{1r}}\left( z \right)} $ | (21) |
| $ {U_b}\left( z \right) = - \frac{{{\rm{i}}gA}}{\omega }\sum\limits_{q = 0}^\infty {{\gamma _q}{u_{1q}}\left( z \right)} $ | (22) |
式中:αr和γq为待定系数;其中,u1r(z)表达式如下
| $ \begin{array}{*{20}{c}} {{u_{1r}}\left( z \right) = }\\ {\frac{{{{\left( { - 1} \right)}^r}\left( {2r} \right)!\mathit{\Gamma }\left( {\frac{1}{6}} \right)}}{{{\rm{ \mathsf{ π} }}{{\left( {h - d} \right)}^{\frac{1}{3}}}\mathit{\Gamma }\left( {2r + \frac{1}{3}} \right)}}\frac{{{\rm{C}}_{2r}^{1/6}\left( {\frac{{z + h}}{{h - d}}} \right)}}{{{{\left[ {{{\left( {h - d} \right)}^2} - {{\left( {z + h} \right)}^2}} \right]}^{\frac{1}{3}}}}}} \end{array} $ | (23) |
式中:u1q(z)的形式与u1r(z)相同,C2r1/6表示特征值为1/6的偶数项盖根堡多项式。
2.4 波浪荷载及反、透射系数求解应用区域间的速度连续条件,并利用特征函数的正交性,可分别求出待定系数Am、Bn、Cn、Dl、El和Fj的表达式。取势函数中待定系数的截断项分别为m=M、n=N、l=L和j=J;速度分布函数中的截断项分别为r=R、s=S和q=Q。再结合相邻区域间公共界面上的压力连续条件,可得到一个未知数分别为B0、D0、αr、βs和γq的线性方程组,方程与未知数个数均为R+S+Q+5。
对压强在作用面上进行积分,求得水平向波浪荷载的振幅为
| $ \begin{array}{*{20}{c}} {{F_x} = \left| {{\rm{i}}\omega \rho \left[ {\int_{ - d}^0 {\left( {{\phi _1}\left| {_{x = - a}} \right. - {\phi _4}\left| {_{x = b}} \right.} \right){\rm{d}}z} + } \right.} \right.}\\ {\left. {\left. {\int_{ - H}^{ - d} {\left( {{\phi _2}\left| {_{x = 0}} \right. - {\phi _3}\left| {_{x = 0}} \right.} \right){\rm{d}}z} } \right]} \right|} \end{array} $ | (24) |
同理可得垂向波浪荷载的振幅:
| $ {F_z} = \left| {{\rm{i}}\rho \omega \left( {\int_{ - a}^0 {{\phi _2}\left| {_{z = - d}} \right.{\rm{d}}x} + \int_0^b {{\phi _3}\left| {_{z = - d}} \right.} } \right){\rm{d}}x} \right| $ | (25) |
采用Garrett[19]的方法对波浪荷载进行无量纲处理,此处用以无量纲化的作用力取Fb=ρgAS0。其中,结构物垂直于计算面的长度为单位1,取S0=0.5 h。为简便,后面依然采用Fx和Fz表示无量纲的波浪荷载。
波浪反射系数Cr和透射系数Ct分别定义为反射波高及透射波高与入射波高的比值。根据x轴无穷远处的波面方程,可求得
| $ {C_r} = N_0^{ - 1/2}\left| {{A_0}} \right|\cosh \left( {kh} \right) $ | (26) |
| $ {C_t} = N_0^{ - 1/2}\left| {{F_0}} \right|\cosh \left( {kh} \right) $ | (27) |
在以下数值计算过程中,若无特殊说明,均取h=10 m,ρ=1 000 kg/m3,g=9.81 m/s2。Garrett[20]得出势函数ϕ1和ϕ4中无限求和序列的截断误差正比于求和项数的倒数。因此在后续计算中,取M=J=400,以精确到小数点后两位。对于其他无限求和的截断项,可通过波浪荷载及反、透射系数的变化情况进行验证,取N=L=50及R=S=Q=6即可使数值计算收敛。
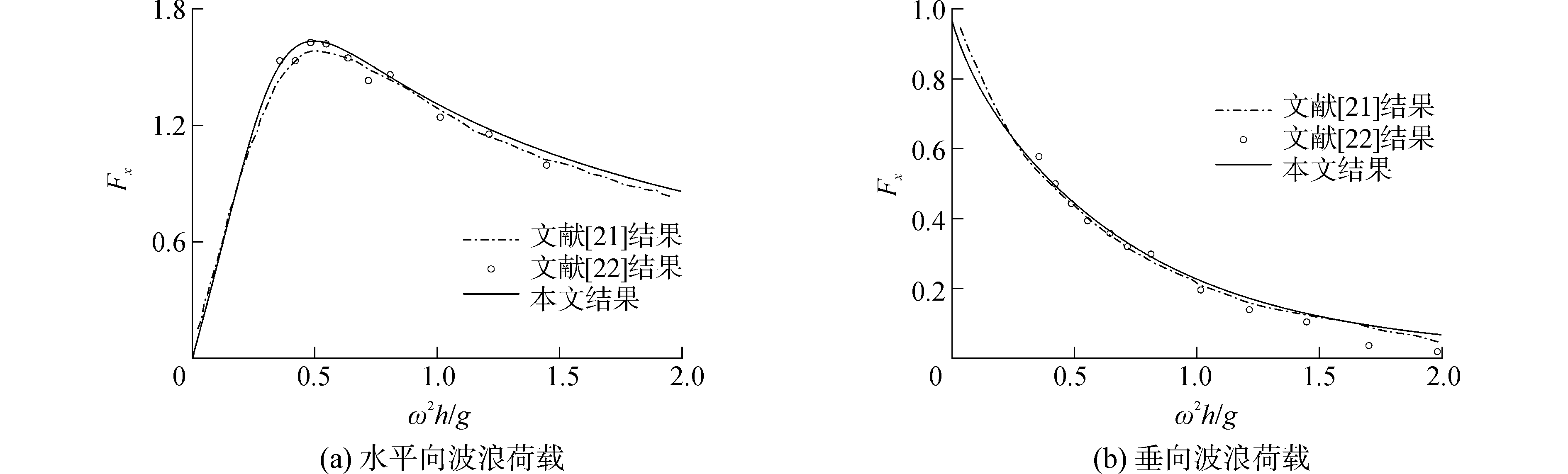
3.1 波浪荷载及反、透射系数验证静水深h设为1个波长,垂向薄板长度设为0,水平板吃水深度d为0.25 m,宽度a+b=0.5 m,其中a=b,T型结构转变为水面固定方箱。分别以ρgAd和ρgA(a+b)对水平向及垂向波浪荷载无量纲化,图 2反映出本文计算结果与文献[21]的理论结果以及文献[22]的试验结果吻合良好。
|
Download:
|
| 图 2 水面固定方箱所受波浪荷载 Fig. 2 Horizontal and vertical wave loads on the fixed rectangular obstacle | |
令水平板吃水深度d/h=0.5,垂向薄板长度c/h=0.000 01。图 3(a)给出水平板长度与吃水深度比值分别为(a+b)/d为0、2、6、10时本文和文献[23]中反射系数Cr的比较情况,可见二者吻合良好。为进一步对计算结果进行验证,就波幅A=0.02 m,静水深h=0.5 m,结构物尺寸a/h=b/h=0.5,c/h=d/h=0.1的工况,采用文献[24]中的CIP方法进行数值模拟,对比结果如图 3(b)所示。基于无粘、无旋假设的势流理论,理论结果中无能量损耗。由图 3(b)可见,理论值与数模结果趋势一致,数模结果由于存在能量耗散而基本小于理论值。

|
Download:
|
| 图 3 波浪反、透射系数的计算结果验证 Fig. 3 Verification for the calculation of wave reflection and transmission coefficients | |
为单独研究水平板长度的影响,设定其吃水深度d/h=0.1,同时固定垂向薄板的长度为c/h=0.1,分别取a/h=b/h为0.2、0.6、1.0、1.4和1.8。如图 4(a)所示,随入射波长的减小,水平向波浪荷载呈先增后减的趋势。当入射波长较大时(kh < 2),水平板长度的延伸会使水平向波浪荷载增大,而当入射波长较小时则呈相反的变化趋势。随着水平板长度的增加,水平向波浪荷载趋于一个稳定值。图 4(b)反映了垂向波浪荷载随水平板长度的变化情况,可见二者几乎成比例增长,这主要是由于垂向受力面积与水平板的长度成正比。在入射波长很大(kh→0)时,水平板长度相较于波长极小,流场内压力变化由波面起伏引起,因此垂向波浪力振幅为ρgA(a+b)。由图 4(c)可见,增大水平板长度能有效减少波浪透射,但其消波性能提升程度呈递减趋势。因此在工程应用中应适当限制防波堤的长度,在保证消波效果的情况下降低建造成本,同时也将垂向波浪荷载控制在合理范围内。

|
Download:
|
| 图 4 不同水平板长度下的波浪荷载及透射系数 Fig. 4 Wave loads and transmission coefficient under different horizontal plate length | |
设定水平板长度为(a+b)/h=1.2,并将垂向薄板安装于水平板正中的位置,其长度为c/h=0.1。从图 5(a)可以看出,由于受力面积的增加,水平向波浪荷载随着水平板吃水深度的增加而增大。同时,水平向波浪荷载峰值位置随水平板吃水深度的增加向低频区偏移,峰值高度几乎成比例增长。当入射波数较大时,随吃水深度的增加,水平向波浪荷载逐渐趋于稳定。图 5(b)中长波情况下垂向波浪力振幅均趋近于2.4,这是由于受力面积均为1.2h。由于波浪能在垂向上指数衰减,垂向波浪荷载也随水平板吃水深度的增加而减小。图 5(c)反映了波浪透射系数随水平板吃水深度的变化情况,可见增大吃水深度能明显减少波浪透射。

|
Download:
|
| 图 5 不同水平板吃水深度下的波浪荷载及透射系数 Fig. 5 Wave loads and transmission coefficient under different draft depth of the horizontal plate | |
为单独讨论垂向薄板对波浪荷载及结构物消波性能的影响,固定水平板长度为1.2倍水深。
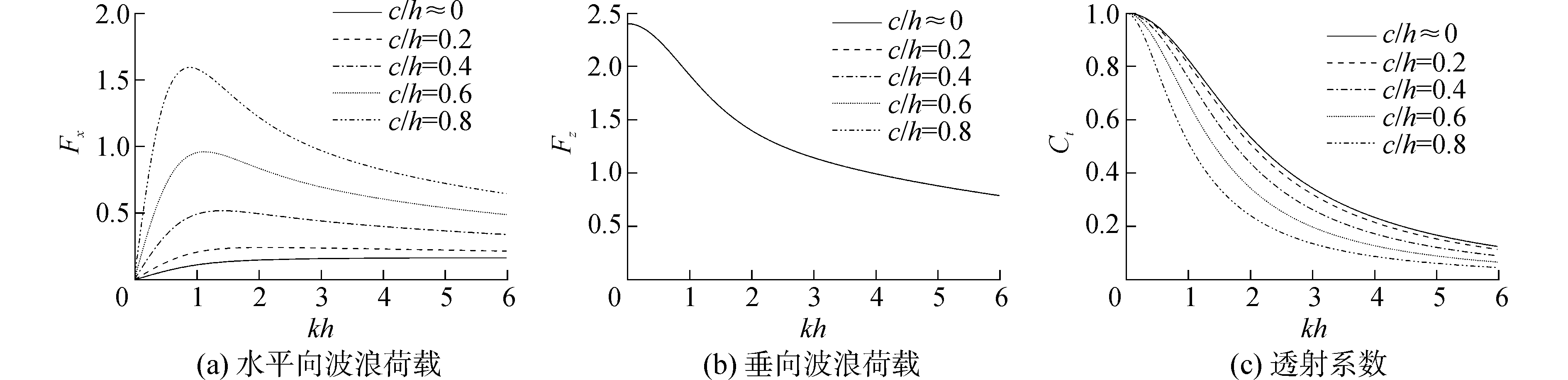
3.3.1 垂向薄板长度的影响设定水平板吃水深度为0.05倍水深,垂向薄板仍安装于水平板的正中位置。由图 6(a)可见,延长垂向薄板长度与增加水平板吃水深度有着类似的效果,不同之处在于其影响程度随着竖板长度的增加而增大。图 6(b)表明垂向薄板长度的增加对结构物所受到的垂向波浪力几乎没有影响,这是因为垂向薄板的存在主要限制水体的水平向运动,同时不会改变结构物的垂向受力面积。如图 6(c)所示,当垂向薄板长度大于0.2倍水深之后,继续增加其长度能有效减少波浪的透射。在实际工程中,延长垂向薄板的长度相较于增加水平板吃水深度更为简便,且成本更低。
|
Download:
|
| 图 6 不同垂向薄板长度下的波浪荷载及透射系数 Fig. 6 Wave loads and transmission coefficient under different vertical sheet length | |
设定水平板吃水深度为0.1倍水深,垂向薄板长度为0.5倍水深,将垂向薄板的安装位置从水平板的迎浪侧向背浪侧移动。图 7(a)反映了结构物受到的水平向波浪荷载随垂向薄板位置移动而变化的情况。当垂向薄板从a/h=0.02处移动到0.31处时,水平向波浪荷载明显减小,而继续移动则变化不大。由图 7(b)可见,结构物受到的垂向波浪力在垂向薄板从水平板的迎浪侧向后移动的过程中持续增大。因为随着垂向薄板后移,水平板下积聚的波浪能越多。如图 7(c)所示,垂向薄板从水平板正中向两侧移动能略微提升结构物的消波性能。当垂向薄板向两侧移动相同距离时,结构物形状一致,且消波性能相同。

|
Download:
|
| 图 7 不同垂向薄板位置下的波浪荷载及透射系数 Fig. 7 Wave loads and transmission coefficient under different position of vertical sheet | |
1) 在低频区(kh < 2)与高频区,水平板长度的增加会使水平向波浪荷载分别沿相反的趋势变化,垂向波浪荷载则大致与水平板长度线性相关。水平向波浪荷载随水平板吃水深度的增加而增大,垂向波浪荷载则呈现出相反的变化趋势。
2) 增加T型结构中水平板的长度及吃水深度,均能有效提升防波堤的消波性能。
3) 垂向薄板长度的增加能显著增大水平向波浪荷载,而垂向波浪荷载几乎不受影响;安装较长的垂向薄板能有效减少波浪透射。
4) 垂向薄板位于水平板迎浪侧时,结构物受到的水平向波浪荷载较大;垂向薄板从水平板的迎浪侧向背浪侧移动会持续增大T型结构受到的垂向波浪荷载。垂向薄板位置对结构物的消波性能影响较小,且位于对称位置时消波性能相同。
| [1] |
王国玉, 黄璐, 任冰, 等. T型透空式防波堤消波性能的理论分析[J]. 水利水电科技进展, 2014, 34(2): 1-5. WANG Guoyu, HUANG Lu, REN Bing, et al. Theoretical analysis of the performance of wave dissipation of T-type open breakwater[J]. Advances in science and technology of water resources, 2014, 34(2): 1-5. (  0) 0)
|
| [2] |
URSELL F. The effect of a fixed vertical barrier on surface waves in deep water[J]. Mathematical proceedings of the Cambridge philosophical society, 1947, 43(3): 374-382. DOI:10.1017/S0305004100023604 (  0) 0)
|
| [3] |
STOKER J J. Water waves[M]. New York: Interscience Publishers, 1957.
(  0) 0)
|
| [4] |
IJIMA T, OZAKI S, EGUCHI Y, et al. Breakwater and quay well by horizontal plates[J]. Coastal engineering proceedings, 1970(12): 1537-1556. (  0) 0)
|
| [5] |
NEELAMANI S, VEDAGIRI M. Wave interaction with partially immersed twin vertical barriers[J]. Ocean engineering, 2002, 29(2): 215-238. DOI:10.1016/S0029-8018(00)00061-5 (  0) 0)
|
| [6] |
USHA R, GAYATHRI T. Wave motion over a twin-plate breakwater[J]. Ocean engineering, 2005, 32(8/9): 1054-1072. (  0) 0)
|
| [7] |
GÜNAYDIN K, KABDASLI M S. Investigation of Π-type breakwaters performance under regular and irregular waves[J]. Ocean engineering, 2007, 34(7): 1028-1043. DOI:10.1016/j.oceaneng.2006.03.015 (  0) 0)
|
| [8] |
顾倩, 张宁川. 斜向波浪作用下双层水平板式防波堤消防浪性能试验研究[J]. 中国科学:物理学力学天文学, 2016, 46(2): 94-107. GU Qian, ZHANG Ningchuan. Experimental studies on oblique wave and twin-plate breakwater[J]. Scientia sinica physica, mechanica & astronomica, 2016, 46(2): 94-107. (  0) 0)
|
| [9] |
CHO I H. Transmission coefficients of a floating rectangular breakwater with porous side plates[J]. International journal of naval architecture and ocean engineering, 2016, 8(1): 53-65. DOI:10.1016/j.ijnaoe.2015.10.002 (  0) 0)
|
| [10] |
DUAN Wenyang, XU Shupeng, XU Qianlong, et al. Performance of an F-type floating breakwater:a numerical and experimental study[J]. Proceedings of the institution of mechanical engineers, part M:journal of engineering for the maritime environment, 2017, 231(2): 583-599. DOI:10.1177/1475090216673461 (  0) 0)
|
| [11] |
ZHAN Jiemin, CHEN Xuebin, GONG Yejun, et al. Numerical investigation of the interaction between an inverse T-type fixed/floating breakwater and regular/irregular waves[J]. Ocean engineering, 2017, 137: 110-119. DOI:10.1016/j.oceaneng.2017.03.058 (  0) 0)
|
| [12] |
NEELAMANI S, RAJENDRAN R. Wave interaction with T-type breakwaters[J]. Ocean engineering, 2002, 29(2): 151-175. DOI:10.1016/S0029-8018(00)00060-3 (  0) 0)
|
| [13] |
何军, 蒋昌波, 李冬, 等. T型防波堤与波浪相互作用数值研究[J]. 海洋工程, 2010, 28(1): 50-57. HE Jun, JIANG Changbo, LI Dong, et al. Numerical study on T-type breakwaters interaction with wave[J]. The ocean engineering, 2010, 28(1): 50-57. DOI:10.3969/j.issn.1005-9865.2010.01.008 (  0) 0)
|
| [14] |
刘宏霄, 董国海, 许条建. T型开孔防波堤消波性能研究[J]. 中国水运, 2017, 17(4): 181-185, 190. LIU Hongxiao, DONG Guohai, XU Tiaojian. Research on the wave dissipating properties of T-type porous breakwaters[J]. China water transport, 2017, 17(4): 181-185, 190. (  0) 0)
|
| [15] |
PORTER R, EVANS D V. Complementary approximations to wave scattering by vertical barriers[J]. Journal of fluid mechanics, 1995, 294: 155-180. DOI:10.1017/S0022112095002849 (  0) 0)
|
| [16] |
LOVAS S, MEI C C, LIU Yuming. Oscillating water column at a coastal corner for wave power extraction[J]. Applied ocean research, 2010, 32(3): 267-283. DOI:10.1016/j.apor.2010.06.004 (  0) 0)
|
| [17] |
DENG Zhengzhi, HUANG Zhenhua, LAW A W K. Wave power extraction by an axisymmetric oscillating-water-column converter supported by a coaxial tube-sector-shaped structure[J]. Applied ocean research, 2013, 42: 114-123. DOI:10.1016/j.apor.2013.05.006 (  0) 0)
|
| [18] |
DENG Zhengzhi, HUANG Zhenhua, LAW A W K. Wave power extraction from a bottom-mounted oscillating water column converter with a V-shaped channel[J]. Proceedings of the royal society A mathematical, physical and engineering sciences, 2014, 470(2167): 20140074. DOI:10.1098/rspa.2014.0074 (  0) 0)
|
| [19] |
GARRETT C J R. Wave forces on a circular dock[J]. Journal of fluid mechanics, 1971, 46(1): 129-139. DOI:10.1017/S0022112071000430 (  0) 0)
|
| [20] |
GARRETT C J R. Bottomless harbours[J]. Journal of fluid mechanics, 1970, 43(3): 433-449. DOI:10.1017/S0022112070002495 (  0) 0)
|
| [21] |
MARUO H. On the increase of the resistance of a ship in Rough Seas (I)[J]. British journal of ophthalmology, 1957, 1957(101): 235-237. (  0) 0)
|
| [22] |
NOJIRI N, MURAYAMA K. A study on the drift force on two-dimensional floating body in regular waves[[J]. Trans west-Japan soc nav arch, 1975, 51: 131-52. (  0) 0)
|
| [23] |
MEI C C, BLACK J L. Scattering of surface waves by rectangular obstacles in waters of finite depth[J]. Journal of fluid mechanics, 1969, 38(3): 499-511. DOI:10.1017/S0022112069000309 (  0) 0)
|
| [24] |
ZHAO Xizeng, HU Changhong. Numerical and experimental study on a 2-D floating body under extreme wave conditions[J]. Applied ocean research, 2012, 35: 1-13. DOI:10.1016/j.apor.2012.01.001 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


