2. 高技术船舶与深海开发装备协同创新中心, 上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
海浪频谱不仅描述了海浪的内部能量结构,同时也间接地表征了其外部特征,是海浪理论研究的核心问题之一。海浪生成机制、海浪预测预报、海洋环境的研究以及海浪对海洋工程、海岸工程的作用等,都与频谱密切相关[1]。
针对海浪频谱的研究,Kitaigorodskii假设可以使用组成波频率、重力加速度、风速、风区四个变量来表示风浪谱,并且当风浪充分成长时,相同风速下的无因次风浪频谱具有相同的形状。目前常使用的理论风浪频谱包括P-M谱、JONSWAP谱等,这些理论谱将谱能量形式表示为与有义波高的关系,能够简化工程问题,但通常只针对特定海域完全适用。为解决理论谱的适用性问题,本文进行了基于实测数据的修正工作[2-5]。
针对海浪特征的单点观测,重力式浮标或浮筒能够测得高精度的波浪数据资料,荷兰Datawell公司生产的“波浪骑士”式测波浮标(WR)为其中典型产品。重力式浮标通过测量自身的垂向加速度,计算波高历程,并根据维纳-辛钦定理,间接完成对海浪频谱的提取。经检测,“波浪骑士”式浮标能够给出可信的实测海浪频谱,其测量得到的数据作为本文的讨论依据[6-8]。
WAVEWATCH-Ⅲ海浪模型是美国国家海洋大气局和环境预报中心联合开发的第三代海浪模型。该模型充分考虑波浪成长和耗散的情况,能够有效地模拟风、浪、流、海冰等不同输入项作用下的海浪演化,其提供的数值结果可以作为实测数据的补充资料。本文采用该模型的计算结果对修正方法进行了补充检验[9-11]
本文以位于目标岛屿处的“波浪骑士”式浮标实测得到的频谱数据为样本,根据谱峰频率的位置,筛选出研究针对的风浪数据点;通过将实测风浪频谱与JONSWAP谱比较,提出增加参数的修正JONSWAP谱,进而完成了对目标海域风浪谱的拟合修正。为验证结果有效性,利用其他月份的实测资料与修正得到的理论谱进行比对,并通过WAVEWATCH-Ⅲ模型对目标海域进行数值模拟,利用计算结果对理论谱做进一步验证。
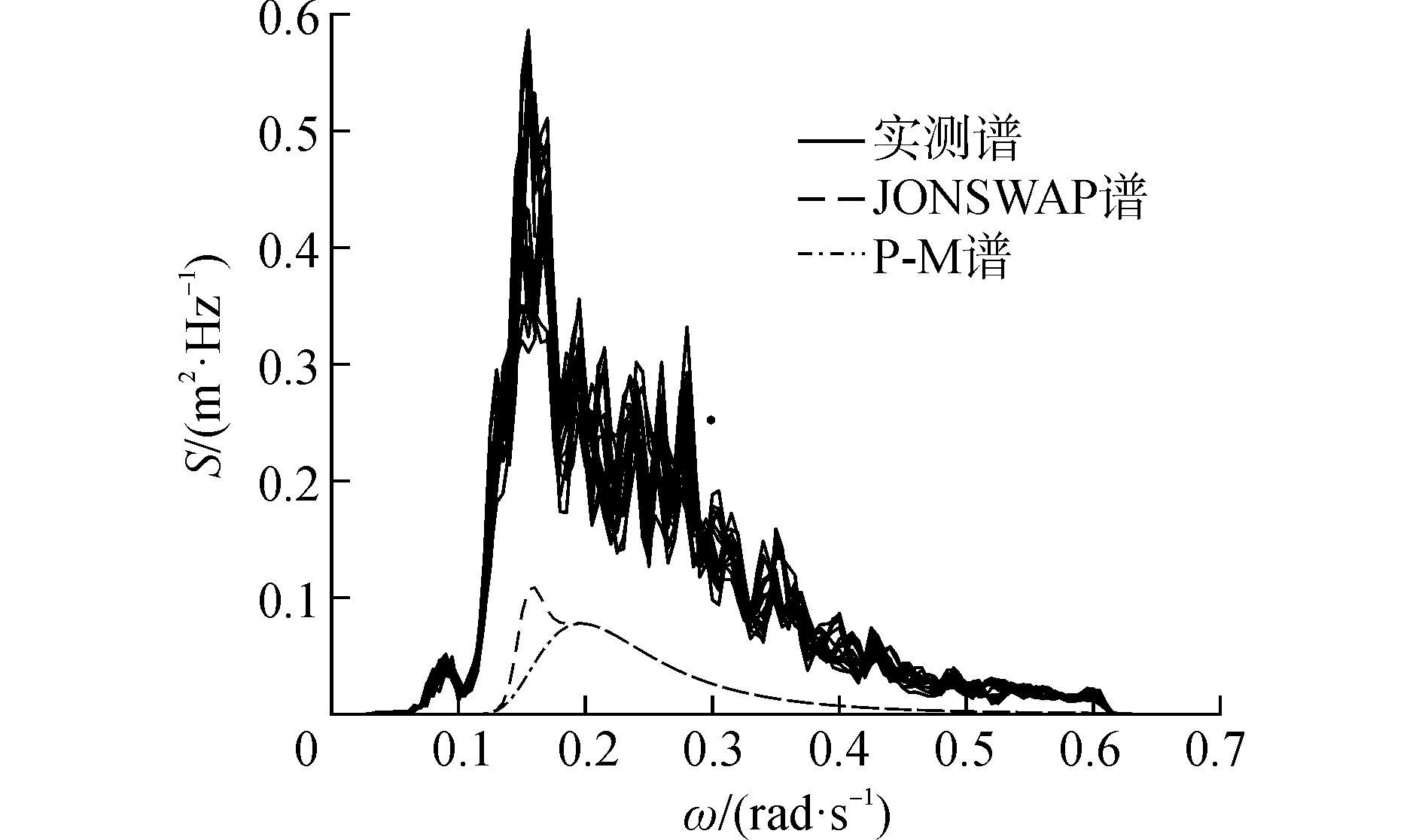
1 实测资料风浪情况筛选针对海浪频谱的拟合,现有根据不同海域实测资料求得的多种理论靶谱,常用的有P-M谱和JONSWAP谱等。为了确定这两种理论谱相对于该特定海域的适用性,利用目标岛屿处2014年8月份的实测资料,将实测谱与这两种理论谱进行比较,得到典型情况如图 1所示。
|
Download:
|
| 图 1 实测频谱与P-M谱、JONSWAP谱对比典型情况 Fig. 1 The typical case of comparison between the measured spectra and P-M and JONSWAP spectrum | |
“波浪骑士”浮标给出的实测频谱是根据30 min内的浮标位移数据经过傅里叶变换得到的。计算两个相邻谱的位移数据起始时间间隔为3 min。图 1共绘制了18个实测谱,也就是谱计算的初始时间最大间隔为54 min。
根据上面典型情况可以看出,P-M谱和JONSWAP谱都不能理想地表达目标海域的海浪频谱情况,同时注意到P-M谱与JONSWAP谱之间的差别不明显。
为了解释两种理论谱差别不明显的原因,分别列出两者的表达展式,并对应到典型情况中进行分析。
P-M谱的表达式为
| $ {{S}_{\text{P-M}}}\left( \omega \right)=\frac{0.78}{{{\omega }^{5}}}\text{exp}\left(-\frac{3.11}{{{H}_{s}}^{2}{{\omega }^{4}}} \right) $ | (1) |
JONSWAP谱的表达式为
| $ S\left( \omega \right)=\frac{0.78}{{{\omega }^{5}}}\text{exp}\left(-\frac{3.11}{{{H}_{s}}^{2}{{\omega }^{4}}} \right){{\gamma }^{\text{exp}\left[\frac{-\left( \omega-{{\omega }_{\text{max}}}^{2} \right)}{2{{\sigma }^{2}}{{\omega }_{\text{max}}}^{2}} \right]}} $ | (2) |
对比式(1)、(2)可知,JONSWAP谱是在P-M谱的基础上乘以一个峰高因子γ,从而改变谱峰频率附近频谱形状,使海浪能量更集中于谱峰频率附近。峰高因子γ项为谱峰值与P-M谱峰值的比值,通常为1~7的随机变量,图 1中JONSWAP谱采用的参数γ为其均值,也是常用值3.3[12]。
结合上述分析,在图 1中发现JONSWAP谱与P-M谱差别不明显的原因是:实测谱的谱峰频谱在理论P-M谱中对应的能量密度很小,更极端的情况甚至会为零。从而导致即使通过乘以峰高因子γ项来提高实测谱峰频率附近的能量密度,也不会对频谱形状产生显著影响。此时针对JONSWAP谱而言,它对P-M谱的修正作用没有得到很好的表达。实质上,这种情况是由于P-M谱与实测谱的谱峰频率相差过大导致的。
根据式(1)可知,P-M谱的谱峰频谱只与有义波高Hs有关。这意味着,在理论谱的描述中,如果有义波高Hs确定,谱峰频率也将随之确定。
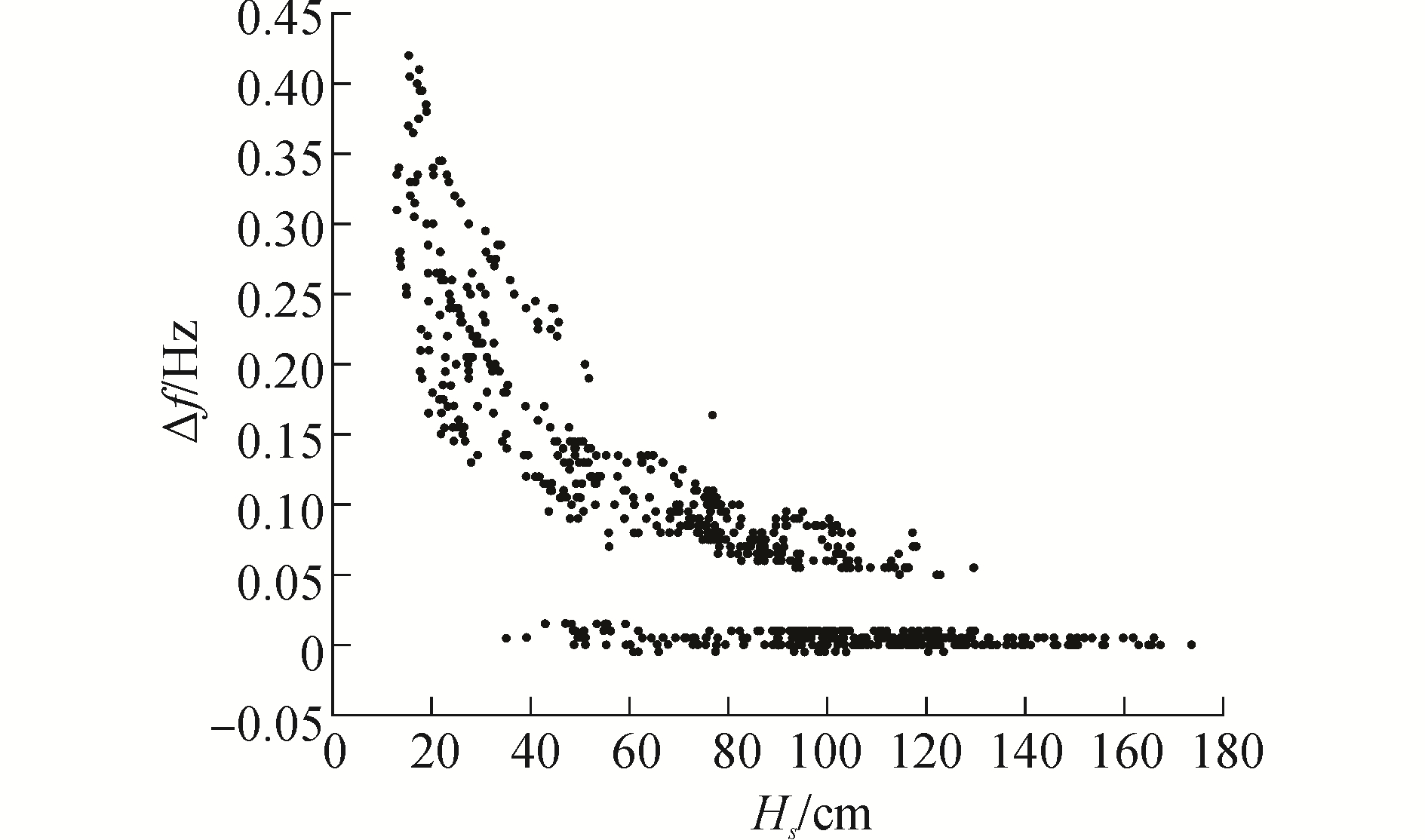
利用“波浪骑士”浮标测得的有义波高,绘制实测数据点的理论P-M谱与实测谱的谱峰频率差Δf相对于有义波高Hs的分布散点图,试图发现谱峰频率差Δf的分布规律,进而找出两者相差过大的原因。散点图如图 2所示。
|
Download:
|
| 图 2 P-M谱与实测谱的谱峰频谱差 Fig. 2 The difference of spectral peak frequency between measured spectrum and P-M spectrum | |
在图 2中能看到,谱峰频谱差Δf呈现为两种分布规律:1)分布在0附近,与有义波高无关的直线;2)恒为正值,且随着有义波高的增大而减小的曲线。
假设理论谱合理,且实际海浪情况符合理论谱的限制条件,那么上述第一种情况描述的现象应该是合理的。所以应从理论谱的限制条件入手,分析出现第二种情况出现的原因。
理论谱的限制条件为充分成长的纯风浪情况。在前面的处理中,已经通过绘制一组实测频谱,并用上包络的方式表示这段时间内的充分成长的谱形状,完成了对谱充分成长的表达。但是实际海浪情况中存在非纯风浪情况,因此还需进行纯风浪的筛选工作。
海浪中的涌浪能量多集中于低频区,当涌浪成分过大时,谱的能量将向低频率区集中。上述Δf的两种分布情况中,一种情况表现为实测谱峰与理论风浪谱峰位置吻合;另一种情况中,实测谱峰的对应频率较小,即谱的能量向低频区集中。推测这种情况是由于实际海浪成分中存在着较大比例的涌浪成分导致的,从而呈现出与理论风浪谱不同的能量结构。所以在进行根据实测资料的南海风浪频谱拟合时,应该先筛选出符合第一种情况的数据点。[13]
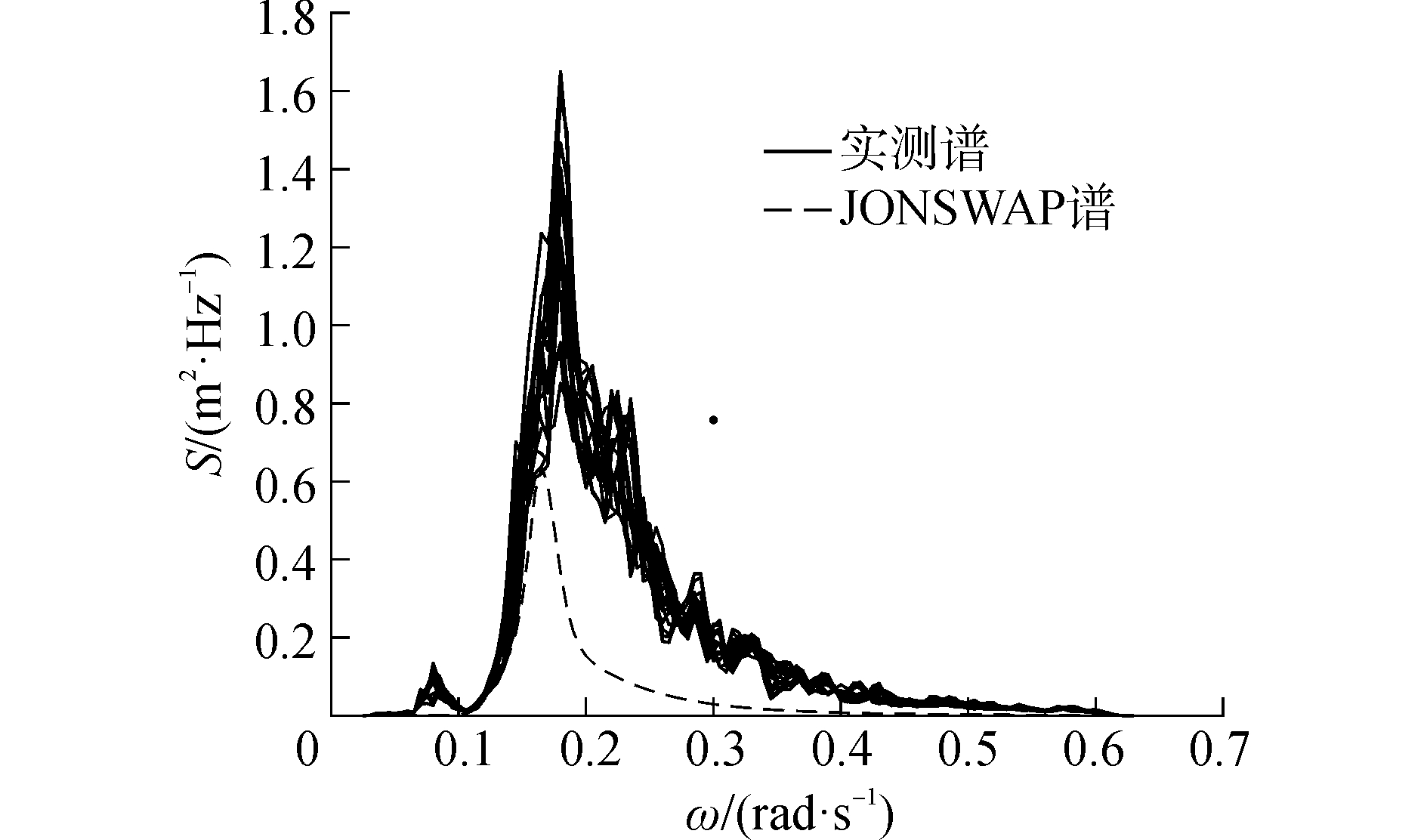
2 增加参数的JONSWAP谱拟合根据已经筛选出的风浪数据点将峰高因子γ为3.3的JONSWAP谱与实测风浪谱进行比较,典型情况如图 3所示。
|
Download:
|
| 图 3 JONSWAP谱与实测风浪谱比较典型情况 Fig. 3 The typical case of comparison between the measured wind-wave spectra and JONSWAP spectrum | |
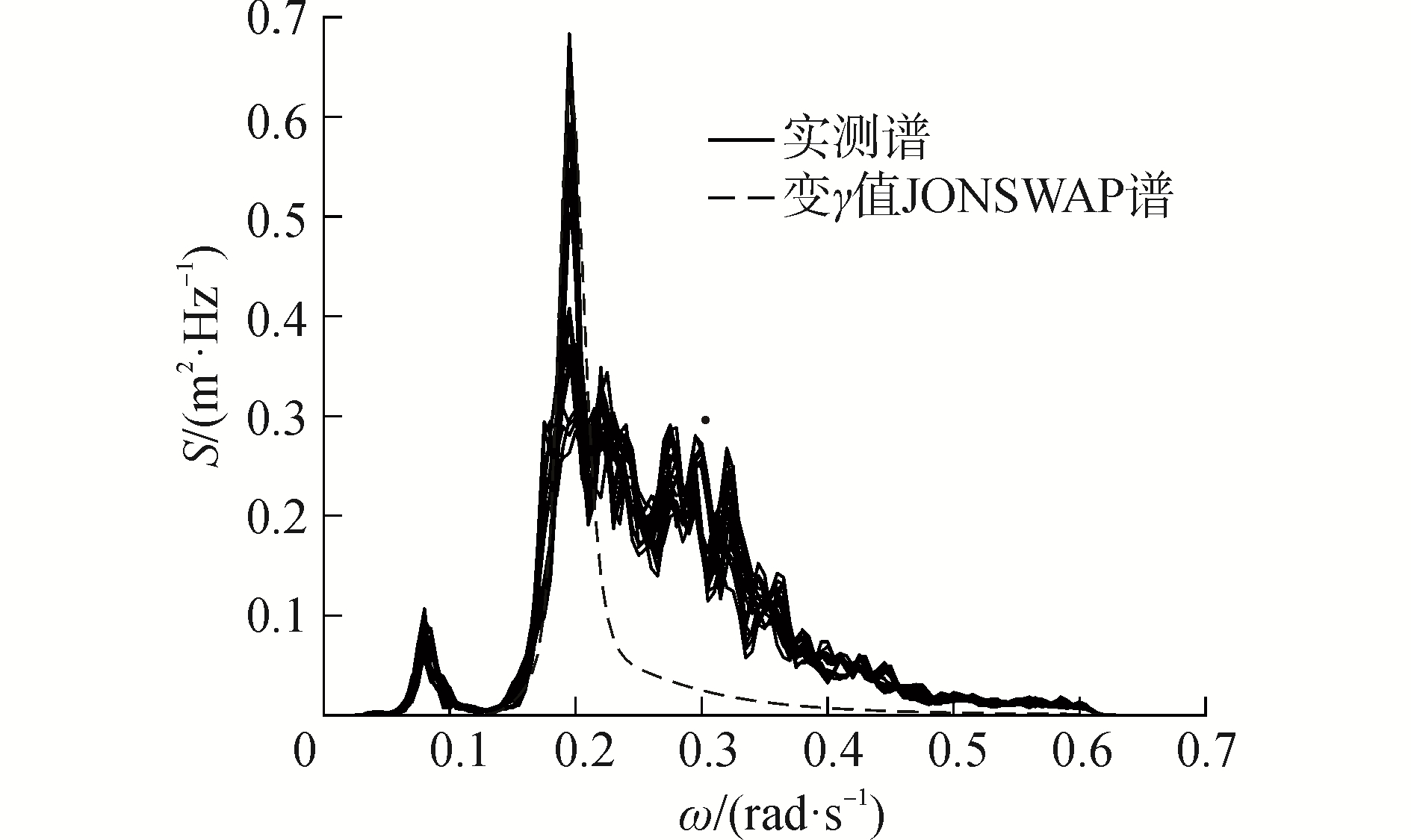
能够看出,峰高因子为3.3的JONSWAP谱不能很好地表达实测风浪谱。于是通过改变谱峰因子,以JONSWAP谱作为靶谱进行拟合。针对各数据点,拟合得到不同的最佳谱峰因子值。其中典型情况如图 4所示,该典型情况对应的峰高因子γ=10.5。
|
Download:
|
| 图 4 变γ值的JONSWAP与实测谱比较典型情况 Fig. 4 The typical case of comparison between the measured spectra and JONSWAP spectrum with variational γ | |
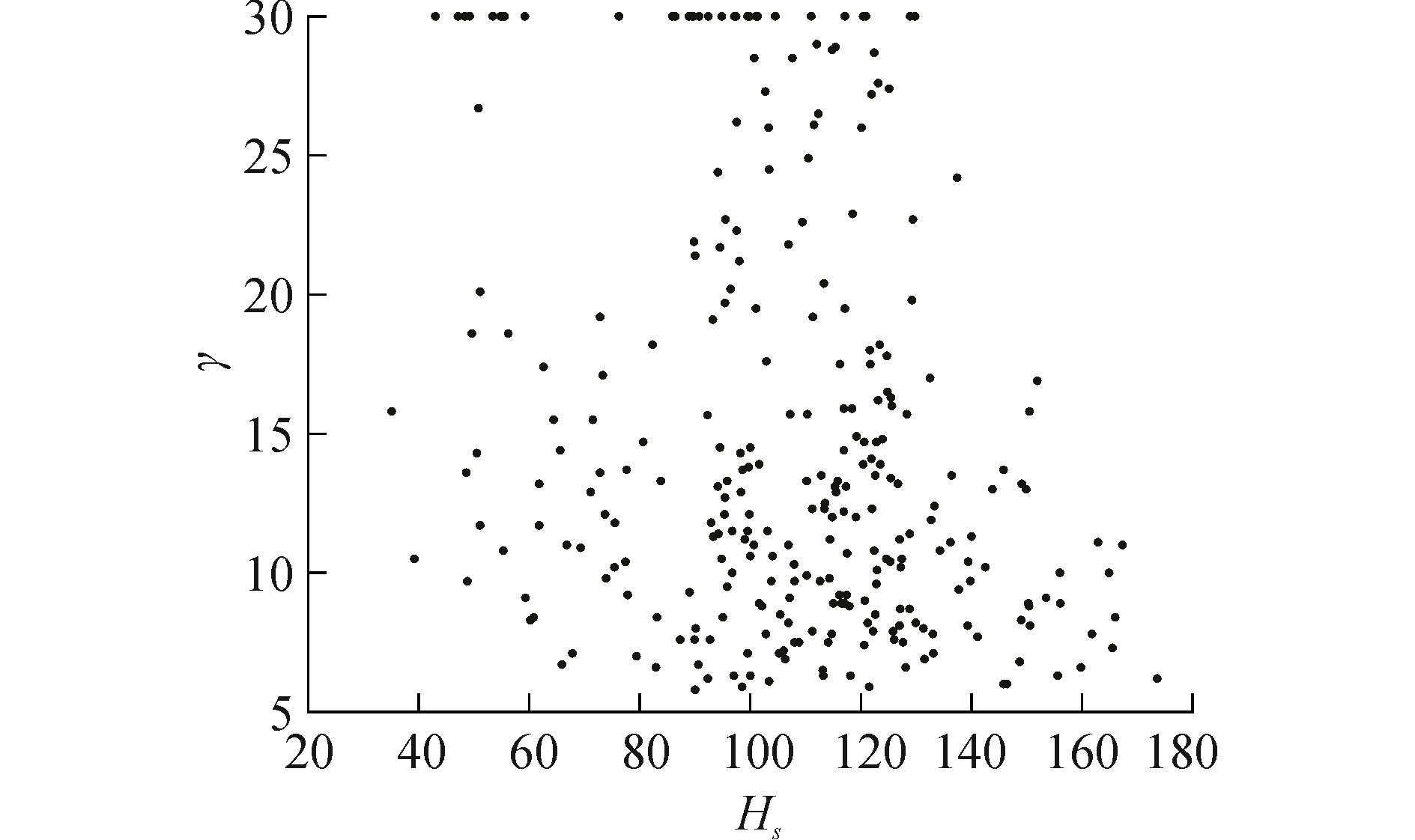
为研究峰高因子γ拟合后的分布规律,绘制各数据点对应的最佳峰高因子与有义波高的散布图如图 5所示。
|
Download:
|
| 图 5 变γ值的JONSWAP谱γ值与Hs值关系 Fig. 5 The relationship between γ and Hs in JONSWAP spectrum | |
根据图 4、5发现,改变峰高因子γ的JONSWAP谱虽然能够在低频和谱峰频率附近处很好地表达实测谱,但是在高频处明显偏小。而且,拟合得到的γ分布也无明显规律性,因此认为JONSWAP谱不能直接作为该海域风浪拟合的靶谱。
增大峰高因子实际上是提升谱峰频率附近的谱能量密度值。为了在高频处更好地拟合实测谱,不能只通过增大峰高因子来升高谱峰值,于是提出双参数拟合方式,表达式如下
| $ \begin{align} &S\left( \omega \right)=\left( 10.797\ 6-\sqrt{3.797\ 9\gamma +55.531\ 0} \right)\times \\ &\ \ \ \ \ \ \ \ \ \ \ \frac{0.78}{{{\omega }^{5}}}\text{exp}\left[-\frac{3.11}{{{H}_{s}}^{2}{{\omega }^{4}}} \right]{{\gamma }^{\text{exp}\left[\frac{-\left( \omega-{{\omega }_{\text{max}}}^{2} \right)}{2{{\sigma }^{2}}{{\omega }_{\text{max}}}^{2}} \right]}} \\ \end{align} $ | (3) |
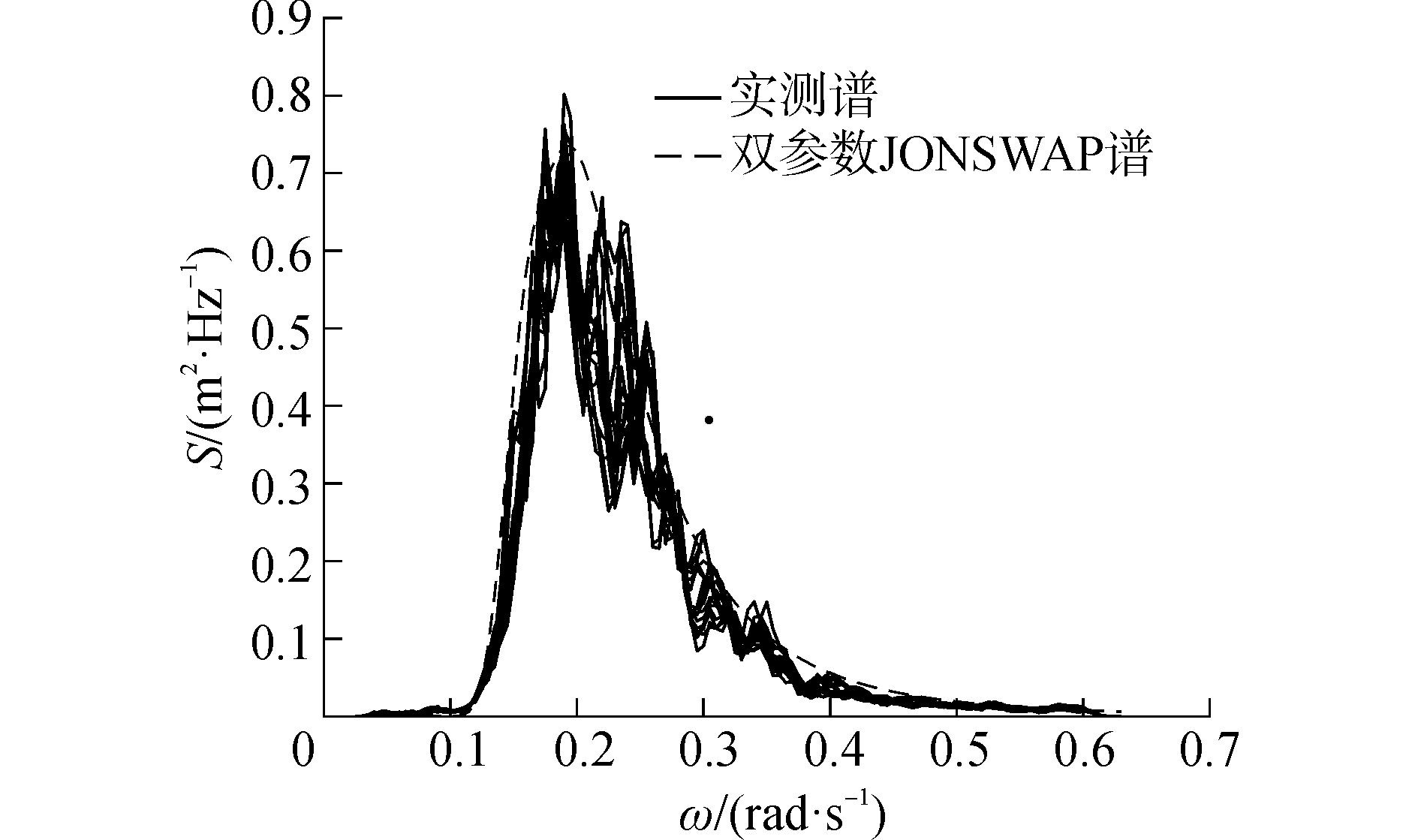
增加参数k,表示在改变峰高因子γ的同时,整体调整谱高度,从而使频谱宽度可以较单参数拟合更宽,典型情况如图 6所示。
|
Download:
|
| 图 6 双参数JONSWAP谱与实测风浪谱比较典型情况 Fig. 6 The typical case of comparison between the measured wind-wave spectra and JONSWAP spectrum with two-parameter | |
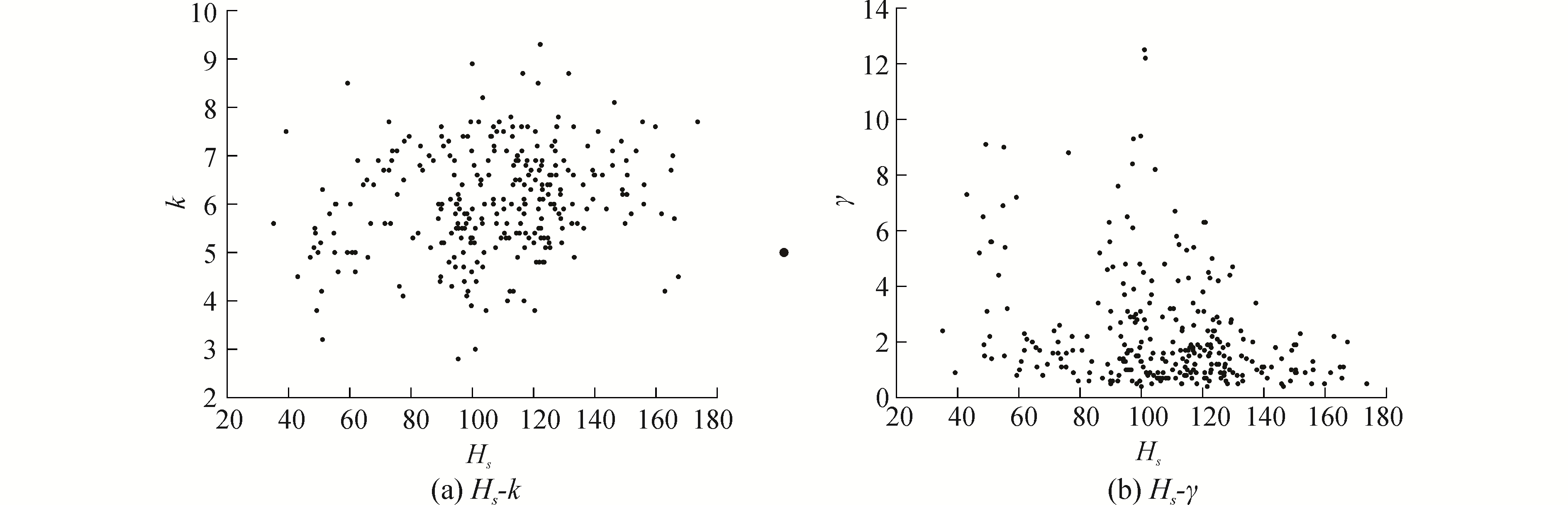
图 6中利用双参数谱作为靶谱能够很好地拟合实测谱。为了完成确定的靶谱形式,需要求出目标海域所对应的两个参数的值,或者找出两参数与有义波高之间的近似关系。针对各数据点,通过同时改变两参数的方式,寻找拟合效果最佳的参数组合,并分别绘制两参数相对于有义波高的散点图,如图 7所示。
|
Download:
|
| 图 7 Hs和k,γ的关系 Fig. 7 The relationship between Hs and k, γ | |
观察图 7发现,使用双参数拟合的方法虽然能够对实测频谱进行较为理想的拟合表达,但是拟合参数的分布依旧无明显的规律性。这种双参数谱无法直接作为靶谱,需要对其进行进一步的修改。
式(3)中包含的两个参数k和γ同时对谱峰高度产生正向的影响,因此在谱峰高度确定的情况下,两参数之间可能存在着负相关的关系。
绘制两参数的分布散点图,发现两参数确实存在着明显的负相关关系。对它们之间的这种关系进行拟合处理,得到拟合的分布散点图如图 8所示。

|
Download:
|
| 图 8 γ值与k值关系 Fig. 8 The relationship between γ and k | |
在选取的三种拟合方式中,二次线性拟合的修正确定系数最大,故采用这种拟合方式,并在95%置信区间内选取最为合适的参数。将拟合结果带回原表达式中,得到单参数谱形式如下
| $ \begin{align} &S\left( \omega \right)=\left( 10.797\ 6-\sqrt{3.797\ 9\gamma +55.531\ 0} \right)\times \\ &\ \ \ \ \ \ \ \ \ \ \ \frac{0.78}{{{\omega }^{5}}}\text{exp}\left[-\frac{3.11}{{{H}_{s}}^{2}{{\omega }^{4}}} \right]{{\gamma }^{\text{exp}\left[\frac{-\left( \omega-{{\omega }_{\text{max}}}^{2} \right)}{2{{\sigma }^{2}}{{\omega }_{\text{max}}}^{2}} \right]}} \\ \end{align} $ | (4) |
利用该修改后的单参数谱对实测谱进行重新拟合,求得γ=1.4,并得到拟合理想的典型情况如图 9所示。

|
Download:
|
| 图 9 修改后的单参数JONSWAP谱与实测风浪谱比较典型情况 Fig. 9 The typical case of comparison between the measured wind-wave spectra and the JONSWAP spectrum with modified parameter | |
经过上面的讨论认为,通过拟合增加参数的JONSWAP谱,并表达两参数间的关系,可以得到修正的单参数风浪谱。将得到的修正谱作为靶谱,能够很好地拟合实测资料。
3 方法有效性验证为检验修正方法的有效性,分别利用拟合数据集外的实测资料和数值结果对修正得到的理论谱进行对比验证。
修正得到的单参数谱是根据目标岛屿处2014年8月份的实测资料求得的,利用9月份的实测资料对修正谱进行验证。
同样需要先筛选9月份的风浪数据点。在筛选数据点时,注意到9月份有“1415”号台风“海鸥”过境并对目标岛屿产生了显著影响。考虑到台风过境时的风浪情况不能采用假设中的固定风区方法推算,因此在对9月份进行风浪资料预处理时,应该筛除有义波高过大的台风风浪[14]。
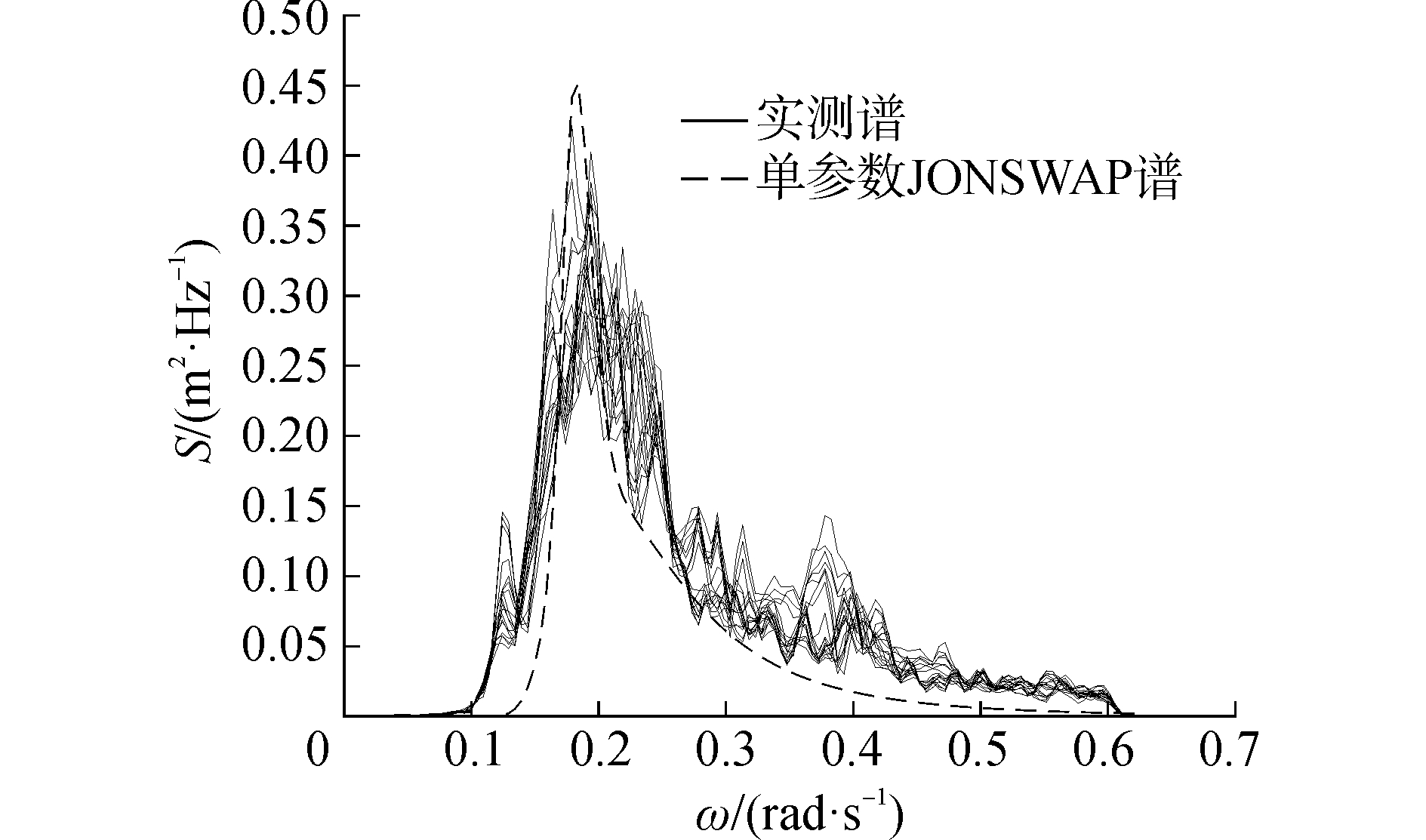
将根据8月份数据资料求得的单参数谱作为靶谱,并带入γ=1.4对9月份进行拟合,得到典型情况如图 10所示。
|
Download:
|
| 图 10 9月份验证结果 Fig. 10 The verification result with measured data of September | |
通过图 10可以看出,利用8月份实测资料求得的海浪频谱对于9月份依然适用。
第三代波浪模式WAVEWATCH-Ⅲ可以在不同输入项的情况下对波浪的演化进行模拟,并得到测量点的波浪参数和频谱数据,能够作为实测数据的补充资料。
以目标岛屿的实测地形为数值模拟地形,以“波浪骑士”浮标的位置为测量点,用WAVEWATCH-Ⅲ对该特定海域进行模拟。
为使目标海域产生充分成长的风浪,在WAVEWATCH-Ⅲ中设海面初始状态为静场,输入项为北向10 m/s的定常风,计算时间为2 h,得到测量点的波参数与谱数据。
此时测量点的有义波高Hs=1.011 m,谱峰频率为fp=0.198 3 Hz。为验证根据上述方法修正得到的理论谱的有效性,先用上述的双参数谱对该数值模拟得到的谱进行拟合,再与γ=1.4时的单参数谱,即式(4)描述的理论谱进行比较,得到图 11。

|
Download:
|
| 图 11 WAVEWATCH-Ⅲ数值模拟频谱与拟合的双参数谱、γ=1.4时的单参数谱对比 Fig. 11 The comparison between the spectrum computed by WAVEWATCH-Ⅲ, the spectrum with two-parameter and the JONSWAP spectrum with modified parameter | |
在图 11中可以看到,WAVEWATCH-Ⅲ在进行数值模拟时在高频处又产生了一个波浪成分,本文对高频处波浪成分的成因和意义不做讨论,仅关注经WAVEWATCH-Ⅲ模拟得到的频谱在受高频波浪影响较小部分的拟合情况。
发现对于充分成长的风浪成分,用双参数谱和γ=1.4的单参数谱都能够很好表达。同时数值模拟谱、双参数谱和单参数谱相差不多,因此认为本文中提出的γ=1.4的单参数谱能够适用于该海域。这也说明:提出在JONSWAP谱中增加参数的双参数谱、通过建立双参数谱中两参数的关系将双参数谱简化、用简化得到的单参数谱来表达目标海域的理论频谱是合理可行的。
4 结论1) 实测资料中的频谱谱峰与对应的理论风浪谱谱峰的位置关系吻合良好,或实测谱峰频率趋向低频区域。结合风、涌浪的能量特征,认为纯风浪情况下的实测谱峰频率应接近理论谱峰频率,可以此为依据筛选风浪数据。
2) JONSWAP谱增加的修正系数与峰高因子呈显著的负相关关系,可将修正谱退化为单参数谱形式。
3) 修正频谱与实测资料及WAVEWATCH-Ⅲ模型计算结果均吻合良好,针对目标海域修正方法有效。
4) 频谱能够直接表达海浪的内部能量结构,是随机波浪理论研究的工程核心问题。本文提出的理论频谱修正方法,可基于实测资料提出适合目标海域范围的修正谱,解决了原有理论谱适用性有限的问题,进而为研究海浪能量分布和波浪环境载荷提供分析手段。
由于实测资料有限,本文仅针对目标岛屿处进行理论谱的修正与检验,具有一定的局限性。如有更多的高精度实测资料,可将本文提出的修正方法应用于其他海域进行有效性验证。
| [1] |
俞聿修, 柳淑学. 随机波浪及其工程应用[M]. 4版. 大连: 大连理工大学出版社, 1992: 137. YU Yuxiu, LIU Shuxue. Random wave and its applications to engineering[M]. 4th ed. Dalian: Dalian University of Technology Press, 1992: 137. (  0) 0)
|
| [2] |
KITAIGORDSKⅡ S A, KRASITSKⅡ V P, ZASLAVSKⅡ M M. On Phillips' theory of equilibrium range in the spectra of wind-generated gravity waves[J]. Journal of physical oceanography, 1975, 5(3): 410-420. DOI:10.1175/1520-0485(1975)005<0410:OPTOER>2.0.CO;2 (  0) 0)
|
| [3] |
PIERSON JR W J, MOSKOWITZ L. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii[J]. Journal of geophysical research, 1964, 69(24): 5181-5190. DOI:10.1029/JZ069i024p05181 (  0) 0)
|
| [4] |
HASSELMYANN D E, DUNCKEL M, EWING J A. Directional wave spectra observed during JONSWAP 1973[J]. Journal of physical oceanography, 1980, 10(8): 1264-1280. DOI:10.1175/1520-0485(1980)010<1264:DWSODJ>2.0.CO;2 (  0) 0)
|
| [5] |
文圣常, 余宙文. 海浪理论与计算原理[M]. 北京: 科学出版社, 1984: 142-146. WEN Shengchang, YU Zhouwen. Wave theory and calculation principle[M]. Beijing: Science Press, 1984: 142-146. (  0) 0)
|
| [6] |
储小青.海浪波谱仪海浪遥感方法及应用基础研究[D].青岛: 中国科学院研究生院(海洋研究所), 2011. CHU Xiaoqing. The algorithm and applied basic study on remote sensing of ocean wave spectrum for ocean wave spectrometer[D]. Qingdao: Physical Oceanography in the Graduate School of Chinese Academy of Sciences, 2011. (  0) 0)
|
| [7] |
左其华. 现场波浪观测技术发展和应用[J]. 海洋工程, 2008, 26(2): 124-139. ZUO Qihua. Advances and applications of ocean wave measurement technology[J]. The ocean engineering, 2008, 26(2): 124-139. DOI:10.3969/j.issn.1005-9865.2008.02.017 (  0) 0)
|
| [8] |
徐曦煜, 王振占, 叶沛, 等. GPS浮标数据反演海浪谱的理论仿真与试验验证[J]. 海洋学报(中文版), 2014, 36(7): 34-44. XU Xiyu, WANG Zhenzhan, YE Pei, et al. Theoretic simulation and campaign validation of ocean wave spectrum retrieval from GPS buoy measurements[J]. Acta oceanologica sinica, 2014, 36(7): 34-44. DOI:10.3969/j.issn.0253-4193.2014.07.005 (  0) 0)
|
| [9] |
MENTASCHI L, BESIO G, CASSOLA F, et al. Performance evaluation of wavewatch Ⅲ in the Mediterranean Sea[J]. Ocean modelling, 2015, 90: 82-94. DOI:10.1016/j.ocemod.2015.04.003 (  0) 0)
|
| [10] |
吴萌萌, 王毅, 万莉颖, 等. WAVEWATCH Ⅲ模式在全球海域的数值模拟试验及结果分析[J]. 海洋预报, 2016, 33(5): 31-40. WU Mengmeng, WANG Yi, WAN Liying, et al. Numerical simulation experiments and analysis using WAVEWATCH Ⅲ in the global ocean[J]. Marine forecasts, 2016, 33(5): 31-40. (  0) 0)
|
| [11] |
孙瑞.南海北部台风浪的时空变化规律和动力机制[D].青岛: 中国科学院研究生院(海洋研究所), 2013. SUN Rui. The variation and mechanism of typhoon waves in the northern part of the South China Sea[D]. Qingdao: Physical Oceanography in the Graduate School of Chinese Academy of Sciences, 2013. (  0) 0)
|
| [12] |
杨生强.南海北部台风影响下海浪谱研究[D].中国科学院研究生院(海洋研究所), 2015. YANG Shengqiang. Research on the northern South China Sea wave spectrum under the influence of typhoon[D]. Qingdao: Physical Oceanography in the Graduate School of Chinese Academy of Sciences, 2015. (  0) 0)
|
| [13] |
潘玉萍, 葛苏放, 沙文钰, 等. 由模拟波面分析双峰谱型海浪的统计特征[J]. 海洋学报(中文版), 2009, 31(4): 13-21. PAN Yuping, GE Sufang, SHA Wenyu, et al. An analysis on the statistical characteristic of sea waves with double-peaked spectrum[J]. Acta oceanologica sinica, 2009, 31(4): 13-21. DOI:10.3321/j.issn:0253-4193.2009.04.002 (  0) 0)
|
| [14] |
陈俊昌, 黎满球, 王文质, 等. 香港附近海区台风海浪谱研究[J]. 热带海洋学报, 1990, 9(4): 1-8. CHEN Junchang, LI Manqiu, WANG Wenzhi, et al. A study on typhoon wave spectrum in the sea area adjacent Hong Kong[J]. Tropic oceanology, 1990, 9(4): 1-8. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


