随着社会经济和科学技术的不断发展，人们对于天然气、石油等资源的依赖也越来越大。从开发的大趋势可以看出，从陆地走向海洋、由浅水去到深水的油气开采难度逐渐增加，另一方面陆地油气开采逐渐枯竭，这就造成了全球油气开发从陆地到海洋、由浅水到深水的大趋向不可逆转^[1]。半潜式平台作为典型的深水平台, 有着抗风浪能力强、工作水深适应范围广泛、钻井能力强、适应恶劣海况、甲板面积和装载量大与转移安装方便等优势。因此，半潜式平台在海洋油气开发和勘探中获得了广泛应用。半潜式钻井平台作为深海作业平台，如何对其水动力性能进行精准计算，一直是科研工作者研宄的热点问题。

海洋平台水动力性能的计算，主要基于三维势流理论^[2]。它将浮式平台作为一个整体结构进行水动力计算。依据三维源汇分布理论，采用面元法求解平台在波浪中受到的载荷^[3]。目前世界范围内典型的三维水动力分析软件如Sesam、HydroStar、AQWA等都是采用上述方法。

虽然利用三维分布源频域方法可以求解二阶波浪力，但基于低阶分布源面元法求解二阶波浪力收敛较差，尤其是对非光滑边界物体，切向诱导速度误差极大^[4]。

针对常值面元法求解物面突变处计算精度低以及高阶边界元方法处理奇异积分复杂和无法直接计算速度势高阶导数的缺点，段文洋^[5]提出了泰勒展开边界元方法(Taylor expansion boundary element method, TEBEM)的思想，即对源偶混合分布方法中的偶极强度进行一阶泰勒展开。段文洋等^[6-10]在泰勒展开边界元方法的基础上，对浮体、潜艇的水动力载荷与运动响应进行研究预报。

本文针对某半潜式钻井平台进行水动力性能及运动响应的研究，并与商业软件AQWA计算结果进行比较，分析总结一阶泰勒展开边界元方法的计算精度与收敛速度。

1 浮式平台水动力分析

对于在规则波中的浮体做摇荡运动，从水动力学的角度来分析浮体对正弦规则入射波的响应。浮体结构物在微幅规则波作用下做六自由度运动，当作用时间足够长，浮体运动和流体的运动就会达到稳态。假设流体无粘，不可压缩且流动无旋。

假设入射波是微幅平面规则波，浮体运动和波幅作为一阶无穷小，应用线性叠加定理进行分析。

流场速度势Φ可分解为入射势Φ₀与扰动势Φ_p^[11]：

$ \mathit{\Phi } = {\mathit{\Phi }_0} + {\mathit{\Phi }_p} = {\mathop{\rm Re}\nolimits} \left( {\left( {{\varphi _0} + {\varphi _p}} \right){{\rm{e}}^{ - {\rm{i}}\omega t}}} \right) $

(1)

式中：$φ$₀是入射势，$φ$_p是扰动势。

由线性叠加定理可以将扰动势分解为辐射势和绕射势，即

$ {\mathit{\Phi }_p} = \sum\limits_{j = 1}^6 {{v_j}{\varphi _j}} + {\varphi _7} $

(2)

式中：v_j是浮体6个自由度的运动速度，$φ$_j是辐射势，$φ$₇是绕射势。

扰动速度势满足的线性化定解问题为

$ \left\{ \begin{array}{l} {\nabla ^2}{\varphi _j} = 0,\;\;\;\;流场内,j = 1,2, \cdots ,7\\ \frac{{\partial {\varphi _j}}}{{\partial z}} - \frac{{{\omega ^2}}}{g}{\varphi _j} = 0,\;\;\;\;z = 0,j = 1,2, \cdots ,7\\ \frac{{\partial {\varphi _j}}}{{\partial n}} = {n_j},\;\;\;\;{S_H}\;上,j = 1,2, \cdots ,6\\ \frac{{\partial {\varphi _7}}}{{\partial \mathit{\boldsymbol{n}}}} = - \frac{{\partial {\varphi _0}}}{{\partial \mathit{\boldsymbol{n}}}},\;\;\;\;{S_H}\;上\\ \mathop {\lim }\limits_{R \to \infty } \sqrt R \left( {\frac{{\partial {\varphi _j}}}{{\partial R}} - {\rm{i}}{k_0}{\varphi _j}} \right) = 0,j = 1,2, \cdots ,7 \end{array} \right. $

(3)

式中：n表示物面法向量，正方向指向浮体内部；g表示重力加速度；S_H表示浮体的平均湿表面；R为径向距离$\sqrt{{{x}^{2}}+{{y}^{2}}}$; k₀为波数。

根据定解条件求解得到浮体在规则波中的速度势，通过伯努利方程可以计算出作用于浮体上的一阶动压力：

$ p = - \rho \frac{{\partial \mathit{\Phi }}}{{\partial t}} $

(4)

在求解得到浮体的水动力系数与入射波浪力及绕射波浪力后，通过对方程组的求解可以得到浮体的运动：

$ \left( {\mathit{\boldsymbol{M}} + \mathit{\boldsymbol{\mu }}} \right)\mathit{\boldsymbol{\ddot \eta }} + \mathit{\boldsymbol{\lambda \dot \eta }} + \mathit{\boldsymbol{C\eta }} = \mathit{\boldsymbol{f}} $

(5)

式中：M表示浮体的质量矩阵，μ表示浮体的附加质量矩阵，λ表示浮体的兴波阻尼矩阵，C表示浮体的静恢复力矩阵，f表示流体载荷列向量，η表示浮体六自由度运动。

通过浮体的运动，可以得到完整的扰动速度势及其相关梯度后，可以通过式(6)求得作用在浮体上的二阶定常力:

$ \begin{gathered} {\mathit{\boldsymbol{F}}^{\left( 2 \right)}} = - \frac{{\rho g}}{4}\int\limits_{wl} {\left( {{\zeta _3} - {\chi _3}} \right){{\left( {{\zeta _3} - {\chi _3}} \right)}^ * }\frac{{\mathit{\boldsymbol{n}}{\text{d}}l}}{{\sqrt {1 - n_3^2} }}} - \hfill \\ \;\;\;\;\;\;\;\;\;\frac{\rho }{4}\iint\limits_{{S_H}} {\left( {\nabla \varphi \cdot \nabla {\varphi ^ * }} \right)\mathit{\boldsymbol{n}}{\text{d}}s} - \frac{{{\text{i}}\omega \rho }}{2}\iint\limits_{{S_H}} {\left( {{\mathit{\boldsymbol{\chi }}^ * } \cdot \nabla \varphi } \right)\mathit{\boldsymbol{n}}{\text{d}}s} + \hfill \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{\eta }}_R^ * \times \left[ {{\mathit{\boldsymbol{F}}^{\left( 1 \right)}} - \rho g{A_{wp}}\left( {{\eta _3} - {\eta _5}{x_f}} \right)\mathit{\boldsymbol{k}}} \right] \hfill \\ \end{gathered} $

(6)

式中:浮体平动位移为η_T=(η₁, η₂, η₃); 角位移为η_R=(η₄, η₅, η₆); 总位移为X=Re(χe^-iωt)，χ=(χ₁, χ₂, χ₃)=η_T+η_R×r; 其中波面升高表达式为ζ₃=iω$φ$/g, r为位置矢量; wl是平均位置水线; 上标*是共轭函数。

2 一阶泰勒展开边界元方法

对于流场速度势的求解，传统的常值面元法用面元网格中心点处的速度势代替整个面元的速度势。

对势函数$φ$(q)和格林函数G(p, q)在流域边界应用格林第三公式，利用流场势满足的线性化定解条件(3)后可获得在浮体平均湿表面的源偶混合分布模型，在浮体湿表面离散后形式为

$ 4{{\rm{\pi }} }\varphi \left( p \right) + \sum\limits_{j = 1}^N {\iint\limits_{\Delta {S_j}} {\varphi \left( q \right)\frac{{\partial G}}{{\partial {n_q}}}{\text{d}}s}} = \sum\limits_{j = 1}^N {\iint\limits_{\Delta {S_j}} {G\frac{{\partial \varphi \left( q \right)}}{{\partial n}}{\text{d}}s}} $

(7)

式中：G=1/r_pq+1/r′_pq′+$2\upsilon \int\limits_{L}{\frac{{{\text{e}}^{k\left( z+\zeta \right)}}}{k-\upsilon }}{{\text{J}}_{0}}\left( kH \right)\text{d}\mathit{k}$，r_pq表示场点p(x, y, z)与源点q(ξ, η, ζ)间的距离，r′_pq′表示场点与源点关于水面的镜像点q′(ξ, η, -ζ)间的距离；H表示场点与源点间的水平距离；J₀为第一类贝塞尔函数；N表示离散面元数。

与常值面元法不同的是, 一阶泰勒展开边界元方法假定速度势在面元内部是一阶连续的。定义(ξ, η, ζ)为源点所在面元的局部坐标，(x, y, z)为场点所在面元的局部坐标。一阶泰勒展开边界元方法通过对源偶混合分布方法中的偶极强度进行泰勒展开, 并且保留切向速度项即一阶导数项。泰勒展开边界元法的未知数是面元中心q₀的速度势与两个正交方向的切向速度，即：

$ \varphi \left( q \right) = \varphi \left( {{q_0}} \right) + \bar \xi \frac{{\partial \varphi }}{{\partial \bar \xi }}\left| {_{{q_0}}} \right. + \bar \eta \frac{{\partial \varphi }}{{\partial \bar \eta }}\left| {_{{q_0}}} \right. $

(8)

将其代入方程(7)可以获得关于$φ$(q₀)，$\frac{\partial \varphi }{\partial \bar{\xi }}\left| {{q}_{0}} \right., \frac{\partial \varphi }{\partial \bar{\eta }}\left| {{q}_{0}} \right.$，的一个方程。

为了补充一阶泰勒展开边界元方法的方程组，对格林第三公式中的场点p，沿着其法向趋于边界时，取场点p垂直于法线平面内的相互正交的$\frac{\partial \varphi \left( p \right)}{\partial \bar{x}}$，$\frac{\partial \varphi \left( p \right)}{\partial \bar{x}}$两个方向上的一阶导数$\frac{\partial \varphi \left( p \right)}{\partial \bar{x}}$，$\frac{\partial \varphi \left( p \right)}{\partial \bar{y}}$。则此时补充方程为

$ 2{{\rm{\pi }} }\frac{{\partial \varphi \left( p \right)}}{{\partial \bar x}} + \frac{\partial }{{\partial \bar x}}\iint\limits_{{S_H}} {\varphi \frac{{\partial G}}{{\partial {n_q}}}{\text{d}}{s_q}} = \frac{\partial }{{\partial \bar x}}\iint\limits_{{S_H}} {\frac{{\partial \varphi }}{{\partial n}}G{\text{d}}{s_q}} $

(9)

$ 2{\rm{\pi }}\frac{{\partial \varphi \left( p \right)}}{{\partial \bar y}} + \frac{\partial }{{\partial \bar y}}\iint\limits_{{S_H}} {\varphi \frac{{\partial G}}{{\partial {n_q}}}{\text{d}}{s_q}} = \frac{\partial }{{\partial \bar y}}\iint\limits_{{S_H}} {\frac{{\partial \varphi }}{{\partial n}}G{\text{d}}{s_q}} $

(10)

同理，对上式两个补充方程中的偶极强度进行泰勒展开，保留其一阶导数项，联立所得的三个方程式，对于任意的面元，有如下简化的一阶泰勒展开边界元方法的离散方程组(i=1, 2, …, N)

$ \sum\limits_{m = 1}^3 {\sum\limits_{j = 1}^N {\left[ {{{\left( {\mathit{\boldsymbol{A}}_m^{ij}} \right)}_k}\left( {\mathit{\boldsymbol{u}}_m^j} \right)} \right]} } = \sum\limits_{j = 1}^N {\left( {\mathit{\boldsymbol{B}}_k^{ij}} \right){{\left( {\frac{{\partial \varphi }}{{\partial n}}} \right)}^j}} $

(11)

式中：i和j表示面元编号；k=1, 2, 3;m=1, 2, 3。矩阵A、u与B推导可参考文献[3-6]。

3 计算模型的建立

本文所研究的半潜式平台是哈尔滨工程大学参与的EXWAVE JIP项目所采用半潜式平台。该JIP项目由挪威海洋技术研究所(Marintek)和DNV-GL船级社联合发起，目的是研究极端海况下半潜式平台等海工平台波浪载荷和系泊浮体总体运动特性，发展合理的数值预报模型，提高相关水动力载荷与运动预报精度。该项目对应的半潜式平台模型实验在2015年由MARINTEK海洋水池开展^[12]。

测量模型的缩尺比为1:50。平台具体主尺度如表 1所示，半潜平台主要质量与静力参数如表 2所示。

该项目在模型试验中通过不规则波中平台运动测试间接获得了平台运动幅值响应函数，可供半潜式平台频域水动力分析算法进行验证，这为基于势流方法进一步开展恶劣海况下半潜式平台运动分析提供了很好的基础验证算例。本文所选取的平台运动幅值传递函数结果对应的是中低海况下的运动响应，目的是为了与线性理论的微幅波假设相对应。

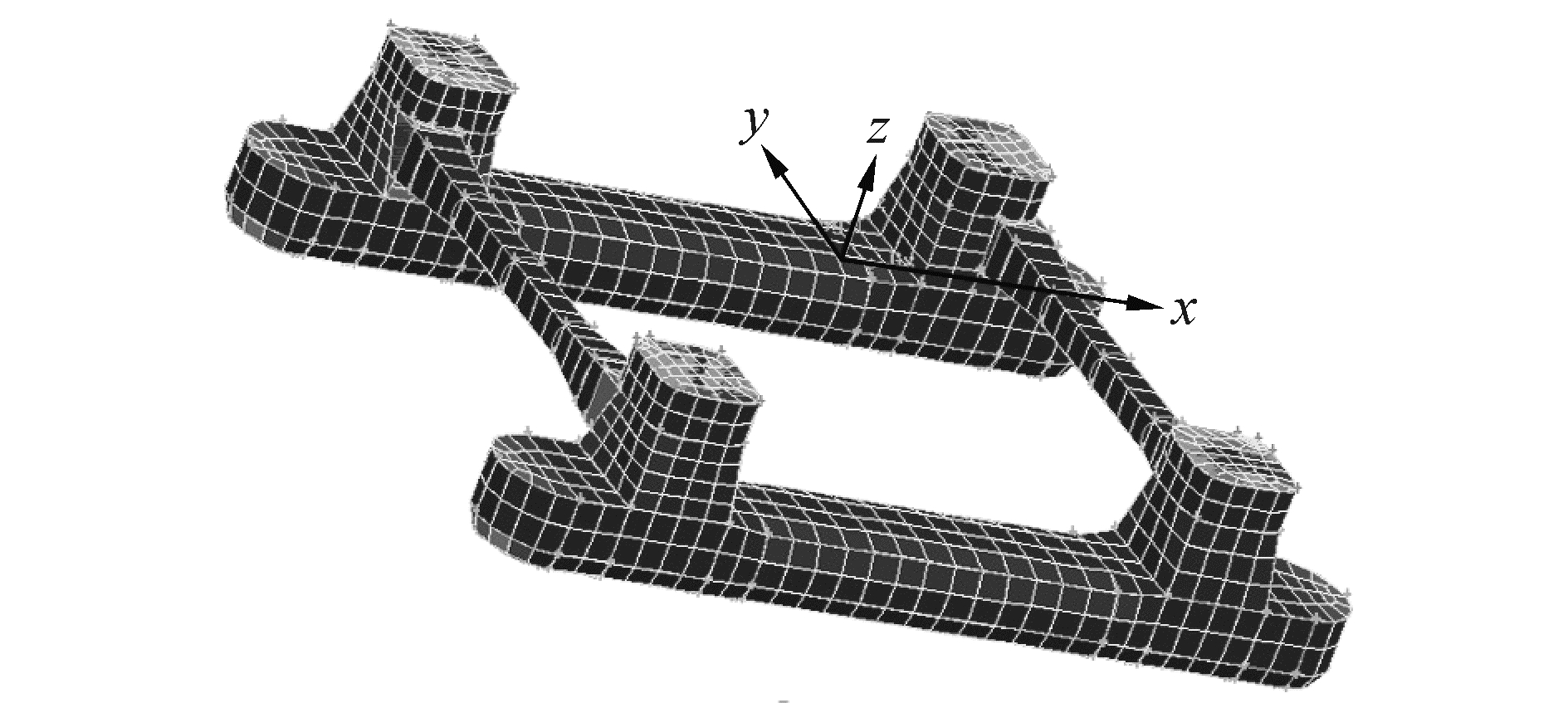
根据以上半潜式平台的全尺度，完成半潜式平台的几何建模^[13]。根据右手螺旋法则，将描述平台运动和入射波的大地坐标系定义为：原点位于水线面中心，x轴平行于中心线，规定指向首部为正；y轴指向左舷为正；z轴垂直于水线面，向上为正。入射波浪向角定义为x轴正向与波浪传播方向间的逆时针夹角。图 1是通过前处理软件Gambit划分的网格离散模型^[14]。本论文中用于一阶泰勒展开边界元方法计算的模型面元网格划分尺度有三种情况：第一种面元网格长度为3.0~3.2 m，网格总数1 690；第二种面元网格长度为2.0~2.3 m，网格总数3 456；第三种面元网格长度为1.5~2.0 m，网格总数4 971。

4 平台计算的结果与比较 4.1 一阶水动力系数比较分析

为了验证一阶TEBEM方法对于预报平台的水动力系数的准确性，本文与基于常值分布源方法的商业软件AQWA计算的数值结果进行对比分析。为保证所划分的网格平均尺度上保持一致大小，本论文中用于AQWA软件计算的模型面元网格数同样有三种情况：第一种面元网格总数1 720；第二种面元网格总数3 502；第三种面元网格总数5 000。以上划分的面元网格统一为四边形单元。

为了方便比较，分别用ρ$\nabla $与ρ$\nabla $(g/D)^0.5对附加质量系数与兴波阻尼系数作无因次化处理，其中ρ表示海水密度，$\nabla $表示平台排水量，D表示平台生存吃水。

图 2(a)与(b)分别给出了平台在纵荡和横荡方向上的附加质量系数的频域变化曲线，将计算结果和基于分布源法的AQWA软件结果对比。从图中可以看出，一阶泰勒展开边界元方法计算得到的结果具有良好的收敛性，与AQWA结果相比，两者的结果吻合较好，相对差别均控制在5%以内。

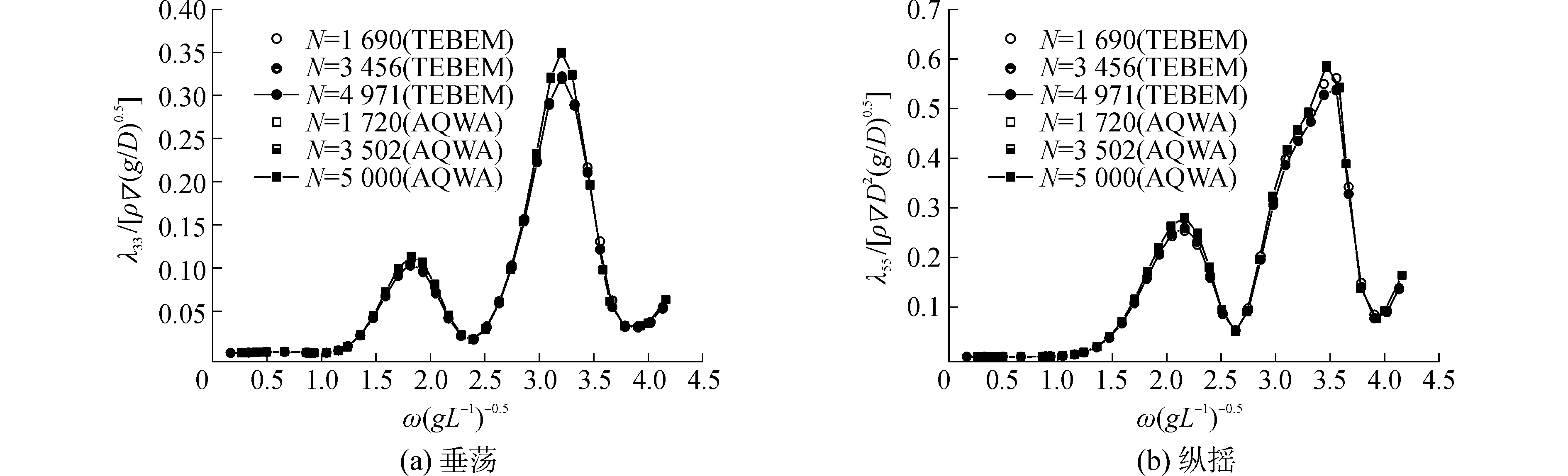
图 3(a)与(b)分别给出了平台在垂荡和纵摇方向上的兴波阻尼系数的频域变化曲线。针对兴波阻尼系数的计算，一阶泰勒展开边界元方法在网格数1 690左右就已经得到收敛结果，两者计算结果吻合较好，只在第二次峰值附近有很小的差别。

4.2 一阶波浪力比较分析

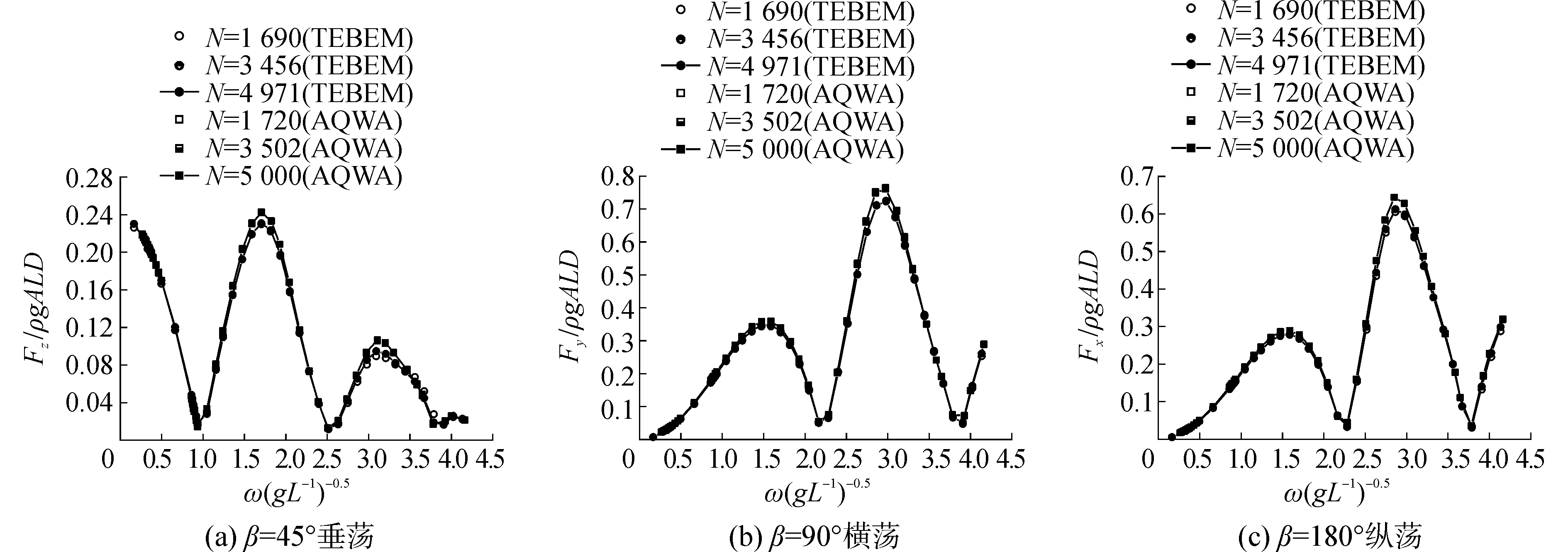
图 4中为采用一阶泰勒展开边界元方法与AQWA软件计算得到的一阶波浪力频域变化曲线。其中F_x、F_y、F_z分别表示平台在纵荡、横荡与垂荡方向的一阶波浪力值。利用ρgALD对波浪力作无因次化处理，其中A表示波幅，L表示浮筒长度。(β表示浪向角，β=180°表示迎浪状态。由于篇幅有限，这里只给出三种不同浪向下具有代表性的波浪力比较结果。)

从图 4中可以看出：对于一阶波浪力的计算，一阶泰勒展开边界元方法在第一种面元网格条件下(网格数为1 690)的计算就已经得到了收敛结果，收敛速度很快；其计算的结果与AQWA的计算结果保持一致。

4.3 一阶运动响应幅值比较分析

图 5中为平台的运动响应幅值的RAO曲线。选取TEBEM计算网格数为1 690的结果，AQWA计算网格数为1 720的结果进行比较分析。

从图 5中可以看出：一阶泰勒展开边界元方法的计算结果与AQWA的计算结果在整个频域上吻合较好，相对差别均控制在1%左右；一阶泰勒展开边界元方法的结果同模型试验结果总体上符合较好。

在共振频率附近，试验结果由于实际流体粘性的存在，比一阶泰勒展开边界元方法与AQWA的计算结果小。对于共振垂荡运动上的差异，主要是由于当前采用的一阶泰勒展开边界元方法与AQWA的计算结果没有考虑垂荡方向的粘性阻尼修正造成的。

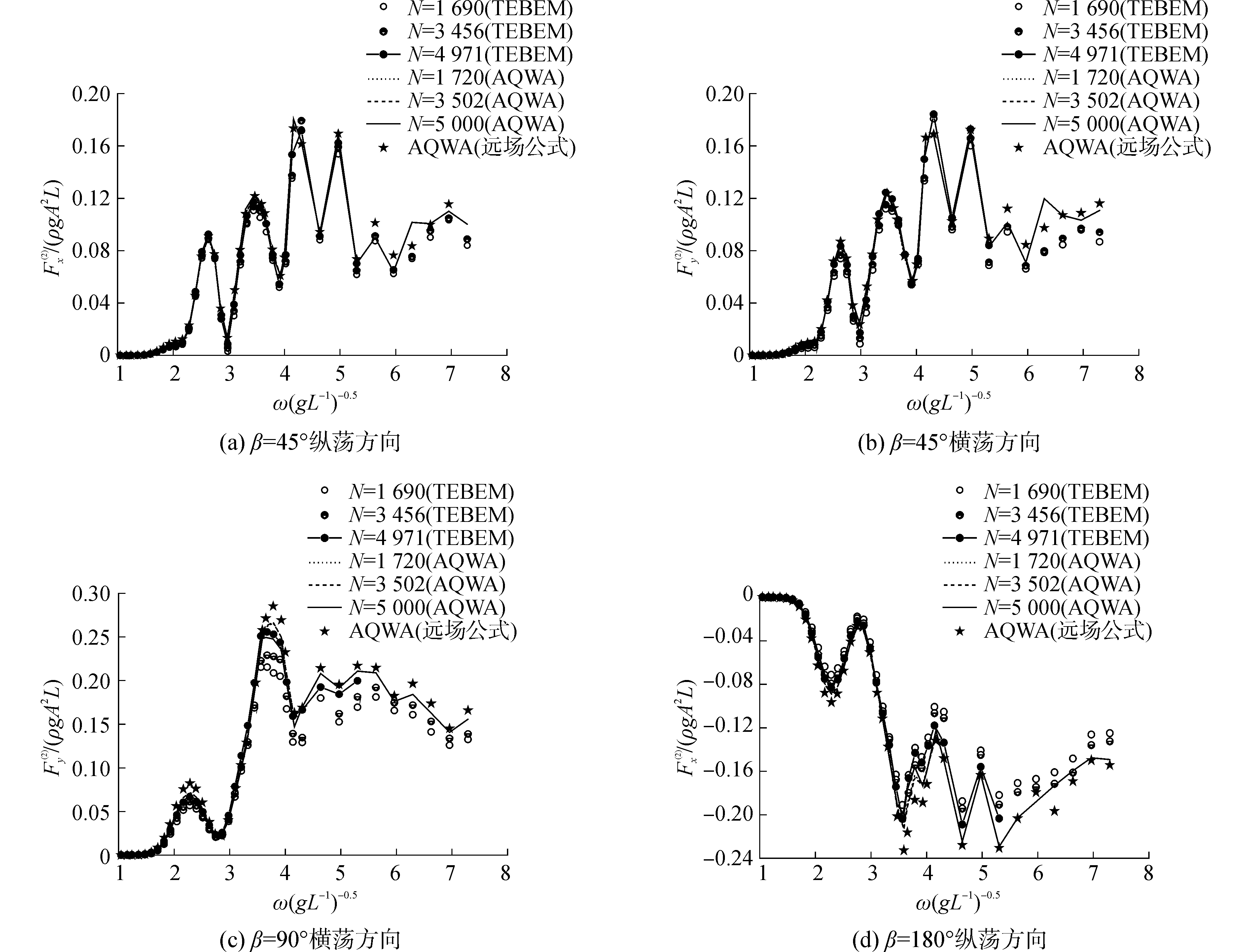
4.4 二阶平均波浪漂移力比较分析

在波浪中的半潜平台除了受到一阶波浪力的作用, 还受到二阶波浪漂移力的作用。特别是浮体水平方向的二阶慢漂力，是系泊浮体水平慢漂运动的主要原因。图 6给出了两种不同方法计算的水平方向平均漂移力结果。其中F_x⁽²⁾、F_y⁽²⁾分别对应于平台在纵荡与横荡方向的平均漂移力值。在图中标注了网格数量的TEBEM方法与AQWA软件均采用近场公式计算平均漂移力，同时利用AQWA远场公式结果(网格数5 000)作比较。

从图 6的计算结果比较上可以看出：一阶泰勒展开边界元方法对于平均漂移力的计算结果与AQWA利用近场公式以及远场公式计算结果吻合良好, 这说明了一阶泰勒展开边界元方法对于二阶波浪力的计算有较高的计算精度。同时可以看出采用一阶泰勒展开边界元方法计算的平均漂移力有着良好的收敛速度。通过比较三种不同网格下的模拟结果可以计算出：当面元网格长度与波长的比值在0.08~0.1时，一阶泰勒展开边界元方法就可以得到平均漂移力的收敛结果。

5 结论

1) 一阶泰勒展开边界元方法在半潜平台的运动响应的预报上，与试验结果吻合较好，有着较高的精度，可用于半潜式平台的运动响应的预报。

2) 一阶泰勒展开边界元方法计算的结果与基于常值分布源方法计算的数值结果吻合较好，尤其在平台的水动力系数与运动响应的计算上。通过对三种不同网格情况下的结果进行比较分析，说明一阶泰勒展开边界元方法具有良好的收敛性。

3) 针对求解具有尖角结构的浮体平均漂移力，本文采用的泰勒展开边界元法利用压力积分近场公式也可给出同远场公式精度一致的收敛性结果，特别适用于考虑多浮体干扰情况下单个浮体上波漂力计算，这是本文方法的一个特色和优势。

4) 当前采用一阶泰勒展开边界元方法对于平台垂荡运动共振频率附近的预报结果与试验结果存在较大的偏差，主要是由于当前采用的一阶泰勒展开边界元方法没有考虑垂荡方向的粘性阻尼修正造成的。