桥梁预拱度设置对于保证线路平顺、运行质量至关重要。我国铁路及公路钢结构设计规范[1-2]均规定,桥跨结构应设置预拱度,以抵消大桥所受恒载和一半活载的挠度。在钢桁梁的设计中,一般通过伸缩杆件以实现起拱目的。预拱度设置合理与否,不但影响桥梁的使用功能,甚至影响结构受力。钢桁梁预拱度设置的科学性首先体现在计算方法上,许多学者对此展开了研究,提出了几何法、温度法及位移荷载法等。几何法[3-5]是根据主桁杆件间的几何关系计算上弦杆变化量与预拱度值之间关系,通常需反复试算才能得到与理论预拱度曲线吻合较好的线形,该方法仅适用于结构形式简单的钢桁梁桥。温度法[6-8]是通过升降温的方式调整杆件的无应力长度,使桁架控制点节点位移逼近理论预拱度。对于超静定结构,采用升降温法起拱会产生起拱次内力及起拱支座反力,通常需建立优化模型,求解约束方程。对于大型钢桁梁桥,约束方程冗杂,求解困难,甚至无解。位移荷载起拱法[9]是将理论预拱度作为输入荷载,杆件伸缩量作为待求解的输出响应,以此达到预设拱度目的。钢桁梁预拱度的设置实质上是通过改变杆件的无应力长度来达到起拱目的。无应力状态控制法理论[10-11]力学平衡方程中包含无应力状态量引起的附加项,该项直接与单元无应力状态量对应。以无应力状态控制法为基础,寻求建立杆件无应力长度变化量与理论预拱度之间关系,从而达到钢桁梁预拱度设置目的,为钢桁梁预拱度设置提供一种新思路,本文即对此问题展开研究。与位移荷载起拱法一样,均是通过杆件伸缩引起结构预拱度的反问题变为通过预拱度求解杆件伸缩量的正问题,故本文公式推导与数值验证均与文献[9]进行对照。
1 位移荷载起拱法对于钢桁梁任意节间,定义两下弦节点的绝对预拱度之差为相对预拱度,由理论预拱度曲线可以得到下弦杆各节点的绝对预拱度值,进而计算节间下弦杆的相对预拱度。节间相对预拱度的实现通过改变杆件的长度得到。
以钢桁梁单片主桁的任意节间作为一个独立单元,假定已安装钢梁给予待安装节间以竖向和水平向约束,各杆件的编号、长度、横截面积、材料弹性模量及节点编号如图 1所示。

|
Download:
|
| 图 1 位移荷载起拱法示意图 Fig. 1 Schematic diagram of the displacement load pre-camber setting method | |
桁架节间在强制位移荷载下,得到节点力与节点位移的关系
| $ \left[ {\begin{array}{*{20}{c}} {{F_{x1}}}\\ {{F_{y1}}}\\ {{F_{x2}}}\\ {{F_{y2}}}\\ {{F_{x3}}}\\ {{F_{y3}}}\\ {{F_{x4}}}\\ {{F_{y4}}} \end{array}} \right] = \mathit{\boldsymbol{K}}\left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {{v_1}}\\ {{u_2}}\\ {{v_2}}\\ {{u_3}}\\ {{v_3}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right] $ | (1) |
式中:(Fxi, Fyi)(i=1, 2, 3, 4)为节点i的节点力;Κ为整个节间刚度矩阵;(ui, vi)(i=1, 2, 3, 4)为第i节点的强制位移。
引入约束条件,即
| $ {u_1} = {v_1} = {u_2} = {v_2} = 0 $ | (2) |
并考虑结构杆端内力之和等于外力之和,即有
| $ \left\{ \begin{array}{l} {F_{x3}} = 0\\ {F_{y3}} = 0\\ {F_{x4}} = 0 \end{array} \right. $ | (3) |
联立式(1)~(3),得到展开式:
| $ \left\{ \begin{array}{l} {g_1}{u_3} + {g_2}{c_2}\left( {{u_3}{c_2} + {v_3}{s_2}} \right) = 0\\ {g_2}{s_2}\left( {{u_3}{c_2} + {v_3}{s_2}} \right) + {g_3}\left( {{v_3} - {v_4}} \right) = 0\\ {g_4}{u_4} = 0 \end{array} \right. $ | (4) |
式中:gi=EiAi/Li;ci=cosθi、si=sinθi;θi为杆件i单元坐标系与整体坐标系之间的夹角,且θ1=θ4=0°、θ3=90°。v4为节间需设置的相对预拱度。由g4不等于零,可得u4=0,即下弦杆件的长度不变。
文献[9]根据下承式钢桁梁预拱度设置特点,在式(4)基础上进一步得出了仅伸缩上弦杆;同时伸缩上弦杆和斜腹杆;同时伸缩上弦杆、竖杆和斜腹杆三种情况下的杆件伸缩公式,此处不赘述。
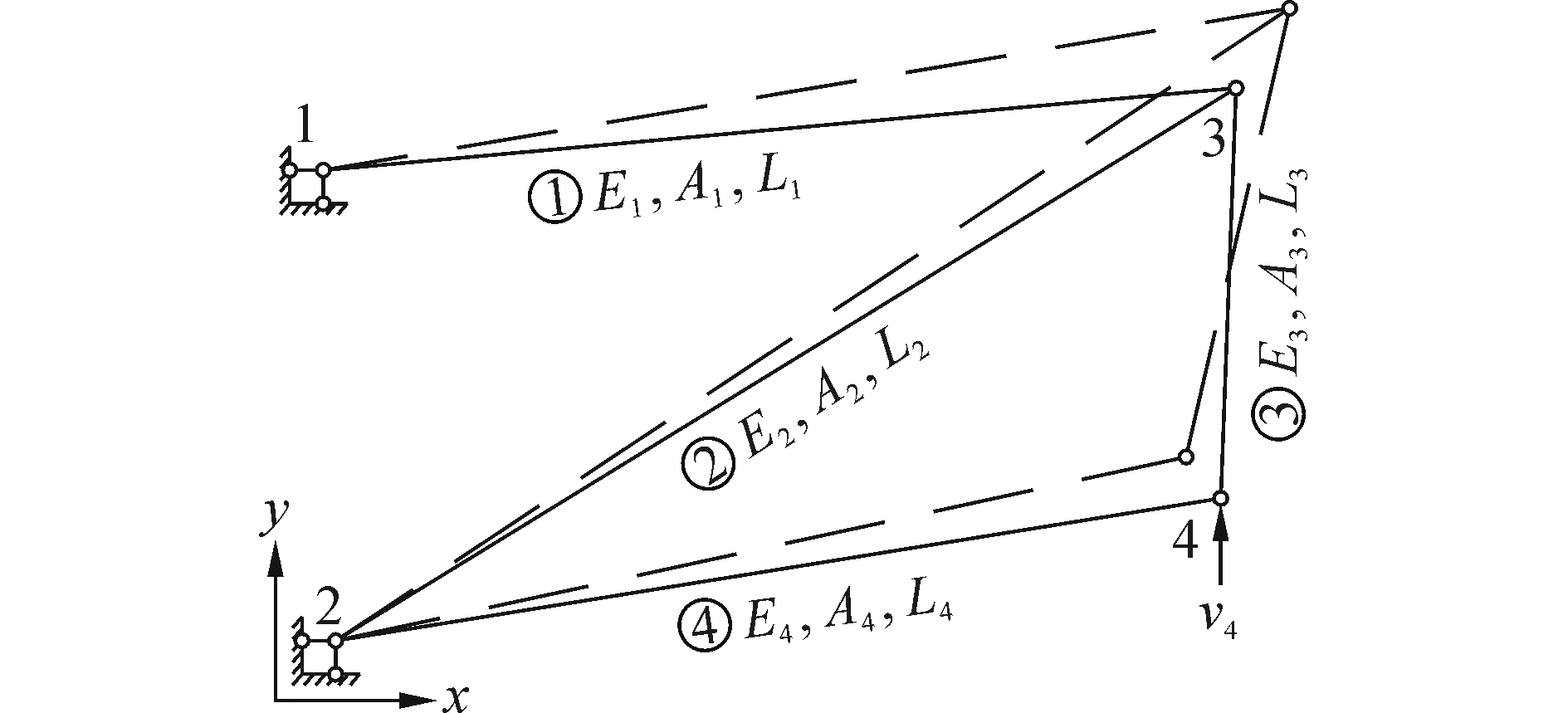
2 无应力状态起拱法 2.1 起拱原理仍以钢桁梁单片主桁的任意节间为例,说明无应力状态起拱法的起拱原理。虚线表示设置了相对预拱度后结构相对位置,杆件编号、节点编号、几何参数及物理参数如图 2所示。
|
Download:
|
| 图 2 无应力状态起拱法示意图 Fig. 2 Schematic diagram of the unstressed pre-camber setting method | |
节间无应力状态法力学平衡方程[10]为
| $ \left( {\sum\limits_{i = 1}^4 {{\mathit{\boldsymbol{k}}_i}} } \right)\mathit{\boldsymbol{\delta = P}} + \sum\limits_{i = 1}^4 {{\mathit{\boldsymbol{P}}_{0i}}} $ | (5) |
式中: ki为整体坐标系下第i根杆件单元刚度矩阵;δ为结构节点位移列阵;P为结构外荷载列阵,对于钢桁梁预拱度设置,此项为零;P0i为第i根杆件无应力状态量改变引起的附加项。其中,
| $ {\mathit{\boldsymbol{k}}_i} = \left[ {\begin{array}{*{20}{c}} {{g_i}c_i^2}&{{g_i}{c_i}{s_i}}&{ - {g_i}c_i^2}&{ - {g_i}{c_i}{s_i}}\\ {{g_i}{c_i}{s_i}}&{{g_i}s_i^2}&{ - {g_i}{c_i}{s_i}}&{ - {g_i}s_i^2}\\ { - {g_i}c_i^2}&{ - {g_i}{c_i}{s_i}}&{{g_i}c_i^2}&{{g_i}{c_i}{s_i}}\\ { - {g_i}{c_i}{s_i}}&{ - {g_i}s_i^2}&{{g_i}{c_i}{s_i}}&{{g_i}s_i^2} \end{array}} \right] $ | (6) |
| $ \mathit{\boldsymbol{\delta }} = {\left[ {\begin{array}{*{20}{c}} {{u_1}}&{{v_1}}&{{u_2}}&{{v_2}}&{{u_3}}&{{v_3}}&{{u_4}}&{{v_4}} \end{array}} \right]^{\rm{T}}} $ | (7) |
| $ {\mathit{\boldsymbol{P}}_{0i}} = {\left[ {\begin{array}{*{20}{c}} {{g_i}{c_i}\Delta {L_i}}&{{g_i}{s_i}\Delta {L_i}}&{ - {g_i}{c_i}\Delta {L_i}}&{ - {g_i}{s_i}\Delta {L_i}} \end{array}} \right]^{\rm{T}}} $ | (8) |
式中:ΔLi为第i根杆件伸缩量。
引入边界约束条件(式(2)),得
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{g_1}c_1^2 + {g_2}c_2^2 + {g_3}c_3^2}&{{g_1}{c_1}{s_1} + {g_2}{c_2}{s_2} + {g_3}{c_3}{s_3}}&{ - {g_3}c_3^2}&{ - {g_3}{c_3}{s_3}}\\ {{g_1}{c_1}{s_1} + {g_2}{c_2}{s_2} + {g_3}{c_3}{s_3}}&{{g_1}c_1^2 + {g_2}c_2^2 + {g_3}c_3^2}&{ - {g_3}{c_3}{s_3}}&{ - {g_3}s_3^2}\\ { - {g_3}c_3^2}&{ - {g_3}{c_3}{s_3}}&{{g_3}c_3^2 - {g_4}c_4^2}&{{g_3}{c_3}{s_3} + {g_4}{c_4}{s_4}}\\ { - {g_3}{c_3}{s_3}}&{ - {g_3}s_3^2}&{{g_3}{c_3}{s_3} + {g_4}{c_4}{s_4}}&{{g_3}s_3^2 - {g_4}s_4^2} \end{array}} \right].}\\ {\left[ {\begin{array}{*{20}{c}} {{u_3}}\\ {{v_3}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {g_1}{c_1}\Delta {L_1} - {g_2}{c_2}\Delta {L_2} - {g_3}{c_3}\Delta {L_3}}\\ { - {g_1}{s_1}\Delta {L_1} - {g_2}{s_2}\Delta {L_2} - {g_3}{s_3}\Delta {L_3}}\\ {{g_3}{c_3}\Delta {L_3} - {g_4}{c_4}\Delta {L_4}}\\ {{g_3}{s_3}\Delta {L_3} - {g_4}{s_4}\Delta {L_4}} \end{array}} \right]} \end{array} $ | (9) |
将式(9)进行初等变换,化简后得
| $ \left[ {\begin{array}{*{20}{c}} { - {c_1}}&{ - {s_1}}&0&0\\ { - {c_2}}&{ - {s_2}}&0&0\\ { - {c_3}}&{ - {s_3}}&{{c_3}}&{{s_3}}\\ 0&0&{ - {c_4}}&{{s_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_3}}\\ {{v_3}}\\ {{u_4}}\\ {{v_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta {L_1}}\\ {\Delta {L_2}}\\ {\Delta {L_3}}\\ {\Delta {L_4}} \end{array}} \right] $ | (10) |
将式(10)表示成伸缩量与节点位移的关系式:
| $ \left\{ \begin{array}{l} \Delta {L_1} = - {u_3}{c_3} - {v_3}{s_3}\\ \Delta {L_2} = - {u_3}{c_2} - {v_3}{s_2}\\ \Delta {L_3} = \left( {{u_4} - {u_3}} \right){c_3} + \left( {{v_4} - {v_3}} \right){s_3}\\ \Delta {L_4} = - {u_4}{c_4} - {v_4}{s_4} \end{array} \right. $ | (11) |
式(11)即为无应力状态起拱法杆件伸缩量的数学表达式,式中不包含任何物理力学参数,故该起拱方法不会产生起拱附加力。该方法并未规定各杆件单元坐标系与整体坐标系间的夹角,故而对此类节间由四根杆件组成的桁梁普遍适用。将各节点位移作为输入,即可确定各杆件的伸缩量。
2.2 杆件伸缩对于下承式钢桁梁桥,仍然针对文献[9]中给出的三种情况进行讨论。由理论预拱度曲线可以得到节段下弦节点的相对预拱度值v4,将v4作为输入,针对不同情况进行分析。
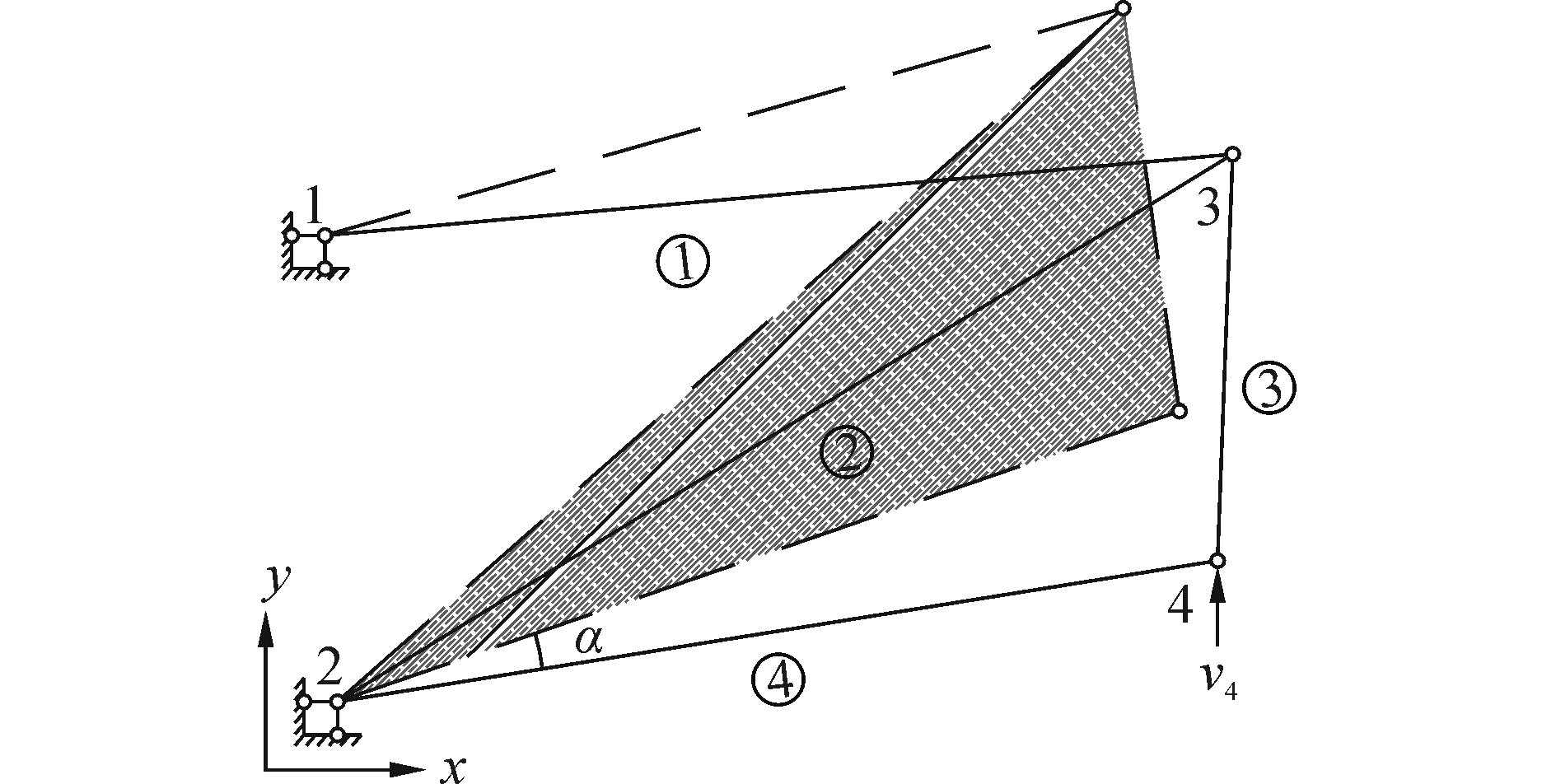
2.2.1 仅伸缩上弦杆如图 3所示,仅伸缩上弦杆,斜腹杆、竖杆和下弦杆长度不变,即有
|
Download:
|
| 图 3 伸缩上弦杆示意图 Fig. 3 Schematic diagram of the length change in upper chords | |
| $ \Delta {L_2} = \Delta {L_3} = \Delta {L_4} = 0 $ | (12) |
v4为已知输入,由图中几何关系知,在上弦杆的伸缩变化过程中,阴影部分形状将不发生变化,它仅发生刚体转动,转角用α表示。联立式(11)~(12)可得上弦杆伸缩量。
由v4已知及ΔL4=-u4c4-v4s4=0得
| $ {u_4} = - {v_4}{t_4} $ | (13) |
式中t4=tanθ4。
由ΔL3=(u4-u3)c3+(v4-v3)s3=0得
| $ {u_3}{c_3} + {v_3}{s_3} = {u_4}{c_3} + {v_4}{s_3} $ | (14) |
由ΔL2=-u3c2-v3s2=0得
| $ {u_3}{c_2} + {v_3}{s_2} = 0 $ | (15) |
由式(14)、(15),并结合式(11)中第一个表达式,可得
| $ \Delta {L_1} = \frac{{\left( {{c_1}{s_2} - {s_1}{c_2}} \right)\left( {{s_3} - {c_3}{t_4}} \right)}}{{{c_2}{s_3} - {s_2}{c_3}}}{v_4} $ | (16) |
阴影部分刚体转角为
| $ \alpha = \frac{{{v_4}}}{{{L_4}}} $ | (17) |
如图 4所示,伸缩上弦杆和斜腹杆,竖杆和下弦杆长度不变,即有

|
Download:
|
| 图 4 同时伸缩上弦杆和斜腹杆 Fig. 4 Length change in both upper chords and diagonal web | |
| $ \Delta {L_3} = \Delta {L_4} = 0 $ | (18) |
仅有相对竖向预拱度v4,还不能得到上弦杆和斜腹杆的伸缩量,需补充条件以确定节点3的位置。若要使竖杆③与计算位置保持一定角度β(当为计算位置顺时针转向指定位置时为正),则可确定上弦杆和斜腹杆的伸缩量。
由v4已知及ΔL4=-u4c4-v4s4=0可得式(13)。
由竖杆指定位置与计算位置保持一定角度β可得节点3的水平及竖向位移
| $ \left\{ \begin{array}{l} {v_3} = {v_4} + {L_3}\left[ {\sin \left( {{\theta _3} - \beta } \right) - {s_3}} \right]\\ {u_3} = {u_4} + {L_3}\left[ {\cos \left( {{\theta _3} - \beta } \right) - {c_3}} \right] \end{array} \right. $ | (19) |
将式(19)代入式(11)第一、二表达式,可得上弦杆和斜腹杆伸缩量
| $ \left\{ \begin{array}{l} \Delta {L_1} = \left( {{c_1}{t_4} - {s_1}} \right){v_4} - {L_3}\left[ {\cos \left( {{\theta _3} - \beta } \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {\sin \left( {{\theta _3} - \beta } \right) - {c_1}{c_3} - {s_1}{s_3}} \right]\\ \Delta {L_2} = \left( {{c_2}{t_4} - {s_2}} \right){v_4} - {L_3}\left[ {\cos \left( {{\theta _3} - \beta } \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {\sin \left( {{\theta _3} - \beta } \right) - {c_2}{c_3} - {s_2}{s_3}} \right] \end{array} \right. $ | (20) |
此时仅下弦杆长度不变,即有ΔL4=0。仅有节点相对预拱度v4,并不能确定节点3的位置,当指定节点3的位移(u3, v3)后,杆件伸缩量可由式(11)确定为
| $ \left\{ \begin{array}{l} \Delta {L_1} = - {u_3}{c_3} - {v_3}{s_3}\\ \Delta {L_2} = - {u_3}{c_2} - {v_3}{s_2}\\ \Delta {L_3} = \left( {{s_3} - {c_3}{t_4}} \right){v_4} - {u_3}{c_3} - {v_3}{s_3} \end{array} \right. $ | (21) |
这样,由理论预拱度得到各节间相对预拱度后,可由式(16)、(20)、(21)快速计算杆件伸缩值,以完成钢桁梁预拱度设置。具体来说,对于钢桁梁普通节间,通常采用伸缩上弦杆的方式进行起拱;大跨钢桁梁结构一般左右对称,跨中位置竖杆倾斜角度容易确定,宜采用同时伸缩上弦杆和斜腹杆的方法。
2.3 两种方法比较本文在荷载位移起拱法[9]基础上,从无应力状态控制法角度对同一起拱问题展开研究,比较两种起拱方法:
1) 两种方法均是以单个节间桁段为研究对象,建立起拱模型,并且都是以节间下弦节点的相对预拱度为输入,杆件的伸缩量作为输出,从而达到起拱目的方法。
2) 荷载位移起拱法将相对预拱度作为强迫位移,根据杆端内力之和与外荷载相等建立关系式,推导出杆件伸缩量的表达式,表达式中含有力学参数;无应力状态起拱法由无应力状态法力学平衡条件直接建立杆件伸缩量与节点位移的关系,表达式中不含物理力学参数,不会产生起拱附加力。
3) 文献[9]在推导位移荷载起拱法时,仅针对竖杆为竖直且弦杆水平的情况进行推导,所以仅适用对此类平面N形钢桁梁的起拱;而无应力状态起拱法在推导时并未限定各杆件的具体倾角,适用于任何平面N形钢桁梁。
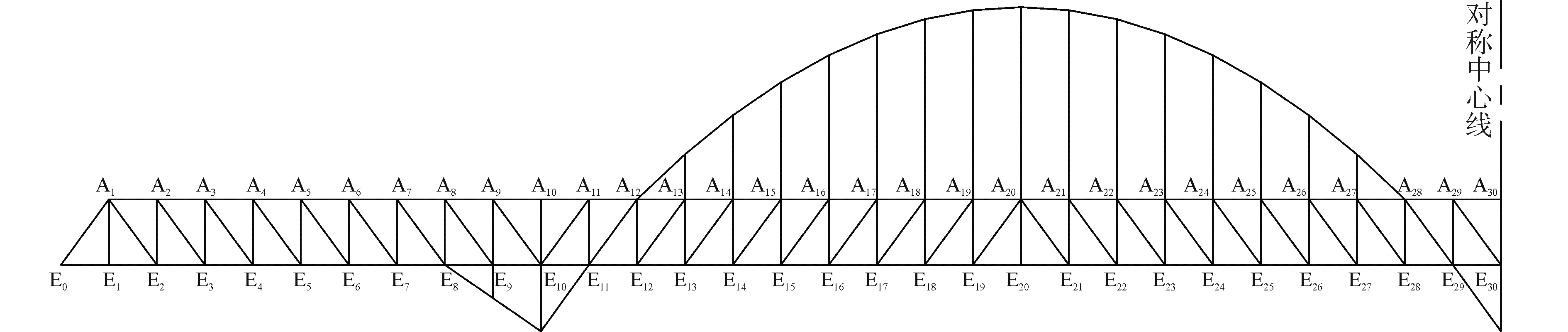
3 数值验证以文献[9]中榕江特大桥的预拱度设置为例进行分析。该桥为110 m+2×220 m+110 m下承式连续刚性梁柔性拱结构。钢桁梁采用带竖杆N型三角桁架,主桁桁高和桁宽均为15.0 m,节间长度为11.0 m。为说明方便,下弦节点由左至右编号为E0~E30,上弦节点由左至右编号为A1~A30。图 5为榕江特大桥主桁结构立面图。
|
Download:
|
| 图 5 榕江特大桥主桁结构立面图 Fig. 5 The elevation of the main truss of the Rongjiang Bridge | |
对于普通节间,通过伸缩上弦杆来进行起拱,由式(16)计算独立节间相对预拱度与上弦伸缩值的对应结果,并同时列出文献[9]的计算值,结果如表 1所示。结果可见,本文计算值与文献[9]计算值十分吻合。
| 表 1 相对预拱度与上弦杆伸缩值对应表 Table 1 Table of relative pre-camber value-length change of upper chord |
榕江特大桥钢桁梁厂设预拱度曲线如图 6所示。

|
Download:
|
| 图 6 榕江特大桥厂设预拱度曲线(mm) Fig. 6 The pre-camber curve of the Rongjiang Bridge (mm) | |
对于普通的N字型节间,采用只伸缩上弦杆的方式;对于跨中对称节间,由于其竖杆的竖向倾角β已知为0,可采用同时伸缩上弦和斜腹杆的方式;对于支座变高度区和端部区域可采用同时伸缩上弦杆、斜腹杆和竖杆的方式来求解其弦杆伸缩量。以图 6所示预拱度作为输入,采用本文方法计算得到各杆件伸缩值,将E20~E30节间的杆件伸缩值列于表 2中。
| 表 2 杆件伸缩值 Table 2 Length change of members |
由表 2可见,本文方法计算值与设计值及文献[9]计算值均吻合很好,说明了本文方法进行预拱度设置的可靠性。
4 结论1) 直接以无应力状态法力学平衡方程得出杆件伸缩量数学表达式,式中不包含任何物理力学参数,为纯几何起拱方法,起拱过程不会产生起拱附加力。
2) 根据下承式钢桁梁桥预拱度设置特点,进一步得出了只伸缩上弦杆;同时伸缩上弦杆和斜腹杆;同时伸缩上弦杆、竖杆和斜腹杆三种情况下的杆件伸缩公式。可针对具体部位进行不同杆件伸缩,对桁梁进行无应力起拱。
3) 数值计算结果与设计值和参考文献计算值吻合,说明采用本文方法进行预拱度设置的可靠性。
4) 与荷载位移起拱法相比,二者的计算原理不同,但二者对N形桁架的起拱效果是一致的。
| [1] |
中铁大桥勘测设计院有限公司. TB 10002.2-2005, 铁路桥梁钢结构设计规范(附条文说明)[S].北京: 中国铁道出版社, 2005. China Railway Bridge Survey and Design Institute Co., Ltd. TB 10002.2-2005, Code for design on steel structure of railway bridge[S]. Beijing: China Railway Publishing House, 2005. (  0) 0)
|
| [2] |
中华人民共和国交通运输部. JTG D64-2015, 公路钢结构桥梁设计规范[S].北京: 人民交通出版社, 2015. People's Republic of China Ministry of Transport. JTG D64-2015, Specifications for design of highway steel bridge[S]. Beijing: People's Transportation Press, 2015. (  0) 0)
|
| [3] |
冯海舟, 熊健民. 大跨度钢桁梁斜拉桥预拱度分析[J]. 北方交通, 2013(3): 57-60. FENG Haizhou, XIONG Jianmin. Analysis on the camber of large-span steel truss cable-stayed bridge[J]. Northern Communications, 2013(3): 57-60. DOI:10.3969/j.issn.1673-6052.2013.03.019 (  0) 0)
|
| [4] |
冯沛. 大跨度铁路连续钢桁梁桥预拱度设置研究[J]. 铁道标准设计, 2016, 60(4): 62-64. FENG Pei. Study on camber-setting of large span railway steel truss bridge[J]. Railway standard design, 2016, 60(4): 62-64. (  0) 0)
|
| [5] |
陈小佳, 崔太雷, 封仁博. 基于几何正装法的N式钢桁梁桥预拱度设置研究[J]. 铁道建筑, 2017(1): 72-75. CHEN Xiaojia, CUI Tailei, FENG Renbo. Study on pre-camber setting for n-type steel truss bridge based on geometric-forward-installation method[J]. Railway engineering, 2017(1): 72-75. (  0) 0)
|
| [6] |
胡步毛, 艾宗良, 袁明, 等. 基于非线性规划实现钢桁连续梁预拱度[J]. 铁道工程学报, 2010, 27(4): 49-52. HU Bumao, AI Zongliang, YUAN Ming, et al. Use nonlinear programming to achieve camber of steel truss continuous bridge[J]. Journal of railway engineering society, 2010, 27(4): 49-52. DOI:10.3969/j.issn.1006-2106.2010.04.011 (  0) 0)
|
| [7] |
李佳莉, 张谢东, 陈卫东, 等. 基于多目标规划的连续钢桁梁预拱度设置研究[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(2): 360-364. LI Jiali, ZHANG Xiedong, CHEN Weidong, et al. Multi-objective programming based study on pre-camber setting of steel truss continuous girder bridge[J]. Journal of Wuhan University of Technology (transportation science & engineering), 2016, 40(2): 360-364. DOI:10.3963/j.issn.2095-3844.2016.02.032 (  0) 0)
|
| [8] |
向律楷, 鄢勇, 袁明, 等. 钢桁梁预拱度设置方法研究[J]. 四川建筑, 2015, 35(1): 150-153. XIANG Lyukai, YAN Yong, YUAN Ming, et al. Study on pre-camber setting of truss bridge[J]. Sichuan architecture, 2015, 35(1): 150-153. DOI:10.3969/j.issn.1007-8983.2015.01.054 (  0) 0)
|
| [9] |
蔡禄荣, 王荣辉, 王钰. 大跨度柏式钢桁梁桥厂制预拱度设置研究[J]. 铁道学报, 2013, 35(4): 96-101. CAI Lurong, WANG Ronghui, WANG Yu. Study on plant precamber setting of large-span n type steel truss bridge[J]. Journal of the China railway society, 2013, 35(4): 96-101. DOI:10.3969/j.issn.1001-8360.2013.04.015 (  0) 0)
|
| [10] |
苑仁安, 秦顺全, 王帆. 分阶段成形杆系结构几何非线性平衡方程[J]. 桥梁建设, 2014, 44(2): 50-55. YUAN Renan, QIN Shunquan, WANG Fan. Equilibrium equation for geometric nonlinearity of frame structure formed in stages[J]. Bridge construction, 2014, 44(2): 50-55. (  0) 0)
|
| [11] |
许磊平, 秦顺全, 马润平. 基于平面壳单元的分阶段成形结构平衡方程[J]. 西南交通大学学报, 2013, 48(5): 857-862. XU Leiping, QIN Shunquan, MA Runping. Equilibrium equation derivation of structures formed by stages based on plane shell element[J]. Journal of Southwest Jiaotong University, 2013, 48(5): 857-862. DOI:10.3969/j.issn.0258-2724.2013.05.012 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


