2. 船舶与海洋水动力湖北省重点实验室, 湖北 武汉 430074
2. Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics, Wuhan 430074, China
圆柱壳作为一种基本结构单元,由于其结构形式简单、自重轻,且抗弯刚度和抗扭刚度都比较大等优点,被广泛应用于航空、航天以及船舶与海洋工程等各种领域。所以,关于结构安全的圆柱壳临界载荷问题成为人们研究的重要课题。随着近年来功能梯度材料(FGM)的研究和应用越来越广泛,功能梯度材料板壳结构也越来受到关注。大量学者开展了功能梯度板壳的静动态特性的研究工作。临界载荷作为功能梯度圆柱壳结构的一个重要指标,关系到结构的安全性和可靠性。
有关圆柱壳结构失稳载荷的预报已经有很多研究。Raymond[1]研究了频率与临界载荷的关系并预测圆柱壳临界载荷的上下限,为基于振动的结构临界载荷无损预报方法奠定了基础。陈忱等[2]利用波传播法分析研究了水下圆柱壳的失稳载荷。李定坤[3]采用力法和三角级数法,定量的分析了边界条件对闭合圆柱薄壳在侧向外压作用下弹性稳定性所产生的影响。郭英涛等[4]基于实验对圆柱壳限制失稳的临界载荷与初始缺陷和不同长度的关系进行了分析。雷勇军等[5]利用实验方法,以结构振动和稳定性的相关性为基础,以振动频率测试值为监控参数,对复合材料圆柱壳失稳状态进行了监测。温登哲等[6]采用Flügge壳体理论,分析了径向内压对复合材料机匣的弹性稳定性的影响,并讨论了几何参数及材料特性对屈曲特性的影响。
对功能梯度材料的自由振动特性的研究也早已开展。梁斌等[7]通过使用Love理论和Rayleigh-Ritz方法,对功能梯度圆柱壳的自由振动进行研究和分析。Iqbal等[8]用波传播法研究了功能梯度材料圆柱壳的振动特性。Naeem等[9]则是研究了浸没在流场中的功能梯度圆柱壳在不同条件下的振动特性。李文达等[10]基于傅里叶级数法对两边弹簧约束的功能梯度圆柱壳的振动特性进行分析。
由于常规的功能梯度材料板壳临界载荷试验具有破坏性,学者们提出了功能梯度板和圆柱壳临界载荷的无损检测法,如利用解析法得到临界载荷的方法[11]。杨科等[11]通过建立功能梯度圆柱壳的几何方程、本构方程、平衡方程, 得到了该圆柱壳的临界屈曲荷载。Chen等[12]用伽辽金法分析非均匀分布载荷、热载荷、压电作用下的压电功能梯度矩形板的屈曲问题。Feldman等[13]对施加单一轴向载荷的功能梯度材料板的屈曲进行了分析。孟凡深等[14]研究了静水压下功能梯度圆柱壳的稳定性特性,得出了临界载荷。基于有限元等数值分析的方法建模工作量大,运算时间较长;而基于试验的方法则需付出较大代价。本文提出一种基于内压预测功能梯度圆柱壳的弹性临界载荷的方法,针对充液的功能梯度圆柱壳,用Flügge方程描述壳体振动,将流体视为理想声介质,采用波动方程描述。将功能梯度圆柱壳中流体内压产生的预应力计入动力平衡方程,研究内压和流—固耦合系统的固有频率之间的关系,并通过插值得到固有频率为零时所对应的静压力,从而得到弹性临界载荷。进而讨论不同的边界条件、不同壳长比、壳厚比以及不同梯度指数等对临界载荷的影响。
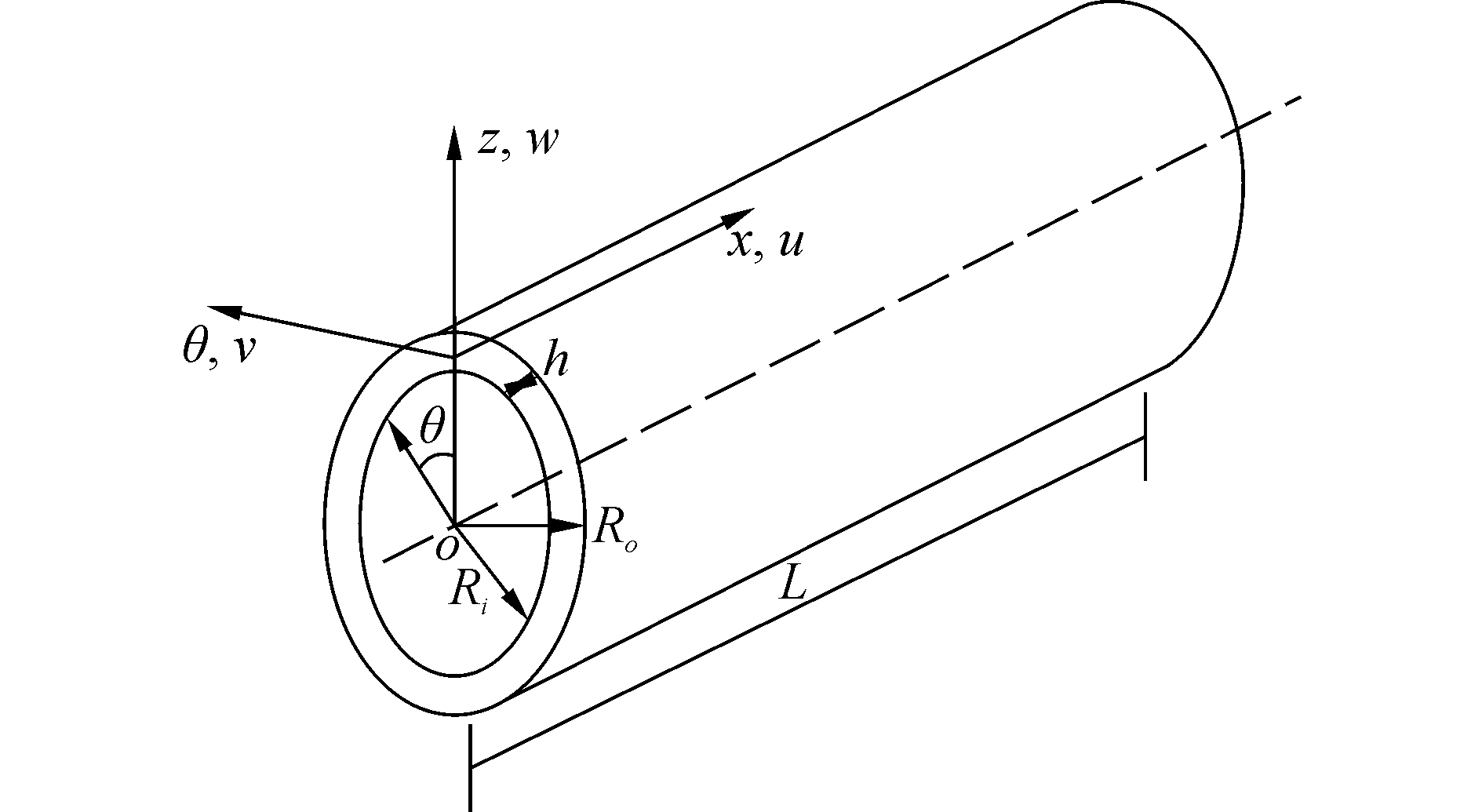
1 结构模型及材料属性 1.1 功能梯度圆柱壳模型在功能梯度圆柱壳的中曲面上建立曲面坐标系(x, θ, z),如图 1所示。x、θ、z分别是轴向坐标、周向坐标和径向坐标。Ro、Ri分别表示功能梯度圆柱壳的外径和内径,h则代表功能梯度圆柱壳的厚度,长度为L, 平均半径为R。位移变量则用u(x, θ, z)、v(x, θ, z)以及w(x, θ, z)来表示。
|
Download:
|
| 图 1 圆柱壳几何模型 Fig. 1 Geometry of cylindrical shell | |
功能梯度材料的特性P取决于材料的温度,可以表示为如下方程[8]:
| $ P = {P_0}\left( {{P_{ - 1}}{T^{ - 1}} + 1 + {P_1}T + {P_2}{T^2} + {P_3}{T^3}} \right) $ | (1) |
式中:P0、P-1、P1、P2、P3是和温度T(K)有关的系数。本文为常温状态,所以不考虑温度对FGM材料的影响。
功能梯度材料的特性通常与材料组分的特性和各组分体积分数相关,可表示为[8]
| $ P = \sum\limits_{k = 1}^t {{P_k}{V_{fk}}} $ | (2) |
式中:Pk、Vfk分别表示某材料组分的特性和组分的体积分数。其中:
| $ \sum\limits_{k = 1}^t {{V_{fk}}} = 1 $ | (3) |
对于厚度一定的功能梯度圆柱壳(以中面为参照面)的体积分数可表示为[8]
| $ {V_f} = {\left( {\frac{z}{h} + 0.5} \right)^N} $ | (4) |
其中梯度指数N为非负实数(0≤N≤∞),幂指数对于体积分数的影响主要表现在N较小的情况。
本文由于是采用由两种不同材料组成的功能梯度材料圆柱壳,则沿厚度方向的各参数:弹性模量E,泊松比μ以及密度可表示为[8]
| $ \left\{ \begin{array}{l} E = \left( {{E_o} - {E_i}} \right){\left( {\frac{z}{h} + 0.5} \right)^N} + {E_i}\\ \mu = \left( {{\mu _o} - {\mu _i}} \right){\left( {\frac{z}{h} + 0.5} \right)^N} + {\mu _i}\\ \rho = \left( {{\rho _o} - {\rho _i}} \right){\left( {\frac{z}{h} + 0.5} \right)^N} + {\rho _i} \end{array} \right. $ | (5) |
式中:Eo、Ei分别代表外表面材料和内表面材料的弹性模量,μo、μi分别代表外表面材料和内表面材料的泊松比,ρo、ρi分别代表外表面材料和内表面材料的质量密度。
2 动力平衡方程由Flügge理论得到壳体静力平衡方程,应变位移方程以及内力矩平衡方程,推导出包含初始应力的壳体自由振动方程[15-16]:
| $ \begin{array}{*{20}{c}} {\left( {1 + {T_1}} \right){u_{xx}} + \left( {{T_2} + \frac{{1 - \mu }}{2}} \right){u_{\theta \theta }} + \frac{{1 + \mu }}{2}{v_{x\theta }} + }\\ {\left( {\mu - {T_2}} \right){w_x} + K\left( {\frac{{1 - \mu }}{2}{u_{\theta \theta }} - {w_{xxx}} + \frac{{1 - \mu }}{2}{w_{x\theta \theta }}} \right) = }\\ {\frac{{{\rho _s}{R^2}\left( {1 - {\mu ^2}} \right)}}{E}{u_{tt}}} \end{array} $ | (6) |
| $ \begin{array}{*{20}{c}} {\frac{{1 + \mu }}{2}{u_{x\theta }} + \left( {{T_1} + \frac{{1 - \mu }}{2}} \right){v_{xx}} + \frac{{1 + \mu }}{2}{v_{\theta \theta }} + }\\ {\left( {1 + {T_2}} \right){w_\theta } + K\left( {\frac{{3\left( {1 - \mu } \right)}}{2}{v_{xx}} - \frac{{3 - \mu }}{2}{w_{xx\theta }}} \right) = }\\ {\frac{{{\rho _s}{R^2}\left( {1 - {\mu ^2}} \right)}}{E}{v_{tt}}} \end{array} $ | (7) |
| $ \begin{array}{*{20}{c}} {\left( {\mu - {T_2}} \right){u_x} - K{u_{xxx}} + K\frac{{1 - \mu }}{2}{u_{x\theta \theta }} + }\\ {\left( {1 + {T_2}} \right){v_\theta } - K\frac{{3 - \mu }}{2}{v_{xx\theta }} + \left( {1 + K} \right)w + }\\ {K{w_{xxxx}} + 2K{w_{xx\theta \theta }} + K{w_{\theta \theta \theta \theta }} + \left( {2K - {T_2}} \right){w_{\theta \theta }} - }\\ {{T_1}{w_{xx}} + \frac{{{R^2}\left( {1 - {\mu ^2}} \right)}}{{Eh}}{P_f} = \frac{{{\rho _s}{R^2}\left( {1 - {\mu ^2}} \right)}}{E}{v_{tt}}} \end{array} $ | (8) |
| $ {\left( {\;\;\;} \right)_x} = R\frac{{\partial \left( {\;\;\;} \right)}}{{\partial x}},{\left( {\;\;\;} \right)_\theta } = \frac{{\partial \left( {\;\;\;} \right)}}{{\partial \theta }}, $ |
| $ {\left( {\;\;\;} \right)_t} = \frac{{\partial \left( {\;\;\;} \right)}}{{\partial t}},K = \frac{{{h^2}}}{{12{R^2}}};{T_1} = \frac{{R\left( {1 - {\mu ^2}} \right)}}{{2Eh}}{p_0}, $ |
| $ {T_2} = \frac{{R\left( {1 - {\mu ^2}} \right)}}{{Eh}}{p_0}, $ |
式中:p0是壳体表面及两端承受的压力,当p0取正值时,表示作用在壳体上为内压,当p0取负值时,表示作用在壳体上为外压;T1和T2则分别为内压在壳体轴向和周向的影响。
由于本文利用充液功能梯度圆柱壳的内压与固有频率的关系来预测,则需要考虑流体对圆柱壳的影响,即求解圆柱壳和水的耦合模态。
假定圆柱壳周围的流体为理想的声介质,则理想流体在柱坐标系下的波动方程:
| $ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {P_f}}}{{\partial r}}} \right) + \frac{1}{{{r^2}}}\frac{{{\partial ^2}{P_f}}}{{\partial {\theta ^2}}} - \frac{1}{{C_f^2}}\frac{{{\partial ^2}{P_f}}}{{\partial {t^2}}} = 0 $ | (9) |
对于壳体的中面位移,利用波传播法可表示为
| $ \left\{ \begin{array}{l} u\left( {x,\theta ,t} \right) = {A_m}\cos \left( {n\theta } \right)\exp \left( {{\rm{i}}\omega t - {\rm{i}}{k_n}x} \right)\\ v\left( {x,\theta ,t} \right) = {B_m}\sin \left( {n\theta } \right)\exp \left( {{\rm{i}}\omega t - {\rm{i}}{k_n}x} \right)\\ w\left( {x,\theta ,t} \right) = {C_m}\cos \left( {n\theta } \right)\exp \left( {{\rm{i}}\omega t - {\rm{i}}{k_n}x} \right) \end{array} \right. $ | (10) |
式中:Am、Bm、Cm分别为x、θ、z方向上的波幅。ω为角频率,kn表示轴向波数,n则为周向模态阶数。
对于声压场,满足上述波动方程的流体声压解可表示为与中面位移类似的方程[16]:
| $ {P_f} = {P_{ns}}\cos \left( {n\theta } \right){\rm{H}}_n^{\left( 2 \right)}\left( {{k_r}r} \right)\exp \left( {{\rm{i}}\omega t - {\rm{i}}{k_n}x} \right) $ | (11) |
式中:Pns表示压力幅值,Hn(2)(krr)是第二型n阶汉克尔函数。径向波数kr满足普通矢量关系kr=(k02-kn2)1/2,其中k0=ω/c是流体声波数,kr是kn的多值函数。
由于流体径向速度必须等于外壳壁和液体的耦合面的法向速度,在耦合面上的连续条件为[16]
| $ - \frac{1}{{{\rm{i}}\omega {\rho _f}}}\frac{{\partial {P_f}}}{{\partial r}}\left| {_{r = R}} \right. = \frac{{\partial w}}{{\partial t}}\left| {_{r = R}} \right. $ | (12) |
由方程(11)以及方程(12)可得到方程[16]:
| $ {P_{ns}} = \left[ {{\omega ^2}{\rho _f}/{k_r}H_n^{\left( 2 \right)}\left( {{k_r}r} \right)} \right]{C_m} $ | (13) |
将方程(13)代入方程(6),得到耦合系统的运动方程,其矩阵形式为
| $ \left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{{c_{13}}}\\ {{c_{21}}}&{{c_{22}}}&{{c_{23}}}\\ {{c_{31}}}&{{c_{32}}}&{{c_{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A_m}}\\ {{B_m}}\\ {{C_m}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}} \right] $ | (14) |
式中:
| $ {c_{11}} = {\mathit{\Omega }^2} - \left( {1 + {T_1}} \right){\left( {{k_n}R} \right)^2} - \left[ {{T_2} + \left( {1 + \frac{{{h^2}}}{{12{R^2}}}} \right)\frac{{1 - \mu }}{2}} \right]{n^2} $ |
| $ {c_{12}} = {c_{21}} = - {\rm{i}}{k_n}Rn\frac{{1 + \mu }}{2} $ |
| $ {c_{13}} = {c_{31}} = - {\rm{i}}\left[ {\left( {\mu - {T_2}} \right){k_n}R + \frac{{{h^2}}}{{12}}{k_n}^3R - \frac{{{h^2}}}{{12R}}\frac{{1 - \mu }}{2}{k_n}{n^2}} \right] $ |
| $ {c_{22}} = \left[ {{T_1} + \left( {1 + \frac{{{h^2}}}{{4{R^2}}}} \right)\frac{{1 - \mu }}{2}} \right]{k_n}^2{R^2} + \left( {1 + {T_2}} \right){n^2} - {\mathit{\Omega }^2} $ |
| $ {c_{23}} = \left( {1 + {T_2}} \right)n + \frac{{{h^2}}}{{12}}\frac{{3 - \mu }}{2}{k_n}^2n $ |
| $ \begin{array}{l} {c_{33}} = 1 + \frac{{{h^2}}}{{12{R^2}}} + \frac{{{h^2}}}{{12}}{k_n}^4{R^2} + \frac{{{h^2}}}{6}{n^2}{k_n}^2 + \frac{{{h^2}}}{{12{R^2}}}{n^4} - \\ \;\;\;\;\;\;\;\left( {\frac{{{h^2}}}{{4{R^2}}} - {T_2}} \right){n^2} + {T_1}{k_n}^2{R^2} - {\mathit{\Omega }^2} + {\rm{FL}} \end{array} $ |
式中:
| $ {\rm{FL}} = - {\mathit{\Omega }^2}\frac{{{\rho _{\rm{f}}}}}{{{\rho _{\rm{s}}}}}\frac{R}{h}\frac{{H_n^{\left( 2 \right)}\left( {{k_r}R} \right)}}{{\left( {{k_r}R} \right)H{'}_n^{\left( 2 \right)}\left( {{k_r}R} \right)}} $ | (15) |
若在真空中则FL=0。
由于方程(14)需要有非零解,则c矩阵的系数行列值必为0:
| $ \left| \mathit{\boldsymbol{c}} \right| = 0 $ | (16) |
则由方程(16)可知,在壳体参数给定的条件下,方程(16)反映了kn和Ω的关系。当给定轴向波数kn,则可得到频率方程:
| $ f\left( \mathit{\Omega } \right) = 0 $ | (17) |
其中轴向波数根据不同边界条件得出,如表 1[16]。通过式(17)以及轴向波数kn,可得到圆柱壳在一定内压条件下的固有频率,从而可以通过得到圆柱壳内压与固有频率之间的关系,预测固有频率为零时所对应的壳体压力,从而求得圆柱壳的临界载荷。
| 表 1 不同边界下的圆柱壳轴向波数 Table 1 Longitudinal wave number on different boundary conditions |
对于圆柱壳结构,失稳时其刚度丧失,固有频率为零,若能求出其固有频率为零时对应的压力即可认为是圆柱壳结构失稳临界压力。由于功能梯度圆柱壳和流场耦合且流体载荷FL为复数,因此方程(17)是一个复系数高阶超越方程,可采用抛物线迭代法,即二次插值法来求解。
3.1 计算方法正确性验证本文从两方面来验证方法的正确性。首先将功能梯度圆柱壳退化为圆柱壳,通过与文献[8]中钢制圆柱壳弹性临界压力的对比,验证本文提出的基于内压条件下壳体固有频率来预测弹性临界压力的准确性;然后计算干模态下功能梯度圆柱壳的固有频率,并与文献[8]对比,验证本文求解干模态下功能梯度圆柱壳固有频率方法的准确性。
3.1.1 钢制圆柱壳的临界载荷预测计算两端简支条件下充液钢质圆柱壳的固有频率,其中钢材料参数如下:杨氏模量Ec=210 GPa,泊松比μc=0.3,质量密度ρc=7 850 kg/m3,壳体长度为L=20 m,厚度为h=0.01 m,半径为R=1 m。流体声速Cf=1 500 m/s,流体密度ρf=1 000 kg/m3。由方程(17)经过退化,可以得出不同内压作用下钢制圆柱壳固有频率如表 2所示。
| 表 2 m=1两端简支状态下圆柱壳在不同内压下的固有频率 Table 2 Natural frequencies of cylindrical shells under different internal pressure with simply supported-simply supported boundary condition m=1 |
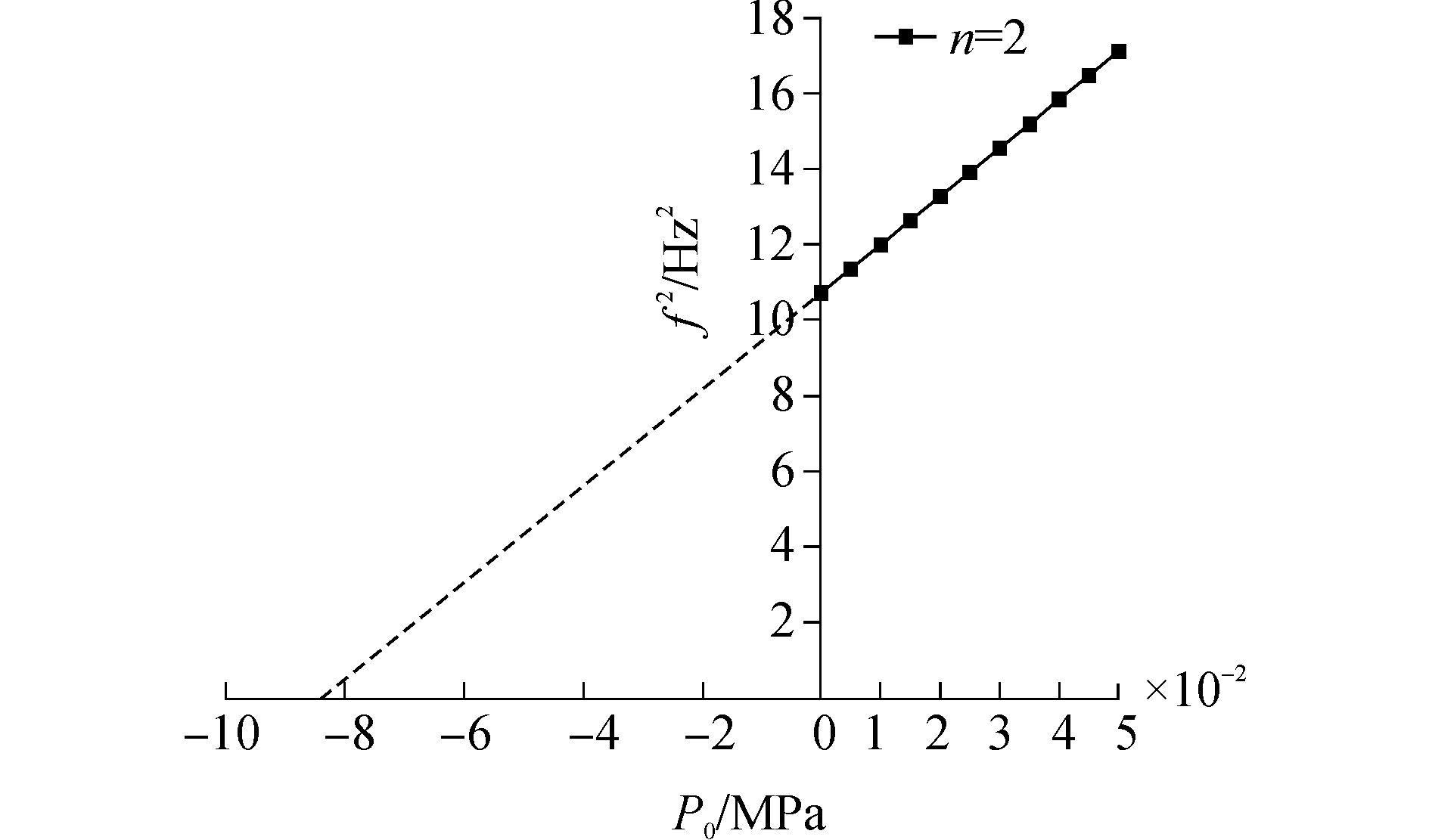
将内压值和固有频率的平方的关系绘制出来,可得n=2时,固有频率为0时对应的压力值最小,如图 2所示。
|
Download:
|
| 图 2 两端简支圆柱壳的固有频率的平方随内压的变化 Fig. 2 Variation of the square of natural frequencies of cylindrical shells with simply supported-simply supported boundary condition as variation of internal pressure | |
由图中可以看出,图中实线部分中的固有频率平方和内压呈线性的关系。虚线部分则是通过对实线中的数据线性插值得到的。图中横坐标中内压为正,外压为负值。对于圆柱壳结构,失稳时其刚度丧失,固有频率为零。根据内压条件下得到的固有频率平方与压力的关系,通过插值预测其固有频率为零时对应的压力,即为圆柱壳弹性临界载荷,由图可得其值为-0.083 901 MPa。与本例相同参数条件下的文献[2]中的结果为0.083 9 MPa。表明本文中采用内压条件下壳体的固有频率与内压关系来求取临界载荷的方法是正确的。
3.1.2 功能梯度圆柱壳固有频率计算为验证本文求取功能梯度圆柱壳固有频率的准确性,采用本文方法对某功能梯度圆柱壳的固有频率进行计算,并和文献[8]数据进行对比。材料参数如表 3所示,h/R=0.002, m=1, L/R=20。
| 表 3 功能梯度材料圆柱壳成分材料属性 Table 3 Material properties of FGM cylindrical shells composition |
表 4为边界条件两端简支时不同体积分数的功能梯度圆柱壳的固有频率,同时与文献[8]进行对比。在此算例中,将功能梯度材料分为Ⅰ型和Ⅱ型,Ⅰ型中不锈钢在外表面,镍在内表面,而Ⅱ型的材料顺序则是相反的。
| 表 4 干模态下两端简支FGM圆柱壳的固有频率 Table 4 Natural frequencies for the FGM cylindrical shells against circumferential wave number with simply supported-simply supported |
通过表 4与文献[8]计算结果的对比,可知本文计算结果与文献结果吻合很好,多数误差不超过1%。由此可知,文本计算功能梯度圆柱壳固有频率的方法和程序是准确的。
3.2 功能梯度材料圆柱壳的临界载荷计算采用本文所提出的方法来预测功能梯度圆柱壳的弹性临界载荷,并对其在不同条件下的临界载荷进行对比分析。
本算例中计算功能梯度材料圆柱壳的组成成分分别为材料o和材料i,各参数如表 5所示。
| 表 5 功能梯度材料圆柱壳成分材料属性 Table 5 Material properties of FGM cylindrical shells composition |
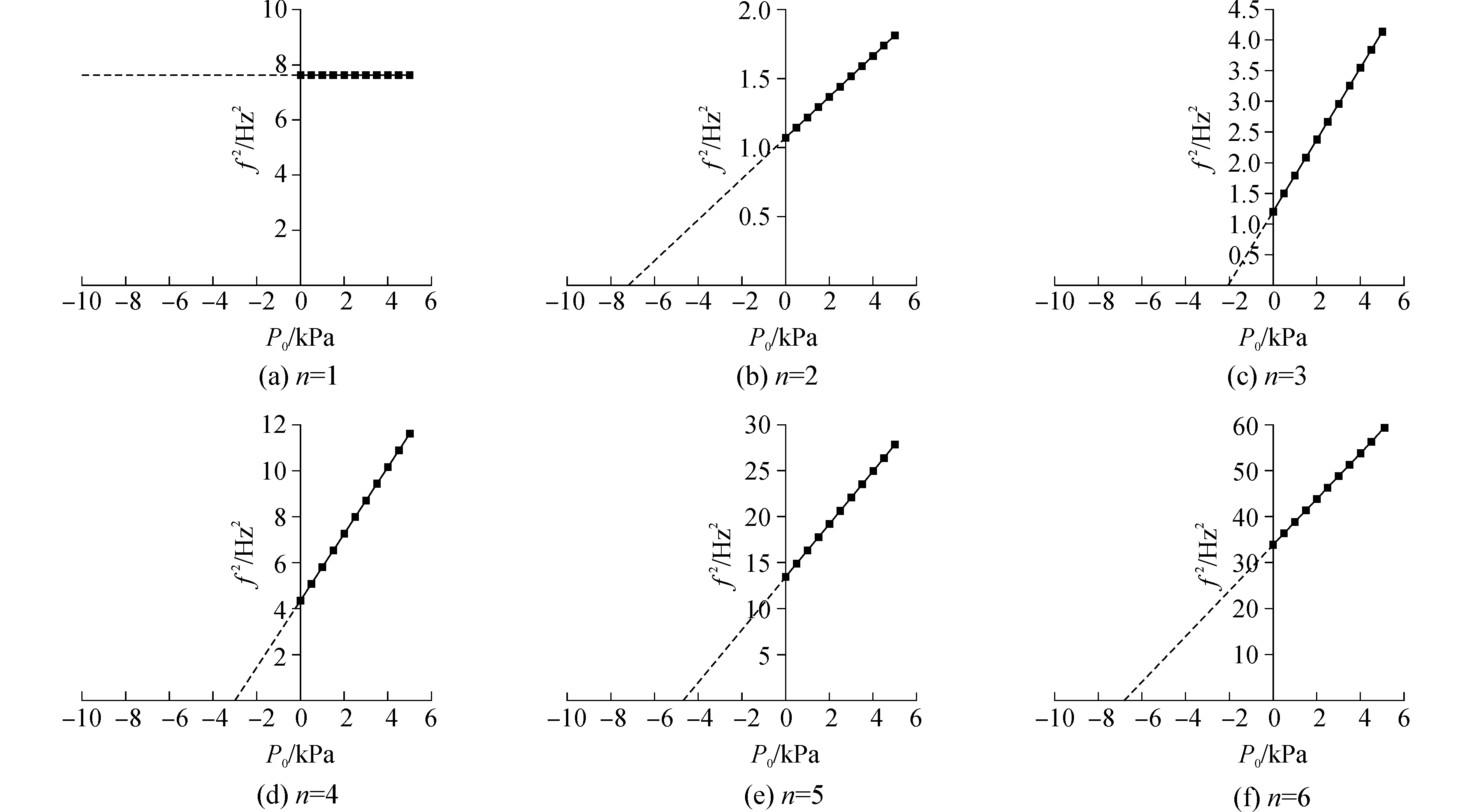
圆柱壳半径R=1 m,h/R=0.002,L/R=20,N=1。流体声速Cf=1 500 m/s,流体密度ρf=1 000 kg/m3。假定充液功能梯度圆柱壳为两端简支状态,取m=1,在不同内压条件下通过计算得到各个周向模态n对应的功能梯度圆柱壳的固有频率,并且将6个不同的周向模态对应的固有频率的平方与内压的关系绘制在图 3中。
|
Download:
|
| 图 3 功能梯度圆柱壳固有频率的平方与内压关系 Fig. 3 Relationship between square of natural frequency and internal pressure of functionally graded cylindrical shell | |
从图 3中可见,周向模态数n不同时,功能梯度圆柱壳固有频率的平方与内压均呈线性关系。在n=1的时候,功能梯度圆柱壳固有频率的平方几乎无变化,这是由于其对应模态类似梁弯曲的情形,临界载荷非常大,所以在本文中不予考虑。在周向模态n为2、3、4、5、6的时候,功能梯度圆柱壳固有频率的平方与压力均近似呈线性关系,曲线斜率各不相同,可由内压计算结果插值预测得到受外压作用时的固有频率,直至固有频率的平方降为零。从图 3中还可发现,当周向模态n=3时,其固有频率为零时对应的压力值最小,则弹性临界载荷应为其对应的压力值,通过插值得到的临界载荷值大小为2.048 0 kPa。由此即可无损预测该功能梯度圆柱壳的临界载荷。
讨论不同参数条件对弹性失稳临界载荷的影响。考虑两端固支(C-C)、两端简支(SS-SS)、一端简支一端固支(C-SS)等条件,利用本文方法得出功能梯度圆柱壳的临界载荷,分别为3.333 4、2.048 0、2.756 2 kPa。由该数据可知功能梯度圆柱壳在两端固支条件下临界载荷较其他两种条件大。这是由于两端刚性固定存在反向弯矩,使得系统刚度较其他两种边界条件大,所以两端刚性固定条件下的临界载荷较大。这也与普通圆柱壳结论一致[5]。
壳厚比不同(h/R为0.002、0.005、0.01、0.05),边界条件为简支时,利用本文方法得到功能梯度圆柱壳的临界载荷值,如表 6所示。
| 表 6 不同h/R两端简支功能梯度圆柱壳的临界载荷值 Table 6 Critical loads of simply supported-simply supported functionally graded cylindrical shells with different h/R |
由表 6中数据可知功能梯度圆柱壳在两端简支条件下壳厚比越大,系统刚度越大,临界载荷值也越大,即在其他参数不变时,厚壳不容易失稳。
壳长比不同(L/R为10、20、30、40、50),边界条件为简支时,利用本文方法得到功能梯度圆柱壳的临界载荷值,如表 7所示。由表 7中数据可知功能梯度圆柱壳在两端简支条件下,壳长比越小,即圆柱壳越短,系统刚度越大,临界载荷值越大,即在其他参数不变时,短壳不容易失稳。
| 表 7 不同L/R两端简支功能梯度圆柱壳的临界载荷值 Table 7 Critical loads of simply supported-simply supported functionally graded cylindrical shells with different L/R |
功能梯度圆柱壳的梯度指数N不同、边界条件为简支条件下,利用本文方法得到功能梯度圆柱壳临界载荷值,如表 8所示。由表 8的数据中可知,梯度指数越大临界载荷越大。原因是梯度指数越大,由式(5)可知材料i成分越多,则壳体的刚度越小,因此临界载荷也越小,且接近于材料i所构成的均质圆柱壳的临界载荷值1.605 4 kPa。
| 表 8 不同梯度指数N两端简支功能梯度圆柱壳的临界载荷 Table 8 Critical loads of simply supported-simply supported functionally graded cylindrical shells with different N |
1) 在相同模态阶数下,固有频率的平方与压力呈线性关系;
2) 通过固有频率的平方和内压的线性关系,插值求得临界载荷,并通过与文献对比,验证了本文方法的正确性;
3) 不同边界条件下,临界载荷在两端固支状态较其他两种状态大;
4) 功能梯度圆柱壳只改变厚度时,厚壳较稳定;
5) 功能梯度圆柱壳只改变长度时,短壳较稳定;
6) 在本文中梯度指数N越大,功能梯度圆柱壳的临界载荷值越小,这是由于N值越大,临界载荷值越接近材料i所构成圆柱壳的临界载荷值。
本文提出的方法基于理论推导和数值求解,相对于外压预测临界载荷的方法,具有一定优势。为无损预测功能梯度圆柱壳的临界载荷提供了一种新的思路。
| [1] |
PLAUT R H, VIRGIN L N. Use of frequency data to predict buckling[J]. Journal of engineering mechanics, 1990, 116(10): 2330-2335. DOI:10.1061/(ASCE)0733-9399(1990)116:10(2330) (  0) 0)
|
| [2] |
陈忱, 李天匀, 朱翔, 等. 基于波传播法的水下圆柱壳临界载荷-频率特性分析[J]. 中国造船, 2012, 53(1): 130-136. CHEN Chen, LI Tianyun, ZHU Xiang, et al. Frequency characteristics analysis for critical load of a submerged cylindrical shell based on wave propagation approach[J]. Shipbuilding of China, 2012, 53(1): 130-136. (  0) 0)
|
| [3] |
李定坤. 边界条件对园柱薄壳稳定性的影响[J]. 福州大学学报, 1978(1): 44-55. LI Dingkun. Influence of boundary conditions on the stability of cylindrical shells[J]. Journal of Fuzhou University, 1978(1): 44-55. (  0) 0)
|
| [4] |
郭英涛, 任文敏. 圆柱壳限制失稳的实验研究[J]. 工程力学, 2006, 23(S1): 6-10. GUO Yingtao, REN Wenmin. Experimental study on confined buckling of cylindrical shells[J]. Engineering mechanics, 2006, 23(S1): 6-10. (  0) 0)
|
| [5] |
雷勇军, 唐国金, 卓曙君, 等. 复合材料圆柱壳失稳载荷的振动监测[J]. 实验力学, 2003, 18(3): 383-388. LEI Yongjun, TANG Guojin, ZHUO Shujun, et al. Determination of the buckling loads of composite cylindrical shells by vibration inspecting[J]. Journal of experimental mechanics, 2003, 18(3): 383-388. DOI:10.3969/j.issn.1001-4888.2003.03.017 (  0) 0)
|
| [6] |
温登哲, 陈予恕, 侯磊, 等. 复合材料机匣的弹性稳定性及振动特性研究[J]. 振动与冲击, 2015, 34(23): 1-7, 24. WEN Dengzhe, CHEN Yushu, HOU Lei, et al. Elastic stability and vibration characteristics of a composite case[J]. Journal of vibration and shock, 2015, 34(23): 1-7, 24. (  0) 0)
|
| [7] |
李戎, 梁斌, NODA N A, 等. 基于波动法的静水压力下功能梯度圆柱壳振动特性研究[J]. 船舶力学, 2013, 17(1): 148-154. LI Rong, LIANG Bin, NODA N A, et al. Study on vibration of functionally graded cylindrical shells subjected to hydrostatic pressure by wave propagation method[J]. Journal of ship mechanics, 2013, 17(1): 148-154. (  0) 0)
|
| [8] |
IQBAL Z, NAEEM M N, SULTANA N, et al. Vibration Characteristics of FGM circular cylindrical shells filled with fluid using wave propagation approach[J]. Applied mathematics and mechanics, 2009, 30(11): 1393-1404. DOI:10.1007/s10483-009-1105-x (  0) 0)
|
| [9] |
NAEEM M N, GAMKHAR M, ARSHAD S H, et al. Vibration analysis of submerged thin FGM cylindrical shells[J]. Journal of mechanical science and technology, 2013, 27(3): 649-656. DOI:10.1007/s12206-013-0119-6 (  0) 0)
|
| [10] |
李文达, 杜敬涛, 杨铁军, 等. 基于改进傅里叶级数方法的旋转功能梯度圆柱壳振动特性分析[J]. 哈尔滨工程大学学报, 2016, 37(3): 388-393. LI Wenda, DU Jingtao, YANG Tiejun, et al. Vibration characteristics analysis of the rotating functionally graded cylindrical shell structure using an improved Fourier series method[J]. Journal of Harbin Engineering University, 2016, 37(3): 388-393. (  0) 0)
|
| [11] |
杨科, 王璠. 功能梯度圆柱壳的屈曲问题[J]. 中山大学学报(自然科学版), 2008, 47(S2): 9-13. YANG Ke, WANG Fan. Buckling of functionally graded cylindrically shells[J]. Acta scientiarum naturalium universitatis sunyatseni, 2008, 47(S2): 9-13. (  0) 0)
|
| [12] |
CHEN X L, ZHAO Z Y, LIEW K M. Stability of piezoelectric FGM rectangular plates subjected to non-uniformly distributed load, heat and voltage[J]. Advances in engineering software, 2008, 39(2): 121-131. DOI:10.1016/j.advengsoft.2006.12.004 (  0) 0)
|
| [13] |
FELDMAN E, ABOUDI J. Buckling analysis of functionally graded plates subjected to uniaxial loading[J]. Composite structures, 1997, 38(1-4): 29-36. DOI:10.1016/S0263-8223(97)00038-X (  0) 0)
|
| [14] |
孟凡深, 李戎, 梁斌, 等. 静水压力下功能梯度圆柱壳稳定性研究[J]. 船舶力学, 2016, 20(1/2): 110-119. MENG Fanshen, LI Rong, LIANG Bin, et al. Study on Stability of functionally graded cylindrical shells Subjected to hydrostatic pressure[J]. Journal of ship mechanics, 2016, 20(1/2): 110-119. (  0) 0)
|
| [15] |
FLÜGGE W. Stresses in shells[M]. 2nd ed. New York: Springer-Verlag, 1973.
(  0) 0)
|
| [16] |
ZHU X, YE W B, LI T Y, et al. The elastic critical pressure prediction of submerged cylindrical shell using wave propagation method[J]. Ocean engineering, 2013, 58: 22-26. DOI:10.1016/j.oceaneng.2012.09.008 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


