2. 中国船舶重工集团第722研究所, 湖北 武汉 430079
2. No. 722 Research Institute of CSIC, Wuhan 430079, China
随着蓝水海军战略的推进,水面无人艇(unmanned surface vehicle,USV)以其高机动性、智能化和无人化的特点,成为未来海上远距离作战的重要装备。当USV上搭载多种传感器和作战模块后,可执行警戒、侦察、监视、跟踪、探雷、灭雷和通信中继等任务。目前服役和在研的USV在基本实现了路径巡航[1-2]、避碰避障[3-5]等初级自主行为后,开始逐步向高级自主行为发展。美国海军已率先在USV高级自主行为研究领域取得重大突破—“蜂群战术”,它们以集群协同作战模式,一旦侦察到“可疑船只”,便自主对其进行包围和拦截。本文以“蜂群战术”为背景,假设我方USV被敌方侦察到后,在机动性不逊于敌方的情况下,提出了一种抗追捕-逃跑策略来动态规划我方USV的逃跑路径,对提高其自主性、智能性和对抗性具有重要意义。
国内外相关专家对追逃问题进行了深入研究,并在机器人[6-9]、无人机对抗[10-11]和导弹拦截[12-13]等领域取得了很多研究成果。针对追逃问题有两种主流解决思路,即分层分解法和状态降维法。前者将问题视为多个并行层面的单追捕-逃跑问题,其核心在于如何加强追捕者之间的协作[14],如哈密顿-雅克比(Hamilton-Jacobi)方程法[13, 15];后者是将连续状态离散化,其核心在于如何保证在离散过程中不降低实际模型的求解精度,如栅格法[8]、时间间隔法[9]、Voronoi图法[11],其中Voronoi图法的求解速度最快,但此类方法往往假设追逃双方具有相同的运动速度,且均能实现瞬时转身。
目前,专门针对USV追逃问题的研究尚处于起步阶段,可以借鉴其他领域追逃问题已取得的研究成果,如文献[7]以追捕机器人的视角,通过基于模糊逻辑规则的分层控制系统,以提高其相互协作追捕的能力;文献[9]研究了无障碍物环境下高速运动机器人的追逃问题,利用构建阿波罗尼奥斯圆的方法,分别提出了相对应的追捕和逃跑策略;文献[15]采用微分对策构建动态方程,并使用解耦的多追捕机器人控制策略来规避次优解,获得最优追捕和逃跑方案;文献[16]研究了无人巡逻队在线路径规划问题,提出了基于随机树快速搜索(RRT)的边界巡逻算法,使其可以同时捕获2~3个入侵者。上述这些方法都给USV的抗追捕-逃跑策略的研究带来了启发,但在具体功能实现过程中还需要联系USV的实际情况。如USV在进行逃跑路径规划的过程中,除了必须要考虑航行海区中障碍物的影响外,还需要考虑USV自身操纵约束对航向、航速控制系统的影响,这使得抗追捕-逃跑策略的研究问题变得异常复杂。
本文将从追逃问题中逃跑者的视角,讨论我方USV在受到“蜂群战术”攻击时,如何动态决策逃跑路径以摆脱敌方USVs的追捕。拟利用阿波罗尼奥斯圆的性质和其自身操纵约束建立相关模型,并以此为依据求解出USV在被追捕时的最优逃跑路径。
1 USV抗追捕-逃跑问题 1.1 USV抗追捕-逃跑问题的数学描述假设在某有界二维连续环境Ω中(含有障碍物),N艘敌方USVs欲追捕我方USV,其动态方程可表示为
| $ \left\{ \begin{array}{l} {{\dot x}_P} = {v_P}\cos {\psi _P}\\ {{\dot y}_P} = {v_P}\sin {\psi _P}\\ {{\dot \psi }_P} = {v_P}/{R_P} \end{array} \right., \left\{ \begin{array}{l} {{\dot x}_E} = {v_E}\cos {\psi _E}\\ {{\dot y}_E} = {v_E}\sin {\psi _E}\\ {{\dot \psi }_E} = {v_E}/{R_E} \end{array} \right. $ | (1) |
式中:P={P1, P2, …, PN}表示敌方USVs;E表示我方USV;(xP, yP)、(xE, yE)分别表示敌我双方在环境Ω中的位置;ψP和ψE表示航向角;RP和RE分别表示最小转弯半径;vP、vE分别表示航速,且满足vP∈[0, VP]、vE∈[0, VE],VP、VE分别表示它们的最大速度,其比值λ为
| $ \lambda = {V_P}/{V_E} $ | (2) |
为了增强问题的可研究性,敌我双方各占优势,如敌方USVs的数量多,相应地我方USV的最大航行速度比敌方USVs快。又由文献[17]可知,当λ < sin(π/N)时追捕者很难追到逃跑者,此时讨论抗追捕-逃跑问题无实际意义。为此,本文主要研究当敌方USVs和我方USV最大速度比λ∈[sin(π/N), 1)时,我方USV抗追捕-逃跑动态路径规划问题。
多艘敌方USVs对我方USV进行追捕,则判定我方USV被敌方USVs捕获的条件为
| $ d(P({x_P}, {y_P}), E({x_E}, {y_E})) \le \varepsilon $ | (3) |
式中:d(·, ·)表示希尔伯特空间的2-范数,ε为敌方USVs捕获半径。若在指定时间内式(3)不成立,或者我方USV提前到达二维连续环境Ω的边界,则判定抗追捕-逃跑成功。
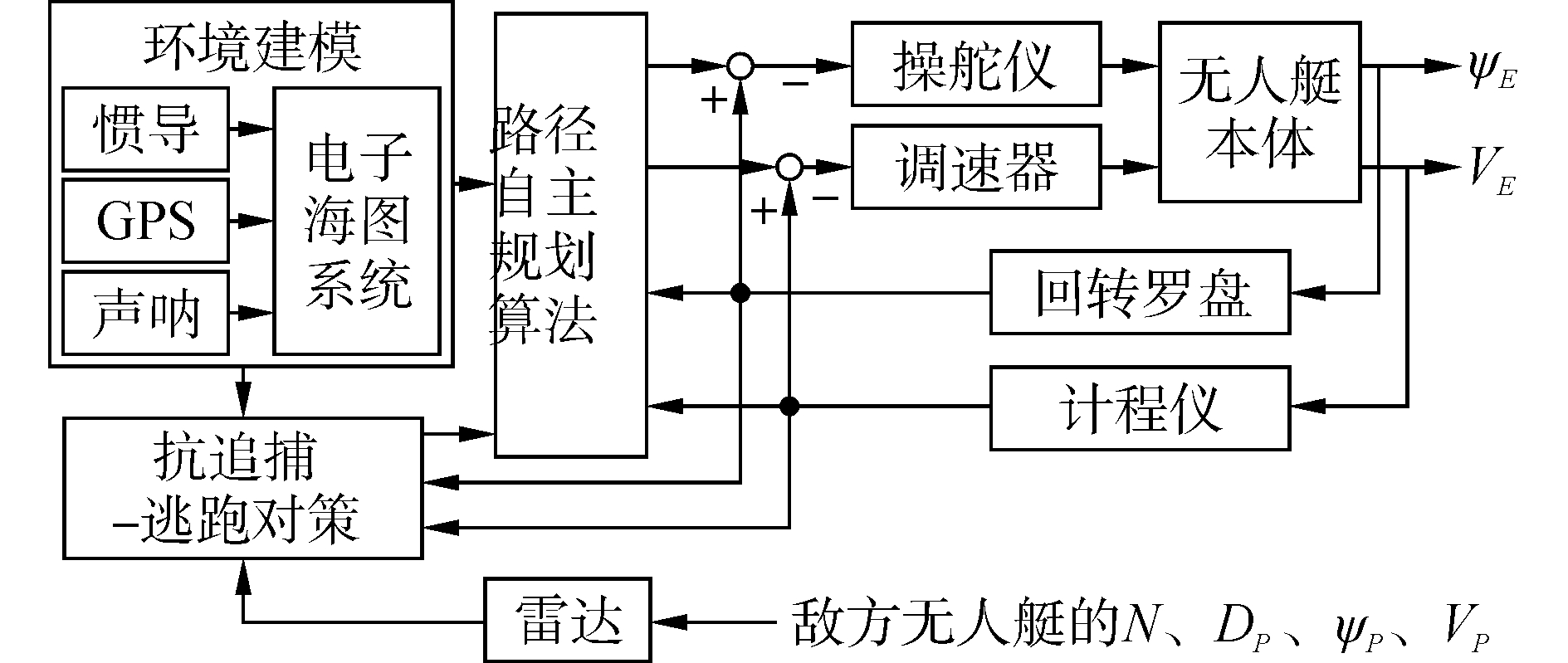
1.2 USV动态逃跑路径规划的系统概述在USV抗追捕-逃跑问题中,其动态路径规划的系统框架如图 1所示。先根据艇载设备(惯导、GPS和声呐等)结合电子海图系统建立环境模型,主要用于获取航行海区的障碍物信息;接着通过路径自主规划算法[5]计算出航向和航速,由回转罗盘和计程仪测得当前实际的航向和航速;最后用计算值和测量值的差值调整操舵仪和调速器,使我方USV按既定的航向和航速航行。
|
Download:
|
| 图 1 动态路径规划的系统框架图 Fig. 1 Framework of the dynamic path planning system | |
当我方USV的航海雷达发现敌方USVs时,其雷达探测到敌艇的数量、距离、航向和速度分别为{N, DP, ψP, VP}。将雷达探测的结果输入到抗追捕-逃跑对策中,并按策略指导路径自主规划算法重新计算航向和航速,使其摆脱敌方USVs的跟踪和追捕。
在抗追捕-逃跑动态路径规划中,主要需要考虑USV的位置、航行方向和速度。因此,可以将航行海区的环境模型简化为二维平面模型,并利用连续环境模型代替离散的棋盘栅格模型。与棋盘栅格模型不同,本文先参考电子海图将该航行海区分为障碍物和可航行海区,其中障碍物包括岛屿、礁石、暗礁、浅滩等可能阻碍航行的区域。采用状态降维法建模对冗余的障碍物轮廓信息进行简化处理,即将该区域中的障碍物抽象成平面多边形。这种模型能较好地反应实际情况,得到的算法更易于工程实现。
1.3 敌方USVs的威胁建模 1.3.1 阿波罗尼奥斯圆先考虑我方USV与单个敌方USV对弈时的情况,且不考虑它们的体量大小,直接将其等效成质点,P(xp, yp)与E(xe, ye)分别表示它们在平面坐标系中的位置坐标。T(x, y)为该平面内的任意点,满足:
| $ PT/{V_P} = ET/{V_E} $ | (4) |
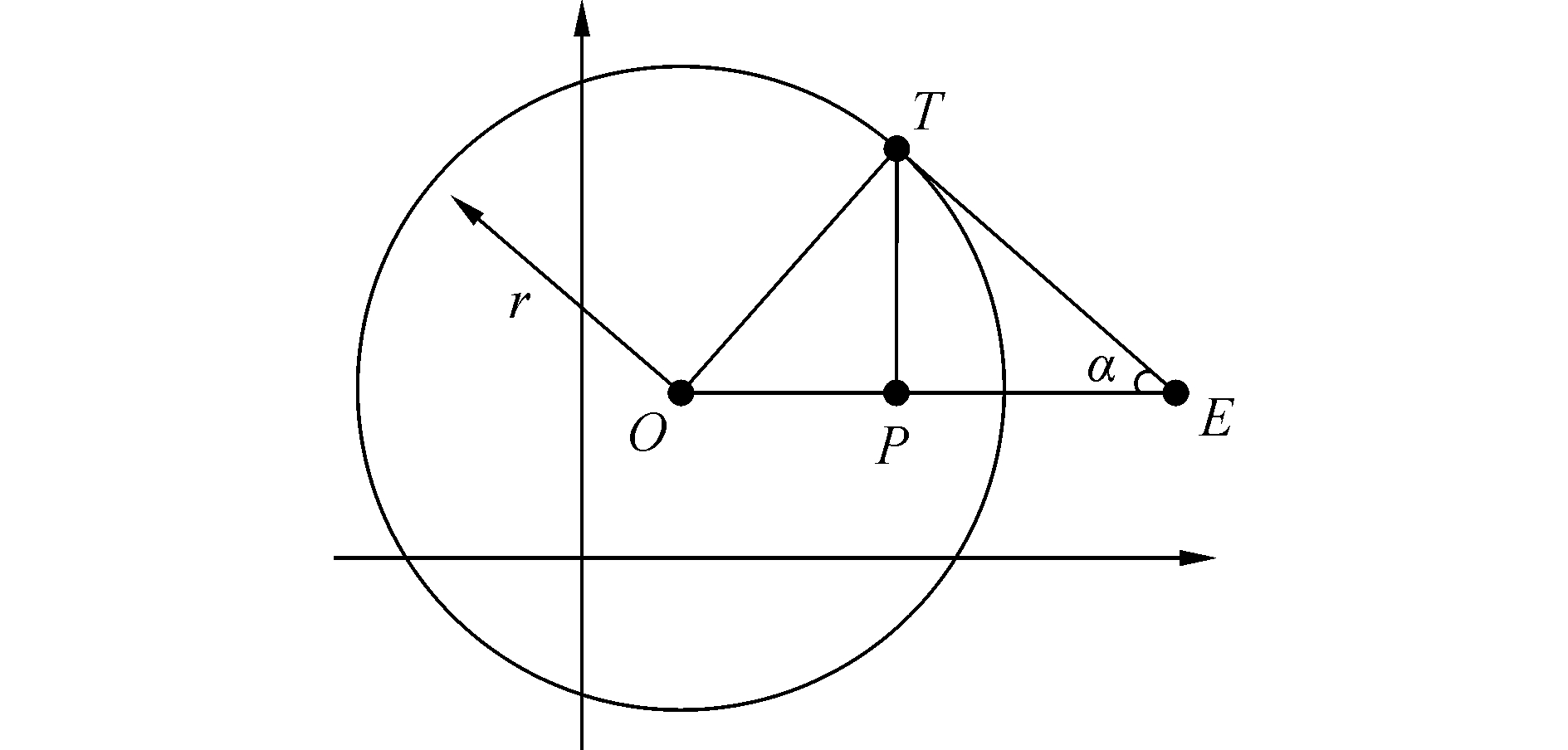
式中:T点的轨迹就形成阿波罗尼奥斯圆(Apollonius circle),如图 2所示。圆上的任意点可以理解为:当敌我双方都采取最大速度航行时,它们能同时到达该点。
|
Download:
|
| 图 2 阿波罗尼奥斯圆 Fig. 2 Apollonius circle | |
由平面几何的相关知识可得该阿波罗尼奥斯圆的圆心为
| $ r = \sqrt {\lambda {{({x_P} - {x_E})}^2} + {{({y_P} - {y_E})}^2}} /(1 - {\lambda ^2}) $ | (5) |
由式(5)可知,r和λ正相关,即敌方USV比我方USV的速度慢得越多,则阿波罗尼奥斯圆的半径就越小,我方USV逃跑成功的几率就越大。根据阿波罗尼奥斯圆的特点,敌方USV能成功追捕到我方USV必须发生在圆的边界上或者圆的内部。因此,将该区域定义为敌方USV的理论威胁区域,而且我方USV在逃跑路径规划过程中应尽量绕开该威胁区域。考虑绕开时的临界情况(见图 2),过点E作阿波罗尼奥斯圆的切线交于点T,由于阿波罗尼奥斯圆的圆心O、敌方USV的位置点P和我方USV的位置点E三者在一条直线上,则存在:
| $ \sin \alpha = OT/OE = \left( {OE \times \lambda } \right)/OE = \lambda $ | (6) |
式(6)说明,α与敌我双方USVs的位置无关,它只与两者的最大速度比λ相关。
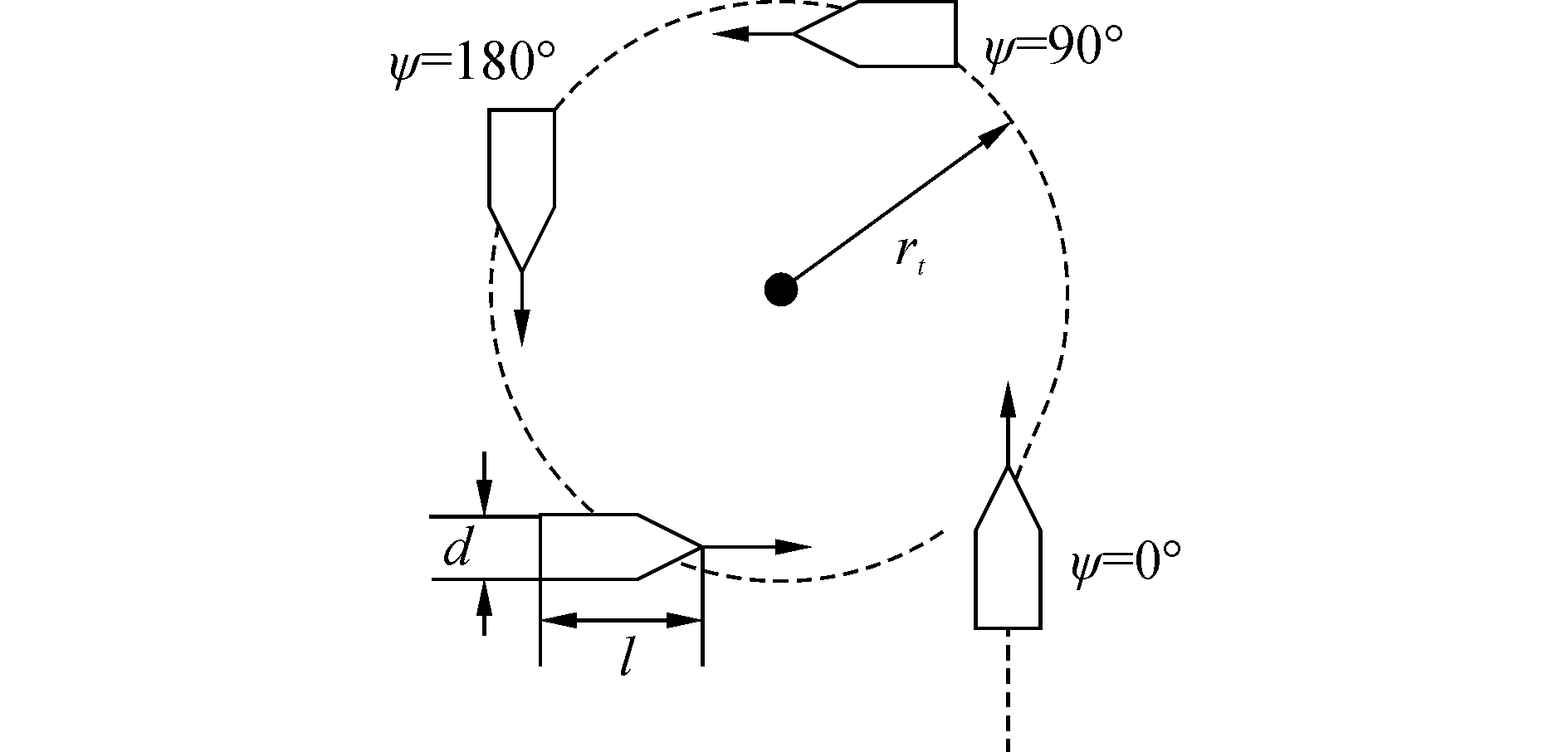
1.3.2 USV的回转特性由于USV本身具有一定的体量大小,无法实现瞬时原点转向。尤其当USV的被捕获半径ε和回转半径rt在一个数量级时,USV的回转性能对捕获结果有重要影响。例如当USV左转舵时,其重心的运动轨迹如图 3所示,其中USV的艇身长度为l、宽度为d,一般有l>d。
|
Download:
|
| 图 3 USV的回转性能 Fig. 3 Turning performance of USV | |
由于USV属于一般小型船舶,本文取回转半径rt=3l/2。从图 3中可以看出转弯的弧度越大,其航行轨迹越长且耗时越多。因此,在“蜂群战术”背景下,必须考虑其回转性能对抗追捕-逃跑策略的影响。
1.3.3 敌方USVs的威胁模型理论上,无论敌方USVs采取何种追捕策略,只要我方USV不进入敌方USVs的阿波罗尼奥斯圆内,就一定不会被捕获。但实际上,受到捕获半径和回转性能的影响,两者之间还需要留有一定的安全裕量,才能保证我方USV的安全。
假设某时刻敌方USV与我方USV的位置和航行方向如图 4所示,若要保证我方USV不被捕获,则它们之间的距离至少要大于捕获半径ε,而且还要预留出足够的回转安全距离2rt。基于此,定义两者之间的安全裕量为

|
Download:
|
| 图 4 安全裕量 Fig. 4 Safety allowance | |
| $ {L_{{\rm{safe}}}} = \varepsilon + 2{r_t} $ | (7) |
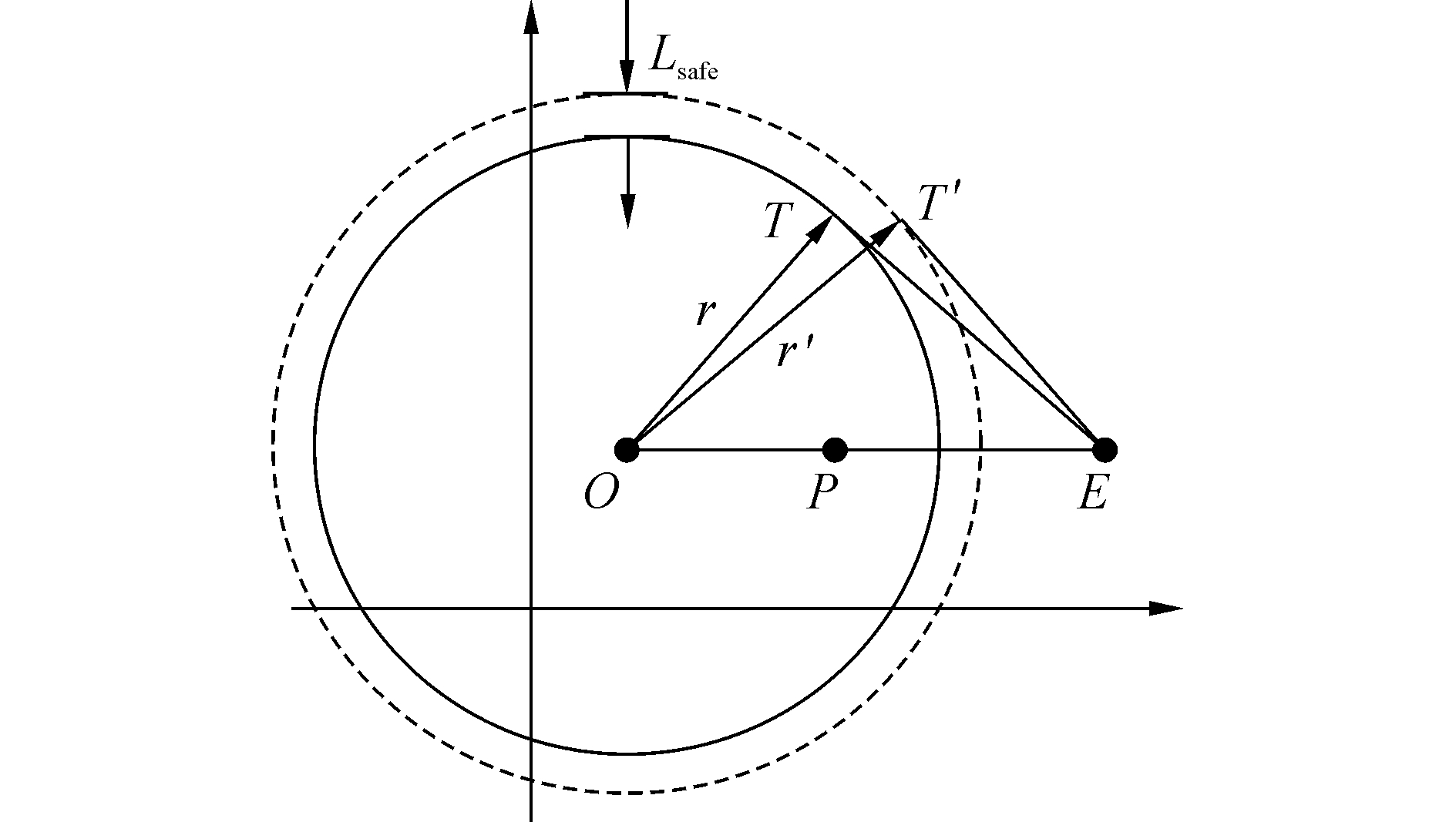
我方USV在抗追捕-逃跑的过程中,除了要尽量避开阿波罗尼奥斯圆定义的威胁区域外,还需要考虑安全裕量。因此,本文对阿波罗尼奥斯圆区域进行“膨胀”处理,具体过程如图 5所示。
|
Download:
|
| 图 5 敌方USV威胁区域 Fig. 5 Threaten area of enemy USV | |
图 5中敌方USV威胁区域和阿波罗尼奥斯圆的圆心重合,半径由r变为r′ (r′=r+Lsafe)。在后续逃跑路径规划过程中,敌方USVs的威胁区域为“膨胀”后的阿波罗尼奥斯圆区域。
2 抗追捕-逃跑策略在敌方USVs的数量多但航行速度略慢的前提条件下,我方USV能否逃跑成功尚待研究。同时,在抗追捕-逃跑策略研究过程中,应考虑与USV密切相关的约束条件,如障碍物、捕获半径、回转特性和航行海区边界等,这些约束条件与被包围状态确定和抗追捕-逃跑对策的执行息息相关。
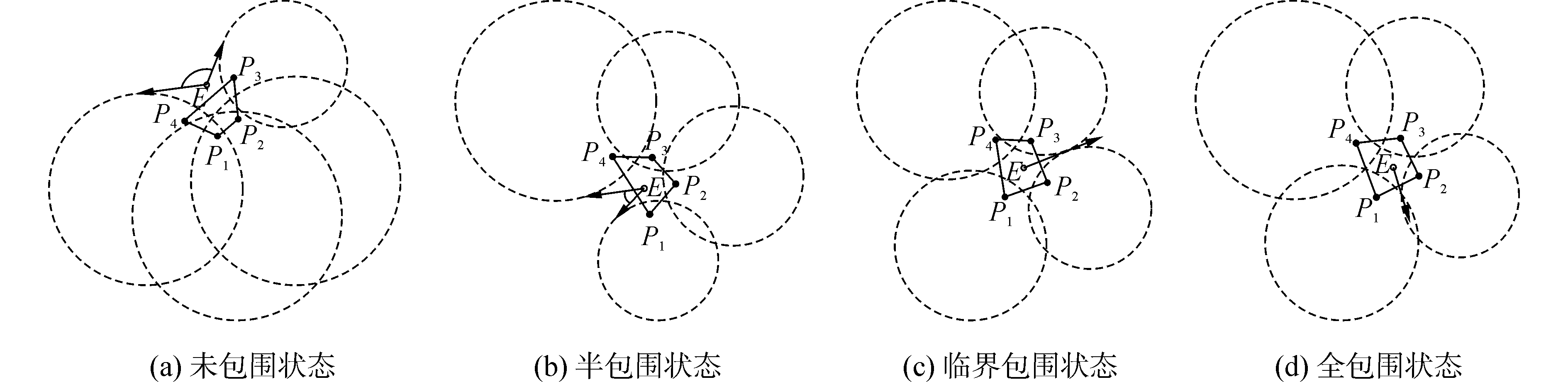
2.1 被包围状态分析通过计算阿波罗尼奥斯圆和安全裕量,可以得到单个敌方USV的威胁区域,而在“蜂群战术”背景下,多艘敌方USVs的追捕威胁范围将会“叠加”。根据我方USV的位置和敌方USVs的威胁区域,可以确定被包围状态集S={S1, S2, S3, S4}:①未包围状态S1,此时我方USV在由敌方USVs构成包围圈的外部;②半包围状态S2,此时我方USV虽然在包围圈内部,但相邻的两艘USVs威胁区域之间有明显缺口;③临界包围状态S3,此时我方USV在敌方USVs包围圈内部,但存在至少两个相邻敌方USVs威胁区域相切,且该切点不属于任何其他敌方USVs的威胁区域;④全包围状态S4,此时我方USV在敌方USVs包围圈内部,且相邻敌方USVs威胁区域全部相交。以N=4为例,上述四种状态的具体情况分别如图 6所示。
|
Download:
|
| 图 6 被包围状态示意图 Fig. 6 Schematic diagram of the bound states | |
无论敌方USVs采取何种追捕策略,我方USV会根据处于被包围的状态做出相应的响应,即抗追捕-逃跑对策集可以表示为S→A,其中A={A1, A2, A3, A4},具体分析如下:
策略A1:在未包围状态S1下,向远离敌方USVs构成的包围圈方向逃跑。
由于我方USV不在敌方USVs包围圈内部,故只要向远离包围圈的方向逃跑,凭借自身速度优势,很容易逃脱敌方USVs的追捕,证明过程略。
策略A2:在半包围状态S2下,向相邻的两艘USVs威胁区域之间的缺口方向逃跑。
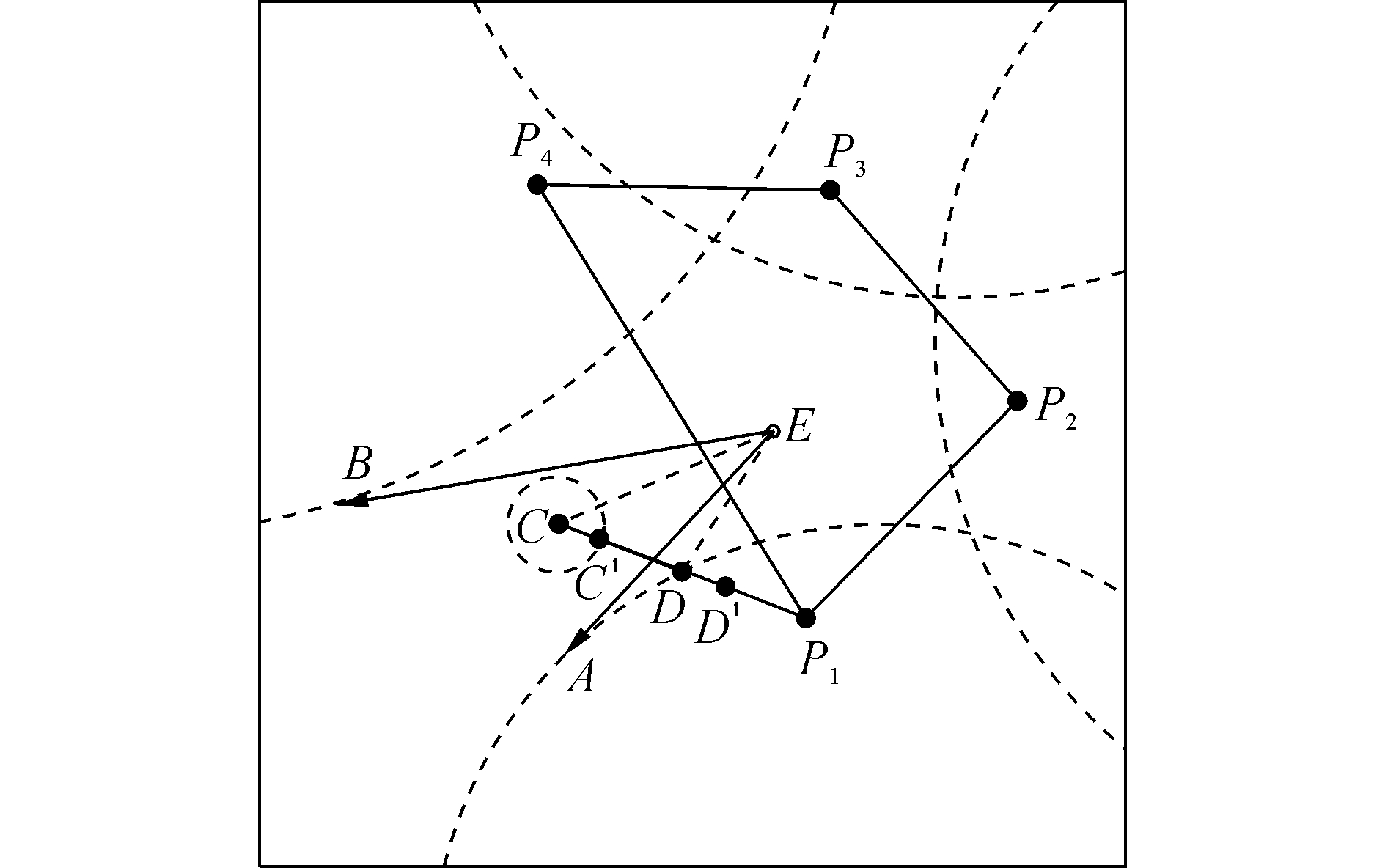
证明:如图 7所示,在∠AEB的方向存在缺口,则我方USV朝着∠AEB的方向逃跑,设C为我方USV航行方向上的任意点,
|
Download:
|
| 图 7 半包围状态下逃跑示意图 Fig. 7 Escape schematic under semi-encircled state | |
若敌方USVs和我方USV分别用时间tP1和tE到达点C′和C,则有:
| $ \begin{array}{*{20}{c}} {{t_E} = \overrightarrow {EC} /{V_E} < \left( {\overrightarrow {ED} + \overrightarrow {DC} } \right)/{V_E} = }\\ {\overrightarrow {ED} /{V_E} + \overrightarrow {DC} /{V_E} = t + \overrightarrow {DC} /{V_E} = }\\ {\overrightarrow {{P_1}D' } /{V_{{P_1}}} + \overrightarrow {DC} /{V_E} = }\\ {(\overrightarrow {{P_1}D} + \overrightarrow {DD' } )/{V_{{P_1}}} + \overrightarrow {DC} /{V_E} < }\\ {(\overrightarrow {{P_1}D} + \overrightarrow {DD' } )/{V_{{P_1}}} + \overrightarrow {DC} /{V_{{P_1}}} = }\\ {(\overrightarrow {{P_1}D} + \overrightarrow {DD' } + \overrightarrow {DC} )/{V_{{P_1}}}} \end{array} $ | (8) |
| $ \because \overrightarrow{DD' }=\overrightarrow{CC' }={{L}_{\text{safe}}} $ | (9) |
| $ \begin{align} &\therefore \ \ \ {{t}_{E}}<(\overrightarrow{{{P}_{1}}D}+\overrightarrow{CC' }+\overrightarrow{DC})/{{V}_{{{P}_{1}}}}= \\ &(\overrightarrow{{{P}_{1}}D}+\overrightarrow{DC' })/{{V}_{{{P}_{1}}}}=\overrightarrow{{{P}_{1}}C' }/{{V}_{{{P}_{1}}}}={{t}_{{{P}_{1}}}} \\ \end{align} $ | (10) |
上述推导过程说明当E到达点C时,P1无法到达点C′,即两者之间的距离大于Lsafe。故P1无法追上E,同理可证其他USVs亦无法追上,故我方USV可以朝着缺口的方向逃脱。
策略A3:在临界包围状态S3下,向相邻两艘USVs威胁区域的切点方向逃跑。
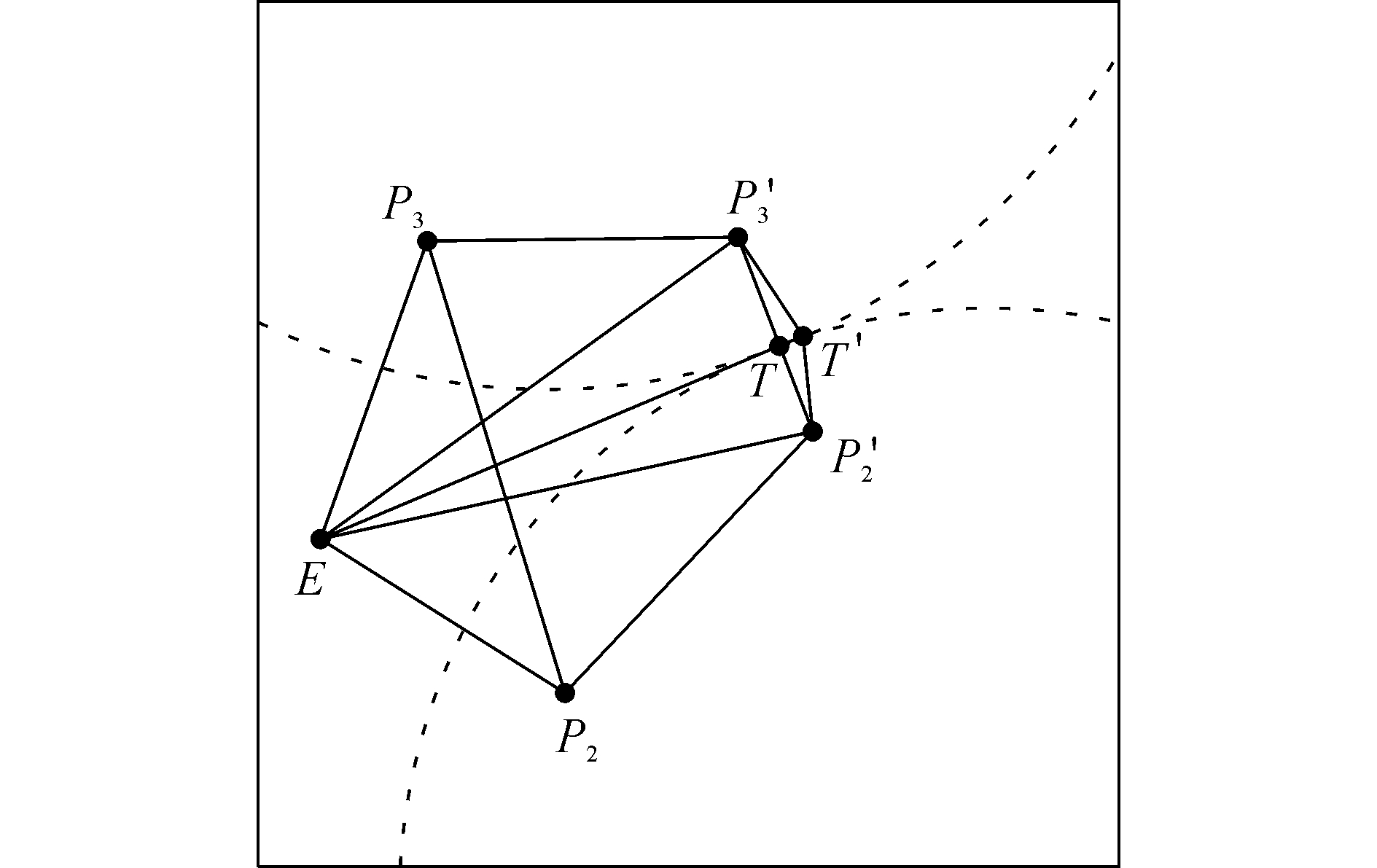
证明:如图 8所示,在临界包围状态下,相邻两艘P2和P3的威胁区域相切于点T。假设在时刻t,P2到达离切点T最近的点P′2,根据阿波罗尼奥斯圆的性质,E亦可到达点P′2,此时有
|
Download:
|
| 图 8 临界包围状态下逃跑示意图 Fig. 8 Escape schematic under critical surround state | |
| $ {t_P} = \overrightarrow {{P_2}P{' _2}} /{V_P} = \overrightarrow {EP{' _2}} /{V_E} $ | (11) |
若我方USV朝着切点T的方向运动,到达点T的时间为
| $ {t_E} = \overrightarrow {ET} /{V_E} $ | (12) |
又由于ΔEP′2T为直角三角形,则存在
| $ {t_E} < \overrightarrow {EP{' _2}} /{V_E} = {t_P} $ | (13) |
式(13)说明当我方USV到达点T时,P2还未到达点P2′,而当P2到达点P2′时,我方USV已到达T′,且存在:
| $ \overrightarrow {T' P{' _2}} > {L_{{\rm{safe}}}} $ | (14) |
上述推导过程说明此时我方USV已安全逃脱。同理,P3亦无法追上我方USV,故我方USV可以朝着切点方向逃脱。
策略A4:在全包围状态S4下,向最远的相邻USVs威胁区域的交点方向逃跑。
在全包围状态下,我方USV不一定能逃脱敌方USVs的追捕。本文选择向最远的相邻USVs的威胁区域的交点方向逃跑,一方面可以最大限度的拖延被捕获时间;另一方面,若敌方USVs没有采用最优追捕方法[17]时,我方USV很可能由全包围状态变成临界包围状态,此时再执行策略A3即可逃脱,证明过程略。
2.3 算法流程根据上文建立的系统模型和抗追捕-逃跑策略,确定我方USV的逃跑路径规划算法流程如下:
1) 确定航行海区的环境模型,利用电子海图系统的数据对该区域进行障碍物建模。初始化我方USV和N艘敌方USVs的位置、航速和航向。
2) 通过式(3)判断此时刻我方USV是否被捕获,若被捕获则我方USV抗追捕-逃跑失败,算法结束;否则,转入步骤3)。
3) 根据当前时刻USV的位置E计算出敌方USVs的威胁区域,确定我方USV被追捕的状态S(t)∈S,执行对应的抗追捕-逃跑策略A(t)∈A,规划出下一时刻我方USV的航行方向ψE(t),并转步骤4)。
4) 按式(1)计算出我方USV以当前速度vE(t)和方向ψE(t)航行Δt(时间间隔)到达的位置
5) 判断我方USV是否到达航行海区的边界,若是,则转步骤6);若否,则转至步骤3)。
6) 我方USV抗追捕-逃跑成功,动态逃跑路径规划结束。
3 仿真实现及结果分析本实验在如图 9所示的环境模型下,其中黑色多边形代表抽象后的障碍物,仿真时间间隔为Δt=1 s。假设有5艘敌方USVs对我方USV进行追捕,敌我双方能实时感知到对方的位置、航向和航速,敌方USVs捕获半径为ε=20 m,且双方的体量大小均为l=6 m, d=2.5 m,则它们的转弯半径均为rt=9 m,保障我方USV不被捕获的安全裕量为Lsafe=38 m。敌我双方USVs的初始仿真参数如表 1所示。

|
Download:
|
| 图 9 抗追捕-逃跑过程 Fig. 9 Process of anti-pursuit evasion | |
| 表 1 仿真参数设置 Tab.1 Simulation parameters initial values |
从仿真开始到我方USV最终逃离敌方无人包围的过程如图 9所示,图 9(a)表示初始时刻,双方USVs均在初始位置,我方USV处于被敌方USVs完全包围状态S4,根据策略A4应向威胁区域的“最远交点”方向逃跑。执行策略A4航行28个时间间隔后,我方USV仍处于被全包围状态如图 9(b)所示,但此时“最远交点”的位置发生变化,则根据策略A4实时调整我方USV的运动方向。在执行该策略114 s后如图 9(c)所示,敌方USVs的包围圈出现可逃生“缺口”,则按策略A2我方USV该缺口方向逃跑。若敌方USVs继续采用最优策略追捕115 s后,如图 9(d)所示我方USV与敌方USVP5之间的距离达到最近,此时P5E=43 m,仍大于安全裕量Lsafe。接下来,执行策略A1朝着远离敌方USVs包围圈的方向航行即可。如图 9(e)所示,我方USV朝着边界方向航行120 s后成功脱险。
为了验证本文策略的有效性,进行了20×100组随机试验, 如表 2所示。在试验过程中,随机生成敌我双方USVs的初始位置和航行方向,并依次模拟敌方USVs的数量N为3、4、5、6、7、9、11、13时,在追逃速度比λ∈[sin(π/N), 1)的情况下,敌方USVs采用最优追捕方法,我方USV采用本文策略能够逃跑成功的概率。
| 表 2 追捕结果 Tab.2 Capture results |
表 2显示在追逃速度比λ不变的情况下,随着敌方USVs的数量增多,我方USV的逃跑成功率整体上呈下降趋势。同时,若敌方USVs的数量一定,我方USV的逃跑成功率随着追逃速度比λ的增大而减小。
4 结论1) 利用阿波罗尼奥斯圆和安全裕量的敌方USVs威胁区域建模方法,提高了抗追捕-逃跑问题模型的准确性。
2) 采用状态降维法对冗余的障碍物轮廓信息进行简化处理,以减少动态路径规划的计算量。
3) 引入被包围状态集及其对应的抗追捕-逃跑策略集,以两者之间的映射关系为依据动态调整逃跑方向,并通过仿真验证了本文提出的策略有助于我方USV突破敌方USVs的包围。
为了进一步提高USV的自主性能,更好的适应未来作战环境,对于多艘USVs协同自主控制是后续研究的重点。
| [1] |
CAMPBELL S, NAEEM W, IRWIN G W. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres[J]. Annual reviews in control, 2012, 36(2): 267-283. DOI:10.1016/j.arcontrol.2012.09.008 (  0) 0)
|
| [2] |
廖煜雷, 刘鹏, 王建, 等. 基于改进人工鱼群算法的无人艇控制参数优化[J]. 哈尔滨工程大学学报, 2014, 35(7): 800-806. LIAO Yulei, LIU Peng, WANG Jian, et al. Control parameter optimization for the unmanned surface vehicle with the improved artificial fish swarm algorithm[J]. Journal of Harbin Engineering University, 2014, 35(7): 800-806. (  0) 0)
|
| [3] |
WU Gongxing, SHI Danda, GUO Jiamin. Deliberative collision avoidance for unmanned surface vehicle based on the directional weight[J]. Journal of Shanghai Jiao Tong University (science), 2016, 21(3): 307-312. DOI:10.1007/s12204-016-1726-z (  0) 0)
|
| [4] |
FUKUTO J, IMAZU H. New collision alarm algorithm using obstacle zone by target (OZT)[J]. IFAC proceedings volumes, 2013, 46(33): 91-96. DOI:10.3182/20130918-4-JP-3022.00044 (  0) 0)
|
| [5] |
苏义鑫, 石兵华, 张华军. 水面无人艇航迹规划算法设计与仿真[J]. 武汉理工大学学报, 2016, 38(6): 84-88. SU Yixin, SHI Binghua, ZHANG Huajun. Design and simulation of a path planning algorithm for unmanned surface vehicle[J]. Journal of Wuhan University of Technology, 2016, 38(6): 84-88. (  0) 0)
|
| [6] |
赵金, 彭刚. 基于NEAT方法的多机器人追捕-逃跑问题[J]. 华中科技大学学报(自然科学版), 2011, 39(S2): 332-334, 339. ZHAO Jin, PENG Gang. A multi-robots pursuit evasion problem based on NEAT solution[J]. Journal of Huazhong University of Science & Technology (natural science edition), 2011, 39(S2): 332-334, 339. (  0) 0)
|
| [7] |
HLADEK D, VAŠČÁÁK J, SINČÁÁK P. Multi-robot control system for pursuit-evasion problem[J]. Journal of electrical engineering, 2009, 60(3): 143-148. (  0) 0)
|
| [8] |
周浦城, 洪炳镕. 基于对策论的群机器人追捕-逃跑问题研究[J]. 哈尔滨工业大学学报, 2003, 35(9): 1056-1059. ZHOU Pucheng, HONG Bingrong. Group robot pursuit-evasion problem based on game theory[J]. Journal of Harbin Institute of Technology, 2003, 35(9): 1056-1059. (  0) 0)
|
| [9] |
RAMANA M V, KOTHARI M. Pursuit-evasion games of high speed evader[J]. Journal of intelligent & robotic systems, 2017, 85(2): 293-306. (  0) 0)
|
| [10] |
龚华军, 杨长锋, 王彪, 等. 无人机的追逃对抗仿真研究[J]. 控制理论与应用, 2009, 26(9): 1019-1022. GONG Huajun, YANG Changfeng, WANG Biao, et al. Simulation of pursuit-evasion among multi-UAV[J]. Control theory & applications, 2009, 26(9): 1019-1022. (  0) 0)
|
| [11] |
PEHLIVANOGLU Y V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV[J]. Aerospace science and technology, 2012, 16(1): 47-55. DOI:10.1016/j.ast.2011.02.006 (  0) 0)
|
| [12] |
李龙跃, 刘付显, 史向峰, 等. 导弹追逃博弈微分对策建模与求解[J]. 系统工程理论与实践, 2016, 36(8): 2161-2168. LI Longyue, LIU Fuxian, SHI Xiangfeng, et al. Differential game model and solving method for missile pursuit-evasion[J]. Systems engineering-theory & practice, 2016, 36(8): 2161-2168. DOI:10.12011/1000-6788(2016)08-2161-08 (  0) 0)
|
| [13] |
刘卫东, 程瑞锋, 高立娥, 等. 水下微分对策协同拦截制导策略[J]. 兵工学报, 2016, 37(9): 1684-1691. LIU Weidong, CHENG Ruifeng, GAO Li'e, et al. Cooperative engagement-based differential guidance law for underwater interceptor[J]. Acta armamentarii, 2016, 37(9): 1684-1691. (  0) 0)
|
| [14] |
FARINELLI A, IOCCHI L, NARDI D. Distributed on-line dynamic task assignment for multi-robot patrolling[J]. Autonomous robots, 2017, 41(6): 1321-1345. DOI:10.1007/s10514-016-9579-8 (  0) 0)
|
| [15] |
JIANHUA G, LIANG Tang, JOHAN R, et al. Suboptimal approaches to multiplayer pursuit-evasion differential games[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Keystone, Colorado, 2006: 261-291. http://arc.aiaa.org/doi/pdf/10.2514/6.2006-6786
(  0) 0)
|
| [16] |
LAU G, LIU H H T. Real-time path planning algorithm for autonomous border patrol:design, simulation, and experimentation[J]. Journal of intelligent & robotic systems, 2014, 75(3/4): 517-539. (  0) 0)
|
| [17] |
方宝富, 潘启树, 洪炳镕, 等. 多追捕者-单-逃跑者追逃问题实现成功捕获的约束条件[J]. 机器人, 2012, 34(3): 282-291. FANG Baofu, PAN Qishu, HONG Bingrong, et al. Constraint conditions of successful capture in multi-pursuers vs one-evader games[J]. Robot, 2012, 34(3): 282-291. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


