高超声速飞行器是指飞行速度在5倍声速以上的飞行器。吸气式高超声速飞行器可以跨越普通飞机飞行区域和部分近空间区域,同时其具有高燃料比冲的特性,使得其运输成本远低于火箭。由于具有以上特点,吸气式高超声速飞行器在军事装备、太空探索和未来航天运输领域均具有重要的潜在应用价值[1]。
吸气式高超声速飞行器具有强耦合、强非线性、快时变和严重不确定性等特性,如何设计出有效的飞行控制系统是高超声速飞行器的关键技术问题之一[2]。高超声速飞行器在实际运行过程中,外部环境和飞行器自身的气动特性以及结构参数均存在明显的不确定性因素[3],其不确定性控制问题已经吸引了众多学者的关注。由于不确定性的影响,一些传统的控制方法已经不能满足控制性能的要求,因此鲁棒控制、自适应控制、滑模控制和模糊控制等先进的控制方法被应用到高超声速飞行器的控制器设计中,并取得了一系列的研究成果。
文献[4]提出了一种基于鲁棒补偿技术和反馈线性化方法的非线性鲁棒控制方法,通过反馈线性化和极点配置的方法设计了标称控制器,通过鲁棒补偿器来抑制参数不确定和外界扰动带来的不利影响。文献[5]在考虑具有模型不确定性情况下高超声速飞行器的控制问题,采用非线性鲁棒自适应控制方法进行了控制器的设计,保证了在弹性干扰情况下飞行器的轨迹跟踪能力。文献[6]针对面向控制的高超声速飞行器模型,在考虑输入限制和模型不确定的情况下,采用鲁棒自适应动态面控制方法设计了控制器。文献[7]考虑具有部分气动参数不确定情况下飞行控制器设计问题,采用了有限时间收敛的滑模观测器来估计扰动项大小,然后使用高阶滑模方法来进行控制器设计,保证系统具有一定的抗干扰能力。文献[8]采用T-S模糊集方法对高超声速飞行器进行了模糊建模,针对模糊模型设计了鲁棒H∞控制器,通过仿真验证了这种控制方法对气动参数摄动的鲁棒性。
本文考虑高超声速飞行器在具有参数不确定性情况下的控制问题,所使用的方法与一般的适用于参数不确定控制问题的方法有所区别,该方法通过对李雅普诺夫函数的直接分析,从而得到对标称控制器的调整方法,进而得到适用于参数不确定系统的控制器,该设计方法具有一定的探索性意义。通过结合自适应反步法和弹性控制方法来进行控制器的设计,以适应高超声速飞行器非线性和强耦合的特点,同时保证了参数不确定性情况下系统的稳定性。最后通过对比仿真实验验证了所提方法的有效性。
1 高超声速飞行器控制问题描述 1.1 高超声速飞行器模型一种典型的锥形体吸气式高超声速飞行器纵向刚体动力学模型如下[9]
| $ \left\{ \begin{array}{l} \dot V = \frac{{T\cos \alpha - D}}{m} - g\sin \gamma \\ \dot h = V\sin \gamma \\ \dot \gamma = \frac{{L + T\sin \alpha }}{{mV}} - \frac{{g\cos \gamma }}{V}\\ \dot \alpha = q - \dot \gamma \\ \dot q = \frac{{{M_{yy}}}}{{{I_{yy}}}} \end{array} \right. $ | (1) |
式中:V为速度,h为飞行高度,γ为航迹倾斜角,α为迎角,q为俯仰角速度,L、D、T、Myy分别为升力、阻力、推力和俯仰力矩。作用在飞行器上的力和力矩的表达式为
| $ \left\{ \begin{array}{l} L = \bar qS{C_L}\left( \alpha \right)\\ D = \bar qS{C_D}\left( \alpha \right)\\ T = \bar qS{C_T}\left( \beta \right)\\ {M_{yy}} = \bar qS\bar c[{C_{M\alpha }}\left( \alpha \right) + {C_{M{\delta _e}}}(\alpha , {\delta _e}) + {C_{Mq}}\left( {V, q, \alpha } \right)] \end{array} \right. $ | (2) |
式中:q为动压,S为等效机翼面积,c为平均气动弦长,β为发动机节流阀调定值,CL为升力系数,CD为阻力系数,CT为推力系数,CMα、CMq、CMδe为俯仰力矩系数。
发动机模型采用如下二阶近似模型:
| $ \ddot \beta = - 2\xi {\omega _n}\dot \beta - \omega _n^2\beta + \omega _n^2{\beta _c} $ | (3) |
式中:ωn为自然频率,ξ为阻尼比。
1.2 高超声速飞行器参数不确定问题高超声速飞行器存在不可忽视的不确定性。由于飞行环境变化大,燃料消耗快,实验数据和工程经验不足以及超高速飞行时所造成的气动加热问题等,飞行器的惯性参数和气动参数均会产生明显的摄动。这种参数的不确定性会对飞行器的特性产生较大的改变[10],所以在控制器的设计时必须要将不确定性因素考虑在内,使得控制器对参数不确定性具有较强的鲁棒性。本文主要考虑对飞行器特性影响较大的一些惯性参数的不确定性问题。结合对飞行过程的分析,参数摄动的表达式如下
| $ \left\{ \begin{array}{l} m = {m_0}(1 + {\mathit{\Delta }_m}), {I_{yy}} = {I_{yy0}}(1 + {\mathit{\Delta }_{{I_{yy}}}})\\ S = {S_0}(1 + {\mathit{\Delta }_S}), \bar c = {{\bar c}_0}(1 + {\mathit{\Delta }_{\bar c}})\\ {c_e} = {c_{e0}}(1 + {\mathit{\Delta }_{{c_e}}}), \rho = {\rho _0}(1 + {\mathit{\Delta }_\rho }) \end{array} \right. $ | (4) |
控制器设计目标为在考虑以上参数摄动情况下,设计出恰当的飞行控制器,以保证飞行器可以平稳、快速和准确地跟踪速度和高度指令信号。
2 弹性自适应控制律设计首先对原系统模型进行输入/输出反馈线性化处理,并分析参数不确定对于系统模型的影响;然后在反步法(Backstepping)的基础上综合采用自适应控制和弹性控制的方法分两步进行控制器的设计,用以消除参数不确定的不利影响;最后利用李雅普诺夫方法证明控制系统的稳定性。
2.1 反馈线性化高超声速飞行器具有强耦合、高度非线性以及大飞行包络的特性。基于微分同胚、李导数和李括号等非线性系统基本理论,利用求导和坐标变换的方法对高超声速飞行器纵向动力学模型进行输入/输出反馈线性化处理,可以使得控制器的设计兼顾原系统的非线性特性和设计与分析的简洁性。
由于考虑的是对于速度和高度的控制,所以将速度V和高度h分别对时间求导,直至表达式中显式出现控制量为止。通过验证可知系统的相对阶为7,所以在标称情况下,通过求导计算可得
| $ \left[ \begin{gathered} {\dddot V} \hfill \\ {h^{(4)}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {f_V} \hfill \\ {f_h} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}{c}} {{b_{11}}}&{{b_{12}}} \\ {{b_{21}}}&{{b_{22}}} \end{array}} \right]\left[ \begin{gathered} {\delta _e} \hfill \\ {\beta _c} \hfill \\ \end{gathered} \right] = \mathit{\boldsymbol{f}} + \mathit{\boldsymbol{Gu}} $ | (5) |
当考虑系统中具有如式(4)所示的参数不确定之后,结合式(5)的表达式可知,式(5)应变为
| $ \left[ \begin{gathered} {\dddot V} \hfill \\ {h^{(4)}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {f_V} \hfill \\ {f_h} \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} \Delta {f_V} \hfill \\ \Delta {f_h} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}{c}} {{b_{11}}}&{{b_{12}}} \\ {{b_{21}}}&{{b_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\Lambda }_{11}}}&0 \\ 0&{{\mathit{\Lambda }_{22}}} \end{array}} \right]\left[ \begin{gathered} {\delta _e} \hfill \\ {\beta _c} \hfill \\ \end{gathered} \right] $ | (6) |
式中:[ΔfV Δfh]T为未知非线性连续函数,Λ11和Λ22为未知常数。由于Λ11和Λ22为1附近的未知常数,故参数摄动不大的情况下, 可以假设2-ε>Λ11, Λ22>ε,其中1>ε>0。
注:对系统进行输入输出线性化之后可以得到系统(6),下面将在此基础上来进行弹性自适应控制律设计。对于考虑了参数不确定性影响之后得到的方程式(6),从其形式可以看出,不确定性的影响可以分为两部分,其中[ΔfV Δfh]T可以看作系统的加性干扰项,
首先在式(6)中忽略掉控制效率干扰项
| $ \left\{ \begin{array}{l} \dot h = {h_1}\\ {{\dot h}_1} = {h_2}\\ {{\dot h}_2} = {h_3}\\ {{\dot h}_3} = {f_h} + \Delta {f_h} + {b_{11}}{\delta _e} + {b_{12}}{\beta _c}\\ \dot V = {V_1}\\ {{\dot V}_1} = V\\ {{\dot V}_2} = {f_V} + \Delta {f_V} + {b_{21}}{\delta _e} + {b_{22}}{\beta _c}_2 \end{array} \right. $ | (7) |
其中
假设[ΔfV Δfh]T是慢时变函数,即忽略其导数项的影响,在后面仿真实验中将会看到这样的假设不会影响控制器的实用效果。
下面针对模型(7)设计了一种自适应Backstepping控制器。记高度指令为hc,速度指令为Vc,控制律和自适应律如下所示。
控制律:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_n} = {\mathit{\boldsymbol{G}}^{ - 1}}\left( { - \left[ \begin{array}{l} {k_{{V_2}}}{z_{{V_2}}}\\ {k_{{h_3}}}{z_{{V_2}}} \end{array} \right] - \left[ \begin{array}{l} {z_{{V_1}}}\\ {z_{{h_2}}} \end{array} \right] - \mathit{\boldsymbol{f}} - \Delta \mathit{\boldsymbol{\hat f}} + \left[ \begin{array}{l} {{\dot \alpha }_{{V_2}}}\\ {{\dot \alpha }_{{h_3}}} \end{array} \right]} \right)\\ {\alpha _{{h_3}}} = - {k_{{h_2}}}{z_{{h_2}}} + {{\dot \alpha }_{{h_2}}} - {z_{{h_1}}}\\ {\alpha _{{h_2}}} = - {k_{{h_1}}}{z_{{h_1}}} + {{\dot \alpha }_{{h_1}}} - {z_h}\\ {\alpha _{{h_1}}} = - {k_h}{z_h} + {{\dot h}_c}\\ {\alpha _{{V_2}}} = - {k_{{V_1}}}{z_{{V_1}}} + {{\dot \alpha }_{{V_1}}} - {z_V}\\ {\alpha _{{V_1}}} = - {k_V}{z_V} + {{\dot V}_c} \end{array} \right. $ | (8) |
式中,zh=h-hc,zh1=h1-αh1,zh2=h2-αh2,zh3=h3-αh3,zV=V-Vc,zV1=V1-αV1,zV2=V2-αV2;kh, kh1, kh2, kh3, kV, kV1, kV2>0为待设计控制器参数。
自适应律:
| $ \mathit{\Delta }\dot{\hat{\mathit{\boldsymbol{f}}}} = {\left[ {\frac{1}{{{k_{\mathit{\Delta }{f_V}}}}}{z_{{V_2}}}\;\;\frac{1}{{{k_{\mathit{\Delta }{f_h}}}}}{z_{{h_3}}}} \right]^{\rm{T}}} $ | (9) |
式中:kΔfV、kΔfh>0为待设计参数。
稳定性证明:选择李雅普诺夫函数为
| $ \begin{array}{l} {V_{{\rm{all}}}} = \frac{1}{2}(z_h^2 + z_{{h_1}}^2 + z_{{h_2}}^2 + z_{{h_3}}^2 + z_V^2 + z_{{V_1}}^2 + \\ \;\;\;\;\;\;z_{{V_2}}^2 + \frac{1}{{{k_{\Delta {f_V}}}}}\Delta \mathit{\boldsymbol{\tilde f}}_V^2 + \frac{1}{{{k_{\Delta {f_h}}}}}\Delta \mathit{\boldsymbol{\tilde f}}_h^2) \end{array} $ | (10) |
对式(10)求导,并将控制律(8)和自适应律(9)代入可得
| $ \begin{array}{l} {{\dot V}_{{\rm{all}}}} = - {k_h}z_h^2 - {k_{{h_1}}}z_{{h_1}}^2 - {k_{{h_2}}}z_{{h_2}}^2 - {k_{{h_3}}}z_{{h_3}}^2 - \\ \;\;\;\;\;\;\;{k_V}z_V^2 - {k_{{V_1}}}z_{{V_1}}^2 - {k_{{V_2}}}z_{{V_2}}^2 \end{array} $ | (11) |
根据拉塞尔不变集定理可知,控制系统稳定。
2.3 弹性控制律设计本文在完全考虑不确定性影响的情况下进行控制律设计。对系统(6),在2.2节得到的控制律un基础上,取如下弹性控制律将可以保证系统的稳定性:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}_n} - {\mathop{\rm sgn}} {\left( {\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {z_3}}}\mathit{\boldsymbol{G}}} \right)^{\rm{T}}}\left( {\left\| {{\mathit{\boldsymbol{u}}_n}} \right\| + \frac{{\left\| {{\mathit{\boldsymbol{u}}_n}} \right\|\beta }}{\varepsilon }} \right) $ | (12) |
式中:z3=[zV2 zh3]T;sgn(·)为符号函数;β为设计参数,满足β+2ε-1>0。
稳定性证明
令
选择李雅普诺夫函数为
| $ \begin{array}{l} {V_{{\rm{res}}}} = \frac{1}{2}(z_h^2 + z_{{h_1}}^2 + z_{{h_2}}^2 + z_{{h_3}}^2 + z_V^2 + z_{{V_1}}^2 + \\ \;\;\;\;\;\;z_{{V_2}}^2 + \frac{1}{{{k_{\Delta {f_V}}}}}\Delta \mathit{\boldsymbol{\tilde f}}_V^2 + \frac{1}{{{k_{\Delta {f_h}}}}}\Delta \mathit{\boldsymbol{\tilde f}}_h^2) \end{array} $ | (13) |
对式(13)求导,并将控制律(12),自适应律(9)代入,可得
| $ {{\dot V}_{{\rm{res}}}} = {{\dot V}_{{\rm{all}}}} + \frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G \boldsymbol{\varOmega} u}} + \frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G\tilde u}} $ | (14) |
式(14)中的第二项满足如下不等式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G \boldsymbol{\varOmega} u}} = \frac{{\partial {V_{{\rm{res}}}}}}{{\partial {z_3}}}\mathit{\boldsymbol{G \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{u}}_n} - \\ \frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G \boldsymbol{\varOmega} }}{\mathop{\rm sgn}} {\left( {\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G}}} \right)^{\rm{T}}}\left( {\left\| {{\mathit{\boldsymbol{u}}_n}} \right\| + \frac{{\left\| {{\mathit{\boldsymbol{u}}_n}} \right\|\beta }}{\varepsilon }} \right) \le \\ \;\;\;\;\;\;\;\;\;\;\left\| {\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G}}} \right\|\left\| \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right\|\left\| {{\mathit{\boldsymbol{u}}_n}} \right\|\left( {2 + \frac{\beta }{\varepsilon }} \right) \le \\ \;\;\;\;\;\;\;\left\| {\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_n}} \right\|\left( {2 + \frac{\beta }{\varepsilon }} \right)\left( {1 - \varepsilon } \right) \end{array} $ | (15) |
式(14)中的第三项满足如下等式:
| $ \begin{array}{l} \frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G\tilde u}} = - \frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G}}{\mathop{\rm sgn}} {\left( {\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G}}} \right)^{\rm{T}}}\left( {\left\| {{\mathit{\boldsymbol{u}}_n}} \right\| + \frac{{\left\| {{\mathit{\boldsymbol{u}}_n}} \right\|\beta }}{\varepsilon }} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\; - \left\| {\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_n}} \right\|\left( {1 + \frac{\beta }{\varepsilon }} \right) \end{array} $ | (16) |
将式(15)、(16)代入式(14),可得
| $ \begin{array}{l} {{\dot V}_{{\rm{res}}}} \le {{\dot V}_{{\rm{all}}}} + \left\| {\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G}}} \right\|\left\| \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right\|\left\| {{\mathit{\boldsymbol{u}}_n}} \right\|\left( {\left( {2 + \frac{\beta }{\varepsilon }} \right) \cdot } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\left( {1 - \varepsilon } \right) - \left( {1 + \frac{\beta }{\varepsilon }} \right)} \right) = \\ {{\dot V}_{{\rm{all}}}}\left\| {\left\| {\frac{{\partial {V_{{\rm{res}}}}}}{{\partial {\mathit{\boldsymbol{z}}_3}}}\mathit{\boldsymbol{G}}} \right.} \right\|\left\| \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right\|\left\| {{\mathit{\boldsymbol{u}}_n}} \right\|\left( {\beta + 2\varepsilon - 1} \right) \le \\ \;\; - {k_h}z_h^2 - {k_{{h_1}}}z_{{h_1}}^2 - {k_{{h_2}}}z_{{h_2}}^2 - {k_{{h_3}}}z_{{h_3}}^2 - \\ \;\;\;\;\;\;\;\;{k_V}z_V^2 - {k_{{V_1}}}z_{{V_1}}^2 - {k_{{V_2}}}z_{{V_2}}^2 \end{array} $ | (17) |
根据拉塞尔不变集定理可知,控制系统稳定。
注:式(12)通过对标称控制器进行修正方式,使得原控制器具有更强的适应性,能抑制控制系统乘性干扰。采用符号函数可能会导致控制器抖振,由于
为了验证所提控制方法的有效性,下面分别采用两种控制方法对高超声速飞行器进行对比仿真实验。仿真时选取的初始状态为h0=33 528 m, V0=4 590.3 m/s, α0=2.7°, γ0=0°,将m、S、Iyy、c、ce、ρ减少10%作为参数的摄动。将阶跃信号通过一个二阶临界阻尼的指令滤波器进行缓冲之后作为系统的指令信号,用以避免反步法控制初期控制指令幅值过大。
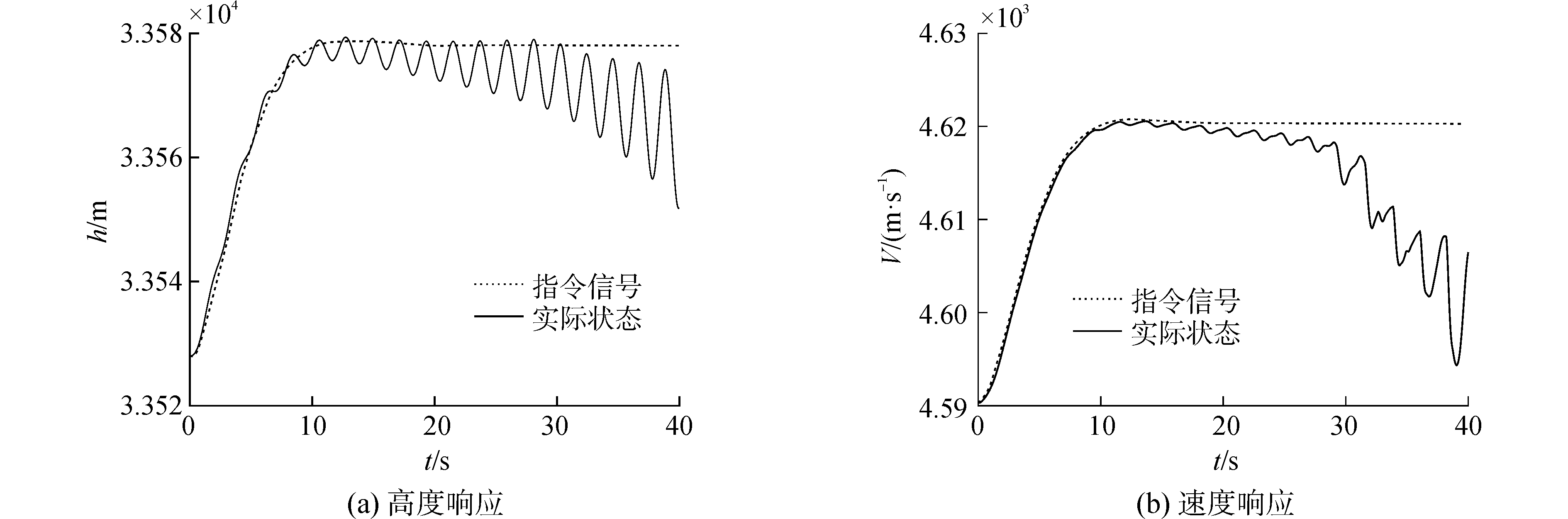
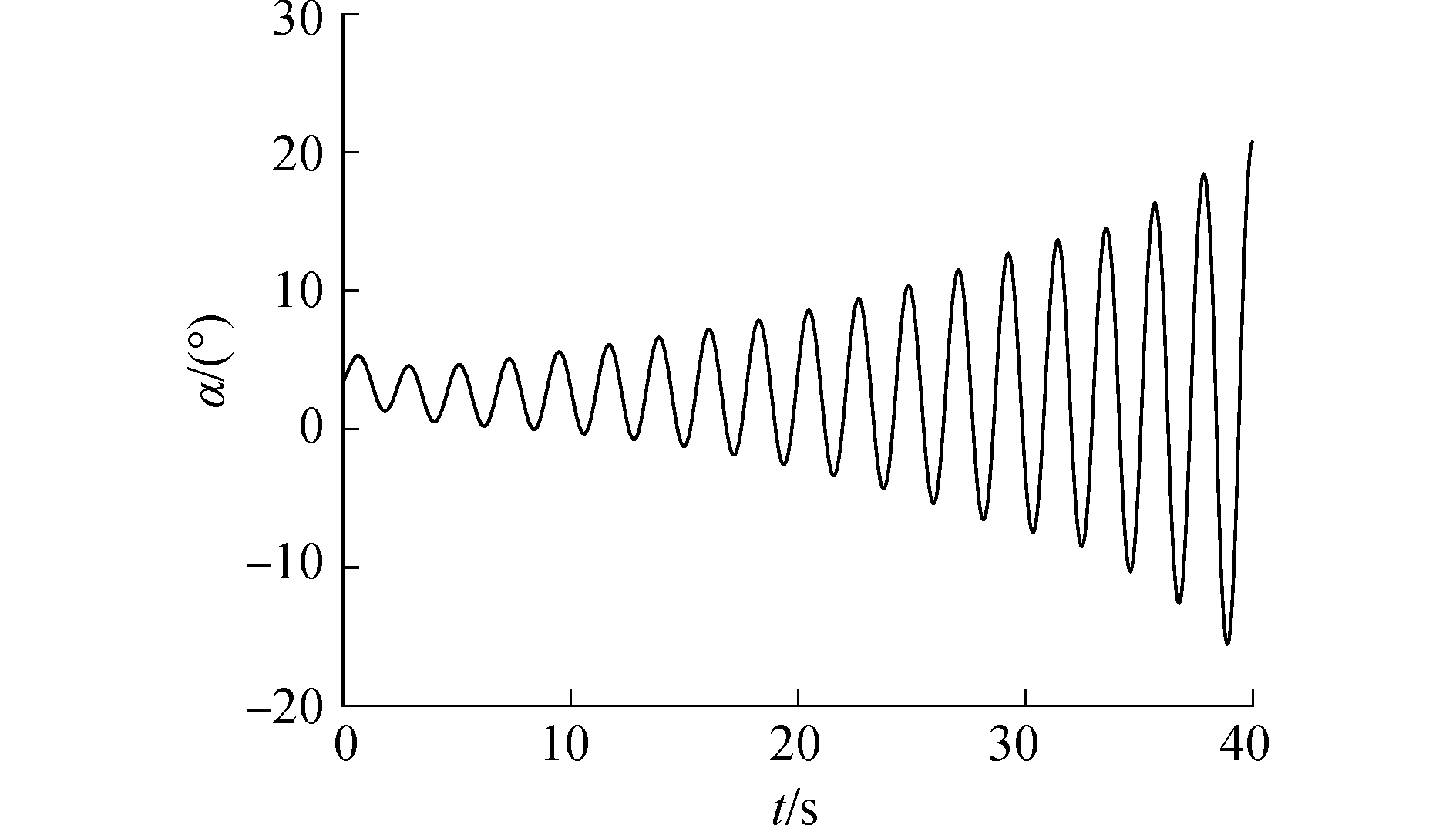
3.1 标准Backstepping控制仿真实验在有参数摄动情况下对高超声速飞行器进行普通反步法进行控制器设计并仿真。仿真的关键结果如图 1和图 2所示。图 1为高度和速度的跟踪曲线,图 2为迎角变化曲线。
|
Download:
|
| 图 1 backstepping控制作用下高度和速度响应曲线 Fig. 1 Response curves of velocity and altitude under backstepping control | |
|
Download:
|
| 图 2 backstepping控制作用下迎角响应曲线 Fig. 2 Response curve of attack angle under backstepping control | |
可以看出此时飞行器对于速度指令和高度指令不能有效跟踪;飞行速度、飞行高度以及飞行迎角均呈现振荡发散状态。这是由于飞行器模型中多个参数均发生了较大的摄动,导致标准Backstepping控制器的失效。所以在参数不确定情况下,标准Backstepping控制方法不能再适用于高超声速飞行器的控制系统设计,需要寻找适应能力更强的控制方法来设计飞行控制器。
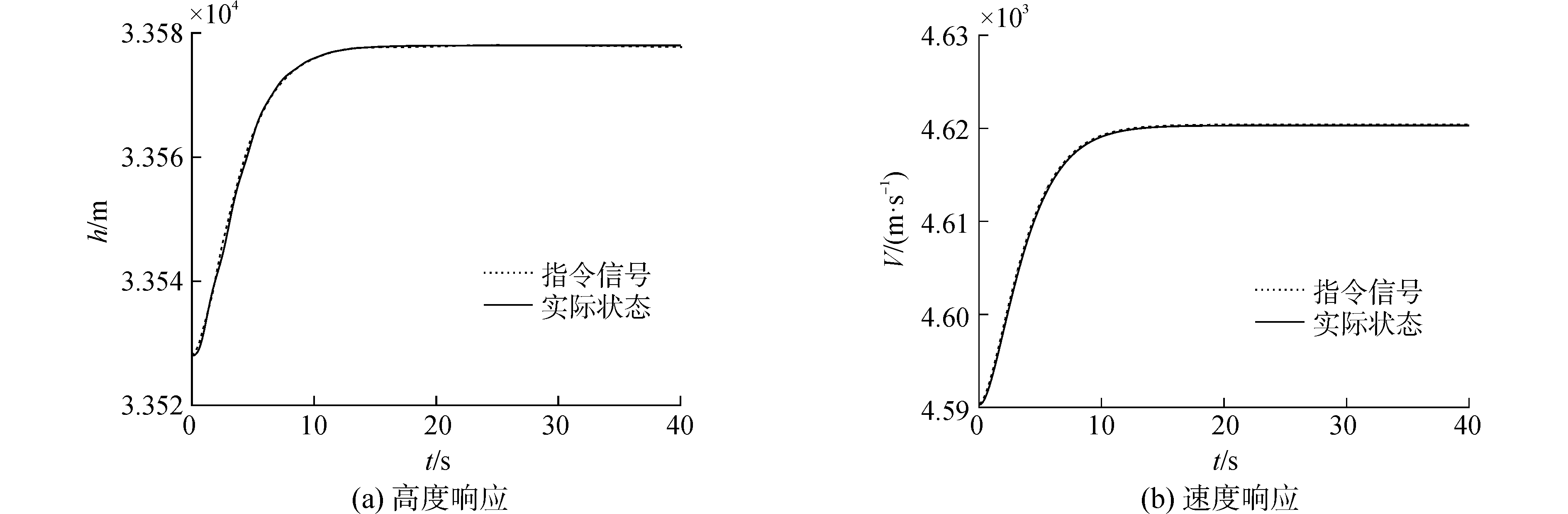
3.2 弹性自适应Backstepping控制仿真实验采用本文所提出的弹性自适应控制方法,对高超声速飞行器进行了控制器设计和仿真分析。在有参数摄动情况下进行仿真实验,仿真结果如图 3~5所示。图 3为高度和速度的跟踪曲线,可以看出飞行器可以迅速地跟上指令信号,无稳态误差。这表明在具有参数摄动时,飞行器对速度和高度信号依然可以具有良好的跟踪性能。图 4为航迹倾斜角、迎角和俯仰角速度的变化曲线,可以看出这些飞行姿态的变化较为平稳。图 5为发动机节流阀调定值和升降舵偏转角的变化曲线,可以看出控制输入量处于合理的范围,并且通过饱和函数替代符号函数的方法,较好地消除了因符号函数的引入而可能带来的抖振问题。
|
Download:
|
| 图 3 高度和速度响应曲线 Fig. 3 Response curves of velocity and altitude | |

|
Download:
|
| 图 4 航迹倾斜角、迎角和俯仰角速度响应曲线 Fig. 4 Response curves of flight path angle, attack angle and pitch angle rate | |

|
Download:
|
| 图 5 控制输入量变化曲线 Fig. 5 Curves of system inputs | |
1) 结合自适应Backstepping控制方法以及弹性控制方法,设计出了抗参数不确定的控制器,并从理论上证明了控制系统的稳定性,这对于高超声速飞行控制器设计方法具有一定的探索意义。
2) 通过与标准Backstepping控制方法的对比仿真实验,表明在具有参数摄动情况下,所提控制方法对于速度指令和高度指令均具有更好的跟踪性能。
3) 所提控制方法通过使用饱和函数替代符号函数,较好地消除了控制器抖振问题。
| [1] |
HU Xiaoxiang, WU Ligang, HU Changhua, et al. Adaptive fuzzy integral sliding mode control for flexible air-breathing hypersonic vehicles subject to input nonlinearity[J]. Journal of aerospace engineering, 2013, 26(4): 721-734. DOI:10.1061/(ASCE)AS.1943-5525.0000193 (  0) 0)
|
| [2] |
黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战[J]. 控制理论与应用, 2011, 28(10): 1496-1505. HUANG Lin, DUAN Zhisheng, YANG Jianying. Challenges of control science in near space hypersonic aircrafts[J]. Control theory & applications, 2011, 28(10): 1496-1505. (  0) 0)
|
| [3] |
孙冲, 方群, 袁建平. 具有模型参数不确定性的高超声速飞行器动态特性分析及控制律设计[J]. 西北工业大学学报, 2012, 30(4): 497-502. SUN Chong, FANG Qun, YUAN Jianping. A useful dynamic analysis of hypersonic vehicle and control law design using uncertainty parameter dynamics model[J]. Journal of Northwestern Polytechnical University, 2012, 30(4): 497-502. (  0) 0)
|
| [4] |
李昭莹, 余令艺, 刘昊, 等. 高超声速飞行器非线性鲁棒控制律设计[J]. 控制理论与应用, 2016, 33(1): 62-69. LI Zhaoying, YU Lingyi, LIU Hao, et al. Nonlinear robust controller design for hypersonic vehicles[J]. Control theory & applications, 2016, 33(1): 62-69. (  0) 0)
|
| [5] |
FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J]. Journal of guidance, control and dynamics, 2009, 32(2): 402-417. DOI:10.2514/1.39210 (  0) 0)
|
| [6] |
ZONG Qun, WANG Fang, TIAN Bailing, et al. Robust adaptive dynamic surface control design for a flexible air-breathing hypersonic vehicle with input constraints and uncertainty[J]. Nonlinear dynamics, 2014, 78(1): 289-315. DOI:10.1007/s11071-014-1440-z (  0) 0)
|
| [7] |
WANG Jie, ZONG Qun, SU Rui, et al. Continuous high order sliding mode controller design for a flexible air-breathing hypersonic vehicle[J]. ISA transactions, 2014, 53(3): 690-698. DOI:10.1016/j.isatra.2014.01.002 (  0) 0)
|
| [8] |
HU Xiaoxiang, WU Ligang, HU Changhua, et al. Dynamic output feedback control of a flexible air-breathing hypersonic vehicle via T-S fuzzy approach[J]. International journal of systems science, 2014, 45(8): 1740-1756. DOI:10.1080/00207721.2012.749547 (  0) 0)
|
| [9] |
XU Haojian, MIRMIRANI M D, IOANNOU P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of guidance, control and dynamics, 2004, 27(5): 829-838. DOI:10.2514/1.12596 (  0) 0)
|
| [10] |
郁嘉, 杨鹏飞, 严德. 高超声速飞行器模型不确定性影响分析[J]. 航空学报, 2015, 36(1): 192-200. YU Jia, YANG Pengfei, YAN De. Influence analysis of hypersonic flight vehicle model uncertainty[J]. Acta aeronautica et astronautica sinica, 2015, 36(1): 192-200. (  0) 0)
|
| [11] |
CHEN Fuyang, LEI Wen, ZHANG Kangkang, et al. A novel nonlinear resilient control for a quadrotor UAV via backstepping control and nonlinear disturbance observer[J]. Nonlinear dynamics, 2016, 85(2): 1281-1295. DOI:10.1007/s11071-016-2760-y (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


