2. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
多孔介质一般指由多相物质占据的共同空间,如岩石、陶瓷、人体骨骼及海底沉积物等[1]。研究多孔介质的声反射和声透射问题对地震勘探、声波测井资料分析、多孔材料的检测以及海底混响和散射特性的研究有重要意义[2-3]。1956年,Biot提出了一种基于流体饱和多孔介质的声传播理论[4-5],为多孔介质声传播规律的研究奠定了重要的基础。Stoll[6]针对Biot模型中固相骨架相连的问题,引入了骨架损耗机制,建立了用于海洋沉积物的Biot-Stoll海底模型,推导并得到了平面声波在水-多孔介质界面上的反射系数,研究发现,即使当声波的入射角比临界角大时,多孔介质和流体介质、弹性介质以及粘弹性介质的性质都不相同,并不会发生全反射[7]。Chotiros等[8-9]认为这是由于多孔介质模型中Biot慢纵波的声透射导致的。Wu等[10]计算了高频声波从水入射到水饱和沙质沉积物的透射系数。Allard等[11-12]采用矩阵分析方法对声波与层状沉积物之间的作用进行了分析,得到了声波从水斜入射到层状多孔介质的法向特性阻抗率表达式。周来江[13]利用广义标准线性体Boltzmann叠加原理的固体流变模型准确地描述了海底介质结构情况,推导了声波在水-粘弹性海底界面处的反射系数和透射系数。王耀俊等[14]用数值分析方法研究了高频声波在多孔介质-流体界面处的反射与透射问题。彭临慧等[15]根据Biot理论,通过分析得到了声波在水-多孔介质层界面处三种透射声波(快纵波、慢纵波和剪切波)的透射系数以及声能的透射系数随入射角和频率的变化关系,给出了各种透射波对透射声能的贡献的表达式。乔文孝等[16]基于Biot理论,对多层水饱和多孔介质中平面波的反射和透射进行了分析,并进行了实验验证。以上研究皆是基于不含气泡的水饱和多孔介质,但对于含气泡非饱和的层状[17]多孔介质的透射问题未见相关报道。
然而对于实际的海底,波浪等会将某些有机物卷入海底,这些有机物经过生物化学作用,产生气体,气体会储存在孔隙较大的沉积物中,其上覆沉积物孔隙足够小,使得气体可以保存,形成气体、砂、孔隙水三态的砂质含气沉积物[18]。海底沉积物的沉积会出现分层,形成了含气泡非饱和的层状多孔介质。为了揭示声波从水入射到这种多孔介质的反射和透射特性,将三种透射波的平面波解代入考虑气泡后修正的Biot波动方程求解相关参数,同时修正引入气泡振动后的Biot弹性模量。通过分析垂直入射时的边界条件,推导出了声波从水入射到含气泡非饱和多孔介质层的反射系数和透射系数,并结合含气泡沉积物声速频散和衰减等特性[19-21],获得了气泡存在下此沉积物的反射系数和透射系数的频率特性。
1 反射系数与透射系数的推导 1.1 Biot波动方程的修正基于Biot理论,文献[22]通过分析气泡线性振动对含气泡非饱和多孔介质的声传播影响,得到了如下修正的Biot波动方程:
| $ \begin{array}{l} \mu {\nabla ^2}\mathit{\boldsymbol{u}} + \left[ {H - \mu } \right]\nabla \left( {\nabla \cdot \mathit{\boldsymbol{u}}} \right) - C\nabla \left( {\nabla \cdot \mathit{\boldsymbol{v}}} \right) = \\ \;\;\;\;\;\frac{{{\partial ^2}}}{{\partial {t^2}}}(\left( {\rho + \gamma \tilde \rho } \right)\mathit{\boldsymbol{u}} - ({\rho _w} + \gamma \tilde \rho )\mathit{\boldsymbol{v}}) \end{array} $ | (1) |
| $ \begin{array}{l} \;\;\;\;\;\;C\nabla \left( {\nabla \cdot \mathit{\boldsymbol{u}}} \right) - M\nabla \left( {\nabla \cdot \mathit{\boldsymbol{v}}} \right) = \\ \frac{{{\partial ^2}}}{{\partial {t^2}}}\left( {(\tilde \rho + {\rho _w})\mathit{\boldsymbol{u}} - \left( {\frac{{\alpha {\rho _w}}}{\beta } + \tilde \rho } \right)\mathit{\boldsymbol{v}}} \right) - \frac{{\eta F}}{\kappa }\frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial t}} \end{array} $ | (2) |
式中:H、C、M为与多孔弹性介质参数有关的Biot弹性模量,μ为骨架的剪切模量,u表示固体骨架的绝对位移,v表示孔隙流体相对于固体框架的相对位移,α表示弯曲度,β表示孔隙度,ρ表示多孔介质混合物的密度,ρw表示孔隙流体的密度,
对于均匀介质,由Biot波动方程可以得到纵波和横波的解[23],此解可以用标量势函数和矢量势函数表示,满足如下关系:
| $ \mathit{\boldsymbol{u}} = \nabla {\mathit{\boldsymbol{\phi}} _s} + \nabla \times {\mathit{\boldsymbol{\psi }}_s} $ | (3) |
| $ \mathit{\boldsymbol{v}} = \nabla {\mathit{\boldsymbol{\phi}} _f} + \nabla \times {\mathit{\boldsymbol{\psi }}_f} $ | (4) |
将式(3)、(4)代入波动方程,可以将Biot波动方程拆分成四个方程,以方便求解各平面波。
| $ H{\nabla ^2}{\mathit{\boldsymbol{\phi}} _s} - C{\nabla ^2}{\mathit{\boldsymbol{\phi}} _f} = - {\omega ^2}\left( {\rho + \gamma \tilde \rho } \right){\mathit{\boldsymbol{\phi}} _s} + {\omega ^2}({\rho _w} + \gamma \tilde \rho ){\mathit{\boldsymbol{\phi}} _f} $ | (5) |
| $ \begin{array}{l} C{\nabla ^2}{\mathit{\boldsymbol{\phi}} _s} - M{\nabla ^2}{\mathit{\boldsymbol{\phi}} _f} = - {\omega ^2}({\rho _w} + \tilde \rho ){\mathit{\boldsymbol{\phi}} _s} + \\ \;\;\;\;{\omega ^2}\left( {\frac{\alpha }{\beta }{\rho _w} + \tilde \rho } \right){\mathit{\boldsymbol{\phi}} _f} + \frac{{i\omega F\eta }}{\kappa }{\mathit{\boldsymbol{\phi}} _f} \end{array} $ |
| $ \mu {\nabla ^2}{\mathit{\boldsymbol{\psi }}_s} = - \omega \left( {^2\rho + \gamma \tilde \rho } \right){\mathit{\boldsymbol{\psi }}_s} + {\omega ^2}({\rho _w} + \gamma \tilde \rho ){\mathit{\boldsymbol{\psi }}_f} $ | (7) |
| $ - \frac{{{\rm{i}}\omega F\eta }}{\kappa }{\mathit{\boldsymbol{\phi}} _f} = - {\omega ^2}\left( {{\rho _w} + \tilde \rho } \right){\mathit{\boldsymbol{\psi }}_s} + {\omega ^2}\left( {\frac{\alpha }{\beta }{\rho _w} + \tilde \rho } \right){\mathit{\boldsymbol{\psi }}_f} $ | (8) |
对于无限延伸的均匀非饱和多孔介质,将弹性理论推广到包含快纵波、慢纵波和横波的情况,设它们的平面波解分别为
| $ {\mathit{\boldsymbol{\phi}} _s} = {{\rm{e}}^{{\rm{i}}{k_q} \cdot r}}, q = 1, 2 $ | (9) |
| $ {\mathit{\boldsymbol{\phi}} _f} = {\gamma _q}{{\rm{e}}^{{\rm{i}}{k_q} \cdot r}}, q = 1, 2 $ | (10) |
| $ {\mathit{\boldsymbol{\psi }}_s} = {\mathit{\boldsymbol{e}}_h}\left( \mathit{\boldsymbol{K}} \right){{\rm{e}}^{{\rm{i}}{k_t} \cdot r}} $ | (11) |
| $ {\mathit{\boldsymbol{\psi }}_f} = {\gamma _t}{\mathit{\boldsymbol{e}}_h}\left( \mathit{\boldsymbol{K}} \right){e^{{\rm{i}}{k_t} \cdot r}} $ | (12) |
式(9)、(10)表示纵波(q=1, 2分别对应快纵波和慢纵波),式(11)、(12)表示横波。kq和kt为波矢量。
将式(9)~(12)代入波动方程,可以分别求得标量势的比γq以及矢量势的比γt。同时,令得到的齐次线性方程组的系数行列式为零,即可分别得到纵波和横波的频散方程:
| $ \left\{ \begin{array}{l} (Hk_q^2 - \rho {\omega ^2} - \gamma \tilde \rho {\omega ^2})\left( {\left( {\frac{{\alpha {\rho _w}}}{\beta } + \tilde \rho } \right){\omega ^2} - Mk_q^2 + i\frac{{F\eta \omega }}{\kappa }} \right) + \\ (Ck_q^2 - {\rho _w}{\omega ^2} - \tilde \rho {\omega ^2})(Ck_q^2 - {\rho _w}{\omega ^2} - \gamma \tilde \rho {\omega ^2}) = 0\\ (\mu k_t^2 - \left( {\rho + \gamma \tilde \rho } \right){\omega ^2})\left( {{\omega ^2}\left( {\frac{{\alpha {\rho _w}}}{\beta } + \tilde \rho } \right) + i\frac{{F\eta \omega }}{\kappa }} \right) + \\ ({\rho _w} + \gamma \tilde \rho )(\tilde \rho + {\rho _w}){\omega ^4} = 0 \end{array} \right. $ | (14) |
通过分别求解式(13)与式(14)两个频散方程,可以得到多孔介质中三种透射波的波数与频率之间的关系:
| $ {k_q} = \sqrt {\frac{{ - {\rm{bb}} \pm \sqrt {{\rm{b}}{{\rm{b}}^2} - 4{\rm{aa}} \cdot {\rm{cc}}} }}{{2{\rm{aa}}}}} , q = 1, 2 $ | (15) |
| $ {k_t} = \frac{{\sqrt {{a_3}{a_4}/{a_2} - {a_1}} }}{\mu } $ | (16) |
式中:
| $ \left\{ \begin{array}{l} {\rm{aa}} = {C^2} - HM, {\rm{bb}} = {a_2}H - {a_1}M - {a_3}C + {a_4}C\\ {\rm{cc}} = {a_1}{a_2} - {a_3}{a_4}, {a_1} = - {\omega ^2}\left( {\rho + \gamma \tilde \rho } \right)\\ {a_2} = {\omega ^2}\left( {\frac{\alpha }{\beta }{\rho _w} + \tilde \rho } \right) - \frac{{{\rm{i}}\omega F\eta }}{\kappa }\\ {a_3} = {\omega ^2}({\rho _w} + \gamma \tilde \rho ), {a_4} = - {\omega ^2}({\rho _w} + \tilde \rho ) \end{array} \right. $ | (17) |
若要得到水-含气泡沉积物-水的边界条件,本文先对含气泡沉积物的Biot弹性模量进行修正。根据文献[24]可以得到流体相对骨架位移v和骨架位移u的比例关系:
| $ \mathit{\boldsymbol{v}} = {\gamma _v}\mathit{\boldsymbol{u}} $ | (18) |
式中:
| $ {\gamma _v} = \frac{{{\rho _w} - \rho }}{{{\rho _m} - {\rho _w}}} $ | (19) |
| $ {\rho _m} = \frac{{\alpha {\rho _w}}}{\beta } - \frac{{{\rm{i}}F\eta }}{{\kappa \omega }} $ | (20) |
等效流体和孔隙流体的运动方程分别为
| $ - \nabla {p_{{\rm{eff}}}} = {\rho _{{\rm{eff}}}}{{\mathit{\boldsymbol{\ddot u}}}_{{\rm{eff}}}} = {\rho _{{\rm{eff}}}}\left( {\mathit{\boldsymbol{\ddot u}} - \mathit{\boldsymbol{\ddot v}}} \right) $ | (21) |
| $ - \nabla p = {\rho _w}\mathit{\boldsymbol{\ddot u}} - {\rho _w}\frac{\alpha }{\beta }\mathit{\boldsymbol{\ddot v}} - \frac{{\eta F}}{\kappa }\mathit{\boldsymbol{\dot v}} $ | (22) |
对式(18)~(22)联立,可以得到如下的等效流体声压和孔隙流体声压的比例关系:
| $ {p_{{\rm{eff}}}} = \frac{{{\rho _{{\rm{eff}}}}(1 - {\gamma _v})}}{{{\rho _w} - {\rho _w}\frac{{\alpha {\gamma _v}}}{\beta } + \frac{{\eta F{\gamma _v}}}{{{\rm{i}}\kappa \omega }}}}p $ | (23) |
文献[22]对含气泡的孔隙流体渗流连续性方程进行了修正,并得到了动态体积分数与多孔介质等效声压之间的表达式:
| $ - p = C{\rm{div}}\mathit{\boldsymbol{u}} - M{\rm{div}}\mathit{\boldsymbol{v}} - M\beta {\beta _g} $ | (24) |
| $ {\beta _g} = - \frac{{4{\rm{ \mathsf{ π} }}N{R_0}}}{{{\rho _w}(\omega _0^2 - {\omega ^2} + 2{\rm{i}}b\omega )}}{p_{{\rm{eff}}}} $ | (25) |
将式(23)代入式(24)、(25),可以得到等价的孔隙流体渗流连续性方程:
| $ - p = \tilde C{\rm{div}}\mathit{\boldsymbol{u}} - \tilde M{\rm{div}}\mathit{\boldsymbol{v}} $ | (26) |
其中
| $ \tilde C = \frac{C}{{1 + \frac{{\tilde \rho }}{{{\rho _{{\rm{eff}}}}}}\frac{{{\rho _{{\rm{eff}}}}(1 - {\gamma _v})}}{{{\rho _w} - {\rho _w}\frac{{\alpha {\gamma _v}}}{\beta } + \frac{{\eta F{\gamma _v}}}{{{\rm{i}}\kappa \omega }}}}}} $ | (27) |
| $ \tilde M = \frac{M}{{1 + \frac{{\tilde \rho }}{{{\rho _{{\rm{eff}}}}}}\frac{{{\rho _{{\rm{eff}}}}(1 - {\gamma _v})}}{{{\rho _w} - {\rho _w}\frac{{\alpha {\gamma _v}}}{\beta } + \frac{{\eta F{\gamma _v}}}{{{\rm{i}}\kappa \omega }}}}}} $ | (28) |
根据以上两式又可得
为了方便分析,本文考虑一个一维问题[25],如图 1所示,有一平面波垂直入射到厚度为L的含气泡非饱和多孔介质层,层的另外两个维度无限延伸。

|
Download:
|
| 图 1 入射、反射和透射示意图 Fig. 1 Incident, reflection and transmission | |
将入射声波和反射声波的位移势函数ϕi和ϕr分别表示为
| $ {\phi _i} = {{\rm{e}}^{ - {\rm{i}}{k_w}x}} $ | (29) |
| $ {\phi _r} = {V_{ww}}{{\rm{e}}^{{\rm{i}}{k_w}x}} $ | (30) |
式中:kw=ω/cw。沉积物中两个纵波的标量位移势的表式为
| $ {\phi _s} = V_{w1}^ - {{\rm{e}}^{{\rm{i}}{k_1}(x - L)}} + V_{w2}^ - {{\rm{e}}^{{\rm{i}}{k_2}(x - L)}} + V_{w1}^ + {{\rm{e}}^{ - {\rm{i}}{k_1}x}} + V_{w2}^ + {{\rm{e}}^{ - {\rm{i}}{k_2}x}} $ | (31) |
| $ \begin{array}{l} {\phi _f} = {\gamma _1}V_{w1}^ - {{\rm{e}}^{{\rm{i}}{k_1}(x - L)}} + {\gamma _2}V_{w2}^ - {{\rm{e}}^{{\rm{i}}{k_2}x(x - L)}} + \\ \;\;\;\;\;\;\;\;{\gamma _1}V_{w1}^ + {{\rm{e}}^{ - {\rm{i}}{k_1}x}} + {\gamma _2}V_{w2}^ + {{\rm{e}}^{ - {\rm{i}}{k_2}x}} \end{array} $ | (32) |
式中:q=1, 2分别代表含气沉积物内快纵波和慢纵波,kq表示对应的波数。
沉积物中的剪切波的矢量势的表示为
| $ {\psi _s} = e_h^ - V_{wt}^ - {{\rm{e}}^{ - {\rm{i}}{k_t}x}} + e_h^ + V_{wt}^ - {{\rm{e}}^{{\rm{i}}{k_t}(x - L)}} $ | (33) |
| $ {\psi _f} = {\gamma _t}e_h^ - V_{wt}^ + {{\rm{e}}^{ - {\rm{i}}{k_t}x}} + {\gamma _t}e_h^ + V_{wt}^ - {{\rm{e}}^{{\rm{i}}{k_t}(x - L)}} $ | (34) |
式中:kt代表沉积物内剪切波的波数,透射声波的位移势函数表示为
| $ {\phi _t} = {V_{tt}}{{\rm{e}}^{ - {\rm{i}}{k_w}(x - L)}} $ | (35) |
文献[7]指出,在分析平面波在海水和孔隙海底之间平坦界面处的反射和透射问题时,通常考虑四个边界条件,即流体流量连续、法向应力连续、流体声压连续、切向应力为零,即四个开孔条件。而在分析此垂直入射情况时,可以推广到如下的边界条件。
1) 流体流量连续:
| $ \left\{ \begin{array}{l} {\left( {\frac{{\partial {\phi _i}}}{{\partial x}} + \frac{{\partial {\phi _r}}}{{\partial x}}} \right)_{x = 0}} = {\left( {\frac{{\partial {\phi _s}}}{{\partial x}} - \frac{{\partial {\phi _f}}}{{\partial x}}} \right)_{x = 0}}\\ {\left( {\frac{{\partial {\phi _t}}}{{\partial x}}} \right)_{x = L}} = {\left( {\frac{{\partial {\phi _s}}}{{\partial x}} - \frac{{\partial {\phi _f}}}{{\partial x}}} \right)_{x = L}} \end{array} \right. $ | (36) |
2) 法向应力连续:
| $ \left\{ \begin{array}{l} {\left( {\tilde H\left( {\frac{{{\partial ^2}{\phi _s}}}{{\partial {x^2}}}} \right) - \tilde C\left( {\frac{{{\partial ^2}{\phi _f}}}{{\partial {x^2}}}} \right)} \right)_{x = 0}} = {( - {\rho _f}{\omega ^2}({\phi _i} + {\phi _r}))_{x = 0}}\\ {\left( {\tilde H\left( {\frac{{{\partial ^2}{\phi _s}}}{{\partial {x^2}}}} \right) - \tilde C\left( {\frac{{{\partial ^2}{\phi _f}}}{{\partial {x^2}}}} \right)} \right)_{x = L}} = {( - {\rho _f}{\omega ^2}{\phi _t})_{x = L}} \end{array} \right. $ | (37) |
3) 流体声压连续:
| $ \left\{ \begin{array}{l} {\left( {\tilde M\frac{{{\partial ^2}{\phi _f}}}{{\partial {x^2}}} - \tilde C\frac{{{\partial ^2}{\phi _s}}}{{\partial {x^2}}}} \right)_{x = 0}} = {\rho _f}{\omega ^2}{({\phi _i} + {\phi _r})_{x = 0}}\\ {\left( {\tilde M\frac{{{\partial ^2}{\phi _f}}}{{\partial {x^2}}} - \tilde C\frac{{{\partial ^2}{\phi _s}}}{{\partial {x^2}}}} \right)_{x = L}} = {({\rho _f}{\omega ^2}{\phi _t})_{x = L}} \end{array} \right. $ | (38) |
4) 切向应力为零:
| $ \left\{ \begin{array}{l} \mu {\left( {\frac{{{\partial ^2}{\psi _s}}}{{\partial {x^2}}}} \right)_{x = 0}} = 0\\ \mu {\left( {\frac{{{\partial ^2}{\psi _s}}}{{\partial {x^2}}}} \right)_{x = L}} = 0 \end{array} \right. $ | (39) |
将上述势函数代入以上边界条件确定的8个方程,可得联立的方程组,写成如下矩阵形式:
| $ \mathit{\boldsymbol{AX = D}} $ | (40) |
其中:
| $ \begin{array}{l} \mathit{\boldsymbol{X}} = {[{V_{ww}}\;\;V_{w1}^ - \;\;V_{w2}^ - \;\;V_{wt}^ - \;\;V_{w1}^ + \;\;V_{w2}^ + \;\;V_{wt}^ + \;\;{V_{tt}}]^{\rm{T}}}\\ \mathit{\boldsymbol{D}} = {[ - {k_w}\;\;0\;\; - {\rho _f}{\omega ^2}\;\;0\;\;{\rho _f}{\omega ^2}\;\;0\;\;0\;\;0]^{\rm{T}}} \end{array} $ |

|
(43) |
解上述方程组即可得到声波从水入射到含气泡非饱和多孔介质层的反射系数Vww,以及透射系数Vtt。
2 数值分析根据上述推导得到的反射系数Vww、透射系数Vtt表达式,利用表 1的参数对透射系数进行计算。
| 表 1 模型参数 Tab.1 Model parameters |
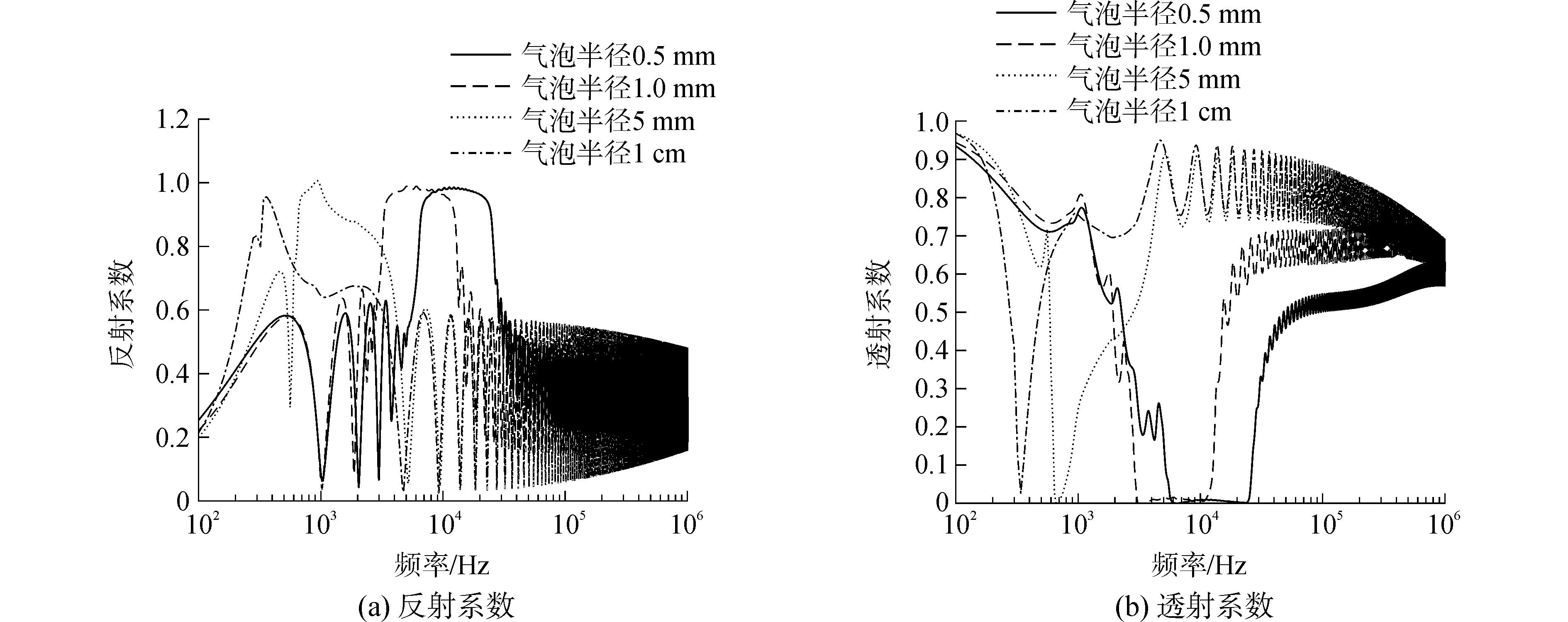
图 2给出了垂直入射情况下含气泡非饱和多孔介质层的声反射系数与声透射系数。数值计算中,气泡体积分数为0.001,含气泡多孔介质层的厚度为0.2 m。由模型计算可知,半径为0.5、1、5以及10 mm的气泡的共振频率分别约为:328、656、3 200、6 558 Hz。可以发现,当入射声波频率远低于气泡共振频率时,不同气泡半径下的反射系数在0.2附近,透射系数都接近于1。这是因为当声波频率很低时,声波的波长很大,远大于层的厚度。例如当声波频率为100 Hz时,波长约为15 m,与层厚0.2 m相差很大,这就使得介质层对声波的作用很小,层可以忽略,使得声能几乎全部透射;但随着频率逐渐增加到气泡共振频率附近,介质层的作用逐渐体现。在低频下含气沉积物中声速很低,使得特性阻抗小于水的特性阻抗,而随着频率增加声速减小,多孔介质层的特性阻抗减小,远离水的特性阻抗,使得两介质的阻抗差异增大,透射系数降低,反射系数增大;当声波频率在气泡共振频率附近时,反射系数则接近于1,透射系数接近于0,即声波很难穿透沉积物。这是因为当声波的频率在气泡共振频率附近时,沉积物呈现高声速和高衰减的特性,使得声波很难穿透。另外,随着气泡半径的增大,气泡共振频率降低;当声波频率远大于气泡共振频率时,反射系数则在0.2~0.5振荡,透射系数在0.5~0.8振荡,并且几种气泡的透射系数与反射系数逐渐逼近。当声波频率很高时,反射波和透射波都是层中多次反射波相干叠加的结果,由于高频声波波长远小于层厚,层中多次反射波相位不一致,使得透射系数与反射系数产生振荡。并且,当频率足够高后,气泡对沉积物的声学特性影响很小,最终会趋近于不含气泡情况。
|
Download:
|
| 图 2 不同气泡半径下反射系数与透射系数随频率的变化 Fig. 2 The variation of reflection coefficient and transmission coefficient with frequency under different bubble radius | |
当气泡半径为5 mm、含气泡多孔介质层厚度为0.2 m时,不同气泡体积分数下的透射系数、反射系数随频率的变化关系见图 3所示,其中气泡的共振频率约为656 Hz。图 3表明,当声波频率在气泡共振频率附近时,反射系数随气泡体积分数的增加成增加的趋势,透射系数呈现下降的趋势,且当气泡体积分数达到0.001时,频率接近气泡共振频率的声波很难穿透该多孔介质层。这是因为在气泡共振频率范围内,随着气泡含量的增大,沉积物衰减增加,使得透射系数减小,反射系数增大;当声波频率大于气泡共振频率时,不同气泡体积分数下的反射系数以及透射系数与无气泡情况基本一致,因为高频下气泡对沉积物的声学特性影响可以忽略。另外发现在非共振频率附近时,只有当气泡体积分数达到0.001时,反射系数和透射系数才与无气泡的情况有明显区别,这是因为在非共振频率附近时,较低的气泡含量对声速和密度的影响很小。当声波频率低于气泡共振频率时,由于低声速,气泡体积分数为0.001下的沉积物特性阻抗要低于不含气泡的特性阻抗,而当声波频率高于气泡共振频率时,高气泡含量的声速又很高,使得这两种情况下的特性阻抗相对于低气泡含量来说都更远离水的特性阻抗,从而透射系数比低气泡含量的低,反射系数则较大。

|
Download:
|
| 图 3 不同气泡体积分数下反射系数与透射系数随频率的变化 Fig. 3 The variation of reflection coefficient and transmission coefficient with frequency under different bubble volume fraction | |
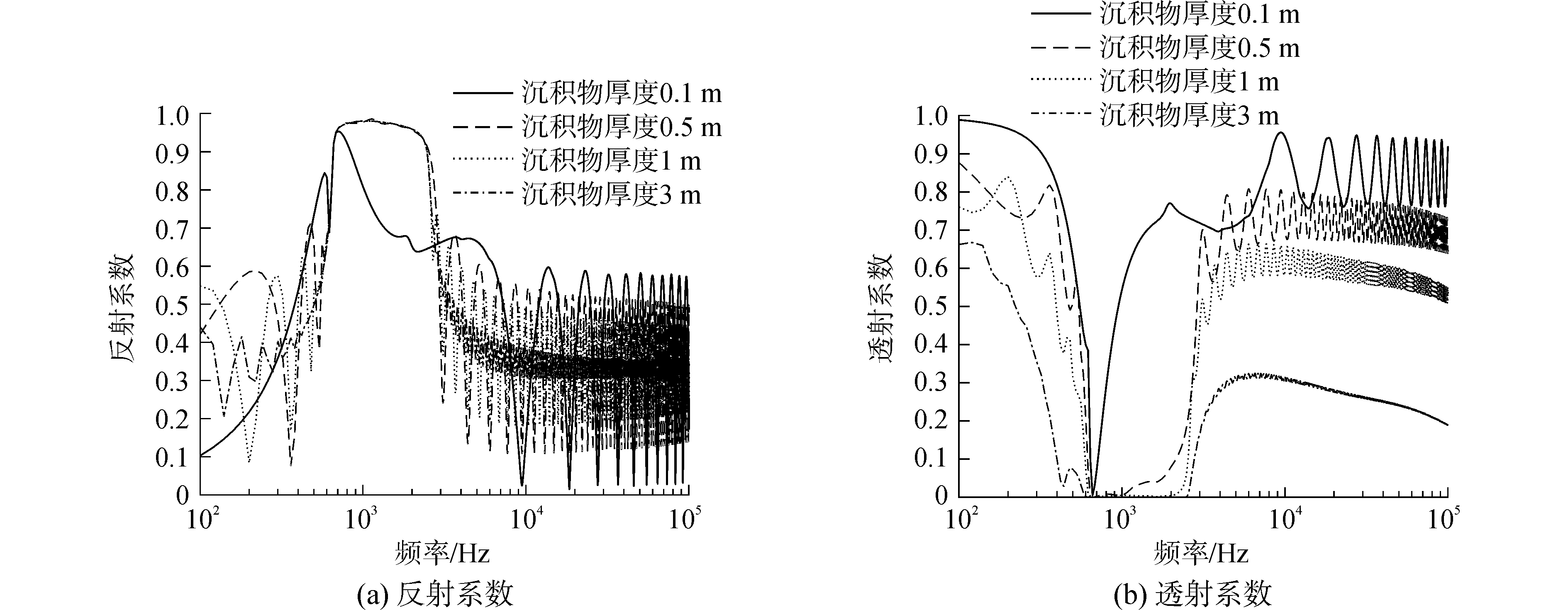
当气泡半径为5 mm、体积分数为0.001时,不同多孔介质层厚下的透射系数、反射系数随频率的变化关系见图 4所示, 其中气泡的共振频率约为656 Hz。由图 4可知,随着沉积物厚度的增加,在不同频率下的透射系数基本呈现减小的趋势;并且厚度越大,透射系数和反射系数的振荡幅度越小。并且发现,当厚度足够大时,透射系数在共振频率附近很大一个频带内都很小。这主要是因为含气泡多孔介质具有较高的声衰减特性,越厚的层衰减效果越明显,透声性能越差。而随着厚度的增加,层中的反射波衰减增大,对反射波和透射波的叠加作用减小,使得透射系数和反射系数振荡幅度减弱。
|
Download:
|
| 图 4 不同层厚度下的反射系数与透射系数随频率的变化 Fig. 4 The coefficient of reflection coefficient and transmission coefficient varies with frequency at different layer thicknesses | |
1) 当入射声波频率远小于气泡共振频率且层厚较小时,声波几乎全透射。
2) 当声波频率逐渐上升至气泡共振频率附近时,若气泡含量足够大,透射系数逐渐减小至0,并且在一定频带内保持稳定,频带的宽度随气泡半径的增大而增大,表明含气泡多孔介质的透声性能与气泡的半径有关,气泡半径越大,不透声的频率越小,不透声的频带越宽。
3) 当声波频率大于气泡共振频率时,随着频率的增大,透射系数逐渐增加随后振荡,而反射系数先减小再振荡。并且发现当频率足够高时,透射系数与反射系数受气泡半径的影响很小;而气泡含量越低,反射系数和透射系数越接近不含气泡的情况。
4) 介质层厚度的影响在透射系数上体现为厚度越大透射系数越小,而反射系数有较大的振荡,厚度越大振荡的范围越小。
| [1] |
张琳. 多孔介质中地震波的频散及衰减机制研究[D]. 青岛: 中国石油大学(华东), 2014: 4-8. ZHANG Lin. A study on seismic wave dispersion and attenuation mechanism in porous media[D]. Qingdao: China University of Petroleum (East China), 2014: 4-8. http://cdmd.cnki.com.cn/Article/CDMD-10425-1016711738.htm (  0) 0)
|
| [2] |
王营, 赵武, 黄丹. 多孔材料声学模型及其应用[J]. 材料导报, 2015, 29(3): 145-149. WANG Ying, ZHAO Wu, HUANG Dan. The acoustic models of porous materials and their applications[J]. Materials review, 2015, 29(3): 145-149. (  0) 0)
|
| [3] |
陈浩, 杨胜来, 于东海. 多孔介质内流体相态特征超声波探测研究进展[J]. 西南石油大学学报(自然科学版), 2013, 35(1): 67-73. CHEN Hao, YANG Shenglai, YU Donghai. Research progress of the ultrasonic detection in phase behavior of fluids in porous media[J]. Journal of southwest petroleum university (science & technology edition), 2013, 35(1): 67-73. (  0) 0)
|
| [4] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. Low-frequency range[J]. The journal of the acoustical society of America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 (  0) 0)
|
| [5] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. Higher frequency range[J]. The journal of the acoustical society of America, 1956, 28(2): 179-191. DOI:10.1121/1.1908241 (  0) 0)
|
| [6] |
STOLL R D, BRYAN G M. Wave attenuation in saturated sediments[J]. The journal of the acoustical society of America, 1970, 47(5B): 1440-1447. DOI:10.1121/1.1912054 (  0) 0)
|
| [7] |
STOLL R D, KAN T K. Reflection of acoustic waves at a water-sediment interface[J]. The journal of the acoustical society of America, 1981, 70(1): 149-156. DOI:10.1121/1.386692 (  0) 0)
|
| [8] |
ALTENBURG R A, CHOTIROS N P, FAULKNER C M. Plane-wave analysis of acoustic signals in a sandy sediment[J]. The journal of the acoustical society of America, 1991, 89(1): 165-170. DOI:10.1121/1.400495 (  0) 0)
|
| [9] |
CHOTIROS N P. Biot model of sound propagation in water-saturated sand[J]. The journal of the acoustical society of America, 1995, 97(1): 199-214. DOI:10.1121/1.412304 (  0) 0)
|
| [10] |
WU Kunyu, XUE Qiang, ADLER L. Reflection and transmission of elastic waves from a fluid-saturated porous solid boundary[J]. The journal of the acoustical society of America, 1990, 87(6): 2349-2358. DOI:10.1121/1.399081 (  0) 0)
|
| [11] |
ALLARD J F, DEPOLLIER C, REBILLARD P, et al. Inhomogeneous Biot waves in layered media[J]. Journal of applied physics, 1989, 66(6): 2278-2284. DOI:10.1063/1.344284 (  0) 0)
|
| [12] |
ALLARD J F, BOURDIER R, DEPOLLIER C. Biot waves in layered media[J]. Journal of applied physics, 1986, 60(6): 1926-1929. DOI:10.1063/1.337244 (  0) 0)
|
| [13] |
周来江, 朴胜春, 杨士莪. 平面波与线性粘弹海底的反射和折射[J]. 声学学报, 2009, 34(2): 136-141. ZHOU Laijiang, PIAO Shengchun, YANG Shi'e. Reflection and refraction of plane wave at a linear viscoelastic ocean bottom[J]. Acta acustica, 2009, 34(2): 136-141. (  0) 0)
|
| [14] |
乔文孝, 王耀俊, 吴文虬. 层状多孔介质中声反射和透射[J]. 声学学报, 1993, 18(2): 99-110. QIAO Wenxiao, WANG Yaojun, WU Wenqiu. Reflection and transmission of acoustic wave on multilayered porous media[J]. Acta acustica, 1993, 18(2): 99-110. (  0) 0)
|
| [15] |
彭临慧, 赵燕鹏, 郁高坤. 声波在水-多孔介质海底界面上的反射与透射[J]. 中国海洋大学学报, 2007, 37(4): 671-675. PENG Linhui, ZHAO Yanpeng, YU Gaokun. Reflection and refraction of acoustic waves at a water-porous sediment interface[J]. Periodical of Ocean University of China, 2007, 37(4): 671-675. (  0) 0)
|
| [16] |
乔文孝, 杜光升, 聂士忠. 声波在液浸多层多孔介质中的反射和透射[J]. 石油大学学报(自然科学版), 1992, 16(4): 113-120. QIAO Wenxiao, DU Guangsheng, NIE Shizhong. Reflection and transmission of elastic wave in layered porous media immersed in liquid[J]. Journal of China University of Petroleum(nature science), 1992, 16(4): 113-120. (  0) 0)
|
| [17] |
徐红玉, 陈殿云, 杨先健. 平面波通过弹性介质中夹层时的传播特性[C]//全国土动力学学术会议. 南京, 2002: 577-584. XU Hongyu, CHEN Dianyun, YANG Xianjian. Popagation characteristics of plan wave while transiting interlining in elastic medium[C]//National Soil Dynamics Academic Conference. Nanjing, 2002: 577-584. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=4107574 (  0) 0)
|
| [18] |
阚光明, 刘保华, 张维冈, 等. 珠江口外伶仃洋海底含气沉积物声波反射及衰减特征[J]. 海洋学报, 2008, 30(2): 26-32. KAN Guangming, LIU Baohua, ZHANG Weigang, et al. Acoustic reflection and attenuation characteristics of gas-containing sediment in the outer lingding bay of the Zhujiang estuary in China[J]. Acta oceanologica sinica, 2008, 30(2): 26-32. (  0) 0)
|
| [19] |
MANTOUKA A, DOGAN H, WHITE P R, et al. Modelling acoustic scattering, sound speed, and attenuation in gassy soft marine sediments[J]. The journal of the acoustical society of America, 2016, 140(1): 274-282. DOI:10.1121/1.4954753 (  0) 0)
|
| [20] |
ZHENG Guangying, HUANG Yiwang, HUA Jian, et al. A corrected effective density fluid model for gassy sediments[J]. The journal of the acoustical society of America, 2017, 141(1): EL32-EL37. DOI:10.1121/1.4973616 (  0) 0)
|
| [21] |
TÓTH Z, SPIESS V, KEIL H. Frequency dependence in seismoacoustic imaging of shallow free gas due to gas bubble resonance[J]. Journal of geophysical research:solid earth, 2015, 120(12): 8056-8072. DOI:10.1002/2015JB012523 (  0) 0)
|
| [22] |
郑广赢, 黄益旺. 气泡线性振动对含气泡水饱和多孔介质声传播的影响[J]. 物理学报, 2016, 65(23): 234301. ZHENG Guangying, HUANG Yiwang. Effect of linear bubble vibration on wave propagation in unsaturated porous medium containing air bubbles[J]. Acta physica sinica, 2016, 65(23): 234301. DOI:10.7498/aps.65.234301 (  0) 0)
|
| [23] |
BIOT M A. Generalized theory of acoustic propagation in porous dissipative media[J]. The journal of the acoustical society of America, 1962, 34(9A): 1254-1264. DOI:10.1121/1.1918315 (  0) 0)
|
| [24] |
JACKSON D R, RICHARDSON M D. High-frequency seafloor acoustics[M]. New York: Springer, 2007: 2497-2498.
(  0) 0)
|
| [25] |
FELLAH Z E A, CHAPELON J Y, BERGER S, et al. Ultrasonic wave propagation in human cancellous bone:application of Biot theory[J]. The journal of the acoustical society of America, 2004, 116(1): 61-73. DOI:10.1121/1.1755239 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


