2. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
海底沉积物对声传播的影响极为明显,其声学特性的准确测量对海洋声传播建模极为重要。已有外场数据表明,海底沉积物声速和衰减都与声波频率有关。海底沉积物的声速频散有时可高达11%[1],在10 kHz以下频段,声速频散尤为显著,对海底掩埋目标探测、海底混响建模具有重要影响。高频段声速频散与衰减实验测量数据与海底沉积物声学模型之一Biot模型吻合良好,然而10 kHz以下频段的声速显著小于模型预报的数据,声速频散却大于模型预报的频散,究其可能原因有海洋环境参数的不确定性,或者中低频段海底沉积物声速频散的机理与高频段存在差异[2-4]。因此,稳定可控条件下海底沉积物声速频散和衰减特性研究具有重要意义,它可能成为解决上述问题的唯一途径。
Biot理论原本是用来描述固体框架和孔隙水组成的双相介质,许多研究工作已将它用于描述海底沉积物,但无论是高频段的衰减还是低频段的声速,理论与海上实验数据的吻合程度还不尽如人意。因此本文将以沙质沉积物为研究对象,在沉积物参数、环境条件均可控的情况下,在实验室中开展沙质沉积物声学参数测量方法的研究,获取高质量的声速和衰减数据,最终为解释海上实验数据与模型预报不符的原因提供数据基础。
沉积物声速频散和衰减数据获取可应用窄带或宽带测量方法。在窄带测量中,发射信号通常为CW脉冲;在宽带测量中,发射信号通常为线性调频脉冲或高斯白噪声脉冲。为了减小发射脉冲的展宽,以减小多途信号的叠加,实际测量中希望发射换能器的带宽尽可能宽,脉冲宽度尽可能短。然而,即使是CW脉冲信号,它也具有一定带宽,并且带宽与脉冲宽度成反比。减小脉宽可以减弱多途与直达波之间的叠加程度,但发射信号带宽的增大对换能器工作带宽及带内平坦程度具有更高要求。由于实验所用声源的频率响应在一定频段内大都是不平坦的,导致发射的窄带CW脉冲信号中心频率发生偏移,造成测量结果的不准确。宽带测量理论上不需要考虑中心频率偏移的问题,但是声源频响的不平坦会降低发射声信号的带宽,利用脉冲压缩等方法进行处理时,会造成匹配滤波器的失配以及脉冲的展宽,同样会造成结果的不准确性。
在通信系统中通常应用的预均衡技术,通过信道的有关先验知识对驱动信号进行补偿,用以来补偿信道衰落,减少码间的干扰,提高系统的传输性能。近年来,许多学者将均衡技术应用到声源驱动信号的补偿中,取得了较好的效果[5-9]。例如文献[6]通过研究数字均衡器的特点,将其引入到宽带系统中用以来补偿匹配换能器;文献[7]通过分段快速傅里叶变换以及频率能量补偿技术实现了回声转发信号的发射声源级差异补偿;文献[8]通过对换能器激励电压进行加权补偿,得到了在约两个倍频程带宽内声源级几乎一致的结果。
本文根据声源的发送电压响应对驱动信号进行补偿,极大抑制了窄带发射声信号中心频率偏移的程度,提高了宽带发射声信号的带宽。驱动信号经补偿之后,拓宽了窄带测量数据的有效带宽,降低了宽带测量数据的起伏,使得窄带和宽带数据更加一致,提高了数据的准确性。本文首先给出驱动信号补偿的原理,其次对补偿之后的效果进行仿真,最后设计实验对实际效果进行验证。
1 驱动信号补偿原理发射换能器一般工作在线性状态,将换能器作为一个线性时不变系统来考虑,则经换能器发射的声信号为
| $ r\left( t \right) = s\left( t \right)*h\left( t \right) $ | (1) |
频率域的表示为
| $ R\left( f \right) = S\left( f \right) \cdot H\left( f \right) $ | (2) |
式中S(f)、H(f)、R(f)分别代表驱动信号s(t)、声源的单位冲击响应函数h(t)和声信号r(t)的傅里叶变换。
由于实际所用声源的发送电压响应在有效的工作带宽内一般是不平坦的,尤其对于谐振式换能器来说更是如此。从频域分析可知,当驱动信号经过一个发送电压响应非平坦的系统后,则发射声信号的频谱形状将发生变化。这将导致窄带测量得到的声速和衰减并非驱动信号中心频率时的数据,宽带测量时会造成匹配滤波器的失配,造成沉积物中声速和衰减测量的不准确性。
因此为了确保实验数据的准确性,需要保持声信号的频谱与驱动信号的频谱尽可能一致,也即H(f)在工作频带内为常数,即需要对发射系统的频响特性进行预均衡。这里在频域上对驱动信号进行补偿,即利用幅度谱为|H(f)|-1的滤波器对驱动信号进行滤波,则经补偿之后的驱动信号为
| $ S'\left( f \right) = S\left( f \right)/H\left( f \right) $ | (3) |
则声源发射的声信号为
| $ R'\left( f \right) = S'\left( f \right)H\left( f \right) = S\left( f \right) $ | (4) |
则理论上驱动信号经过补偿之后,声源发射的声信号与原驱动信号的频谱形状相同。
在实验室中进行沙质沉积物声速频散和衰减的测量时,由于水箱尺寸有限,为了避免多途的严重干扰,窄带测量发射信号通常采用窄脉冲。脉冲越窄,其带宽则越宽。当一个具有一定带宽的信号经过一个窄带系统时,不仅声信号的频谱形状发生变化,其时间波形也将展宽,在低频情况下很难与多途信号分离开,带来衰减的测量误差。而宽带测量时由于频谱形状变化,会造成声信号带宽降低,匹配滤波器失配。而经式(4)补偿之后,发射声信号的频谱形状将与电信号的特征相类似,并且由于系统带宽不足造成的脉冲展宽现象也能够得到很好的抑制。
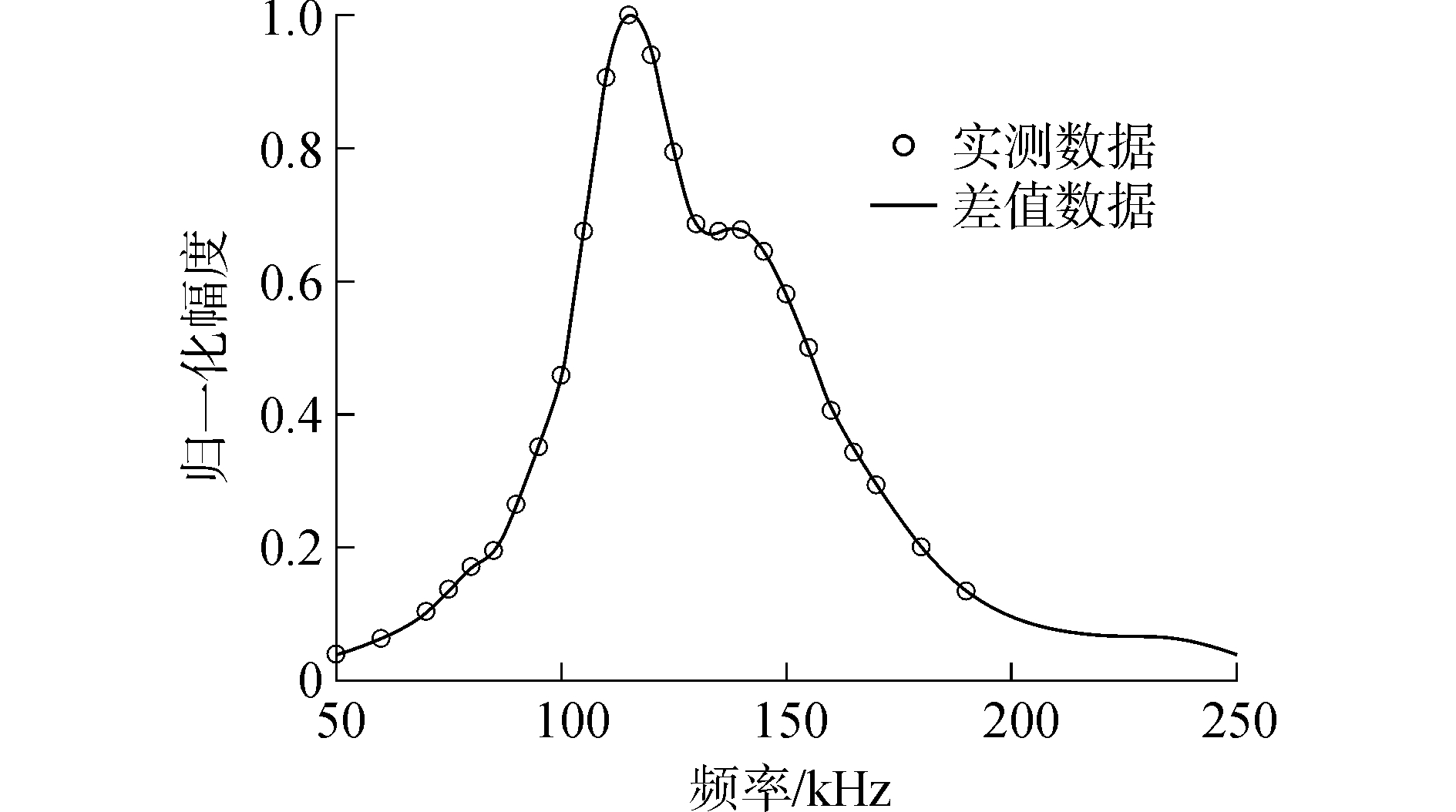
2 驱动信号补偿理论仿真为了验证方法的有效性,根据换能器的发送电压响应进行发射声信号的仿真以及窄带和宽带驱动信号的补偿,对比和分析补偿前后的效果。图 1为实验中发射换能器的归一化发送电压响应曲线(对实测数据进行了三次样条插值)。该换能器的最大响应频率约115 kHz,-3 dB工作带宽约23 kHz。
|
Download:
|
| 图 1 发射换能器的发送电压响应 Fig. 1 Transmitting voltage response of the transmitter | |
窄带测量时驱动信号采用经Blackman窗调制的CW脉冲信号,填充5个周期,频率范围90~170 kHz。
仿真结果如图 2所示,驱动电信号的中心频率分别为90 kHz和170 kHz,但经过发射换能器转换成声信号后,声信号的中心频率偏移到了108 kHz和147 kHz。同时可以看到,由于仿真时对换能器发送电压响应的截断,声源发射的声信号脉冲展宽明显。

|
Download:
|
| 图 2 窄带驱动信号补偿前后结果对比 Fig. 2 The contrast before and after compensation for narrowband driving signal | |
出现中心频率偏移的原因可以由声源的发送电压响应曲线进行解释,换能器的谐振频率在115 kHz左右。发射CW脉冲信号时,由于驱动信号具有一定的带宽。当驱动信号的中心频率低于115 kHz时,此时由于声源的发送电压响应随着频率的升高而增大,因此换能器发射的声信号高频成分增大,使得声信号幅度谱的峰值向高频端偏移,因而造成发射声信号中心频率的增大;相反,当驱动信号的中心频率高于115 kHz时,声源的发送电压响应随着频率的升高而减小,因此换能器发射的声信号低频成分增大,使得声信号幅度谱的峰值向低频端移动,因而造成发射声信号中心频率的减小。
如图 2中经补偿后的发射声信号所示,通过对驱动信号的补偿,换能器发射的声信号中心频率与驱动信号中心频率基本一致,抵消了声源发送电压响应不平坦的影响。
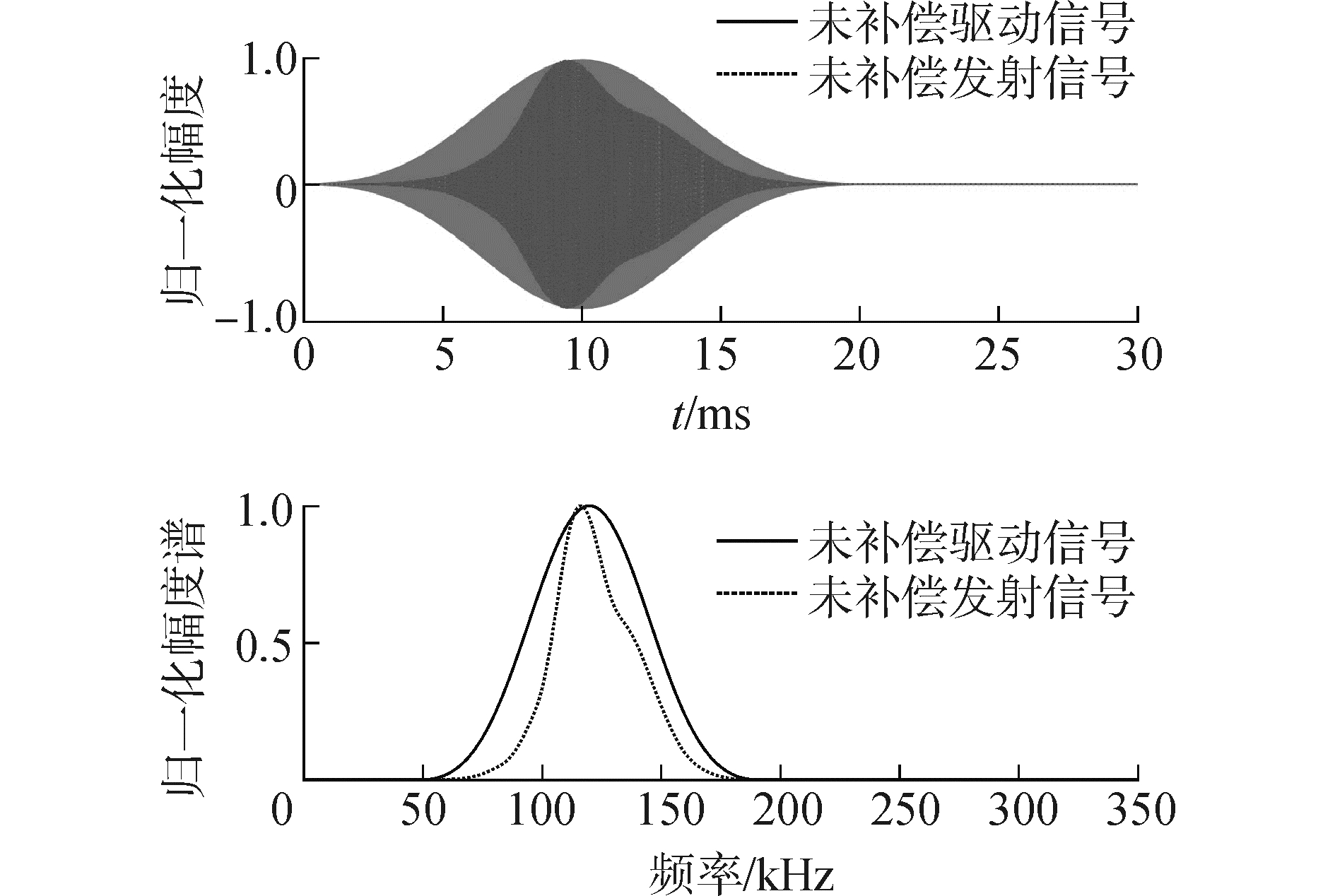
2.2 宽带信号宽带测量时驱动信号采用经Blackman窗调制的脉冲长度为20 ms、扫频范围为50~190 kHz的LFM信号,这里加Blackman窗调制是为了实验测量时压低脉冲压缩后信号旁瓣对直达波提取的影响。
宽带信号未补偿时信号如图 3所示,同窄带发射声信号中心频率的偏移分析,当驱动信号为宽带LFM信号时,发射声信号的频谱形状发生了变化。由于谐振式换能器发送电压响应的不平坦,系统的带宽受限,使得发射声信号发生明显畸变,带宽降低。
|
Download:
|
| 图 3 宽带信号未补偿结果 Fig. 3 No compensation for broadband signal | |
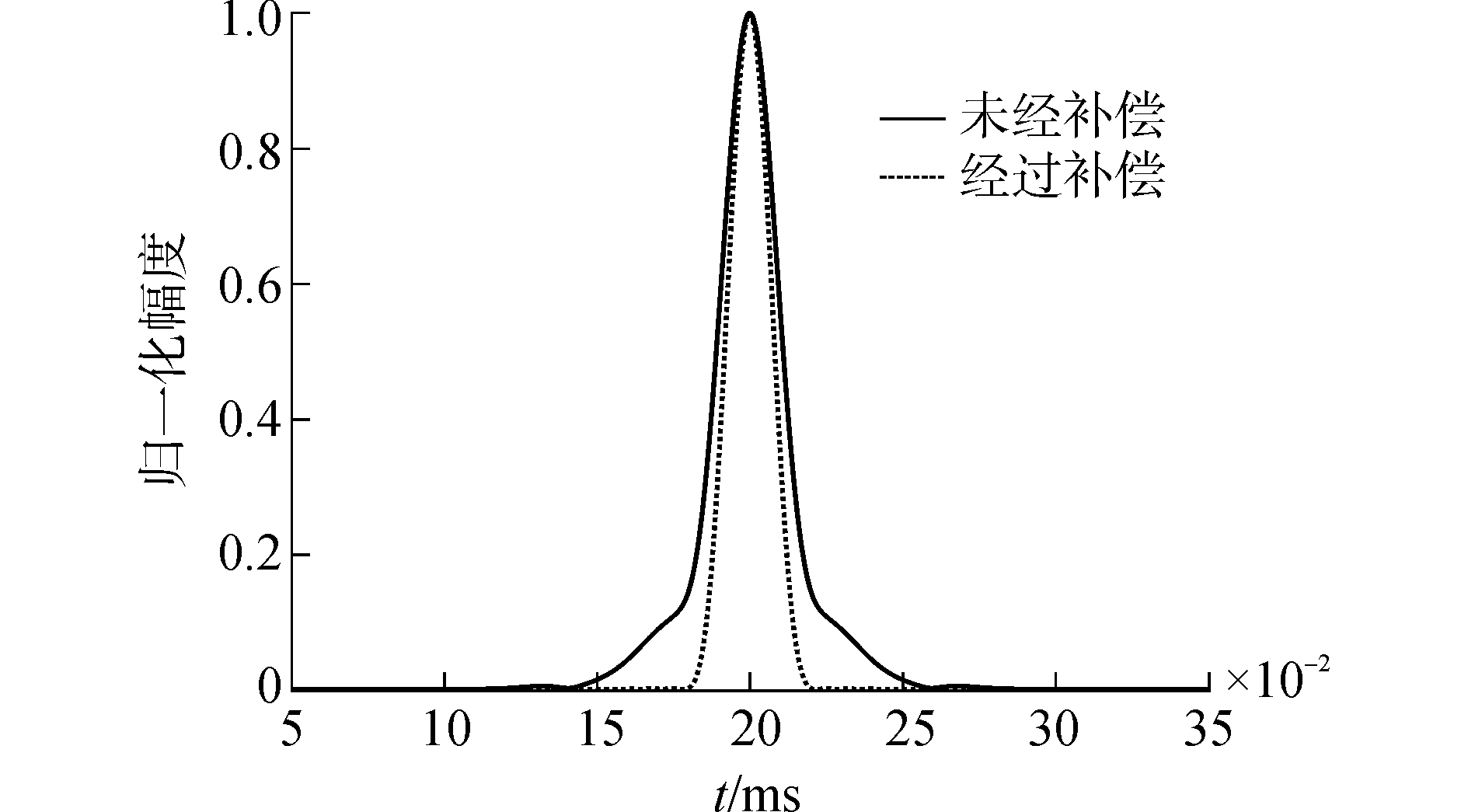
宽带测量时,利用脉冲压缩方法分离直达波与多途信号,仿真得到直达波经脉冲压缩后信号的包络(参考信号为图 3中未补偿的驱动信号)如图 4所示。由于发射声信号波形发生了明显畸变,造成匹配滤波器的失配;同时由于发射声信号的带宽降低,降低了脉冲压缩的压缩比,使得压缩得到的信号更宽,更易受多途信号叠加的影响。

|
Download:
|
| 图 4 脉冲压缩后信号包络 Fig. 4 Envelops after pulse compression | |
经过补偿后的发射声信号如图 5所示,通过对驱动信号的补偿,换能器发射的声信号时域波形和频谱形状与未补偿时的驱动信号基本一致,抵消了声源发送电压响应不平坦性的影响。从图 4中经补偿之后脉冲压缩的信号包络可以看出,驱动信号补偿后,匹配滤波器的失配得到了抑制,并且由脉冲压缩压缩比降低引起的脉宽展宽也得到了很好的抑制。
|
Download:
|
| 图 5 宽带信号经过补偿结果 Fig. 5 Compensation for broadband signal | |
由窄带和宽带信号的仿真结果可以看出,由于声源带宽受限以及发送电压响应的不平坦,使得实际发射声信号的频谱形状发生了变化。其中窄带发射信号中心频率发生偏移,宽带发射信号的波形发生畸变以及带宽降低。这对沉积物中声速和衰减系数的测量造成影响,不仅会使测量数据的频带范围受限,而且会造成测量结果的不准确,这对于沉积物模型的验证是极其不利的。而通过对驱动信号进行补偿,使得通过换能器发射的声信号与驱动电信号能够保持一致,提高了实验测量结果的准确性。
3 实验结果与分析实验在长宽高为1.2 m×1.2 m×1m的水箱中进行,设备布放示意图如图 6所示。铝合金框架上有三个玻璃缸,玻璃缸底面的玻璃厚度相同。玻璃缸长宽约30 cm,装满水饱和沙的两个玻璃缸的深度分别为10.100 cm和20.030 cm。柱形指向性发射换能器和B & K8105水听器固定在可滑动的框架上,声源辐射面和水听器的几何中心在水中的深度分别为4 cm和64 cm。声源声轴对准水听器,垂直向下发射声波。

|
Download:
|
| 图 6 设备布放示意图 Fig. 6 Sketch map of the experiment equipment | |
分别采用窄带和宽带脉冲信号测量水饱和沙的声速和衰减。窄带测量时,驱动信号分别为加Blackman窗的CW脉冲信号和补偿的CW脉冲信号(见图 2中经过补偿的驱动信号),脉冲填充周期数为5,驱动信号频率范围为90~170 kHz,步长为10 kHz;宽带测量时,驱动信号分别为加Blackman窗的线性调频脉冲和补偿的线性调频脉冲(见图 4中经过补偿的驱动信号),脉冲长度20 ms、扫频范围50~190 kHz。
窄带测量中,可根据有无沙样品时信号的到达时差获得声速,根据穿透不同厚度沙样品的信号幅度获得衰减。声速和衰减表示为[10]
| $ {c_p} = \frac{{{c_w}}}{{1 - {c_w}\Delta t/{d_2}}} $ | (5) |
| $ {\alpha _p} = - \frac{{20}}{{\Delta d}}\lg \left( {\frac{{{V_2}}}{{{V_1}}}} \right) $ | (6) |
式中:cw为水中声速;Δt为声速测量中脉冲信号的到达时差,采用互相关法估计得到;d1、d2为沙样品厚度,Δd=d2-d1;V1、V2分别表示穿透薄沙和厚沙信号的幅度。
宽带测量中,由于脉冲宽度较大,直达波与多途信号叠加严重,为此首先应用脉冲压缩方法从接收信号中提取直达波,在此基础上根据有无沙样品时接收信号的相位差计算声速,根据穿透不同厚度沙样品的信号幅度谱计算衰减,声速和衰减的表达式如下
| $ {c_p} = {c_w}{\left( {1 + \frac{{{c_w}\Delta \phi }}{{\omega \Delta d}}} \right)^{ - 1}} $ | (7) |
| $ {\alpha _p} = - \frac{{20\lg e}}{{\Delta d}}\ln |{H_r}\left( {{\rm{j}}\omega } \right)| $ | (8) |
式中:Δϕ为接收信号的相位差,|Hr(jω)|表示接收信号的幅度谱之比。
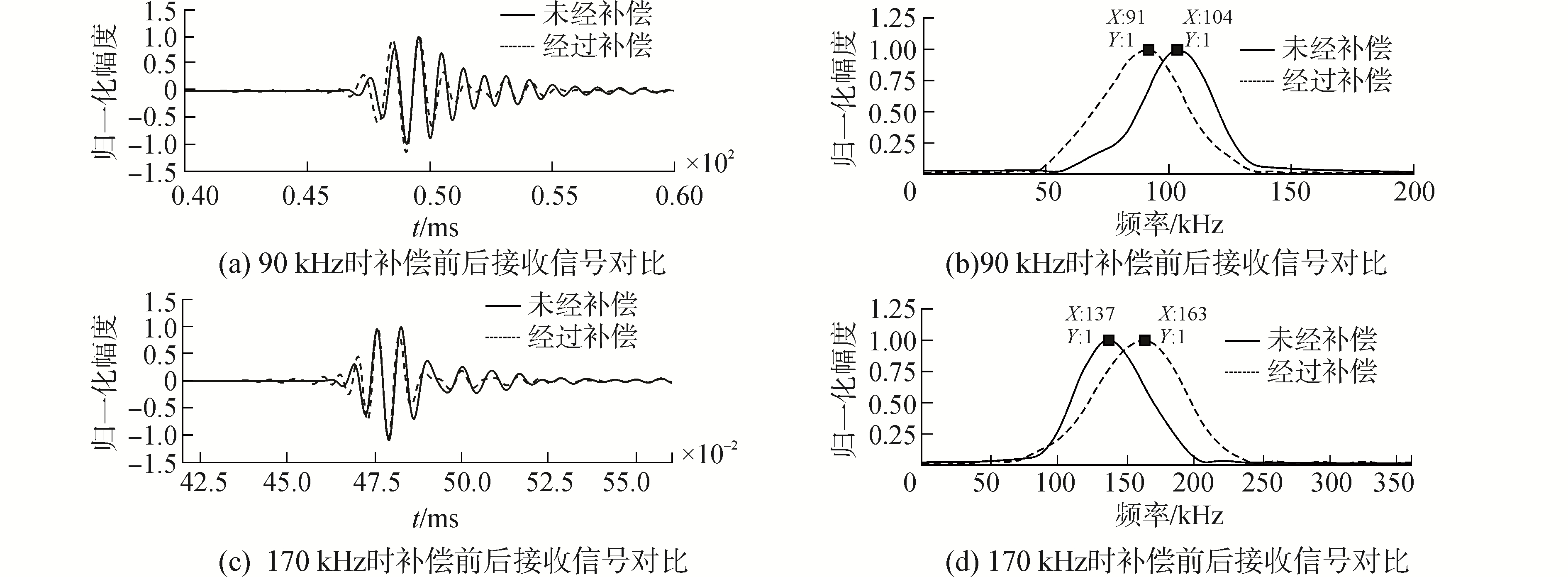
窄带实验时,透过缸的接收信号如图 7所示,驱动信号中心频率分别为90 kHz和170 kHz。驱动信号未补偿时,接收信号中心频率分别偏移到了104 kHz和137 kHz,与仿真结果基本一致;驱动信号补偿后,接收信号中心频率分别为91 kHz和163 kHz,与驱动信号中心频率较为相近。实验数据表明,驱动信号补偿抑制了接收信号的中心频率偏移。
|
Download:
|
| 图 7 窄带测量时补偿前后接收信号对比 Fig. 7 The contrast between received narrowband signals before and after compensation | |
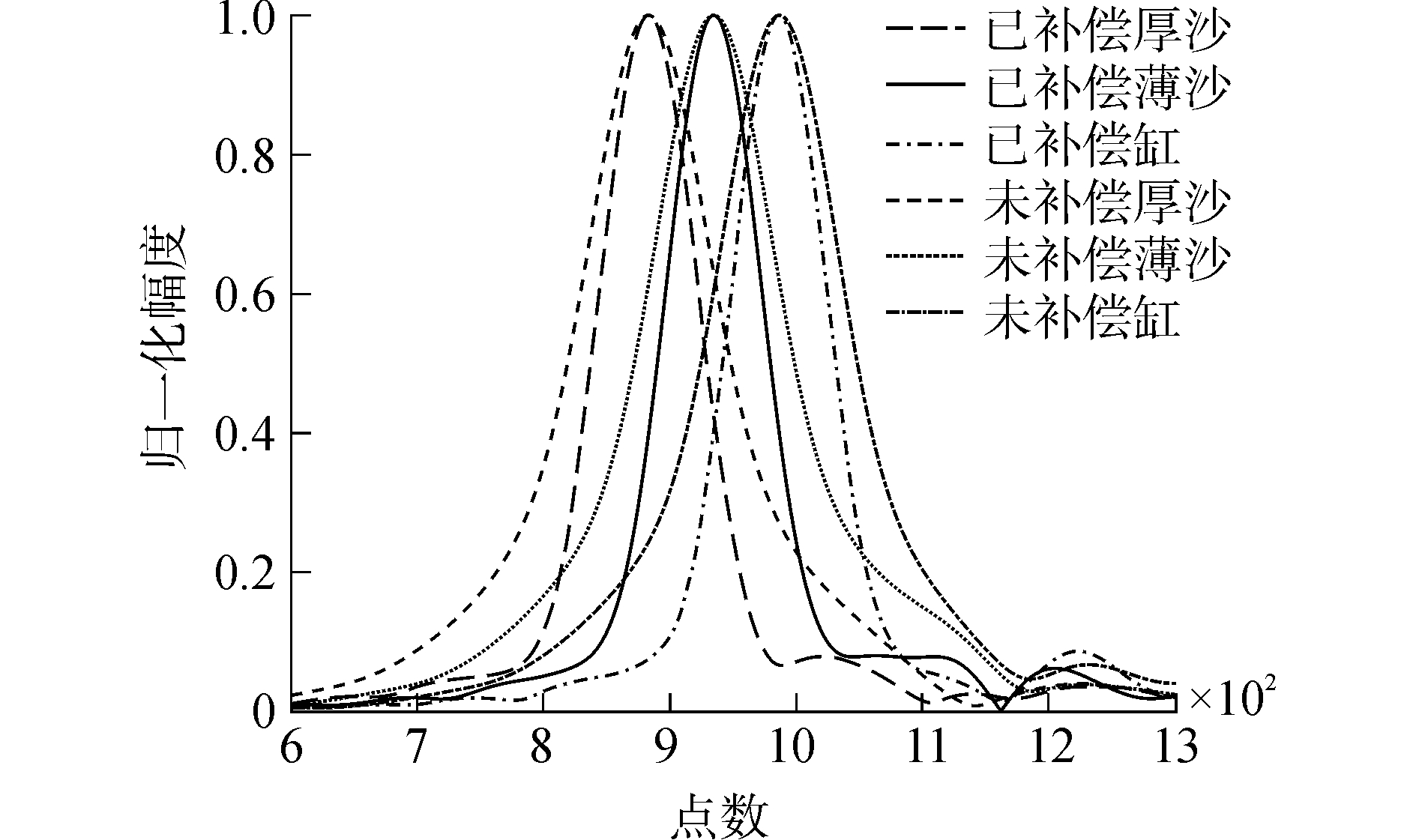
宽带实验时,无玻璃缸情况下水听器接收的信号如图 8(a)所示,经过脉冲压缩后,提取的直达波波形和幅度谱如图 8(b)和图 8(c)所示。从图 8(c)中可以看出,驱动信号未经补偿时,水听器接收信号的带宽比原宽带信号的带宽小了很多;经过补偿后,接收信号带宽得到改善。当然,在应用脉冲压缩提取直达波的过程中,由于匹配滤波器的失配以及多途信号叠加的影响,会造成所提取的直达波产生偏差。图 9为宽带测量时水听器接收信号脉冲压缩的结果(参考信号为经补偿后提取的直达波,如图 8(b)所示),可以看出,驱动信号补偿后,接收信号脉冲压缩后的脉宽更窄,降低了直达波与多途叠加的程度,此时还原得到的直达波更准确,由此测量方法得到的声速和衰减数据将更可靠。

|
Download:
|
| 图 8 宽带测量时无玻璃情况下的接收信号 Fig. 8 Received broadband signals without glass jar | |
|
Download:
|
| 图 9 接收信号脉冲压缩后的包络 Fig. 9 Envelops of received signals after pulse compression | |
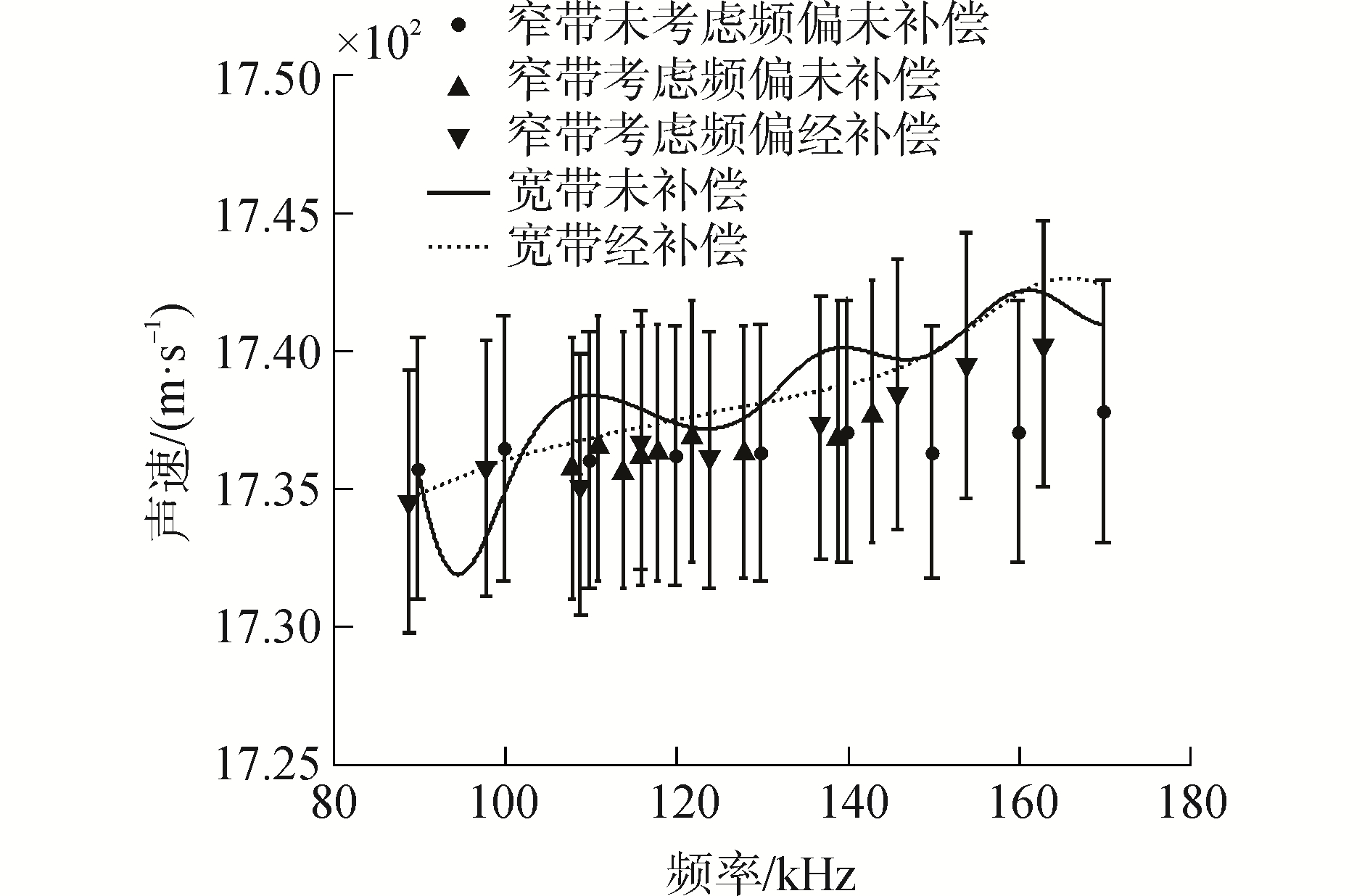
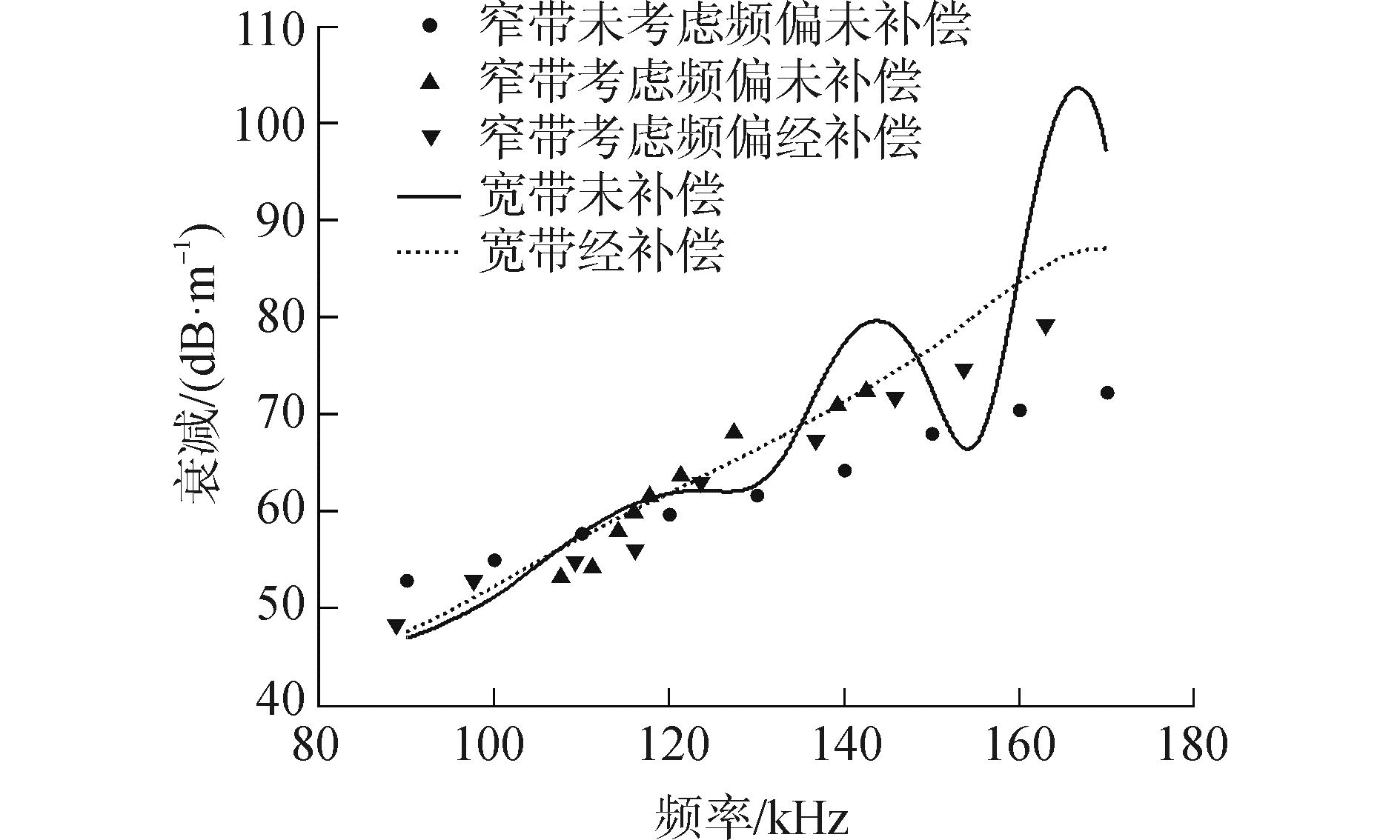
图 10和11给出了窄带和宽带测量方法获取的水饱和沙质沉积物的声速和衰减。
|
Download:
|
| 图 10 补偿前后声速结果对比 Fig. 10 Comparison of sound speed results befor and after compensation | |
|
Download:
|
| 图 11 补偿前后衰减结果对比 Fig. 11 Comparison of attenuation results befor and after compensation | |
根据水饱和沙质沉积物声学模型的预报结果可知,在实验测量频段内,沉积物声速具有弱的正频散特性,衰减随着频率增大而增大[11-13]。在图 10和图 11中,实心圆点表示的是未考虑中心频率偏移时的测量结果(即测量结果对应于驱动信号的中心频率),三角形表示的是考虑中心频率偏移时的测量结果(即测量结果对应于实际接收信号的中心频率)。从窄带测量时未考虑中心频率偏移影响的测量结果可以看出,其与考虑中心频率偏移补偿前后的窄带测量结果以及宽带测量结果相比偏差很大,尤其是对衰减系数的影响。而驱动信号经过补偿后窄带测量声速呈现明显的正频散特性,声速和衰减的测量结果与宽带测量的结果更加逼近,窄带测量的频段范围比未补偿时得到了明显提高。
宽带测量中,当驱动信号未补偿时,由于发射换能器的工作带宽较窄,导致其发射声信号的带宽显著减小,脉冲压缩的时间分辨力降低,直达波与多途未能完全分离,最终导致声速和衰减产生起伏。而驱动信号补偿后,换能器发射的声信号的带宽增大,脉冲压缩的时间分辨力提高,多途叠加带来的影响降低,测量结果的起伏明显减弱。
4 结论1) 仿真与实验研究表明,本文提出的沙质沉积物声速频散和衰减测量的换能器驱动信号补偿方法是可行的。通过应用发射换能器的发送电压响应对驱动信号进行补偿,显著降低了换能器工作频带窄、带内不平坦带来的影响。
2) 驱动信号经补偿后,发射声信号中心频率的偏移得到有效抑制,信号带宽得到了保持,保证了宽带测量中脉冲压缩的时间分辨力,获得了更为可靠的声速频散和衰减数据,为沉积物声学模型的验证提供了保障。
3) 在驱动信号补偿中只应用了换能器的发送电压响应数据,这在工程上也是易于实现的。
| [1] |
BEST A I, HUGGETT Q J, HARRIS A J K. Comparison of in situ and laboratory acoustic measurements on Lough Hyne marine sediments[J]. The Journal of the acoustical society of America, 2001, 110(2): 695-709. DOI:10.1121/1.1382616 (  0) 0)
|
| [2] |
WILLIAMS K L, JACKSON D R, THORSOS E I, et al. Comparison of sound speed and attenuation measured in a sandy sediment to predictions based on the Biot theory of porous media[J]. IEEE journal of oceanic engineering, 2002, 27(3): 413-428. DOI:10.1109/JOE.2002.1040928 (  0) 0)
|
| [3] |
STOLL R D. Velocity dispersion in water-saturated granular sediment[J]. The journal of the acoustical society of America, 2002, 111(2): 785-793. DOI:10.1121/1.1432981 (  0) 0)
|
| [4] |
ZIMMER M A, BIBEE L D, RICHARDSON M D. Measurement of the frequency dependence of the sound speed and attenuation of seafloor sands from 1 to 400 kHz[J]. IEEE journal of oceanic engineering, 2010, 35(3): 538-557. DOI:10.1109/JOE.2010.2056230 (  0) 0)
|
| [5] |
胡智兵, 王清池, 许鹭芬, 等. 水声信道高速率数据传输中换能器频谱特性的均衡[J]. 厦门大学学报(自然科学版), 1999, 38(4): 524-528. HU Zhibing, WANG Qingchi, XU Lufen, et al. Equalization of transducers' spectral characteristic in high-speed data transmission within underwater acoustic channel[J]. Journal of Xiamen University (natural science), 1999, 38(4): 524-528. (  0) 0)
|
| [6] |
周伟江, 景永刚, 陈梦英. 数字均衡技术在水声宽带系统中的应用[J]. 声学技术, 2012, 31(2): 219-222. ZHOU Weijiang, JING Yonggang, CHEN Mengying. Application of digital equalizer technology in underwater broadband system[J]. Technical acoustics, 2012, 31(2): 219-222. (  0) 0)
|
| [7] |
曹清刚, 吴亮, 王晋. 水下回波模拟器频率补偿技术[J]. 舰船科学技术, 2012, 34(7): 96-100, 103. CAO Qinggang, WU Liang, WANG Jin. Equalize technique of underwater echo simulator research and achieve[J]. Ship science and technology, 2012, 34(7): 96-100, 103. (  0) 0)
|
| [8] |
刘望生, 俞宏沛, 周利生. 纵振水声换能器发送电压响应频带展宽补偿[J]. 压电与声光, 2008, 30(5): 577-578, 581. LIU Wangsheng, YU Hongpei, ZHOU Lisheng. Analyse of broadband longitudinal vibrating underwater transducer transmitting voltage response compensating[J]. Piezoelectrics & acoustooptics, 2008, 30(5): 577-578, 581. (  0) 0)
|
| [9] |
赵鹏涛, 曹振宇. 发射换能器频域补偿算法研究[J]. 水雷战与舰船防护, 2012, 20(1): 78-80. ZHAO Pengtao, CAO Zhenyu. Compensatory algorithns of transmitting transducer in frequency domain[J]. Mine warfare & ship self-defence, 2012, 20(1): 78-80. (  0) 0)
|
| [10] |
于盛齐, 黄益旺, 刘保华, 等. 沉积物中声速和衰减系数的宽带测量方法[J]. 声学学报, 2015, 40(5): 682-694. YU Shengqi, HUANG Yiwang, LIU Baohua, et al. A wide-band method for sound speed and attenuation measurement in sediments[J]. Acta acustica, 2015, 40(5): 682-694. (  0) 0)
|
| [11] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. Low-frequency range[J]. The journal of the acoustical society of America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 (  0) 0)
|
| [12] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. Higher frequency range[J]. The journal of the acoustical society of America, 1956, 28(2): 179-191. DOI:10.1121/1.1908241 (  0) 0)
|
| [13] |
WILLIAMS K L. An effective density fluid model for acoustic propagation in sediments derived from Biot theory[J]. The journal of the acoustical society of America, 2001, 110(5): 2276-2281. DOI:10.1121/1.1412449 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


