过去40年有限元法被广泛的应用到求解固体力学问题中,而有限体积法主要被应用到求解流体问题上[1],2000年开始,有限体积法由于其实施方法简单、对求解域的强守恒性,被逐步广泛的应用到了求解固体力学问题中:如线弹性问题、热粘塑问题、结构的磨损、铸造过程、杆件几何非线性大变形问题以及材料非线性大应变问题等[2-13]。
文献[14]中采用OPENFOAM对非正交材料进行了孔板大应变以及大旋转问题的分析,并在文献[15]中针对不同插值方法以及是否进行边界非正交修正的球体大旋转问题进行了对比,其单元中心梯度采用最小二乘法进行计算,对比结果显示在小增量载荷下,采用非正交边界修正的最小二乘法插值网格移动要优于未进行边界非正交修正的距离加权法插值网格移动。
本文在原有GTEA软件计算流体问题的基础上,将计算流体方法应用到求解结构大应变问题,基于更新拉格朗日描述,提出了求解几何非线性问题的LS-FVM,研究了GTEA中两种常用不同精度的梯度算法对文献[15]中圆盘大旋转问题的影响,并提出了一种改进的距离加权插值法,对比了改进后的距离加权法与传统插值方法对网格移动精度的影响,最后研究了圆盘在大增量载荷下内应力的分布。
1 非线性问题控制方程 1.1 线动量守恒方程不考虑体积力,采用更新的拉格朗日描述法,以现时构型为参考构型稳态线动量守恒方程为
| $ \oint\limits_{{A_u}} {{\mathit{\boldsymbol{n}}_u} \cdot \left( {\delta {\mathit{\boldsymbol{S}}_{\rm{u}}} + {\mathit{\boldsymbol{S}}_{\rm{u}}} \cdot \delta \mathit{\boldsymbol{F}}_{\rm{u}}^{\rm{T}} + \delta {\mathit{\boldsymbol{S}}_{\rm{u}}} \cdot \delta \mathit{\boldsymbol{F}}_{\rm{u}}^{\rm{T}}} \right){\rm{d}}{A_u}} = 0 $ | (1) |
式中:下标u表示以更新位移后的现时构型为参看构型,nu为界面单位外法向量,δSu为第二皮奥拉基尔霍夫应力增量,δFu=(▽u)T为变形梯度增量,Au为面积元。
1.2 本够关系对于弹性材料,采用广义虎克定律,应力应变的增量的表达式为
| $ \delta S = 2\mu \left( {\delta E} \right) + \lambda {\rm{tr}}\left( {\delta E} \right)I $ | (2) |
式中:μ、λ表示拉梅系数,E为格林应变张量,其增量表达式为
| $ \begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{E}} = \frac{1}{2}\left[ {\nabla \delta \mathit{\boldsymbol{u}} + {{\left( {\nabla \delta \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}} + \nabla \delta \mathit{\boldsymbol{u}} \cdot {{\left( {\nabla \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}} + } \right.}\\ {\left. {\nabla \mathit{\boldsymbol{u}} \cdot {{\left( {\nabla \delta \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}} + \nabla \delta \mathit{\boldsymbol{u}} \cdot {{\left( {\nabla \delta \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}} \right]} \end{array} $ | (3) |
代入格林应变增量表达式得到更新构型拉格朗日法的本够方程:
| $ \begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{S}} = \mu \left[ {\nabla {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u + }}{{\left( {\nabla {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}} \right] + \lambda {\rm{tr}}\left( {\nabla {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u}}} \right)\mathit{\boldsymbol{I}} + }\\ {\mu \nabla {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u}} \cdot {{\left( {\nabla {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u}}} \right)}^{\rm{T}}} + \frac{1}{2}\left( {\nabla {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u}}:\nabla {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u}}} \right)\mathit{\boldsymbol{I}}} \end{array} $ | (4) |
其中拉梅系数的表达式:
| $ \mu = \frac{E}{{2\left( {1 + \nu } \right)}} $ | (5) |
| $ \lambda = \left\{ {\begin{array}{*{20}{l}} {\frac{{\mathit{\boldsymbol{\nu }}E}}{{\left( {1 + \mathit{\boldsymbol{\nu }}} \right)\left( {1 - \mathit{\boldsymbol{\nu }}} \right)}},\;\;\;\;\;{\rm{平面应力}}}\\ {\frac{{\mathit{\boldsymbol{\nu }}E}}{{\left( {1 + \mathit{\boldsymbol{\nu }}} \right)\left( {1 - 2\mathit{\boldsymbol{\nu }}} \right)}},\;\;\;{\rm{平面应变和三维问题}}} \end{array}} \right. $ | (6) |
当采用更新的拉格朗日法进行大应变、大旋转问题分析时,网格移动后需进行应力更新,其表达式如下
| $ {\mathit{\boldsymbol{S}}_{\rm{u}}} = {J^{ - 1}}\mathit{\boldsymbol{F}} \cdot {\mathit{\boldsymbol{S}}_{\rm{u}}} \cdot {\mathit{\boldsymbol{F}}^{\rm{T}}} $ | (7) |
式中:F表示初始构型到现时构型的变形梯度,J为雅克比矩阵F的行列式,J=det(F),变形梯度矩阵F的位移表达为
| $ \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{I}} + {\left( {\nabla \mathit{\boldsymbol{u}}} \right)^{\rm{T}}} $ | (8) |
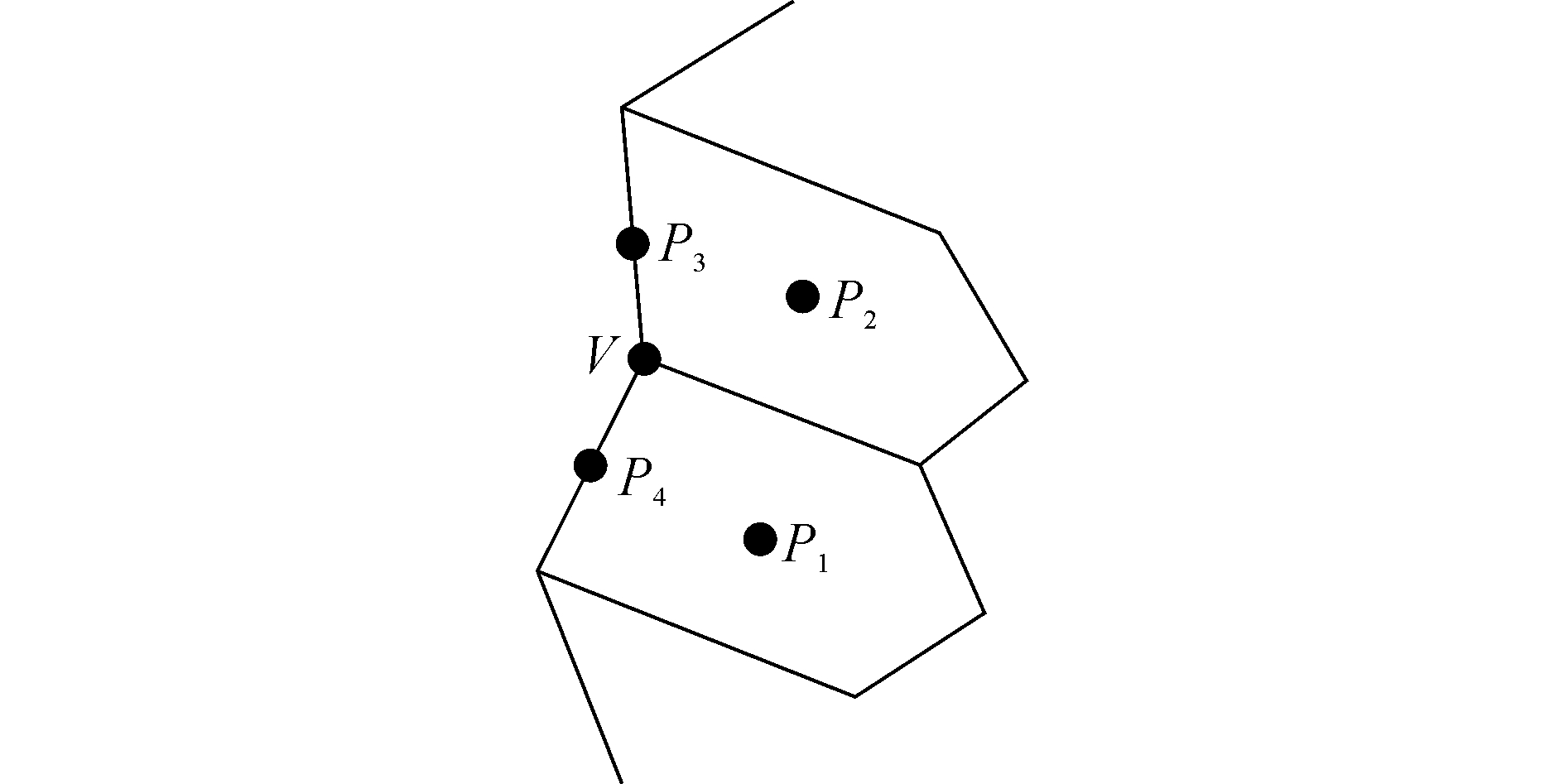
距离加权法采用每个单元中心处的变量值对单元节点进行距离加权插值,示意图如图 1所示,其计算公式如下
| $ {f_V} = \frac{{\sum\limits_{i = 1}^P {{\omega _{{P_i}}}{f_{{P_i}}}} }}{{\sum\limits_{i = 1}^P {{\omega _{{P_i}}}} }} $ | (9) |

|
Download:
|
| 图 1 距离加权插值法 Fig. 1 Inverse distance interpolation | |
式中:fV为所需要计算节点值,fPi为相邻单元中心的值,Pi为所围绕单元中心的节点数,ωPi为距离加权的函数,其表达式为
| $ {\omega _{{P_i}}} = \frac{1}{{\left| {{\mathit{\boldsymbol{r}}_V} - {\mathit{\boldsymbol{r}}_{{P_i}}}} \right|}} $ | (10) |
式中:rV表示节点V的位置矢量,rPi为所围绕节点Pi的位置矢量。
1.4.2 改进的距离加权插值法传统的距离插值法在计算边界节点V1时仅用到相邻单元中心P1和P5的节点值,当边界条件影响较大时,采用上述方法网格移动质量会很差,因此本文中对传统距离插值方法进行了改进(图 1空心节点),增加边界节点B1和B2对节点V1的影响,同时考虑单元中心节点P1、P5以及边节点B1、B2计算节点V1处的位移。
1.4.3 最小二乘插值法最小二乘法利用节点周围单元中心以及边界点Pi处的值拟合一个平面,通过使Pi在拟合平面上的近似解和其真实解余量的平方和最小,确定得到拟合平面的待定系数,进而得到所需插值节点V处的待求解变量(如图 2),设拟合平面为
| $ f\left( {x,y,z} \right) = ax + by + cz + d $ | (11) |
|
Download:
|
| 图 2 最小二乘插值法 Fig. 2 Least squares interpolation method | |
式中:x、y、z分别为笛卡尔坐标系空间坐标,a、b、c、d为待求解系数。
1.5 边界条件本文中圆盘旋转考虑第一类边界条件,在圆板周向施加Dirichlet边界:
| $ \delta {u_i} = \delta {u_{iB}} $ | (12) |
基于格心型有限体积法对空间区域进行离散,采用分离迭代求解器对两个方向分别进行求解,增量载荷迭代步收敛残差为1.0×10-16。应用Fortran语言对其进行编写求解程序,其主要流程如下:1)初始化,读入网格信息以及物性参数;2)网格移动并进行应力更新计算与结构相关的矩阵系数;3)施加增量载荷进行分离迭代求解;4)方程组达到收敛残差后进行总应力以及总位移计算;5)判断是否到达总载荷步,如果未到预设总载荷,返回到2)继续进行求解,如累加的增量载荷增量达到总载荷,输出真实应力以及总位移。总流程图如图 3所示。

|
Download:
|
| 图 3 计算大应变程序流程图 Fig. 3 Computation procedure for large strain problems | |
线动量方程最终离散为
| $ {a_P}{\phi _P} = \sum\limits_{nf} {{a_N}{\phi _N} + \mathit{\boldsymbol{R}}} $ | (13) |
式中:aP为单元中心系数,aN为相邻单元中心系数,ϕP和ϕN分别单元中心以及相邻单元中心的待解量,nf为单元周围总单元面,R为源项,式(13)中各项系数表达式为
| $ \left\{ \begin{array}{l} \phi = \delta \mathit{\boldsymbol{u}}\\ {a_P} = \frac{{{{\left( {{\rho _u}{V_u}} \right)}_p}}}{{{{\left( \mathit{\Delta t} \right)}^2}}} + \sum\limits_{f = 1}^{{n_i}} {{a_N}} \\ {a_N} = \left( {2{\mu _f} + {\lambda _f}} \right) \cdot \left( {\frac{{{\mathit{\boldsymbol{A}}_{fu}} \cdot {\mathit{\boldsymbol{A}}_{fu}}}}{{{\mathit{\boldsymbol{A}}_{fu}} \cdot {\mathit{\boldsymbol{d}}_f}}}} \right)\\ {\mathit{\boldsymbol{R}} = \sum\limits_{f = 1}^{{n_i}} {\left( {2{\mu _f} + {\lambda _f}} \right)\left( {\nabla \delta {\mathit{\boldsymbol{u}}^{t - 1}}} \right) \cdot \left( {{\mathit{\boldsymbol{A}}_{fu}} - {\mathit{\boldsymbol{d}}_f}\frac{{{\mathit{\boldsymbol{A}}_{fu}} \cdot {\mathit{\boldsymbol{A}}_{fu}}}}{{{\mathit{\boldsymbol{A}}_{fu}} \cdot {\mathit{\boldsymbol{d}}_f}}}} \right)} + }\\ \;\;\;\;\sum\limits_{f = 1}^{{n_i}} {{\mathit{\boldsymbol{A}}_{fu}} \cdot \left[ {{\mu _f}\left( {\nabla \delta {\mathit{\boldsymbol{u}}^{t - 1}}} \right)_f^{\rm{T}} + {\lambda _f}{\rm{tr}}{{\left( {\nabla \delta {\mathit{\boldsymbol{u}}^{t - 1}}} \right)}_f}\mathit{\boldsymbol{I}} - } \right.} \\ {\;\;\;\;{\left( {\mu + \lambda } \right)_f}\left( {\nabla \delta {\mathit{\boldsymbol{u}}^{t - 1}}} \right)_f^{\rm{T}} + \mu {\left( {\nabla \delta {\mathit{\boldsymbol{u}}^{t - 1}}} \right)_f} \cdot \left( {\nabla \delta {\mathit{\boldsymbol{u}}^{t - 1}}} \right)_f^{\rm{T}} + }\\ {\;\;\;\;0.5 \cdot {\lambda _f}{\left( {\nabla \delta {\mathit{\boldsymbol{u}}^{t - 1}}:\nabla \delta {\mathit{\boldsymbol{u}}^{t - 1}}} \right)_f}\mathit{\boldsymbol{I }} + }\\ \;\;\;\;\left. {\left( {\mathit{\boldsymbol{S}}_{fu}^{t - 1} + \delta \mathit{\boldsymbol{S}}_{fu}^{t - 1}} \right) \cdot {{\left( {\delta \mathit{\boldsymbol{F}}_{fu}^T} \right)}^{t - 1}}} \right] \end{array} \right. $ | (14) |
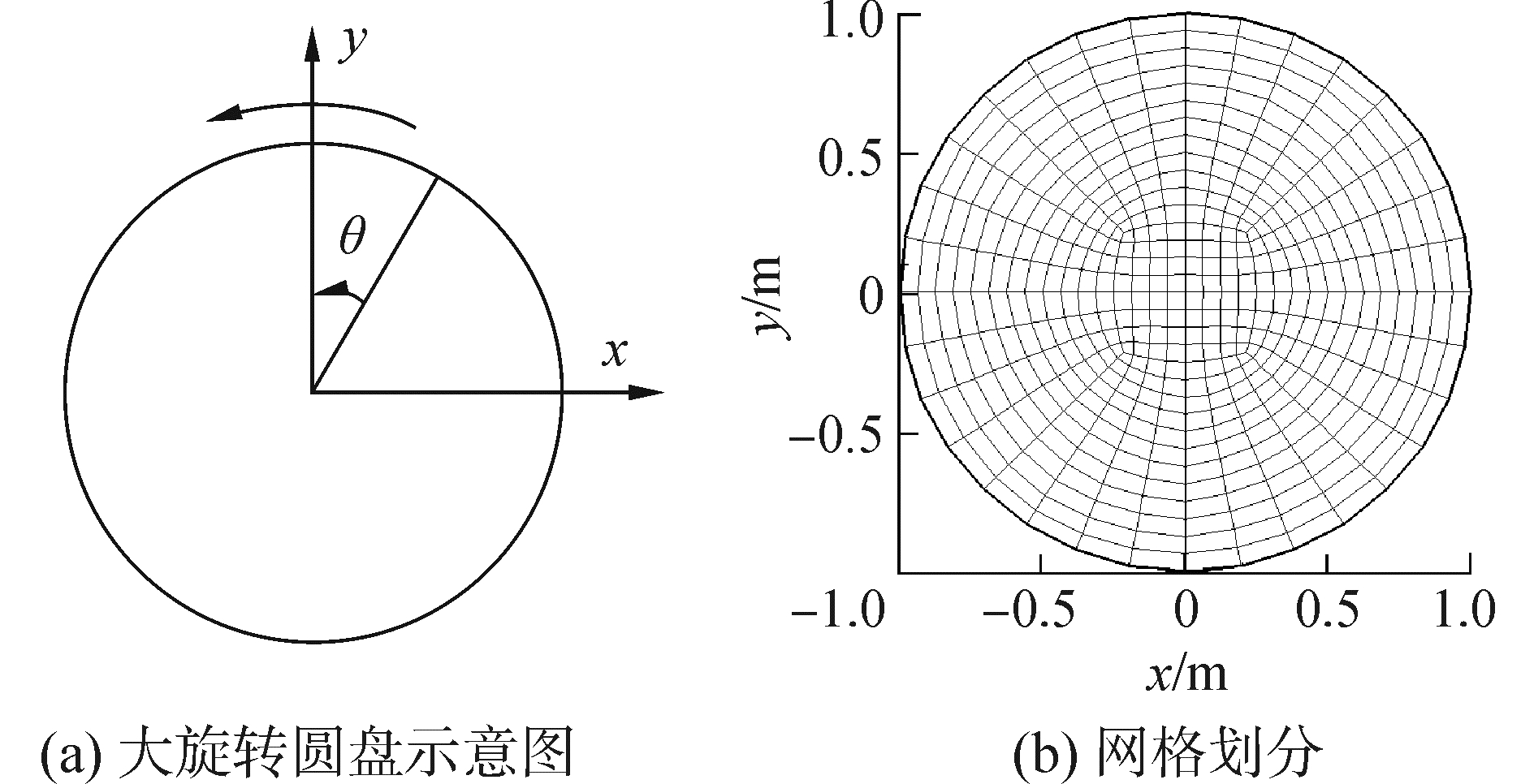
为了验证不同网格移动算法以及梯度算法对圆盘大旋转问题的影响,计算了圆盘在不同增量位移载荷下的应力分布。圆盘半径r=1 m,杨氏模量E=210 GPa,泊松比υ=0.3。采用448个非正交四边形单元对圆盘进行网格划分。几何模型及其网格如图 4所示。
|
Download:
|
| 图 4 大旋转圆盘示意图以及网格划分 Fig. 4 Sketch up of large rotating disk and mesh | |
圆盘外周施加位移边界条件。在笛卡尔坐标系下,其位移增量的表达式为
| $ \left\{ \begin{array}{l} \delta {u_x} = \cos \theta \cdot x + \sin \theta \cdot y - x\\ \delta {u_y} = \sin \theta \cdot x - \cos \theta \cdot y - y \end{array} \right. $ | (15) |
式中:x和y为边界面中心的位置矢量,θ为边界中心的旋转角度。
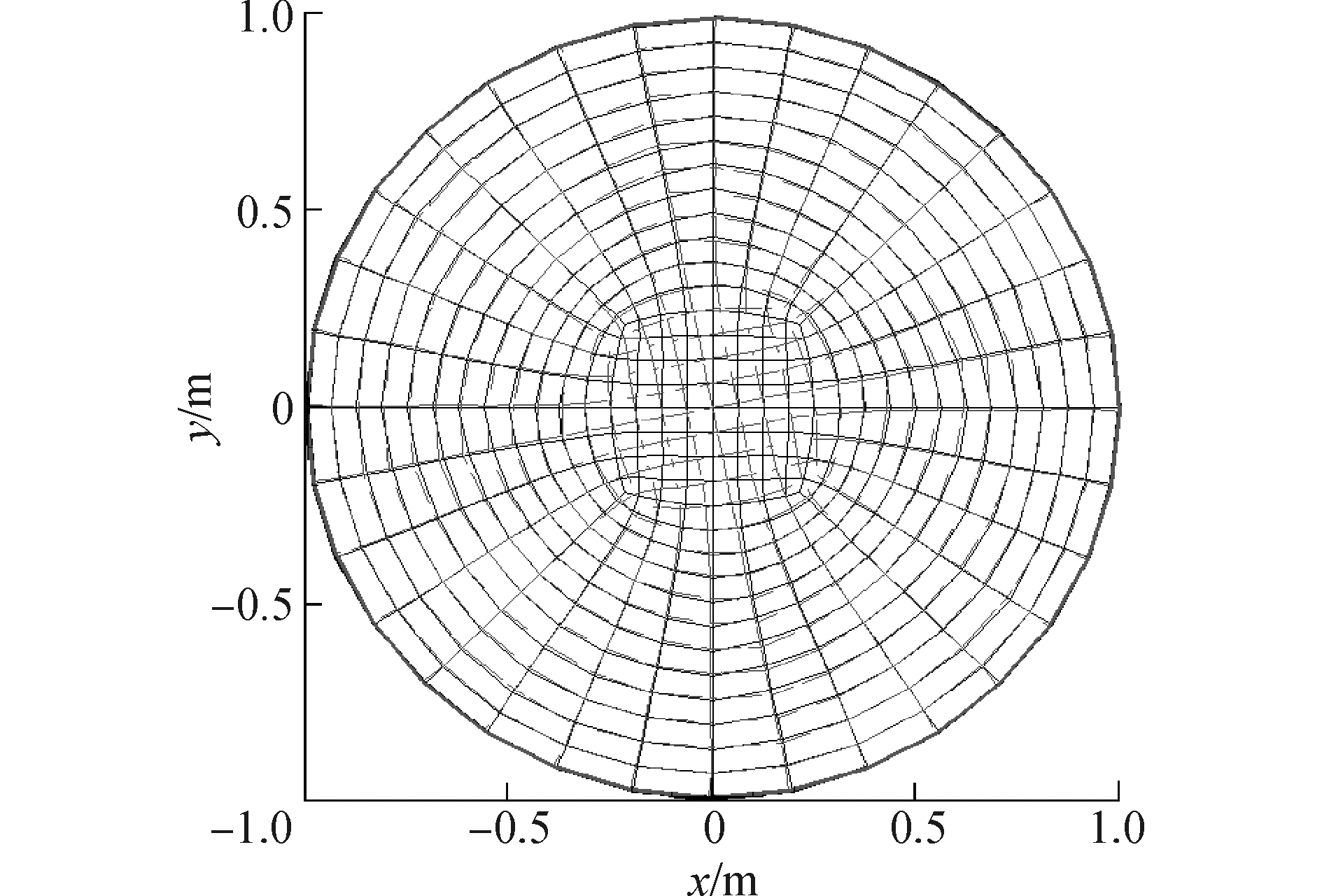
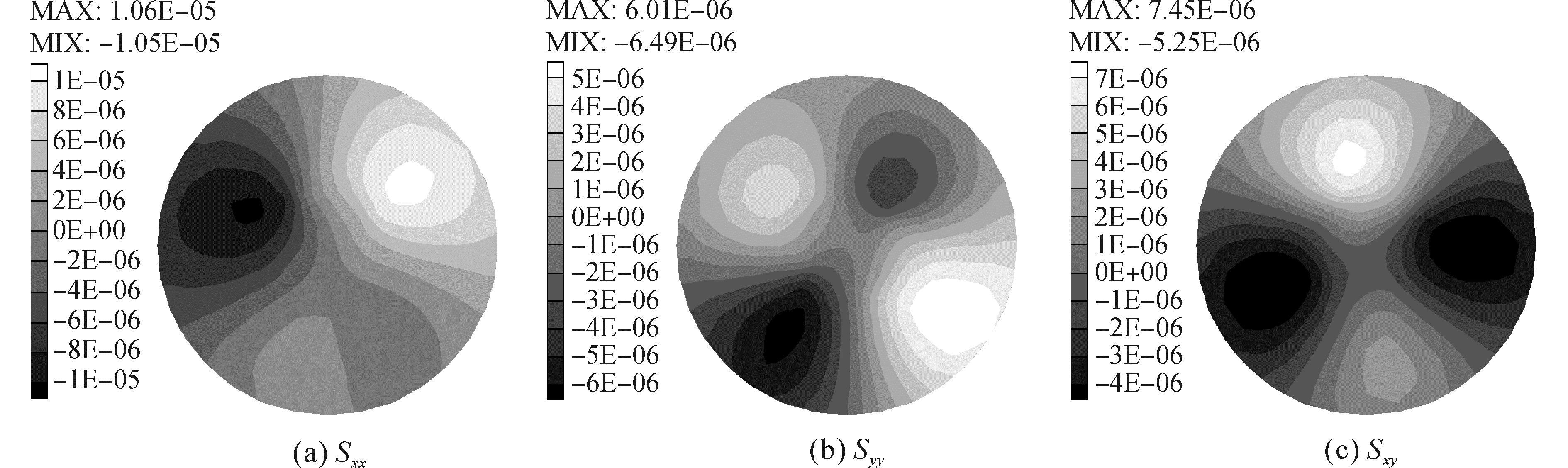
3.1 不同网格移动插值方法对圆盘旋转的影响圆盘在准静态刚体旋转时,其内部的应力分布为0。对比最小二乘法和改进的距离加权插值法对圆盘内部应力以及网格移动的影响。上述两种网格移动方法均采用最小二乘梯度算法计算单元中心梯度,旋转圆盘的增量角度为θ=11.25°。1个载荷步下,采用最小二乘法的网格移动示意图如图 5所示。从图中可以看出,应用最小二乘法的网格移动在网格边界有较好的插值解,在1个载荷步后,移动后的网格在边界上可以很好的和初始网格吻合,圆盘内应力分布与预期的一样,几乎为0(如图 6)。
|
Download:
|
| 图 5 应用最小二乘法插值网格移动 Fig. 5 Mesh movement using least squares interpolation | |
|
Download:
|
| 图 6 采用最小二乘法圆盘应力分布 Fig. 6 True stress distributions based on least square method | |
图 7为网格移动采用距离加权插值法圆盘内应力分布,圆盘内应力分布与预期的一样,几乎为0。

|
Download:
|
| 图 7 采用距离加权法圆盘应力分布 Fig. 7 True stress distributions based on inverse distance interpolation method | |
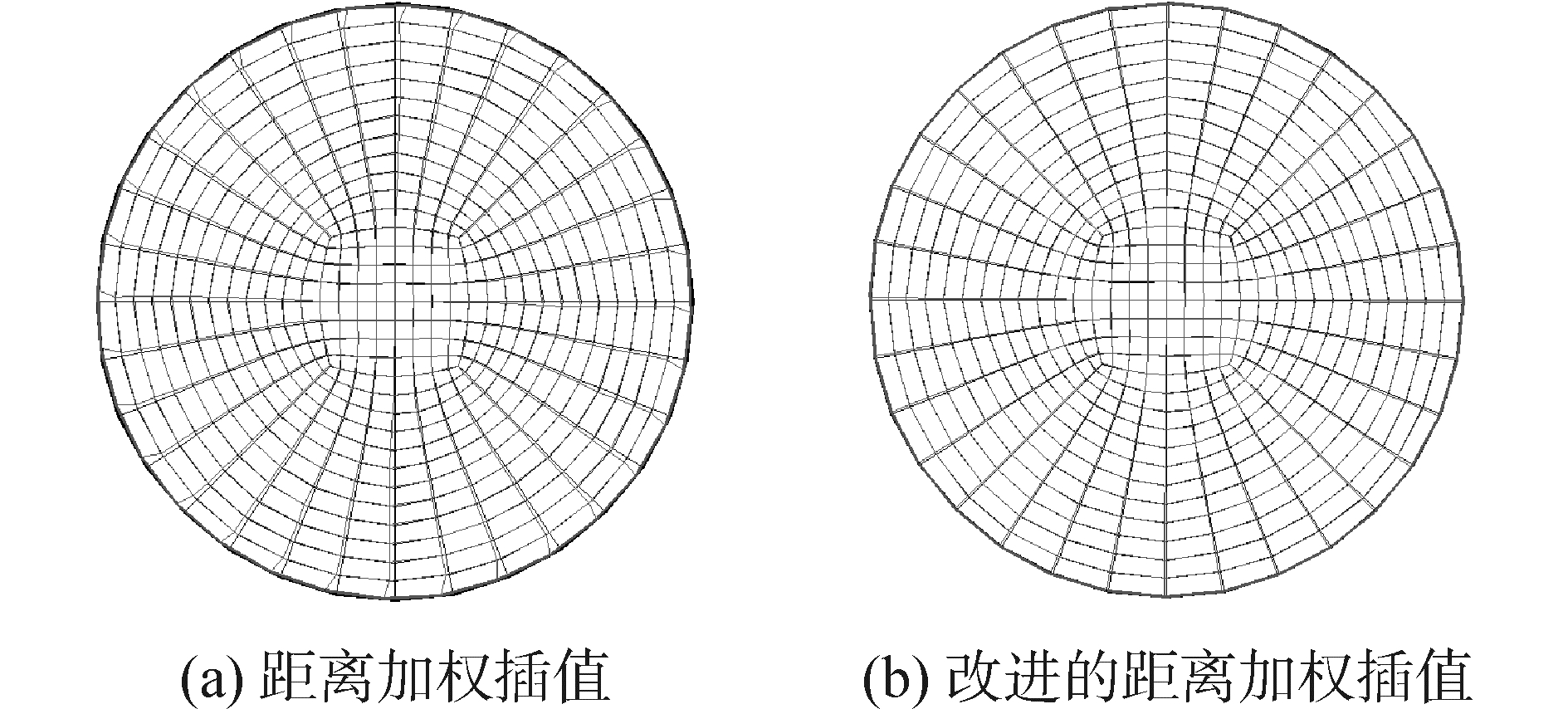
虽然采用距离加权法也可以正确求解圆盘大旋转问题,但其采用的网格移动方法在其边界上会产生不理想的位移偏差,如图 8(a)所示,在1个载荷步下,应用传统距离加权插值法边界网格最大位移误差约为0.008。当圆盘旋转8个载荷步后,由于每一步网格移动误差的积累,网格在边界上将会出现严重的扭曲,如图 9(a)所示。采用改进的距离加权插值法进行网格移动,通过考虑边界的中点对网格节点的影响,可以有效的减小由于插值所带来的误差,1个载荷步边界位移的误差约为0.001,如图 8(b)所示,同时在圆盘旋转8个载荷步后,仍可以很好的预测网格移动(图 9(b))。

|
Download:
|
| 图 8 1载荷步距离加权插值及改进的距离加权插值网格移动 Fig. 8 Mesh movement using traditional and advanced inverse distance interpolation after 1 load step | |
|
Download:
|
| 图 9 8载荷步距离加权插值及改进的距离加权插值网格移动 Fig. 9 Mesh movement using traditional and advanced inverse distance interpolation after 8 load steps | |
采用上述参数以及载荷增量对大圆盘旋转问题进行求解,单元中心梯度由Gauss算法进行计算,计算结果如图 10所示,通过与采用最小二乘法求解单元中心梯度结果的对比(图 6),采用Gauss法求解单元中心梯度时会导致严重错误的应力分布,同时易导致程序发散。单元中心的梯度算法对非线性大旋转问题影响较大,应选择更高精度的最小二乘法进行单元梯度的计算。

|
Download:
|
| 图 10 应用高斯法计算单元中心梯度圆盘应力分布 Fig. 10 Results of the rotating disk using Gauss method to calculate the cell central gradient | |
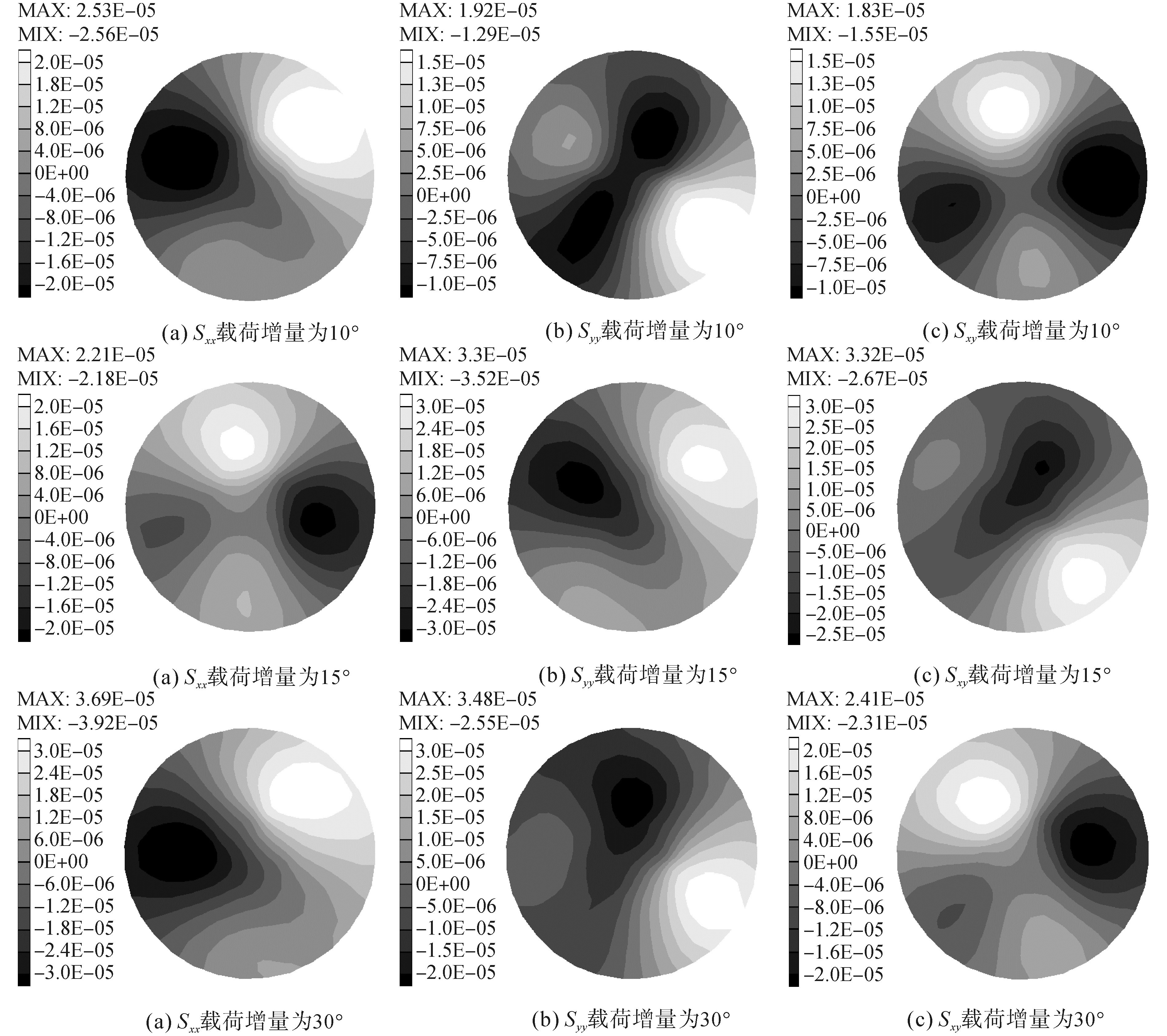
为研究增量载荷大小对大旋转问题的影响,分别对载荷增量为10°、15°、30°进行应力对比。采用改进的距离加权插值法进行网格移动,单元中心梯度应用最小二乘梯度法进行计算,总旋转角度为90°。计算结果如图 11所示,从图中可以看出在30°增量载荷下,采用大应变有限体积法仍可以得到较好的数值解。同时,采用该方法对40°的增量载荷进行了计算,计算结果发散,其原因为在大增量梯度下待解方程非线性项的影响远远大于线性项,导致矩阵病态。
|
Download:
|
| 图 11 不同增量载荷应力分布对比 Fig. 11 Comparisons of the true stress under different increment sizes | |
图 12为不同增量载荷下应用小应变理论求解大旋转问题应力分布示意图。从图中可以看出圆盘内正应力σx随着增量载荷的增加而逐步增大。结果表明即使在很小的载荷增量下,采用小应变理论仍会产生错误的应力分布。

|
Download:
|
| 图 12 小应变理论求解大旋转问题 Fig. 12 Results of the rotating disk using small theory | |
1) 采用传统距离加权插值法的网格移动质量最差,当构形移动较大时,优先采用最小二乘法或改进的距离加权法。
2) 大旋转问题对单元中心梯度的计算精度要求较高,采用Gauss梯度算法会产生不合理的应力分布,应选择具有更高精度的最小二乘梯度算法。
3) 应用小应变理论求解大旋转问题时,在很小的增量载荷下,仍会产生错误的应力分布,而LS-FVM在较大的载荷增量步下仍可以得到较好的收敛解,但载荷不宜过大,过大的增量载荷会导致病态矩阵的出现,导致发散。
| [1] |
JASAK H, WELLER H G. Application of the finite volume method and unstructured meshes to linear elasticity[J]. International journal for numerical methods in engineering, 1998, 48(2): 267-287. (  0) 0)
|
| [2] |
FRYER Y D, BAILEY C, CROSS M, et al. A control volume procedure for solving the elastic stress-strain equations on an unstructured mesh[J]. Applied mathematical modelling, 1991, 15(11/12): 639-645. (  0) 0)
|
| [3] |
WHEEL M A. A geometrically versatile finite volume formulation for plane elastostatic stress analysis[J]. The journal of strain analysis for engineering design, 1996, 31(2): 111-116. DOI:10.1243/03093247V312111 (  0) 0)
|
| [4] |
WHEEL M A. A finite volume method for analysing the bending deformation of thick and thin plates[J]. Computer methods in applied mechanics and engineering, 1997, 147(1/2): 199-208. (  0) 0)
|
| [5] |
DEMIRDŽIĆ I, MARTINOVIĆ D. Finite volume method for thermo-elasto-plastic stress analysis[J]. Computer methods in applied mechanics and engineering, 1993, 109(3/4): 331-349. (  0) 0)
|
| [6] |
DEMIRDŽIĆ I, DŽAFEROVIĆ E, IVANKOVIĆ A. Finite-volume approach to the rmoviscoelasticity[J]. Numerical heat transfer part B fundamentals, 2005, 47(3): 213-237. DOI:10.1080/10407790590901675 (  0) 0)
|
| [7] |
IVANKOVIC A, DEMIRDZIC I, WILLIAMS J G, et al. Application of the finite volume method to the analysis of dynamic fracture problems[J]. International journal of fracture, 1994, 66(4): 357-371. DOI:10.1007/BF00018439 (  0) 0)
|
| [8] |
FALLAH N A, BAILEY C, CROSS M, et al. Comparison of finite element and finite volume methods application in geometrically nonlinear stress analysis[J]. Applied mathematical modelling, 2000, 24(7): 439-455. DOI:10.1016/S0307-904X(99)00047-5 (  0) 0)
|
| [9] |
BIJELONJA I, DEMIRDŽIĆ I, MUZAFERIJA S. A finite volume method for large strain analysis of incompressible hyperelastic materials[J]. International journal for numerical methods in engineering, 2005, 64(12): 1594-1609. DOI:10.1002/(ISSN)1097-0207 (  0) 0)
|
| [10] |
BIJELONJA I, DEMIRDŽIĆ I, MUZAFERIJA S. A finite volume method for incompressible linear elasticity[J]. Computer methods in applied mechanics and engineering, 2006, 195(44/45/46/47): 6378-6390. (  0) 0)
|
| [11] |
BIJELONJA I. A numerical method for almost incompressible body problem[C]//Annals of DAAAM for 2011 & Proceedings of the 22nd International DAAAM Symposium. Vienna, Austria, 2011.
(  0) 0)
|
| [12] |
TUKOVIĆ Ž, JASAK H. Updated Lagrangian finite volume solver for large deformation dynamic response of elastic body[J]. Transactions of FAMENA, 2007, 31(1): 55-70. (  0) 0)
|
| [13] |
GONG Jingfeng, XUAN Lingkuan, MING Pingjian, et al. An unstructured finite-volume method for transient heat conduction analysis of multilayer functionally graded materials with mixed grids[J]. Numerical heat transfer, part B:fundamentals, 2013, 63(3): 222-247. DOI:10.1080/10407790.2013.751251 (  0) 0)
|
| [14] |
CARDIFF P, KARAC A, IVANKDVI'C A. A large strain finite volume method for orthotropic bodies with general material orientations[J]. Computer methods in applied mechanics & Engineering, 2014, 268: 318-335. (  0) 0)
|
| [15] |
CARDIFF P. Development of the finite volume method for hip joint stress analysis[D]. Dublin: University College Dublin, 2012: 28-71.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


