钢筋混凝土圆柱因强度高、造价低、施工方便和整体性好等优点在土木工程中应用广泛。但钢筋混凝土构件在桥梁、港口和化工厂等侵蚀环境中使用时,结构性能因钢筋锈蚀而降低,关键部位钢筋混凝土构件的失效甚至会引起整个结构的倒塌。
纤维增强复合材料(fiber rein-forced polymer, FRP)筋密度为钢筋密度1/5~1/4,抗拉强度高于普通钢筋的屈服强度,轻质高强且具有绝缘、耐腐蚀等优点,在建筑领域逐渐成为一种可以替代钢筋的材料。但是FRP筋材料为线弹性,在破坏前无屈服阶段,因此在混凝土中加入聚乙烯醇(polyvinyl alcohol, PVA)纤维,可以克服混凝土脆性大的缺点和弥补FRP筋线弹性的不足,从而提高FRP筋混凝土构件的延性[1]。近年来,众多学者对FRP筋混凝土梁的抗弯性能及FRP筋混凝土柱的受压性能进行了研究[2-8],但关于GFRP筋纤维混凝土柱受压性能的研究鲜见报道,我国规程[9]仅对FRP筋受弯构件作了相应规定。本文对GFRP筋纤维混凝土圆柱进行轴压试验,了解其受力过程,分析其破坏机理,研究配筋种类、纵筋配筋率、箍筋间距和箍筋直径对其受力性能的影响,提出适合于GFRP筋纤维混凝土柱的轴压承载力计算公式和本构模型。
1 轴压试验概述 1.1 试件的设计与制作9个试件高度为1 300 mm、直径为400 mm、保护层厚度为25 mm。试件以配筋种类、纵筋配筋率、箍筋间距及箍筋直径为变化参数,见表 1。
| 表 1 试件参数 Tab.1 Details of specimens |
绑扎后的试件见图 1,所有试件均采用连续箍筋,无搭接。试件在上下两端250 mm范围内箍筋加密,防止试件两端局部受压提前破坏。试验所用模板为内径400 mm的钢管,试件均为垂直浇筑,自然养护28 d。

|
Download:
|
| 图 1 绑扎后的GFRP筋及钢筋笼 Fig. 1 Photos of the assembled GFRP and steel cages | |
钢筋和GFRP筋基本参数见表 2。钢筋纵筋为HRB400钢筋,箍筋为HPB300钢筋。GFRP筋材质均为无碱玻璃纤维增强乙烯基酯树脂,纤维含量80%,GFRP筋由南京峰晖复合材料有限公司制造。
| 表 2 钢筋和GFRP筋基本参数 Tab.2 Parameters of steel bars and GFRP bars |
混凝土含水泥、水、沙、石、矿粉、粉煤灰、减水剂和纤维的质量分别是453、178、730、943、64、64、4.1和3 g/m3。材料组成为:P·O42.5R普通硅酸盐水泥、中砂(细度模数2.3)、碎石(连续级配)、减水剂(减水率大于30%)。纤维为PVA纤维,直径20 μm,长度10 mm,抗拉强度1 600 MPa。
每批试件制备6个150 mm×150 mm×300 mm的混凝土棱柱体试块,抗压强度fcp和弹性模量Ec均根据标准试验方法[10]测定。结果如表 3所示。
| 表 3 试验结果 Tab.3 Test results |
在钢筋和GFRP筋骨架上,沿周边等间距选取三根纵筋,并在其1/2高度处布置纵筋应变片。在钢筋和GFRP筋骨架1/2高度处的箍筋上,等间距布置四个箍筋应变片。在混凝土柱外表面的1/2高度处,分别等间距布置四个纵向和四个横向混凝土应变片。
为保证试件受力均匀,加载前分别在试件顶部和底部铺一层细石英砂,并预压至40 kN。预压过程中,观察四个纵筋和四个混凝土竖向应变片读数,若各读数与平均值之差不大于平均值5%,认为试件处于轴心受压状态,可正式对试件加载,否则重新调整试件位置,直到试件满足轴心受压的条件。
试验加载首先采用力控制,加载速度为150 kN/min,当力达到预估峰值荷载的80%时改用位移控制,加载速度为0.12 mm/min。当荷载下降至峰值荷载的70%或总竖向位移达到30 mm时,停止加载。加载仪器为20 000 kN长柱微机控制电液伺服压力试验机如图 2所示。

|
Download:
|
| 图 2 试验加载装置 Fig. 2 Test set-up | |
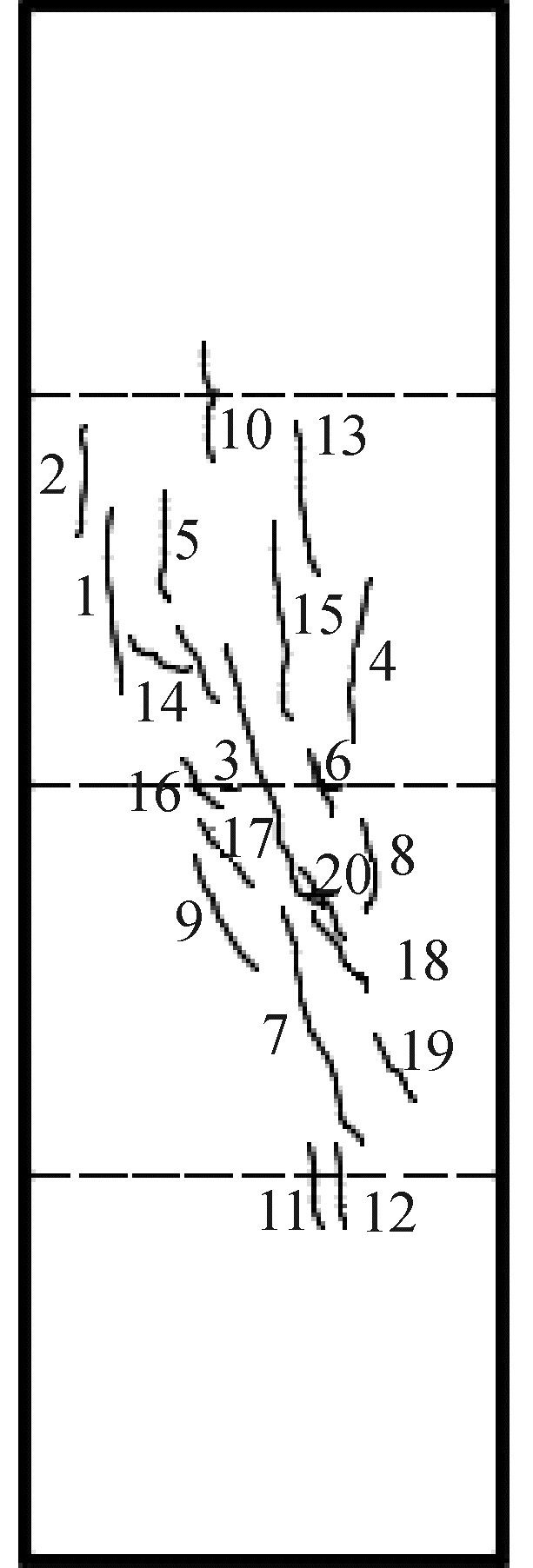
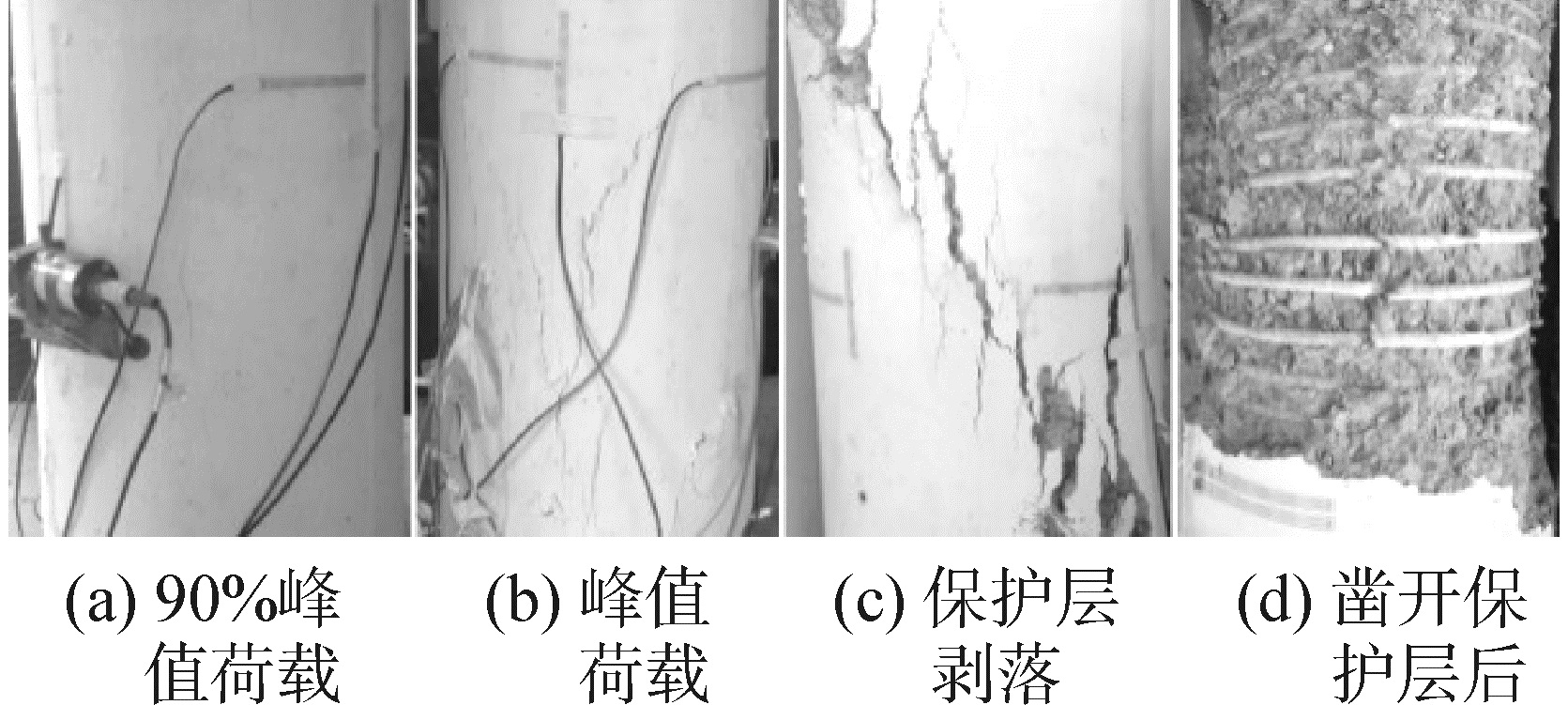
GFRP筋纤维混凝土柱裂纹发展情况见图 3,试件破坏后的形态如图 4所示,试件(G6V-12H73)在不同受力阶段的开裂情况如图 5所示。未配筋纤维混凝土柱加载初期混凝土轴向应变和环向应变较小,试件处于弹性阶段。当加载至峰值荷载的80%左右时,有轻微的混凝土开裂声,试件中部出现第一条竖向裂缝;达到峰值荷载后,裂缝宽度突然增大,荷载迅速下降。试件破坏时,裂缝数量较少,宽度较大,因无箍筋的约束作用,峰后破坏过程较快,呈脆性破坏,但试件的完整性较好,体现了纤维的桥联作用。
|
Download:
|
| 图 3 裂纹发展情况分布 Fig. 3 Distribution of crack development | |

|
Download:
|
| 图 4 试件破坏后的形态 Fig. 4 Overview of the test specimens after failure | |
|
Download:
|
| 图 5 试件在不同阶段的开裂情况(G6V-12H73) Fig. 5 Cracking appearance of test specimens at different loading stages(G6V-12H73) | |
配筋混凝土柱加载初期的变形与未配筋混凝土柱相似,混凝土轴向应变和环向应变较小,箍筋应变较小,约束作用尚未被激活,试件处于弹性阶段。当加载至峰值荷载73%~88%时,听到轻微的混凝土开裂声,试件中部出现微裂缝,随着荷载增加,微裂缝数量增多,宽度增大。峰值荷载后,裂缝加宽速度变大,混凝土轴向应变和环向应变增加,箍筋约束作用被激活。试件破坏时均表现出一定延性,试件破坏后没有严重的保护层剥落现象,体现了纤维的桥联作用。
与GFRP筋PVA纤维混凝土柱相比,未加纤维的GFRP筋混凝土柱[13],裂缝开展速度较快,且试件破坏时,裂缝数量少,宽度大。试件破坏后,保护层剥落严重。
2.2 试验数据及分析试验结果如表 3所示,Pmax为峰值荷载,kN;εspiral、εbar、εch和εcc分别为峰值荷载时箍筋应变、纵筋应变、混凝土环向应变和混凝土轴向应变,με;fco为未约束纤维混凝土强度,MPa;fcc为GFRP筋约束纤维混凝土强度,MPa。
混凝土轴向应力计算式为
| $ \sigma \left( {P - {P_{{\rm{bar}}}}} \right)/A $ | (1) |
式中:σ为混凝土轴向应力, MPa; P为加载过程中试件承受的荷载,kN;Pbar为加载过程中纵筋承受的荷载,kN;Pbar=εbEbAfrp;εb为纵筋应变,με;Eb为纵筋弹性模量,MPa;Afrp为GFRP纵筋截面面积,mm2; A为混凝土受力面积,mm2。
图 6中曲线OABC和ODEF为计算的混凝土轴向应力-轴向应变曲线,曲线OAEF为实际加载过程中的混凝土轴向应力-轴向应变曲线。

|
Download:
|
| 图 6 混凝土应力-应变曲线计算方法(G6V-12H73) Fig. 6 Calculation method of concrete stress-strain curves of specimens | |
曲线OABC和ODEF中混凝土轴向应力均按式(1)计算,面积分别取混凝土全截面面积和混凝土核心面积。加载过程中,混凝土保护层开裂前(开裂荷载为峰值荷载的80%左右),混凝土轴向应力-轴向应变曲线取OA段;混凝土保护层剥落后,混凝土轴向应力-轴向应变曲线取EF段。点A与点E之间光滑过渡,OA、AE和EF三段结合形成整个加载过程中的混凝土轴向应力-轴向应变曲线。
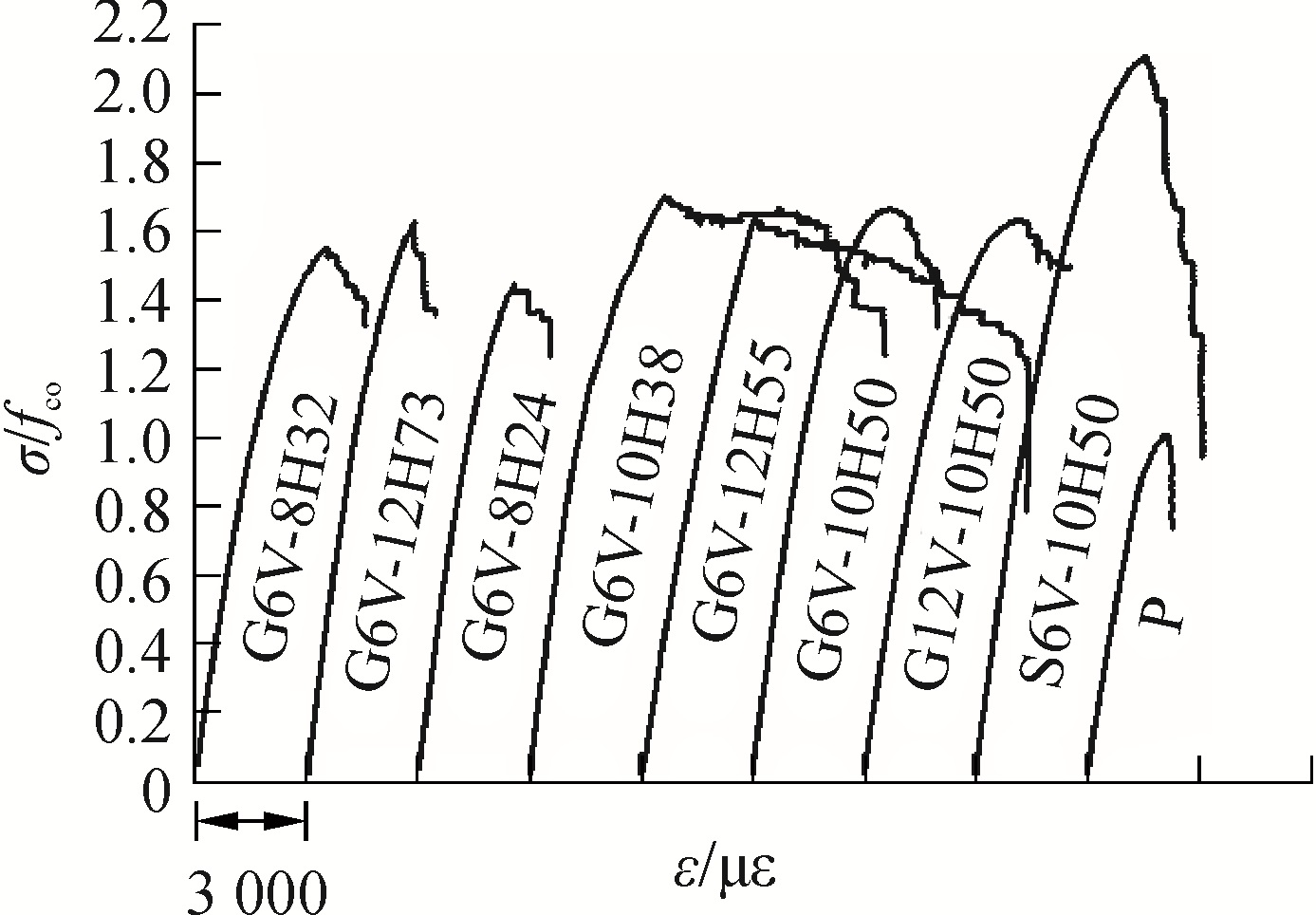
混凝土轴向标准化应力-轴向应变曲线见图 7。将混凝土轴向应力除以各自未约束混凝土强度,得到混凝土轴向标准化应力。
|
Download:
|
| 图 7 混凝土轴向标准化应力-轴向应变曲线 Fig. 7 Concrete normalized axial stress- axial strain curves | |
试件S6V-10H50峰值荷载时,钢筋纵筋承担的力占总承载力的8.23%,而钢筋普通混凝土柱中钢筋纵筋承担的力占总承载力的15%[13],说明混凝土中掺入纤维,延缓了混凝土保护层的开裂,增加了试件中混凝土承担的轴力。
试件G12 V-10H50在峰值荷载时的环向应变和轴向应变分别比试件P高348.76%和37.29%。其他GFRP筋纤维混凝土柱在峰值荷载时的混凝土环向应变平均值为1 801.41 με,比试件P高311.72%;轴向应变平均值为2 520.83 με,比试件P高14.84%;GFRP筋试件中混凝土轴向应变接近GFRP纵筋应变,说明混凝土与GFRP纵筋粘结良好,变形协调。试件破坏后,凿开保护层,观察到GFRP筋纤维混凝土柱基本因箍筋拉断而破坏,钢筋纤维混凝土柱因箍筋屈曲而破坏。
2.3 受力性能的影响因素 2.3.1 配筋种类试件G6V-10H50和S6V-10H50配筋种类不同,试件G6V-10H50的承载力、核心混凝土强度提高系数和延性系数分别为试件S6V-10H50的0.81、0.79和0.94倍。可见在提高承载力和核心混凝土强度方面,GFRP筋不及钢筋,但在提高延性方面,GFRP筋与钢筋接近。
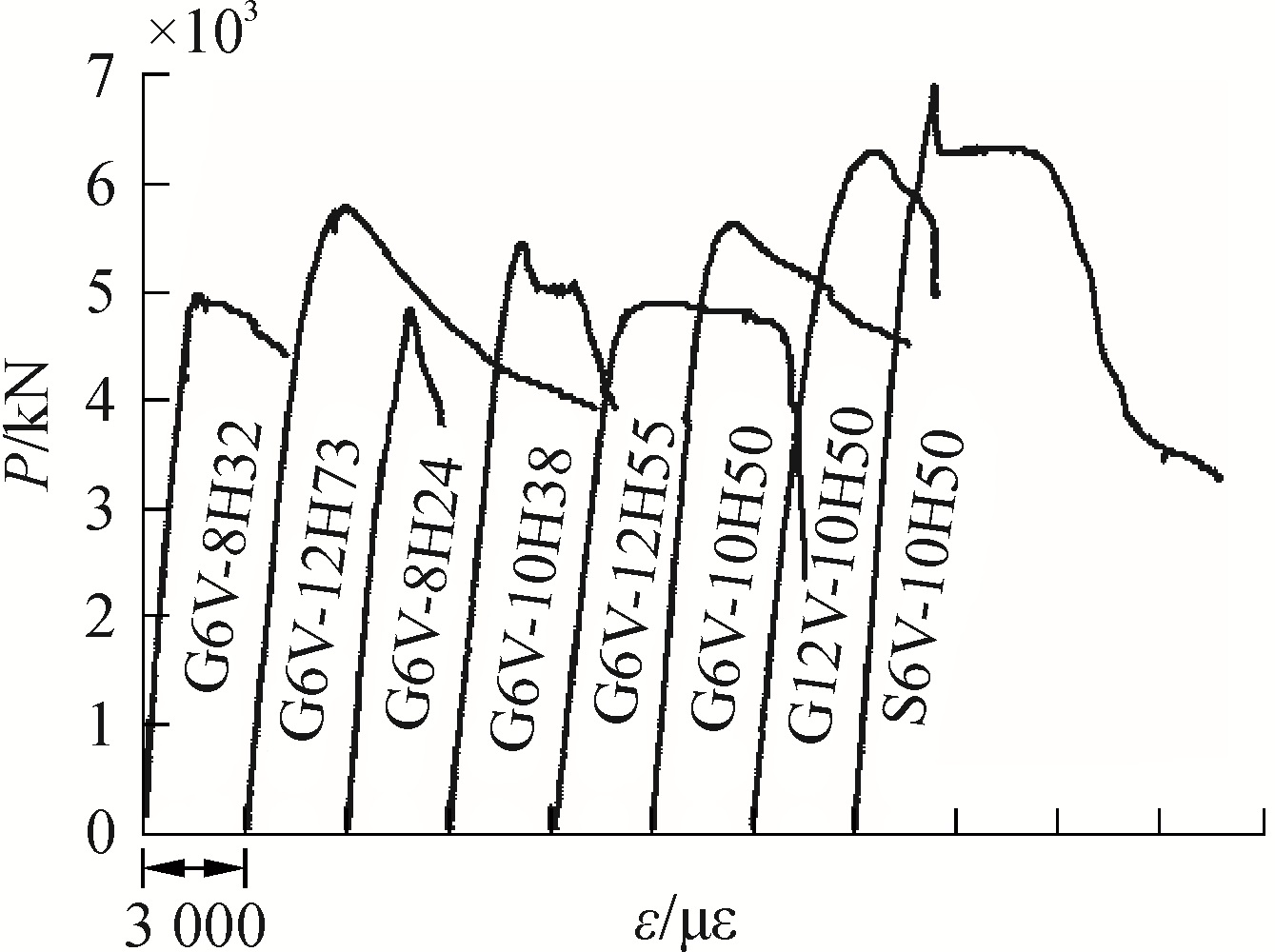
峰值荷载时,GFRP纵筋和钢筋纵筋承受的力分别占试件承载力的2.15%和8.23%,因为GFRP筋的弹性模量小于钢筋的弹性模量,所以GFRP纵筋承担的力较小。试件G6V-10H50纵筋峰值应变为限应变的29.65%;试件S6V-10H50纵筋峰值应变为极限应变的21.00%。由图 8可见,GFRP纵筋和钢筋纵筋在峰后阶段都能发生较大变形,说明两种纵筋在峰后阶段都能充分发挥作用,继续承担轴力。
|
Download:
|
| 图 8 轴力-纵筋应变曲线 Fig. 8 Load-longitudinal bar strain curves | |
试件G6V-10H50和G12 V-10H50纵筋配筋率分别为0.96%和1.92%。试件G6V-10H50的承载力、核心混凝土强度提高系数和延性系数分别为试件G12 V-10H50的0.90、1.02和1.00倍。可见提高纵筋配筋率能显著提高试件承载力,但是提高纵筋配筋率对核心混凝土强度及试件延性的影响不明显。
2.3.3 箍筋间距试件G6V-12H73和G6V-12H55,当箍筋间距由73 mm减小到55 mm时,箍筋峰值应变增加210.97%,核心混凝土强度提高系数增加0.61%,延性系数增加68.40%,混凝土轴向标准化应力-轴向应变曲线峰后下降段变平缓(见图 7)。说明当箍筋间距适当时,随着箍筋间距减小,箍筋约束作用增大,试件延性显著提高,但核心混凝土强度提高系数几乎不变。
试件G6V-10H50和G6V-10H38,当箍筋间距由50 mm减小到38 mm时,箍筋的峰值应变没有增加,反而降低41.07%,是因为较小的箍筋间距有效的限制了混凝土的开裂,约束了核心混凝土的膨胀,从而箍筋的变形较小。试件G6V-10H38与试件G6V-10H50相比,核心混凝土强度提高系数增加1.78%,延性系数增加96.90%,混凝土轴向标准化应力-轴向应变曲线峰后下降段变平缓(见图 7)。说明当箍筋间距适当时,随着箍筋间距减小,试件延性显著提高,但核心混凝土强度提高系数几乎不变,结论与第一组试件一致。
试件G6V-8H32和G6V-8H24,当箍筋间距由32 mm减小到24 mm时,箍筋峰值应变降低51.47%,核心混凝土强度提高系数降低7.64%,延性系数降低6.00%,混凝土轴向标准化应力-轴向应变曲线峰后下降段变陡(见图 7)。说明箍筋间距小于32 mm时,随着箍筋间距减小,核心混凝土强度提高系数及延性均降低。因为过小的箍筋间距既降低了混凝土保护层和核心混凝间的粘结,又降低了箍筋上下两侧混凝土间的粘结,导致混凝土过早开裂,试件受力性能变差。
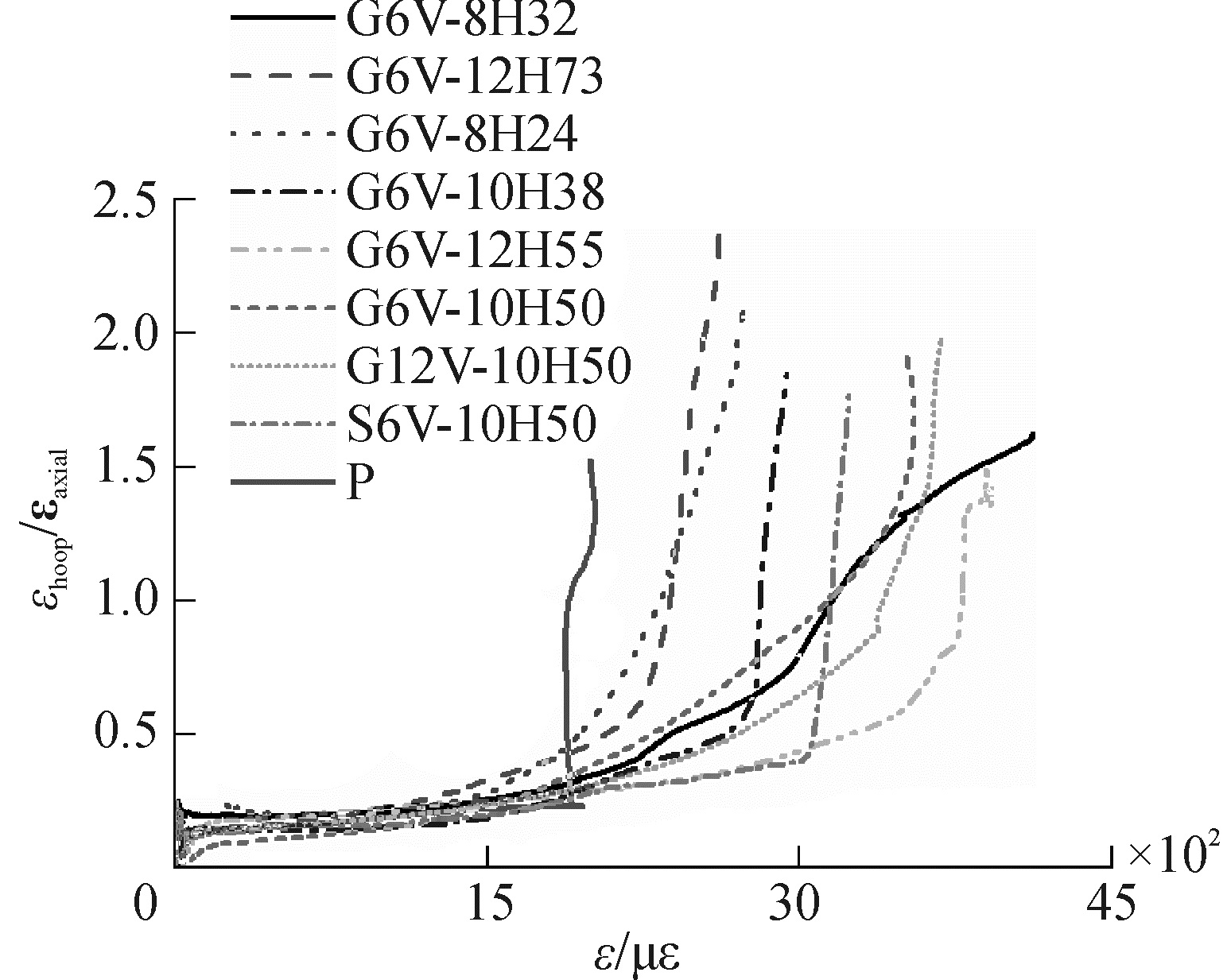
混凝土膨胀率(混凝土环向应变/轴向应变)-轴向应变曲线见图 9,试件加载初期,曲线基本为水平直线,试件处于弹性阶段,膨胀率为0.2左右。随试件参数不同,各试件在膨胀率为0.5~0.8时进入不稳定裂缝发展阶段,此后曲线斜率急剧增加,曲线基本为竖直直线。试件P、G6V-12H73和G6V-8H24混凝土膨胀率骤增时,轴向应变较小,说明未配筋、箍筋间距过大或过小都会导致试件过早破坏。因为箍筋间距过小削弱了混凝土的整体性,箍筋间距过大则不能对核心混凝土提供足够约束以延缓裂缝开展。
|
Download:
|
| 图 9 体积膨胀率-轴向应变关系 Fig. 9 Dilation-axial strain of specimens | |
试件G6V-8H32、G6V-10H50和G6V-12H73配箍率为1.90%,箍筋直径分别为8、10和12 mm,峰值荷载时箍筋应变分别为1 063.38、1 364.13和957.11 με,核心混凝土强度提高系数分别为1.55、1.66和1.62,延性系数分别为2.30、2.29和1.64。说明配箍率相同时,随着箍筋直径增大,试件延性系数明显降低,核心混凝土强度提高系数变化不明显。
试件G6V-8H24、G6V-10H38和G6V-12H55配箍率为2.50%,箍筋直径分别为8、10和12 mm,峰值荷载时箍筋应变分别为516.11、803.90和2 976.34 με,核心混凝土强度提高系数分别为1.44、1.69和1.63,延性系数分别为2.17、4.51和5.19。试件G6V-8H24间距过小,受力性能较差。试件G6V-10H38的强度提高系数及延性系数高于试件G6V-12H55,说明箍筋间距适当时,保持配箍率不变,随箍筋直径增大,试件延性系数明显降低,强度提高系数变化不明显,结论与第一组试件一致。
3 承载力计算公式试验结果表明:峰值荷载时,GFRP箍筋变形较小,对混凝土的约束作用较弱。以往理论研究及工程设计中均未考虑箍筋对承载力的提高作用,普遍采用文献[14-15]中FRP筋约束普通混凝土柱的承载力计算公式如下
| $ {P_{\rm{o}}} = 0.85{{f'}_{\rm{c}}}\left( {{A_{\rm{g}}} - {A_{{\rm{frp}}}}} \right) + 0.35{f_{{\rm{frp}}}}{A_{{\rm{frp}}}} $ | (2) |
| $ {P_{\rm{o}}} = 0.85{{f'}_{\rm{c}}}\left( {{A_{\rm{g}}} - {A_{{\rm{frp}}}}} \right) + {\varepsilon _{{\rm{cc}}}}{E_{{\rm{frp}}}}{A_{{\rm{frp}}}} $ | (3) |
式中:f′c为混凝土圆柱体轴心抗压强度,MPa;Ag为试件全截面面积,mm2;Afrp为GFRP纵筋截面面积,mm2;ffrp为GFRP纵筋抗拉强度,MPa;εcc为峰值荷载时混凝土轴向应变,με;Efrp为GFRP纵筋弹性模量,MPa;0.85为考虑构件中混凝土强度与混凝土试块强度差异采用的折减系数[16],0.35为GFRP纵筋抗压强度与抗拉强度的比值。
本文中不考虑箍筋对承载力的提高作用,承载力由纤维混凝土和GFRP纵筋两部分组成:
| $ {P_{\rm{o}}} = 0.89{f_{{\rm{cp}}}}\left( {{A_{\rm{g}}} - {A_{{\rm{frp}}}}} \right) + {{f'}_{{\rm{frp}}}}{A_{{\rm{frp}}}} $ | (4) |
式中:fcp为混凝土棱柱体轴心抗压强度,MPa;f′frp为GFRP筋抗压强度实测值,MPa,见表 2;0.89为考虑构件中混凝土强度与混凝土棱柱体轴心抗压强度差异采用的折减系数,参照本试验未配筋柱中混凝土强度与混凝土棱柱体轴心抗压强度之间的关系确定。
承载力试验值与计算值之比Pmax/Po,见图 10。

|
Download:
|
| 图 10 承载力试验值与计算值的对比 Fig. 10 Comparison between experimental values and calculated values of bearing capacity | |
试验值与式(2)计算值之比Pmax/Po的范围为0.98~1.25,平均值1.14;试验值与式(3)计算值之比Pmax/Po的范围为1.03~1.32,平均值1.20;试验值与式(4)计算值之比Pmax/Po的范围为0.92~1.16,平均值1.05。式(2)、(3)的承载力计算值低于试验值,低估了GFRP纵筋承担的轴力,造成材料浪费。式(4)得出的承载力计算值与试验值较接近,能准确预测GFRP筋纤维混凝土柱的承载力。
4 GFRP筋约束混凝土本构模型 4.1 峰值应力和峰值应变为计算GFRP筋约束混凝土的峰值强度,采用Ottosen混凝土破坏准则[17],它以试验数据为基础,过镇海[18]认为Ottosen混凝土破坏准则比较合理。统一表达式为
| $ {\sigma _{\rm{o}}} = a - b{\tau _{\rm{o}}} - c\tau _{\rm{o}}^2 $ | (5) |
式中:σo为相对八面体正应力,τo为相对八面体剪应力,a、b、c为与试验有关的参数。
| $ {\sigma _{\rm{o}}} = \left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)/3{f_{{\rm{co}}}} $ | (6) |
| $ {\tau _{\rm{o}}} = \sqrt {\left( {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _3} - {\sigma _1}} \right)}^2}} \right)} /3{f_{{\rm{co}}}} $ | (7) |
对于GFRP筋约束纤维混凝土,σ1=σ2=-fl,σ3=-fcc,把式(6)、(7)代入式(5),混凝土峰值强度计算式为
| $ {f_{{\rm{cc}}}} = {f_{{\rm{co}}}}\left[ {\frac{{1 - 3\sqrt 2 b}}{{12c}} + \sqrt {\frac{{3 - 9\sqrt 2 b + \sqrt 2 a}}{{36c}} + \frac{{\sqrt 2 {f_1}}}{{36c{f_{{\rm{co}}}}}}} + \frac{{{f_1}}}{{{f_{{\rm{co}}}}}}} \right] $ | (8) |
其中,
式中:fl为箍筋有效约束强度,MPa; ke为有效系数; ffv为箍筋的抗拉强度值,MPa[9];Atf为箍筋的截面面积,mm2;s为箍筋间距,mm;dcor为混凝土柱核心直径,mm;s′为箍筋净间距,mm;ρcc为纵筋配筋率;Ef为箍筋弹性模量,MPa;ff为箍筋未弯曲时的抗拉强度,MPa;rv为箍筋弯折半径,mm;dv为箍筋直径,mm。
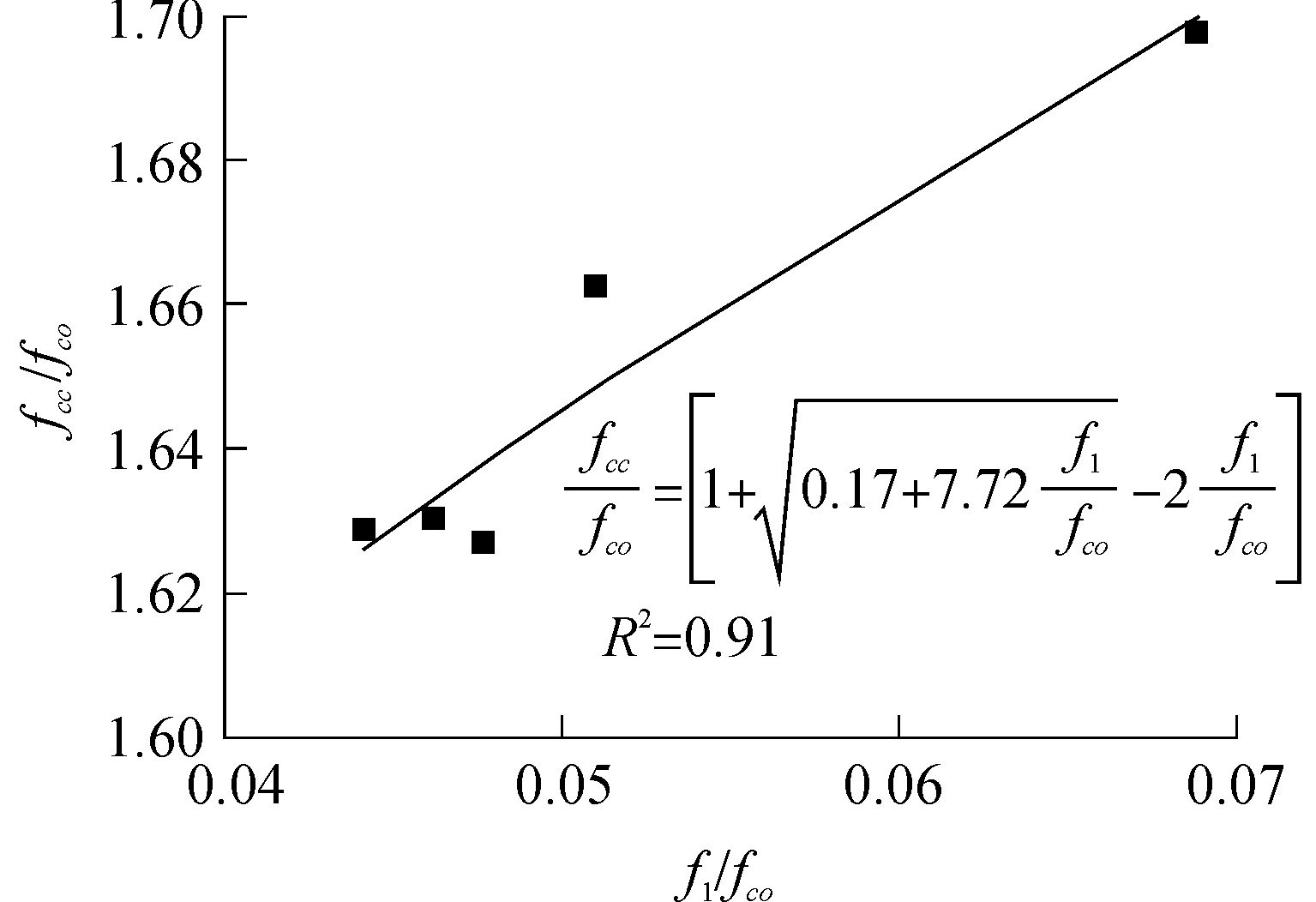
根据试验结果回归式(8),峰值强度计算式见图 11,拟合度R2为0.91。因为试件G6V-8H32和G6V-8H24箍筋间距较小,混凝土过早开裂,试件破坏较早,故分析时不考虑其相关数据。
|
Download:
|
| 图 11 fcc/fco-fl/fco曲线 Fig. 11 fcc/fco-fl/fco curve | |
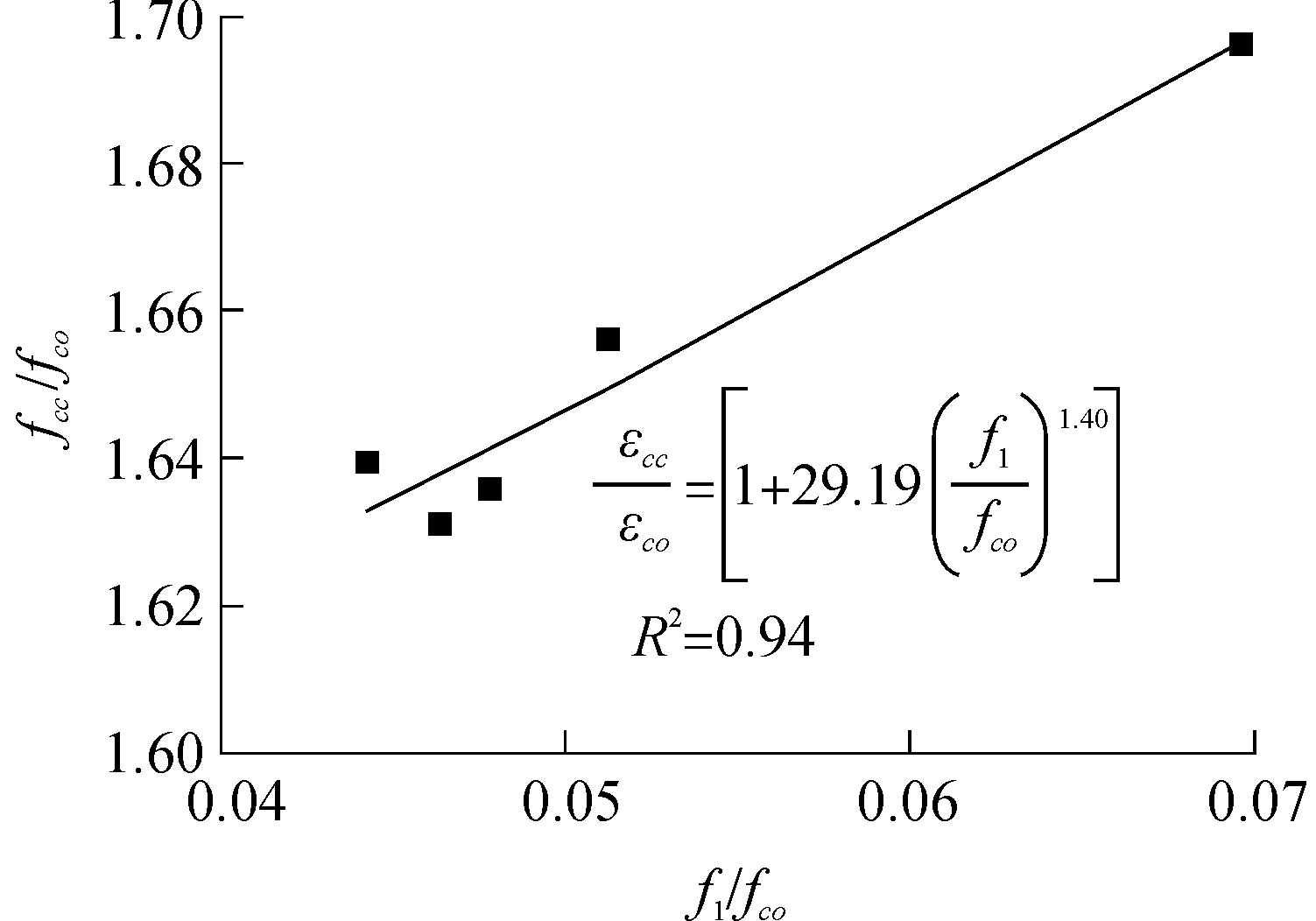
根据试验数据回归出峰值应变计算式见图 12,拟合度R2为0.94,分析时也不考虑试件G6V-8H32和G6V-8H24的相关数据。
|
Download:
|
| 图 12 εcc/εco-fl/fco曲线 Fig. 12 εcc/εco-fl/fco curve | |
混凝土轴压应力-应变关系是结构非线性分析的基础,对分析纤维混凝土柱承载力、延性等力学性能具有重要意义。关于GFRP筋约束纤维混凝土轴压应力-应变关系的研究较少,本文以Lam-Teng提出的FRP布约束混凝土轴压应力-应变关系[19]为基础,建立适合于GFRP筋约束纤维混凝土的轴压应力-应变关系。
Lam-Teng轴压应力-应变表达式为
| $ {\sigma _{\rm{c}}} = \left\{ \begin{array}{l} {E_{\rm{c}}}{\varepsilon _{\rm{c}}} - \frac{{{{\left( {{E_{\rm{c}}} - {E_2}} \right)}^2}}}{{4{f_{{\rm{co}}}}}}\varepsilon _{\rm{c}}^2,\;\;\;\;0 \le {\varepsilon _{\rm{c}}} < {\varepsilon _{{\rm{cc}}}}\\ {f_{{\rm{co}}}} - \frac{{{f_{{\rm{co}}}} - {f_{{\rm{cu}}}}}}{{{\varepsilon _{{\rm{cu}}}} - {\varepsilon _{{\rm{co}}}}}}\left( {{\varepsilon _{\rm{c}}} - {\varepsilon _{{\rm{co}}}}} \right),\;\;{\varepsilon _{{\rm{cc}}}} \le {\varepsilon _{\rm{c}}} < {\varepsilon _{{\rm{cu}}}} \end{array} \right. $ | (13) |
式中:εcc为混凝土峰值应变,με;εcc=2fco/(Ec-E2);εcu为混凝土极限应变,με;E2为下降段斜率,E2=(fcc-fco)/εcu;fco为未约束混凝土强度, MPa。
FRP布约束混凝土与FRP筋约束混凝土受力机理不完全相同,Lam-Teng本构模型不能直接用于GFRP筋约束混凝土。本文引入参数n,提出GFRP筋约束纤维混凝土轴压应力-应变本构模型,表达式由抛物线上升段和直线下降段组成:
| $ {\sigma _{\rm{c}}} = \left\{ \begin{array}{l} {E_{\rm{c}}}{\varepsilon _{\rm{c}}} - \frac{{nE_{\rm{c}}^2}}{{{f_{{\rm{co}}}}}}\varepsilon _{\rm{c}}^2,\;\;\;\;0 \le {\varepsilon _{\rm{c}}} < {\varepsilon _{{\rm{cc}}}}\\ {E_1}\left( {{\varepsilon _{\rm{c}}} - {\varepsilon _{{\rm{co}}}}} \right) + {f_{{\rm{cc}}}},\;\;{\varepsilon _{{\rm{cc}}}} \le {\varepsilon _{\rm{c}}} < {\varepsilon _{{\rm{cu}}}} \end{array} \right. $ | (14) |
| $ n = 2.49{\left( {\frac{{{f_1}}}{{{f_{{\rm{co}}}}}}} \right)^{0.48}}{\left( {\frac{{{\varepsilon _{{\rm{cc}}}}}}{{{\varepsilon _{{\rm{co}}}}}}} \right)^{0.29}}{\left( {\frac{{{f_{{\rm{cc}}}}}}{{{f_{{\rm{co}}}}}}} \right)^{ - 3.04}} $ | (15) |
| $ {E_1} = - \frac{{6.28{E_{\rm{c}}}}}{{{{10}^6}{\rho _{{\rm{st}}}}^{2.83}}}{\left| {s - 42} \right|^{0.84}}{\left( {\frac{{{f_1}}}{{{f_{{\rm{co}}}}}}} \right)^{1.18}} $ | (16) |
式中:n为与约束强度比、峰值应变比及强度提高系数有关的系数;E1为直线下降段的斜率;Ec为混凝土弹性模量实测值,MPa,见表 3;ρst为体积配箍率,%;s为箍筋间距,mm;fco为未约束混凝土强度,MPa。
理论与试验混凝土轴压应力-应变曲线见图 13,理论曲线与试验曲线吻合较好。

|
Download:
|
| 图 13 理论与试验混凝土轴压应力-应变曲线对比 Fig. 13 Comparison between predictions of proposed concrete axial stress-strain curves and experimental results | |
1) GFRP筋纤维混凝土柱与钢筋纤维混凝柱破坏过程相近,破坏形态相似;虽然前者核心混凝土强度提高系数比后者核心混凝土强度提高系数低20%左右,但两者延性系数相近,因此GFRP筋能够代替钢筋用于侵蚀环境中的混凝土受压构件。
2) 提高GFRP纵筋配筋率能显著提高试件轴压承载力,但对延性影响较小。
3) 减小箍筋间距或配箍率不变时减小箍筋直径,均能显著提高试件延性,但是对承载力及约束效率的提高作用较小;箍筋间距小于32 mm时减小箍筋间距或箍筋间距大于73 mm时增加箍筋间距,试件核心混凝土强度和试件延性均降低。
4) 提出的GFRP筋纤维混凝土柱轴压承载力计算公式及混凝土轴压应力-应变本构模型与试验结果吻合较好,预测精度较高,可供应用参考。
| [1] |
林晖.掺PVA纤维混凝土的力学及变形性能研究[D].南京: 南京航空航天大学, 2006: 6-12. LIN Hui. Research on the performance of mechanics and deformation of concrete with PVA fiber[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006: 6-12. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D038354 (  0) 0)
|
| [2] |
祁皑, 翁春光. FRP筋混凝土连续梁力学性能试验研究[J]. 土木工程学报, 2008, 41(5): 1-7. QI Ai, WENG Chunguang. Experimental study on the mechanical behavior of continuous beams reinforced with FRP rebars[J]. China civil engineering journal, 2008, 41(5): 1-7. DOI:10.3321/j.issn:1000-131X.2008.05.001 (  0) 0)
|
| [3] |
薛伟辰, 郑乔文, 杨雨. FRP筋混凝土梁正截面抗弯承载力设计研究[J]. 工程力学, 2009, 26(1): 79-85. XUE Weichen, ZHENG Qiaowen, YANG Yu. Design recommendations on flexural capacity of FRP-reinforced concrete beams[J]. Engineering mechanics, 2009, 26(1): 79-85. (  0) 0)
|
| [4] |
王作虎, 杜修力, 詹界东. 有粘结和无粘结相结合的预应力FRP筋混凝土梁抗弯承载力研究[J]. 工程力学, 2012, 29(3): 67-74. WANG Zuohu, DU Xiuli, ZHAN Jiedong. The flexural capacity of concrete beams prestressed with bonded and/or unbonded FRP tendons[J]. Engineering mechanics, 2012, 29(3): 67-74. (  0) 0)
|
| [5] |
ZHANG Jiwen, GE Wenjie, DAI Hang, et al. Study on the flexural capacity of concrete beam hybrid reinforced with frp bars and steel bars[C]//Proceedings of the 5th International Conference on FRP Composites in Civil Engineering. Beijing, China, 2010: 304-307.
(  0) 0)
|
| [6] |
PANTELIDES C P, GIBBONS M E, REAVEELEY L D. Axial load behavior of concrete columns confined with GFRP spirals[J]. Journal of composites for construction, 2013, 17(3): 305-313. DOI:10.1061/(ASCE)CC.1943-5614.0000357 (  0) 0)
|
| [7] |
DE L A, MATTA F, NANNI A. Behavior of full-scale glass fiber-reinforced polymer reinforced concrete columns under axial load[J]. ACI structural journal, 2010, 107(5): 589-596. (  0) 0)
|
| [8] |
AFIFI M Z, MOHAMED H M, CHAALLAL O, et al. Confinement model for concrete columns internally confined with carbon FRP spirals and hoops[J]. Journal of structural engineering, 2015, 141(9): 04014219. DOI:10.1061/(ASCE)ST.1943-541X.0001197 (  0) 0)
|
| [9] |
中冶建筑研究总院有限公司. GB 50608-2010, 纤维增强复合材料建设工程应用技术规范[S].北京: 中国计划出版社, 2011. Central Research Institute of Building and Construction Co., Ltd. GB 50608-2010, Technical code for infrastructure application of FRP composites[S]. Beijing: China Planning Press, 2011. (  0) 0)
|
| [10] |
中国建筑科学研究院. GB/T 50081-2002, 普通混凝土力学性能试验方法标准[S].北京: 中国建筑工业出版社, 2003. China Academy of Building Research. GB/T 50081-2002, Standard for test method of mechanical properties on ordinary concrete[S]. Beijing: China Architecture & Building Press, 2003. (  0) 0)
|
| [11] |
中国建筑科学研究院. GB 50010-2010, 混凝土结构设计规范(2015年版)[S].北京: 中国建筑工业出版社, 2011. China Academy of Building Research. GB 50010-2010, Code for design of concrete structures[S]. Beijing: China Architecture & Building Press, 2011 (  0) 0)
|
| [12] |
PESSIKI S, PIERONI A. Axial load behavior of large-scale spirally-reinforced high-strength concrete columns[J]. ACI structural journal, 1997, 94(3): 304-314. (  0) 0)
|
| [13] |
AFIFI M Z, MOHAMED H M, BENMOKRANE B. Axial capacity of circular concrete columns reinforced with GFRP bars and spirals[J]. Journal of composites for construction, 2014, 18(1): 04013017. DOI:10.1061/(ASCE)CC.1943-5614.0000438 (  0) 0)
|
| [14] |
TOBBI H, FARGHALY A S, BENMOKRANE B. Behavior of concentrically loaded fiber-reinforced polymer reinforced concrete columns with varying reinforcement types and ratios[J]. ACI structural journal, 2014, 111(2): 375-385. (  0) 0)
|
| [15] |
KOBAYASHI K, FUJISAKI T. Compressive behavior of FRP reinforcement in non-prestressed concrete members[C]//Proceedings of the 1995 2nd International RILEM Symposium. Ghent, Belgium, 1995: 267-274.
(  0) 0)
|
| [16] |
TOBBI H, FARGHALY A S, BENMOKRANE B. Strength model for concrete columns reinforced with fiber-reinforced polymer bars and ties[J]. ACI structural journal, 2014, 111(4): 789-798. (  0) 0)
|
| [17] |
OTTOSEN N S. A failure criterion for concrete[J]. Journal of engineering mechanics, 1977, 103(4): 527-535. (  0) 0)
|
| [18] |
过镇海, 时旭东. 钢筋混凝土原理和分析[M]. 北京: 清华大学出版社, 2003: 103-114. GUO Zhenhai, SHI Xudong. Reinforced concrete theory and analyse[M]. Beijing: Tsinghua University Press, 2003: 103-114. (  0) 0)
|
| [19] |
LAM L, TENG J G. Design-oriented stress-strain model for FRP-confined concrete[J]. Construction and building materials, 2003, 17(6/7): 471-489. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


