2. 同济大学 土木工程防灾国家重点实验室, 上海 200092
2. State Key Laboratory of Disaster Prevention in Civil Engineering, Tongji University, Shanghai 200092, China
钢结构与其他结构相比,其自身重量小、延性大、抗震性能好、可重复使用、施工速度快,钢结构在各个领域大量使用,但是钢结构在铸造和使用过程中会产生一些初始缺陷,这些缺陷会引起构件和结构失效。Anderson[1]收集了近百年来钢结构事故事例,Biggs[2]对事故进行了详细的分析。目前在材料裂纹扩展方面各国学者提出了断裂力学理论、有限元理论、扩展有限元理论。断裂力学的疲劳裂纹扩展驱动力和各种影响机理方面存在不同意见,这些问题各国学者仍在进一步探索。有限元方法不足在于:裂纹限制在网格上,尖端附近需要布置高密度网格,网格随裂纹扩展必须重新划分[3]。扩展有限元的缺点:加进裂尖位移场并不是真实的裂尖渐进位移场;裂尖只加强一层单元,裂尖位置直接影响计算精度。正是由于各种方法在解决裂纹扩展问题中存在不足,提出了近场动力学(peridynamic, PD)[4]理论,这种理论不依靠空间导数,采用积分的方法,当物体在外力作用下用质点间距离的变化来描述物体受力状态。在近场动力学理论发展方面,Silling等[5-6]提出了一维无限杆近场动力学的解,还得到了近场动力学断裂力学路径与扩展有限元和内聚力非常接近的结果。刘一鸣等[7]模拟了脆性材料的断裂特性。赖欣等[8]模拟了干燥土和饱和土受内压冲击作用的破坏过程。刘立胜等[9]模拟了双材料界面力学性能。顾鑫等[10]模拟了混凝土侵蚀问题。朱其志等[11]模拟类岩石裂纹扩展。黄丹等[12]提出了准静态问题的分析。赵金海等[13-14]采用延伸率断裂准则模拟了双边裂纹及中心双裂纹扩展。还提出了PD-COD裂纹扩展准则。本文采用近场动力学通过降低质点间键的连接强度,模拟了钢铁在铸造过程产生的气孔、夹杂、未熔合等初始缺陷。同时采用无缺陷和有缺陷不同纵向裂纹间距情况下的裂纹扩展路径进行对比,得到了初始缺陷对不同纵向间距中心双裂纹扩展路径的影响规律。
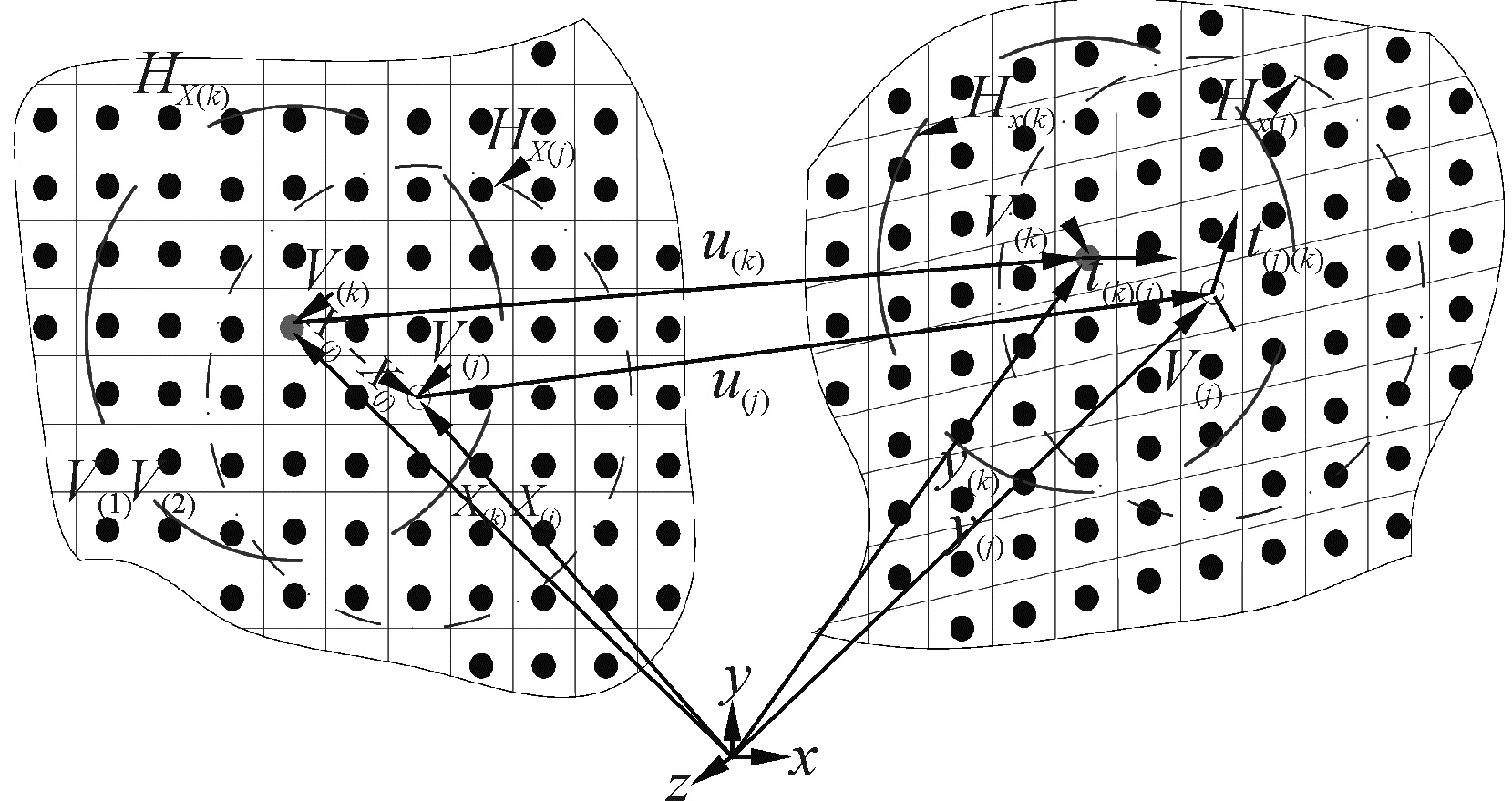
1 近场动力学理论近场动力学主要考虑力状态T和变状态Y,两质点初始相对位置矢量(x(j)-x(k)),定义为
| $ {\mathit{\boldsymbol{\xi }}_{\left( k \right)\left( j \right)}} = {x_{\left( j \right)}} - {x_{\left( k \right)}} $ | (1) |
在外荷载作用下变形后两质点的位置矢量为[5]
| $ \left( {{y_{\left( j \right)}} - {y_{\left( k \right)}}} \right) = \mathit{\boldsymbol{\underline Y}} \left( {{x_{\left( k \right)}},t} \right) = \left[ {\begin{array}{*{20}{c}} {{y_{\left( 1 \right)}} - {y_{\left( k \right)}}}\\ {{y_{\left( 2 \right)}} - {y_{\left( k \right)}}}\\ \vdots \\ {{y_{\left( \infty \right)}} - {y_{\left( k \right)}}} \end{array}} \right] $ | (2) |
假定质点x(k)的体积V(k),且在半径δ的圆区域Hx(k)内含有质点x(j)j=1, 2, …,则质点x(k)作用在质点x(j)上的近场动力学力t(j)(k)为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{t}}_{\left( k \right)\left( j \right)}}\left( {{\mathit{\boldsymbol{u}}_{\left( j \right)}} - {\mathit{\boldsymbol{u}}_{\left( k \right)}},{x_{\left( j \right)}} - {x_{\left( k \right)}},t} \right) = }\\ {\mathit{\boldsymbol{\underline T}} \left( {{x_{\left( k \right)}},t} \right)\left\langle {{x_{\left( j \right)}} - {x_{\left( k \right)}}} \right\rangle } \end{array} $ | (3) |
在区域Hx(k)以外的质点,x(k)与其相互作用可以忽略,如图 1所示,u(k)和u(j)表示质点x(k)和x(j)的变形量,变形后两质点间的延伸s(k)(j)为
| $ \begin{array}{l} {s_{\left( k \right)\left( j \right)}} = s\left( {{\mathit{\boldsymbol{u}}_{\left( j \right)}} - {\mathit{\boldsymbol{u}}_{\left( k \right)}},{x_{\left( j \right)}} - {x_{\left( k \right)}}} \right) = \\ \frac{{\left( {\left| {{y_{\left( j \right)}} - {y_{\left( k \right)}}} \right| - \left| {{x_{\left( j \right)}} - {x_{\left( k \right)}}} \right|} \right)}}{{\left| {{x_{\left( j \right)}} - {x_{\left( k \right)}}} \right|}} \end{array} $ | (4) |
|
Download:
|
| 图 1 近场动力学质点的运动 Fig. 1 The movement of peridynamic particles | |
式中:y(k)为质点x(k)变形后的位置矢量,y(j)为质点x(j)变形后的位置矢量。
质点x(k)和质点x(j)相互作用的应变能标量微应变能w(k)(j)为
| $ {w_{\left( k \right)\left( j \right)}} = {w_{\left( k \right)\left( j \right)}}\left( {{y_{\left( {{1^k}} \right)}} - {y_{\left( k \right)}},{y_{\left( {{2^k}} \right)}} - {y_{\left( k \right)}}, \cdots } \right) $ | (5) |
式中:y(k)为质点x(k)的变形矢量,y(1k)为与质点x(k)相互作用的第一个质点。
质点x(k)同其周围作用的应变能密度的总和可以表示为
| $ \begin{array}{l} {W_{\left( k \right)}} = \frac{1}{2}\sum\limits_{j = 1}^\infty {\left( {\frac{1}{2}{w_{\left( k \right)\left( j \right)}}\left( {{y_{\left( {{1^k}} \right)}} - {y_{\left( k \right)}},{y_{\left( {{2^k}} \right)}} - {y_{\left( k \right)}}, \cdots } \right) + } \right.} \\ \left. {\frac{1}{2}{w_{\left( j \right)\left( k \right)}}\left( {{y_{\left( {{1^j}} \right)}} - {y_{\left( j \right)}},{y_{\left( {{2^j}} \right)}} - {y_{\left( j \right)}}, \cdots } \right)} \right) \cdot {V_{\left( j \right)}} \end{array} $ | (6) |
式中当k=j时, w(k)(j)=0。
应用拉格朗日方程,近场动力学方程表示为
| $ \begin{array}{*{20}{c}} {{\rho _{\left( k \right)}}{{\mathit{\boldsymbol{\ddot u}}}_{\left( k \right)}} = \sum\limits_{j = 1}^\infty {\left[ {{\mathit{\boldsymbol{t}}_{\left( k \right)\left( j \right)}}\left( {{\mathit{\boldsymbol{u}}_{\left( j \right)}} - {\mathit{\boldsymbol{u}}_{\left( k \right)}},{x_{\left( j \right)}} - {x_{\left( k \right)}},t} \right) - } \right.} }\\ {\left. {{\mathit{\boldsymbol{t}}_{\left( j \right)\left( k \right)}}\left( {{\mathit{\boldsymbol{u}}_{\left( k \right)}} - {\mathit{\boldsymbol{u}}_{\left( j \right)}},{x_{\left( k \right)}} - {x_{\left( j \right)}},t} \right)} \right]{V_{\left( j \right)}} + {\mathit{\boldsymbol{b}}_{\left( k \right)}}} \end{array} $ | (7) |
其中:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{t}}_{\left( k \right)\left( j \right)}}\left( {{\mathit{\boldsymbol{u}}_{\left( j \right)}} - {\mathit{\boldsymbol{u}}_{\left( k \right)}},{x_{\left( j \right)}} - {x_{\left( k \right)}},t} \right) = }\\ {\frac{1}{2} \cdot \frac{1}{{{V_{\left( k \right)}}}}\left( {\sum\limits_{i = 1}^\infty {\frac{{\partial {w_{\left( k \right)\left( i \right)}}}}{{\partial \left( {{y_{\left( j \right)}} - {y_{\left( k \right)}}} \right)}}{V_{\left( i \right)}}} } \right)} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{t}}_{\left( j \right)\left( k \right)}}\left( {{\mathit{\boldsymbol{u}}_{\left( k \right)}} - {\mathit{\boldsymbol{u}}_{\left( j \right)}},{x_{\left( k \right)}} - {x_{\left( j \right)}},t} \right) = }\\ {\frac{1}{2} \cdot \frac{1}{{{V_{\left( j \right)}}}}\left( {\sum\limits_{i = 1}^\infty {\frac{{\partial {w_{\left( i \right)\left( k \right)}}}}{{\partial \left( {{y_{\left( k \right)}} - {y_{\left( j \right)}}} \right)}}{V_{\left( i \right)}}} } \right)} \end{array} $ | (9) |
最终质点x(k)的近场动力学方程可以表示为
| $ \begin{array}{*{20}{c}} {{\rho _{\left( k \right)}}{{\mathit{\boldsymbol{\ddot u}}}_{\left( k \right)}} = \int_H {\mathit{\boldsymbol{t}}\left( {\mathit{\boldsymbol{u'}} - \mathit{\boldsymbol{u}},x' - x,t} \right)} - }\\ {\mathit{\boldsymbol{t'}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{u'}},x - x',t} \right){\rm{d}}H + \mathit{\boldsymbol{b}}\left( {x,t} \right)} \end{array} $ | (10) |
近场动力学理论认为当质点x(k)、x(j)的相互近场动力学力消失时,就认为质点x(k)、x(j)间产生了损伤。假设当两质点间的延伸量s(k)(j)超过了临界值sc认为损伤开始形成。
近场动力学引进了一个依靠历史的标量值函数:
| $ \mu \left( {{x_{\left( j \right)}} - {x_{\left( k \right)}},t} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 1,\\ 0, \end{array}&\begin{array}{l} {s_{\left( k \right)\left( j \right)}} < {s_c}\\ 其他 \end{array} \end{array}} \right. $ | (11) |
在外力作用下,物体中质点间的距离(y(j)-y(k))与延伸率值s(k)(j)不断变化。当两质点x(k),x(j)的延伸率值s(k)(j) < sc时,物体没有发生损伤,两质点间存在作用力,μ(x(j)-x(k), t)=1;当s(k)(j)≥sc时,损伤开始发生,两质点间的作用力逐渐失效为0,此时μ(x(j)-x(k), t)=0。
物体的局部损伤定义为质点x(k)与其圆区域Hx(k)内质点x(j),j=1, 2, …,作相互作用力的权重函数:
| $ \varphi \left( {x,t} \right) = 1 - \frac{{\int\limits_H {\mu \left( {{x_{\left( j \right)}} - {x_{\left( k \right)}},t} \right){\rm{d}}V'} }}{{\int\limits_H {{\rm{d}}V'} }} $ | (12) |
局部损伤函数值φ(x, t)∈[0, 1]。当φ(x, t)=1时,质点间的相互作用力完全消失,当φ(x, t)=0时,表示质点间的作用力没有受到外荷载的影响。
3 含缺陷中心平行双裂纹扩展分析本文采用长宽均为0.05 m的二维平钢板,弹性模量E=203 GPa,泊松比ν=0.3,密度为ρ=7 850 kg/m3。钢板厚为一个质点直径5×10-4 m,板中有两条裂纹长为2a=0.01 m的裂纹,裂纹纵向间距分别为3、4和5 mm。不同纵向间距双裂纹周围随机分布有初始缺陷(气孔、夹杂、未熔合)。垂直裂纹方向在板的端部分别施加速度为v=20 m/s的荷载,考虑随机分布的初始缺陷对不同纵向间距的双平行裂纹扩展路径的影响。如图 2所示,双平行线表示裂纹,类椭圆物体表示初始缺陷。

|
Download:
|
| 图 2 二维板质点位置分布 Fig. 2 The particles position distribution in 2D plate | |
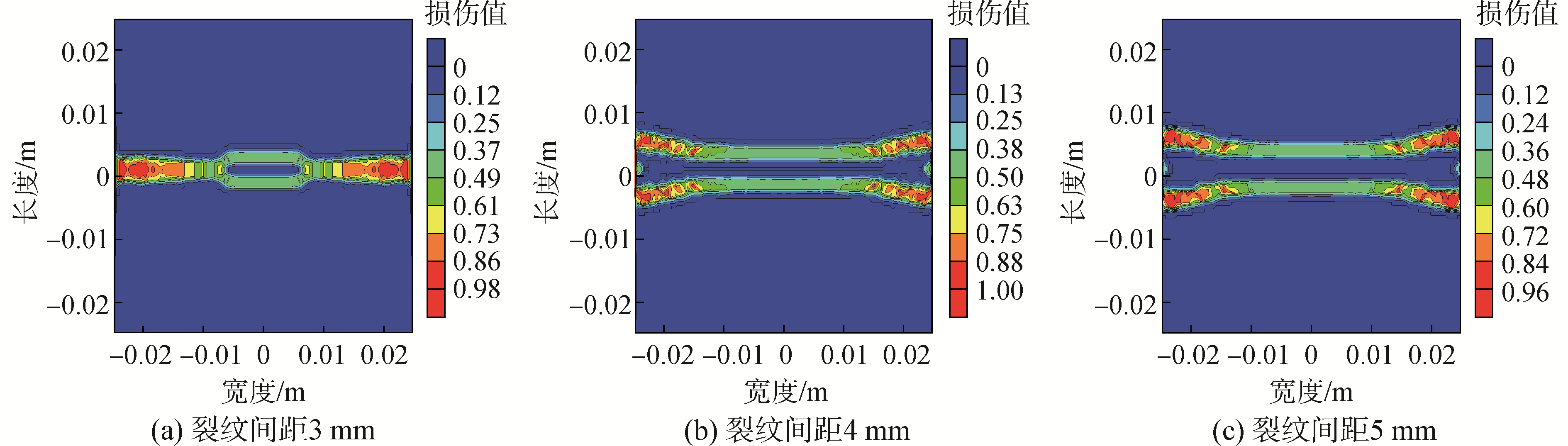
图 3为无随机分布初始缺陷的不同纵向间距双平行裂纹模型。图 4为无初始缺陷纵向间距分别为3、4和5 mm中心双平行裂纹扩展路径。由图 4(a)可知,纵向间距为3 mm的双平行裂纹在荷载作用下两条裂纹融合为一条水平裂纹;图 4(b)可知,裂纹纵向间距为4 mm的双平行裂纹在荷载作用下,两条平行裂纹先沿着水平方向扩展,后裂纹相向扩展,裂纹纵向间距变大;图 4(c)可知,纵向间距为5 mm的双平行裂纹在荷载作用下,两条裂纹先沿着水平方向扩展,然后裂纹扩展路径发生偏移,裂纹相向扩展,纵向间距变大。间距5 mm的裂纹扩展路径与间距4 mm的裂纹扩展路径虽然相似,但是,间距5 mm的裂纹,裂纹扩展方向发生改变部位先于间距4 mm的裂纹。

|
Download:
|
| 图 3 无缺陷的双裂纹 Fig. 3 Double cracks without defects | |
|
Download:
|
| 图 4 无缺陷双裂纹扩展路径 Fig. 4 Double crack propagation path without defects | |
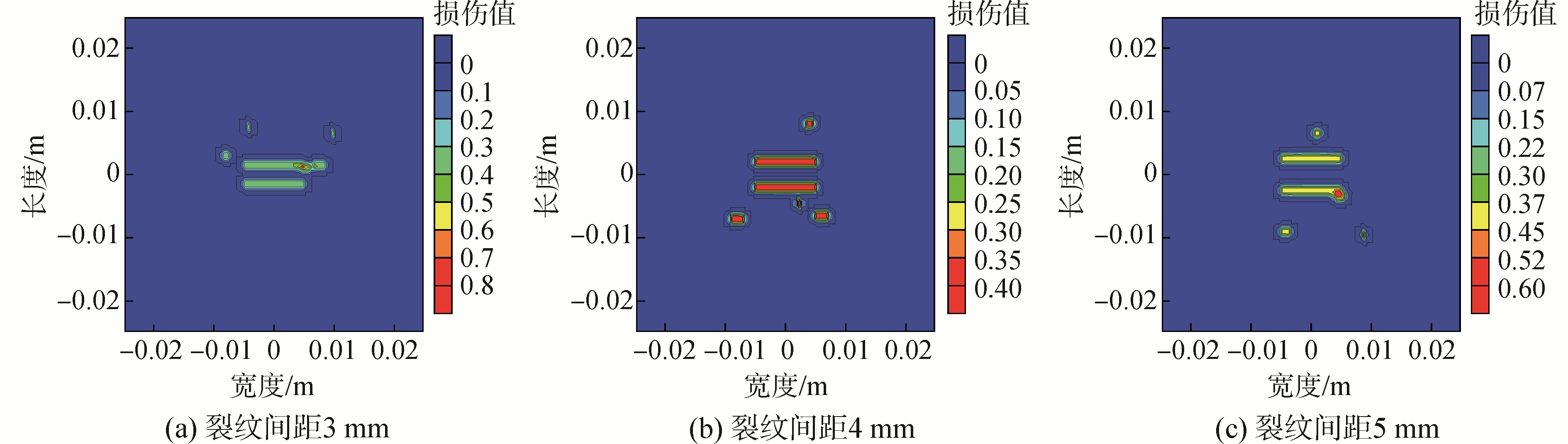
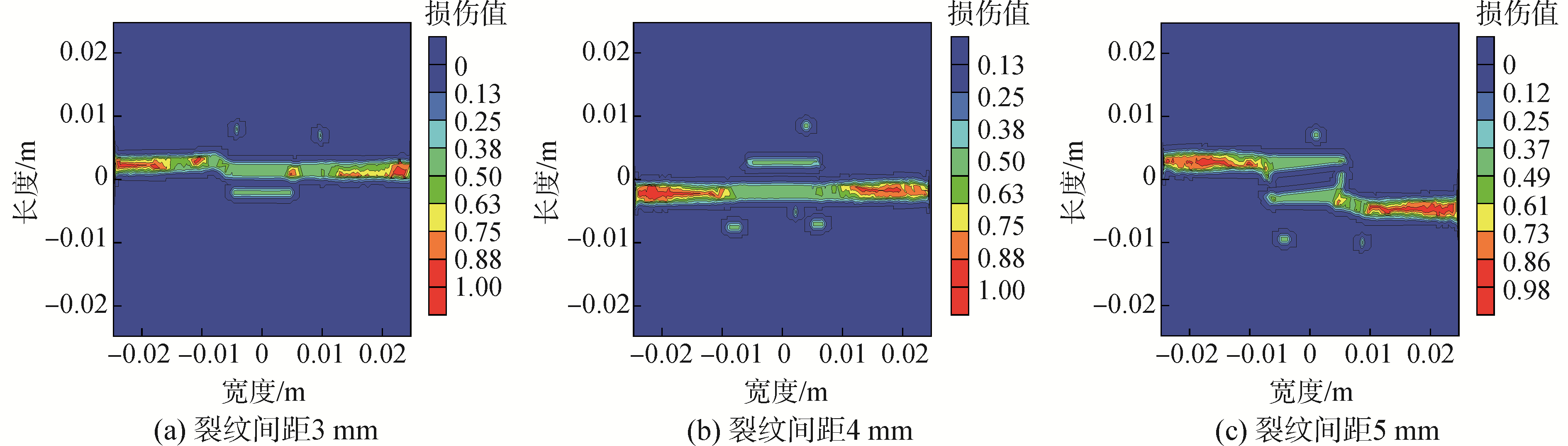
图 5为含随机分布初始缺陷的不同纵向间距双平行裂纹模型,初始缺陷为随机长度0~2 mm的5个气孔、夹杂或未熔合的缺陷,随机分布于平行双裂纹周围。图 6为含随机分布初始缺陷的双裂纹模型,在速度荷载为v=20 m/s情况下裂纹扩展路径。间距为3 mm的双裂纹在缺陷的影响下只有上边裂纹扩展为一条水平贯通试件宽度方向的裂纹,下边的裂纹几乎没有扩展。间距为4 mm的双裂纹在随机缺陷影响下,只有下边裂纹扩展为一条贯通试件宽度方向的裂纹,上边裂纹几乎没有扩展。间距为5 mm的双裂纹受随机缺陷的影响下,上边的裂纹只有裂纹左边尖端沿着水平方向扩展,下边的裂纹只有裂纹右边的尖端扩展贯通试件的宽度方向。
|
Download:
|
| 图 5 随机初始缺陷分布 Fig. 5 Random initial defect distribution | |
|
Download:
|
| 图 6 含随机缺陷双裂纹扩展路径 Fig. 6 Double crack propagation path with random defects | |
1) 无缺陷的中心双平行裂纹在外荷载作用下,随着双裂纹纵向间距的变化,裂纹扩展路径也随之改变。
2) 裂纹间距小于3 mm时,双裂纹融合为一条水平裂纹;当平行裂纹间距增大后,裂纹扩展为两条间距不断变大的裂纹,且初始裂纹间距越大,裂纹尖端就越早改变扩展路径的方向。
3) 含随机缺陷(气孔、夹杂、未熔合)的不同纵向间距的平行双裂纹扩展路径与无缺陷裂纹扩展路径对比可知,初始缺陷不仅改变了中心双裂纹扩展路径,同时对中心双裂纹扩展也有一定的抑制作用。
| [1] |
ANDERSON W E. An engineer views brittle fracture history[R]. Boeing Report, 1969.
(  0) 0)
|
| [2] |
BIGGS W D. The brittle fracture of steel[M]. London: MacDonald and Evans, 1960.
(  0) 0)
|
| [3] |
BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. International journal for numerical methods in engineering, 1999, 45(5): 601-620. DOI:10.1002/(ISSN)1097-0207 (  0) 0)
|
| [4] |
SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the mechanics and physics of solids, 2000, 48(1): 175-209. DOI:10.1016/S0022-5096(99)00029-0 (  0) 0)
|
| [5] |
SILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling[J]. Journal of elasticity, 2007, 88(2): 151-184. DOI:10.1007/s10659-007-9125-1 (  0) 0)
|
| [6] |
SILLING S A, ASKARI E. Peridynamic modeling of impact damage[C]//Proceedings of ASME/JSME 2004 Pressure Vessels and Piping Conference. San Diego, 2004: 197-205.
(  0) 0)
|
| [7] |
刘一鸣, 黄丹.脆性裂纹扩展的近场动力学分析[C]//中国力学大会-2015论文摘要集.上海, 2015: 331-331. LIU Yiming, HUANG Dan. Based on peridynamic the analysis of brittle crack propagation[C]//Chinese Congress of Theoretical and Applied Mechanics. Shanghai, 2015: 331-331. (  0) 0)
|
| [8] |
赖欣, 刘立胜, 刘齐文, 等.土受内压冲击作用破坏过程的近场动力学模拟[C]//中国力学大会-2015论文摘要集.上海, 2015: 331-331. LAI Xin, LIU Lisheng, LIU Qiwen, et al. Based on peridynamics the numerical simulation of failure process of soil subjected to internal pressure[C]//Chinese Congress of Theoretical and Applied Mechanics. Shanghai, 2015: 331-331. (  0) 0)
|
| [9] |
王芳.双材料界面及其力学性能的近场动力学研究[D].武汉: 武汉理工大学, 2015: 39-46. WANG Fang. Studies of bimaterial interface and its mechanical property with peridynamics[D]. Wuhan: Wuhan University of Technology, 2015: 39-46. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D794744 (  0) 0)
|
| [10] |
顾鑫, 章青, 黄丹. 基于近场动力学方法的混凝土板侵彻问题研究[J]. 振动与冲击, 2016, 35(6): 52-58. GU Xin, ZHANG Qing, HUANG Dan. Peridynamics used in solving penetration problem of concrete slabs[J]. Journal of vibration and shock, 2016, 35(6): 52-58. (  0) 0)
|
| [11] |
朱其志, 倪涛, 赵伦洋, 等. 岩石类材料裂纹扩展贯通的近场动力学方法模拟[J]. 岩石力学与工程学报, 2016, 34(S2): 3507-3515. ZHU Qizhi, NI Tao, ZHAO Lunyang, et al. Simulations of crack propagation in rock-like materials using peridynamic method[J]. Chinese journal of rock mechanics and engineering, 2016, 34(S2): 3507-3515. (  0) 0)
|
| [12] |
黄丹, 卢广达, 章青. 准静态变形破坏的近场动力学分析[J]. 计算力学学报, 2016, 33(5): 657-662. HUANG Dan, LU Guangda, ZHANG Qing. A peridynamic study on quasi-static deformation and failure[J]. Chinese journal of computational mechanics, 2016, 33(5): 657-662. (  0) 0)
|
| [13] |
ZHAO Jinhai, TANG Hesheng, XUE Songtao. Peridynamics versus XFEM:a comparative study for quasistatic crack problems[J]. Frontiers of structural and civil engineering, 2017. DOI:10.1007/s11709-017-0434-6 (  0) 0)
|
| [14] |
ZHAO Jinhai, TANG Hesheng, XUE Songtao. A new fracture criterion for peridynamic and dual-horizon peridynamics[J]. Frontiers of structural and civil engineering, 2017. DOI:10.1007/s11709-017-0447-1 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


