2. 哈尔滨建成集团有限公司, 黑龙江 哈尔滨 150030
2. Harbin Construction Group Co., LTD, Harbin 150030, China
遥控作业型水下机器人[1](remotely operated vehicle,ROV)的最大特点是能在危险复杂的深海环境中完成大负荷、高强度和高精度作业,是实施深海资源开发不可或缺的重大技术装备之一。作业型ROV通常安装7台或8台呈矢量布置的液压推进器,以保证较强的水下作业能力和作业安全性。为了实现在最小能耗条件下过驱动ROV或船舶的运动控制,必须解决过驱动矢量推进系统的推力优化分配问题[2-3]。此外推进器作为一个典型的惯性环节[2],若推力分配控制策略不当,容易引起水下机器人控制性能变差和作业效率降低,严重甚至会导致水下作业任务失败。因此,水下机器人矢量推进系统建模及推力分配方法成当前研究的热点和关键问题之一[3-5]
Fossen[3]针对过驱动海上航行器的推力分配方法进行深入分析,指出直接分配法和伪逆法是一种实时性较性高的推力分配方法,但必须解决推进器推力的饱和输出问题[4]。李新飞等[2]针对某作业型ROV所安装的液压推进器建立了控制电压和推力响应之间对应关系,为推力分配方法的研究奠定基础。俞建成[5]针对过驱动矢量推进载人潜器,对每个推进器的期望控制量进行归一化处理后,研究了过驱动推力分配问题。贾立娟[6]针对某观测型ROV的推进器进行动力学建模,分析了螺旋桨动力学响应问题。范士波[7]使用原始对偶路径跟踪方法解决了过驱动ROV推力分配时可能出现的饱和问题,但是该方法计算过程复杂,且实时性不高。Soylu等[8]研究了考虑饱和约束特性的推力优化分配方法,但是没有考虑该方法的实时性问题。Akmal等[9]针对某性ROV研究了一种主动容错的推力分配方法。黄海等[10]建立了一种矢量推进微型ROV的推力分配模型,基于递归神经网络设计了推力容错分配控制器,但是没有考虑推力饱和问题。魏延辉[11]研究了一种基于能量最优原则的推力分配方法,但没有考虑推力饱和问题。可以看出:国内外一些学者在对矢量推进系统和推力分配方法进行研究时,往往没有考虑推进器饱和约束条件,或者虽然考虑了推进器约束条件[12],但使用推力分配方法复杂、计算量大、实时性不高。
本文针对某深海过驱动作业型ROV推进器呈矢量对称安装的特点,推导建立了一种过驱动水下机器人矢量推进学系统的数学模型,直接反映了推进器推力和作用于ROV本体上六自由度合推力之间的关系。然后将八台推进器分成两组,以分别控制水平面和垂直面运动。对推力分配过程中可能出现的推进器饱和输出问题,先将控制电压进行归一化处理,再根据推进器矢量对称安装的特点,提出一种水平面和垂直面分开控制的直接逻辑分配方法。在Matlab中构建过驱动ROV六自由度运动控制和推力分配仿真模型[13-14],分析作业型ROV六自由度运动和推进器推力的动态响应过程,并对各种推力分配方法的仿真结果进行了深入对比分析。
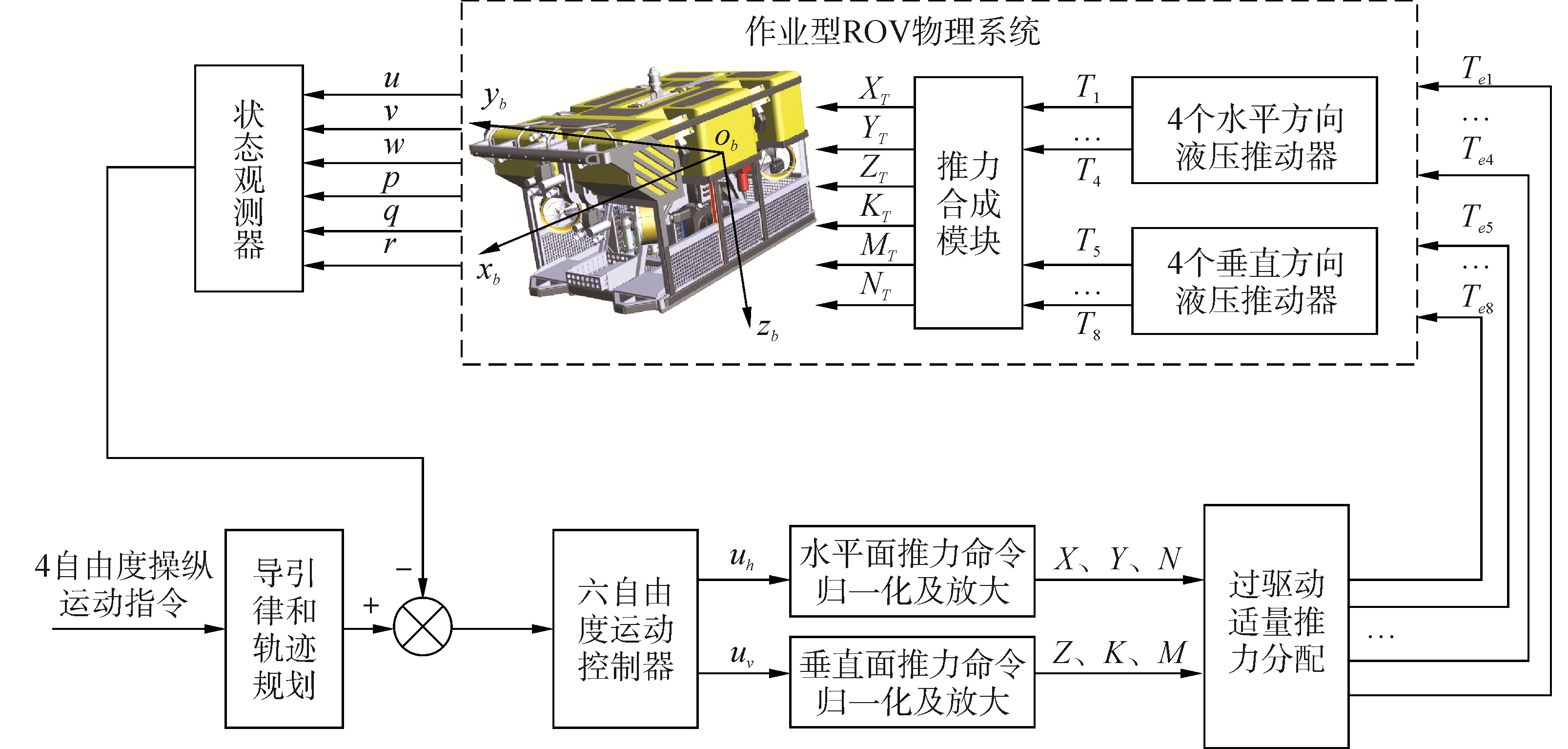
1 ROV推进系统建模及推力分配 1.1 ROV运动控制系统组成及工作原理如图 1,本文以英国SMD公司的Quantum系列遥控作业型ROV为研究对象,分析ROV运动控制系统的组成及工作原理。图 1中,Quantum系列作业型ROV上安装8台液压导管式推进器,其中垂直方向安装4台,水平方向安装4台。建立水下机器人本体坐标系[15]ob-xbybzb,其坐标原点ob取在ROV重心上,坐标轴obxb、obyb、obzb分别与ROV惯性主轴一致。
|
Download:
|
| 图 1 作业型ROV运动控制系统的组成及其工作原理 Fig. 1 The working principle of Work-Class ROV | |
表 1是8台成矢量对称安装的推进器及其在ROV本体坐标系{b}中安装位置和角度。
| 表 1 作业型ROV推进器的安装角度及位置参数 Tab.1 Arrangement parameters of vector thrusters |
1) 水平推进器的合推力
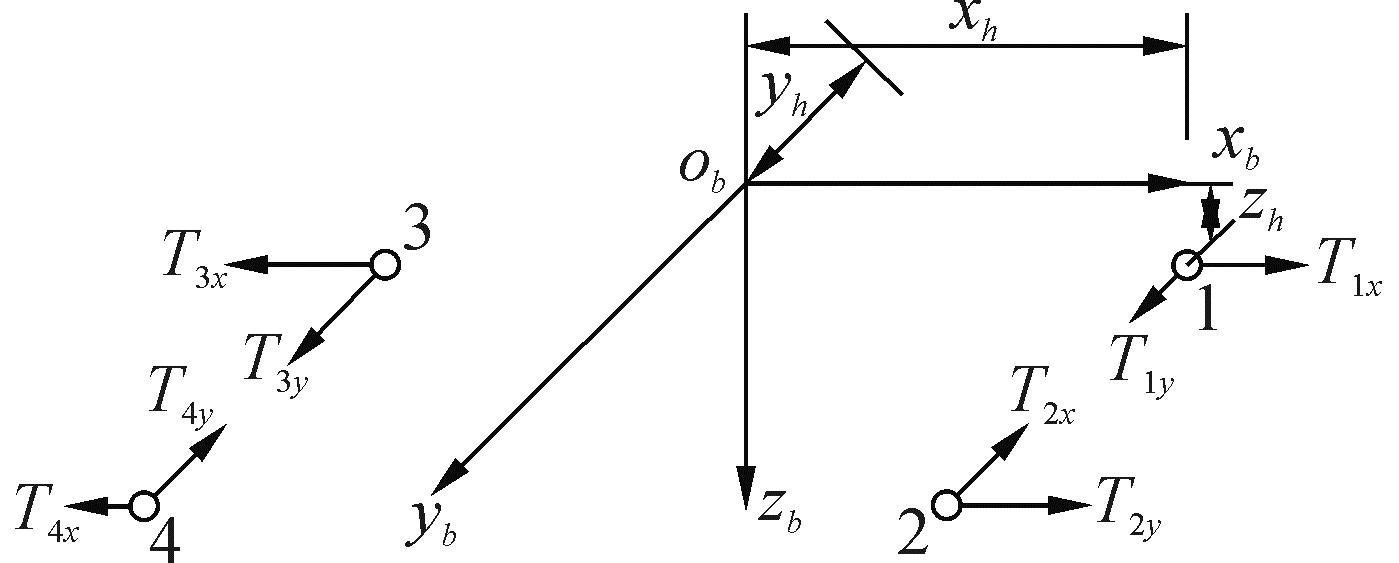
图 2中,ROV本体受到4台水平推进器的推力作用,其受到推力正方向与obxb轴的夹角都为50°,经过推力分解,水平推进器推力对ROV本体产生的合推力在本体坐标系{b}各轴上下式表示:
| $ \left\{ \begin{array}{l} {X_{\rm{h}}} = {T_1}\cos {\beta _{\rm{h}}} + {T_2}\cos {\beta _{\rm{h}}} - {T_3}\cos {\beta _{\rm{h}}} - {T_4}\cos {\beta _{\rm{h}}}\\ {Y_{\rm{h}}} = {T_1}\sin {\beta _{\rm{h}}} - {T_2}\sin {\beta _{\rm{h}}} + {T_3}\sin {\beta _{\rm{h}}} - {T_4}\sin {\beta _{\rm{h}}}\\ {Z_{\rm{h}}} = 0 \end{array} \right. $ | (1) |
式中:T1、T2、T3、T4分别为ROV本体受到1#、2#、3#、4#推进器的推力;Xh、Yh、Zh分别为本体受到水平推进器沿obxb轴、obyb轴、obzb轴的合推力;βh为推进器推力与obxb轴的夹角。
2) 水平推进器的合推力矩。
由于4台水平推进器安装于ROV重心的下方,且成矢量对称布置,因此会对ROV本体产生相应的三个自由度的推力矩,图 2是4台水平推进器推力对坐标系{b}各轴产生的推力矩的示意图。水平推进器推力经过力分解后,其各自分解力的正方向如图 2。则4台水平推进器对ROV本体产生合推力在坐标系{b}的三个轴上可用下式表示:
| $ \left\{ \begin{array}{l} {K_{\rm{h}}} = - {T_{1y}}{z_{\rm{h}}} + {T_{2y}}{z_{\rm{h}}} - {T_{3y}}{z_{\rm{h}}} + {T_{4y}}{z_{\rm{h}}}\\ {M_{\rm{h}}} = {T_{1x}}{z_{\rm{h}}} + {T_{2x}}{z_{\rm{h}}} - {T_{3x}}{z_{\rm{h}}} - {T_{4x}}{z_{\rm{h}}}\\ {N_{\rm{h}}} = {T_{1x}}{y_{\rm{h}}} + {T_{1y}}{x_{\rm{h}}} - {T_{2x}}{y_{\rm{h}}} - {T_{2y}}{x_{\rm{h}}} - {T_{3x}}{y_{\rm{h}}} - \\ \;\;\;\;\;\;\;\;{T_{3y}}{x_{\rm{h}}} + {T_{4x}}{y_{\rm{h}}} + {T_{4y}}{x_{\rm{h}}} \end{array} \right. $ | (2) |
|
Download:
|
| 图 2 水平推进器的推力对ROV本体的推力矩示意图 Fig. 2 The thrust moment of horizontal propeller on ROV | |
式中:Kh、Mh、Nh分别为水平推进器对ROV本体在obxb轴、obyb轴、obzb轴方向的合推力矩。
1.2.2 垂直面矢量推进系统的数学建模1) 垂直推进器的合推力。
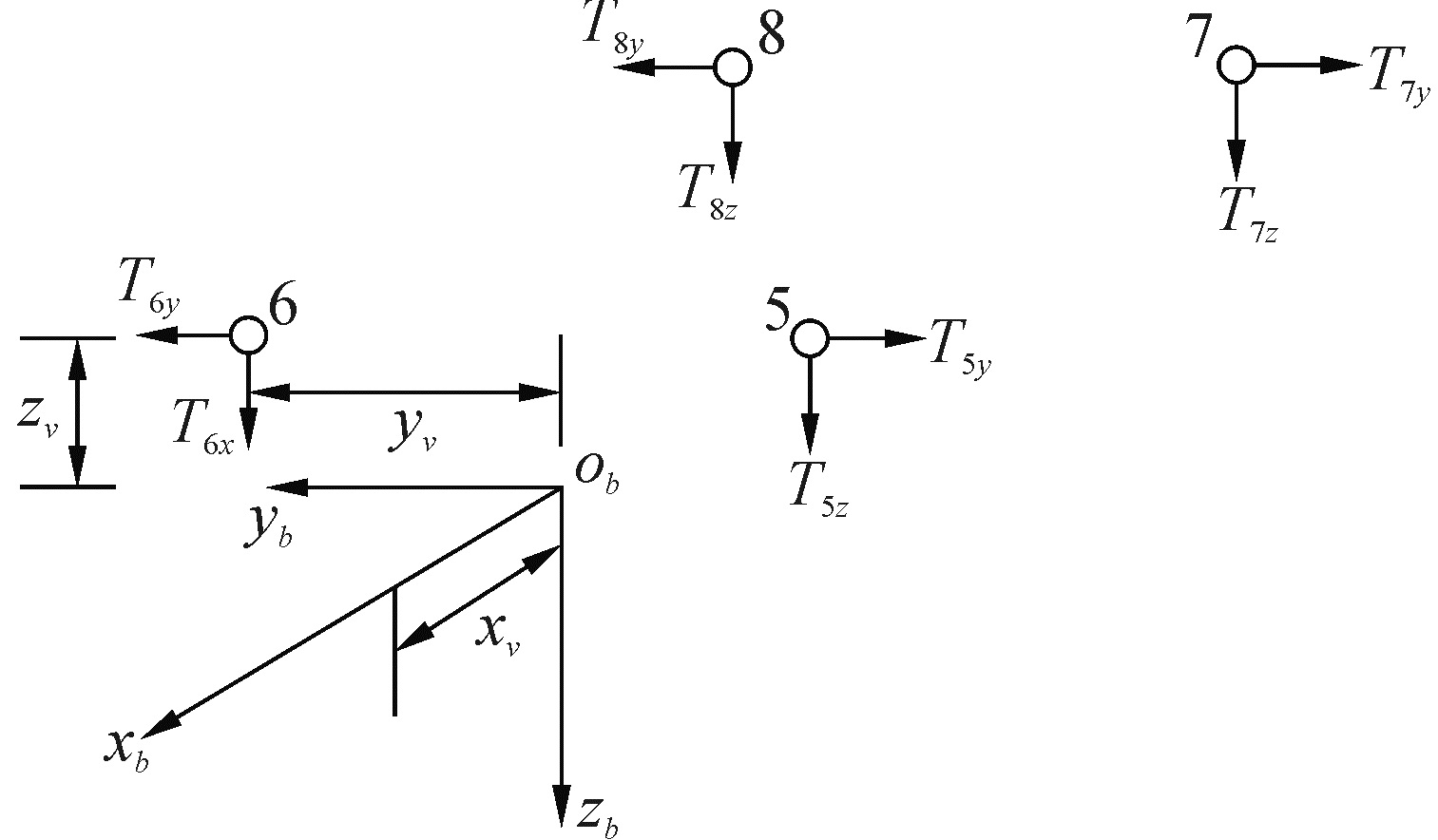
图 3中,ROV本体受到4台垂直推进器的推力作用,其受到推力正方向与obzb轴的夹角都为20°,经过推力分解,则垂直推进器推力对ROV本体产生的合推力可分别用下式表示:
| $ \left\{ \begin{array}{l} {X_{\rm{v}}} = 0\\ {Y_{\rm{v}}} = - {T_5}\sin {\beta _{\rm{v}}} + {T_6}\sin {\beta _{\rm{v}}} - {T_7}\sin {\beta _{\rm{v}}} + {T_8}\sin {\beta _{\rm{v}}}\\ {Z_{\rm{v}}} = {T_5}\cos {\beta _{\rm{v}}} + {T_6}\cos {\beta _{\rm{v}}} + {T_7}\cos {\beta _{\rm{v}}} + {T_8}\cos {\beta _{\rm{v}}} \end{array} \right. $ | (3) |
|
Download:
|
| 图 3 垂直推进器的推力对ROV本体的推力矩示意图 Fig. 3 The thrust moment of vertical propeller on ROV | |
式中:T5、T6、T7、T8分别为ROV本体受到5#、6#、7#、8#垂推的推力;Xv、Yv、Zv分别为ROV本体受到垂推沿obxb轴、obyb轴、obzb轴的合推力;βv为垂推的推力方向与obzb轴的夹角。
2) 垂直推进器的合推力矩。
从图 3及表 1可知,由于4台垂直推进器安装于ROV重心的上方,且成矢量对称布置,因此会对ROV本体产生相应的三个自由度的推力矩,图 3所示的是4台垂直推进器推力对坐标系{b}的各轴产生的推力矩的示意图。
4台垂直推进器的推力经过力的分解后,其各自分解力的正方向如图 3所示。则4台垂直推进器推力对ROV本体产生的合推力矩在坐标系{b}上的三个轴上可用下式表示:
| $ \left\{ \begin{array}{l} {K_{\rm{v}}} = - {T_{5y}}{z_{\rm{v}}} - {T_{5z}}{y_{\rm{v}}} + {T_{6y}}{z_{\rm{v}}} + {T_{6z}}{y_{\rm{v}}} - {T_{7y}}{z_{\rm{v}}} - \\ \;\;\;\;\;\;\;{T_{7z}}{y_{\rm{v}}} + {T_{8y}}{z_{\rm{v}}} + {T_{8z}}{y_{\rm{v}}}\\ {M_{\rm{v}}} = - {T_{5z}}{x_{\rm{v}}} - {T_{6z}}{x_{\rm{v}}} + {T_{7z}}{x_{\rm{v}}} + {T_{8z}}{x_{\rm{v}}}\\ {N_{\rm{v}}} = - {T_{5y}}{x_{\rm{v}}} + {T_{6y}}{x_{\rm{v}}} + {T_{7y}}{x_{\rm{v}}} - {T_{8y}}{x_{\rm{v}}} \end{array} \right. $ | (4) |
式中:Kv、Mv、Nv分别为垂直推进器对ROV本体在obxb轴、obyb轴、obzb轴方向的合推力矩。
1.2.3 过驱动推进系统合推力由方程组(1)~(4),ROV所安装的8台推进器对ROV本体产生六自由运动度的合推力:
| $ \left\{ \begin{array}{l} {X_{\rm{T}}} = {X_{\rm{h}}} + {X_{\rm{v}}}\\ {Y_{\rm{T}}} = {Y_{\rm{h}}} + {Y_{\rm{v}}}\\ {Z_{\rm{T}}} = {Z_{\rm{h}}} + {Z_{\rm{v}}}\\ {K_{\rm{T}}} = {K_{\rm{h}}} + {K_{\rm{v}}}\\ {M_{\rm{T}}} = {M_{\rm{h}}} + {M_{\rm{v}}}\\ {N_{\rm{T}}} = {N_{\rm{h}}} + {N_{\rm{v}}} \end{array} \right. $ | (5) |
式中:XT、YT、ZT分别为8台推进器对ROV本体产生的纵向推力、横向推力和垂向推力;KT、MT、NT分别为8台推进器对本体产生的横倾推力矩、纵倾推力矩、偏航推力矩。
由式(1)~(5),作用在ROV本体上的六自由度的控制矢量可用下式表示:
| $ \mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{B}}\left( \beta \right)\mathit{\boldsymbol{T}} $ | (6) |
式中:τ=[XT YT ZT KT MT NT]T为作用在ROV本体上的六自由度推力矢量;T=[T1 T2 T3 T4 T5 T6 T7 T8]T为推进器输出的推力矢量;B(β)为推进器矢量布置矩阵。
1.3 ROV推力分配方法 1.3.1 水平面运动推力分配方法当水平面三个期望推力对应的控制电压同时输出时,可能导致水平面的某个推进器的推力饱和。为了避免这种现象,首先可将水平面的三个期望控制电压进行归一化:
| $ \left\{ \begin{array}{l} {\delta _1} = \left| {{u_X}} \right|/{u_{\rm{H}}}\\ {\delta _2} = \left| {{u_Y}} \right|/{u_{\rm{H}}}\\ {\delta _3} = \left| {{u_Z}} \right|/{u_{\rm{H}}} \end{array} \right. $ | (7) |
式中:uH=|uX|+|uY|+|uN|为水平方向推力对应的控制电压的绝对值之和;δ1、δ2、δ3分别为归一化后纵向控制电压、横向控制电压和偏航控制电压。
然后根据纵向、横向和偏航力矩的权重,分别将归一化后的期望控制电压进行放大:
| $ \left\{ \begin{array}{l} X = {k_1}{u_X}{\delta _1}\\ Y = {k_2}{u_Y}{\delta _2}\\ N = {k_3}{u_N}{\delta _3} \end{array} \right. $ | (8) |
式中:X、Y、N为分别为期望的纵向推力、期望的横向推力和期望偏航力矩;k1、k2、k3为分别为纵向、横向推力和偏航力矩对应权重系数。
最后,根据ROV的4水平台推进器成矢量对称布置的特点,可将纵向推力、横向推力和偏航推力矩按照下式进行分配:
| $ \left\{ \begin{array}{l} {T_{{e_1}}} = X + Y + N\\ {T_{{e_2}}} = X - Y - N\\ {T_{{e_3}}} = - X + Y - N\\ {T_{{e_4}}} = - X - Y + N \end{array} \right. $ | (9) |
式中:Te1、Te2、Te3、Te4分别为1#、2#、3#、4#推进器的期望推力。
1.3.2 垂直面运动推力分配方法当垂直面三个期望推力对应的控制电压同时输出时,可能导致垂直面某个推进器的推力输出饱和。为了避免这种现象,首先可将垂直面的三个期望控制量进行归一化:
| $ \left\{ \begin{array}{l} {\varepsilon _1} = \left| {{u_Z}} \right|/{u_{\rm{V}}}\\ {\varepsilon _2} = \left| {{u_K}} \right|/{u_{\rm{V}}}\\ {\varepsilon _3} = \left| {{u_M}} \right|/{u_{\rm{V}}} \end{array} \right. $ | (10) |
式中:uV=|uZ|+|uK|+|uM|为垂直推力对应控制电压的绝对值之和;ε1、ε2、ε3分别为归一化的期望垂向控制电压、横倾控制电压和纵倾控制电压。
然后,将归一化后的垂直面期望控制量放大,如下式
| $ \left\{ \begin{array}{l} Z = {l_1}{u_Z}{\varepsilon _1}\\ K = {l_2}{u_K}{\varepsilon _2}\\ M = {l_3}{u_M}{\varepsilon _3} \end{array} \right. $ | (11) |
式中:Z、K、M为分别为期望的纵向推力、横向推力和偏航力矩, l1、l2、l3分别为垂向推力、横倾力矩和纵倾推力矩对应的权重系数。
最后,根据ROV的4台垂直推进器成矢量对称布置的特点,由推力合成原则,可将垂向推力、横倾力矩和纵倾力矩分别按照下式进行推力分配:
| $ \left\{ \begin{array}{l} {T_{{e_5}}} = Z - K - M\\ {T_{{e_6}}} = Z + K - M\\ {T_{{e_7}}} = Z - K + M\\ {T_{{e_8}}} = Z + K + M \end{array} \right. $ | (12) |
式中:Te5、Te6、Te7、Te8分别为5#、6#、7#、8#推进器的期望推力。
1.3.3 螺旋桨数学模型作业型ROV采用的都是液压控制的螺旋桨推进器,螺旋桨转矩的计算式为
| $ Q = {K_{\rm{Q}}}\rho {n^2}{D^5} $ | (13) |
式中:Q为螺旋桨转矩,N·m;KQ为螺旋桨的转矩系数;ρ为海水密度,kg/m3;n为螺旋桨转速,r/s;D为螺旋桨直径,m。
螺旋桨输出推力的计算式为
| $ T = {K_{\rm{T}}}\rho {n^2}{D^4} $ | (14) |
式中KT为螺旋桨的推力系数。
推进器的功率可由下式计算:
| $ P = Q\omega $ | (15) |
式中ω为螺旋桨转速,rad/s。
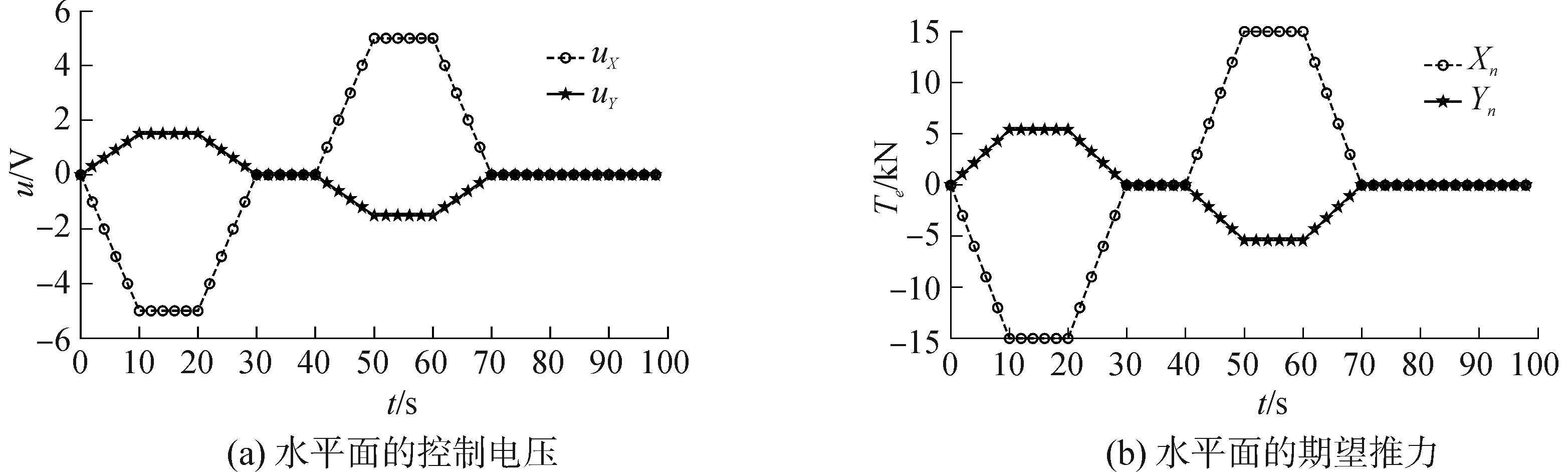
3 仿真结果及分析 3.1 仿真初始条件查阅相关资料可知:每台水平推进器最大输出推力为6 kN,根据表 1中推进器安装参数,4台水平推进器可输出最大纵向推力为15 kN、最大横向推力为18 kN。每台垂直推进器最大输出推力为5 kN,则4台垂直推进器可输出最大垂向推力18 kN。仿真初开始时,北东坐标系下水下机器人的初始位置和速度为0,姿态角和角速度为0。从零时刻开始,操纵手柄(Joystick)输出水平面2个自由度(纵向、横向运动)控制电压,如图 4所示,同时其他四个自由度度自动控制有效。
|
Download:
|
| 图 4 期望推力及控制电压 Fig. 4 Expected thrust and control voltage | |
图 4(a)中uX代表Joystick输出的纵向控制电压,uX∈[-5 5] V,uX=5 V对应图 4(b)中纵向推力Xn为15 kN。图 4(a)中uY代表Joystick输出的纵向控制电压,uY∈[-5 5] V,uY=5 V对应图 4(b)中的横向推力Yn为18 kN。
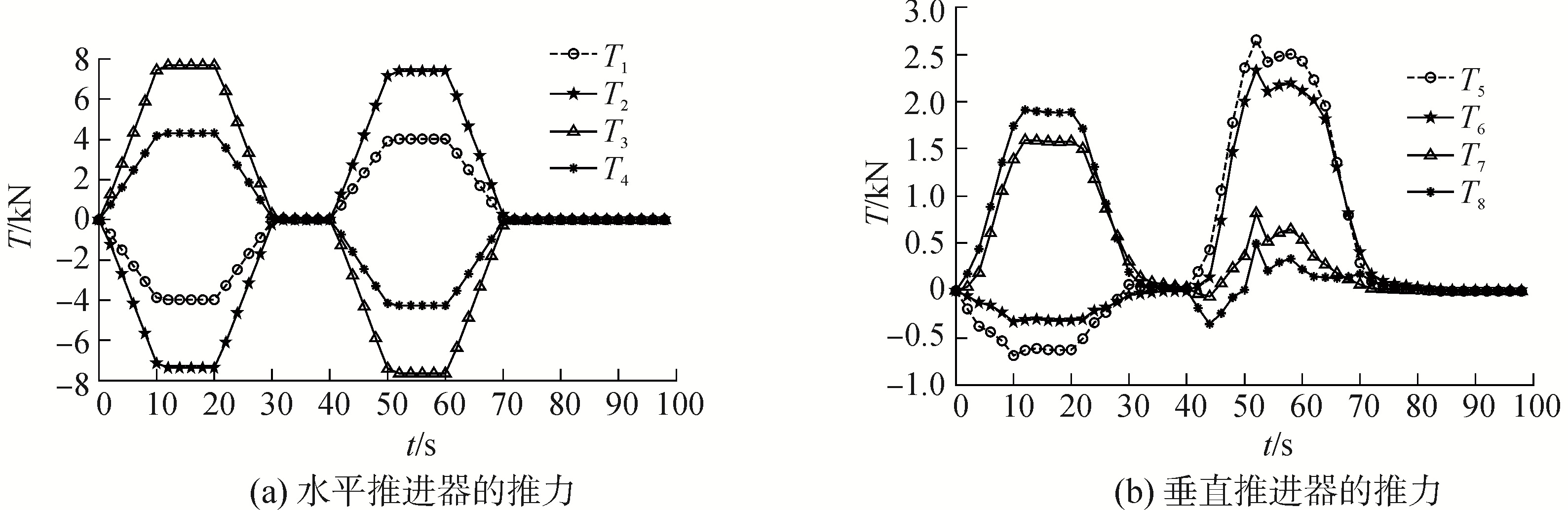
3.2 未归一化伪逆推力分配仿真将未归一化的期望控制推力使用伪逆分配方法进行水下机器人推力分配仿真,即图 4(b)中的纵向和横向推力输入到仿真模型中,其他仿真初始条件设置和3.1节一致,推力分配的结果如图 5所示。
|
Download:
|
| 图 5 未归一化伪逆法的推进器响应 Fig. 5 Thrust response based on pseudo inverse method | |
图 5(a)中,可以看出推进器T1和T4出现的最大推力为4 kN,推进器T2和T3出现的最大推力为7.4 kN,超过了水平推进器最大推力6 kN,T2和T3出现了推力饱和现象。
图 5(b)中,推进器T5出现的最大推力为2.7 kN,推进器T6出现的最大推力为2.3 kN,推进器T7出现的最大推力为1.6 kN,推进器T8出现的最大推力为1.9 kN,垂直推进器未出现了推力饱和现象。
可以看出:在没有对水平面和垂直面的控制量进行归一化条件下,而直接使用伪逆方法进行推力分配时,水平推进器推力出现了饱和现象。
3.3 归一化直接逻辑推力分配仿真图 6(a)中所示的是归一化后期望推力,可以看出归一化后的期望推力值减小,纵向最大推力由15 kN减小至11.5 kN,横向最大推力值由5.4 kN减小至1.25 kN,与图 4(b)相比较,归一化后的期望纵向和横向推力减小。图 6(b)中所示的是归一化的力矩,其中横倾力矩最大值为0.2 kN·m,纵倾力矩最大值为2.5 kN·m,偏航力矩最大值为2.1 N·m。

|
Download:
|
| 图 6 归一化后期望推力及推力矩 Fig. 6 The normalized desired forces and moments | |
可已看出:对控制电压进行归一化后,可使每个自由度期望推力或推力矩可按照期望权重减小。
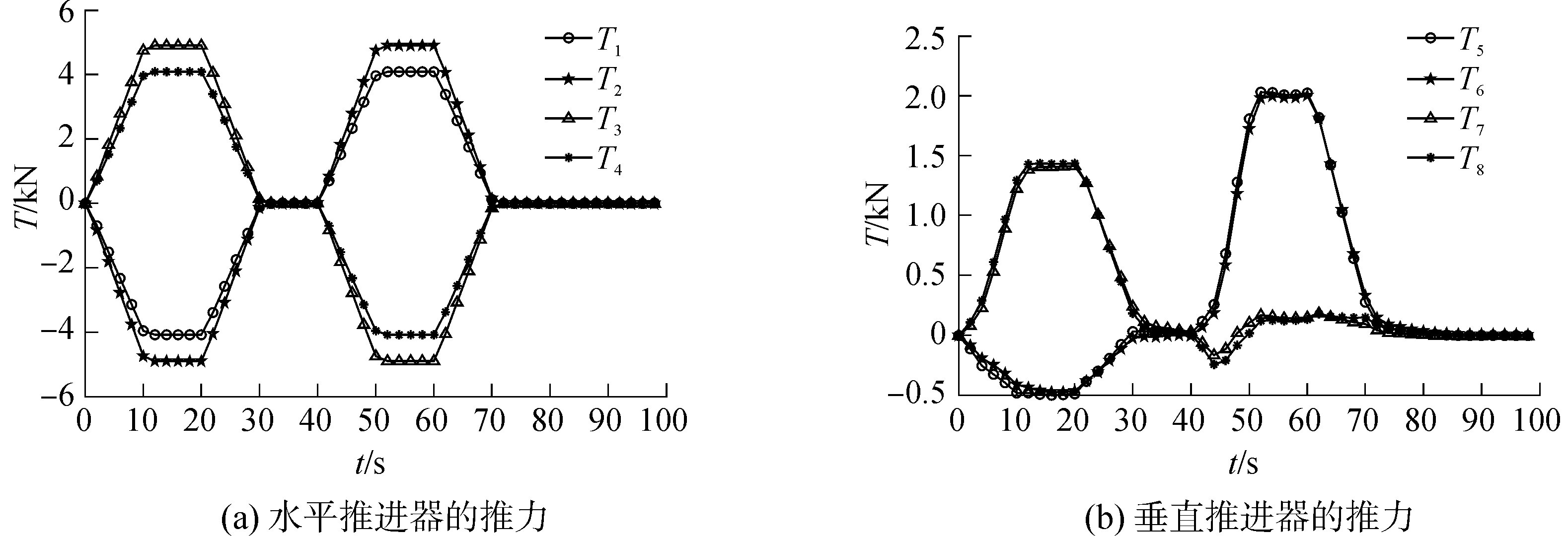
图 7(a)是4台水平推进器的推力分配结果,T1和T4最大推力为4.1 kN,和T3最大推力为4.9 kN,没有出先推力饱和情况。
|
Download:
|
| 图 7 归一化直接逻辑法的推力分配结果 Fig. 7 Thrust allocation by normalized direct logical | |
图 7(b)是4台垂直推进器的推力分配结果,T5最大推力为2.1 kN,T6最大推力为2 kN,T7最大输出力为1.4 kN,T8最大推力为1.45 kN,没有出先推力饱和情况。
可以看出:在对水平面和垂直面的控制量归一化后,再对ROV进行推力分配,实现了ROV的推力分配目标,且所有推进器都没有出现饱和现象。
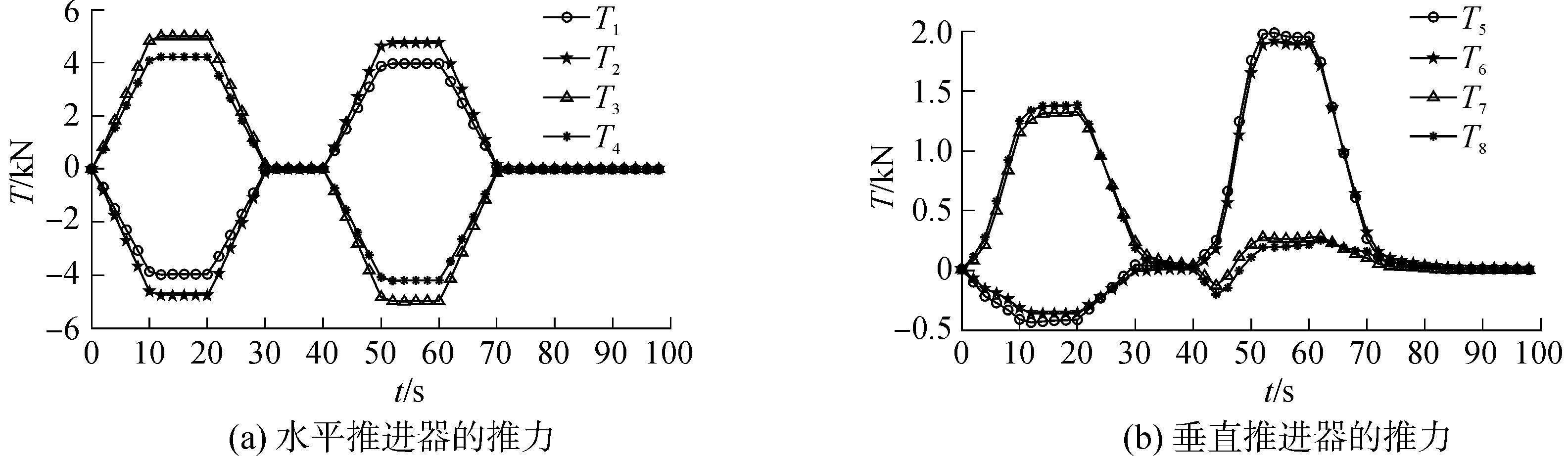
3.4 归一化伪逆推力分配仿真将图 6(a)中的纵向和横向推力输入到仿真模型中,其他仿真初始条件设置和3.1节一致,使用伪逆分配方法进行水下机器人的运动控制仿真,但进行推力分配的输入是归一化水平面和垂直面控制量,推力分配的仿真结果如图 8所示。
|
Download:
|
| 图 8 归一化伪逆法的面推进器响应 Fig. 8 Thrust allocation of normalized pseudo inverse method | |
图 8(a)是水平推进器的推力分配结果,其中,推进器T1出现的最大推力为4 kN,T2出现的最大推力为4.8 kN,T3出现最大推力为5 kN,T4出现的最大推力为4.2 kN,水平推进器没有饱和情况。
图 8(b)是垂直推进器的推力分配结果,其中,推进器T5出现的最大推力为2 kN,T6出现的最大推力为1.9 kN,T7出现的最大输出力为1.3 kN,T8出现的最大推力为1.4 kN,垂直推进器没有饱和情况。
可以看出:在对水平面和垂直面的控制量归一化后,再利用伪逆推力分配方法对ROV进行推力分配,实现了ROV运动控制目标,且所有推进器推力都没有出现过饱和现象。因此,为了防止多个自由度控制量同时输出而导致推力分配的饱和现象,必须对控制电压进行归一化处理。
3.5 三种推力分配方法消耗功率对比在3.1节所设置的仿真初始条件下,可通过计算作业型运动控制所消耗功率,来比较三种推力分配方法的优化效果。每台推进器的推力、转速和转矩可由式(13)、(14)计算,所消耗功率可由式(15)计算,则ROV所消耗功率为8台推进器功率之和。三种推力分配方法所消耗功率对比如图 9。

|
Download:
|
| 图 9 三种分配方法消耗功率对比 Fig. 9 Power consumption of three allocation methods | |
图 9中,未归一化伪逆方法所消耗功率最高,其峰值为122 kW,查询相关资料可知,目标ROV的最功率容量为112 kW,这种推力分配时的功率消耗不允许的。将水平面和垂直面的控制量分别进行归一化后,直接逻辑分配和伪逆分配法所消耗功率基本一致,两者的峰值功率有所差别,伪逆法的为80.1 kW,直接分配阀的为79.7 kW,差别为0.5%。因此,可以认为归一化的直接逻辑分配法是一种近似的优化分配方法。
4 结论1) 根据过驱动作业型ROV总体结构中推进器的空间分布关系,推导出推进器的推力和作用到ROV本体上合力之间的关系,建立了过驱动ROV推进系统的数学模型。
2) 先将水平面控制电压和垂直面控制电压进行归一化,然后分别按照权重进行放大后,再对ROV进行推力分配,可有效解决推进器饱和问题。
3) 根据多个推进器成矢量对称布置的特点,提出一种先将控制电压归一化,再进行直接逻辑推力分配方法,可实现ROV的六自由度运动控制。
4) 直接逻辑分配法是一种非常接近最优能耗的推力分配方法,具有直观、简单、效率高和实时性强等显著优点。
| [1] |
CHRIST R D. The ROV manual: a user guide for observation-class remotely operated vehicles[R]. Butterworth Heinemann, 2007.
(  0) 0)
|
| [2] |
李新飞, 姜述强, 崔洪斌. 考虑螺旋桨负载的液压推进器动力学响应分析[J]. 华中科技大学学报, 2017, 45(2): 23-28. LI Xinfei, JIANG Shuqiang, CUI Hongbin. Dynamics analysis of hydraulic thruster with propeller load[J]. J Huazhong Univ of Sci & Tec, 2017, 45(2): 23-28. (  0) 0)
|
| [3] |
JOHANSEN T A, FOSSEN T I. Control allocation-a survey[J]. Automatica, 2013(49): 1087-1103. (  0) 0)
|
| [4] |
JOHANSEN T A, FOSSEN T I, BERGE S P. Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming[J]. IEEE Transactions on control system technology, 2004, 12(1): 211-216. DOI:10.1109/TCST.2003.821952 (  0) 0)
|
| [5] |
俞建成, 张艾群, 王晓辉. 7000米载人潜水器推进器故障容错控制分配研究[J]. 机器人, 2006, 33(5): 519-524. YU Jiancheng, ZHANG Aiqun, WANG Xiaohui. Research on thruster fault tolerant control allocation of a 7 000 m manned submarine[J]. Robot, 2006, 33(1): 519-524. (  0) 0)
|
| [6] |
贾立娟, 秦玉峰, 张选明, 等. 微型缆控水下观测机器人推进动力分析[J]. 海洋技术学报, 2014, 33(2): 104-110. JIA Lijuan, QIN Yufeng, ZHANG Xuanming, et al. Analysis on the propulsive power of a novel micro-ROV[J]. Journal of ocean technology, 2014, 33(2): 104-110. (  0) 0)
|
| [7] |
范士波.深海作业型ROV水动力试验及运动控制技术研究[D].上海: 上海交通大学, 2013: 1-16. FAN Shibo. Hydrodynamics test and research on motion control for deep sea work-class remotely operated vehicle[D]. Shanghai: Shanghai Jiao Tong University, 2013: 1-16. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2335511 (  0) 0)
|
| [8] |
SOYLU S, BUCKHAM B J, PODHORODESKI R P. A chattering free sliding-mode controller for underwater vehicles with fault-tolerant infinity-norm thrust allocation[J]. Ocean engineering, 2008, 35(16): 1647-1659. DOI:10.1016/j.oceaneng.2008.07.013 (  0) 0)
|
| [9] |
AKMAL M, YUSOFF M, ARSHAD M R. Active fault tolerant control of a remotely operated vehicle propulsion system[J]. Procedia engineering, 2012, 41: 622-628. DOI:10.1016/j.proeng.2012.07.221 (  0) 0)
|
| [10] |
黄海, 万磊, 庞永杰, 等. SY_遥控式水下机器人推力器容错控制的研究[J]. 应用基础与工程科学学报, 2012, 20(6): 1118-1127. HUANG Hai, WAN Lei, PANG Yongjie, et al. Fault tolerance control of SY-Ⅱ remote operated vehicle[J]. Journal of basic seience and engineering, 2012, 20(6): 1118-1127. DOI:10.3969/j.issn.1005-0930.2012.06.018 (  0) 0)
|
| [11] |
魏延辉, 陈巍, 杜振振, 等. 深海ROV伺服控制方法研究及仿真[J]. 控制与决策, 2015, 33(10): 1785-1790. WEI Yanhui, CHEN Wei, DU Zhenzhen, et al. Servo control method of ROV and Simulation[J]. Control and decision, 2015, 33(10): 1785-1790. (  0) 0)
|
| [12] |
YANG Shizhi, WANG Lei, SUN Pan. Optimal thrust allocation logic design of dynamic positioning with pseudo-inverse method[J]. Journal of Shanghai Jiao Tong University, 2011, 16(1): 118-123. DOI:10.1007/s12204-011-1104-9 (  0) 0)
|
| [13] |
KIRKEBY M. Comparison of controllers for dynamic positioning and tracking of ROV minerva[D].[s.l.]: NTNU, 2010.
(  0) 0)
|
| [14] |
CANDELORO M. Design of observers for DP and tracking of ROV minerva with experimental results[D].[s.l.], NTNU, 2011.
(  0) 0)
|
| [15] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. New York: John Wiley & Sons Ltd, 2011: 1-10.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


