高光谱遥感(hyperspectral remote sensing)是指利用很多窄的电磁波波段获取物体有关数据的技术。实现了地物空间信息、光谱信息的同步获取,在相关领域中具有很高的应用价值和广阔的发展前景。
高光谱图像的三个显著特点可以概括如下[1]:1)高光谱图像具有高的光谱分辨率,这使得它能够解决许多多光谱不能解决的问题;2)相邻谱带间存在较强的相关性,这一特点为其降维处理(包括波段选择、特征提取等)和谱间压缩提供可能;3)高光谱图像随着维数的增加,超立方体的体积集中于角端,超球体和椭球体的体积集中在外壳,这些特点进一步为高光谱图像处理提供了理论依据。
高光谱图像拥有较高的谱分辨力,但这种优越性是以其较大的数据量及较高的数据维为代价,使得数据中包含了大量的冗余信息,给高光谱图像数据的分析与处理带来较大的困难。空间分辨率是指传感器所能分辨的最小的目标大小,或指影像中一个像素点所表示的地面面积,它是评价传感器性能和遥感信息的重要指标之一,也是识别地物形状大小的重要依据[2]。高光谱图像的低空间分辨率导致了混合像素的广泛存在,从而只能展示出模糊的类别信息[3]。在实际应用中,分析者常常需要更为简洁精确的信息,为此,各种高光谱图像处理技术相继发展起来。
SVM(support vector machine)是在统计学习理论的基础上发展起来的新一代机器学习理论,根据有限的样本信息为基础,寻求模型的复杂度和学习能力之间的最佳折衷,以期获得最好的推广能力[4]。SVM有着坚实的理论基础和较强的推广能力,因此在解决小样本、非线性和高维模式问题中表现出特有的优势[5]。在高光谱数据处理中,SVM显著的优势和良好的效果已得到了充分的显示,并已在波段选择、据压缩、光谱分类、光谱端元选择、光谱解混、亚像元定位及异常检测等领域被广泛应用。
1 SVM理论 1.1 SVMSVM理论从分类的角度来说,是一种广义的线性分类器,它是在线性分类器的基础上,通过引入结构风险最小化原则、最优化理论和核函数演化而成的[6]。原始的SVM理论用于处理两类分类问题,其示意图见图 1。分类原理可概括为:寻找一个分类超平面,使得训练样本中的两类样本点能被分开,并且距离该平面尽可能地远。

|
Download:
|
| 图 1 最优分类面示意图 Fig. 1 Diagram of optimization classification surface | |
核技术的成功应用使得SVM的分类性能发生质的提高。引入核函数的概念之后,SVM的基本思想可以概括简单为:首先通过非线性变换将输入空间变换到一个高维空间,然后在这个新空间中求取最优线性分类面,而这种非线性变换是通过定义适当的内积函数来加以实现的。较为常用的核函数有线性核函数、多项式核函数、高斯核函数等。文献[7]对SVM的机理及应用进行了详细的研究和讨论。
SVM的潜在应用价值吸引了众多学者的关注,近几年出现了许多发展和变形的SVM类型,如v-SVM[8]、最小二乘SVM(least squares support vector machine,LSSVM)[9]、加权SVM[10]、鲁棒SVM[10-11]、关联向量机RVM[12]、超球体支持向量机(也称支持向量数据描述(support vector data description,SVDD))[13]、半监督支持向量机(semi-supervised support vector machines,SSSVM)等,文献[14]对其中一些类型SVM进行了对比介绍。SVM的优化算法也得到了长足的发展,其中较为著名的有分解算法[15]、最近邻法[16]和序贯最小优化算法(sequential minimal optimization,SMO)[17],等。
1.2 LSSVM在众多SVM的发展类型中,最小二乘SVM(LSSVM)因其高效的分类和回归功能而得到广泛的使用。更为主要的,LSSVM的数学模型是一个仅带有等式约束的误差代价函数平方和的优化问题,其求解可在线性系统中进行,并拥有高效的分类和回归功能,因而在各个领域得到广泛的使用。LSSVM的数学形式描述如下
| $ \begin{array}{c} \mathop {{\rm{min}}}\limits_{w, b, e} \left( {w, e} \right)\; = \;\frac{1}{2}\;\left\| \mathit{\boldsymbol{w}} \right\|{\;^2} + \frac{\gamma }{2}\sum\limits_{i = 1}^n {e_i^2} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{y_i} = \; < \mathit{\boldsymbol{w}}, \varphi ({x_i}) > + b + {e_i}, \\ i = 1, 2, \ldots , n, \;\;\;\;\gamma \; > \;0 \end{array} $ | (1) |
相应的的对偶问题为
| $ \begin{array}{c} \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{w}}, b, e, a} \;L\left( {\mathit{\boldsymbol{w}}, b, e, \alpha } \right) = \;\\ \mathit{\boldsymbol{J}}\left( {w, e} \right) - \sum\limits_{i = 1}^n {\{ < \mathit{\boldsymbol{w}}, \varphi ({x_i}) > + b + {e_i} - {y_i}\} } \end{array} $ | (2) |
其最优KKT条件为
| $ \left[ {\begin{array}{*{20}{c}} 0&{1_v^{\rm{T}}}\\ {{1_v}}&{K + 1/\gamma } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} b\\ \alpha \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ y \end{array}} \right] $ | (3) |
基本的SVM的分类理论是用来处理两类分类问题的。对于多类问题,SVM的解决途径一般有两种:1)直接使用一个优化公式实现多分类设计;2)通过多个SVM二值分类器的相互组合实现多类分类。第一种方法以Weston提出的多值分类算法为代表,在经典的SVM理论的基础之上重新构造多值分类模型[18]。但这种算法选择的目标函数过于复杂而难以实现,不仅计算量大,而且在分类精度上也不占优势。因此,第二种方法更为常用。组合多个二值分类器常见构造方法有:1-a-r SVMs法和1-a-1SVMs法[19-20]、有向无环图支持向量机(DAG-SVM)[21]、纠错编码支持向量机(ECOC-SVMS)[22]、层次支持向量机(H-SVMS)[23]等。
对大量类别进行识别时,当前常用的1-a-r SVMs和1-a-1SVMs的训练速度将会大大降低;ECOC-SVMS的训练速度较“一对多”有明显改进,但其分类效果受错误码的相关性影响很大,另外对类别数量较多时效果不佳[24];DAG-SVMS方法简单易行,但因自上而下的“误差积累”现象而产生误差的积累效应,将会严重影响分类性能。为解决以上问题,文献[25]对多类目标分类器的结构进行了简化,大大减少了子分类器数目,进而提高分类速度。文献[26]改进了二叉树支持向量机多类分类方法,能够克服类别数量悬殊大、数据干扰等测量带来的不利因素,同时获得更大的划分空间。
2 SVM在高光谱图像波段选择技术中的应用波段选择能够有效地去除高光谱图像较高数据维所导致的冗余信息,不仅能够减少后续处理中的计算量,还能够避免数据处理时的过适应现象。
目前的波段选择方法多为将原始数据各波段按照某种规则排序和去除,最终选取最优的几个波段。但传统的波段选择方法需要训练的分类器过多而导致计算量过大,或者缺乏类别可分性的反馈指导[27]。随后提出的基于平均可分性统计的波段选择方法[28]抗噪声能力又较差。文献[29]将支持向量机应用于波段选择。该方法首先定义各波段相应的单位向量,再计算决策函数的梯度与这些向量的夹角作为各波段的排序模糊因子,但该方法存在一定的选择误差[29]。此外,以上两种算法所选择的波段易于集中在若干个连续的波段子空间上,这也将影响低分类精度。
文献[30]中提出一种基于支持向量机和子空间划分的波段选择方法。在该文献中,敏感度分析方法被用于支持向量机判决函数,同时配合子空间划分,最后在每个子空间选择支持向量机敏感度分析排序靠前的波段。为减少统计分类影响的计算量,该文利用SVM自动选择支持向量,仅考查各波段对支持向量分类的整体影响作为全局统计的近似。该方法避免了所选取的波段过于集中的缺点,减小了冗余并携带了更多的信息,进而改善了分类精度,并有利于数据的其他后续应用。
但是已有研究表明,不一定所有和分类目标相关度高的特征组合就一定能取得最高分类正确率[31]。高光谱遥感图像的波段选择作为一个非常复杂的组合优化问题,一些含有较少信息量的波段反而可能对分类有重要的作用[32]。为此,利用搜索算法结合评估函数来搜寻优化的波段子集将成为较为有效的方法。
例如文献[32]中,使用支持向量机和遗传算法相结合的搜索算法(GA-SVM)进行波段选择。首先利用条件互信息将波段分组,使用GA-SVM方法搜索出相对最优的波段组合,然后剔除并合并相应的波段分组,最后再次利用GA-SVM对初优化波段组进行搜索得到相对更优的结果。该法缩小了遗传算法的搜索空间,减少了计算量,还避免了仅依赖单波段信息进行剔除的绝对性,从组合优化的角度对问题进行求解,而且避免了由于噪音扰动使得条件互信息分组法出现冗余和噪音分组的情况,一定程度上提高了波段组合的分类准确率[32]。
另外,SVM因其在高光谱遥感分类方面的优越性,通常用于波段选择后数据的分类,因此亦可将其作为波段选择算法的性能衡量标准,用以评价各种波段选择算法的性能及类别区分度[33]。而在采用SVM方法对高光谱遥感影像进行分类时,通常情况下波段选择和SVM参数优化是分开实现的[34]。文献[35]提出一种结合粒子群优化(PSO)方法的PSO-BSSVM分类模型,能够自动选择合适的波段影像并同时对SVM核函数参数进行优化。该方法能够智能地在分类精度和波段之间取得很好的平衡,自动寻找到合适的波段影像和SVM参数,进而提高了高光谱遥感影像的分类精度[35]。
3 SVM在高光谱图像压缩编码技术中的应用高光谱遥感图像可以看作由二维的空间域和一维的光谱域组成的三维立体图像,在空间相关性的基础上还增加了谱间相关性,数据的压缩主要是去除这两类相关性。
目前,高光谱遥感图像压缩方法主要分为预测方式、矢量量化、变换编码及多种方法结合使用的综合方法。高光谱遥感图像编码中的变换方法,主要有离散余弦变换(discrete co-sine transform,DCT)、KLT(karhunen-loeve transform)和离散小波变换(discrete wavelet transform,DWT)[36]。
Robinson首次将SVM应用于静态图像压缩,提出了结合SVM与DCT的压缩方法,利用SVM对DCT系数进行压缩,得到了比JPEG明显好的压缩效果[37]。此后,文献[38]提出基于SVM的小波图像压缩方法,文献[39]将其用于遥感图像压缩。
由于小波支持向量回归(wavelet support vector regression,WSVR)具有对突变信号逐步精细的描述的特性,因而WSVR能够以更高的精度逼近任意函数[36]。为此,文献[36]提出一种结合WSVR和三维小波变换的方法,用于实现高光谱遥感图像的压缩。该方法首先对图像进行三维整数小波变换,然后通过小波支持向量回归学习逼近小波系数,最后对所得结果进行熵编码[36]。
支持向量数据描述(SVDD)奇异检测算法也可用于高光谱图像的压缩,此时能够解决现有高光谱图像压缩方法存在的问题,如压缩比与恢复信息准确性的矛盾[24]。该方法首先根据光谱相似性进行空间聚类实现区域分割,大块区域像元光谱取均值作为背景光谱,用SVDD算法检测与局部邻域背景不同的小目标,接着对背景和小目标光谱数据进行无损压缩,最后对整个数据立方体进行大比例有损压缩[24]。
4 SVM在高光谱图像分类技术中的应用分类是高光谱数据处理的起步最早、研究最多、最基本、最重要的研究内容之一。它是人们从遥感影像上提取有用信息的重要途径之一。分类后产生的专题地图可以清晰地反映出地物的空间分布,便于人们从中认识和发现其规律,使高光谱遥感图像具有真正的使用价值并有效的投入到实际应用中。
高光谱图像处理中常用的几种典型分类方法有:光谱角匹配(spectral angle match,SAM)、最大似然(maximal likelyhood,ML)(又称Bayes准则)、Fisher判别分析等。具有特有优势的分类器SVM,在高光谱图像分类中同样表现出良好的性能,并在遥感图像分类领域已得到广泛关注。文献[40]对SVM在高维多光谱数据分类中的快速算法、多类分类算法,边界样本提取等问题分别进行了研究。文献[41]系统研究了SVM在光谱遥感影像分类中的相关问题。文献[42]利用高光谱图像中地物的谱域信息和空域信息分别生成核函数,并采用不同策略构造组合核函数,用于SVM分类器。文献[6]提出一种二次分类的多类支持向量机解决高光谱图像数据分类问题。
J.A.K,Suykens提出的LSSVM的加权方法,能够有效控制高光谱图像中受到噪声干扰严重的像元和野值点,从而获得了更加良好的鲁棒特性和推广能力[17]。但这种加权的方法一次训练所需要的计算量一般较大,尤其是当训练样本较多时,该方法将变得极为耗时[43]。为进一步提高分类分析效果,基于LSSVM理论,文献[43]中提出了一种像元、特征和类别进行多重加权处理的复选性加权分类方法。
像元加权,即是将不同样本相应的分类误差在代价函数分配不同的权值,能够使异常程度不同的样本在分类模型中加以体现。特征加权,即将Fisher线性判别分析中的类内散度矩阵的逆矩阵,应用于高光谱图像分类之中。该矩阵可以很好地体现不同特征对于分类效果的不同贡献[44]。类别加权,即指通过重置式(3)矩阵中特定类别样本对应位置的对角元素值,以达到改变对各个类别的重视程度,从而保护感兴趣类别,抑制非重要类别的目的[43]。因此,该方法能有效地提高感兴趣类别的分类精度。
以上三种加权方法可以单独使用,也可以以任何复选方式组合使用,以达到最佳分类效果。这种方法能够使异常程度不同的训练样本得到不同的控制;类别可分性不同的特征得到不同的体现;重要性不同的数据类别得到不同的对待,最终实现更好的数据分析效果[43]。
近年SVM算法在高光谱分类领域也得到了一定的发展。文献[45]将超球体多类支持向量机、最小二乘超球体多类支持向量机、半模糊最小二乘超球体多类支持向量机用于高光谱遥感影像分类中。文献[46]提出了基于遗传算法的关联向量分类算法(GA-RVM),该方法使用遗传算法(GA)搜索面向RVM的最优参数和特征子空间。文献[47]提出的一种综合利用地物的空域和光谱域信息的SVM高光谱图像分类算法。随着半监督学习发展,半监督支持向量机在高光谱图像分类中也有了长足进步[48],如基于图理论的半监督学习分类[49]、基于直推式支持向量的分类方法(TSVM)[50]、基于拉普拉斯支持向量机(LapSVM)的分类方法[51]、基于one-class SVM的分类[52]等。文献[53]中提出一种变形核函数的半监督SVM,使用一种组合核函数的方法将空谱信息进行融合。
5 SVM在高光谱图像端元选择技术中的应用高光谱图像较低的空间分辨率导致混合像素的广泛存在,即一个像素可能是几种类别的混合。传统的硬分类技术对于混合像素的处理因误差较大而难以满足现实要求。分析各类别成分在混合像素内所占的比例的技术称为光谱解混。光谱解混实施的必要前提是要知道高光谱数据中包含哪些地物类别,在此背景下提取各类别代表性纯光谱的技术称为光谱端元选择,简称端元选择。
近年来,多种高光谱图像光谱端元选择方法相继发展起来,如:像素纯度索引(PPI)算法、N-FINDR算法、SGA算法、迭代误差分析(IEA)等。N-FINDR算法与SGA算法因其具有全自动、选择效果较好等优点而受到广泛应用。然而大量的体积计算限制了这两种算法的应用。一些N-FINDR算法的改进方案[36, 38-39]对原方法不足的改进仍然有限,且容易受到野值点的影响。
5.1 LSVM的距离测算功能对于LSVM (线性SVM)理论,人们了解更多的是它的分类和回归功能,文献[54-55]中则开发利用了其距离测算功能。
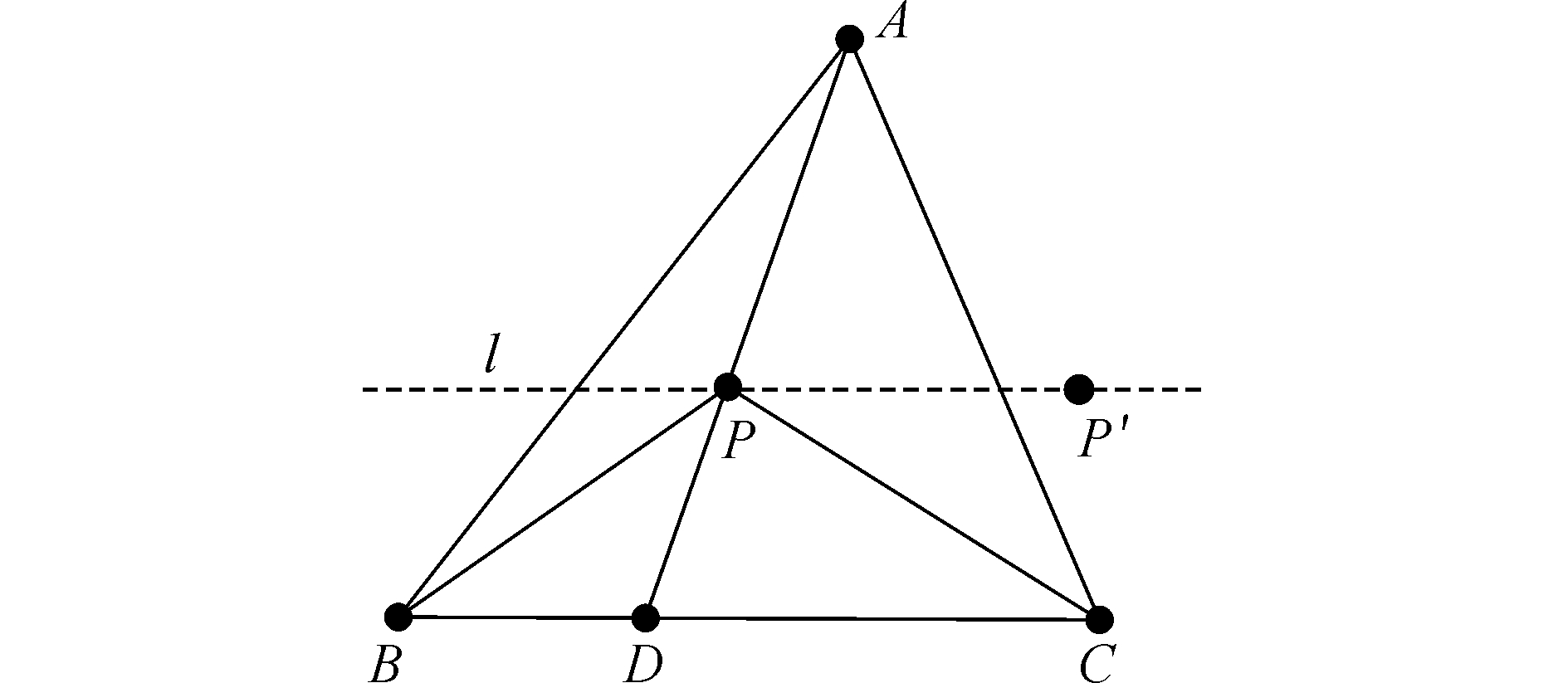
3类分类问题见图 2。则下面关系成立:
| $ f\left( P \right) = \lambda f\left( A \right) + \left( {1 - \lambda } \right)f\left( D \right) = \lambda , 0 < \lambda < 1 $ | (4) |
|
Download:
|
| 图 2 LSVM的距离测算功能 Fig. 2 Distance measurement function of LKSSVM | |
此时,判别函数f(·)即定义了一种由点“·”到直线BC的正比于欧氏距离的有向距离,同理可得另外2个子分类器。推而广之,对于N类分类问题,LSVM的N个子分类器定义了N种方向的有向距离函数。
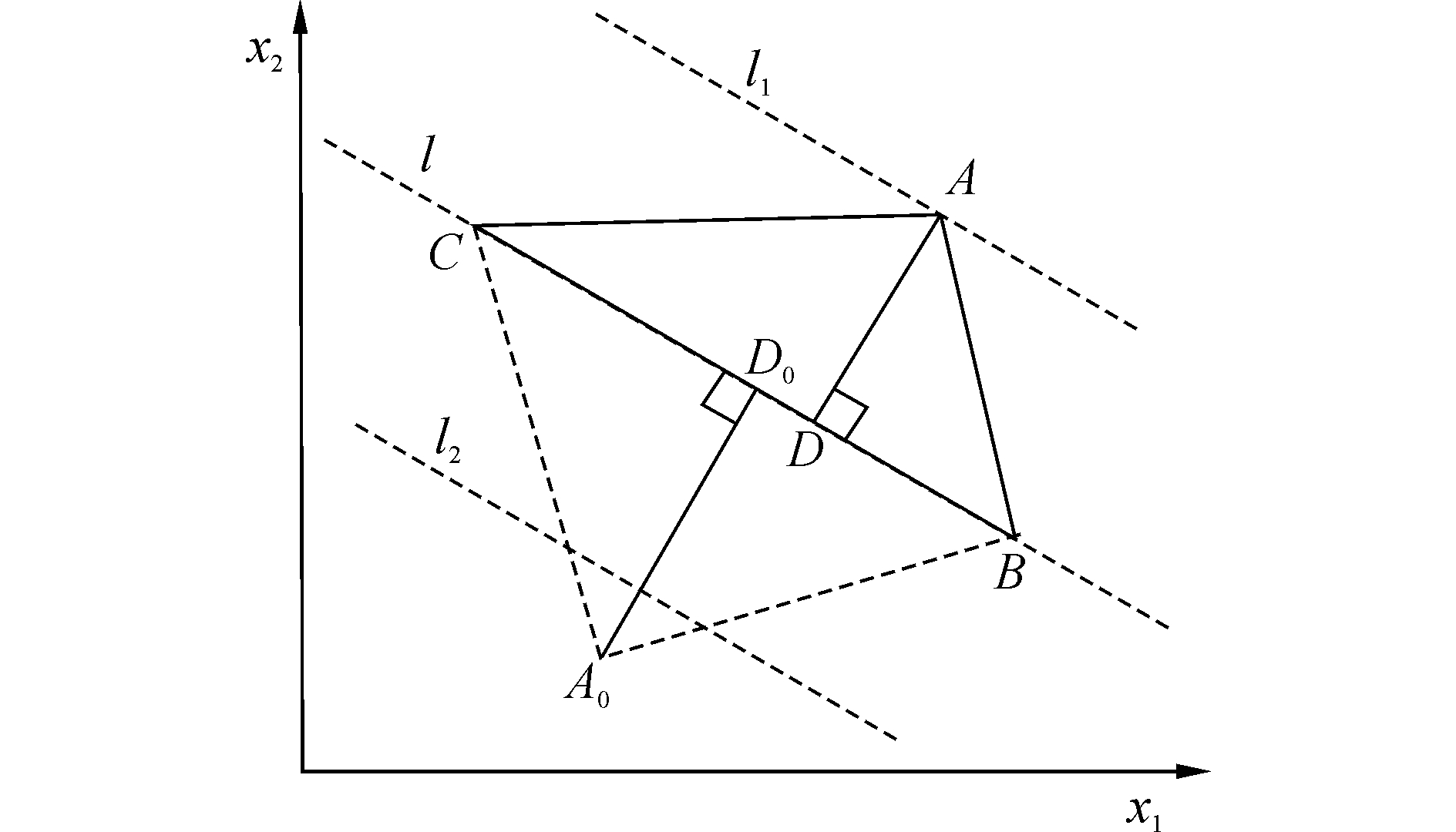
5.2 SVM在高光谱图像光谱端元选择技术中的应用基于线性最小二乘支持向量机,利用SVM的距离测算功能,文献[54-55]分别提出在原始空间实施、免于体积计算的N-FINDR和SGA的改进算法。这种方法无需降维预处理,且采用SVM计算低复杂度的距离尺度从而代替复杂的体积尺度来加速算法。这两种方式在选择结果上与原始算法等价,而在执行效率上却明显优于原始方法,所选择的光谱端元数目越大,新算法的优势越明显。文献[55]端元选择方法如图 3所示,比较ABC和A0BC两个二维凸多面体体积可以通过比较AD和A0D0来完成。利用SVM判别函数进行距离比较,仅当A0落在两虚线外侧时才可选作当前端元。
|
Download:
|
| 图 3 N-FINDR算法中的尺度替换示意图 Fig. 3 Scale replacement diagram of N-FINDR | |
这种方法同样可以推广到多端元组合或高维空间,而以上提及的距离测算功能对于其他线性支持向量机(LSVM)均有效[49]。
此外,文献[56]在上述算法基础上,提出改进的算法停机准则和数据特征预处理方法,引入了支持向量机的多类分类模型,在原始搜索到的端元基础上,进行二次端元提取,提高了端元提取的精度。并使用支持向量机对提取到的端元进行二次提取。而文献[57]通过探究端元选择与波段选择之间的关系,又将端元选择算法应用到波段选择领域之中。
6 SVM在高光谱图像光谱解混技术中的应用传统的硬分类技术对于混合像素的处理因误差较大而难以满足现实要求,光谱解混技术正是为解决该问题而发展起来的。现有的光谱解混有多种实现算法,但从效率和效果角度来说,基于线性光谱混合模型(linear spectral mixing modeling, LSMM)[58]的解混方法由于具有模型简单和物理意义明确等优点,目前为止是光谱解混中最为常用的方法,但该方法需先对数据进行降维处理,并计算较为复杂。
几何模型方法可以把光谱解混问题转化为高光谱数据空间中的体积比,进而应用距离比代替体积比来减小计算的复杂度。由4.1节可知,SVM的判别函数f(·)可以定义为一种由点“·”到直线的正比于欧氏距离的有向距离。因此基于SVM的方法能够应用低复杂度的距离尺度代替复杂的体积尺度进行光谱解混。此时该方法使光谱解混效率大幅度提高,并且无需进行降维处理。
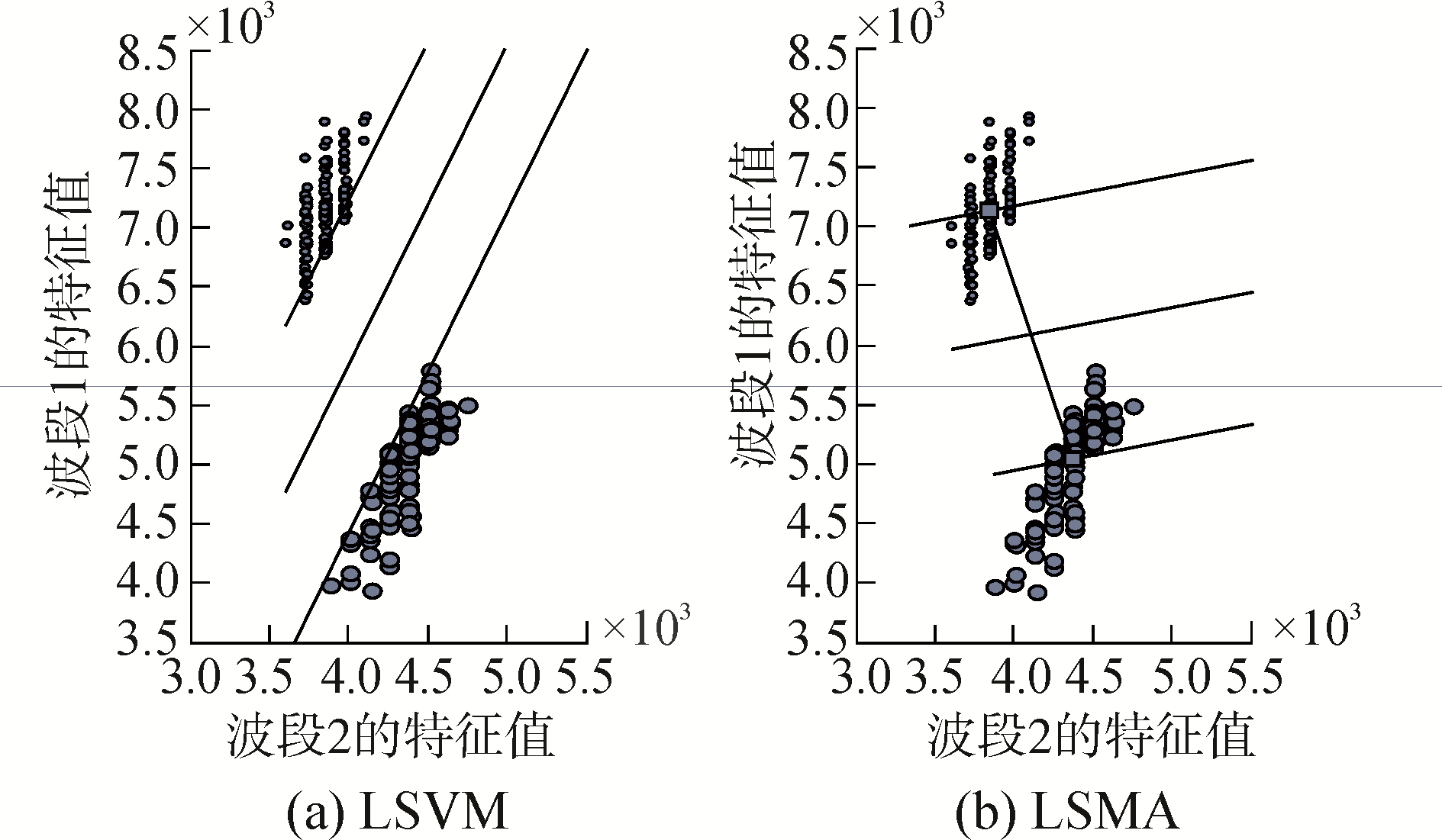
6.1 LSVM解混的独特优势LSVM解混在信息的扩展利用和非线性推广中具有独特优势。传统LSMM中每类地物只能用一个端元信息来表示,而这种方式对类内光谱变化较大的高光谱图解译精度较低。文献[43]中提出的逐步解译思想,但实施较为复杂,文献[59-60]的方法虽更为简单合理,但解译精度不高。LSVM可以利用多个训练样本刻画一个类别,从而获得更为合理的分析模型。一组真实数据下的LSMM和SVM两模型分划效果见图 4所示。同时,LSVM也优于将多端元光谱解混方法中等同看待每个端元光谱的做法,并且能够利用混合监督数据训练LSVM模型。
|
Download:
|
| 图 4 LSVM与LSMA的分划模型对比 Fig. 4 Comparison of division model of LSVM and LSMA | |
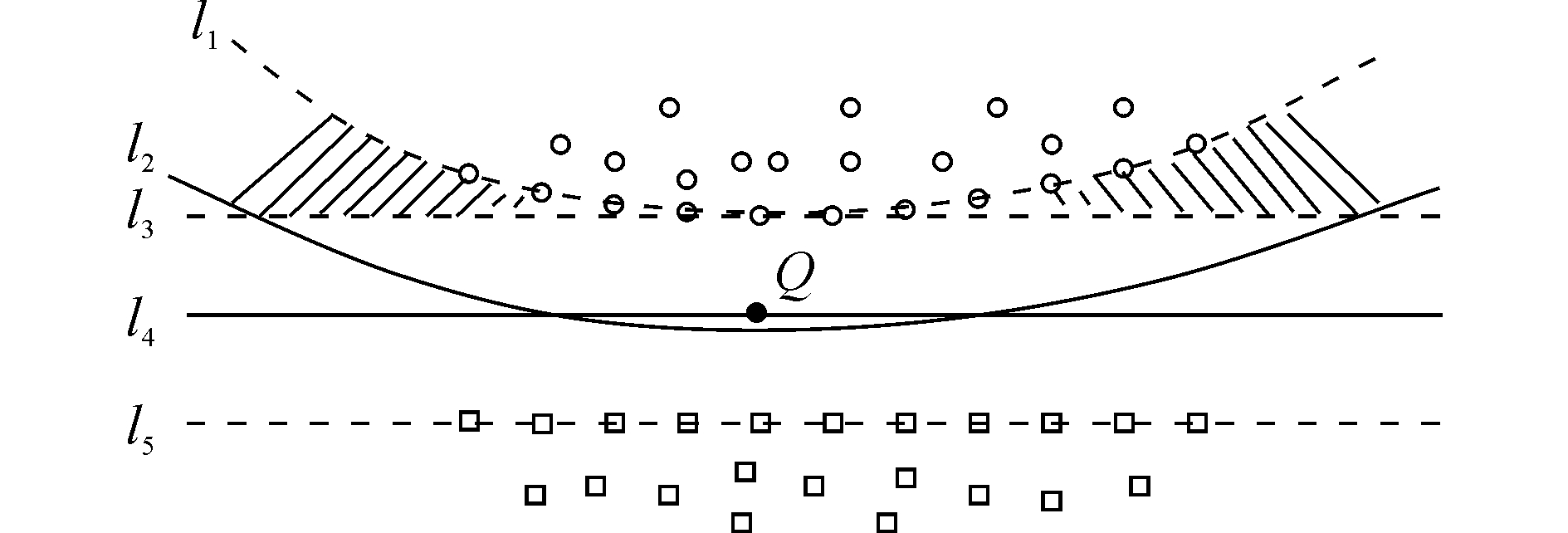
同时,LSVM可以通过引入非线性映射,解决高光谱图像光谱解混的非线性问题。如图 5是一个2维数据的非线性解混示意图,相比于LSVM错误地判决阴影区域的数据,非线性SVM(NLSVM)会对其做出更为合理的混合判定。虽然在处理某些数据点时NLSVM可能会弱于LSVM,但从总体效果来讲,NLSVM的解混优势仍非常明显。
|
Download:
|
| 图 5 LSVM与NLSVM非线性分化模型对比 Fig. 5 Comparison of nonlinear differentiation models of LSVM and NLSVM | |
在只利用光谱端元信息和无约束条件下,LSVM与LSMA两种光谱解混模型除距离测算的方向不同外,具有等效性[61],且在文献[62]中的约束方法下,LSVM与LSMA仍然等效。
实际上,基于统计学习理论的结构风险最小化原则的SVM,其距离测算性能,还可以看做识别对象属于某一类别的后验概率。而混合像元分解即是基于后验概率分类的一种特殊情况,通过后验概率能够有效地提取亚像元的信息[63]。此时,该方法更适用于影像中非线性特性的表达,且不需要具体的光谱混合模型。
文献[64]中提出了一种利用SVM后验概率进行高光谱影像的混合像元分解的方法,此后文献[65]又验证了改进SVM两两配对求解多类问题后验概率方法的有效性。文献[66]中提出一种结合空间信息的基于线性最小平方支持向量机(LLSSVM)的解混方法,该方法利用空间信息进行智能性判别、相关类别选择和应用LLSSVM进行解译,并通过赋予LLSSVM鲁棒特性来提高解译精度。该方法通过引入权值向量可以使LLSSVM获得具有鲁棒性,即将式(1)中的误差项
高光谱图像中虽然混合像元大量存在,但每个混合像元往往只包含少量的相关类别,并且这些类别与其邻域像元类别关系密切。因此利用光谱的空间相关性能够有效提高解混精度。基于邻域的混合像元LLSSVM解混的详细步骤参见文献[62, 66]。
文献[67]在改进SVM求解多类问题基础上利用相关向量机的后验概率进行高光谱影像混合像元分解。该方法将RVM学习转化为最大化边缘似然函数估计问题,采用快速序列稀疏贝叶斯学习算法求解,并通过两两配对的方法实现多类RVM分类,最后利用后验概率进行高光谱影像的混合像元分解[68]。文献[69]结合自动形态学端元提取方法,通过支持向量得到像元组分,支持向量机后验概率作为地物的组分信息,进而达到光谱解混的目的。
现有的SVM模型都是将硬分类误差约束条件纳入优化函数中,而光谱解混的一般评价原则为解混误差也即软分类误差。为此,带有软约束的最小二乘型SVM新模型应运而生。
原始SVM模型用多个纯样本来描述一个类别,克服了LSMM模型的缺陷。具有等式约束的LSSVM新模型从约束条件上进行了改进,但却再次引入了这种僵化表示。为此,可将纯像元作为变化端元,用以全面刻画高光谱数据的类内变化。这样,对于每个混合训练样本xi,总有与之相关的特有的端元组合
光谱解混技术虽然求解了混合像素内各个类别所占的比例,但类别空间分布的不确定性仍然存在。亚像元定位(sub-pixel mapping)是一种以子像素尺度表示边缘混合像素的重要技术。空间相关性作为亚像元定位的理论基础,以最大化像元之间和像元内部的空间相关性为基本原则。以空间相关性理论为基石,许多亚像元定位技术相继发展起来[70-72]。随后,马尔可夫随机场模型、MAP、BP神经网络(BPNN)等模型也被用于解决该问题。但以上方法仍存在一些问题,如,附加信息的难以获得,较大的计算量或只限用于相对简单的光谱解混分量图的超分辨处理等。
作为一种学习的亚像元定位方法,BPNN拥有一些特定优势,但同时也存在着一系列的缺陷,如收敛速度偏慢、易陷入局部最优,训练效果依赖于大量的训练样本等[71]。LSSVM能够有效处理高维度、小样本和非线性等模式识别问题,同时其训练过程时间极短。这些优势使得LSSVM可用于亚像元定位,且能够可克服BPNN学习上的缺陷。因此,文献[73]提出了一种基于最小二乘支持向量机的亚像元定位方法。该文献中同时提出一种人工合成训练样本的方法,为摆脱制图方法对先验信息的完全依赖。
基于LSSVM的亚像元定位方法需要训练样本信息,但很多时候这些先验信息难以获取。利用大规模地物在整体视觉上呈现的线性分布状态,可以通过人工合成训练样本的方式,对线性特征地物的亚像元定位,从而摆脱对先验信息的完全依赖[7]。
8 SVM在高光谱异常检测技术中的应用异常检测作为遥感技术中最重要的应用之一,已在军事及民用领域广泛应用。通常情况下,比起在普通图像中利用形状特征进行检测,高光谱图像检测还可利用其丰富的光谱维信息。异常检测无需先验信息,如RX检测及其有关的派生算法。光谱匹配检测需要使用目标光谱的先验信息,可以在有附加约束或无附加约束条件下实施,如光谱角度填图法(SAM)、匹配滤波器(MF)法,及有约束能量最小化(CEM)等算法。
8.1 支持向量数据描述传统模式识别方法设计两类和多类的分类器时存在单类分类(one-class)问题[74]。在SVM的基础上,Schelkopf等提出了最小包围球的概念来解决此问题。随后Tax等又将最此概念推广到数据域描述问题中,并称之为支持向量数据描述(support vector data description,SVDD)[75]。
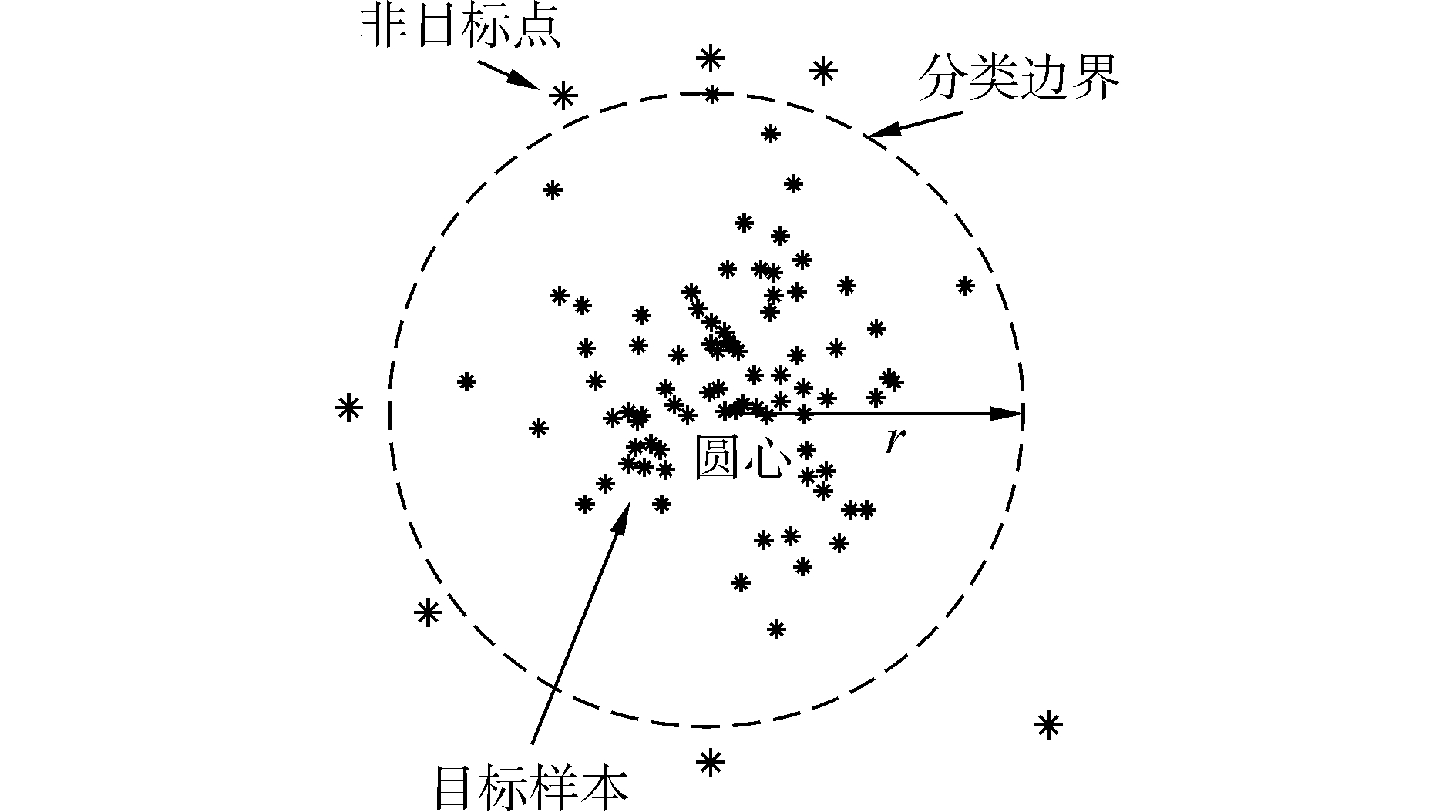
该方法的重要思想是[76]:将具有共同特性的一类样本约束于能够将该类中样本包围的超球内,寻找满足该要求的最小封闭超球并用判别准则使该类与其它类样本分开。二维空间为例的超球体示意图见图 6。
|
Download:
|
| 图 6 支持向量数据描述示意图 Fig. 6 The diagram of support vector data description | |
如果训练过程中有非目标样本数据,则由于非目标样本数据的存在,使得超球面在两边都得到了支撑,相比只有目标样本数据的情况,其超球面可能更符合数据点的实际分布情况,从而提高分类效果[77]。SVDD方法不仅可以解决非线性问题,自动寻找到最小包围半径,还可以有效地利用背景信息,进而提高异常检测性能。在提供同样的少量正样本时,SVDD方法与SAM和CEM算法在较好阈值时的检测效果基本相当,而在增加部分负样本的情况时,SVDD算法检测结果优于这两种算法[77]。
SVDD方法分类时,分类边界附近样本的噪声会影响分类面。因此,文献[78]提出了样本错误加权支持向量数据描述(WSVDD)方法。该方法用于高光谱小异常检测时可抑制小目标形状对背景选择的干扰。SVDD及其改进方法同样可用于高光谱图像的异常检测,详见文献[76, 79-80]。
8.2 LSVM在图像检测中的应用遥感图像变化检测是利用对同一地区在不同时期拍摄的两幅或多幅遥感图像,采用图像处理和模式识别等手段,检测出该地区的地物变化信息的过程[81]。这些信息可用于地理系统更新,环境监测以及军事评估等,因此在多个领域受到广泛的应用,成为遥感信息科学研究的一个重要方面。
Lorenzo Bruzzone[82]提出的运用半监督的支撑向量机(semi-supervised support vector machines,SSSVM)的方法,将变化检测问题归结为分类问题,即将图像分类为发生变化和未发生变化的两类。该方法是一种无监督的变化检测方法,同时又结合了支撑向量在多维向量分类中的优越性能,获得了较好的检测结果。文献[83]提出了一种基于分割窗的变化检测方法,对SSSVM方法进行了改进。该方法把SSSVM的变化检测方法和分割窗的思想结合起来,能较好地解决遥感图像中变化区域相对较大或较小时半监督支撑向量机分类法不能准确检测的问题,具有很好的变化检测性能。
此外,SMV在目标含量检测[84]、无损检测[85-86]等领域也已受到关注。
9 结论高光谱遥感图像以它独有的优势已经渐渐取代多光谱遥感图像在遥感成像中的重要性,并日益受到广泛关注。因SVM在解决小样本、非线性和高维模式等问题中特有的优势,已被广泛用于高光谱数据处理。本文分析了当今高光谱数据处理中的几个主要领域模型,总结了当前各领域的发展现状及主要的处理方法,针对不同领域的特点及需求,重点对SVM方法在各领域中的应用及优势进行了阐述。尽管在这些领域中,基于SVM的模型都显示出其特有的优势,但是如何进一步改进SVM模型,同时将改进的模型应用于各种领域,仍然值得高光谱遥感科学工作者们进一步研究。
| [1] |
JIMENEZ L O, LANDGREBE D A. Supervised classification in high-dimensional space:geometrical, statistical, and asymptotical properties of multivariate data[J]. IEEE transactions on systems, man, and cybernetics, part C (applications and reviews), 1998, 28(1): 39-54. DOI:10.1109/5326.661089 (  0) 0)
|
| [2] |
杨永崇, 郭岚. 数字地图的分辨率[J]. 测绘科学, 2007, 32(4): 185-186, 165. YANG Yongchong, GUO Lan. Resolution of digital maps[J]. Science of surveying and mapping, 2007, 32(4): 185-186, 165. (  0) 0)
|
| [3] |
顾松刚, 史培军. 基于混合象元分解的辽东湾海冰资源量估算[J]. 北京师范大学学报(自然科学版), 2004, 40(3): 411-416. GU Songgang, SHI Peijun. Estimation of sea ice resources in Liaodong Bay on decomposing mixed pixels[J]. Journal of Beijing normal university (natural science), 2004, 40(3): 411-416. (  0) 0)
|
| [4] |
EVGENIOU T, PONTIL M. Support vector machines: theory and applications[C]//Proceeding of Machine Learning and Its Applications. London, UK, 2001: 249-257.
(  0) 0)
|
| [5] |
VAPNIK V N. 统计学习理论的本质[M]. 张学工, 译. 北京: 清华大学出版社, 2000: 2-6. VAPNIK V N. Statistical learning theory[M]. ZHANG Xuegong. Beijing: Tsinghua University Press, 2000: 2-6. (  0) 0)
|
| [6] |
郭春燕. 基于支持向量机的高光谱遥感图像分类[D]. 哈尔滨: 哈尔滨工程大学, 2007. GUO Chunyan. Hyperspectral imagery classification based on support vector machine[D]. Harbin: Harbin Engineering University, 2007. (  0) 0)
|
| [7] |
SMOLA A J. Learning with kernels[M]. Sankt Augustin: Gmd Forschungszentrum Informationstechnik, 1998.
(  0) 0)
|
| [8] |
宋杰, 唐焕文. 基于线性规划的ν-支持向量机分类器[J]. 大连理工大学学报, 2005, 45(2): 303-307. SONG Jie, TANG Huanwen. ν-support vector machine classifier based on linear programming[J]. Journal of Dalian University of Technology, 2005, 45(2): 303-307. (  0) 0)
|
| [9] |
SUYKENS J A K, DE BRABANTER J, LUKAS L, et al. Weighted least squares support vector machines:robustness and sparse approximation[J]. Neurocomputing, 2002, 48(1/2/3/4): 85-105. (  0) 0)
|
| [10] |
SONG Qing, HU Wenjie, XIE Wenfang. Robust support vector machine with bullet hole image classification[J]. IEEE transactions on systems, man, and cybernetics, part C (applications and reviews), 2002, 32(4): 440-448. DOI:10.1109/TSMCC.2002.807277 (  0) 0)
|
| [11] |
TRAFALIS T B, ALWAZZI S A. Robust optimization in support vector machine training with bounded errors[C]//Proceedings of the International Joint Conference on Neural Networks. Portland, United States, 2003: 2039-2042.
(  0) 0)
|
| [12] |
TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of machine learning research, 2001, 1: 211-244. (  0) 0)
|
| [13] |
TAX D M J, DUIN R P W. Support vector data description[J]. Machine learning, 2004, 54(1): 45-66. DOI:10.1023/B:MACH.0000008084.60811.49 (  0) 0)
|
| [14] |
范昕炜. 支持向量机算法的研究及其应用[D]. 杭州: 浙江大学, 2003: 1-24. FAN Xinwei. Support vector machine and its applications[D]. Hangzhou: Zhejiang University, 2003. (  0) 0)
|
| [15] |
SCHÖLKOPF B, BURGES C J C, SMOLA A J. Advances in kernel methods:support vector learning[M]. Cambridge: MIT Press, 1999.
(  0) 0)
|
| [16] |
KEERTHI S S, SHEVADE S K, BHATTACHARYYA C, et al. A fast iterative nearest point algorithm for support vector machine classifier design[J]. IEEE transactions on neural networks, 2000, 11(1): 124-136. DOI:10.1109/72.822516 (  0) 0)
|
| [17] |
SHEVADE S K, KEERTHI S S, BHATTACHARYYA C, et al. Improvements to the SMO algorithm for SVM regression[J]. IEEE transactions on neural networks, 2000, 11(5): 1188-1193. DOI:10.1109/72.870050 (  0) 0)
|
| [18] |
WESTON J, WATKINS C. Multi-class support vector machines: SD2TR298204[R]. London: Royal Holloway University of London, 1998.
(  0) 0)
|
| [19] |
BOTTOU L, CORTES C, DENKER J S, et al. Comparison of classifier methods: a case study in handwritten digit recognition[C]//Proceedings of the 12th IAPR International Conference on Pattern Recognition. Jerusalem, 1994: 77-87.
(  0) 0)
|
| [20] |
PLATT J C, CRISTIANINI N, SHAWE-TAYLOR J. Large margin DAGs for multiclass classification[C]//Advances in Neural Information Processing Systems. Dener, United States, 2000: 547-553.
(  0) 0)
|
| [21] |
ALLWEIN E L, SCHAPIRE R E, SINGER Y. Reducing multiclass to binary:a unifying approach for margin classifiers[J]. Journal of machine learning research, 2000, 1: 113-141. (  0) 0)
|
| [22] |
MELGANI F, BRUZZONE L. Classification of hyperspectral remote sensing images with support vector machines[J]. IEEE transactions on geoscience and remote sensing, 2004, 42(8): 1778-1790. DOI:10.1109/TGRS.2004.831865 (  0) 0)
|
| [23] |
马波. 支持向量机多类分类算法的分析与设计[D]. 扬州: 扬州大学, 2008. MA Bo. The analysis and design for the algorithms of multiclass classification based on SVM[D]. Yangzhou: Yangzhou University, 2008. (  0) 0)
|
| [24] |
王立国, 张晔, 谷延锋. 支持向量机多类目标分类器的结构简化研究[J]. 中国图象图形学报, 2005, 10(5): 571-574. WANG Liguo, ZHANG Ye, GU Yanfeng. The research of simplification of structure of multi-class classifier of support vector machine[J]. Journal of image and graphics, 2005, 10(5): 571-574. DOI:10.11834/jig.200505114 (  0) 0)
|
| [25] |
刘健, 刘忠, 熊鹰. 改进的二叉树支持向量机多类分类算法研究[J]. 计算机工程与应用, 2010, 46(33): 117-120. LIU Jian, LIU Zhong, XIONG Ying. Improved multi-category support vector machines based on binary tree[J]. Computer engineering and applications, 2010, 46(33): 117-120. (  0) 0)
|
| [26] |
DEVIJVER P A, KITTLER J. Pattern recognition:a statistical approach[M]. Englewood Cliffs, NJ: Prentice-Hall, 1982.
(  0) 0)
|
| [27] |
HERMES L, BUHMANN J M. Feature selection for support vector machines[C]//Proceedings of the 15th International Conference on Pattern Recognition. Barcelona, 2000, 2: 712-715.
(  0) 0)
|
| [28] |
WEBB A R, COPSEY K D. Statistical pattern recognition[M]. 3rd ed. Chichester: Wiley, 2011.
(  0) 0)
|
| [29] |
王立国, 谷延锋, 张晔. 基于支持向量机和子空间划分的波段选择方法[J]. 系统工程与电子技术, 2005, 27(6): 974-977. WANG Liguo, GU Yanfeng, ZHANG Ye. Band selection method based on combination of support vector machines and subspatial partition[J]. Systems engineering and electronics, 2005, 27(6): 974-977. (  0) 0)
|
| [30] |
PENG Hanchuan, LONG Fuhui, DING C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(8): 1226-1238. DOI:10.1109/TPAMI.2005.159 (  0) 0)
|
| [31] |
吴昊, 李士进, 林林, 等. 多策略结合的高光谱图像波段选择新方法[J]. 计算机科学与探索, 2010, 4(5): 464-472. WU Hao, LI Shijin, LIN Lin, et al. Multiple-strategy combination based approach to band selection for hyper-spectral image classification[J]. Journal of frontiers of computer science and technology, 2010, 4(5): 464-472. (  0) 0)
|
| [32] |
苏红军, 盛业华, YANGHe, 等. 基于正交投影散度的高光谱遥感波段选择算法[J]. 光谱学与光谱分析, 2011, 31(5): 1309-1313. SU Hongjun, SHENG Yehua, YANG He, et al. Orthogonal projection divergence-based hyperspectral band selection[J]. Spectroscopy and spectral analysis, 2011, 31(5): 1309-1313. (  0) 0)
|
| [33] |
CHION C, LANDRY J A, DA COSTA L. A genetic-programming-based method for hyperspectral data information extraction:agricultural applications[J]. IEEE transactions on geoscience and remote sensing, 2008, 46(8): 2446-2457. DOI:10.1109/TGRS.2008.922061 (  0) 0)
|
| [34] |
丁胜, 袁修孝, 陈黎. 粒子群优化算法用于高光谱遥感影像分类的自动波段选择[J]. 测绘学报, 2010, 39(3): 257-263. DING Sheng, YUAN Xiuxiao, CHEN Li. Automatic band selection of hyperspectral remote sensing image classification using particle swarm optimization[J]. Acta geodaetica et cartographica sinica, 2010, 39(3): 257-263. (  0) 0)
|
| [35] |
吴一全, 吴超. 基于小波和支持向量回归的高光谱遥感图像压缩[J]. 宇航学报, 2011, 32(3): 620-626. WU Yiquan, WU Chao. Hyperspectral remote sensing image compression based on wavelet and support vector regression[J]. Journal of astronautics, 2011, 32(3): 620-626. (  0) 0)
|
| [36] |
ROBINSON J, KECMAN V. Combining support vector machine learning with the discrete cosine transform in image compression[J]. IEEE transactions on neural networks, 2003, 14(4): 950-958. DOI:10.1109/TNN.2003.813842 (  0) 0)
|
| [37] |
李元诚, 焦润海, 李波. 一种基于支持向量机的小波图像压缩方法[J]. 北京航空航天大学学报, 2006, 32(5): 598-602. LI Yuancheng, JIAO Runhai, LI Bo. Wavelet image compression based on support vector machines[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(5): 598-602. (  0) 0)
|
| [38] |
张丽萍, 李元诚. 基于支持向量机的遥感图像压缩方法[J]. 计算机工程与应用, 2006, 42(27): 200-202. ZHANG Liping, LI Yuancheng. Remote sensing image compression based on support vector machines[J]. Computer engineering and applications, 2006, 42(27): 200-202. DOI:10.3321/j.issn:1002-8331.2006.27.061 (  0) 0)
|
| [39] |
夏建涛. 基于机器学习的高维多光谱数据分类[D]. 西安: 西北工业大学, 2002. XIA Jiantao. High dimensional multispectral data classification by machine learning[D]. Xi'an: Northwestern Polytechnical University, 2002. (  0) 0)
|
| [40] |
刘志刚. 支撑向量机在光谱遥感影像分类中的若干问题研究[D]. 武汉: 武汉大学, 2004. LIU Zhigang. Key problems of applying support vector machines to the classification of spectral remote sensing imagery[D]. Wuhan: Wuhan University, 2004. (  0) 0)
|
| [41] |
CAMPS-VALLS G, GOMEZ-CHOVA L, MUNOZ-MARI J, et al. Composite kernels for hyperspectral image classification[J]. IEEE geoscience and remote sensing letters, 2006, 3(1): 93-97. DOI:10.1109/LGRS.2005.857031 (  0) 0)
|
| [42] |
WINTER M E, LUCEY P G, STEUTEL D. Examining hyperspectral unmixing error reduction due to stepwise unmixing[C]//Proceedings of the SPIE Volume 5093, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery. Orlando, Florida, 2003, 5093: 380-389.
(  0) 0)
|
| [43] |
JI Bahong, CHANG C I, JENSEN J L, et al. Unsupervised constrained linear fisher's discriminant analysis for hyperspectral image classification[C]//Proceedings of the 49th Annual Meeting. Denver, 2004, 5546: 2-4.
(  0) 0)
|
| [44] |
林超. 基于超球体多类支持向量机的高光谱遥感影像分类[D]. 长沙: 中南大学, 2011. LIN Chao. The classification of hyperspectral remote sensing image based on hyper sphere multi-class support vector machine[D]. Changsha: Central South University, 2011. (  0) 0)
|
| [45] |
董超, 田联房, 赵慧洁. 遗传关联向量机高光谱影像分类[J]. 上海交通大学学报, 2011, 45(10): 1516-1520. DONG Chao, TIAN Lianfang, ZHAO Huijie. Hyperspectral image classification by genetic relevance vector machine[J]. Journal of Shanghai Jiaotong university, 2011, 45(10): 1516-1520. (  0) 0)
|
| [46] |
高恒振, 万建伟, 粘永健, 等. 一种基于谱域-空域组合特征支持向量机的高光谱图像分类算法[J]. 宇航学报, 2011, 32(4): 917-921. GAO Hengzhen, WAN Jianwei, NIAN Yongjian, et al. Hyperspectral image classification algorithm based on spectral-spatial hybrid features and SVM[J]. Journal of astronautics, 2011, 32(4): 917-921. (  0) 0)
|
| [47] |
王立国, 邓禄群, 张晶. 基于线性最小二乘支持向量机的光谱端元选择算法[J]. 光谱学与光谱分析, 2010, 30(3): 743-747. WANG Liguo, DENG Luqun, ZHANG Jing. Endmember selection algorithm based on linear least square support vector machines[J]. Spectroscopy and spectral analysis, 2010, 30(3): 743-747. (  0) 0)
|
| [48] |
HAJIGHORBANI M, HASHEMI S M R, BROUMANDNIA A, et al. A review of some semi-supervised learning methods[J]. Knowl-Based Eng Innov, 2016, 2(4): 250-259. (  0) 0)
|
| [49] |
CAMPS-VALLS G, MARSHEVA T V B, ZHOU Dengyong. Semi-supervised graph-based hyperspectral image classifycation[J]. IEEE transactions on geoscience and remote sensing, 2007, 45(10): 3044-3054. DOI:10.1109/TGRS.2007.895416 (  0) 0)
|
| [50] |
郝思媛. 空谱协作的高光谱图像分类方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2015. HAO Siyuan. Research on spatial-spectral collaborative classification for hyperspectral image[D]. Harbin: Harbin Engineering University, 2015. (  0) 0)
|
| [51] |
GU Yanfeng, FENG Kai. Optimized laplacian SVM with distance metric learning for hyperspectral image classification[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2013, 6(3): 1109-1117. DOI:10.1109/JSTARS.2013.2243112 (  0) 0)
|
| [52] |
MUNOZ-MARI J, BOVOLO F, GOMEZ-CHOVA L, et al. Semisupervised one-class support vector machines for classification of remote sensing data[J]. IEEE transactions on geoscience and remote sensing, 2010, 48(8): 3188-3197. DOI:10.1109/TGRS.2010.2045764 (  0) 0)
|
| [53] |
HUO Lianzhi, TANG Ping, ZHANG Zheng, et al. Semisupervised classification of remote sensing images with hierarchical spatial similarity[J]. IEEE geoscience and remote sensing letters, 2015, 12(1): 150-154. DOI:10.1109/LGRS.2014.2329713 (  0) 0)
|
| [54] |
王立国, 张晶, 刘丹凤, 等. 从端元选择到光谱解混的距离测算方法[J]. 红外与毫米波学报, 2010, 29(6): 471-475. WANG Liguo, ZHANG Jing, LIU Danfeng, et al. Distance measurement based methods from endmember selection to spectral unmixing[J]. Journal of infrared and millimeter waves, 2010, 29(6): 471-475. (  0) 0)
|
| [55] |
赵春晖, 齐滨, 王玉磊. 一种改进的N-FINDR高光谱端元提取算法[J]. 电子与信息学报, 2012, 34(2): 499-503. ZHAO Chunhui, QI Bin, WANG Yulei. An improved N-FINDR hyperspectral endmember extraction algorithm[J]. Journal of electronics & information technology, 2012, 34(2): 499-503. (  0) 0)
|
| [56] |
王立国, 赵春晖, 毕晓君. 端元选择算法在波段选择中的应用[J]. 吉林大学学报(工学版), 2007, 37(4): 915-919. WANG Liguo, ZHAO Chunhui, BI Xiaojun. Application of endmember extraction method to band selection[J]. Journal of Jilin University (engineering and technology edition), 2007, 37(4): 915-919. (  0) 0)
|
| [57] |
CHANG C I, JI Baohong. Weighted abundance-constrained linear spectral mixture analysis[J]. IEEE transactions on geoscience and remote sensing, 2006, 44(2): 378-388. DOI:10.1109/TGRS.2005.861408 (  0) 0)
|
| [58] |
何青, 熊桢. 基于邻域的混合象元解译[J]. 北方交通大学学报, 1999, 23(4): 118-121. HE Qing, XIONG Zhen. Neighbor-field-based mixed pixel interpretation[J]. Journal of northern Jiaotong university, 1999, 23(4): 118-121. (  0) 0)
|
| [59] |
LUO Junwu, KING R L, YOUNAN N. An unmixing algorithm based on vicinal information[C]//Proceedings of International Geoscience and Remote Sensing Symposium. Toronto, Ontario, Canada, 2002: 1453-1455.
(  0) 0)
|
| [60] |
BROWN M, LEWIS H G, GUNN S R. Linear spectral mixture models and support vector machines for remote sensing[J]. IEEE transactions on geoscience and remote sensing, 2000, 38(5): 2346-2360. DOI:10.1109/36.868891 (  0) 0)
|
| [61] |
王立国, 张晔, 陈浩. 基于鲁棒支持向量机的光谱解译[J]. 吉林大学学报(工学版), 2007, 37(1): 155-159. WANG Liguo, ZHANG Ye, CHEN Hao. Spectral unmixing based on robust support vector machine[J]. Journal of Jilin University (engineering and technology edition), 2007, 37(1): 155-159. (  0) 0)
|
| [62] |
FOODY G M. Relating the land-cover composition of mixed pixels to artificial neural network classification output[J]. Photogrammetric engineering and remote sensing, 1996, 62(5): 491-499. (  0) 0)
|
| [63] |
吴波, 张良培, 李平湘. 基于支撑向量机概率输出的高光谱影像混合像元分解[J]. 武汉大学学报(信息科学版), 2006, 31(1): 51-54. WU Bo, ZHANG Liangpei, LI Pingxiang. Unmixing of hyperspectral imagery based on probabilistic outputs of support vector machines[J]. Geomatics and information science of Wuhan University, 2006, 31(1): 51-54. (  0) 0)
|
| [64] |
李慧, 王云鹏, 李岩, 等. 基于SVM和PWC的遥感影像混合像元分解[J]. 测绘学报, 2009, 38(4): 318-323. LI Hui, WANG Yunpeng, LI Yan, et al. Unmixing of remote sensing images based on support vector machines and pairwise coupling[J]. Acta geodaetica et cartographica sinica, 2009, 38(4): 318-323. (  0) 0)
|
| [65] |
王立国, 张晶. 基于线性光谱混合模型的光谱解混改进模型[J]. 光电子·激光, 2010, 21(8): 1222-1226. WANG Liguo, ZHANG Jing. An improved spectral unmixing modeling based on linear spectral mixing modeling[J]. Journal of optoelectronics·laser, 2010, 21(8): 1222-1226. (  0) 0)
|
| [66] |
杨国鹏, 周欣, 余旭初, 等. 基于相关向量机的高光谱影像混合像元分解[J]. 电子学报, 2010, 38(12): 2751-2756. YANG Guopeng, ZHOU Xin, YU Xuchu, et al. Relevance vector machine for hyperspectral imagery unmixing[J]. Acta electronica sinica, 2010, 38(12): 2751-2756. (  0) 0)
|
| [67] |
李慧, 王云鹏, 李岩, 等. 基于形态学和支持向量的遥感图像混合像元分解[J]. 遥感技术与应用, 2009, 24(1): 114-119. LI Hui, WANG Yunpeng, LI Yan, et al. Unmixing remote sensing imagery based on morphology and support vector machines[J]. Remote sensing technology and application, 2009, 24(1): 114-119. DOI:10.11873/j.issn.1004-0323.2009.1.114 (  0) 0)
|
| [68] |
ATKINSON P M. Super-resolution target mapping from soft classified remotely sensed imagery[C]//Proceedings of the 5th International Conference on GeoComputation. Leeds, 2001.
(  0) 0)
|
| [69] |
TATEM A J, LEWIS H G, ATKINSON P M, et al. Multiple-class land-cover mapping at the sub-pixel scale using a hopfield neural network[J]. International journal of applied earth observation and geoinformation, 2001, 3(2): 184-190. DOI:10.1016/S0303-2434(01)85010-8 (  0) 0)
|
| [70] |
VERHOEYE J, DE WULF R. Land cover mapping at sub-pixel scales using linear optimization techniques[J]. Remote sensing of environment, 2002, 79(1): 96-104. DOI:10.1016/S0034-4257(01)00242-5 (  0) 0)
|
| [71] |
MERTENS K, VERBEKE L, DE WULF R. Sub-pixel mapping with neural networks: real-world spatial configurations learned from artificial shapes[C]//Proceedings of the 4th International Symposium on Remote Sensing and Urban Areas. Regensburg, 2003.
(  0) 0)
|
| [72] |
MAULIK U, CHAKRABORTY D. Learning with transductive SVM for semi-supervised pixel classification of remote sensing imagery[J]. ISPRS journal of photogrammetry and remote sensing, 2013, 77: 66-78. DOI:10.1016/j.isprsjprs.2012.12.003 (  0) 0)
|
| [73] |
WANG Qunming, WANG Liguo, LIU Danfeng, et al. Sub-pixel mapping for land class with linear features using least square support vector machine[J]. Infrared and laser engineering, 2012, 41(6): 1669-1675. (  0) 0)
|
| [74] |
潘志松, 陈斌, 缪志敏, 等. One-Class分类器研究[J]. 电子学报, 2009, 37(11): 2496-2503. PAN Zhisong, CHEN Bin, MIAO Zhimin, et al. Overview of study on one-class classifiers[J]. Acta electronica sinica, 2009, 37(11): 2496-2503. DOI:10.3321/j.issn:0372-2112.2009.11.025 (  0) 0)
|
| [75] |
TAX D M J, DUIN R P W. Support vector data description[J]. Machine learning, 2004, 54(1): 45-46. DOI:10.1023/B:MACH.0000008084.60811.49 (  0) 0)
|
| [76] |
谌德荣, 宫久路, 陈乾, 等. 基于样本分割的快速高光谱图像异常检测支持向量数据描述方法[J]. 兵工学报, 2008, 29(9): 1049-1053. CHEN Derong, GONG Jiulu, CHEN Qian, et al. Support vector data description for fast anomaly detection in hyperspectral imagery based on sample segmentation[J]. Acta armamentarii, 2008, 29(9): 1049-1053. (  0) 0)
|
| [77] |
王晓飞. 高光谱图像分辨率增强及在小目标检测中的应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. WANG Xiaofei. Hyperspectral image resolution enhancement and its application on small target detection[D]. Harbin: Harbin Institute of Technology, 2011. (  0) 0)
|
| [78] |
燕继坤, 王勇, 曹春霞, 等. 样本错误加权的支持向量数据描述[J]. 计算机工程, 2005, 31(2): 24-26. YAN Jikun, WANG Yong, Cao Chunxia, et al. Example error weighted support vector data description[J]. Computer engineering, 2005, 31(2): 24-26. (  0) 0)
|
| [79] |
谌德荣, 宫久路, 何光林, 等. 高光谱图像全局异常检测RFS-SVDD算法[J]. 宇航学报, 2010, 31(1): 228-232. CHEN Derong, GONG Jiulu, HE Guanglin, et al. A RFS-SVDD algorithm for hyperspectral global anomaly detection[J]. Journal of astronautics, 2010, 31(1): 228-232. (  0) 0)
|
| [80] |
梅锋, 赵春晖, 王立国, 等. 基于支持向量描述的自适应高光谱异常检测算法[J]. 光子学报, 2009, 38(11): 2820-2825. MEI Feng, ZHAO Chunhui, WANG Liguo, et al. Support vector data description based on adaptive anomaly detection method in hyperspectral imagery[J]. Acta photonica sinica, 2009, 38(11): 2820-2825. (  0) 0)
|
| [81] |
SING A. Review article digital change detection techniques using remotely-sensed data[J]. International journal of remote sensing, 1989, 10(6): 989-1003. DOI:10.1080/01431168908903939 (  0) 0)
|
| [82] |
BOVOLO F, BRUZZONE L, MARCONCINI M. A novel approach to unsupervised change detection Based on a semisupervised SVM and a similarity measure[J]. IEEE transactions on geoscience and remote sensing, 2008, 46(7): 2070-2082. DOI:10.1109/TGRS.2008.916643 (  0) 0)
|
| [83] |
赵磊, 王斌, 张立明. 基于分割窗半监督支持向量机的遥感图像变化检测[J]. 复旦学报(自然科学版), 2010, 49(2): 190-196. ZHAO Lei, WANG Bin, ZHANG Liming, et al. Change detection for remotely sensed images based on split window and semi-supervised SVM[J]. Journal of Fudan University (natural science), 2010, 49(2): 190-196. (  0) 0)
|
| [84] |
彭彦昆, 黄慧, 王伟, 等. 基于LS-SVM和高光谱技术的玉米叶片叶绿素含量检测[J]. 江苏大学学报(自然科学版), 2011, 32(2): 125-128, 174. PENG Yankun, HUANG Hui, WANG Wei, et al. Rapid detection of chlorophyll content in corn leaves by using least squares-support vector machines and hyperspectral images[J]. Journal of Jiangsu University (natural science edition), 2011, 32(2): 125-128, 174. (  0) 0)
|
| [85] |
万相梅, 黄敏, 朱启兵. 基于高光谱散射图像的苹果压缩硬度和汁液含量无损检测[J]. 食品工业科技, 2012, 33(6): 71-74, 78. WANG Xiangmei, HUANG Min, ZHU Qibing, et al. Non-destructive detection for compression hardness and juiciness in apple based on hyperspectral scattering image[J]. Science and technology of food industry, 2012, 33(6): 71-74, 78. (  0) 0)
|
| [86] |
王晓. 基于高光谱图像及近红外光谱技术的水果表面农药残留的无损检测研究[D]. 南昌: 江西农业大学, 2011. WANG Xiao. The nondestructive inspection research of pesticide residues contamination on fruit surface based on hyperspectral imaging and near infrared spectroscopy technology[D]. Nanchang: Jiangxi Agricultural University, 2011. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


