近年来,由于陆地资源的枯竭和海上油气田的大量发现,世界各国都开始重视海上油气田的开发和利用,因此海底管线在海工建筑中应用越来越广泛,但由于受复杂海洋环境的影响,铺设在沙质海床上的海底管线极易发生局部冲刷,造成管线悬空,从而引起涡激振动,而这种振动是造成管线失事的主要原因[1]。为了降低管线的失事率,国内外许多学者对床面的局部冲刷进行了大量的试验和数值模拟研究,如:冲刷的临界条件、冲刷机理、管道上的作用力、海床与管道相互作用、冲刷坑的深度及宽度[2-7]等均取得相应的研究成果。在此冲刷的基础上,管道的防护方法也得到了多方面的探讨。主要有两种方法:一种是防止床面冲刷,如:将混凝土沉排或“人工草”覆盖于管道上,以此增大泥沙的起动流速[8-9];初新杰[10]在人工草的基础上通过试验提出了管线淘空仿生防护技术,对解决胜利油田粉土地基保护问题有重要意义。崔华等[11]对埕岛油田悬空管线采用仿生草进行防护研究,发现仿生草防护促淤效果明显,且治理效果受管线走向和潮流方向的影响,与潮流方向一致或与潮流方向夹角较小(< 40°)的海底管线,治理效果良好。或者在管道上安装柔性浮帘截沙促淤[12];又或在管道与床面间安装柔性阻流器,减少管道两侧的渗压力防止床面冲刷[13]。另一种方法是将管线埋于床面以下,如:人为的埋入或者在管道上方安装阻流器实现管道的自埋[14]。王怡等[15]根据弗劳德数Fr相等原理,采用缩放法对悬空管线采用抛石防护进行研究,可得出流体对抛石的冲刷机理、抛石防护的薄弱位置以及抛石防护的极限抗流速度等结论,为抛石治理管线悬空提供试验依据。王召堂[16]对南堡海底管线存在的一系列问题进行了研究,并提出了抛石护坡、碎石覆盖和后挖沟填埋的措施,为海底管线的安全运营提供了保障。Hulsbergen[17-18]研究发现安装于管道顶部的阻流器能明显增加冲刷的深度及宽度,同时加速冲刷进程。相关的结果显示,管道安装阻流器后,其自埋过程比无阻流器的情况快10倍,并且阻流器越长其进程越迅速。Chiew[19]研究了波浪作用下阻流器对冲刷深度的影响,发现当附加的阻流器角度为α=±30°时,能有效加速冲刷;而当安装角度为α=±120°和±135°时,会形成二次冲刷坑。通过数学模型,Cheng等[20]模拟了稳定流条件下,安装阻流器后管道周围的流场,发现阻流器改变了其周围压力分布并加速了冲刷与自埋进程。Zhao等[21]通过数值模拟研究发现,阻流器的存在,明显增加了拖曳力、管下流速及其附近的床面切应力,从而加速床面冲刷,且产生一个向下的力促使管道自埋。Oner[22]通过试验研究发现阻流器的存在能增加管道上下游分离区域的长度。曾威[23]从应用的角度研究了阻流器促进管道自埋的技术原理、应用的水文地质条件及安装方法。赵恩金等[24]采用数值模拟研究了冲刷坑形成后管线自埋前导流板对管线涡激振动的影响,发现安装导流板后,管线的升力系数均值为负值,随着导流板高度与管径之比(h/D)的增加,升力系数幅值逐渐减少,在h/D为0.375时,基本达到最小值,且管线合力向下,有利于管线的自埋。在(h/D)为0.25时,发生了涡激振动中的“准周期拍击现象”,而拖曳力随着导流板高度的增加而增加,管线受到的横向作用力增加,其对管线的强度要求增加。
尽管学者们对阻流器进行了大量的研究,但关于管道无阻流器、安装阻流器及间隙比作用下管道冲刷深度计算的研究还较少。本文从力学平衡角度出发,拟探讨管径、阻流器高度、间隙比对管道冲刷深度的影响, 并推导有阻流器和间隙比情况下冲刷深度的计算公式。
1 物理模型试验 1.1 试验的建立本文中的试验的包括两组,试验一是在波流环形水槽中进行的,水槽长24.8 m,宽0.5 m,深0.6 m。水槽中央填有非均匀沙,用来模拟沙质海床,沙床高0.15 m,长5 m, 其布置如图 1(a)所示。试验二是在波流水槽中进行的,水槽长30 m、宽0.6 m、深1.0 m,沙质床面的高度为0.20 m、长20 m,边坡为1:2,试验布置如图 1(b)所示。

|
Download:
|
| 图 1 模型试验布置图 Fig. 1 Experiment arrangement | |
试验一主要研究无间隙比时(管道及床面的间隙S与管径D的比值,e=S/D),不同管径、流速及阻流器高度对冲刷坑内的流速分布、冲刷深度的影响。管线模型长0.5 m,直径分别为0.07、0.09、0.11 m。试验中阻流器高度分别为0.25D、0.5D(D为管道直径),安装方式如图 1(c)所示,试验水温为16 ℃,运动粘滞系数为ν=1.118×10-6 m2/s。试验水深H=0.4 m, 管线上游距床面D/2高度处的来流流速分别为0.24、0.3、0.4 m/s,沙样的中值粒径为d50=0.3 mm。
试验二主要研究同一雷诺数条件下,不同间隙比及阻流器高度对冲刷深度的影响。试验管线长0.6 m,直径为0.1 m,模型沙高度为0.20 m,在管线顶端分别安装0.125D、0.25D、0.375D、0.5D,4种高度的阻流器,间隙比分别为0、0.3、0.5,管线上游距床面D/2高度处的流速为0.24 m/s,具体试验参数如表 1所示。表 1中1~9组主要是研究各种参数对冲刷深度的影响并用于验证推导的计算公式,10~11组研究了不同间隙比对冲刷深度的影响;12及13组则用来确定休止角参数k′。
| 表 1 试验参数 Tab.1 Experimental parameters |
试验值的获取主要集中在动床上,管道上游、管道迎流面及冲刷坑内的流场分布采用ADV(acoustic doppler velocimeter)进行测量。试验所用ADV探头为侧向的,测量的是其侧方5 cm处的流速, 对测点影响较小。通过流场的试验值可以确定管道上游驻点的高度及流速分布指数。本文中的驻点高度即管道迎流面上流速为零的点与床面间的高度,其可由管道迎流面的断面流速分布确定。冲刷稳定后,将水槽内水缓慢完全排出,然后采用精度为0.1 mm的测针对冲刷坑的断面进行测量,动水休止角及冲刷深度均由冲刷坑断面值获取。
2 冲刷坑深度理论推导 2.1 冲止流速冲刷稳定时,将冲刷坑最深点床面上d高度处沿床面方向的流速定义为“冲止流速”。Shi等[25]假设泥沙颗粒为球体,根据力学平衡原理,对泥沙颗粒进行简单的理论分析,推导出了在清水冲刷的条件下泥沙的冲止流速公式为
| $ {u_{es}} = {\left\{ {\frac{{8dg\left( {{S_0} - 1} \right)\sin {\varphi _0}}}{{3\left( {{C_L}\tan {\varphi _0} + {C_D}} \right)}}} \right\}^{\frac{1}{2}}} $ | (1) |
式中:d为泥沙颗粒的平均粒径;S0为泥沙容重与水流容重的比值;CL为上举力系数,爱因斯坦根据埃尔-萨姆尼的试验成果,发现距理论床面0.35 d处的流速对应的CL为常数可取为0.178[26];CD为推移力系数,当试验条件为紊流时其为定值,本文中取CD=0.45[27];φ0为泥沙的动水休止角,其受结构物影响,并随管径及来流流速的变化而变化。
2.2 冲刷深度对于无阻流器及间隙(S=0),有阻流器但无间隙,有阻流器且有间隙三种工况的冲刷深度,Shi等[25]已进行了研究,并提出了冲刷深度的计算公式。在Yang[28]的研究结果,本人对安装阻流器且间隙不为零的冲刷深度公式进行了分析,得出了另一计算公式,过程如下:
|
Download:
|
| 图 2 安装阻流器且S>0时管道周围流速分布 Fig. 2 The velocity distribution around pipe with spoiler for S>0 condition | |
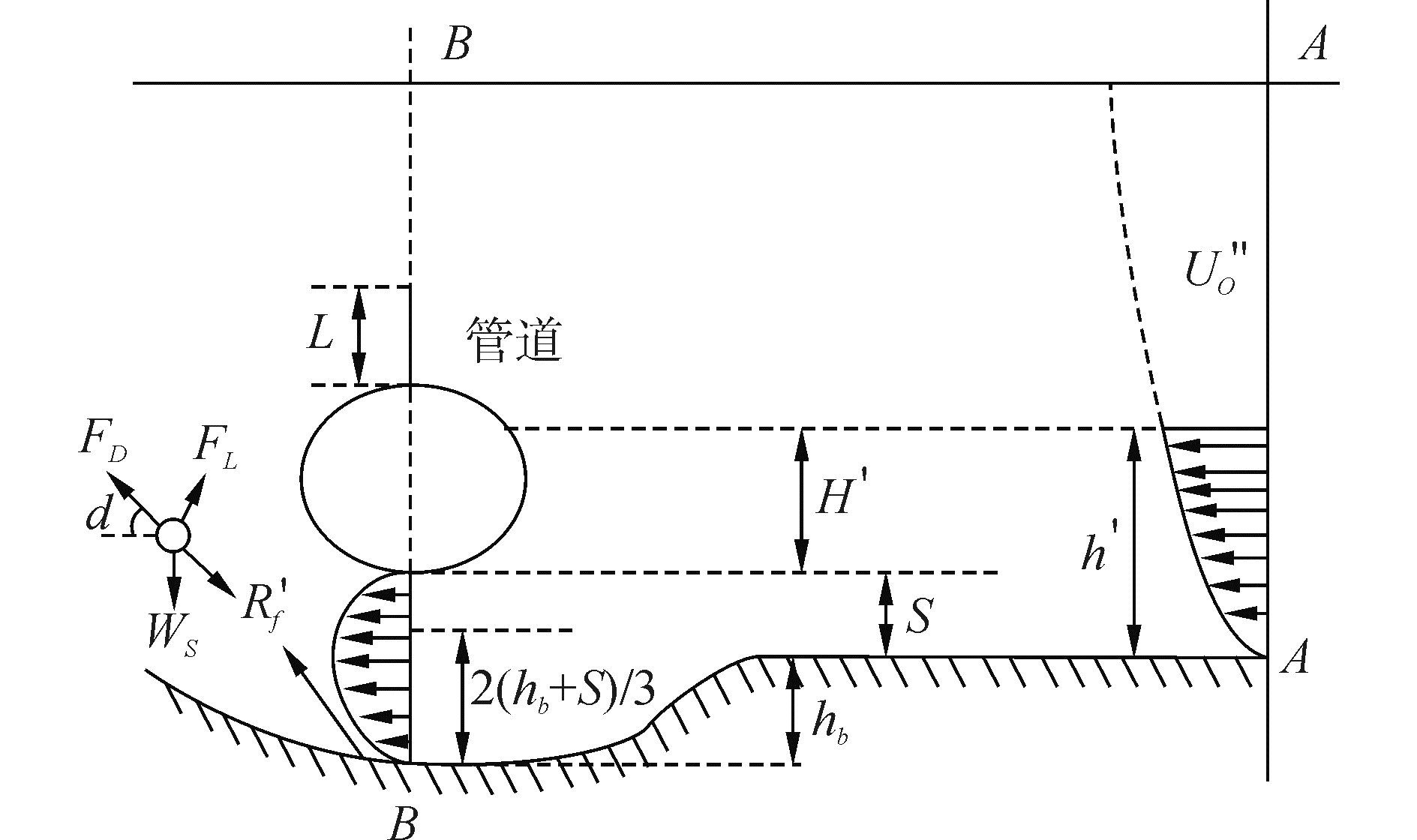
安装阻流器且间隙不为零(S>0)。管道与床面间隙大于零时,冲刷坑内颗粒受力未发生变化,故其冲止流速的公式不变。但间隙S的存在减小了管道下方床面的冲刷及泥沙输移,试验发现,与没有间隙的工况相比,冲刷宽度降低,泥沙动水休止角增大,可由φ′表示。
经试验观测,管道下方流速最大值出现在距冲刷坑床面2(hb+S)/3处(hb为冲刷坑深度),且呈指数分布,则床面至2(hb+S)/3的流速关系式u(y)为
| $ \frac{{u\left( y \right)}}{{{u_b}}} = {\left( {\frac{y}{d}} \right)^m},\;\;\;y \in \left[ {0,\frac{2}{3}\left( {{h_b} + S} \right)} \right] $ | (2) |
2(hb+S)/3处至管壁处流速u'(y)可以表达为
| $ \frac{{u'\left( y \right)}}{{{{u'}_b}}} = {\left( {\frac{{y'}}{{\left( {{h_b} + S'} \right)/3}}} \right)^m},\;\;\;\;\;y' \in \left[ {0,\frac{1}{3}\left( {{h_b} + S} \right)} \right] $ | (3) |
| $ {{u'}_b} = {u_b}{\left[ {\frac{{2\left( {{h_b} + S} \right)}}{{3d}}} \right]^m} $ | (4) |
式中:u′b为冲刷坑内2(hb+S)/3处流速,y、y′为竖向坐标,m为冲刷坑内流速分布指数。
对管线迎流面上的流速数据(R12)进行分析后发现:驻点高度随流速及阻流器高度L的变化而略有变化,Yang[28]提出驻点与管线底端的距离H′可表示为H′=Y+Y1, Y为无导流板时驻点与床面的距离, Y1为安装导流板后驻点上升的高度,故假设床面与驻点直接的高度为h′,其关系可表示为:h′=S+H′,同理,假设断面A-A的流速分布也呈指数分布,则其流速分布表达式为
| $ \frac{{U\left( y \right)}}{{{{U''}_0}}} = {\left( {\frac{{{y_0}}}{{h'}}} \right)^n},\;\;\;\;{y_0} \in \left[ {0,h'} \right] $ | (5) |
| $ {{U''}_0} = {u_0}{\left( {\frac{{2h'}}{D}} \right)^n} $ | (6) |
式中:U″0为断面A-A上距床面h′处对应的行进流速,u0为断面A-A上D/2处对应的行进流速,n为断面A-A上流速分布指数(对于明渠流n=1/6[29])。
利用流体的连续性条件可知:
| $ \int_0^{\frac{2}{3}\left( {{h_b} + S} \right)} {u\left( y \right){\rm{d}}y} + \int_0^{\frac{1}{3}\left( {{h_b} + S} \right)} {u'\left( y \right){\rm{d}}y} = \int_0^{h'} {U\left( y \right){\rm{d}}y} $ | (7) |
将各参数代入式(7)有
| $ {h_b} = {\left[ {\frac{{{3^m}{2^{n - m}}{u_0}\left( {m + 1} \right){d^m}{{\left( {S + Y + {Y_1}} \right)}^{n + 1}}}}{{{D^n}\left( {n + 1} \right){u_b}}}} \right]^{\frac{1}{{m + 1}}}} - S $ | (8) |
试验测量了不同阻流器高度、间隙比及来流流速条件下,管道周围床面的冲刷。结果显示:管道下方冲刷坑的深度及宽度随管径、阻流器高度、来流流速的增大而显著增加(如图 3(a)、(b)及(c)所示);并且冲刷坑的最深点有向下游偏移的趋势(如图 5所示)。但动水休止角与冲止流速的规律与冲刷深度相反,随阻流器的高度及流速的增大而减小,并最终趋于稳定。冲刷深度与间隙比成反比,阻流器越高,此规律越明显(如图 3(d)所示)。图 4为图 3(b)、(c)两种阻流器高度下的试验照片,该组照片表明阻流器能够明显的增加泥沙输移,加速冲刷。

|
Download:
|
| 图 3 冲刷深度宽度随来流流速、阻流器高度及间隙比的变化规律 Fig. 3 Variations of scour depth and width with incoming velocity, spoiler heights and gap-ratios | |
|
Download:
|
| 图 5 k′与S/D的关系曲线 Fig. 5 The relationship curve between k′ and S/D | |

|
Download:
|
| 图 4 管径D=9 cm时有、无阻流器冲刷试验图 Fig. 4 Experimental photos show the scour around the pipe for D=9 cm with and without a spoiler | |
Yang等[28]通过对试验数据进行拟合分析,提出了管道上无阻流器及间隙和管道上安装阻流器且无间隙的休止角表达式,发现管道上无阻流器及间隙时,休止角是仅与沙粒雷诺数有关的系数,关系式为φ0=1.8[lg(Re*)]2-6.7lg(Re*)+6.3,而当管道上安装阻流器且无间隙时,休止角φ是与导流板高度L、沙粒雷诺数及管径有关的参数。Yang通过数据进行分析认为φ可由φ0乘以修正系数k表示,其表达式为
| $ \frac{\varphi }{{{\varphi _0}}} = k = f\left( {\frac{L}{D}} \right) $ |
故k的关系式可表示为
| $ k = 2.9{\left( {\frac{L}{D}} \right)^2} - 2.8\left( {\frac{L}{D}} \right) + 1 $ |
在次基础上对Yang未深入研究的管道安装阻流器且有间隙时的工况进行研究,发现动水休止角φ′与间隙S、阻流器高度及管径有关。对(R12)
(R13)结果进行分析,发现与有阻流器但无间隙的工况类似,φ′可由φ与修正系数k′表示,即
| $ k' = - 1.8{\left( {\frac{S}{D}} \right)^2} + 4.5\left( {\frac{S}{D}} \right) + 1 $ | (9) |
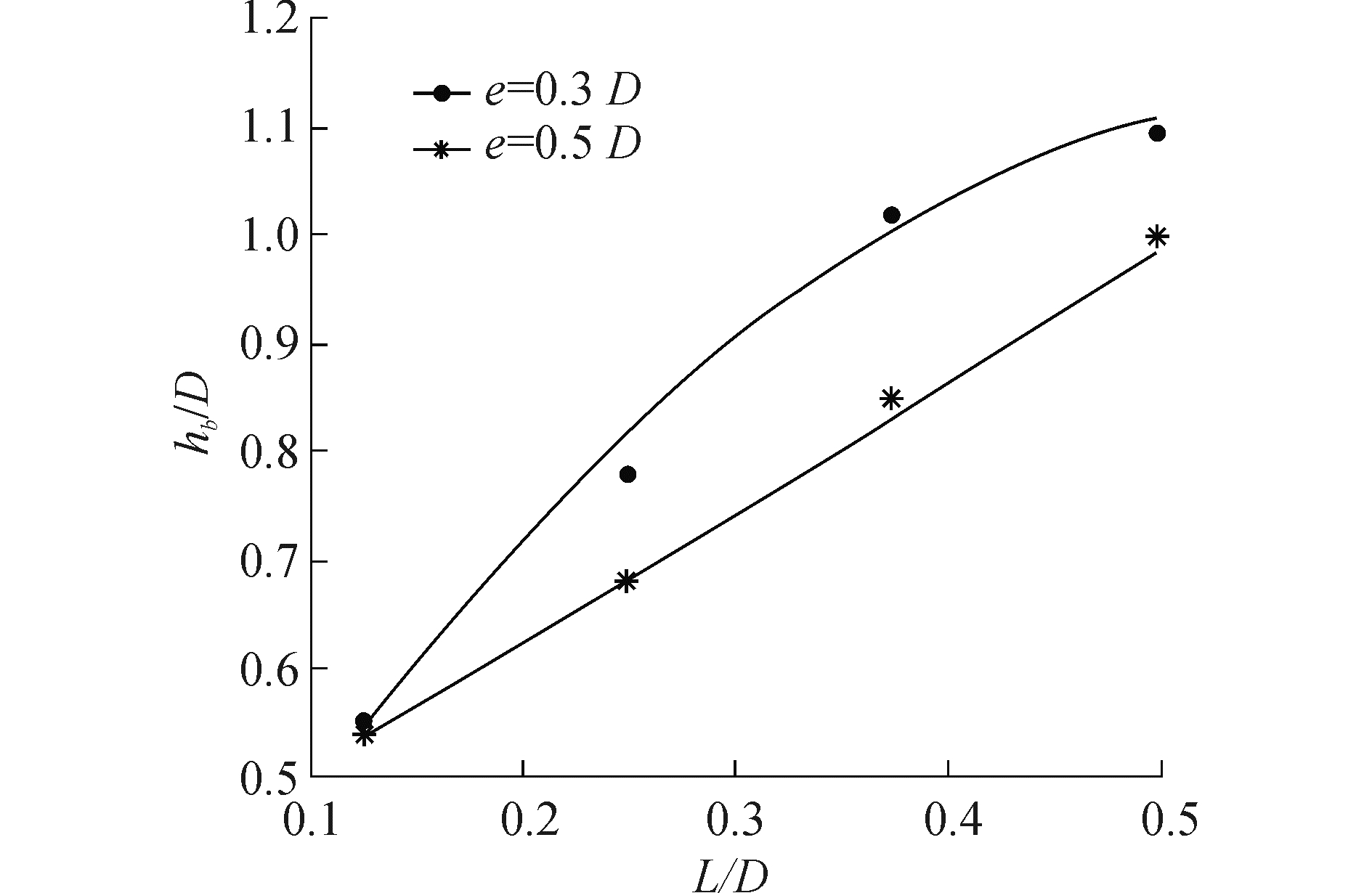
对试验数据进行分析发现,当管道与床面间有间隙时,冲刷深度将随间隙比的增大而减小(如图 6所示),e=0.5的深度略小于e=0.3的情况。对于相同间隙比的情况,深度随阻流器高度增加而增加。Yang[28]的试验数据与本文计算值的对比发现,公式的计算值(式(8))与试验值具有很好的一致性。

|
Download:
|
| 图 6 有间隙及阻流器时计算值与试验值的对比曲线 Fig. 6 Comparison of calculating values and test data for the gap and spoiler condition | |
1) 根据力学平衡原理,对阻流器及间隙作用下冲刷坑内泥沙颗粒的冲止流速计算公式进行研究,发现冲止流速的主要影响参数为动水休止角;二者均随阻流器的高度及雷诺数的增大而减小,最终趋于稳定。
2) 采用流体的连续性条件,推导了安装阻流器且有间隙情况下冲刷稳定时的冲刷深度计算公式。流速分布及冲止流速是决定冲刷深度的主要因素。
3) 由经试验值与计算值的对比分析可知,冲刷坑深度公式基本反应了阻流器及间隙作用下冲刷坑深度的变化规律。
| [1] |
GAO Fuping, YANG Bing, WU Yingxiang, et al. Steady current induced seabed scour around a vibrating pipeline[J]. Applied ocean research, 2006, 28(5): 291-298. DOI:10.1016/j.apor.2007.01.004 (  0) 0)
|
| [2] |
浦群, 李坤. 管线振荡绕流对砂床的冲蚀[J]. 力学学报, 1999, 31(6): 677-681. PU Qun, LI Kun. Scour of the sand bed below the pipeline in oscillating flow[J]. Acta mechanica sinica, 1999, 31(6): 677-681. (  0) 0)
|
| [3] |
潘冬子, 王立忠, 潘存鸿, 等. 推进波作用下海底管线周围局部冲刷试验研究[J]. 海洋工程, 2007, 25(4): 27-32. PAN Dongzi, WANG Lizhong, PAN Cunhong, et al. Local scour around pipeline due to progressive wave[J]. The ocean engineering, 2007, 25(4): 27-32. (  0) 0)
|
| [4] |
ZANG Zhipeng, CHENG Liang, ZHAO Ming, et al. A numerical model for onset of scour below offshore pipelines[J]. Coastal engineering, 2009, 56(4): 458-466. DOI:10.1016/j.coastaleng.2008.10.001 (  0) 0)
|
| [5] |
李玉成, 陈兵, 王革. 波浪对海底管线作用的物理模型实验及数值模拟研究[J]. 海洋通报, 1996, 15(4): 58-65. LI Yucheng, CHEN Bing, WANG Ge. Physical model test and numerical simulation of pipeline under wave action[J]. Marine science bulletin, 1996, 15(4): 58-65. (  0) 0)
|
| [6] |
栾茂田, 曲鹏, 杨庆, 等. 波浪引起的海底管线周围海床动力响应分析[J]. 岩石力学与工程学报, 2008, 27(4): 789-795. LUAN Maotian, QU Peng, YANG Qing, et al. Wave-induced dynamic response of seabed around submarine pipeline[J]. Chinese journal of rock mechanics and engineering, 2008, 27(4): 789-795. (  0) 0)
|
| [7] |
秦崇仁, 彭亚. 波浪作用下海底裸置管道周围的冲刷[J]. 港工技术, 1995(3): 7-12. QIN Chongren, PENG Ya. Washing around the seabed pipeline placed barely by wave action[J]. Port engineering technology, 1995(3): 7-12. (  0) 0)
|
| [8] |
GAO F P, GU X Y, JENG D S. Physical modeling of untrenched submarine pipeline instability[J]. Ocean engineering, 2003, 30(10): 1283-1304. DOI:10.1016/S0029-8018(02)00108-7 (  0) 0)
|
| [9] |
赵冬岩, 余建星, 李广雪, 等. 海底管线防冲刷技术试验研究[J]. 哈尔滨工程大学学报, 2009, 30(6): 597-601. ZHAO Dongyan, YU Jianxing, LI Guangxue, et al. An experimental scour-prevention technique for subsea pipelines[J]. Journal of Harbin Engineering University, 2009, 30(6): 597-601. (  0) 0)
|
| [10] |
初新杰. 海底管线淘空仿生防护技术试验研究[J]. 装备制造技术, 2011(7): 19-21, 30. CHU Xinjie. Test study on bionic technology of anti-scouring protection for subsea pipelines[J]. Equipment manufacturing technology, 2011(7): 19-21, 30. (  0) 0)
|
| [11] |
崔华, 曹立华, 陈义兰, 等. 埕岛海域平台周围悬跨海底管线仿生草治理效果研究[J]. 海岸工程, 2015, 34(3): 77-86. CUI Hua, CAO Lihua, CHEN Yilan, et al. Study on the effect of bionic grass treatment for the suspended span of submarine pipelines around the oil platforms in the Chengdao Sea Area[J]. Coastal engineering, 2015, 34(3): 77-86. (  0) 0)
|
| [12] |
喻国良, 陈琴琴, 李艳红. 海底管道防冲刷保护技术的发展现状与趋势[J]. 水利水电技术, 2007, 38(11): 30-33. YU Guoliang, CHEN Qinqin, LI Yanhong. Status and tendency of development of scour-prevention technique for submarine pipeline[J]. Water resources and hydropower engineering, 2007, 38(11): 30-33. DOI:10.3969/j.issn.1000-0860.2007.11.008 (  0) 0)
|
| [13] |
韩艳, 拾兵, 任兴月, 等. 导流板对海底管线防护功能的试验研究[J]. 四川大学学报(工程科学版), 2010, 42(2): 100-106. HAN Yan, SHI Bing, REN Xingyue, et al. Experimental study on the function of spoilers in protecting submarine pipeline[J]. Journal of Sichuan University(engineering science edition), 2010, 42(2): 100-106. (  0) 0)
|
| [14] |
CHIEW Y M. Effect of spoilers on scour at submarine pipelines[J]. Journal of hydraulic engineering, 1992, 118(9): 1311-1317. DOI:10.1061/(ASCE)0733-9429(1992)118:9(1311) (  0) 0)
|
| [15] |
王怡, 李俊, 孙长保. 局部抛石法治理海底管道悬空的试验研究[J]. 油气储运, 2016, 35(7): 784-787. WANG Yi, LI Jun, SUN Changbao. Experiment study on the local rock dumping methods for submarine pipeline spans[J]. Oil & gas storage and transportation, 2016, 35(7): 784-787. (  0) 0)
|
| [16] |
王召堂. 南堡油田海底管道勘测及问题管段治理[J]. 石油工程建设, 2012, 38(6): 21-23. WANG Zhaotang. Submarine pipeline survey and troubled pipeline section treatment in Nanpu Oilfield[J]. Petroleum engineering construction, 2012, 38(6): 21-23. (  0) 0)
|
| [17] |
HULSBERGEN C H. Spoilers for stimulated self-burial of submarine pipelines[C]//Offshore Technology Conference. Houston, Texas: OTC, 1986: 441-444.
(  0) 0)
|
| [18] |
HULSBERGEN C H, BIJKER R. Effect of spoilers on submarine pipeline stability[C]//Offshore Technology Conference. Houston, Texas: OTC, 1989: 337-350.
(  0) 0)
|
| [19] |
CHIEW Y M. Effect of spoilers on wave-induced scour at submarine pipelines[J]. Journal of waterway, port, coastal and ocean engineering, 1993, 119(4): 417-428. DOI:10.1061/(ASCE)0733-950X(1993)119:4(417) (  0) 0)
|
| [20] |
CHENG Liang, CHEW L W. Modelling of flow around a near-bed pipeline with a spoiler[J]. Ocean engineering, 2003, 30(13): 1595-1611. DOI:10.1016/S0029-8018(02)00148-8 (  0) 0)
|
| [21] |
ZHAO Jianping, WANG Xuechao. CFD numerical simulation of the submarine pipeline with a spoiler[J]. Journal of offshore mechanics and arctic engineering, 2009, 131(3): 031601. DOI:10.1115/1.3124127 (  0) 0)
|
| [22] |
ONER A A. The flow around a pipeline with a spoiler[J]. Proceedings of the institution of mechanical engineers, part C:journal of mechanical engineering science, 2010, 224(1): 109-121. DOI:10.1243/09544062JMES1699 (  0) 0)
|
| [23] |
曾威. 一种新型的海底管道自埋施工技术[J]. 油气储运, 2007, 26(5): 57-58. ZENG Wei. The improved spoiler——a new self-burying applied technology in the pipeline laying for submarine pipeline[J]. Oil & gas storage and transportation, 2007, 26(5): 57-58. (  0) 0)
|
| [24] |
赵恩金, 拾兵, 曹坤. 导流板对海底管线涡激振动的影响[J]. 哈尔滨工程大学学报, 2016, 37(3): 320-325. ZHAO Enjin, SHI Bing, CAO Kun. Influence of reflectors on vortex-induced vibration of subsea pipelines[J]. Journal of Harbin Engineering University, 2016, 37(3): 320-325. (  0) 0)
|
| [25] |
SHI Bing, YANG Lipeng, HAN Yan. Study on scour hole depth of submarine pipeline with spoiler, Chinese-German joint symposium on hydraulic and ocean engineering (CG JOINT 2010)[M]. Tianjin: Tianjin University Press, 2010: 416-421.
(  0) 0)
|
| [26] |
钱宁, 万兆惠. 泥沙运动力学[M]. 北京: 科学出版社, 1983.
(  0) 0)
|
| [27] |
MAO Yi. The interaction between a pipeline and an erodible bed[D]. Kongens Lyngby, Denmark: Technical University of Denmark, 1987.
(  0) 0)
|
| [28] |
YANG Lipeng, SHI Bing, GUO Yakun, et al. Calculation and experiment on scour depth for submarine pipeline with a spoiler[J]. Ocean engineering, 2012, 55: 191-198. DOI:10.1016/j.oceaneng.2012.07.031 (  0) 0)
|
| [29] |
CHEN C L. Unified theory on power laws for flow resistance[J]. Journal of hydraulic engineering, 1991, 117(3): 371-389. DOI:10.1061/(ASCE)0733-9429(1991)117:3(371) (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


