目前,长江经济带的出口集装箱有两种运输路径:1)经公路运抵洋山港,再经海运运抵目的地港;2)经公路运抵内河港口,再经长江水道运抵洋山港,后经海运运抵目的地港。在两种路径上,货物都需多次转运、重复装卸,导致运输成本上升,因此有必要依托长江水道和公/铁路网络,实施更高效的出口集装箱运输组织。目前,有关海上班轮运输的研究较多,有关内河航道班轮的研究较少。海上班轮运输研究主要涉及的是船舶调度、靠泊港与航行路径选择。Shintani等[1]研究了考虑靠泊港选择、靠泊顺序、航速与空箱调运的集装箱班轮航线优化问题。陈康等[2]提出了基于运营者、货主和政府三方博弈的短途班轮航线优化模型。陈康等[3]基于混合航线结构,构建双层规划模型,优化集装箱航线与空重箱运输方案。Maras等[4]考虑空箱调运,以船公司利润最大化为目标建立内河集装箱驳船运输路径优化模型。Zheng等[5]考虑内河船型和江海直达船型的区别,设计长江集装箱运输的轴辐式网络。Konings等[6]研究了英国和德国之间莱茵河段的江海直达运输,设计江海推驳船二程组织模式。Southworth等[7]提出了两种由公、铁和水路三种方式构成的多式联运网络的表现方法。汪传旭[8]基于轴-辐式港口近洋运输系统和经济腹地与港口之间的集疏运系统,建立了区域港口群二级物流运输系统的非线性优化模型。魏航等[9]考虑运输成本和运输时间的变化特性,设计时变网络条件下多式联运的最短路径算法。Arnold等[10]研究了多式联运网络中公路枢纽和铁路枢纽的选址问题,建立整数0-1规划模型,设计启发式算法进行求解。Hansse等[11]提出一种分析多式联运网络中广义运输成本的模型,并以挪威到欧洲大陆的水产品运输为例验证模型。Resat等[12]研究了考虑时间窗的多式联运网络设计问题,以运输费用和时间最小建立多目标优化模型,基于土耳其的马尔马拉地区验证模型。
上述研究的重点在于枢纽选址和制定运输方案,模型多为整数规划模型,不考虑载运工具数量、运输能力。本文基于出口集装箱运输需求,在设置干港和枢纽河港以及考虑江海直达与江海联运两种模式下,构建长江经济带出口集装箱运输组织优化模型,优化内陆干港和枢纽河港的选址方案,研究出口集装箱的路径选择行为,确定运输方案。
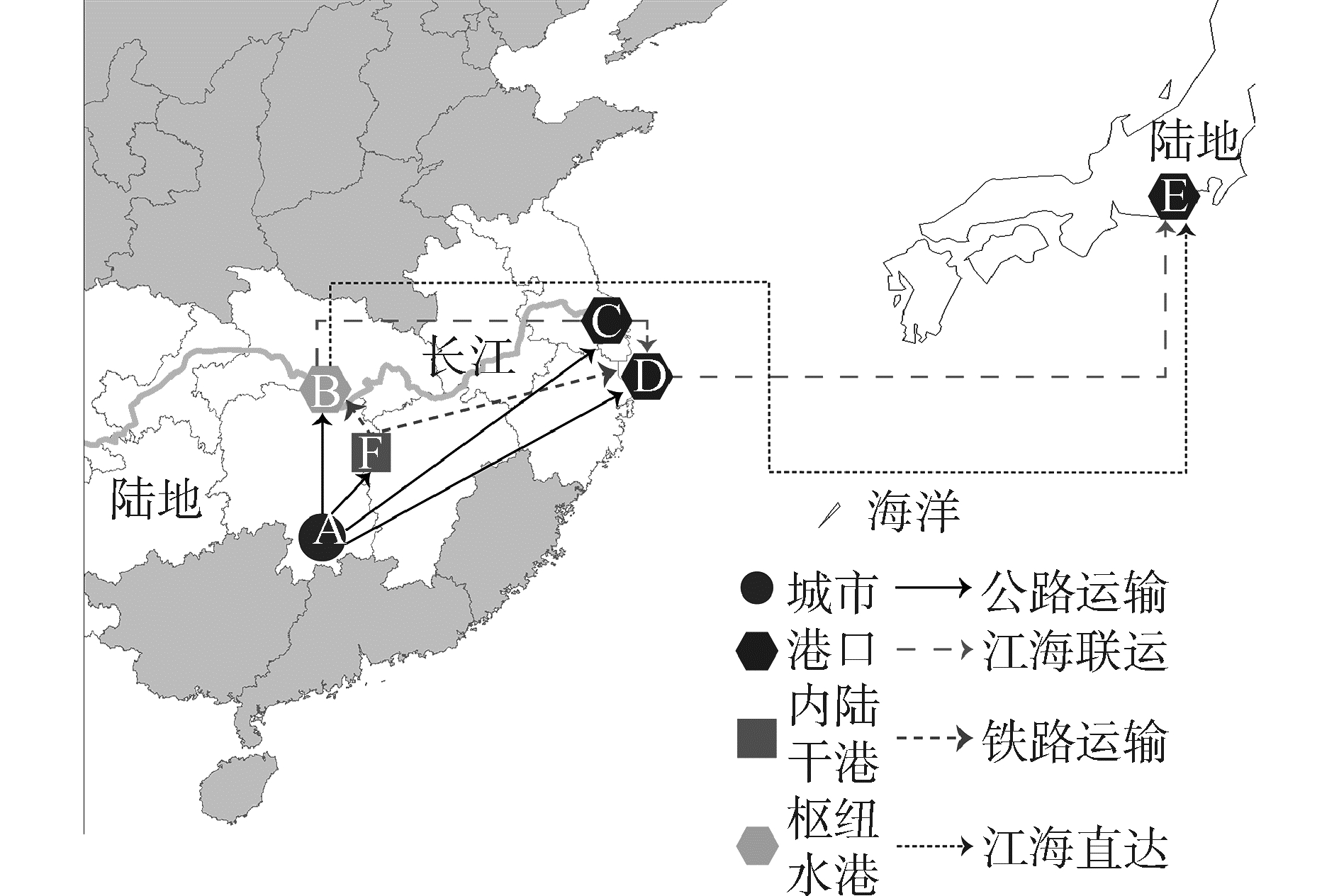
1 长江经济带超级网络构建图 1是设想的长江经济带上多种运输方式协同的运输路径状况,在城市A设置干港F,把河港B作为枢纽河港,开通F到B的集装箱班列与B到E的江海直达航线。此时,出口集装箱面临的路径有:P1:由A先经公路到B,再经江海直达航线到E;P2:由A先经公路至F,后经铁路班列到D,再在D换装到海轮上到E;P3:由A先经公路至F,后经班列到B,再从B以江海直达的方式到E。
|
Download:
|
| 图 1 长江经济带出口集装箱运输路径示意图 Fig. 1 Paths of export containers from YZREB | |
为研究长江经济带的出口集装箱的路径选择行为,基于由长江航道、铁路班列、高速公路、换装设施以及海上航线构成的综合运输系统构建超级网络,其中的实链接表示公路、铁路、内河航道和海上航线,虚链接表示两种方式间的换装。
用(NG, AG)表示超级网络G;用(NE, AE)表示公路网,NE为公路节点,AE为公路段;用(NR, AR)表示铁路网,NR为铁路节点,AR为铁路段;用(NWt, AWt)表示江海联运网,NWt为江海联运网络中的港口节点,NWt=NWt1∪NWt2,其中,NWt1为江海联运网络与水陆换装路段所连接的河港节点,NWt2为江海联运网络中的海港节点,AWt为江海联运航段;用(NWk, AWk)表示江海直达航线,NWk=NWk1∪NWk2, 其中,NWk1为江海直达航线网络与水陆换装路段所连接的河港节点,NWk2为江海直达航线网络中的海港节点,AWk为江海直达航段,用{NWk, AWk, mk, fk}表示江海直达航线方案k,其中mk为江海直达的船舶类型,fk为江海直达航线的发班频率;用AS表示公铁、铁水和公水之间的换装路段,AB表示江海联运时中转港内的换装路段。
基于超级网络,优化出口集装箱运输方案需要决策的问题为:1)根据起运地到目的地港的运输需求,在部分城市设置干港;2)将长江沿线的部分河港设置为枢纽河港,在干港与枢纽河港间开行班列;3)确定枢纽河港与国外目的地港间的江海直达航线方案,包括:确定船舶类型、船舶数量以及发班频率;4)根据路径选择行为,提出集装箱的运输方案。此决策可用两阶段规划来描述,第一阶段给出干港、枢纽河港的选址方案、集装箱班列方案以及江海直达航线方案,第二阶段基于用户平衡原理确定集装箱的走行路径。然后根据费用判断第一阶段确定的方案是否合理。
2 两阶段运网优化模型结构 2.1 第一阶段的模型结构假设:1)水运只有江海直达和江海联运两种方式,且江海联运的船型、发班频率和挂靠港固定;2)陆运运费率不变,江海联运的换装时间随货流量增加而增加;3)一条江海直达航线仅使用一种船舶;4)船舶在各港口的在港时间相同;5)船舶在一条航线上的航行速度固定不变;6)决策周期为7 d。
| $ \begin{array}{*{20}{c}} {\min {Z_1} = {c^e}\sum\limits_{a \in {A_E}} {{l_a}{q_a}} + {c^s}\sum\limits_{a \in {A_S}} {{q_a}} + }\\ {{c^r}\sum\limits_p {\sum\limits_i {\sum\limits_k {{x_p}{y_{ik}}{l_{pi}}{q_{pi}}} } } }\\ {{c^{wt}}\sum\limits_i {\sum\limits_j {{l_{ij}}{q_{ij}}} } + \sum\limits_k {{z_k}{c^k}} + \mu \sum\limits_{a \in {A_G}} {{t_a}{q_a}} } \end{array} $ | (1) |
式中:ce、cr分别为公路和铁路的单位集装箱运输成本,cs为换装的单位成本,cwt为江海联运的单位集装箱运输成本,ck为江海直达航线方案k的运营成本,la为链接a的长度,qa-链接a上的货流量,ta为链接a的通行时间。在上述决策模型中,当a∈AR、a∈AWt和a∈AWk时,用lpi和qpi分别表示铁路路段(p, i)的长度和货流量;用lij、tij和qij表示航运路段(i, j)的长度、通行时间和货流量;μ表示时间价值系数;xp为0-1变量,若城市p设置干港取值1,否则为0;yik为0-1变量,若河港i为江海直达航线k的枢纽水港取值1,否则为0;zk为0-1变量,若江海直达航线方案k被选中取值1,否则为0。目标函数式(1)表示综合运输费用最小,右侧第一项为公路运输费用,第二项为换装费用,第三项为铁路运输费用,第四项为江海联运费用,第五项为江海直达费用,第六项为超级网络上花费时间的时间价值。模型的约束条件为
s.t.
| $ \sum\limits_k {{z_k}} = 1 $ | (2) |
| $ \sum\limits_p {{x_p}} = {n_1} $ | (3) |
| $ \sum\limits_i {{y_{ik}}} = {n_2},i \in {P_1},\forall k \in K $ | (4) |
| $ \begin{array}{*{20}{c}} {{c^k} = 7c_k^{{\rm{fix}}}n_k^{{\rm{ship}}} + {c^{{\rm{bunker1}}}}h_k^{{\rm{bunker1}}}\sum\limits_i {\sum\limits_j {{t_{ij}}} } + }\\ {\left( {\sum\limits_i {\left( {\sum\limits_j {{t_{ij}}} } \right)} + t_i^{{\rm{handle}}} + t_i^{{\rm{wait}}}} \right){c^{{\rm{bunker2}}}}h_k^{{\rm{bunker2}}} + c_k^{{\rm{port}}}} \end{array} $ | (5) |
| $ c_{ij}^k = \left( {{l_{ij}}/\sum\limits_i {\sum\limits_j {{l_{ij}}} } } \right)/\left( {{c^k}/{\rm{Ca}}{{\rm{p}}_k}} \right) $ | (6) |
| $ n_k^{{\rm{ship}}} = {f_k}\left( {\sum\limits_i {\left( {\sum\limits_j {{t_{ij}}} } \right)} + t_i^{{\rm{handle}}} + t_i^{{\rm{wait}}}} \right)/7 $ | (7) |
| $ {y_p} \in \left\{ {0,1} \right\},\forall p \in P $ | (8) |
| $ {y_{ik}} \in \left\{ {0,1} \right\},\forall i \in {A_{Wk}},\forall k \in K $ | (9) |
| $ {z_k} \in \left\{ {0,1} \right\},\forall k \in K $ | (10) |
式中:P为干港集合;n1为干港数;P1为河港集合;n2为枢纽河港数;K为江海直达航线方案集;ckfix为江海直达船舶mk的日租金;cbunker1、cbunker2分别为江海直达船舶mk的重油价格和轻油价格;hkbunker1、hkbunker2分别为江海直达船舶mk的日重油和日轻油消耗;ckport为江海直达航线方案k的港口使费,由挂靠的港口数决定;tihandle、tiwait分别为船舶在港口i的装卸和等待时间;Capk为江海直达船舶mk的单船的载箱量;cijk为江海直达航线方案k上航段(i, j)间的单位运力的运营成本;nkship为江海直达航线k所需江海直达船舶mk的数量。式(2)表示只能有一个航线方案,式(3)表示有n1个干港,式(4)表示有n2个枢纽河港,式(5)用于计算江海直达航线方案k的运营成本,式(6)用于计算江海直达航线方案k上港口i至港口j航段上的单位运力的运营成本,式(7)用于计算江海直达航线方案k所需要江海直达船舶mk的数量,式(8)~(10)为变量约束。
2.2 第二阶段的模型结构| $ \min {Z_2} = \sum\limits_{a \in {A_G}} {\int_0^{{q_a}} {{c_a}\left( w \right){\rm{d}}w} } $ | (11) |
| $ {\rm{s}}.\;{\rm{t}}.\sum\limits_{r \in R} {f_r^{{\rm{od}}}} = {Q_{{\rm{od}}}},\forall o \in O,\forall d \in D $ | (12) |
| $ \begin{array}{*{20}{c}} {\sum\limits_o {\sum\limits_d {\sum\limits_r {\delta _{a,r}^{{\rm{od}}}f_r^{{\rm{od}}}} } } = {q_a},\forall o \in O,\forall d \in D,}\\ {\forall r \in R} \end{array} $ | (13) |
| $ f_r^{{\rm{od}}} \ge 0,\forall o \in O,\forall d \in D $ | (14) |
式中:O为出发地集合;D为目的地海港集合;Qod为出发地o到目的地海港d的货流总量;frod为出发地o到目的地海港d的第r条路径上的货流量;δa, rod为0-1变量,若链接a属于从出发地o到目的港d的第r条路径取值为1,否则为0。式(11)为用户平衡的交通分配模型的目标函数,式(12)表示OD间各条路径上的集装箱流量之和等于OD间的集装箱流总量,式(13)表示各路段集装箱流量等于各od对的途经该路段的路径集装箱流量之和,式(14)为变量约束。
3 实例分析 3.1 数据收集选取无锡、苏州、杭州等40个城市所在的长江中下游地区为出口地,对应的起运港有宜昌港、荆州港、武汉港、黄石港、九江港、安庆港、铜陵港、芜湖港、南京港、镇江港、张家港港、南通港、外高桥港、洋山港。选取日本的东京港、横滨港、名古屋港和神户港作为目的地港。
由于荆门、长沙、合肥、南昌、杭州、景德镇位于公路主枢纽处,因此可作为干港的选址地。以设置2个干港和2个枢纽河港为前提,假设班列发班频率为1班/日、载箱量为60TEU。参数θ=1.7、α=2、β=2.5。公路基本运价为6元/TEU/km,铁路运价为:基价1+基价2×运距,其中基价1=449元/TEU,基价2=1.98元/TEU/km。公路、铁路和水路的装卸费分别为49.5、70.2和425.5元/TEU。
集装箱运输的时间价值系数为[13]
| $ \mu = {V_g} \times i/365 $ | (23) |
式中:μ为集装箱货物运输的时间价值系数,Vg为货物的价值,年利率i=4.35%。单位集装箱的货物价值为27394USD[14]
考虑长江中下游航段差异,以丰水期通航的最大船舶为限制,选择5 000 MT、7 000 MT、10 000 MT、12 000 MT、19 000 MT和23 000 MT六种江海直达船作为备选船型,其各种指标如表 1所示。
| 表 1 江海直达船舶数据 Tab.1 Specification of the river-sea ships |
由《2015年度航道计划水深》可知,武汉长江大桥至安庆皖河口段,丰水期水深6 m,可通航10 000 t级船舶;安庆皖河口至芜湖长江大桥段,丰水期水深8 m,可通航12 000 t级船舶;芜湖长江大桥至南京燕子矶段丰水期水深至9 m,可通航19 000 t级以上船舶;南京燕子矶以下航道水深在10 m以上,全年可通航23 000 t级船舶。
3.2 求解及结果分析1) 第一阶段模型的求解算法。
第一阶段模型所优化的是干港选择、枢纽河港选择以及靠泊港口与靠泊顺序选择的混合优化问题,该类问题属于NP-Hard,且决策变量的定义域以及变化规律等差异较大,而遗传算法能针对其决策变量的特点设计出简单科学的编码,可以大幅缩小算法的探索空间,提高算法的效率,用遗传算法求解,把总运输费用做为适应度函数值,其编码、交叉和变异步骤如下。
① 编码
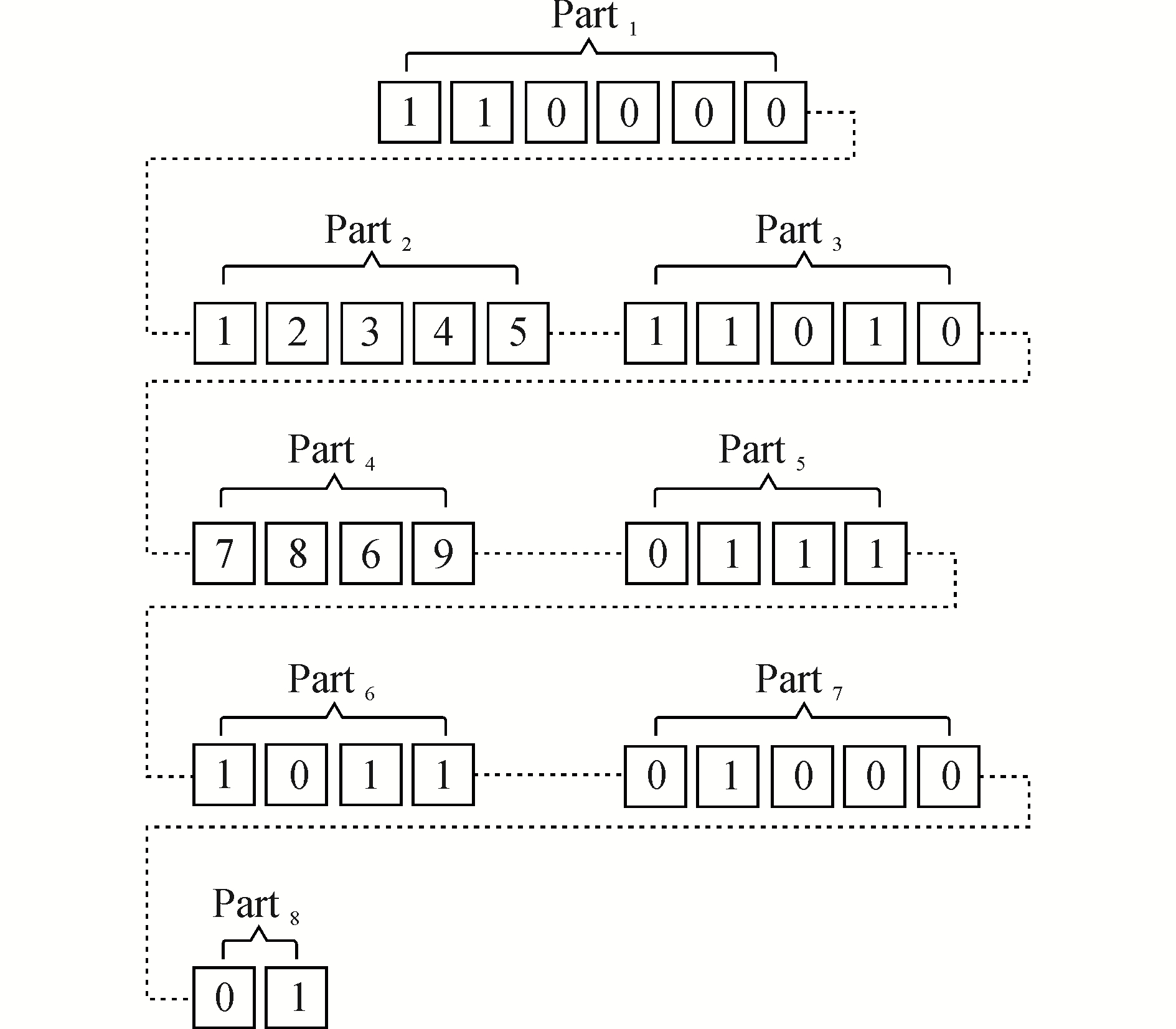
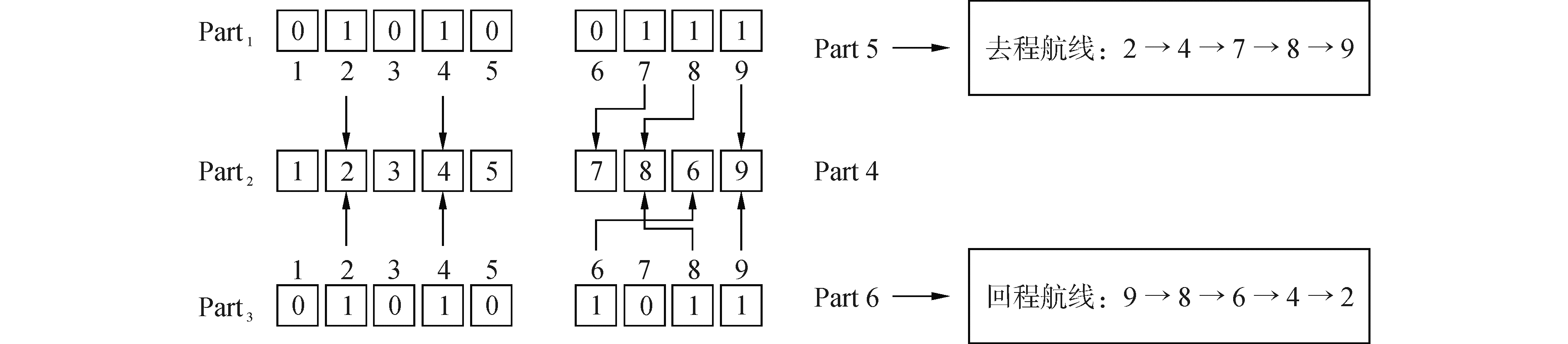
染色体由8部分构成(图 2),Part1的基因位数等于干港的备选地个数,基因值为1表示有干港;Part2为内河港口序列;Part3的基因位数等于河港的个数,基因值为1的表示枢纽河港;Part4为备选海港序号;Part5和Part6的基因位数等于海港个数,分别用于选择去程航线和回程航线的靠泊海港;Part7为船型编码,位数等于备选船型数;Part8为船舶发班频率编码。Part2、Part3、Part4、Part5和Part6共同确定江海直达航线的靠泊港。例如,Part1的1、2号基因位为1,表示在城市1和城市2设置干港。Part2为1-2-3-4-5,由于Part3的2、4号基因位的编码为1,因此枢纽河港为2和4;Part4为7-8-6-9,由于Part5的7、8、9号基因位的编码为1,因此去程子航线为2-4-7-8-9;Part6的6、8、9号基因位编码为1,因此回程子航线为9-8-6-4-2(图 3)。
|
Download:
|
| 图 2 编码方法 Fig. 2 Coding method | |
|
Download:
|
| 图 3 解码方法 Fig. 3 Decoding method | |
② 交叉操作
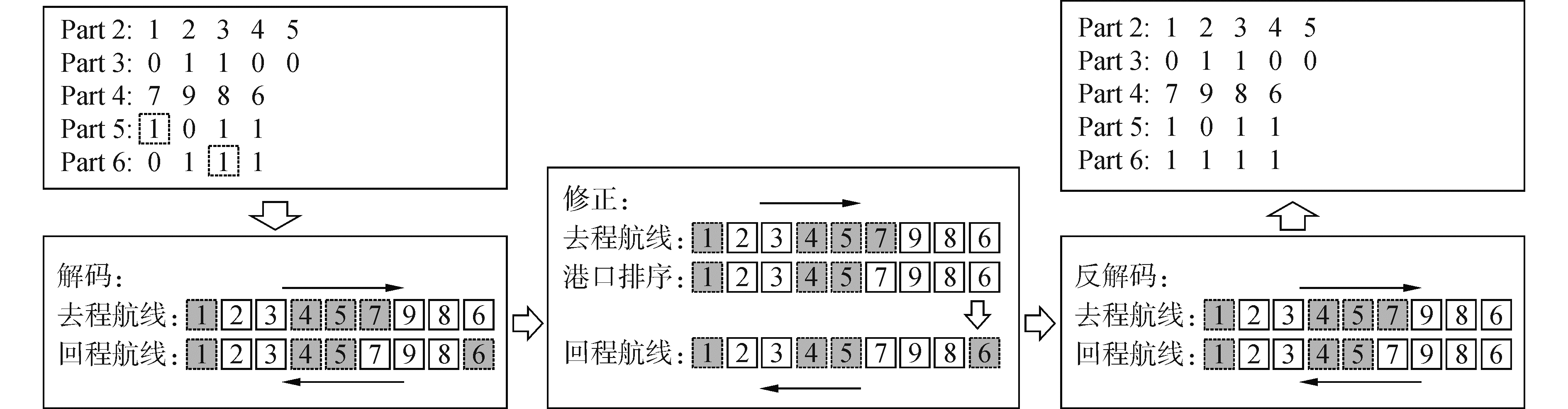
对Part1、Part7和Part8采用单点交叉,对Part3、Part5和Part6采用两点交叉,对Part4采用实数交叉。如果交叉得到的Part3、Part4、Part5和Part6不满足条件,需修正Part5和Part6。方法为将Part4的序列分别与去程子航线的终到港与回程子航线的起始港相比较,若不相同则根据港口序列将相关的首/末港插入到子航线中(图 4)。
|
Download:
|
| 图 4 编码修正方法 Fig. 4 Correct method of genetic code | |
③ 变异操作
针对Part1、Part3、Part5、Part6、Part7和Part8上的某个基因进行0-1变换。若变异得到的Part3、Part4、Part5和Part6不满足条件,同样需修正。例如,Part1上的基因为1-1-0-0-0-0,如果第2个基因变异,则变异后Part1上的基因变成1-0-0-0-0。经交叉变异后,如果子代个体Part1中“数值”为1的基因个数发生变化,则随机调整子代编码中的部分基因进行调整以保证数值为“1”的基因个数与父代相同。
2) 第二阶段模型的求解算法。
基于文献[15]的思想以集装箱货物通过各路段的成本(包括运费与时间)作为评定各链接阻抗的依据。公路路段的运费与时间都较稳定,但铁路路段与水路路段的成本受运力限制,换装路段的成本受运力限制及运输需求量等因素的影响波动较大,因此,本文设置了如下的阻抗函数来描述运输路段和换装路段的成本的变化特点,用Frank-Wolfe法求解下层模型。求解时各种链接的阻抗函数设置如下:
公路路段的阻抗函数:当a∈AE时,U(qa)=θcela+μLa/va,θ为运价转换系数,ce为公路的单位集装箱运输成本,la为公路路段a的长度,va为卡车在公路路段a上的运行速度。
铁路路段的阻抗函数:当a∈AR时,U(qa)=θcrla+μLa/va-M1min{0, ca2-qa2},cr为铁路的单位集装箱运输成本,la为铁路路段a的长度,va为火车在铁路路段a的运行速度,M1为一个足够大的正数,ca为铁路路段a的运输能力,qa为铁路路段a的集装箱流量。
换装路段的阻抗函数:当a∈As时,U(qa)=θcsla+μta,cs为单位集装箱换装成本,换装总时间ta=tahandle+tawait;tahandle和tawait分别为集装箱在换装路段a上的操作时间和等待时间。
江海直达运输路段的阻抗函数:当a∈AWk时,U(qa)=θcak+μLa/vk-M1min{0, (fkCapk)2-qa2}, cak为江海直达航线方案k上航段a的单位运力的运营成本,la为航段a的长度,vk为江海直达船舶mk的速度,M1为一个足够大的数,fk为江海直达航线方案k的发班频率,Capk为江海直达船舶mk的单船载箱量,qa为航段a的集装箱流量。使用惩罚项M1min{0, (fkCapk)2-qa2}来解决航线运力受限的问题,当(fkCapk)2-qa2≥0时,取值为0,当(fkCapk)2-qa2<0时,取值为一个足够大的数。
江海联运运输路段的阻抗函数:当a∈AWt时,U(qa)=θcwtla+μLa/va,cwt为江海联运航线上的单位集装箱运输成本,la为江海联运航段a的长度,va为船舶在江海联运航段a的航速。
江海联运中转港内换装路段的阻抗函数:当a∈AB时, U(qa)=μta(1+α(qa/Va)β),μ为时间价值系数,ta为在中转港的换装时间,Va为海轮的载箱量,α, β为相关参数。
3) 第一阶段的结果及分析。
基于输出结果可知,要在长沙和荆门两地设置干港,武汉港和南京港是枢纽水港,江海直达航线为:武汉-南京-东京-横滨-名古屋-南京-武汉,需配置10艘800 TEU的江海直达型船舶(图 5),总运输成本为6.99千万元。
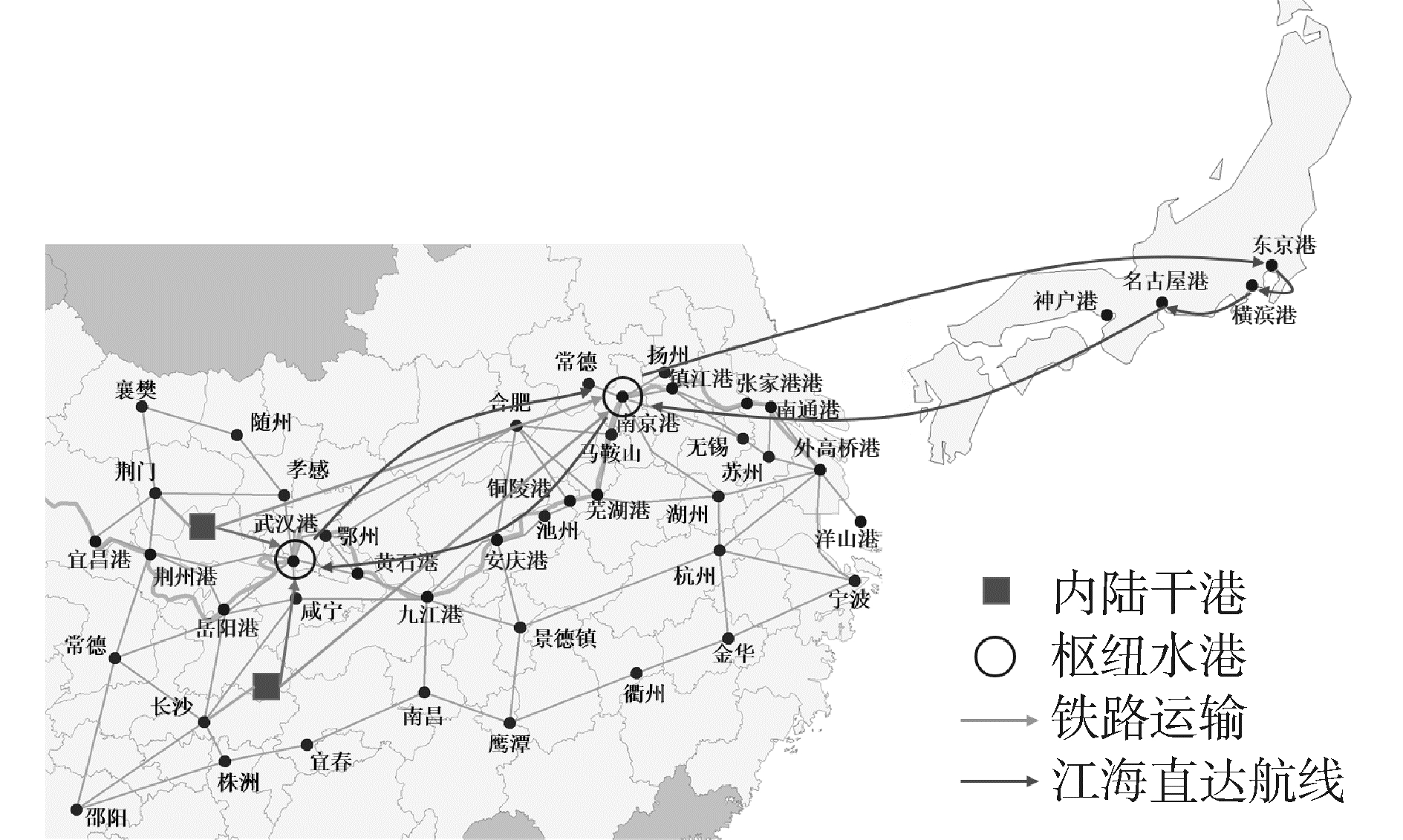
|
Download:
|
| 图 5 设置2个干港和2个枢纽河港时的选址与航线情况 Fig. 5 Cases of setting 2 dry ports and 2 hub river ports | |
4) 第二阶段的结果及分析。
① 干港及其换装量
由长沙干港和荆门干港开往武汉港与南京港班列每周的运量分别为:420 TEU、412 TEU、418 TEU和285 TEU,装载率为100%、98.1%、99.5%和67.9%。从装载率看,在长沙和荆门设干港是合理的,他们都位于长江中游公路枢纽处,距长江水道约300 km,属中距离干港。岳阳、常德、邵阳、株洲和咸宁的集装箱可经长沙干港转运,宜昌、荆州、襄樊和孝感的集装箱可经荆门干港转运。
表 2显示了2个干港城市的集装箱发生/吸引量、运入/运出量与中转量。其中,荆门干港的中转比例为84.9%,是典型的中转型干港。长沙的中转比例为47.8%,是偏腹地型的干港。
| 表 2 设置2个枢纽水港时干港的运输情况 Tab.2 Cases of dry ports when setting 2 river hub ports |
② 枢纽河港及其江海直达量
每周武汉和南京到日本的外贸出口箱量分别为1 059 TEU和1 720 TEU,排在第3、2位。从货运需求来看,武汉港和南京港作为枢纽河港是合理的。从空间位置看,武汉、南京分别地处长江中游和上游公路枢纽处,武汉港作为枢纽河港可吸引武汉城市圈的货物以江海直达的方式运至目的地港,南京港作为枢纽河港可使南京经济圈和中游其他地区的出口货物以江海直达的方式运至目的地港。
表 3显示了两个枢纽河港的集疏运量及其比例,武汉港的铁路运入比例为37.9%,江海直达运至目的地港的比例为60.4%,而经长江运至洋山港中转的比例为39.6%,说明武汉港是典型的江海直达枢纽河港。南京港的铁路运入比例为24.8%,江海直达运至目的地港的比例为37.8%,经长江运至洋山港再中转到目的地港的比例为62.2%,说明南京港属于江海直达与江海联运混合型枢纽河港。
| 表 3 两个枢纽河港的运输量 Tab.3 Container volumes in the two hub river portsTEU |
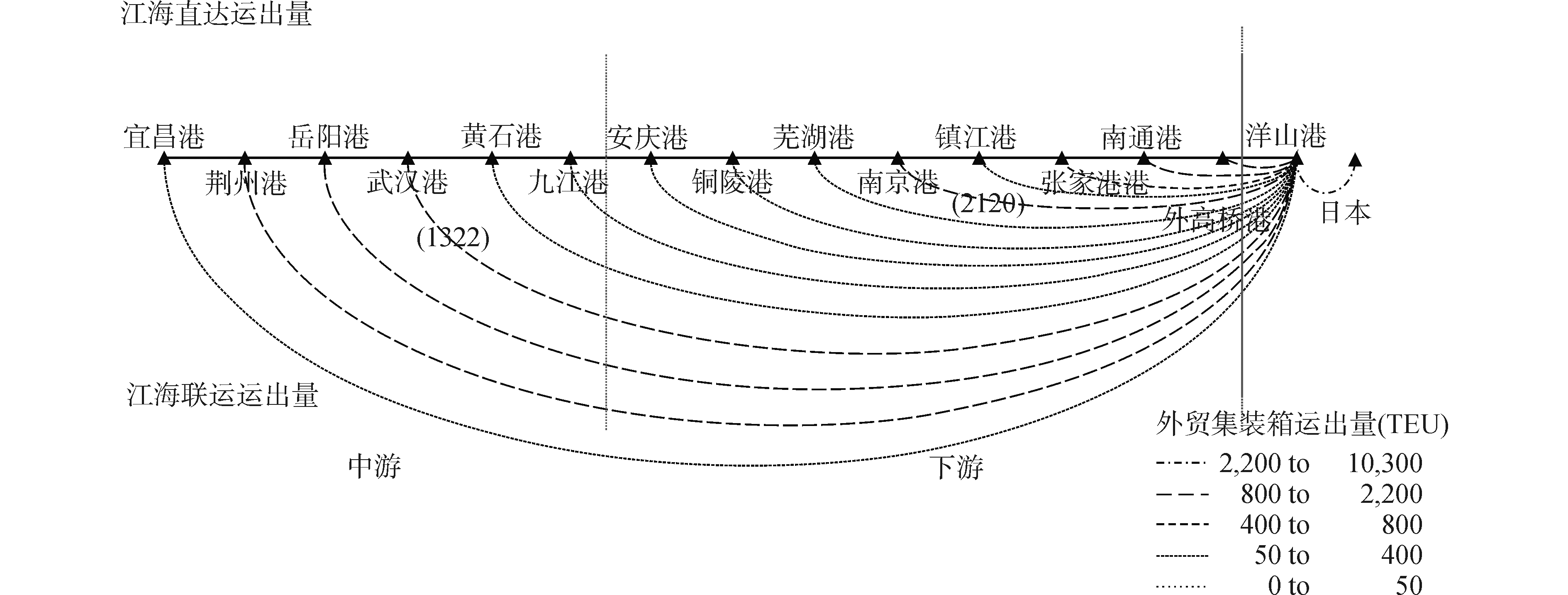
③ 河港运输至洋山港的中转量
图 6显示各河港运输至洋山港中转的箱量,在洋山港出口的集装箱中,长三角地区(南京港、镇江港、张家港港、南通港、外高桥港)的箱量的比例大。说明该地区更倾向于选择在洋山港中转出口。长江中游的出口箱量所占的比重较小,说明中游地区更倾向于在武汉或南京枢纽河港选择江海直达模式。

|
Download:
|
| 图 6 设置2个枢纽河港时内河港口的运量 Fig. 6 Volume in inland ports when setting 2 hub river ports | |
1) 无枢纽河港(n2=0,干港数量不变,即n1=2)
此时,河港运至洋山港的箱量如图 7所示,运输总成本为9.07千万元。与图 6相比,由宜昌港、荆州港、岳阳港和黄石港江海联运的出口箱明显增多,增幅分别为74.4%、370.3%、230.9%和10.6%。说明原本由武汉港或南京港以江海直达运输的部分集装箱从这些河港以江海联运的方式前往目的地港,由武汉港和南京港以江海联运的方式前往目的港的外贸集装箱将分别增加50.7%和20.9%。
|
Download:
|
| 图 7 设置2个干港、0个枢纽河港时内河港口的运量 Fig. 7 Volumes in inland ports when setting 2 dry ports and 0 hub river port | |
2) 1枢纽河港(n2=1,干港数量不变,即n1=2)
此时,江海直达的航线为:武汉-东京-名古屋-神户-武汉(图 8),航线配置7艘800 TEU的船,综合运输成本为7.82千万元。表 6显示2个干港城市的集装箱发生/吸引量、运入/运出量与中转量,与有2个枢纽河港(n2=2)相比,此时长沙和荆门两干港的中转比例降低,分别为39.1%和59.8%,因为随着武汉港货量的增多,出口箱的换装时间增加,阻碍了他们从长沙干港和荆门干港运到武汉港中转出口。
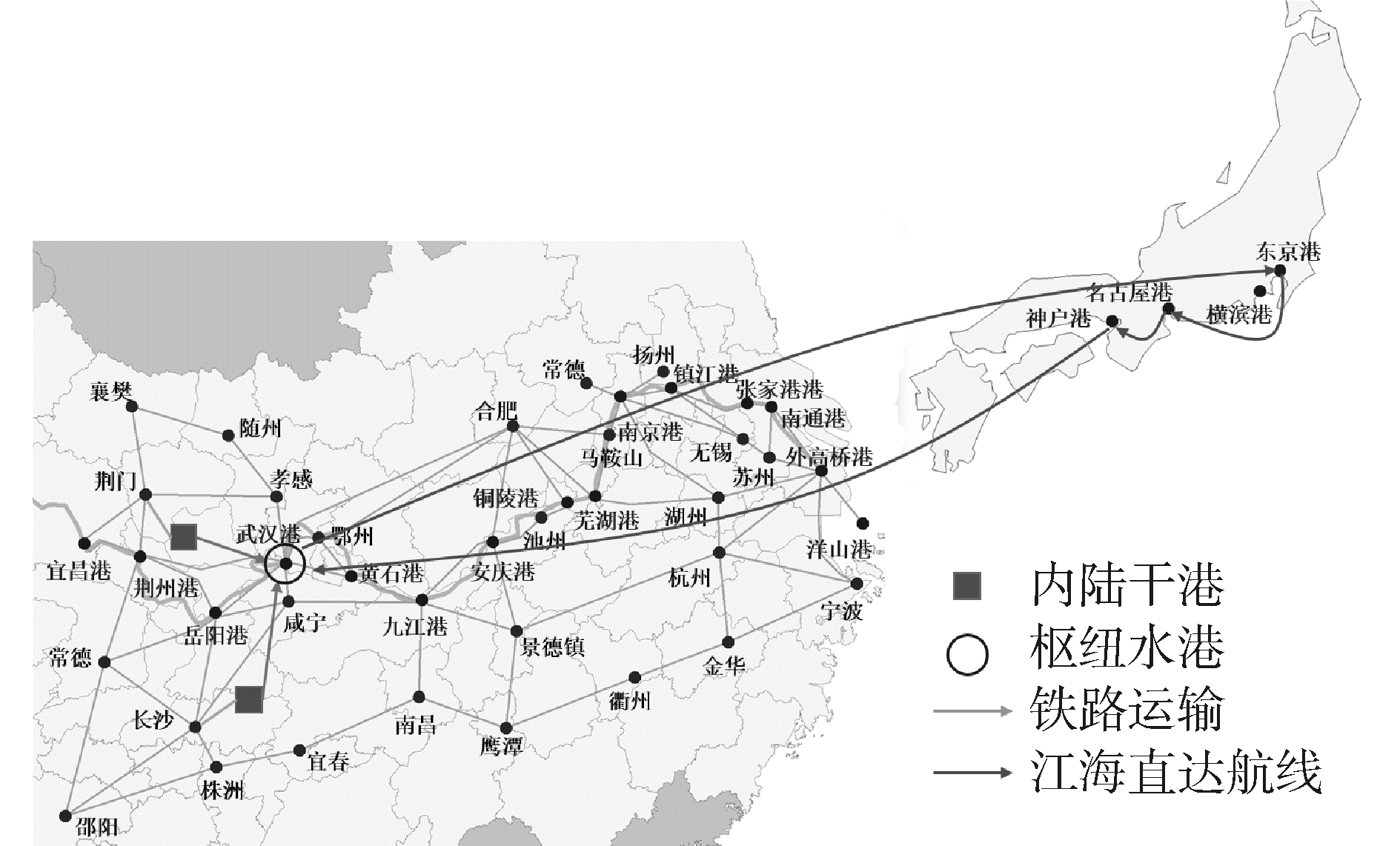
|
Download:
|
| 图 8 设置2个干港和1个枢纽河港时的选址与航线情况 Fig. 8 Cases of setting 2 dry ports and 1 hub river port | |
| 表 4 设置1个枢纽水港时干港的运输情况 Tab.4 Cases of dry ports when setting 1 hub river port TEU |
河港运至洋山港的中转量如图 9所示,与设置2个枢纽河港相比,此时(n2=1),由宜昌港、荆州港、岳阳港江海联运的箱量明显增加,增幅分别为34.9%、120.9%和87.7%。说明原本由武汉港或南京港江海直达的部分集装箱改为从本地河港以江海联运的方式出口,由武汉港和南京港以江海联运的方式出口的集装箱也分别增加17.0%和20.9%。
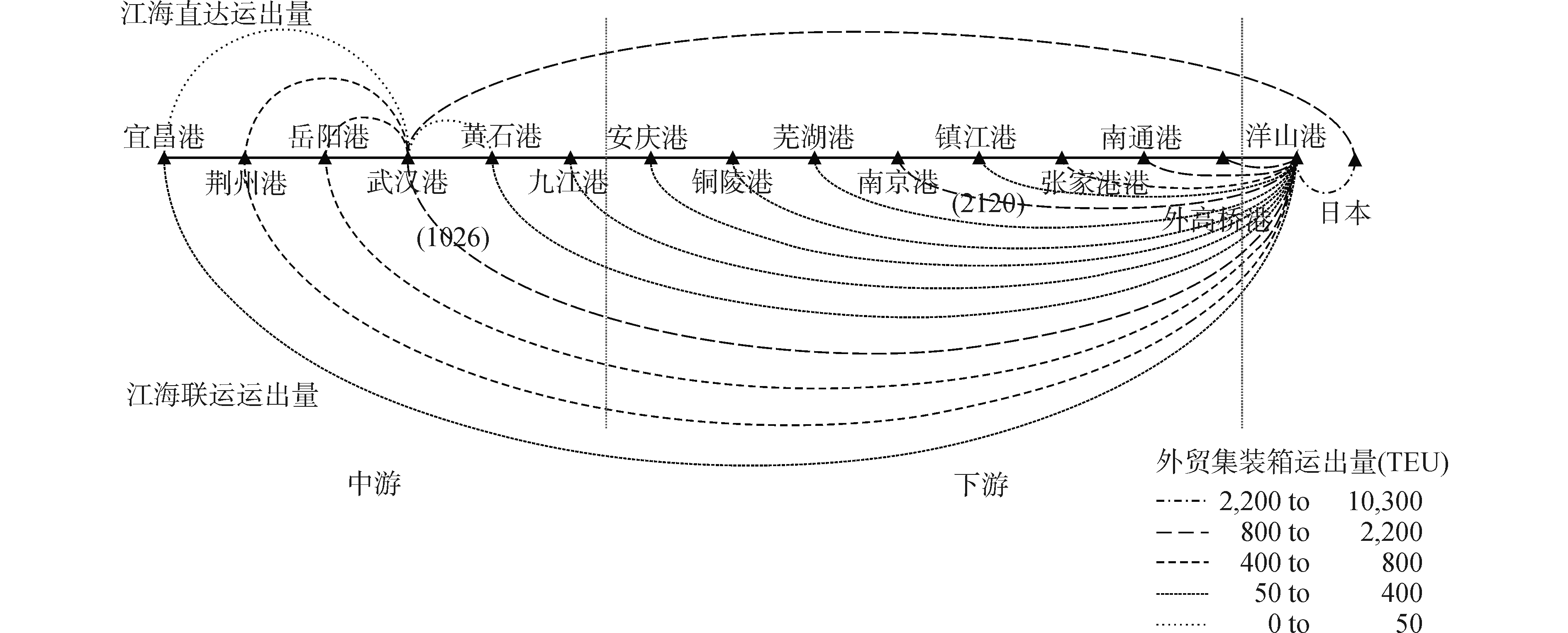
|
Download:
|
| 图 9 设置2个干港和1个枢纽水港时内河港口的运量 Fig. 9 Volumes in inland ports when setting 2 dry ports and 1 hub river port | |
1) 干港适合选址在公路枢纽处且距离河港300 km左右的城市;
2) 武汉港和南京港拥有大量出口运输需求,适合作为长江中游和下游的枢纽河港,其中武汉港适合发展江海直达运输,南京港在发展江海直达运输的同时,还应重点发展江海联运模式;
3) 本文提出的模型、理论以及方法对于构建长江经济带综合交通运输枢纽,实施外贸货物的陆-铁-海联运具有重要的参考价值。
| [1] |
SHINTANI K, IMAI A, NISHIMURA E, et al. The container shipping network design problem with empty container repositioning[J]. Transportation research part E:logistics and transportation review, 2007, 43(1): 39-59. DOI:10.1016/j.tre.2005.05.003 (  0) 0)
|
| [2] |
陈康, 杨忠振. 基于三方博弈的短途班轮航线优化模型[J]. 交通运输工程学报, 2011, 11(6): 74-81, 88. CHEN Kang, YANG Zhongzhen. Optimization model of short-distance liner ship route based on tripartite game[J]. Journal of traffic and transportation engineering, 2011, 11(6): 74-81, 88. (  0) 0)
|
| [3] |
陈康, 郭利泉, 杨忠振. 基于混合航线结构的集装箱航线与空重箱运输综合优化模型[J]. 系统工程理论与实践, 2014, 34(1): 122-128. CHEN Kang, GUO Liquan, YANG Zhongzhen. Optimization model for container ship routing and empty/full container transport in the context of mixed route structure[J]. Systems engineering-theory & practice, 2014, 34(1): 122-128. DOI:10.12011/1000-6788(2014)1-122 (  0) 0)
|
| [4] |
MARAŠ V, LAZIĆ J, DAVIDOVIĆ T, et al. Routing of barge container ships by mixed-integer programming heuristics[J]. Applied soft computing, 2013, 13(8): 3515-3528. DOI:10.1016/j.asoc.2013.03.003 (  0) 0)
|
| [5] |
ZHENG Jianfeng, YANG Dong. Hub-and-spoke network design for container shipping along the Yangtze River[J]. Journal of transport geography, 2016, 55: 51-57. DOI:10.1016/j.jtrangeo.2016.07.001 (  0) 0)
|
| [6] |
KONINGS R, LUDEMA M. The competitiveness of the river-sea transport system:market perspectives on the United Kingdom-Germany corridor[J]. Journal of transport geography, 2000, 8(3): 221-228. DOI:10.1016/S0966-6923(00)00015-6 (  0) 0)
|
| [7] |
SOUTHWORTH F, PETERSON B E. Intermodal and international freight network modeling[J]. Transportation research part C:emerging technologies, 2000, 8(1/2/3/4/5/6): 147-166. (  0) 0)
|
| [8] |
汪传旭. 基于轴-辐运输系统的区域港口群二级物流运输网络优化[J]. 系统工程理论与实践, 2008, 28(9): 152-158. WANG Chuanxu. Optimization of hub-and-spoke based regional port cluster two stage logistics system network[J]. Systems engineering-theory & practice, 2008, 28(9): 152-158. (  0) 0)
|
| [9] |
魏航, 李军, 蒲云. 时变网络下多式联运的最短路径问题研究[J]. 系统工程学报, 2007, 22(2): 205-209. WEI Hang, LI Jun, PU Yun. Study on the multi-modal shortest path in time-varying network[J]. Journal of systems engineering, 2007, 22(2): 205-209. (  0) 0)
|
| [10] |
ARNOLD P, PEETERS D, THOMAS I. Modelling a rail/road intermodal transportation system[J]. Transportation research part E:logistics and transportation review, 2013, 40(3): 255-270. (  0) 0)
|
| [11] |
HANSSEN T E S, MATHISEN T A, JØRGENSEN F. Generalized transport costs in intermodal freight transport[J]. Procedia-social and behavioral sciences, 2012, 54: 189-200. DOI:10.1016/j.sbspro.2012.09.738 (  0) 0)
|
| [12] |
RESAT H G, TURKAY M. Design and operation of intermodal transportation network in the Marmara region of Turkey[J]. Transportation research part E:logistics and transportation review, 2015, 83: 16-33. DOI:10.1016/j.tre.2015.08.006 (  0) 0)
|
| [13] |
宋炳良. 国际集装箱多式联运与东部港口竞争力分析[J]. 中国航海, 2003(3): 61-64. SONG Bingliang. Analysis of international multi-modal transportation and eastern coastal ports competitiveness[J]. Navigation of China, 2003(3): 61-64. (  0) 0)
|
| [14] |
刘腾远. 内贸集装箱多式联运成本分析[J]. 甘肃科学学报, 2013, 25(2): 142-144. LIU Tengyuan. Analysis of the costs of domestic container intermodal[J]. Journal of Gansu sciences, 2013, 25(2): 142-144. (  0) 0)
|
| [15] |
MENG Qiang, WANG Xinchang. Intermodal hub-and-spoke network design:Incorporating multiple stakeholders and multi-type containers[J]. Transportation research part B:methodological, 2011, 45(4): 724-742. DOI:10.1016/j.trb.2010.11.002 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


